Производная 2 sinx: Y=2sinx найти производную из функции

{2}}\dfrac{d\left( \sin x \right)}{dx}\] 9{n-1}}\],
\[\dfrac{d}{dx}\left( \sin x \right)=\cos x\]
А также мы должны знать аддитивное правило, правило вычитания, мультипликативное правило и частное правило дифференцирования. Формулы этих правил:
Аддитивное правило: \[\dfrac{d}{dx}\left( u(x)+v(x) \right)=\dfrac{d\left( u(x) \ right)}{dx}+\dfrac{d\left( v(x) \right)}{dx}\]
Правило вычитания: \[\dfrac{d}{dx}\left( u(x)- v(x) \right)=\dfrac{d\left( u(x) \right)}{dx}-\dfrac{d\left( v(x) \right)}{dx}\]
Правило произведения это: \[\dfrac{d}{dx}\left( u(x)\times v(x) \right)=v(x)\dfrac{d\left( u(x) \right)}{dx }+u(x)\dfrac{d\left( v(x) \right)}{dx}\] 9{2}}}\]
В этом вопросе мы использовали правило произведения для решения.

3.5: Производные тригонометрических функций

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

2494

• Гилберт Странг и Эдвин «Джед» Герман
• OpenStax

Цели обучения

• Найти производные функции синуса и косинуса.
• Найдите производные стандартных тригонометрических функций.
• Вычислить высшие производные синуса и косинуса.

Одним из важнейших видов движения в физике является простое гармоническое движение, которое связано с такими системами, как объект с массой, колеблющейся на пружине. Простое гармоническое движение может быть описано с помощью функции синуса или косинуса. В этом разделе мы расширим наши знания о формулах производных, включив в них производные этих и других тригонометрических функций. Мы начнем с производных функций синуса и косинуса, а затем используем их для получения формул для производных оставшихся четырех тригонометрических функций. Способность вычислять производные функций синуса и косинуса позволит нам найти скорость и ускорение простого гармонического движения.

Производные функции синуса и косинуса

Мы начнем исследование производной функции синуса, используя формулу, чтобы сделать обоснованное предположение о ее производной. Напомним, что для функции \(f(x),\)

\[f′(x)=\lim_{h→0}\dfrac{f(x+h)−f(x)}{h}. \nonumber \]

Следовательно, для значений \(h\), очень близких к \(0\),

\[f′(x)≈\dfrac{f(x+h)−f(x)} {час}. \nonumber \]

Мы видим, что, используя \(h=0,01\),

\[\dfrac{d}{dx}(\sin x)≈\dfrac{\sin (x+0,01)−\sin х}{0,01} \номер\]

Установив

\[D(x)=\dfrac{\sin (x+0.01)−\sin x}{0.01} \nonumber \]

и используя графическую утилиту, мы можем получить график приближение к производной \(\sin x\) (рисунок \(\PageIndex{1}\)).

Рисунок \(\PageIndex{1}\): График функции \(D(x)\) очень похож на косинусоидальную кривую.

При осмотре график \(D(x)\) кажется очень близким к графику функции косинуса. Действительно, мы покажем, что

\[\dfrac{d}{dx}(\sin x)=\cos x. \номер\]

Если бы мы проделали те же шаги для аппроксимации производной функции косинуса, мы бы обнаружили, что

\[\dfrac{d}{dx}(\cos x)=-\sin x. \nonumber \]

Производные от \(\sin x\) и \(\cos x\)

Производной функции синуса является косинус, а производной функции косинуса является отрицательный синус.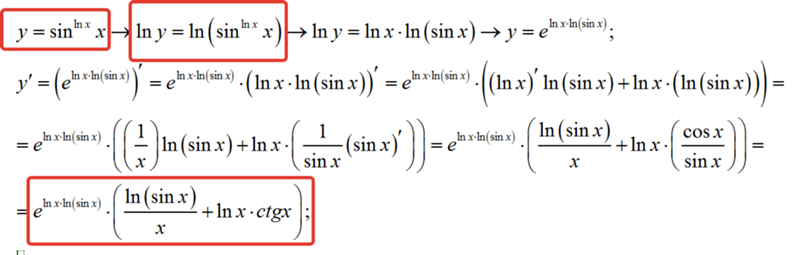

\[\dfrac{d}{dx}(\sin x)=\cos x \nonumber \]

\[\dfrac{d}{dx}(\cos x)=-\sin x \nonumber \ ]

Доказательство

Поскольку доказательства для \(\dfrac{d}{dx}(\sin x)=\cos x\) и \(\dfrac{d}{dx}(\cos x)=-\sin x\) используют аналогичные методы, мы приводим только доказательство для \(\dfrac{d}{dx}(\sin x)=\cos x\). Прежде чем начать, вспомните два важных тригонометрических предела:

\(\displaystyle \lim_{h→0}\dfrac{\sin h}{h}=1\) и \(\displaystyle \lim_{h→0}\dfrac {\ cos ч-1} {ч} = 0 \).

Графики \(y=\dfrac{\sin h}{h}\) и \(y=\dfrac{\cos h−1}{h}\) показаны на рисунке \(\PageIndex{2 }\).

Рисунок \(\PageIndex{2}\): На этих графиках показаны два важных предела, необходимых для установления формул производных для функций синуса и косинуса.

Напомним также следующее тригонометрическое тождество для синуса суммы двух углов:

\[\sin (x+h)=\sin x\cos h+\cos x\sin h. \nonumber \]

Теперь, когда мы собрали все необходимые уравнения и тождества, приступим к доказательству.

\[\begin{align*} \dfrac{d}{dx}(\sin x) &=\lim_{h→0}\dfrac{\sin(x+h)−\sin x}{h} & & \text{Применить определение производной.}\\[4pt]
&=\lim_{h→0}\dfrac{\sin x\cos h+\cos x\sin h−\sin x}{h } & & \text{Используйте тождество триггера для синуса суммы двух углов.}\\[4pt]
&=\lim_{h→0}\left(\dfrac{\sin x\cos h−\sin x}{h}+\dfrac{\cos x\sin h}{h}\right) & & \ text{Перегруппировать.}\\[4pt]
&=\lim_{h→0}\left(\sin x\left(\dfrac{\cos h−1}{h}\right)+(\cos x) \left(\dfrac{\sin h}{h}\right)\right) & & \text{Вынести за скобки}\sin x\text{и}\cos x \\[4pt]
&=(\sin x )\lim_{h→0}\left(\dfrac{\cos h−1}{h}\right)+(\cos x)\lim_{h→0}\left(\dfrac{\sinh}{ h}\right) & & \text{Коэффициент }\sin x\text{ и }\cos x \text{ вне пределов.} \\[4pt]
&=(\sin x)(0)+(\ cos x)(1) & & \text{Применить формулы ограничения триггеров.}\\[4pt]

&=\cos x & & \text{Упростить.} \end{align*} \nonumber \]

□

На рисунке \(\PageIndex{3}\) показано соотношение между графиком \(f( x)=\sin x\) и его производная \(f′(x)=\cos x\).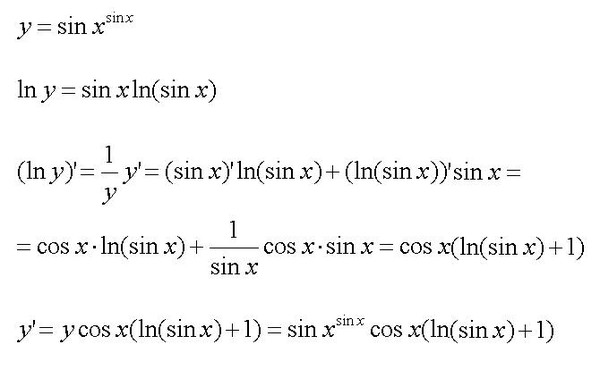 Обратите внимание, что в точках, где \(f(x)=\sin x\) имеет горизонтальную касательную, ее производная \(f′(x)=\cos x\) принимает нулевое значение. Мы также видим, что где f\((x)=\sin x\) возрастает, \(f′(x)=\cos x>0\) и где \(f(x)=\sin x\) убывает, \(f′(x)=\cos x<0.\)

Рисунок \(\PageIndex{3}\): где \(f(x)\) имеет максимум или минимум, \(f’ (x)=0\), то есть \(f'(x)=0\), где \(f(x)\) имеет горизонтальную касательную. Эти точки отмечены точками на графиках 92x}\)

Пример \(\PageIndex{3}\): приложение к скорости

Частица движется вдоль координатной оси таким образом, что ее положение в момент времени \(t\) определяется выражением \(s(t)= 2\sin t−t\) при \(0≤t≤2π.\) В какие моменты времени частица покоится?

Решение

Чтобы определить, когда частица находится в состоянии покоя, установите \(s′(t)=v(t)=0.\) Начните с нахождения \(s′(t).\) Мы получим

\[s′(t)=2 \cos t−1, \nonumber \]

поэтому мы должны решить

\[2 \cos t−1=0\text{ для }0≤t≤2π. \nonumber \]

Решениями этого уравнения являются \(t=\dfrac{π}{3}\) и \(t=\dfrac{5π}{3}\). Таким образом, частица покоится в моменты времени \(t=\dfrac{π}{3}\) и \(t=\dfrac{5π}{3}\).

Упражнение \(\PageIndex{3}\)

Частица движется вдоль координатной оси. Его положение в момент времени \(t\) определяется как \(s(t)=\sqrt{3}t+2\cos t\) для \(0≤t≤2π.\) В какие моменты времени частица находится в отдых?

Подсказка

Используйте предыдущий пример в качестве руководства.

Ответить

\(t=\dfrac{π}{3},\quad t=\dfrac{2π}{3}\)

Производные других тригонометрических функций

Поскольку оставшиеся четыре тригонометрические функции могут быть выражены в виде частных, содержащих синус, косинус или и то, и другое, мы можем использовать правило частных, чтобы найти формулы для их производных.

Пример \(\PageIndex{4}\): производная касательной функции 92x\\[4pt]

\dfrac{d}{dx}(\sec x)&=\sec x \tan x\\[4pt]
\dfrac{d}{dx}(\csc x)&=- \csc х \кот х. 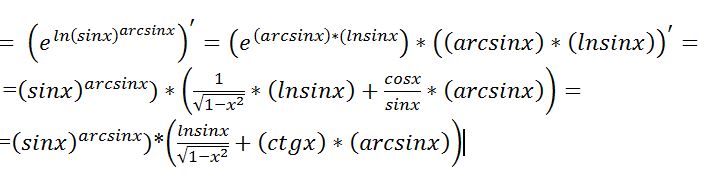\end{align} \nonumber \]

Пример \(\PageIndex{5}\): нахождение уравнения касательной

Найдите уравнение касательной к графику \(f(x)=\ кроватка x \) в точке \(x=\frac{π}{4}\).

Решение

Чтобы найти уравнение касательной, нам нужна точка и наклон в этой точке. Чтобы найти точку, вычислите

\(f\left(\frac{π}{4}\right)=\cot\frac{π}{4}=1\). 92 \ влево (\ гидроразрыва {π} {4} \ вправо) = −2 \).

Используя уравнение точки-наклона линии, мы получаем

\(y−1=−2\left(x−\frac{π}{4}\right)\)

или эквивалентно,

\ (y=−2x+1+\frac{π}{2}\).

Пример \(\PageIndex{6}\): нахождение производной тригонометрических функций

Найдите производную \(f(x)=\csc x+x\tan x .\)

Решение

Чтобы найти эту производную, мы должны использовать как правило сумм, так и правило произведения. По правилу сумм находим 92 х\)

Упражнение \(\PageIndex{6}\)

Найдите наклон линии, касательной к графику \(f(x)=\tan x \) в точке \(x=\dfrac{π}{6} \).

Подсказка

Вычислить производную в точке \(x=\dfrac{π}{6}\).

Ответить

\(\dfrac{4}{3}\)

Производные высшего порядка

Производные высшего порядка от \(\sin x\) и \(\cos x\) повторяются. Следуя шаблону, мы можем найти любую производную более высокого порядка от \(\sin x\) и \(\cos x.\) 9{4⋅14+3}}(\sin x)\)

Ответить

\(-\cos х\)

Пример \(\PageIndex{9}\): приложение к ускорению

Частица движется вдоль координатной оси таким образом, что ее положение в момент времени \(t\) определяется выражением \(s(t)= 2−\sint\). Найдите \(v(π/4)\) и \(a(π/4)\). Сравните эти значения и решите, ускоряется или замедляется частица.

Раствор

Сначала найдите \(v(t)=s′(t)\)

\[v(t)=s′(t)=−\cos t .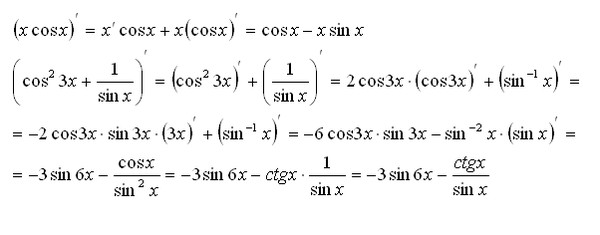 \nonumber \]

Таким образом,

\(v\left(\frac{π}{4}\right)=-\dfrac{1}{\sqrt{2}}=-\dfrac{\sqrt{2 }}{2}\).

Затем найдите \(a(t)=v′(t)\). Таким образом, \(a(t)=v′(t)=\sin t\), и мы имеем

\(a\left(\frac{π}{4}\right)=\dfrac{1}{\ sqrt{2}}=\dfrac{\sqrt{2}}{2}\).

Поскольку \(v\left(\frac{π}{4}\right)=-\dfrac{\sqrt{2}}{2}<0\) и \(a\left(\frac{π} {4}\right)=\dfrac{\sqrt{2}}{2}>0\), мы видим, что скорость и ускорение действуют в противоположных направлениях; то есть объект ускоряется в направлении, противоположном направлению, в котором он движется. Следовательно, частица замедляется.

Упражнение \(\PageIndex{9}\)

Блок, прикрепленный к пружине, движется вертикально. Его положение в момент времени t определяется выражением \(s(t)=2\sin t\). Найдите \(v\left(\frac{5π}{6}\right)\) и \(a\left(\frac{5π}{6}\right)\). Сравните эти значения и решите, ускоряется блок или замедляется.

Подсказка

Используйте пример \(\PageIndex{9}\) в качестве руководства.

Ответить

\(v\left(\frac{5π}{6}\right)=-\sqrt{3}<0\) и \(a\left(\frac{5π}{6}\right)=-1 <0\). Блок ускоряется.

Ключевые понятия

• Мы можем найти производные от \(\sin x\) и \(\cos x\), используя определение производной и формулы предела, найденные ранее. Результат

\(\dfrac{d}{dx}\big(\sin x\big)=\cos x\quad\text{and}\quad\dfrac{d}{dx}\big(\cos x\big )=−\sin x\).

• С помощью этих двух формул мы можем определить производные всех шести основных тригонометрических функций. 92x\)
  • Производная секущей функции

  \(\dfrac{d}{dx}(\sec x)=\sec x\tan x \)

  • Производная функции косеканса

  \(\dfrac{d}{dx}(\csc x)=-\csc x\cot x \)

  ---

  Эта страница под названием 3.5: Производные тригонометрических функций распространяется под лицензией CC BY-NC-SA 4. 0 и была создана, изменена и/или курирована Гилбертом Стрэнгом и Эдвином «Джедом» Херманом (OpenStax) через исходный контент, который был отредактировано в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.

  1. Вернуться к началу
  • Была ли эта статья полезной?

  1. Тип изделия

     Раздел или Страница

     Автор

     ОпенСтакс

     Лицензия

     СС BY-NC-SA

     Версия лицензии

     4,0

     Программа OER или Publisher

     ОпенСтакс

     Показать страницу TOC

     нет

  2. Теги

     1. автор @ Эдвин «Джед» Герман
     2. автор@Гилберт Странг
     3. Производная функции косеканса
     4. Производная функции косинуса
     5. Производная функции котангенса
     6. Производная секущей функции
     7. Производная синусоидальной функции
     8. Производная функции тангенса
     9. https://math.

        No related posts.