Открытый урок Элементы комбинаторики
Место проведения: КГБПОУ «Волчихинский политехнический колледж»
Дата проведения: 26 октября 2015 года
Продолжительность: 45 мин
Дисциплина: ПД.01 Математика
Тема: Основные понятия комбинаторики.
Тип урока: комбинированный урок
Цель: организовать деятельность обучающихся по изучению и первичному закреплению учебного материала по теме «Основные понятия комбинаторики»
Задачи:
Образовательные: создать условия для осознанного понимания решения простейших задач на применение элементов комбинаторики; изучить формулы размещения, перестановки и сочетания; сформировать у обучающихся первичные умения и навыки решения задач.
Развивающие: развивать познавательный интерес студентов, логическое мышление, умение применять знания в изменённой ситуации, делать выводы и обобщения; развивать умения сравнивать, систематизировать, обобщать; навыки контроля и самоконтроля.
Воспитательные: формировать научное мировоззрение у обучающихся, культуру математической речи, информационную и коммуникативную культуру студентов; воспитание дружелюбного отношения друг другу, умение работать в коллективе.
9. Планируемый результат: формирование положительной мотивации, знания основных формул комбинаторики, формирование у обучающихся первичных умений и навыков решения простейших комбинаторных задач; развитие коммуникативных умений.
Основой дидактический метод: проблемно-поисковый.
Частные методы: метод эвристической беседы, методы организации и осуществления учебно-познавательной деятельности, методы контроля и самоконтроля за эффективностью учебно-познавательной деятельности.
Формы работы: фронтальная, групповая, работа в парах, индивидуальная работа.
Дидактические средства: мультимедиапроектор, презентация по теме «Основные понятия комбинаторики».
Список используемых источников:
УМК: Спирина М.
С. Теория вероятности и математическая статистика: учебник для студ. учреждений среднего профессионального образования / М.С. Спирина, П.А. Спирин. – 5-е изд., стер. – М.: Издательский центр «Академия», 2013. – 352 с.
План урока
1. Организационное начало урока.
2. Актуализация знаний, умений и навыков.
3. Этап подготовки студентов к активному и сознательному усвоению нового материала
4.Этап изучения и усвоения новых знаний.
5. Первичный контроль знаний.
6. Подведение итогов занятия.
7. Рефлексия.
8. Домашнее задание.
9. Организационное завершение урока.
Этапы урока | Содержание учебного материала | Формирование УУД | |
Деятельность преподавателя | Деятельность студентов | ||
1.Организационный этап. Слайд 1. | Преподаватель проверяет готовность к уроку. Я рада приветствовать всех Вас на сегодняшнем уроке. Все мы с вами пришли на урок с разным настроением, но я надеюсь что в конце нашего занятия у нас у всех будут только положительные эмоции. Девизом нашего занятия я предлагаю взять слова английского математика Д. Сильвестра «Число, положение и комбинация — три взаимно пересекающиеся, но различные сферы мысли, к которым можно отнести все математические идеи» Английский математик Джеймс Джозеф Сильвестр | Обучающиеся настраиваются на урок, приветствуют гостей и друг друга, быстрое включение в деловой ритм, установка внимания всей группы. | Установление обучающимися связи между учебной деятельностью и ее мотивом. |
2.Актуализация знаний, умений и навыков. Сайды 2-9. | Прежде чем перейти к изучению нового материала, проведем небольшую разминку по ранее изученному материалу. Что называется соединениями? Группы, составленные из каких-либо элементов. Дайте определение факториала числа. Факториал числа – это произведение натуральных чисел от 1 до самого числа (включая данное число). Обозначается факториал восклицательным знаком. Факториал 0 и 1 равен единице. Вычислите факториалы следующих чисел. 3! =6 5! = 120 6! = 720 7! = 5040 Вычислите значения выражений. 5!+6! = 120+720=840 15!/ (13!(15-13)!) = 15*7=105 Как Вы думаете, для чего мы повторили данные понятия? | Обучающиеся работают самостоятельно. | Коррекция знаний обучающихся |
3.Этап подготовки студентов к активному и сознательному усвоению нового материала Слайд 10-13. | Настроить на позитив. Математику, физику и психологу задают одну и ту же задачу: «Монету бросили 100 раз, и все 100 раз выпала решка. Что выпадет в 101-ый раз?» Математик: «С вероятностью 1/2 выпадет орёл» Физик: «Эксперимент показал, что должна выпасть решка» Психолог: «Выпадет орёл». Математик с физиком: «Но почему?» -Ну, как же, всё решка да решка! Орлу ведь тоже хочется! Сейчас я предлагаю Вам решить задачу. Туристическая фирма планирует посещение туристами в Италии трех городов: Венеции, Рима и Флоренции. Сколько существует вариантов такого маршрута? ВРФ ВФР РФВ РВФ ФРВ ФВР (6) Как называются задачи такого типа? Задачи такого типа называются комбинаторными задачами. Как называется раздел математики, в котором решаются задачи на составление различных комбинаций? Комбинаторика. Как Вы думаете, какова тема нашего занятия? Какую цель можно поставить? (знакомство с новой темой, применение на практике и в жизни человека) Каковы задачи нашего занятия? | Студенты работают в парах. Студенты отвечают на вопросы преподавателя. Формулируют тему урока «Основные понятия комбинаторики». Раскрывают подробно, о чем пойдет речь на уроке. Формулируют задачи на урок. | Самостоятельное выделение, анализ и формулирование познавательной цели и учебной задачи. Развитие умения формулировать тему и задачи урока. Прогнозирование результатов. Формирование умения прогнозировать свою работу. |
4.Этап изучения и усвоения новых знаний. Слайд 14-19 | Вы сейчас предложили несколько способов решения выше указанной задачи. Но есть более простой способ решения данной задачи – это решение с использованием основных понятий комбинаторики (перестановки, размещения, сочетания). Давайте более подробно остановимся на каждом понятии. 1. Перестановки. Перестановками из n элементовназываются такие соединения из всех n элементов, которые отличаются друг от друга порядком расположения элементов. Число перестановок из n элементов обозначается символом Pn и вычисляется по формуле: Pn = n! Вернемся к нашей задаче. Нам известно, что туристическая фирма планирует посещение туристами в Италии трех городов: Венеции, Рима и Флоренции. Сколько существует вариантов такого маршрута? Pn = n! = 3! = 1*2*3=6 (способов) Ответ: 6 способов. Рассмотрим еще одну задачу. В ящике находится 15 деталей. Сколькими способами можно взять 4 детали? 2. Сочетания. Сочетаниями из n элементов по k в каждом называются такие соединения, которые отличаются друг от друга хотя бы одним элементом. Количество сочетаний обозначается и вычисляется по формуле Вернемся к задаче. | Студенты записывают определения в формулу в тетрадь. Студенты решают задачу с помощью формулы, записывают в тетрадь. Студенты предлагают способы решения задачи. Студенты записывают определения в формулу в тетрадь. Студенты решают задачу с помощью формулы, записывают в тетрадь. | Обучение работе с источниками знаний: — формирование умений решения простейших комбинаторных задач; Выявление, идентификация проблемы Самостоятельное создание алгоритмов деятельности при решении проблем поискового характера. Инициативное сотрудничество в поиске и сборе информации. |
Предлагают способы решения данной задачи.
Мы рассмотрели два основных понятия комбинаторики. Скажите, о каком понятии мы еще не говорили. Размещения. Совершенно верно – размещения. 3. Размещения. Размещениями изn элементов по k в каждом называются такие соединения, которые отличаются друг от друга либо самими элементами (хотя бы одним), либо порядком их расположения. Количество размещений обозначается и вычисляется по формуле Предлагаю Вам составить задачу на нахождения количества размещений. Пример. Сколько различных двузначных чисел можно составить из множества цифр , причем так, чтобы цифры числа были различны? | Студенты решают задачу с помощью формулы, записывают в тетрадь. Студенты пытаются составить задачу в парах. | ||
5. Первичный контроль знаний. Слайд 20-27 | 1) Решение простейших комбинаторных задач 2) Найти ошибки в решениях задач: | Студенты работают у доски, решают простейшие комбинаторные задачи. Сколькими способами можно рассадить 5 человек за столом? В студенческой группе 23 человека. Сколькими способами можно выбрать старосту и его заместителя? способами. Сколькими способами из колоды в 36 карт можно выбрать 3 карты? Проверьте, верно, ли решены задачи: Сколькими способами из восьми человек можно избрать комиссию, состоящую из пяти членов? С = Ответ: 56. (верно) Сколько четырехбуквенных слов можно образовать из букв слова сапфир? P4=4! = 1*2*3*4 =24 (неверно) А. | Умение применять полученные знания в конкретной ситуации. Умение применять полученные знания в конкретной ситуации. Контроль, самооценка. |
3) Самостоятельная работа по вариантам. | Студенты работают самостоятельно по вариантам. Взаимопроверка. 1 вариант. Сколько различных четырехзначных чисел можно составить из цифр 1, 2, 3, 4, 5, 6? Решение. Общее число комбинаций равно числу размещений из 6 элементов по 4 2 вариант. В группе 10 студентов. Сколькими способами можно выбрать из этой группы троих студентов для участия в конференции? Решение. Число способов равно числу сочетаний из 10 элементов по 3 элемента: =120 | Умение применять полученные знания в конкретной ситуации. | |
6. Подведение итогов занятия | Подведем итоги нашего занятия. Обсуждение и выставление оценок за урок. | Вспоминают, что изучали на данном уроке. | Формирование умения строить речевые высказывания в соответствии с поставленными задачами урока. |
7.Рефлексия Слайд 28 | Достиг ли ты своих целей? _____________________ Оцени степень усвоения: ________________________ Продолжи одно из предложений: “Мне понятно… “Я запомнил… “Мне на уроке… “Я думаю… | Высказывают свое мнение по уроку. | Формировать умение осуществлять познавательную и личностную рефлексию. |
8.Домашнее задание Слайд 29 | Творческое. Составить сводную таблицу по изученному материалу. Решить задачу (дифференцированные задачи) Задача на «3» Сколько различных четырехзначных чисел можно составить из цифр 2, 3, 5, 7. Задачи на «4» Восемь студентов обменялись рукопожатиями. Сколькими способами можно составить трехцветный полосатый флаг из пяти различных по цвету отрезков материи? Задача на «5» Сколько словарей надо издать, чтобы можно было выполнять переводы с любого из шести языков на любой из них? | Запись домашнего задания | Саморегуляция как способность к мобилизации сил и энергии, к волевому усилию (к выбору в ситуации мотивационного конфликта) и преодоления препятствий. |
9.Логическое завершение урока. Слайд 30 | Вы молодцы! Каждый из вас «научился тому, что следует знать». Спасибо за урок! | Психологический настрой на окончание урока | Формирование положительной мотивации, развитие коммуникативных умений |
Сколько было рукопожатий?Адрес публикации: https://www.prodlenka.org/metodicheskie-razrabotki/174971-otkrytyj-urok-jelementy-kombinatoriki
Понятия пространства элементарных событий и случайного события.
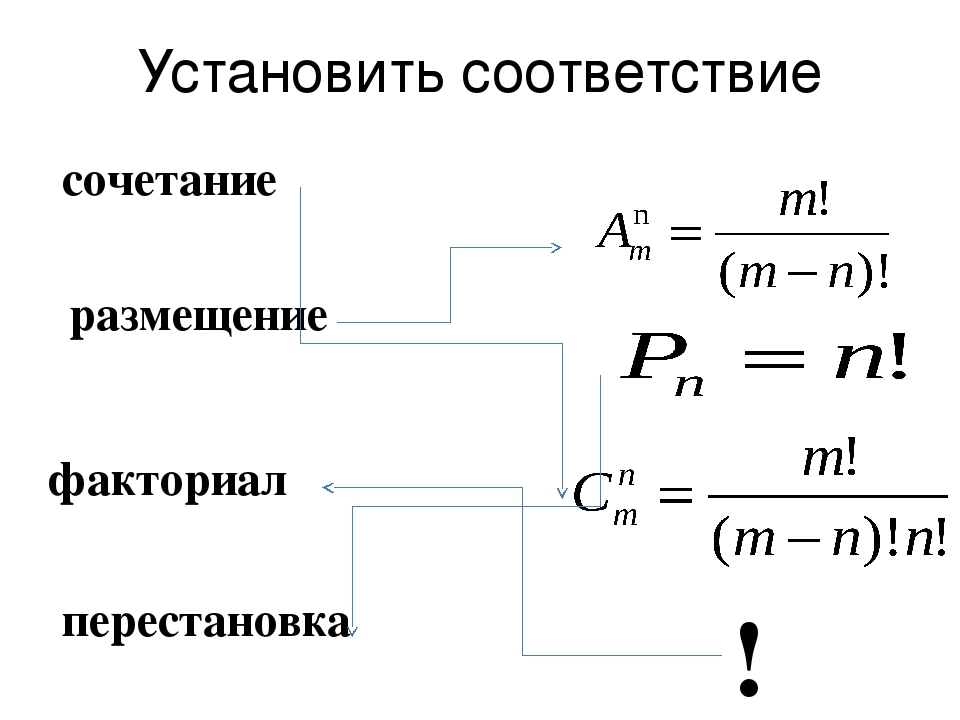Основные формулы комбинаторики.Лучшие смартфоны на Android в 2022 году
Серия iPhone от Apple редко чем удивляет. Когда вы получаете новый iPhone, общее впечатление, скорее всего, будет очень похожим на ваше предыдущее устройство. Однако всё совсем не так в лагере владельцев устройств на Android. Существуют телефоны Android всех форм и размеров, не говоря уже о разных ценовых категориях. Другими словами, Android-телефон может подойти многим. Однако поиск лучших телефонов на Android может быть сложной задачей.
1424 0
Конструирование Математика
- Главная /
- Статьи /
- Математика
(34.1.) В рамках теории вероятностей исследуются модели экспериментов, результат которых зависит от условий опыта. Иными словами, данная теория изучает модели стохастических экспериментов.
О: В качестве элементарных событийопределяют возможные результаты эксперимента. Пространство элементарных событийесть множество элементарных событий конкретного опыта:
Предположим, чтоявляется конечным или счетным множеством.
Пример 1: Выбрасывают игральную кость. Число возможных результатов эксперимента- выпадение.
Пример 2: Подбрасывается монета. Число возможных результатов
— открывается герб,- открывается решка.
Пример 3: Подбрасываются две монеты. Число возможных результатов
При вычилении количества элементарных событий, содержащихся в конечном пространстве, применяют следующими понятиями комбинаторного анализа: перестановка, сочетание, размещение.
О: В качестве соединений определяют разные комбинации, предполагающие наличие элементов множества, которые зависят от определенных условий. Перестановки изэлементов — это соединения, включающие в себяэлементов и отличающиеся их порядком. Размещениями изэлементов поэлементов, отличия между которыми заключаются в элементах или в их порядках.
Определение числа осуществляется в соответствии со следующими формулами:
1) число перестановок изэлементов:
2) число размещений изэлементов по:
3) число сочетаний изэлементов по:
Пример:
1) Перестановки:
2) Размещения из трех элементов по два:
3) Сочетания из трех элементов по два:
О: Случайное событиеявляется достоверным событием,обозначает невозможное событие.
По итогам опыта случайное событие может возникнуть, а может и не произойти.
Пример 1:
1) Бросают игральную кость. Событие, получается, всодержатся 3 элементарных события.
2) Выбрасывают две игральные кости.представляет собой появление таких цифр (), их сумма составляет
3) Слово «победа», состоящее из шести букв, образовано из карточек.
Произвольно выбираем две буквы,- две выбранные буквы — согласные. Пространство элементарных событий образовано изсостоит ихэлементарных событий.
Нравится
Твитнуть
Теги Математика
Сюжеты Математика
Понятие об автоматах, их задание графами
(38.4.) Сформулируем понятие конечного автомата, обозначим входной алфавит, выходной алфавит, алфавит состояний, функцию переходов, функцию выходов, на рисунке изобразим граф переходов.
4150 0
Некоторые классы графов
(38.3.) Большинство графов, которые используются в приложениях (например, графы сортировок, классификаций) предполагают наличие диаграмм, именуемых деревьями. Связный неориентированный граф без циклов, в частности, предполагающий отсутствие петель и кратных ребер, именуют деревом. Несвязный неориентированный граф без цикла — лес, его связные компоненты являются деревьями.
10128 0
Маршруты, цепи и циклы
(38.2.) В рамках обозначенной темы рассмотрим случай определения связного неориентированного мультиграфа в качестве эйлерова и гамильтонова графа.
13662 0
Комментарии (0)
Вы должны авторизоваться, чтобы оставлять комментарии.
Вход
Калькулятор перестановок и комбинаций
| Перестановки , n P r = |
| = | 30 |
| Комбинации , N C R = |
| = | 15 |
Калькулятор связанных вероятностей | Калькулятор размера выборки
Перестановки и комбинации являются частью раздела математики, называемого комбинаторикой, который включает изучение конечных дискретных структур.
Перестановки — это определенный выбор элементов в наборе, где важен порядок расположения элементов, тогда как комбинации включают выбор элементов без учета порядка. Например, типичный кодовый замок технически должен называться замком перестановки по математическим стандартам, поскольку важен порядок вводимых чисел; 1-2-9не то же самое, что 2-9-1, тогда как для комбинации любого порядка этих трех чисел будет достаточно. Существуют различные типы перестановок и комбинаций, но приведенный выше калькулятор рассматривает только случай без замены, также называемый без повторения. Это означает, что для приведенного выше примера с кодовым замком этот калькулятор не вычисляет случай, когда кодовый замок может иметь повторяющиеся значения, например, 3-3-3.
Перестановки
Предоставленный калькулятор вычисляет одну из наиболее типичных концепций перестановок, где расположение фиксированного числа элементов r , берутся из заданного набора n . По сути, это можно назвать R-перспективами N или частичных перестановок
, или P(n,r) среди прочих. В случае перестановок без замены рассматриваются все возможные способы перечисления элементов в наборе в определенном порядке, но количество вариантов выбора уменьшается каждый раз при выборе элемента, а не в таком случае, как «комбинированный» замок. , где значение может встречаться несколько раз, например 3-3-3. Например, при попытке определить количество способов, которыми капитан команды и вратарь футбольной команды могут быть выбраны из команды, состоящей из 11 членов, капитан команды и вратарь не могут быть одним и тем же лицом, и после выбора они должны быть удалены из набора. Буквы A от до K будет представлять 11 различных членов команды:A B C D E F G H I J K 11 участников; A выбран капитаном
B C D E F G H I J K 10 членов; B выбран в качестве вратаря
Как видно, первым выбором был A в качестве капитана из 11 первоначальных членов, но поскольку A не может быть капитаном команды, а также вратарем, A был снят со сета перед вторым выбором вратаря B можно изготовить.
Общие возможности, если бы была указана позиция каждого отдельного члена команды, были бы 11 × 10 × 9 × 8 × 7 × … × 2 × 1, или 11 факториалов, записанных как 11 !. Однако, поскольку в этом случае важны только выбор капитана команды и вратаря, релевантными являются только первые два выбора, 11 × 10 = 110. Таким образом, уравнение для расчета перестановок удаляет остальные элементы, 9 × 8 × 7 × … × 2 × 1 или 9 !. Таким образом, обобщенное уравнение для перестановки можно записать так:
| n P r = |
|
Или в данном случае специально:
| 11 P 2 = |
| = | = 11 × 10 = 110 |
Опять же, предоставленный калькулятор не вычисляет перестановки с заменой, но для любопытства ниже приведено уравнение: в том, что они по существу являются перестановками, в которых удалены все избыточности (как будет описано ниже), поскольку порядок в комбинации не важен.
. Как и в случае с перестановками, предоставленный калькулятор рассматривает только случай комбинаций без замены, а случай комбинаций с заменой обсуждаться не будет. Снова используя пример футбольной команды, найдите количество способов выбрать 2 нападающих из команды из 11 человек. В отличие от случая, приведенного в примере с перестановкой, где сначала был выбран капитан, а затем вратарь, порядок, в котором нападающие выбраны не имеет значения, так как они оба будут нападающими. Снова обращаясь к футбольной команде как буквы 9От 0006 A
Возможное количество договоренностей для всех n человек равно n! , как описано в разделе перестановок. Чтобы определить количество комбинаций, необходимо удалить избыточности из общего количества перестановок (110 из предыдущего примера в разделе перестановок) путем деления избыточности, которая в данном случае равна 2!. Опять же, это потому, что порядок больше не имеет значения, поэтому уравнение перестановки нужно сократить на количество способов, которыми можно выбрать игроков, A , затем B или B , затем A , 2 или 2!. Это дает обобщенное уравнение для комбинации, как и для перестановки, деленное на количество избыточностей, и обычно известное как биномиальный коэффициент:| n C r = |
|
Или в данном случае специально:
| 11 С 2 = |
| = |
| = 55 |
Логично, что вариантов для комбинации меньше, чем для перестановки, поскольку избыточность убирается.
Опять же для любопытных, уравнение для комбинаций с заменой приведено ниже:
| n C r = |
|
Урок Видео: Комбинация | Nagwa
Стенограмма видео
В этом видео мы узнаем, как
использовать свойства комбинации для решения проблем и использовать комбинации для подсчета возможных
результаты. Комбинация 𝑛𝐶𝑘 представляет
количество различных способов выбора 𝑘 объектов из 𝑛 различных
объекты. При работе с комбинациями
порядок не имеет значения. Важно отметить, что 𝑛 и
𝑘 должно быть целым неотрицательным числом, а 𝑛 должно быть больше или равно 𝑘. Напомним, что перестановка
𝑛𝑃𝑘 очень похоже. Однако в этом случае порядок
иметь значение.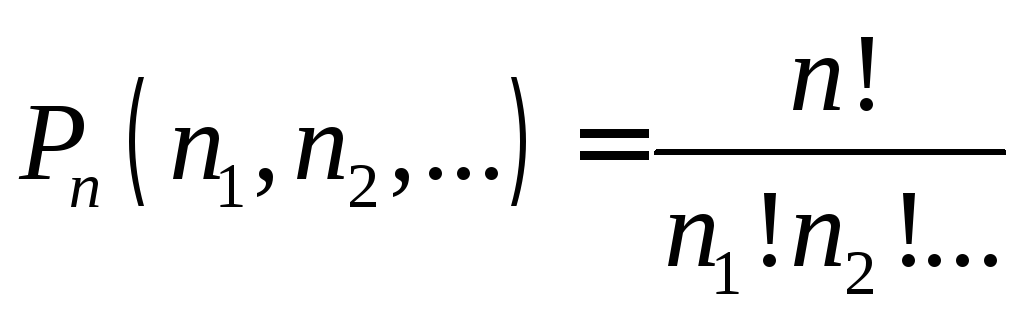
Мы начнем это видео с
сравнение перестановок и сочетаний в контексте.
Как уже было сказано, ключ Разница между перестановкой и комбинацией заключается в том, имеет ли значение порядок. Обозначение, используемое для обоих этих аналогично, где 𝑛 — общее количество различных объектов, а 𝑘 — количество объекты упорядочиваются или выбираются. Давайте представим гонку, в которой у нас есть 𝑛 бегуны. И в первом случае верхний 𝑘 бегуны получают медали с их разрядами. Если 𝑘 равно трем, двум возможные способы назначения медалей показаны на рисунке. Хотя те же три бегуна заняли первые три места в обоих случаях, в результате медалисты выиграли разные медали.
Это потому, что порядок имеет значение. Количество различных способов
назначать медали за эту гонку — это количество различных способов заказать 𝑘 объектов из
𝑛 Всего объектов.
Это дается перестановкой
𝑛𝑃𝑘. Если, с другой стороны, вершина
трем финишерам были вручены одинаковые медали, в отличие от тех, у кого
позиции, то есть только один способ выбрать тех же трех финишеров. Это потому, что приказ не
иметь значение. Это значение дается
сочетание 𝑛𝐶𝑘. Сейчас мы рассмотрим, как мы можем
рассчитайте это, используя фундаментальный принцип подсчета.
Основной принцип счета
утверждает, что если у нас есть два независимых события 𝐴 и 𝐵 такие, что количество
возможных исходов события 𝐴 равно 𝑥 и количество возможных исходов события
𝐵 равно 𝑦, то общее количество различных возможных исходов этих двух событий
вместе это произведение 𝑥, умноженное на 𝑦. Применяя это к нашему примеру, мы
видим, что количество способов выбрать 𝑘 бегунов из 𝑛, умноженное на количество
способов заказать 𝑘 бегунов равно количеству способов заказать 𝑘 бегунов из
𝑛.
Используя наши обозначения для комбинаций
и перестановок, первый член в левой части равен 𝑛𝐶𝑘, а член в
правая сторона 𝑛𝑃𝑘.
Поскольку существует 𝑘 факториальных способов заказываем 𝑘 бегунов, имеем 𝑛𝐶𝑘, умноженное на 𝑘 факториал, равно 𝑛𝑃𝑘, напоминая, что 𝑘 факториал — это произведение всех положительных целых чисел, меньших или равно 𝑘. Разделив обе части нашего уравнения по факториалу 𝑘 имеем 𝑛𝐶𝑘 равно 𝑛𝑃𝑘, деленному на факториал 𝑘. Используя тот факт, что 𝑛𝑃𝑘 равно на 𝑛 факториал над 𝑛 минус 𝑘 факториал, мы перепишем правую часть так у нас есть формула для комбинаций. Формальное определение комбинация показана, где 𝑛𝐶𝑘 равно 𝑛 факториалу, деленному на 𝑛 минус 𝑘 факториал, умноженный на 𝑘 факториал.
Стоит отметить, что есть
эквивалентные обозначения, включая два показанных. Сейчас мы рассмотрим пару
примеры, подтверждающие это.
Что из следующего равно 41 𝐶 пять? Это (A) 41 𝑃 пять разделить на пять факториал, (B) 41 𝑃 пять разделить на пять, (C) 41 𝑃 пять умножить на пять факториал, или (D) 41 𝑃 пять умножить на пять?
Начнем с того, что вспомним наши формулы для перестановки и комбинации. Перестановка 𝑛𝑃𝑘 равна 𝑛 факториал разделить на 𝑛 минус 𝑘 факториал. А комбинация 𝑛𝐶𝑘 равна на 𝑛 факториал, деленный на 𝑛 минус 𝑘 факториал, умноженный на 𝑘 факториал. Объединив эти две формулы, мы видим, что 𝑛𝐶𝑘 равно 𝑛𝑃𝑘, деленному на 𝑘 факториал. В этом вопросе 𝑛 равно 41 и 𝑘 равно пяти. Это означает, что 41 𝐶 пять равно до 41 𝑃 пять разделить на пять факториал. Поэтому правильный ответ вариант (А).
В нашем следующем примере нам нужно оценить комбинацию.
Оценка 23 𝐶 19.
Чтобы ответить на этот вопрос,
начнем с того, что вспомним формулу комбинаций.
𝑛𝐶𝑘 равно 𝑛 факториалу
разделить на 𝑛 минус 𝑘 факториал, умноженный на 𝑘 факториал. В этом вопросе 𝑛 равно 23
а 𝑘 равно 19. Следовательно, 23 𝐶 19 равно 23
факториал разделить на 23 минус 19 факториал умножить на 19факториал. Знаменатель упрощается до четырех
факториал умножить на 19 факториал. Мы можем переписать числитель как 23
умножить на 22 умножить на 21 умножить на 20 умножить на 19 факториал. И, разделив числитель на
знаменатель на 19 факториал, имеем 23 умножить на 22 умножить на 21 умножить
на 20 разделить на четыре факториала.
Запись четырех факториалов как четырех умножить на три умножить на два умножить на один, мы можем уменьшить множители как показано. Это оставляет нам 23 умноженных на 11 умножить на семь умножить на пять, что равно 8855. 23 𝐶 19равно 8855.
В нашем следующем примере мы
рассмотреть задачу на подсчет комбинаций.
Сколько трехкарточных комбинаций может быть выбрать из колоды из 52 карт?
Начнем с того, что вспомним, что комбинация 𝑛𝐶𝑘 представляет собой количество различных способов выбора 𝑘 объектов из 𝑛 отдельные объекты. Это можно рассчитать, разделив 𝑛 факториал на 𝑛 минус 𝑘 факториал, умноженный на 𝑘 факториал. В этом вопросе у нас есть колода 52 карты, поэтому 𝑛 равно 52, и мы хотим выбрать три из них, поэтому 𝑘 равно до трех. Это означает, что нам нужно вычислить 52 𝐶 три, что равно делению факториала 52 на 49факториал умножить на три факториал.
Используя наши знания о факториалах,
мы знаем, что факториал 52 можно переписать как 52 умножить на 51 умножить на 50
умножить на 49 факториал. Это позволяет нам отменить 49
факториал на числитель и знаменатель. Три факториала равны трем
умножить на два умножить на один.
Затем мы можем сократить множители трех
и два, как показано. 26 умножить на 17 умножить на
50 равно 22 100. Поскольку 52 𝐶 три равно 22 100,
это количество трехкарточных комбинаций, которые можно выбрать из колоды из 52 карт.
карты.
В нашем последнем примере мы рассмотрим, как идентифицировать неизвестные параметры в комбинациях.
Если 𝑛 𝐶 три равно 120, найти 𝑛.
Начнем с того, что вспомним формулу
для комбинаций. 𝑛𝐶𝑘 равно 𝑛 факториалу
разделить на 𝑛 минус 𝑘 факториал, умноженный на 𝑘 факториал. В этом вопросе нам говорят, что
𝑘 равно трем, и мы также знаем, что 𝑛 𝐶 три равно 120. Подставив эти значения в наш
формула, у нас есть 𝑛 факториал, деленный на 𝑛 минус три факториала, умноженные на
три факториала равно 120. Используя тот факт, что три факториала
равно шести, то умножаем обе части нашего уравнения на три факториала
дает нам 𝑛 факториал над 𝑛 минус три факториала равно 720.
𝑛 факториал можно переписать как показано. Тогда мы можем разделить числитель а знаменатель левой части на 𝑛 минус три факториала. Это оставляет нас с уравнением 𝑛 умножить на 𝑛 минус один умножить на 𝑛 минус два равно 720. Произведение трех последовательных целых чисел равно 720. Мы могли бы вычислить значение 𝑛 с помощью проб и улучшений. Однако мы можем использовать и тот факт, что для любого 𝑛 больше двух произведение этих трех целых чисел больше чем 𝑛 минус два в кубе и меньше 𝑛 в кубе. В этом вопросе 720 больше чем 𝑛 минус два в кубе и меньше 𝑛 в кубе. Затем мы можем вычислить кубический корень из каждой части неравенство.
До двух знаков после запятой куб
корень из 720 равен 8,96. Следовательно, это больше, чем 𝑛
минус два и меньше 𝑛. Решение двух частей этого
неравенство, мы видим, что 𝑛 должно быть меньше 10,96 и должно быть больше
8.
96. Это означает, что у нас есть два
возможные значения для 𝑛: девять или 10. Подстановка 𝑛 равняется девяти в
в левой части нашего уравнения девять умножить на восемь умножить на
Семь. Это равно 504, что не
верно, так как правая часть равна 720. Когда 𝑛 равно 10, у нас есть 10
умножить на девять умножить на восемь. Это равно 720. Таким образом, мы можем заключить, что если
𝑛 𝐶 три равно 120, тогда 𝑛 равно 10.
Сейчас мы закончим это видео,
повторение ключевых моментов. Комбинация 𝑛𝐶𝑘 представляет
количество различных способов выбрать 𝑘 объектов из 𝑛 общего числа различных объектов,
где порядок объектов 𝑘 не имеет значения. Три разных обозначения
все написанное эквивалентно. Перестановка 𝑛𝑃𝑘 представляет
количество различных способов упорядочить 𝑘 объектов из 𝑛 всего объектов. На этот раз заказ 𝑘
объекты имеют значение.