Онлайн калькулятор умножения вектора на число
| 0 | ||||
| AC | +/- | ÷ | ||
| 7 | 8 | 9 | × | |
| 4 | 5 | 6 | — | |
| 1 | 2 | 3 | + | |
| 0 | 00 | , | = | |
Укажите размерность пространства 23
Укажите форму представления вектора Координаты точек начала и конца вектораКоординаты вектора
Задайте координаты вектора
Задайте значение числа q на которое нужно умножить вектор
q =
Как умножить вектор на число
Пример 1.
Умножим вектор плоскости на число q. Координаты вектора заданны точками.
Координаты точки А вектора AB: (5 ; 9)
Координаты точки B вектора AB: (-2 ; 11)
Числа q на которое нужно умножить вектор AB = 12
Для того, чтобы вектор умножить на число, необходимо каждую координату вектора умножить на данное число.
Вычислим координаты первого вектора по двум точкам A и B:
AB = {Bx — Ax; By — Ay} = {-2 — 5 ; 11 — 9} = {-7 ; 2}
AB ⋅ q = {ABx ⋅ q ; ABy ⋅ q} = {-7 ⋅ 12 ; 2 ⋅ 12} = {-84 ; 24}
Пример 2. Умножим вектор пространства на число q.
Координаты вектора a: (5 ; 9 ; -2)
Числа q на которое нужно умножить вектор a = 2.6
Для того, чтобы вектор умножить на число, необходимо каждую координату вектора умножить на данное число.
a ⋅ q = {ax ⋅ q ; ay ⋅ q ; az ⋅ q} = {5 ⋅ 2.
6 ; 9 ⋅ 2.6 ; -2 ⋅ 2.6} = {13 ; 117/5 ; -26/5} = {13 ; 23.4 ; -5.2}
| Вам могут также быть полезны следующие сервисы |
| Калькуляторы линейная алгебра и аналитическая геометрия |
| Калькулятор сложения и вычитания матриц |
| Калькулятор умножения матриц |
| Калькулятор транспонирование матрицы |
| Калькулятор нахождения определителя (детерминанта) матрицы |
| Калькулятор нахождения обратной матрицы |
| Длина отрезка. Онлайн калькулятор расстояния между точками |
| Онлайн калькулятор нахождения координат вектора по двум точкам |
| Калькулятор нахождения модуля (длины) вектора |
| Калькулятор сложения и вычитания векторов |
| Калькулятор скалярного произведения векторов через длину и косинус угла между векторами |
| Калькулятор скалярного произведения векторов через координаты |
| Калькулятор векторного произведения векторов через координаты |
| Калькулятор смешанного произведения векторов |
| Калькулятор умножения вектора на число |
| Калькулятор нахождения угла между векторами |
| Калькулятор проверки коллинеарности векторов |
| Калькулятор проверки компланарности векторов |
| Калькуляторы (Комбинаторика) |
| Калькулятор нахождения числа перестановок из n элементов |
| Калькулятор нахождения числа сочетаний из n элементов |
| Калькулятор нахождения числа размещений из n элементов |
| Калькуляторы систем счисления |
| Калькулятор перевода чисел из арабских в римские и из римских в арабские |
| Калькулятор перевода чисел в различные системы счисления |
| Калькулятор сложения, вычитания, умножения и деления двоичных чисел |
| Системы счисления теория |
| N2 | Двоичная система счисления |
| N3 | Троичная система счисления |
| N4 | Четырехичная система счисления |
| N5 | Пятеричная система счисления |
| N6 | Шестеричная система счисления |
| N7 | Семеричная система счисления |
| N8 | Восьмеричная система счисления |
| N9 | Девятеричная система счисления |
| N11 | Одиннадцатиричная система счисления |
| N12 | Двенадцатеричная система счисления |
| N13 | Тринадцатеричная система счисления |
| N14 | Четырнадцатеричная система счисления |
| N15 | Пятнадцатеричная система счисления |
| N16 | Шестнадцатеричная система счисления |
| N17 | Семнадцатеричная система счисления |
| N18 | Восемнадцатеричная система счисления |
| N19 | Девятнадцатеричная система счисления |
| N20 | Двадцатеричная система счисления |
| N21 | Двадцатиодноричная система счисления |
| N22 | Двадцатидвухричная система счисления |
| N23 | Двадцатитрехричная система счисления |
| N24 | Двадцатичетырехричная система счисления |
| N25 | Двадцатипятеричная система счисления |
| N26 | Двадцатишестеричная система счисления |
| N27 | Двадцатисемеричная система счисления |
| N28 | Двадцативосьмеричная система счисления |
| N29 | Двадцатидевятиричная система счисления |
| N30 | Тридцатиричная система счисления |
| N31 | Тридцатиодноричная система счисления |
| N32 | Тридцатидвухричная система счисления |
| N33 | Тридцатитрехричная система счисления |
| N34 | Тридцатичетырехричная система счисления |
| N35 | Тридцатипятиричная система счисления |
| N36 | Тридцатишестиричная система счисления |
| Дроби |
| Калькулятор интервальных повторений |
| Учим дроби наглядно |
| Калькулятор сокращения дробей |
| Калькулятор преобразования неправильной дроби в смешанную |
| Калькулятор преобразования смешанной дроби в неправильную |
| Калькулятор сложения, вычитания, умножения и деления дробей |
| Калькулятор возведения дроби в степень |
| Калькулятор перевода десятичной дроби в обыкновенную |
| Калькулятор перевода обыкновенной дроби в десятичную |
| Калькулятор сравнения дробей |
| Калькулятор приведения дробей к общему знаменателю |
| Калькуляторы (тригонометрия) |
| Калькулятор синуса угла |
| Калькулятор косинуса угла |
| Калькулятор тангенса угла |
| Калькулятор котангенса угла |
| Калькулятор секанса угла |
| Калькулятор косеканса угла |
| Калькулятор арксинуса угла |
| Калькулятор арккосинуса угла |
| Калькулятор арктангенса угла |
| Калькулятор арккотангенса угла |
| Калькулятор арксеканса угла |
| Калькулятор арккосеканса угла |
| Калькулятор нахождения наименьшего угла |
| Калькулятор определения вида угла |
| Калькулятор смежных углов |
| Калькуляторы (Теория чисел) |
| Калькулятор выражений |
| Калькулятор упрощения выражений |
| Калькулятор со скобками |
| Калькулятор уравнений |
| Калькулятор суммы |
| Калькулятор пределов функций |
| Калькулятор разложения числа на простые множители |
| Калькулятор НОД и НОК |
| Калькулятор НОД и НОК по алгоритму Евклида |
| Калькулятор НОД и НОК для любого количества чисел |
| Калькулятор делителей числа |
| Представление многозначных чисел в виде суммы разрядных слагаемых |
| Калькулятор деления числа в данном отношении |
| Калькулятор перевода числа с Е в десятичное |
| Калькулятор экспоненциальной записи чисел |
| Калькулятор нахождения факториала числа |
| Калькулятор нахождения логарифма числа |
| Калькулятор квадратных уравнений |
| Калькулятор остатка от деления |
| Калькулятор корней с решением |
| Калькулятор нахождения периода десятичной дроби |
| Калькулятор больших чисел |
| Калькулятор округления числа |
| Калькулятор свойств корней и степеней |
| Калькулятор комплексных чисел |
| Калькулятор среднего арифметического |
| Калькулятор арифметической прогрессии |
| Калькулятор геометрической прогрессии |
| Калькулятор модуля числа |
| Калькулятор абсолютной погрешности приближения |
| Калькулятор абсолютной погрешности |
| Калькулятор относительной погрешности |
| Калькуляторы площади геометрических фигур |
| Площадь квадрата |
| Площадь прямоугольника |
| КАЛЬКУЛЯТОРЫ ЗАДАЧ ПО ГЕОМЕТРИИ |
| Генератор Pdf с примерами |
| Тренажёры решения примеров |
| Тренажёр таблицы умножения |
| Тренажер счета для дошкольников |
| Тренажер счета на внимательность для дошкольников |
Тренажер решения примеров на сложение, вычитание, умножение, деление. Найди правильный ответ. |
| Тренажер решения примеров с разными действиями |
| Тренажёры решения столбиком |
| Тренажёр сложения столбиком |
| Тренажёр вычитания столбиком |
| Тренажёр умножения столбиком |
| Калькуляторы решения столбиком |
| Калькулятор сложения, вычитания, умножения и деления столбиком |
| Калькулятор деления столбиком с остатком |
| Конвертеры величин |
| Конвертер единиц длины |
| Конвертер единиц скорости |
| Конвертер единиц ускорения |
| Цифры в текст |
| Калькуляторы (физика) |
Механика |
| Калькулятор вычисления скорости, времени и расстояния |
| Калькулятор вычисления ускорения, скорости и перемещения |
| Калькулятор вычисления времени движения |
| Калькулятор времени |
Второй закон Ньютона. Калькулятор вычисления силы, массы и ускорения. |
| Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния. |
| Импульс тела. Калькулятор вычисления импульса, массы и скорости |
| Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы. |
| Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения |
Оптика |
| Калькулятор отражения и преломления света |
Электричество и магнетизм |
| Калькулятор Закона Ома |
| Калькулятор Закона Кулона |
| Калькулятор напряженности E электрического поля |
| Калькулятор нахождения точечного электрического заряда Q |
| Калькулятор нахождения силы F действующей на заряд q |
| Калькулятор вычисления расстояния r от заряда q |
| Калькулятор вычисления потенциальной энергии W заряда q |
| Калькулятор вычисления потенциала φ электростатического поля |
| Калькулятор вычисления электроемкости C проводника и сферы |
Конденсаторы |
| Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе |
| Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе |
| Калькулятор вычисления энергии W заряженного конденсатора |
Калькулятор вычисления энергии W заряженного конденсатора. Для плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов |
| Калькуляторы по астрономии |
| Вес тела на других планетах |
| Ускорение свободного падения на планетах Солнечной системы и их спутниках |
| Генераторы |
| Генератор примеров по математике |
| Генератор случайных чисел |
| Генератор паролей |
Умножение вектора на число.
Навигация по странице:
- Геометрическая интерпретация умножения вектора на число.
- Алгебраическая интерпретация умножения вектора на число.
- Формулы умножения вектора на число
- для плоских задач
- для пространственных задач
- для n -мерного вектора
- Свойства вектора умноженного на число
- Примеры задач на умножение вектора и числа
- плоская задача
- пространственных задача
Онлайн калькулятор.
Умножение вектора на число.
Геометрическая интерпретация.
Произведение ненулевого вектора на число — это вектор, коллинеарный данному (сонаправленный данному, если число положительное, имеющий противоположное направление, если число отрицательное), а его модуль равен модулю данного вектора, умноженному на модуль числа.
Алгебраическая интерпретация. Произведение ненулевого вектора на число — это вектор, координаты которого равны соответствующим координатам данного вектора, умноженным на число.
Формулы умножения вектора на число
Формула умножения вектора на число для плоских задач
В случае плоской задачи произведение вектора a = {ax ; ay} и числа k можно найти воспользовавшись следующей формулой:
k · a = {k · ax; k · ay}
Формула умножения вектора на число для пространственных задач
В случае пространственной задачи произведение вектора a = {ax ; ay ; az} и числа k можно найти воспользовавшись следующей формулой:
k · a = {k · ax ; k · ay ; k · az}
Формула умножения n -мерного вектора
В случае n-мерного пространства произведение вектора a = {a1 ; a2; .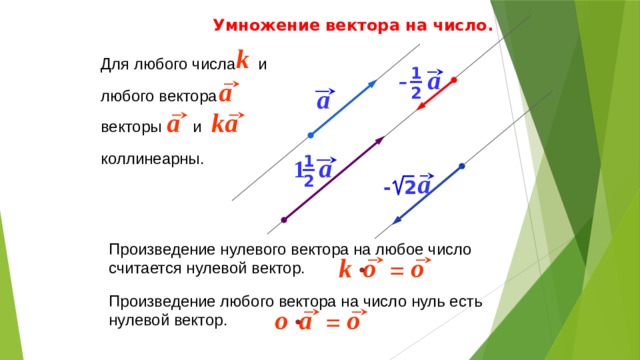
.. ; an} и числа k можно найти воспользовавшись следующей формулой:
k · a = {k · a1; k · a2; … ; k · an}
Свойства вектора умноженного на число
Если вектор b равен произведению ненулевого числа k и ненулевого вектора a, то есть b = k · a, тогда:
b || a — вектора b и a параллельны
a↑↑b, если k > 0 — вектора b и a сонаправленные, если число k > 0
a↑↓b, если k < 0 — вектора b и a противоположно направленные, если число k < 0
|b| = |k| · |a| — модуль вектора b равен модулю вектора a умноженному на модуль числа k
Примеры задач на умножение вектора и числа
Пример умножения вектора на число для плоских задачи
Пример 1. Найти произведение вектора a = {1; 2} на 3.
Решение: 3 · a = {3 · 1; 3 · 2} = {3; 6}.
Пример умножения вектора на число для пространственных задачи
Пример 2.
Найти произведение вектора a = {1; 2; -5} на -2.
Решение: (-2) · a = {(-2) · 1; (-2) · 2; (-2) · (-5)} = {-2; -4; 10}.
Вектора Вектор: определение и основные понятия Определение координат вектора заданного координатами его начальной и конечной точки Модуль вектора. Длина вектора Направляющие косинусы вектора Равенство векторов Ортогональность векторов Коллинеарность векторов Компланарность векторов Угол между векторами Проекция вектора Сложение и вычитание векторов Умножение вектора на число Скалярное произведение векторов Векторное произведение векторов Смешанное произведение векторов Линейно зависимые и линейно независимые вектора Разложение вектора по базису
Онлайн калькуляторы с векторами
Онлайн упражнения с векторами на плоскости
Онлайн упражнения с векторами в пространстве
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Скалярное умножение векторов
Горячая математика Чтобы умножить вектор на скаляр, умножьте каждый компонент на скаляр.
Если ты → «=» 〈 ты 1 , ты 2 〉 имеет величину | ты → | и направление г , затем н ты → «=» н 〈 ты 1 , ты 2 〉 «=» 〈 н ты 1 , н ты 2 〉 где н положительное действительное число, величина равна | н ты → | , а его направление г .
Обратите внимание, что если н отрицательно, то направление н ты является противоположностью г .
Пример :
Позволять
ты
«=»
〈
−
1
,
3
〉
, Находить
7
ты
.
7 ты «=» 7 〈 − 1 , 3 〉 «=» 〈 7 ( − 1 ) , 7 ( 3 ) 〉 «=» 〈 − 7 , 21 〉
Позволять
ты
и
в
быть векторами, пусть
с
и
г
быть скалярами.
Тогда верны следующие свойства.
Свойства скалярного умножения | |
| Величина масштабированного вектора равна абсолютному значению скаляра, умноженному на величину вектора. | ‖ с в ‖ «=» | с | в |
| Ассоциативное свойство | с ( г ты ) «=» ( с г ) ты |
| Коммутативное свойство | с ты «=» ты с |
| Распределительное свойство | ( с + г ) ты «=» с ты + г ты с ( ты + в ) «=» с ты + с в |
| Идентификационное свойство | 1 ⋅ ты «=» ты |
| Мультипликативное свойство − 1 | ( − 1 ) с «=» − с |
| Мультипликативное свойство 0 | 0 ( ты ) «=» 0 |
Как умножать векторы — скалярное (точечное) произведение
Как умножать векторы
Ключевые термины
Цели
В этой статье мы рассмотрим другое представление векторов, а также основы умножения векторов.
Единичные векторы
Хотя форма координат для представления векторов ясна, мы также можем представить их в виде алгебраических выражений, используя единичные векторы. В наших стандартных прямоугольных (или евклидовых) координатах ( x, y, и z ) единичный вектор представляет собой вектор длины 1, параллельный одной из осей. В двумерной координатной плоскости единичные векторы часто называют i и j, , как показано на графике ниже. Для трех измерений мы добавляем единичный вектор k , соответствующий направлению оси z . Эти векторы определяются алгебраически следующим образом. или 03
к = (0, 0, 1)
Прежде чем представить алгебраическое представление векторов с помощью единичных векторов, мы должны сначала ввести умножение векторов — в данном случае на скаляры.
Умножение векторов на скаляры
Умножение с участием векторов является более сложным, чем умножение только скаляров. Начнем с самого простого случая: умножения вектора на скаляр. Ниже приведено определение умножения скаляра 9.0121 c вектором a, , где a = ( x, y ). (Опять же, мы можем легко распространить эти принципы на три измерения.) мутативный, поэтому . Но что означает это умножение? Как оказалось, умножение на скаляр c приводит к увеличению длины вектора в 9 раз.0121 в. Наиболее четко это видно для единичных векторов, но это применимо к любому вектору. (Однако умножение на отрицательную скалярную величину меняет направление вектора на противоположное.) На приведенном ниже графике показаны некоторые примеры использования c = 2. (Напомним, что положение вектора не влияет на его значение.)
Практическая задача: Для заданного вектора a = (3, 1) найдите вектор в том же направлении, что и a , но в два раза длиннее.
Решение: Когда мы умножаем вектор на скаляр, направление вектора произведения совпадает с направлением множителя. Единственная разница в том, что длина умножается на скаляр. Таким образом, чтобы получить вектор, который в два раза длиннее a , но в том же направлении, что и a, просто умножьте на 2. 0010 = 2 • ( 3, 1) = (2 • 3, 2 • 1) = (6, 2)
Алгебраическое представление векторов s алгебраически. Обратите внимание, что любой двумерный вектор v может быть представлен как сумма длины, умноженной на единичный вектор i , и другой длины, умноженной на единичный вектор j. Например, рассмотрим вектор (2, 4). Примените правила векторов, которые мы уже изучили:
(2, 4) = (2, 0) + (0, 4) (правило сложения векторов) • (1, 0) + 4 • (0, 1) (правило умножения скаляров и векторов)
(2, 4) = 2 i + 4 j
2 0
9 0 0 2 Графически мы добавляем два вектора в единичных направлениях, чтобы получить наш произвольный вектор.
Хотите узнать больше? Почему бы не пройти онлайн-курс Precalculus?
Обратите внимание, что единичные векторы действуют почти так же, как переменные. Таким образом, мы можем сложить два вектора a и b следующим образом.
а = 3 i – 2 j b = i + 3 j
а + б = (3 i – 2 j0 0009 я + 3 я ) = 3 я + я – 2 + 3 = 4 +
03 9002
Это представление обеспечивает большую гибкость, чем представление координат, но оно эквивалентно.
Практическая задача: Вычислить сумму и разность ( t0 — u векторов 9 t = -2 i + 3 j и u = 6 i — 4 j.
Решение: Мы можем довольно легко решить эту задачу алгебраически.
t + u = (-2 i + 3 j ) + (6 i — 4 j ) = 4 i — 0 j = (9,00010 j -1) 03 t — u = (-2 i + 3 j ) — (6 i — 4 j ) = -2 0 i 3 Умножение векторов: скалярное (точечное) произведение . Однако на данный момент значение этого продукта может быть вам не совсем ясно. 3 32 Таким образом, v • i является «частью» вектора v 90 90 9 0 9 0 0 0 3 9 0 0 0 0 0 3 I. Однако это объяснение работает только для векторов длины 1. Когда два произвольных вектора перемножаются, скалярное произведение имеет аналогичный смысл, но величина числа немного отличается. Мы не будем углубляться в это, но мы можем рассмотреть частный случай, когда скалярное произведение дает ценную информацию. Длина вектора сам с собой. Рассмотрим эту ситуацию графически. Результатом здесь является прямоугольный треугольник с горизонтальной стороной длиной x и вертикальной стороной длиной y. Эти длины соответствуют длинам составляющих векторов x i и y j, соответственно. Но мы знаем из теоремы Пифагора, что есть квадрат длины вектора против . Не случайно это то же самое, что и скалярное произведение v сам с собой. Таким образом, длина любого вектора v, , записанного как (или иногда ), является квадратным корнем скалярного произведения. В простом случае единичного вектора Эти простые случаи помогают проверить эту интерпретацию скалярного произведения. Практическая задача: Вычислите длины следующих векторов. — 6 я + 4 j = -8 i + 7 j = (-8, 7) 
Определены два типа умножения с участием двух векторов: так называемое скалярное произведение (или «точечный продукт») и так называемое векторное произведение (или «перекрестное произведение»). Для простоты мы рассмотрим только скалярное произведение, но на этом этапе у вас должна быть достаточная математическая база, чтобы понимать и векторное произведение. 9Скалярное произведение 0009 (или скалярное произведение ) двух векторов определяется следующим образом в двух измерениях. Как всегда, это определение можно легко распространить на три измерения — просто следуйте шаблону. Обратите внимание, что операция всегда должна обозначаться точкой (•), чтобы отличить ее от векторного произведения, в котором используется символ умножения () — отсюда и названия скалярное произведение и перекрестное произведение . 
Мы можем проиллюстрировать это, рассмотрев простой случай: скалярное произведение произвольного вектора v и единичных векторов i и j. 933 
3
