4. Определение значений тригонометрических функций углов
Значения синуса и косинуса данного угла α на НЛ-10М определяются по шкалам 3 и 5, значения тангенса и котангенса — по шкалам 4 и 5.
Чтобы определить синус и косинус данного угла, необходимо 90° шкалы 3 или треугольный индекс шкалы 4 установить на деление 100 шкалы 5 и с помощью риски визирки отсчитать против значения данного угла α шкалы 3 по шкале 5 искомое значение синуса (в долях единицы). Значение косинуса угла α отсчитывается против угла 90° — α (рис. 4.3).
Для определения тангенса и котангенса угла треугольный индекс шкалы 4 необходимо установить на деление 100 шкалы 5 и против значения
заданного угла α шкалы 4 отсчитать на шкале 5 искомое значение тангенса, а против значений 90°—α отсчитать искомое значение котангенса (см. рис. 4.3).
Пример. Дан
угол α=40°. Определить синус, косинус,
тангенс и котангенс этого угла.
Дан
угол α=40°. Определить синус, косинус,
тангенс и котангенс этого угла.
Решение, sin 40°=0,64; cos 40°=0,77; tg 40°=0,84; ctg 40°= 1,19.
5. Умножение данного числа на тригонометрические функции углов
Умножение данного числа на синус и косинус угла на НЛ-10М производится по шкалам 3 и 5, а умножение на тангенс и котангенс угла — по шкалам 4 и 5. Для умножения числа на синус и косинус угла а необходимо 90° шкалы 3 или треугольный индекс шкалы 4 установить на заданное число и против угла α шкалы 3 отсчитать на шкале 5 искомое произведение числа на синус угла α, a против угла 90° — α — искомое произведение числа на косинус угла α (рис. 4.4).
Пример. Дан угол α = 42°; число С=250. Определить произведение числа 250 на синус и косинус 42°.
Решение. 250. sin 42°= 167; 260. cos 42° =186.
Для
умножения числа на тангенс и котангенс
угла α необходимо треугольный индекс
шкалы 4 установить
на заданное число и против угла а шкалы 4 отсчитать
на шкале 5 искомое произведение числа
на тангенс угла, α против угла 90°—α—искомое
произведение числа на котангенс угла
а.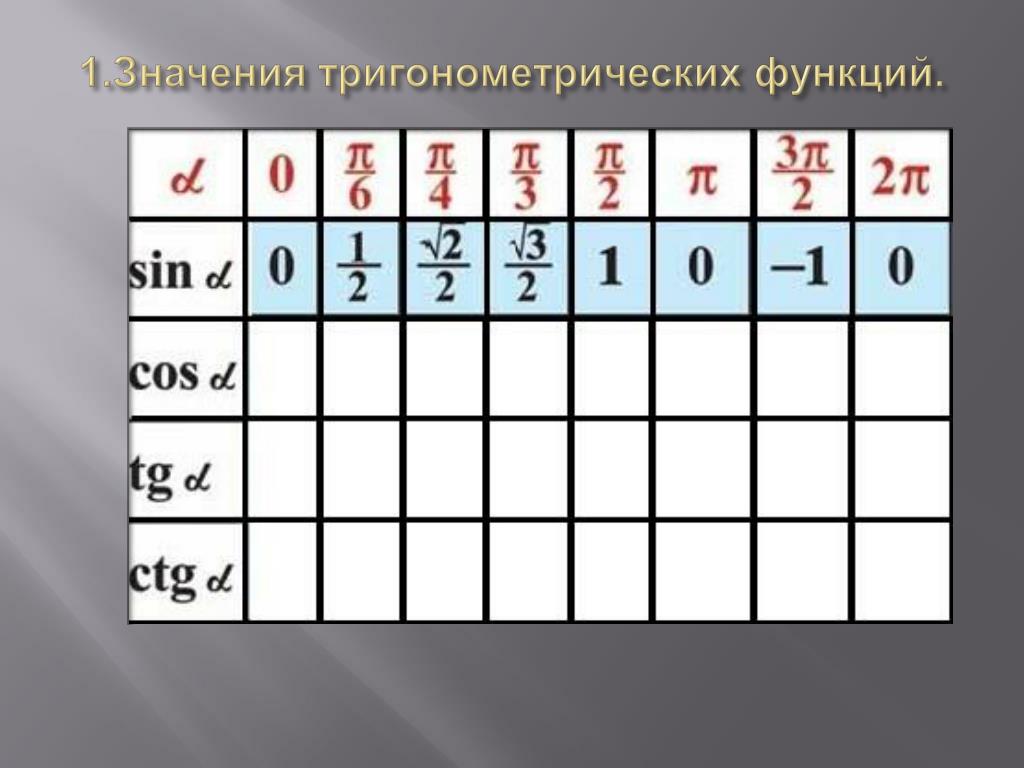
Пример. Дан угол α=42°; число С=250. Определить произведение числа 260 на тангенс и котангенс 42°.
Решение: 250-tg 42°=225; 250-ctg 42°=277.
6. Деление данного числа на тригонометрические функции углов
Деление данного числа на тригонометрические функции углов выполняется с помощью тех же шкал, что и умножение числа на тригонометрические функции углов.
Для деления заданного числа на синус или косинус угла на НЛ-10М необходимо установить риску визирки на заданное число по шкале 5, затем подвести против риски визирки значение заданного угла α шкалы 3 (при делении числа на синус угла) или угла 90° — α (при делении числа на косинус α)
Пример. Дан
угол α=50°; число равно 250. Определить
частное от деления 250 на синус и
косинус угла 50°.
Решение. 250 : sin 50°=326; 250 : cos 50° = 389.
Чтобы разделить число на тангенс угла α, на НЛ-10М необходимо деление угла α шкалы 4 совместить с делением заданного числа шкалы 5 и против треугольного индекса шкалы 4 отсчитать на шкале 5 искомое частное.
При делении числа на котангенс угла α против заданного числа подводят деление 90°—α.
Пример. Дан угол α=40°; число С=160. Определить частное от деления 160 на тангенс и котангенс 40°.
Решение. 160:tg40°=191; 160:ctg40°= 134.
Основные тригонометрические свойства. Тригонометрические функции
Тригонометрия — раздел математической науки, в котором изучаются тригонометрические функции и их использование в геометрии. Развитие тригонометрии началось еще во времена античной Греции. Во времена средневековья важный вклад в развитие этой науки внесли ученые Ближнего Востока и Индии.
Данная статья посвящена базовым понятиям и дефинициям тригонометрии. В ней рассмотрены определения основных тригонометрических функций: синуса, косинуса, тангенса и котангенса. Разъяснен и проиллюстрирован их смысл в контексте геометрии.
Yandex.RTB R-A-339285-1
Изначально определения тригонометрических функций, аргументом которых является угол, выражались через соотношения сторон прямоугольного треугольника.
Определения тригонометрических функций
Синус угла (sin α) — отношение противолежащего этому углу катета к гипотенузе.
Косинус угла (cos α) — отношение прилежащего катета к гипотенузе.
Тангенс угла (t g α) — отношение противолежащего катета к прилежащему.
Котангенс угла (c t g α) — отношение прилежащего катета к противолежащему.
Данные определения даны для острого угла прямоугольного треугольника!
Приведем иллюстрацию.
В треугольнике ABC с прямым углом С синус угла А равен отношению катета BC к гипотенузе AB.
Определения синуса, косинуса, тангенса и котангенса позволяют вычислять значения этих функций по известным длинам сторон треугольника.
Важно помнить!
Область значений синуса и косинуса: от -1 до 1. Иными словами синус и косинус принимают значения от -1 до 1. Область значений тангенса и котангенса — вся числовая прямая, то есть эти функции могут принимать любые значения.
Определения, данные выше, относятся к острым углам. В тригонометрии вводится понятие угла поворота, величина которого, в отличие от острого угла, не ограничена рамками от 0 до 90 градусов.Угол поворота в градусах или радианах выражается любым действительным числом от — ∞ до + ∞ .
В данном контексте можно дать определение синуса, косинуса, тангенса и котангенса угла произвольной величины. Представим единичную окружность с центром в начале декартовой системы координат.
Начальная точка A с координатами (1 , 0) поворачивается вокруг центра единичной окружности на некоторый угол α и переходит в точку A 1 . Определение дается через координаты точки A 1 (x , y).
Синус (sin) угла поворота
Синус угла поворота α — это ордината точки A 1 (x , y).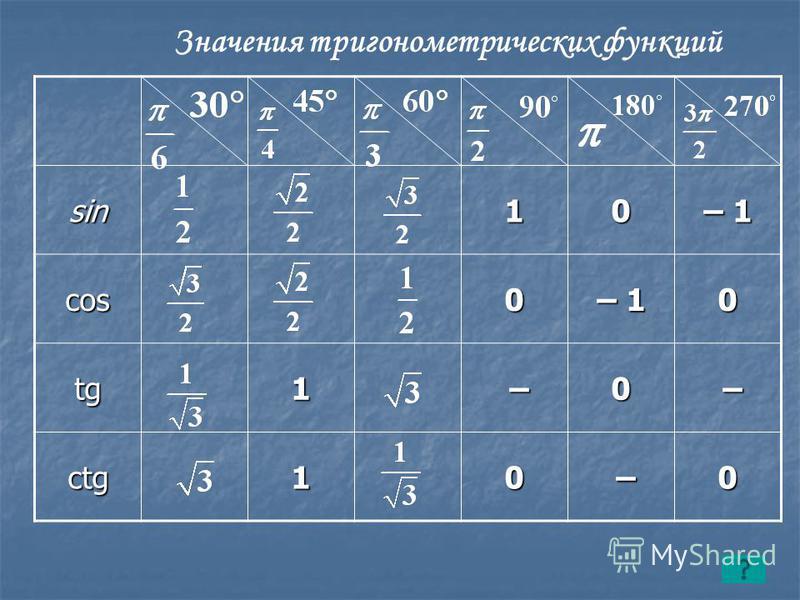 sin α = y
sin α = y
Косинус (cos) угла поворота
Косинус угла поворота α — это абсцисса точки A 1 (x , y). cos α = х
Тангенс (tg) угла поворота
Тангенс угла поворота α — это отношение ординаты точки A 1 (x , y) к ее абсциссе. t g α = y x
Котангенс (ctg) угла поворота
Котангенс угла поворота α — это отношение абсциссы точки A 1 (x , y) к ее ординате. c t g α = x y
Синус и косинус определены для любого угла поворота. Это логично, ведь абсциссу и ординату точки после поворота можно определить при любом угле. Иначе обстоит дело с тангенсом и котангенсом. Тангенс не определен, когда точка после поворота переходит в точку с нулевой абсциссой (0 , 1) и (0 , — 1). В таких случаях выражение для тангенса t g α = y x просто не имеет смысла, так как в нем присутствует деление на ноль. Аналогично ситуация с котангенсом. Отличием состоит в том, что котангенс не определен в тех случаях, когда в ноль обращается ордината точки.
Важно помнить!
Синус и косинус определены для любых углов α .
Тангенс определен для всех углов, кроме α = 90 ° + 180 ° · k , k ∈ Z (α = π 2 + π · k , k ∈ Z)
Котангенс определен для всех углов, кроме α = 180 ° · k , k ∈ Z (α = π · k , k ∈ Z)
При решении практических примеров не говорят «синус угла поворота α «. Слова «угол поворота» просто опускают, подразумевая, что из контекста и так понятно, о чем идет речь.
Числа
Как быть с определением синуса, косинуса, тангенса и котангенса числа, а не угла поворота?
Синус, косинус, тангенс, котангенс числа
Синусом, косинусом, тангенсом и котангенсом числа t называется число, которое соответственно равно синусу, косинусу, тангенсу и котангенсу в t радиан.
Например, синус числа 10 π равен синусу угла поворота величиной 10 π рад.
Существует и другой подход к определению синуса, косинуса, тангенса и котангенса числа. Рассмотрим его подробнее.
Любому действительному числу t ставится в соответствие точка на единичной окружности с центром в начале прямоугольной декартовой системы координат.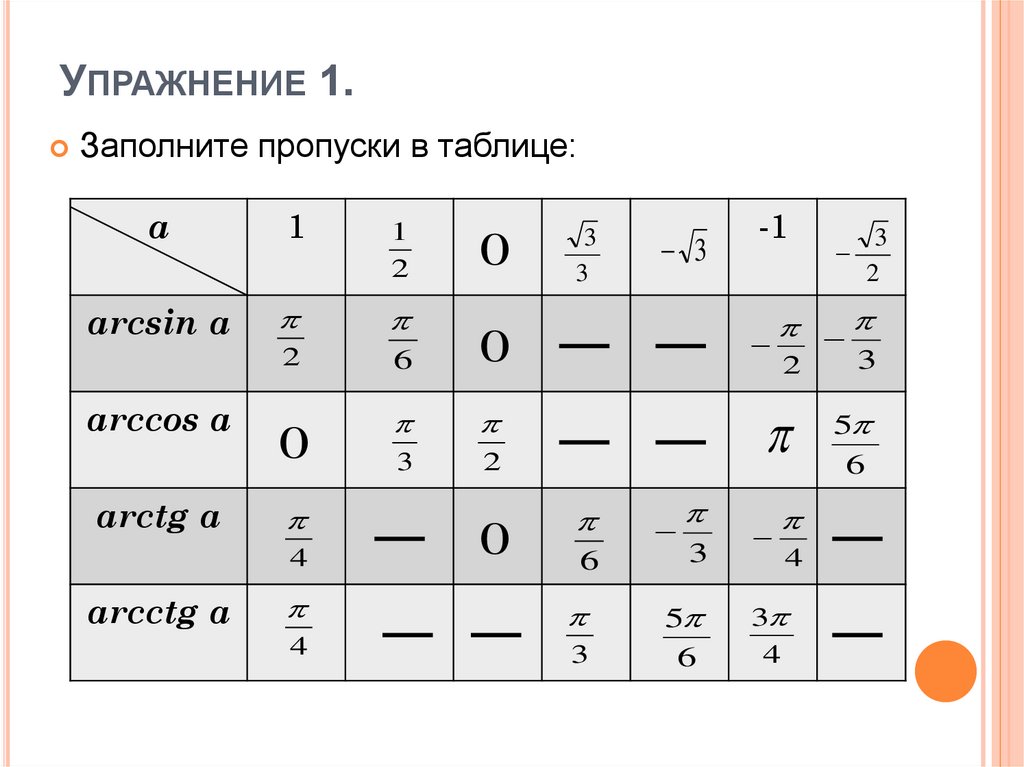
Начальная точка на окружности — точка A c координатами (1 , 0).
Положительному числу t
Отрицательному числу t соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t .
Теперь, когда связь числа и точки на окружности установлена, переходим к определению синуса, косинуса, тангенса и котангенса.
Синус (sin) числа t
Синус числа t — ордината точки единичной окружности, соответствующей числу t. sin t = y
Косинус (cos) числа t
Косинус числа t — абсцисса точки единичной окружности, соответствующей числу t. cos t = x
Тангенс (tg) числа t
Тангенс числа t — отношение ординаты к абсциссе точки единичной окружности, соответствующей числу t. t g t = y x = sin t cos t
Последние определения находятся в соответствии и не противоречат определению, данному в начале это пункта. Точка на окружности, соответствующая числу t , совпадает с точкой, в которую переходит начальная точка после поворота на угол t радиан.
Точка на окружности, соответствующая числу t , совпадает с точкой, в которую переходит начальная точка после поворота на угол t радиан.
Тригонометрические функции углового и числового аргумента
Каждому значению угла α соответствует определенное значение синуса и косинуса этого угла. Также, как всем углам α , отличным от α = 90 ° + 180 ° · k , k ∈ Z (α = π 2 + π · k , k ∈ Z) соответствует определенное значение тангенса. Котангенс, как сказано выше, определен для всех α , кроме α = 180 ° · k , k ∈ Z (α = π · k , k ∈ Z).
Можно сказать, что sin α , cos α , t g α , c t g α — это функции угла альфа, или функции углового аргумента.
Аналогично можно говорить о синусе, косинусе, тангенсе и котангенсе, как о функциях числового аргумента. Каждому действительному числу

Основные функции тригонометрии
Синус, косинус, тангенс и котангенс — основные тригонометрические функции.
Из контекста обычно понятно, с каким аргументом тригонометрической функции (угловой аргумент или числовой аргумент) мы имеем дело.
Вернемся к данным в самом начале определениям и углу альфа, лежащему в пределах от 0 до 90 градусов. Тригонометрические определения синуса, косинуса, тангенса и котангенса полностью согласуются с геометрическими определениями, данными с помощью соотношений сторон прямоугольного треугольника. Покажем это.
Возьмем единичную окружность с центром в прямоугольной декартовой системе координат. Повернем начальную точку A (1 , 0) на угол величиной до 90 градусов и проведем из полученной точки A 1 (x , y) перпендикуляр к оси абсцисс. В полученном прямоугольном треугольнике угол A 1 O H равен углу поворота α , длина катета O H равна абсциссе точки A 1 (x , y) . Длина катета, противолежащего углу, равна ординате точки A 1 (x , y) , а длина гипотенузы равна единице, так как она является радиусом единичной окружности.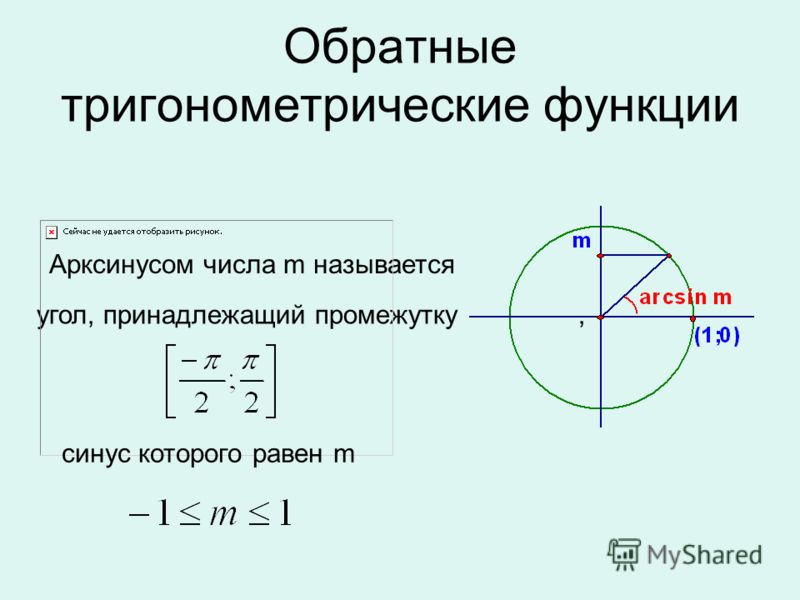
В соответствии с определением из геометрии, синус угла α равен отношению противолежащего катета к гипотенузе.
sin α = A 1 H O A 1 = y 1 = y
Значит, определение синуса острого угла в прямоугольном треугольнике через соотношение сторон эквивалентно определению синуса угла поворота α , при альфа лежащем в пределах от 0 до 90 градусов.
Аналогично соответствие определений можно показать для косинуса, тангенса и котангенса.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
С центром в точке A .
α — угол, выраженный в радианах.
Определение
Синус (sin α) — это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины противолежащего катета |BC| к длине гипотенузы |AC|.
Косинус (cos α) — это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины прилежащего катета |AB| к длине гипотенузы |AC|.
Принятые обозначения
;
;
.
;
;
.
График функции синус, y = sin x
График функции косинус, y = cos x
Свойства синуса и косинуса
Периодичность
Функции y = sin x и y = cos x периодичны с периодом 2 π .
Четность
Функция синус — нечетная. Функция косинус — четная.
Область определения и значений, экстремумы, возрастание, убывание
Функции синус и косинус непрерывны на своей области определения, то есть для всех x (см. доказательство непрерывности). Их основные свойства представлены в таблице (n — целое).
| y = sin x | y = cos x | |
| Область определения и непрерывность | — ∞ | — ∞ |
| Область значений | -1 ≤ y ≤ 1 | -1 ≤ y ≤ 1 |
| Возрастание | ||
| Убывание | ||
| Максимумы, y = 1 | ||
| Минимумы, y = -1 | ||
| Нули, y = 0 | ||
| Точки пересечения с осью ординат, x = 0 | y = 0 | y = 1 |
Основные формулы
Сумма квадратов синуса и косинуса
Формулы синуса и косинуса от суммы и разности
;
;
Формулы произведения синусов и косинусов
Формулы суммы и разности
Выражение синуса через косинус
;
;
;
.
Выражение косинуса через синус
;
;
;
.
Выражение через тангенс
; .
При ,
имеем:
;
.
При :
;
.
Таблица синусов и косинусов, тангенсов и котангенсов
В данной таблице представлены значения синусов и косинусов при некоторых значениях аргумента.
Выражения через комплексные переменные
;
Формула Эйлера
Выражения через гиперболические функции
;
;
Производные
; . Вывод формул > > >
Производные n-го порядка:
{ -∞
Секанс, косеканс
Обратные функции
Обратными функциями к синусу и косинусу являются арксинус и арккосинус , соответственно.
Арксинус, arcsin
Арккосинус, arccos
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Отношение противолежащего катета к гипотенузе называют синусом острого угла прямоугольного треугольника.
\sin \alpha = \frac{a}{c}
Косинус острого угла прямоугольного треугольника
Отношение близлежащего катета к гипотенузе называют косинусом острого угла прямоугольного треугольника.
\cos \alpha = \frac{b}{c}
Тангенс острого угла прямоугольного треугольника
Отношение противолежащего катета к близлежащему катету называют тангенсом острого угла прямоугольного треугольника.
tg \alpha = \frac{a}{b}
Котангенс острого угла прямоугольного треугольника
Отношение близлежащего катета к противолежащему катету называют котангенсом острого угла прямоугольного треугольника.
ctg \alpha = \frac{b}{a}
Синус произвольного угла
Ордината точки на единичной окружности , которой соответствует угол \alpha называют синусом произвольного угла поворота \alpha .
\sin \alpha=y
Косинус произвольного угла
Абсцисса точки на единичной окружности, которой соответствует угол \alpha
называют косинусом произвольного угла поворота \alpha
.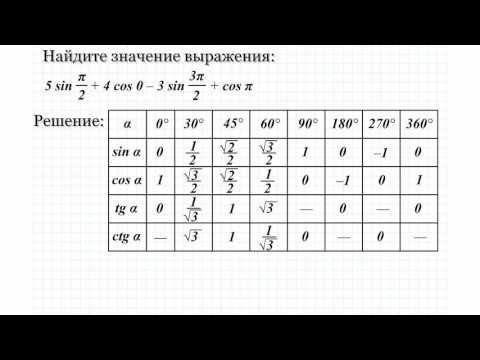
\cos \alpha=x
Тангенс произвольного угла
Отношение синуса произвольного угла поворота \alpha к его косинусу называют тангенсом произвольного угла поворота \alpha .
tg \alpha = y_{A}
tg \alpha = \frac{\sin \alpha}{\cos \alpha}
Котангенс произвольного угла
Отношение косинуса произвольного угла поворота \alpha к его синусу называют котангенсом произвольного угла поворота \alpha .
ctg \alpha =x_{A}
ctg \alpha = \frac{\cos \alpha}{\sin \alpha}
Пример нахождения произвольного угла
Если \alpha — некоторый угол AOM , где M — точка единичной окружности, то
\sin \alpha=y_{M} , \cos \alpha=x_{M} , tg \alpha=\frac{y_{M}}{x_{M}} , ctg \alpha=\frac{x_{M}}{y_{M}} .
Например, если \angle AOM = -\frac{\pi}{4} , то: ордината точки M равна -\frac{\sqrt{2}}{2} , абсцисса равна \frac{\sqrt{2}}{2} и потому
\sin \left (-\frac{\pi}{4} \right)=-\frac{\sqrt{2}}{2} ;
\cos \left (\frac{\pi}{4} \right)=\frac{\sqrt{2}}{2} ;
tg ;
ctg
\left (-\frac{\pi}{4} \right)=-1
.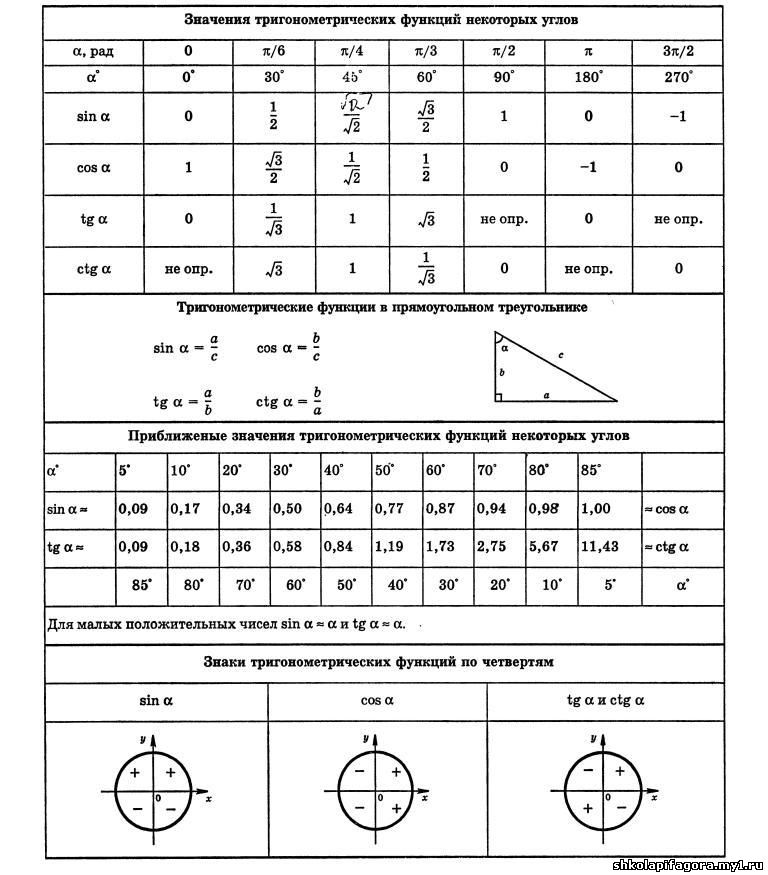 {\circ}\left(2\pi\right)
{\circ}\left(2\pi\right)
В этой статье будут рассмотрены три основных свойства тригонометрических функций: синуса, косинуса, тангенса и котангенса.
Первое свойство — знак функции в зависимости от того, какой четверти единичной окружности приналдежит угол α . Второе свойство — периодичность. Согласно этому свойству, тигонометрическая функция не меняет значения при изменении угла на целое число оборотов. Третье свойсто определяет, как меняются значения функций sin, cos, tg, ctg при противоположных углах α и — α .
Третье свойсто определяет, как меняются значения функций sin, cos, tg, ctg при противоположных углах α и — α .
Yandex.RTB R-A-339285-1
Часто в математическом тексте или в контексте задачи можно встретить фразу: «угол первой, второй, третьей или четвертой координатной четверти». Что это такое?
Обратимся к единичной окружности. Она разделена на четыре четверти. Отметим на окружности начальную точку A 0 (1 , 0) и, поворачивая ее вокруг точки O на угол α , попадем в точку A 1 (x , y) . В зависимости от того, в какой четверти будет лежать точка A 1 (x , y) , угол α будет называться углом первой, второй, третьей и четвертой четвети соответственно.
Для наглядности приведем иллюстрацию.
Угол α = 30 ° лежит в первой четверти. Угол — 210 ° является углом второй четверти. Угол 585 ° — угол третьей четверти. Угол — 45 ° — это угол четвертой четверти.
При этом углы ± 90 ° , ± 180 ° , ± 270 ° , ± 360 ° не принадлежат ни одной четверти, так как лежат на координатных осях.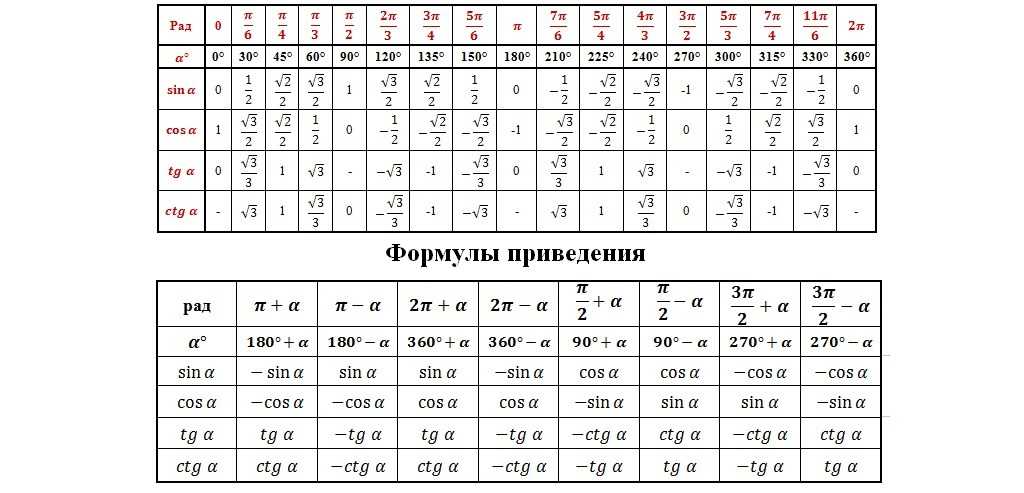
Теперь рассмотрим знаки, которые принимают синус, косинус, тангенс и котангенс в зависимости от того, в какой четверти лежит угол.
Чтобы определить знаки синуса по четвертям, вспомним опредение. Синус — это ордината точки A 1 (x , y) . Из рисунка видно, что в первой и второй четвертях она положительна, а в третьей и четверной — отрицательна.
Косинус — это абсцисса точки A 1 (x , y) . В соответсии с этим, определяем знаки косинуса на окружности. Косинус положителен в первой и четвертой четвертях, а отрицателен во второй и третьей четверти.
Для определения знаков тангенса и котангенса по четвертям также вспоминаем определения этих тригонометрических функций. Тангенс — отношение ординаты точки к абсциссе. Значит, по правилу деления чисел с разными знаками, когда ордината и абсцисса имеют одинаковые знаки, знак тангенса на окружности будет положительным, а когда ордината и абсцисса имеют разные знаки — отрицательным. Аналогично определяются знаки котангенса по четвертям.
Важно помнить!
- Синус угла α имеет знак плюс в 1 и 2 четвертях, знак минус — в 3 и 4 четвертях.
- Косинус угла α имеет знак плюс в 1 и 4 четвертях, знак минус — в 2 и 3 четвертях.
- Тангенс угла α имеет знак плюс в 1 и 3 четвертях, знак минус — в 2 и 4 четвертях.
- Котангенс угла α имеет знак плюс в 1 и 3 четвертях, знак минус — в 2 и 4 четвертях.
Свойство периодичности
Свойство периодичности — одно из самых очевидных свойств тригонометрических функций.
Свойство периодичности
При изменении угла на целое число полных оборотов значения синуса, косинуса, тангенса и котангенса данного угла остаются неизменными.
Действительно, при изменении угла на целое число оборотов мы всегда будем попадать из начальной точки A на единичной окружности в точку A 1 с одними и теми же координатами. Соответственно, не будут меняться и значения синуса, косинуса, тангенса и котангенса.
Математически данное свойство записывается так:
sin α + 2 π · z = sin α cos α + 2 π · z = cos α t g α + 2 π · z = t g α c t g α + 2 π · z = c t g α
Какое применение на практике находит это свойство? Свойство периодичности, как и формулы приведения, часто используется для вычисления значений синусов, косинусов, тангенсов и котангенсов больших углов.
Приведем примеры.
sin 13 π 5 = sin 3 π 5 + 2 π = sin 3 π 5
t g (- 689 °) = t g (31 ° + 360 ° · (- 2)) = t g 31 ° t g (- 689 °) = t g (- 329 ° + 360 ° · (- 1)) = t g (- 329 °)
Вновь обратимся к единичной окружности.
Точка A 1 (x , y) — результат поворота начальной точки A 0 (1 , 0) вокруг центра окружности на угол α . Точка A 2 (x , — y) — результат поворота начальной точки на угол — α .
Точки A 1 и A 2 симметричны относительно оси абсцисс. В случае, когда α = 0 ° , ± 180 ° , ± 360 ° точки A 1 и A 2 совпадают. Пусть одна точка имеет координаты (x , y) , а вторая — (x , — y) . Вспомним определения синуса, косинуса, тангенса, котангенса и запишем:
sin α = y , cos α = x , t g α = y x , c t g α = x y sin — α = — y , cos — α = x , t g — α = — y x , c t g — α = x — y
Отсюда следует свойство синусов, косинусов, тангенсов и котангенсов противоположных углов.
Свойство синусов, косинусов, тангенсов и котангенсов противоположных углов
sin — α = — sin α cos — α = cos α t g — α = — t g α c t g — α = — c t g α
Согласно этому свойству, справедливы равенства
sin — 48 ° = — sin 48 ° , c t g π 9 = — c t g — π 9 , cos 18 ° = cos — 18 °
Рассмотренное свойство часто используется при решении практических задач в случаях, когда нужно избавиться от отрицательных знаков углов в агрументах тригонометрических функций.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
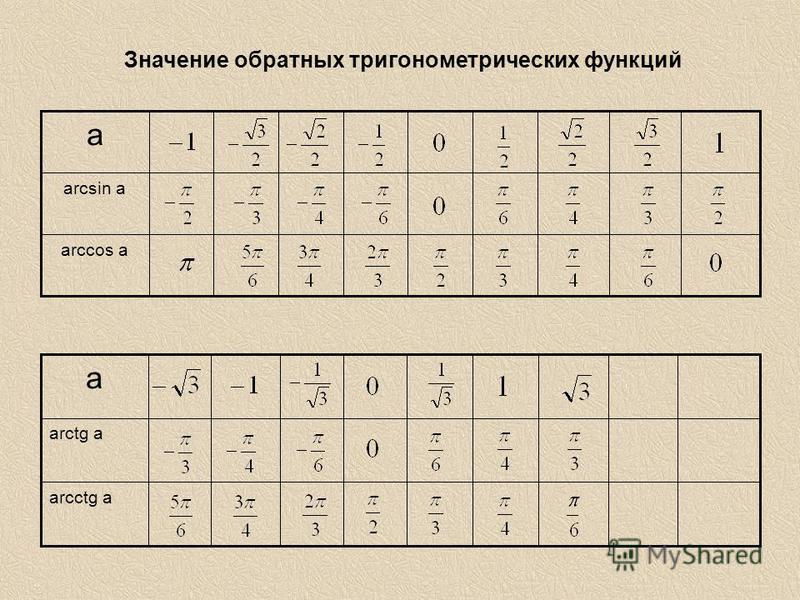
В этой статье собраны таблицы синусов, косинусов, тангенсов и котангенсов . Сначала мы приведем таблицу основных значений тригонометрических функций, то есть, таблицу синусов, косинусов, тангенсов и котангенсов углов 0, 30, 45, 60, 90, …, 360 градусов (0, π/6, π/4, π/3, π/2, …, 2π радиан). После этого мы дадим таблицу синусов и косинусов, а также таблицу тангенсов и котангенсов В. М. Брадиса, и покажем, как использовать эти таблицы при нахождении значений тригонометрических функций.
Навигация по странице.
Таблица синусов, косинусов, тангенсов и котангенсов для углов 0, 30, 45, 60, 90, … градусов
Список литературы.
- Алгебра: Учеб. для 9 кл. сред. шк./Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под ред. С. А. Теляковского.- М.: Просвещение, 1990.- 272 с.: ил.- ISBN 5-09-002727-7
- Башмаков М. И. Алгебра и начала анализа: Учеб.
 для 10-11 кл. сред. шк. — 3-е изд. — М.: Просвещение, 1993. — 351 с.: ил. — ISBN 5-09-004617-4.
для 10-11 кл. сред. шк. — 3-е изд. — М.: Просвещение, 1993. — 351 с.: ил. — ISBN 5-09-004617-4. - Алгебра и начала анализа: Учеб. для 10-11 кл. общеобразоват. учреждений / А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын и др.; Под ред. А. Н. Колмогорова.- 14-е изд.- М.: Просвещение, 2004.- 384 с.: ил.- ISBN 5-09-013651-3.
- Гусев В. А., Мордкович А. Г. Математика (пособие для поступающих в техникумы): Учеб. пособие.- М.; Высш. шк., 1984.-351 с., ил.
- Брадис В. М. Четырехзначные математические таблицы: Для общеобразоват. учеб. заведений. — 2-е изд. — М.: Дрофа, 1999.- 96 с.: ил. ISBN 5-7107-2667-2
Тригонометрическая таблица — определение, как создать, примеры и часто задаваемые вопросы °. Тригонометрическая таблица содержит все шесть тригонометрических соотношений: синус, косинус, тангенс, косеканс, секанс, котангенс. Тригонометрические функции, также известные как гониометрические функции, угловые функции или круговые функции, — это функции, которые устанавливают связь между углом и отношением двух сторон прямоугольного треугольника.
 Тригонометрические функции полезны для изучения различных типов углов, треугольников и других объектов.
Тригонометрические функции полезны для изучения различных типов углов, треугольников и других объектов.Определение тригонометрической таблицы
Табличное представление значений всех шести тригонометрических функций для их общих углов называется тригонометрической таблицей. Значение различных тригонометрических отношений можно узнать с помощью приведенной ниже таблицы:
Тригонометрические функции
Тригонометрия имеет 6 основных тригонометрических функций: синус, косинус, тангенс, косеканс, секанс и котангенс. Теперь давайте рассмотрим тригонометрические функции. Для любого прямоугольного треугольника с перпендикуляром (P), основанием (B) и гипотенузой (H) шесть тригонометрических функций следующие:0003
Советы по изучению тригонометрических соотношенийСинус: Определяется как отношение перпендикуляра к гипотенузе и представляется как sin θ
Косинус: Определяется как отношение основания к гипотенузе и представляется как cos θ
Тангенс: Определяется как отношение синуса и косинуса угла.
Таким образом, определение тангенса представляет собой отношение перпендикуляра к основанию и представляется как tan θ
Косеканс: Это величина, обратная sin θ, и представляется как cosec θ.
Секанс: Это величина, обратная cos θ, обозначается как sec θ.
Котангенс: Это величина, обратная тангенсу θ, и представляется как cot θ.
Изучите приведенную ниже таблицу, чтобы легко запомнить тригонометрические соотношения.
| Некоторые люди носят вьющиеся черные волосы, чтобы создать красоту0056 |
|---|
| cos θ (кудрявый) = основание (черный) / гипотенуза (волосы) |
| загар θ (к) = перпендикуляр (производство) / основание (красота) |
Как создать тригонометрическую таблицу?
Изучите следующие шаги, чтобы создать тригонометрическую таблицу стандартных углов.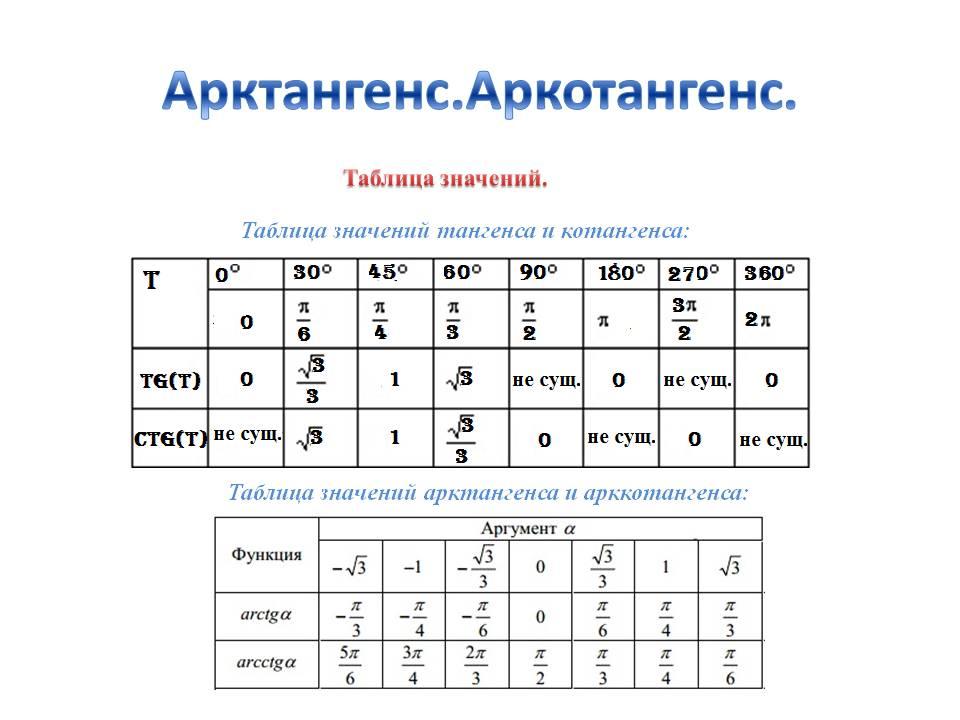
Шаг 1: Создайте таблицу
Создайте таблицу и перечислите все углы, такие как 0°, 30°, 45°, 60° и 90°, в верхней строке. Введите все тригонометрические функции sin, cos, tan, cosec, sec и cot в первый столбец.
Шаг 2: Оцените значение для всех углов функции sin.
Для нахождения значений функции sin разделите 0, 1, 2, 3 и 4 на 4 и возьмите под корень каждого значения соответственно как
Для значения sin 0° = √( 0/4) = 0
Аналогично,
sin 30° = √(1/4) = 1/2
sin 45° = √(2/4) = 1/√2
sin 60° = √(3/ 4) = √3/2
sin 90° = √(4/4) = 1
| sin 0° | sin 30° | SIN 45 ° | SIN 60 ° | SIN 90 ° | ||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1/2 | 1/√2 | √3/2 | 1/a Оценить значение для всех углов функции cos Значение функции cos противоположно значению функции sin, т.
Шаг 4: Оценка значения для всех углов функции тангенса Значение функции тангенса равно функции sin, деленной на функцию cos, т. е. tan x = sin x / cos x . Значение всех углов в функции тангенса рассчитывается как tan 0 ° = sin 0 ° / cos 0 ° = 0/1 = 0, аналогично
Шаг 5: Оценить значение для всех углов от функции COSEC 9000 3 9000 3 9000 3 функция равна обратной функции sin. Значение cosec 0° получается путем взятия обратной величины sin 0° Значение cosec 0° получается путем взятия обратной величины sin 0°cosec 0° = 1 / sin 0° = 1 / 0 = не определено. Similarly,
Шаг 6: Оцените значение для всех углов функции sec Значение функции sec равно обратному значению функции cos. Значение sec 0° получается путем взятия обратной величины cos 0° с 0 ° = 1 / cos 0 ° = 1 /1 = 1. Аналогично,
Шаг 7: Оценить значение для всех углов от Cot Fecund функция равна обратной функции тангенса. с 0 ° = 1 / cos 0 ° = 1 /1 = 1. Аналогично,
Расположите все полученные значения тригонометрической таблицы в тригонометрическую таблицу. Тригонометрические тождества (дополнительные и дополнительные углы)
Также проверка 9212 Решенные примеры по тригонометрии Пример 1: Если sin θ = 4/5, то найти все тригонометрические значения. Решение:
Пример 2: Найдите значение COS 45 ° + 2 sin 60° – тангенс 60°. Решение:
Пример 3. Найдите значение cos 75°. Решение:
Часто задаваемые вопросы по тригонометрии ТаблицаВопрос 1: Что такое тригонометрия? Ответ:
Вопрос 2. Что такое тригонометрическая таблица? Ответ:
Вопрос 3: Что такое стандартные углы в тригонометрической таблице? Ответ:
Вопрос 4: Каково значение тангенса 45 градусов? Ответ:
тригонометрия: | InfopleaseОсновные тригонометрические функцииТригомометрия возникла как изучение определенных математических соотношений, первоначально определенных в терминах углов и сторон прямоугольного треугольника, т. е. треугольника, содержащего прямой угол ( ).0°). Определены шесть основных соотношений, или тригонометрических функций. ;;;;;;слева;стопка;2745n;;; ;t35;нет;1;t35;63360n ;;заблокировать;;;;нет;1;139392n;201963n;;;;;63360n;;left;stack;2745n;;;Хотя действительные длины сторон прямоугольного треугольника могут иметь любые значения, отношения длин будут одинаковыми для всех подобных прямоугольных треугольников, большой или маленький; эти отношения зависят только от углов, а не от фактических длин. Функции встречаются парами — синус и косинус, тангенс и котангенс, секанс и косеканс — называемые кофункциями. В уравнениях они обычно представлены как sin, cos, tan, cot, sec и csc. Поскольку в обычной (евклидовой) планиметрии сумма углов треугольника равна 180°, сумма углов А и В должна составлять 90° и, следовательно, являются дополнительными углами. Из определений функций видно, что sin B=cos A, cos B=sin A, tan B=cot A и sec B=csc A; в общем случае функция угла равна кофункции его дополнения. Поскольку гипотенуза (с) всегда является наибольшей стороной прямоугольного треугольника, значения синуса и косинуса всегда находятся между нулем и единицей, значения секанса и косеканса всегда равны или больше единицы, а значения тангенса и котангенса не ограничены, неограниченно возрастая с нуля. ;t35;нет;1;t35;63360n ;;заблокировать;;;;нет;1;139392n;201963n;;;;;63360n;;left;stack;2745n;;;Хотя действительные длины сторон прямоугольного треугольника могут иметь любые значения, отношения длин будут одинаковыми для всех подобных прямоугольных треугольников, большой или маленький; эти отношения зависят только от углов, а не от фактических длин. Функции встречаются парами — синус и косинус, тангенс и котангенс, секанс и косеканс — называемые кофункциями. В уравнениях они обычно представлены как sin, cos, tan, cot, sec и csc. Поскольку в обычной (евклидовой) планиметрии сумма углов треугольника равна 180°, сумма углов А и В должна составлять 90° и, следовательно, являются дополнительными углами. Из определений функций видно, что sin B=cos A, cos B=sin A, tan B=cot A и sec B=csc A; в общем случае функция угла равна кофункции его дополнения. Поскольку гипотенуза (с) всегда является наибольшей стороной прямоугольного треугольника, значения синуса и косинуса всегда находятся между нулем и единицей, значения секанса и косеканса всегда равны или больше единицы, а значения тангенса и котангенса не ограничены, неограниченно возрастая с нуля. Для некоторых специальных прямоугольных треугольников значения функций могут быть легко вычислены; например, в прямоугольном треугольнике с острыми углами 30° и 60° стороны относятся как 1 :3 : 2, так что sin 30°=cos 60°=1/2, cos 30°=sin 60°=3 /2, tan 30°=cot 60°=1/3, cot 30°=tan 60°=3, sec 30°=csc 60°=2/3 и csc 30°=sec 60°=2. Для других углов значения тригонометрических функций обычно находятся из набора таблиц или научного калькулятора. Для предельных значений 0° и 90°, длина одной стороны треугольника стремится к нулю, в то время как другая приближается к длине гипотенузы, что приводит к значениям sin 0°=cos 90°=0, cos 0°=sin 90°=1, tan 0°= cot 90°=0, а sec 0°=csc 90°=1; поскольку деление на ноль не определено, cot 0°, tan 90°, csc 0° и sec 90° не определены и имеют бесконечно большие значения. Общий треугольник, не обязательно содержащий прямой угол, также можно проанализировать с помощью тригонометрия, и обнаруживаются различные соотношения между сторонами и углами общего треугольника. Для некоторых специальных прямоугольных треугольников значения функций могут быть легко вычислены; например, в прямоугольном треугольнике с острыми углами 30° и 60° стороны относятся как 1 :3 : 2, так что sin 30°=cos 60°=1/2, cos 30°=sin 60°=3 /2, tan 30°=cot 60°=1/3, cot 30°=tan 60°=3, sec 30°=csc 60°=2/3 и csc 30°=sec 60°=2. Для других углов значения тригонометрических функций обычно находятся из набора таблиц или научного калькулятора. Для предельных значений 0° и 90°, длина одной стороны треугольника стремится к нулю, в то время как другая приближается к длине гипотенузы, что приводит к значениям sin 0°=cos 90°=0, cos 0°=sin 90°=1, tan 0°= cot 90°=0, а sec 0°=csc 90°=1; поскольку деление на ноль не определено, cot 0°, tan 90°, csc 0° и sec 90° не определены и имеют бесконечно большие значения. Общий треугольник, не обязательно содержащий прямой угол, также можно проанализировать с помощью тригонометрия, и обнаруживаются различные соотношения между сторонами и углами общего треугольника.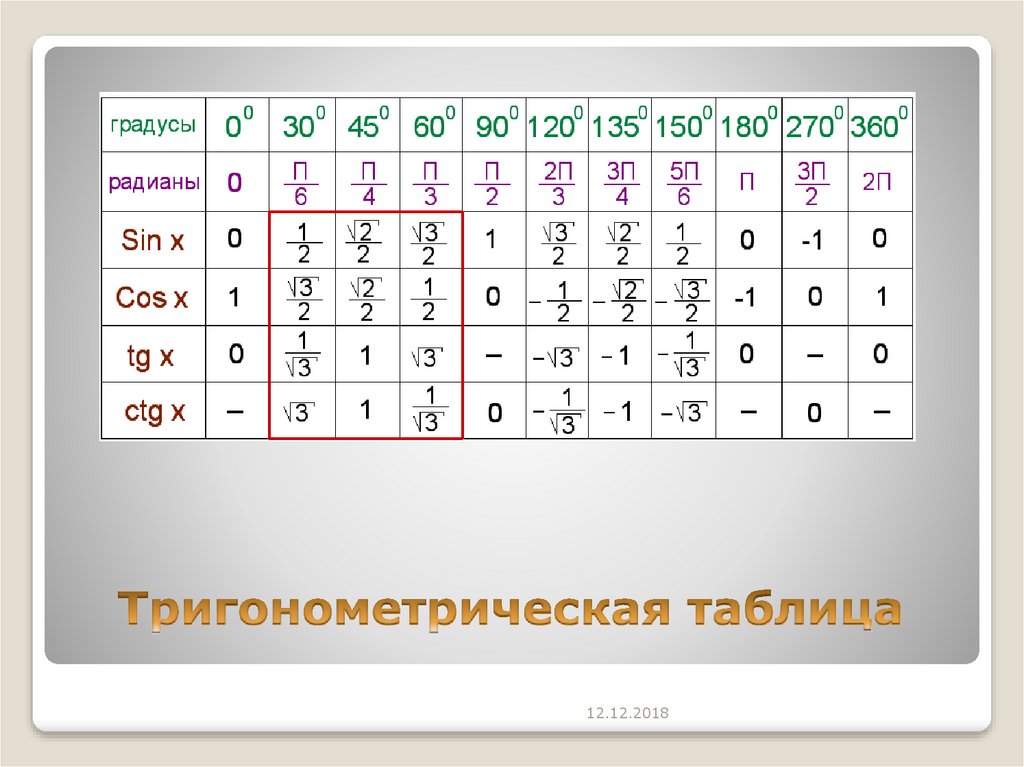 |

 для 10-11 кл. сред. шк. — 3-е изд. — М.: Просвещение, 1993. — 351 с.: ил. — ISBN 5-09-004617-4.
для 10-11 кл. сред. шк. — 3-е изд. — М.: Просвещение, 1993. — 351 с.: ил. — ISBN 5-09-004617-4. Таким образом, определение тангенса представляет собой отношение перпендикуляра к основанию и представляется как tan θ
Таким образом, определение тангенса представляет собой отношение перпендикуляра к основанию и представляется как tan θ е. cos 0° = sin 90°, cos 30° = sin 60° и cos 45° = sin 45°, поэтому
е. cos 0° = sin 90°, cos 30° = sin 60° и cos 45° = sin 45°, поэтому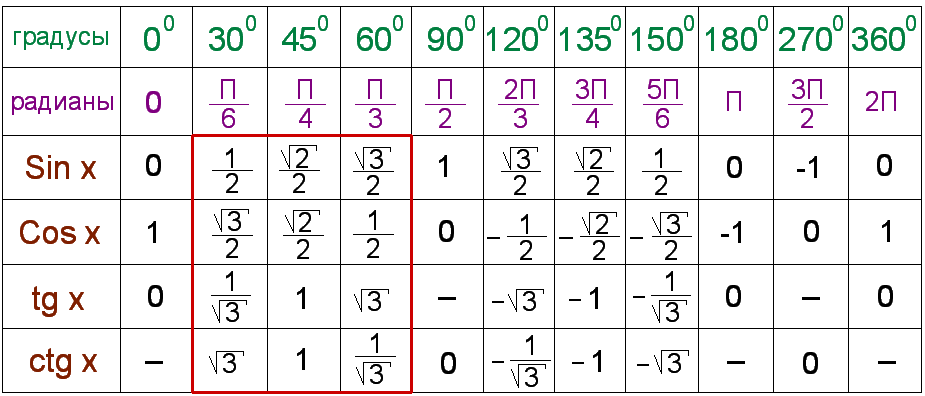 Значение cot 0° получается путем взятия обратной величины cos 0°
Значение cot 0° получается путем взятия обратной величины cos 0°