Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия
Углом называют часть плоскости, ограниченную двумя лучами, выходящими из одной точки. Лучи,ограничивающие угол, называют сторонами угла. Точку, из которой выходят лучи, называют вершиной угла.
Схему обозначения углов рассмотрим на примере угла, изображенного на рисунке 1.
Рис.1
Изображенный на рисунке 1 угол можно обозначить тремя способами:
Углы называют равными углами, если их можно совместить.
Если при пересечении двух прямых образуются четыре равных угла, то такие углы называют прямыми углами (рис.2). Пересекающиеся прямые линии, образующие прямые углы, называют перпендикулярными прямыми.
Рис.2
Если через точку A, не лежащую на прямой l, проведена прямая, перпендикулярная к прямой l и пересекающая прямую l точке B, то говорят, что из точки B опущен перпендикупяр AB на прямую l (рис.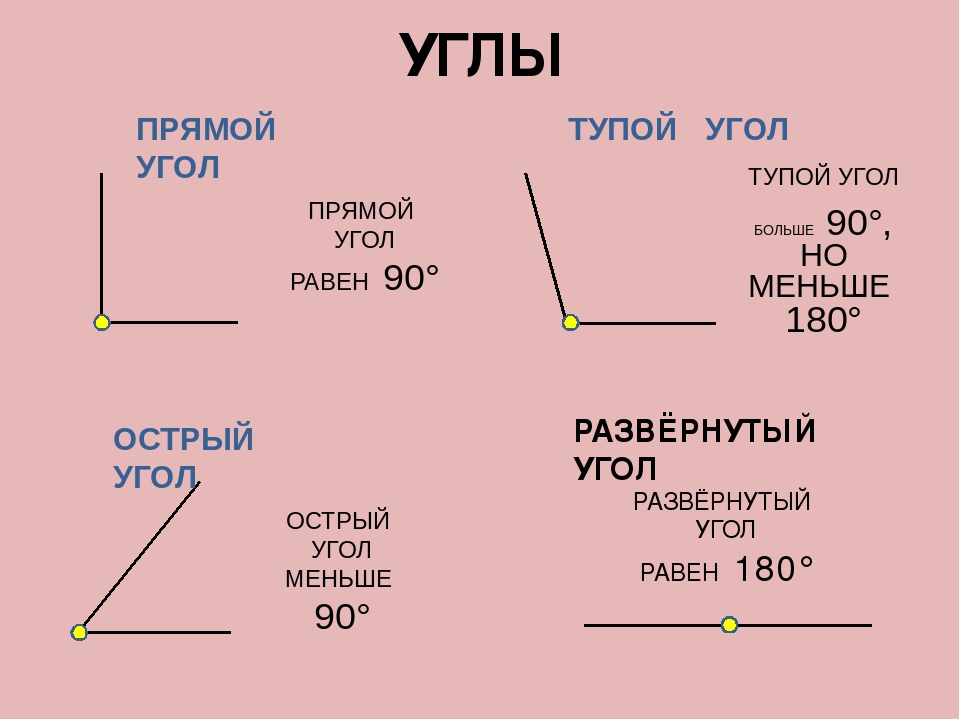 3). Точку B называют основанием перпендикуляра AB.
3). Точку B называют основанием перпендикуляра AB.
Рис.3
Замечание. Длину отрезка AB называют расстоянием от точки A до прямой l.
Углом в 1° (один градус) называют угол, составляющий одну девяностую часть прямого угла.
Угол, в k раз больший угла в 1°, называют углом в k° ( k градусов).
Углы измеряют также и в радианах. О радианах можно прочитать в разделе нашего справочника «Измерение углов. Градусы и радианы».
Таблица 1 – Типы углов в зависимости от величины в градусах
| Прямой угол |
Свойство: Прямой угол равен 90° |
| Острый угол |
Свойство: Острый угол меньше 90° |
| Тупой угол |
Свойство: Тупой угол больше 90°, но меньше 180° |
| Развернутый угол |
Свойство: Развернутый угол равен 180° |
| Угол больший, чем развернутый |
Свойство: Такой угол больше 180°, но меньше 360° |
| Полный угол |
Свойство: Полный угол равен 360° |
| Угол, равный нулю |
Свойство: Такой угол равен 0° |
Таблица 2 – Типы углов в зависимости расположения сторон
| Вертикальные углы |
Свойство вертикальных углов: Вертикальные углы равны |
| Смежные углы |
Свойство смежных углов: Сумма смежных углов равна 180° |
| Углы с соответственно параллельными сторонами |
Свойство углов с соответственно параллельными сторонами: Углы с соответственно параллельными сторонами равны, если оба являются острыми или оба являются тупыми |
Свойство углов с соответственно параллельными сторонами: Сумма углов с соответственно параллельными сторонами равна 180°, если один из них острый, а другой тупой |
| Углы с соответственно перпендикулярными сторонами |
Свойство углов с соответственно перпендикулярными сторонами: Углы с соответственно перпендикулярными сторонами равны, если оба являются острыми или оба являются тупыми |
Свойство углов с соответственно перпендикулярными сторонами: Сумма углов с соответственно перпендикулярными сторонами равна 180°, если один из них острый, а другой тупой |
Определение. Биссектрисой угла называют луч, делящий угол пополам.
Биссектрисой угла называют луч, делящий угол пополам.
Задача. Доказать, что биссектрисы смежных углов перпендикулярны.
Решение. Рассмотрим рисунок 4.
Рис.4
На этом рисунке углы AOB и BOC – смежные, а лучи OE и OD – биссектрисы этих углов. Поскольку
2α + 2β = 180°.
то
α + β = 90°,
что и требовалось доказать.
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Как определить тупой острый и прямой угол. Виды углов. Как разметить острый угол
Каждый угол, в зависимости от его величины, имеет своё название:
Два угла называются смежными , если у них одна сторона общая, а две другие стороны составляют прямую линию:
Углы MOP и PON смежные, так как луч OP — общая сторона, а две другие стороны — OM и ON составляют прямую.
Общая сторона смежных углов называется наклонной к прямой , на которой лежат две другие стороны, только в том случае, когда смежные углы не равны между собой. Если смежные углы равны, то их общая сторона будет перпендикуляром .
Сумма смежных углов равна 180°.
Два угла называются вертикальными , если стороны одного угла дополняют до прямых линий стороны другого угла:
Углы 1 и 3, а также углы 2 и 4 — вертикальные.
Вертикальные углы равны.
Докажем, что вертикальные углы равны:
Сумма ∠1 и ∠2 составляет развёрнутый угол. И сумма ∠3 и ∠2 составляет развёрнутый угол. Значит, эти две суммы равны:
∠1 + ∠2 = ∠3 + ∠2.
В этом равенстве слева и справа есть по одинаковому слагаемому — ∠2. Равенство не нарушится, если это слагаемое в левой и в правой части опустить. Тогда мы получаем.
Посмотрите на картинку. (Рис. 1)
Рис. 1. Иллюстрация к примеру
Из каких знакомых вам геометрических фигур она состоит?
Конечно, вы увидели, что картинка состоит из треугольников и прямоугольников. Какое слово спряталось в названии обеих этих фигур? Это слово — угол (рис. 2).
Какое слово спряталось в названии обеих этих фигур? Это слово — угол (рис. 2).
Рис. 2. Определение угла
Сегодня мы будем учиться чертить прямой угол.
В названии этого угла уже есть слово «прямой». Чтобы правильно изобразить прямой угол, нам понадобится угольник. (Рис. 3)
Рис. 3. Угольник
В самом угольнике уже есть прямой угол. (Рис. 4)
Рис. 4. Прямой угол
Он и поможет нам изобразить эту геометрическую фигуру.
Чтобы правильно изобразить фигуру, мы должны приложить угольник к плоскости (1), обвести его стороны (2), назвать вершину угла (3) и лучи (4).
1.
2.
3.
4.
Давайте определим, есть ли среди имеющихся углов прямые (Рис. 5). В этом нам поможет угольник.
Рис. 5. Иллюстрация к примеру
Найдем прямой угол угольника и приложим его к имеющимся углам (рис. 6).
Рис. 6. Иллюстрация к примеру
Мы видим, что прямой угол совпал с углом ВОМ. Это значит, что угол ВОМ прямой. Проделаем эту же операцию еще раз. (Рис. 7)
Это значит, что угол ВОМ прямой. Проделаем эту же операцию еще раз. (Рис. 7)
Рис. 7. Иллюстрация к примеру
Мы видим, что прямой угол нашего угольника не совпал с углом СOD. Это значит, что угол COD не прямой. Еще раз приложим прямой угол угольника к углу АОТ. (Рис. 8)
Рис. 8. Иллюстрация к примеру
Мы видим, что угол АОТ гораздо больше, чем прямой угол. Это значит, что угол АОТ не является прямым.
На этом уроке мы учились строить прямой угол с помощью угольника.
Слово «угол» дало название многим вещам, а также геометрическим фигурам: прямоугольник, треугольник, угольнику, с помощью которого можно начертить прямой угол.
Треугольник — это геометрическая фигура, которая состоит из трех сторон и трех углов. Треугольник, у которого есть прямой угол, называется прямоугольным треугольником.
Посмотрите на картинку. (Рис. 1)
Рис. 1. Иллюстрация к примеру
Из каких знакомых вам геометрических фигур она состоит?
Конечно, вы увидели, что картинка состоит из треугольников и прямоугольников.
Рис. 2. Определение угла
Сегодня мы будем учиться чертить прямой угол.
В названии этого угла уже есть слово «прямой». Чтобы правильно изобразить прямой угол, нам понадобится угольник. (Рис. 3)
Рис. 3. Угольник
В самом угольнике уже есть прямой угол. (Рис. 4)
Рис. 4. Прямой угол
Он и поможет нам изобразить эту геометрическую фигуру.
Чтобы правильно изобразить фигуру, мы должны приложить угольник к плоскости (1), обвести его стороны (2), назвать вершину угла (3) и лучи (4).
1.
2.
3.
4.
Давайте определим, есть ли среди имеющихся углов прямые (Рис. 5). В этом нам поможет угольник.
Рис. 5. Иллюстрация к примеру
Найдем прямой угол угольника и приложим его к имеющимся углам (рис. 6).
Рис. 6. Иллюстрация к примеру
Мы видим, что прямой угол совпал с углом ВОМ.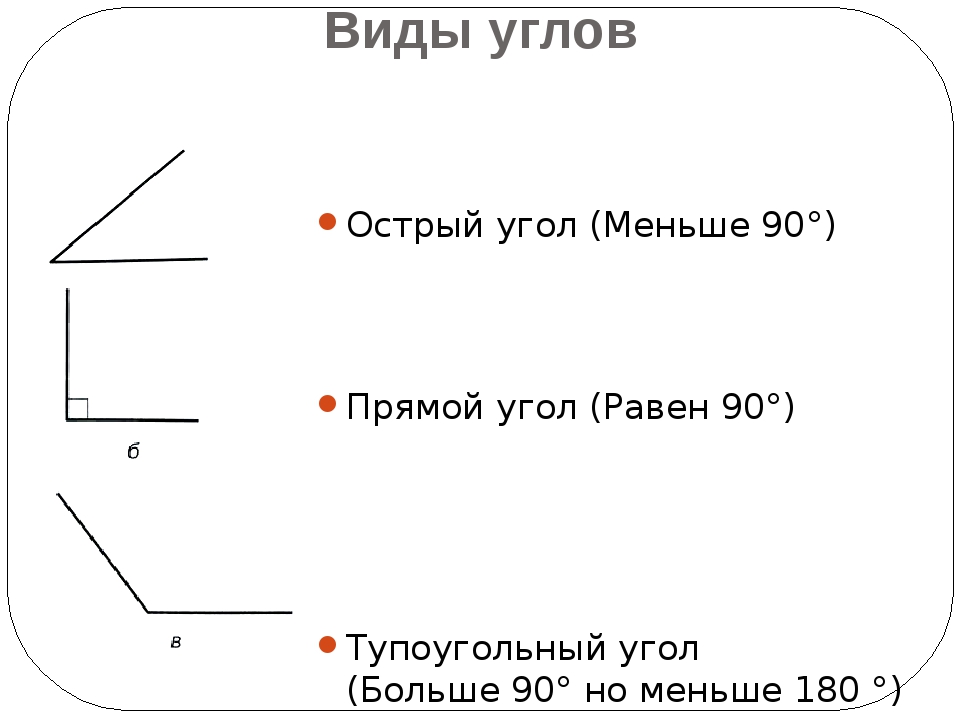 Это значит, что угол ВОМ прямой. Проделаем эту же операцию еще раз. (Рис. 7)
Это значит, что угол ВОМ прямой. Проделаем эту же операцию еще раз. (Рис. 7)
Рис. 7. Иллюстрация к примеру
Мы видим, что прямой угол нашего угольника не совпал с углом СOD. Это значит, что угол COD не прямой. Еще раз приложим прямой угол угольника к углу АОТ. (Рис. 8)
Рис. 8. Иллюстрация к примеру
Мы видим, что угол АОТ гораздо больше, чем прямой угол. Это значит, что угол АОТ не является прямым.
На этом уроке мы учились строить прямой угол с помощью угольника.
Слово «угол» дало название многим вещам, а также геометрическим фигурам: прямоугольник, треугольник, угольнику, с помощью которого можно начертить прямой угол.
Треугольник — это геометрическая фигура, которая состоит из трех сторон и трех углов. Треугольник, у которого есть прямой угол, называется прямоугольным треугольником.
Посмотрите на картинку. (Рис. 1)
Рис. 1. Иллюстрация к примеру
Из каких знакомых вам геометрических фигур она состоит?
Конечно, вы увидели, что картинка состоит из треугольников и прямоугольников. Какое слово спряталось в названии обеих этих фигур? Это слово — угол (рис. 2).
Какое слово спряталось в названии обеих этих фигур? Это слово — угол (рис. 2).
Рис. 2. Определение угла
Сегодня мы будем учиться чертить прямой угол.
В названии этого угла уже есть слово «прямой». Чтобы правильно изобразить прямой угол, нам понадобится угольник. (Рис. 3)
Рис. 3. Угольник
В самом угольнике уже есть прямой угол. (Рис. 4)
Рис. 4. Прямой угол
Он и поможет нам изобразить эту геометрическую фигуру.
Чтобы правильно изобразить фигуру, мы должны приложить угольник к плоскости (1), обвести его стороны (2), назвать вершину угла (3) и лучи (4).
1.
2.
3.
4.
Давайте определим, есть ли среди имеющихся углов прямые (Рис. 5). В этом нам поможет угольник.
Рис. 5. Иллюстрация к примеру
Найдем прямой угол угольника и приложим его к имеющимся углам (рис. 6).
Рис. 6. Иллюстрация к примеру
Мы видим, что прямой угол совпал с углом ВОМ. Это значит, что угол ВОМ прямой. Проделаем эту же операцию еще раз. (Рис. 7)
Это значит, что угол ВОМ прямой. Проделаем эту же операцию еще раз. (Рис. 7)
Рис. 7. Иллюстрация к примеру
Мы видим, что прямой угол нашего угольника не совпал с углом СOD. Это значит, что угол COD не прямой. Еще раз приложим прямой угол угольника к углу АОТ. (Рис. 8)
Рис. 8. Иллюстрация к примеру
Мы видим, что угол АОТ гораздо больше, чем прямой угол. Это значит, что угол АОТ не является прямым.
На этом уроке мы учились строить прямой угол с помощью угольника.
Слово «угол» дало название многим вещам, а также геометрическим фигурам: прямоугольник, треугольник, угольнику, с помощью которого можно начертить прямой угол.
Треугольник — это геометрическая фигура, которая состоит из трех сторон и трех углов. Треугольник, у которого есть прямой угол, называется прямоугольным треугольником.
ПРЯМОЙ, ая, ое; прям, пряма, прямо, прямШы и прямы. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
прямой угол — — Тематики нефтегазовая промышленность EN right angle …
прямой угол — угол, равный своему смежному. * * * ПРЯМОЙ УГОЛ ПРЯМОЙ УГОЛ, угол, равный своему смежному … Энциклопедический словарь
* * * ПРЯМОЙ УГОЛ ПРЯМОЙ УГОЛ, угол, равный своему смежному … Энциклопедический словарь
ПРЯМОЙ УГОЛ — угол, равный своему смежному; в градусном измерении равен 90° … Естествознание. Энциклопедический словарь
Прямой угол — см. Угол … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
ПРЯМОЙ УГОЛ — 1) угол, равный своему смежному. 2) Внесистемная ед. плоского угла. Обозначение L. 1 L = 90° = ПИ/2 рад 1,570 796 рад (см. Радиан) … Большой энциклопедический политехнический словарь
ПРЯМОЙ — прямая, прямое; прям, пряма, прямо. 1. Ровно вытянутый в каком–н. направлении, не кривой, без изгибов. Прямая линия. «Прямая дорога обрывалась и уж шла вниз.» Чехов. Прямой нос. Прямая фигура. 2. Беспересадочный (ж.–д. и разг.). Прямой маршрут.… … Толковый словарь Ушакова
ПРЯМОЙ — ПРЯМОЙ, ая, ое; прям, пряма, прямо, прямы и прямы. 1. Ровно идущий в каком н. направлении, без изгибов. Прямая линия (линия, образом к рой может служить бесконечная туго натянутая нить). Провести прямую (т. е. прямую линию; сущ.). Дорога идёт… … Толковый словарь Ожегова
Провести прямую (т. е. прямую линию; сущ.). Дорога идёт… … Толковый словарь Ожегова
угол основного профиля витка — (αb) Угол между основным профилем витка эвольвентного червяка и прямой, составляющей с осью червяка прямой угол скрещивания. Примечание Угол прямолинейного основного профиля витка эвольвентного червяка αb равен основному углу подъема… … Справочник технического переводчика
Книги
- Таблицы для численного решения граничных задач теории гармонических функций , Канторович Л. В., Крылов В. И., Чернин К. Е.. Граничные задачи для гармонических функций часто возникают при математическом анализе многих важных вопросов физики и техники (задачи расчета электрического и теплового поля, задачи… Купить за 610 руб
- Математика. 2 класс. Учебник. В 2-х частях. Часть 2 , Моро М.И.. Учебник «Математика» входит в образовательную систему» Школа России» . Материал учебника позволяет реализовать системно-деятельностный подход, организовать дифференцированное обучение и…
Сколько градусов в остром угле — Дом своими руками
Сколько градусов прямой, тупой и острый углы?
Сколько градусов прямой угол ?
Сколько градусов тупой угол?
Сколько градусов острый угол ?
Углом в геометрии называют точку, из которой выходят два луча.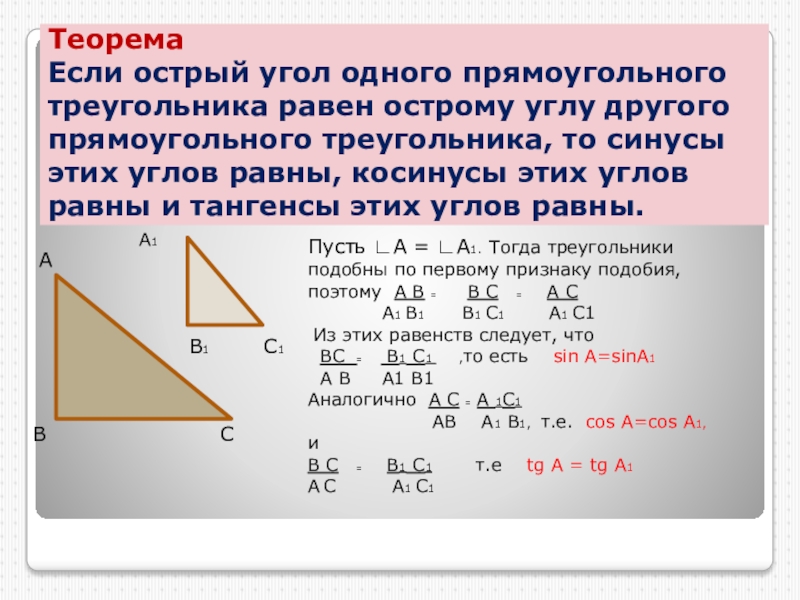
В зависимости от того, насколько отличаются направления лучей, определяются характеристики самого угла.
Мера углов меряется в градусах.
Если лучи угла расходятся один от одного под угол в 90 градусов — это прямой угол.
Если лучи угла расходятся один от одного под угол больше 90 градусов (от 90 до 180 градусов, потому как 180 градусов — это развернутый угол), то угол тупой.
Если лучи угла расходятся меньше чем угол 90 градусов (от 0 до 90 градусов) — угол острый.
Прямой угол собой представляет половину развернутого. А потому как величина развернутого угла в градусах равна 180-ти, то градусная мера прямого угла равна 90°.
Углы, меньшие 90°, называют острыми. Углы же, чья градусная мера превосходит все те же 90 градусов, однако при этом меньше 180°, называют тупыми.
Подобным образом, величина острого угла в градусах может принимать любое значение из диапазона (0; 90), ну а тупого — исходя из этого из диапазона (90; 180).
И только прямой угол из всех обозначенных в вопросе имеет вполне конкретную (не колеблющуюся ни в каких диапазонах) градусную меру — 90.
Какой угол именуется острым, прямым, тупым?
Какой угол в геометрии именуется острым, прямым, тупым? Сколько градусов в остом угле, тупом угле, прямом угле? Как определить острый угол, прямой угол, тупой угол?
Угол грамотный пересечением 2-ух поперечных прямых именуется прямым. Также прямой угол может появиться при делении окружности на ровные 4-ре части (1/4 окружности).
Прямой угол равён 90 градусам.
Когда стороны угла совпадают, подобный угол именуется нулевым
Нулевой угол равён 0 градусам.
Все углы, значения в градусах которых больше нулевого и меньше прямого именуется острыми.
Острый угол — больше 0 градусов и меньше 90 градусов.
Если стороны угла лежат в разных направлениях и создают прямую, подобный угол именуется развернутым и равён он 180 градусам.
Углы, значения в градусах которых больше прямого и меньше развернутого называются тупыми.
Тупой угол — больше 90 градусов и меньше 180 градусов.
Всех их соединяет одно:
острый, прямой и тупой углы — они все рельефные.
Все очень просто. Проведём аналогию с обыкновенными часами. Если одну из стрелок установить таким образом, чтобы она указывала на двенадцать часов, а другою, чтобы указывала на три — то они создают прямой угол в 90 градусов. Если же начать двигать стрелку указывающую на 3 часа в обратном направлении( в двухчасовой метки на циферблате) — то она будет образовывать, одновременно со второй стрелкой, острые углы(менее 90 градусов). Когда же стрелки будут указывать в одну точку — они создают нулевой угол в ноль градусов.А если вернуть вторую стрелку к исходной( трехчасовой отметке) и начать перемещать её вперед по циферблату — то аж до шестичасовой метки она одновременно с первой будут образовывать тупые углы( более 90 градусов). Когда стрелки будут указывать, одна на 12, а остальная на 6 — это будет, говоря иначе, развёрнутый угол в 180 градусов.
Острый угол сколько градусов
Добрый день!
Как понять острый угол сколько градусов равён? Как можно усвоить?
Благодарю!
Усвоить и разобраться очень легко.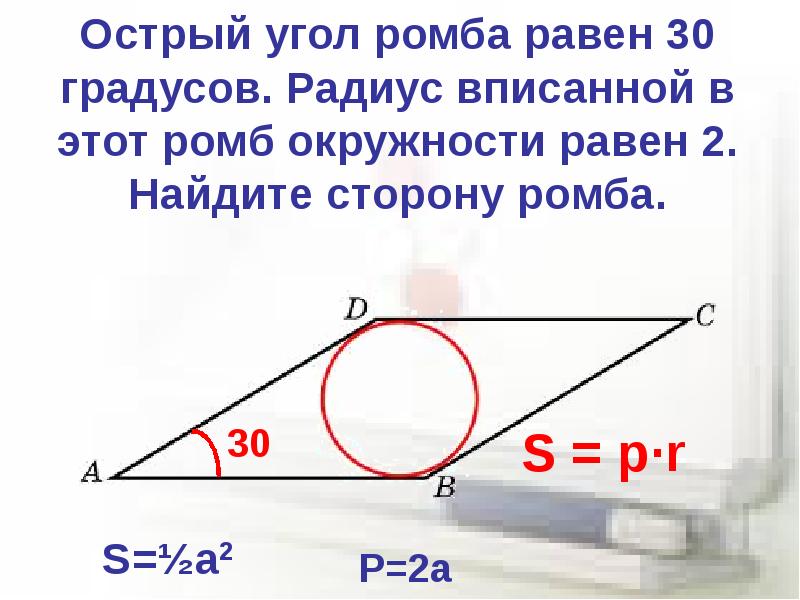 Начинаем учиться на циферблате обыкновенных часов.
Начинаем учиться на циферблате обыкновенных часов.
Установим одну стрелку так, что она будет указывать на 12- часов, а остальная будет указывать на 3 часа. В этом положении стрелки создают прямой угол, который равён девяносто град.
Начинаем сдвигать стрелку, которая указывает на 3 часа, против хода часовой стрелки, о есть к двенадцати часам через 2 часа и один час. В этом случае две стрелки будут образовывать острый угол, который окажется меньшей 90 град., но больше 0 град.
Если же стрелки объединить на одной цифре, к примеру, на двенадцати, то стрелки создают угол в ноль град., другими словами нулевой.
Если же первую стрелку оставить на 12-ти часах, а вторую опять уместить на 3 часа и начать двигать по ходу часовой стрелки, другими словами через определения четырех, пяти до 6-ти часов, то полученные углы будут тупыми (больше 90 и меньше 180 градусов).
Когда вторая стрелка будет стоять на 6-ти часах, то подобный угол будет равным 180 градусов, а его называют развернутым.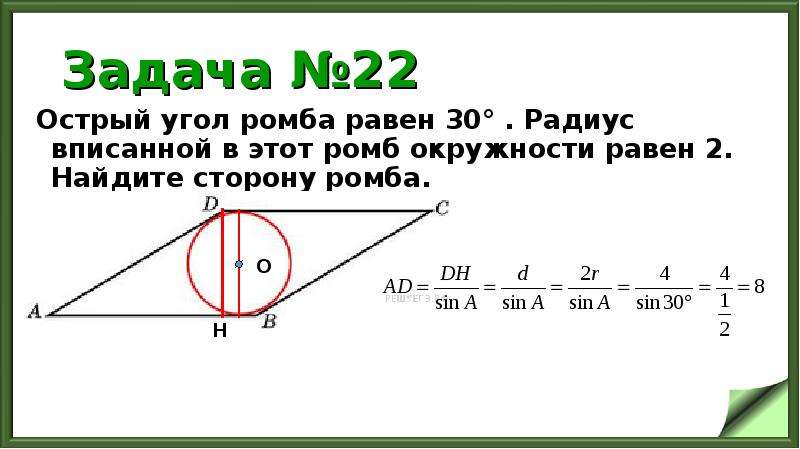
Полный оборот циферблата равён 360 градусам.
Надеюсь, этот подход поможет Вам хорошо разобраться и усвоить какой из углов каким должен быть и скольким градусам быть равным.
Острый, прямой и тупой углы
Навигация по записям
1. Острые углы прямоугольного треугольника равны и. Найдите угол между высотой и биссектрисой, проведенными из вершины прямого угла. Ответ дайте в градуса
Для подготовки к контрольной.ИГА
1. Острые углы прямоугольного треугольника равны и . Найдите угол между высотой и биссектрисой, проведенными из вершины прямого угла. Ответ дайте в градусах.
3. Найдите скалярное произведение векторов и .
4. Найдите синус угла наклона отрезка, соединяющего точки и , с осью абсцисс.
6. На клетчатой бумаге нарисовано два круга. Площадь внутреннего круга равна 4. Найдите площадь заштрихованной фигуры.
Площадь внутреннего круга равна 4. Найдите площадь заштрихованной фигуры.
11. В треугольнике ABC угол C равен 90°, CH — высота, , . Найдите AH.
13. В треугольнике , — высота, . Найдите .
17. Основания равнобедренной трапеции равны 14 и 26, а ее периметр равен 60. Найдите площадь трапеции.
18. Сторона ромба равна 20, острый угол равен . Найдите радиус вписанной окружности этого ромба.
20. В треугольнике , синус внешнего угла при вершине равен Найдите .
21. Найдите угол прямоугольного параллелепипеда, для которого =5, =4, =4. Дайте ответ в градусах.
24. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2. Площадь поверхности параллелепипеда равна 16. Найдите его диагональ.
26. В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в раза больше, чем у первого? Ответ выразите в сантиметрах.
В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в раза больше, чем у первого? Ответ выразите в сантиметрах.
30. В прямоугольном параллелепипеде известны длины рёбер: , , . Найдите площадь сечения, проходящего через вершины , и .
31. Длины всех ребер правильной четырёхугольной пирамиды PABCD с вершиной P равны между собой. Найдите угол между прямой BM и плоскостью BDP, если точка M — середина бокового ребра пирамиды AP.
35. В правильной треугольной пирамиде SABC с вершиной S? все рёбра которой равны 4, точка N — середина ребра AC, точка O центр основания пирамиды, точка P делит отрезок SO в отношении 3:1, считая от вершины пирамиды.
а) Докажите, что прямая NP перпендикулярна прямой BS.
б) Найдите расстояние от точки B до прямой NP.
36. В правильной четырёхугольной пирамиде SABCD с основанием ABCD точка M — середина ребра SA, точка K — середина ребра SC. Найдите угол между плоскостями BMK и ABC, если AB = 8, SC = 6.
39. Площадь основания правильной четырёхугольной пирамиды SABCD равна 64.
а) Постройте прямую пересечения плоскости SAC и плоскости, проходящей через вершину S этой пирамиды, середину стороны АВ и центр основания.
б) Найдите площадь боковой поверхности этой пирамиды, если площадь сечения пирамиды плоскостью SAC равна 64.
44. Две окружности касаются внешним образом в точке K. Прямая AB касается первой окружности в точке A, а второй — в точке B. Прямая BK пересекает первую окружность в точке D, прямая AK пересекает вторую окружность в точке C.
Прямая BK пересекает первую окружность в точке D, прямая AK пересекает вторую окружность в точке C.
а) Докажите, что прямые AD и BC параллельны.
б) Найдите площадь треугольника AKB, если известно, что радиусы окружностей равны 4 и 1.
46. В прямоугольном треугольнике ABC с прямым углом C известны стороны AC = 12, BC = 5. Окружность радиуса с центром O на стороне BC проходит через вершину C. Вторая окружность касается катета AC, гипотенузы треугольника, а также внешним образом касается первой окружности.
а) Докажите, что радиус второй окружности меньше, чем длины катета AC.
б) Найдите радиус второй окружности.
Достарыңызбен бөлісу:
§12. Виды углов. Измерение углов
ПОВТОРЯЕМ ТЕОРИЮ125. Заполните пропуски.
Заполните пропуски.
1) Угол, стороны которого образуют прямую, называют развернутым.
2) Единицу измерения углов называют градусом.
3) Измерить угол — значит подсчитать, сколько градусов входит в этот угол.
4) Величина развернутого угла составляет 180 градусов.
5) Углы измеряют с помощью прибора, который называют транспортиром.
6) Равные углы имеют равные градусные меры.
7) Из двух неравных углов большим считают тот, у которого градусная мера больше другого.
8) Если между сторонами угла АВС провести луч ВD, то градусная мера угла АВС равна сумме градусных мер углов ABD и DBC.
9) Острым называют угол, градусная мера которого меньше 90 градусов.
10) Прямым называют угол, градусная мера которого равна 90 градусам.
11) Тупым называют угол, градусная мера которого больше 90 градусов.
12) Биссектриса развернутого угла делит его на два прямых угла.
РЕШАЕМ ЗАДАЧИ
126. Начертите:
1) острый угол ACD;
2) прямой угол HTR;
3) тупой угол M;
4) развернутый угол KBO.
127. Известно, что . Заполните таблицу.
| Острые углы | А, Е |
| Тупые углы | В, D, N |
| Прямые углы | C, M |
| Развернутые углы | F |
128. Найдите, пользуясь транспортиром, градусные меры углов, изображенных на рисунке. Отпределите вид каждого угла.
129. 1) Отлоите от луча ВА угол АВС, величина которого равна 60 градусов.
2) Отложите от луча CD угол DCB, величина которого равна 140 градусов.
3) Отложите от луча ОК угол КОМ, величина которого равна 90 градусов.
4) Отложите от луча ST угол TSK, величина которого равна 26 градусов.
5) Отложите от луча QP угол PQR, величина которого равна 118 градусов.
6) Отложите от луча EF угол FEK, величина которого равна 180 градусов.
130. На данном рисунке угол EDK равен 43 градуса. Тогда угол CDE равен 180-43 = 137 градусов.
131. Начертите два угла с общей стороной так, чтобы они: 1) составляли развернутый угол; 2) не составляли развернутый угол.
132. Углы АВС и DBC составляют развернутый угол. Определите вид угла DBC, если угол АВС: 1) острый; 2) прямой; 3) тупой.
Ответ: 1) тупой; 2) прямой; 3) острый.
133. Из вершины прямого угла МОК проведены два луча ОР и ON так, что МON=64, РОК=57. Вычислити величину угла РON.
134. Развернутый угол АВС разделили лучами ВD, ВМ и ВК на четыре равных угла. Заполните пропуски.
1) Градусную меру 45 градусов имеют углы ABD, DBM, MBK, KBC.
2) Градусную меру 90 градусов имеют углы ABM, MBC, DBK.
3) Градусную меру 135 градусов имеют углы ABK, DBC.
135. Начертите угол COD, равный 163 градусам. Лучом OA разделите этот угол на два угла так, чтобы угол AOD был равен 88 градусам. Вычислите величину угла AOC.
Лучом OA разделите этот угол на два угла так, чтобы угол AOD был равен 88 градусам. Вычислите величину угла AOC.
136. Известно, что луч DE — биссектриса угла ADC, угол ADE=54 градусам. Тогда угол ADC = ? Пользуясь транспортиром, начертите угол ADC и проведите луч DE.
137. Нарисуйте на циферблате часов часовую и минутную стрелки так, чтобы часы показывали заданное время, и найдите градусную меру угла между стрелками часов.
1) 2 ч; 2) 6 ч; 3) 8 ч
138. Угол АВС равен 30 градусам. Проведите луч BD так, чтобы: 1) луч ABD был равен 90 градусам, а угол CBD — 120; 2) угол ABD был равен 90 градусам, а угол CBD — 60.
Тест «Углы». 5 класс.Вариант 1. | Тест «Углы». 5 класс.Вариант 2. |
№1. | №1 . Представлены градусные величины углов. Выберите острый угол. А) 90°. Б) 6°. В) 91°. Г) 158° |
№2 . Представлены градусные величины углов. Выберите острый угол. А) 90°. Б) 6°. В) 91°. Г) 158° | №2. Даны градусные меры четырёх углов. Какой из углов тупой? А) 90°. Б) 106°. В) 9°. Г) 58° |
№3. Представлены градусные величины углов. Выберите прямой угол. А) 180°. Б) 90°. В) 1°. Г) 45°. | №3. Укажите величину прямого угла. А) 180°. Б) 45°. В) 1°. Г) 90°. |
№4. Вычисли неизвестный угол по готовому рисунку. | №4. Вычисли неизвестный угол по готовому рисунку. |
№5. | №5. Угол, равный половине развернутого угла, называется: А) острый. Б) тупой. В) прямой. Г) Полуразвёрнутый. |
№6. Угол, стороны которого образуют прямую, называется: А) развернутый. Б) линейный. В) прямой. Г) нулевой. | №6. Угол, стороны которого образуют прямую, называется: А) нулевой. Б) линейный. В) прямой. Г) развернутый. |
№7. Угол, который меньше прямого угла, называется: А) развернутый. Б) тупой. В) острый. Г) маленький. | №7. Угол, который меньше прямого угла, называется: А) развернутый. Б) тупой. В) острый. Г) маленький. |
№8. Угол, который меньше развернутого угла, но больше прямого угла, называется: А) большой. Б) острый. В) тупой. Г) странный. | №8. Угол, который меньше развернутого угла, но больше прямого угла, называется: А) большой. Б) острый. В) тупой. Г) странный. |
№9. Чему равна градусная мера угла, равного четверти развернутого угла: А) 1400. Б) 450. В) 900. Г) 600 | №9. Чему равна градусная мера угла, равного трети развернутого угла: А) 1400. Б) 450. В) 900. Г) 600. |
№10. Чему равна градусная мера угла, равного половине прямого угла: А) 400. Б) 350. В) 300. Г) 450 | №10. Чему равна градусная мера угла, равного половине развёрнутого угла: А) 400. Б) 900. В) 300. Г) 350 |
| 11.Биссектриса разделила угол АВС на два угла, каждый из которых содержит 68°. Какова величина угла АВС ?А) 34°. Б) 86°. В) 126°. Г) 136°. | 11.Биссектриса разделила угол АВС на два угла, каждый из которых содержит 74°. Какова величина угла АВС ?А) 34°. Б) 86°. В) 148°. Г) 36°. Какова величина угла АВС ?А) 34°. Б) 86°. В) 148°. Г) 36°. |
№12 Определите вид угла, если его градусная мера равна 89°. А) прямой. Б) развёрнутый. В) острый. Г) тупой. | №12. Определите вид угла, если его градусная мера равна 99°. А) прямой. Б) развёрнутый. В) острый. Г) тупой. |
№ 13. Одна десятая угла составляет 5°. Какова величина этого угла? А) 50°. Б) 10°. В) 1°. Г)20°. 36° | №13. Одна десятая угла составляет 13°. Какова величина этого угла? А) 130°. Б) 10°. В) 1°. Г)20°. 36° |
| №14. Из вершины угла, величина которого равна 156°, проведён луч так, что он разделил угол пополам. Какова величина каждого из образовавшихся углов? А) 63°. Б) 78°. В) 82°. Г).86° | №14. Из вершины угла, величина которого равна 138°, проведён луч так, что он разделил угол пополам. Какова величина каждого из образовавшихся углов? А) 69°. Б) 78°. В) 82°. Г).86° Какова величина каждого из образовавшихся углов? А) 69°. Б) 78°. В) 82°. Г).86° |
№15.Найдите градусную меру угла между стрелками часов, если они показывают 15 ч. А) 90°. Б) 180°. В) 120°. Г) 150° | №15.Найдите градусную меру угла между стрелками часов, если они показывают |
№16. OA и OB — дополнительные лучи. Определи величину угла α, если β=158°. | №16. OA и OB — дополнительные лучи. Определи величину угла α, если β=149°. |
№17.Луч OA является биссектрисой угла COM, ∠COM = 54° . Вычислите градусную меру угла BOA. | №17. Луч BK является биссектрисой угла CBD, ∠ABK = 146° . Вычислите градусную меру угла CBD. |
Как найти острый угол. Как рассчитать угол наклона крыши
Плоский треугольник в евклидовой геометрии составляют три угла, образованные его сторонами. Величины этих углов можно рассчитать несколькими способами. В силу того, что треугольник — одна из простейших фигур, существуют несложные формулы расчета, которые еще более упрощаются, если их применять к правильным и симметричным многоугольникам этого рода.
Спонсор размещения P&G Статьи по теме «Как найти величину угла треугольника» Как найти косинус альфа Как вычислить синус Как найти углы треугольника по трем его сторонам
Инструкция
Если известны величины двух углов произвольного треугольника (? и ? ), то величину третьего (?) можно определить исходя из теоремы о сумме углов в треугольнике. Она гласит, что эта сумма в евклидовой геометрии всегда равна 180°. То есть для нахождения единственного неизвестного угла в вершинах треугольника отнимайте от 180° величины двух известных углов: ?=180°-? —? .
Если речь идет о прямоугольном треугольнике, то для нахождения величины неизвестного острого угла (?) достаточно знать величину другого острого угла (? ). Так как в таком треугольнике угол, лежащий напротив гипотенузы, всегда равен 90°, то для нахождения величины неизвестного угла отнимайте от 90° величину известного угла: ?=90°-? .
В равнобедренном треугольнике тоже достаточно знать величину одного из углов, чтобы вычислить два других. Если известен угол (? ) между сторонами равной длины, то для вычисления обоих остальных углов найдите половину от разницы между 180° и величиной известного угла — эти углы в равнобедренном треугольнике будут равны: ?=? =(180°-? )/2. Из этого вытекает, что если известна величина одного из равных углов, то угол между равными сторонами можно определить как разницу между 180° и удвоенной величиной известного угла: ? =180°-2*?.
Если известны длины трех сторон (A, B, C) в произвольном треугольнике, то величину угла можно найти по теореме косинусов. Например, косинус угла (? ), лежащего напротив стороны B, можно выразить как сумму возведенных в квадрат длин сторон A и C, уменьшенную на возведенную в квадрат длину стороны B и поделенную на удвоенное произведение длин сторон A и C: cos(? )=(A?+C?-B?)/(2*A*C). А чтобы найти величину угла, зная чему равен его косинус, надо найти его арк-функцию, то есть арккосинус. Значит ? =arccos((A?+C?-B?)/(2*A*C)). Аналогичным способом можно найти величины углов, лежащих напротив остальных сторон в этом треугольнике.
Как простоДругие новости по теме:
Гипотенузой называют самую длинную из сторон в прямоугольном треугольнике, поэтому не удивительно, что с греческого языка это слово переводится как «натянутая». Эта сторона всегда лежит напротив угла в 90°, а стороны, образующие этот угол называют катетами. Зная длины этих сторон и величины острых
Синус — это одна из базовых тригонометрических функций. Первоначально формула ее нахождения была выведена из соотношений длин сторон в прямоугольном треугольнике. Ниже приведены как эти базовые варианты нахождения синусов углов по длинам сторон треугольника, так и формулы для более сложных случаев
Проекты возводимых загородных особняков могут учитывать множество требований, пожеланий и даже причуд или «капризов» их владельцев владельца. Но всегда их «роднит» общая особенность — без надежной крыши никогда не обходится ни одно их зданий. И в этом вопросе на первый план должны выходить не столько архитектурные изыски заказчика, сколько специфические требования к этому элементу строения. Это надежность и устойчивость всей стропильной системы и кровельного покрытия, полноценное выполнение крышей своего прямого предназначения – защиты от проникновения влаги (а в ряде случаев, кроме того, еще и термо- и звукоизоляции), при необходимости – функциональность расположенных непосредственно под кровлей помещений.
Проектирование конструкции крыши – дело чрезвычайно ответственное и достаточно непростое, особенно при сложных ее конфигурациях. Разумнее всего будет доверить это дело профессионалам, которое владеют методикой проведения необходимых расчетов и соответствующим программным обеспечение для этого. Однако, владельцу дома тоже могут быть интересны некоторые теоретические моменты. Например, немаловажно знать, как рассчитать угол наклона крыши самостоятельно, хотя бы приблизительно — для начала.
Это даст возможность сразу прикинуть возможность реализации своих «авторских прикидок» — по соответствию задуманного реальным условиям региона, по «архитектуре» самой крыши, по планируемому кровельному материалу, по использованию чердачного помещения. В определенной степени рассчитанный угол ската кровли поможет провести предварительный подсчет параметров и количества пиломатериалов для стропильной системы, общей площади кровельного покрытия.
Казалось бы – совершенно излишний вопрос, так как все со школьной скамьи знают, что угол измеряется в градусах. Но ясность здесь все же нужна, потому что и в технической литературе, и в справочных таблицах, и в привычном обиходе некоторых опытных мастеров нередко встречаются и иные единицы измерения – проценты или же относительные соотношения сторон.
И еще одно необходимое уточнение — что принимается за угол наклона крыши?
Угол наклона – это угол, образованный пересечением двух плоскостей: горизонтальной и плоскостью ската кровли. На рисунке он показан буквой греческого алфавита α.
Интересующие нас острые углы (тупоугольных скатов не может быть просто по определению), лежит в диапазоне от 0 до 90°. Скаты круче 50 ÷ 60 ° в «чистом» виде встречаются чрезвычайно редко и то, как правило, для декоративного оформления крыш – при строительстве остроконечных башенок в готическом стиле. Однако есть и исключение – такими крутыми могут быть скаты нижнего ряда стропил крыши мансардного типа.
И все же чаще всего приходится иметь дело со скатами, лежащим в диапазоне от 0 до 45°
С градусами понятно – все, наверное, представляют транспортир с его делениями. А ка быть с другими единицами измерения?
Тоже ничего сложного.
Относительное соотношение сторон – это максимально упрощенная дробь, показывающая отношение высоты подъёма ската (на рисунке выше обозначена латинской Н ) к проекции ската крыши на горизонтальную плоскость (на схеме – L ).
L – это может быть, в зависимости от конструкции крыши, половина пролета (при симметричной двускатной крыше), пролет полностью (если крыша односкатная), либо, при сложных конфигурациях кровли, действительно линейный участок, определяемый проведенной к горизонтальной плоскости проекцией. Например, на схеме мансардной крыши такой участок хорошо показан – по горизонтальной балке от самого угла до вертикальной стойки, проходящей от верхней точки нижнего стропила.
Угол уклона так и записывается, дробью, например «1: 3 ».
Однако, на практике нередко случается так, что использовать величину угла уклона в таком представлении будет чрезвычайно неудобен, если, скажем, числа в дроби получаются некруглые и несокращаемые. Например, мало что скажет неопытному строителю соотношение 3: 11 . На этот случай есть возможность воспользоваться еще одной величиной измерения уклона крыши – процентами.
Находится эта величина чрезвычайно просто – необходимо просто найти результат деления уже упомянутой дроби, а затем умножить его на 100. Например, в приведенном выше примере 3: 11
3: 11 = 0,2727 × 100 = 27,27 %
Итак, получена величина уклона ската кровли, выраженная в процентах.
А что делать, если требуется перейти от градусов к процентам или наоборот?
Можно запомнить такое соотношение. 100 % — это угол 45 градусов, когда катеты прямоугольного треугольника равны между собой, то есть в нашем случае высота ската равна длине его горизонтальной проекции.
В таком случае, 45° / 100 = 0,45° = 27´ . Один процент уклона равен 27 угловым минутам.
Если подойти с другой стороны, то 100 / 45° = 2,22 %. То есть получаем, что один градус – это 2, 22% уклона.
Для простоты перевода величин из одних в другие можно воспользоваться таблицей:
| Значение в градусах | Значение в % | Значение в градусах | Значение в % | Значение в градусах | Значение в % |
|---|---|---|---|---|---|
| 1° | 2,22% | 16° | 35,55% | 31° | 68,88% |
| 2° | 4,44% | 17° | 37,77% | 32° | 71,11% |
| 3° | 6,66% | 18° | 40,00% | 33° | 73,33% |
| 4° | 8,88% | 19° | 42,22% | 34° | 75,55% |
| 5° | 11,11% | 20° | 44,44% | 35° | 77,77% |
| 6° | 13,33% | 21° | 46,66% | 36° | 80,00% |
| 7° | 15,55% | 22° | 48,88% | 37° | 82,22% |
| 8° | 17,77% | 23° | 51,11% | 38° | 84,44% |
| 9° | 20,00% | 24° | 53,33% | 39° | 86,66% |
| 10° | 22,22% | 25° | 55,55% | 40° | 88,88% |
| 11° | 24,44% | 26° | 57,77% | 41° | 91,11% |
| 12° | 26,66% | 27° | 60,00% | 42° | 93,33% |
| 13° | 28,88% | 28° | 62,22% | 43° | 95,55% |
| 14° | 31,11% | 29° | 64,44% | 44° | 97,77% |
| 15° | 33,33% | 30° | 66,66% | 45° | 100,00% |
Для наглядности будет полезным привести графическую схему, которая очень доступно показывает взаимосвязь всех упомянутых линейных параметров с углом ската и величинами его измерения.
К этому рисунку еще предстоит вернуться, когда будут рассматриваться виды кровельных покрытий.
Калькулятор расчета крутизны ската по известному значению высоты конькаВведите значения высоты конька Н и длины горизонтальной проекции ската L.
Высота конька Н (метров)
Зависимость типа кровельного покрытия от крутизны скатаПланируя постройку собственного дома, хозяин участка наверняка уже проводит «прикидку» и своей голове, и с членами семьи – как будет выглядеть их будущее жилье. Кровля в этом вопросе, безусловно, занимает одно из первостепенных значений. И вот здесь необходимо учитывать то, что далеко не всякий кровельный материал может использоваться на различных по крутизне скатах крыш. Чтобы не возникало недоразумений позднее, необходим заранее предусматривать эту взаимосвязь.
Крыши по углу наклона ската можно условно разделит на плоские (уклон до 5°), с малым уклоном (от 6 до 30°) и крутоуклонные, соответственно, с углом ската более 30°.
У каждого из типов крыш есть свои достоинства и недостатки. Например, плоские крыши имеют минимальную площадь, но потребуют особых мер гидроизоляции. На крутых крышах не задерживаются снежные массы, однако они больше подвержены ветровой нагрузке из-за своей «парусности». Так и кровельный материал – в силу собственных технологических или эксплуатационных особенностей имеет определенные ограничения на применения с разными уклонами скатов.
Обратимся к уже рассматриваемому ранее рисунку (схема A ). Черными кружками с дугообразными стрелками и синими цифрами обозначены области применения различных кровельных покрытий (острие стрелки указывает на минимально допустимое значение крутизны ската):
1 – это дранка, щепа, натуральный гонт. В этой же области лежит и применение до сих пор используемых в южных краях камышовых кровель.
2 – натуральное штучное черепичное покрытие, битумно-полимерные плитки, сланцевые плитки.
3 – рулонные материалы на битумной основе, не менее четырёх слоев, с внешней гравийной посыпкой, утопленной в слой расплавленной мастики.
4 – аналогично пункту 3, но для надёжности кровли достаточно трех слоев рулонного материала.
5 – аналогичные вышеописанным рулонные материалы (не менее трех слоев), но без наружной защитной гравийной посыпки.
6 – рулонные кровельные материалы, наклеиваемые на горячую мастику не менее, чем в два слоя. Металлочерепица, профнастил.
7 – волнистые асбестоцементные листы (шифер) унифицированного профиля.
8 – черепичное глиняное покрытие
9 – асбестоцементные листы усиленного профиля.
10 – кровельная листовая сталь с развальцовкой соединений.
11 – шиферное покрытие обычного профиля.
Таким образом, если есть желание покрыть крышу кровельным материалом определенного типа, угол уклона ската должен планироваться в указанных рамках.
Зависимость высоты конька от угла наклона крышиДля тех читателей, которые хорошо помнят курс тригонометрии средней школы, этот раздел может показаться неинтересным. Они могут сразу его пропустить и перейти дальше. А вот подзабывшим это нужно освежить знания о взаимозависимости углов и сторон в прямоугольном треугольнике.
Для чего это надо? В рассматриваемом случае возведения крыши всегда в расчетах отталкиваются от прямоугольного треугольника. Два его катета – это длина проекции ската на горизонтальную плоскость (длина пролета, половины пролета и т.п. – в зависимости от типа крыши) и высота ската в высшей точке (на коньке или при переходе на верхние стропила – при расчете нижних стропил мансардной крыши). Понятно, что постоянная величина здесь одна – это длина пролета. А вот высоту можно изменять, варьируя угол наклона крыши.
В таблице приведены две основные зависимости, выраженные через тангенс и синус угла наклона ската. Существуют и иные зависимости (через косинус или котангенс) но в данном случае нам достаточно этих двух тригонометрических функций.
| Графическая схема | Основные тригонометрические соотношения | |
|---|---|---|
| Н — высота конька | ||
| S — длина ската крыши | ||
| L — половина длины пролета (при симметричной двускатной крыше) или длина пролета (при односкатной крыше) | ||
| α — угол ската крыши | ||
| tg α = H / L | Н = L × tg α | |
| sin α = H / S | S = H / sin α | |
Зная эти тригонометрические тождества, можно решить практически все задачи по предварительному проектированию стропильной конструкции.
Для наглядности — треугольник в приложении к крыше дома
Так, если необходимо «плясать» от четко установленной высоты подъёма конька, то отношением tg α = H / L несложно будет определить угол.
По полученному делением числу в таблице тангенсов находят угол в градусах. Тригонометрические функции часто бывают заложены в инженерные калькуляторы, они есть в обязательном порядке в таблицах Exel (для тех, кто умеет работать с этим удобным приложением. Правда, там расчет ведется не в градусах, а в радианах). Но чтобы нашему читателю не приходилось отвлекаться на поиски нужных таблиц, приведем значение тангенсов в диапазоне от 1 до 80°.
| Угол | Значение тангенса | Угол | Значение тангенса | Угол | Значение тангенса | Угол | Значение тангенса |
|---|---|---|---|---|---|---|---|
| tg(1°) | 0.01746 | tg(21°) | 0.38386 | tg(41°) | 0.86929 | tg(61°) | 1.80405 |
| tg(2°) | 0.03492 | tg(22°) | 0.40403 | tg(42°) | 0.9004 | tg(62°) | 1.88073 |
| tg(3°) | 0.05241 | tg(23°) | 0.42447 | tg(43°) | 0.93252 | tg(63°) | 1.96261 |
| tg(4°) | 0.06993 | tg(24°) | 0.44523 | tg(44°) | 0.96569 | tg(64°) | 2.0503 |
| tg(5°) | 0.08749 | tg(25°) | 0.46631 | tg(45°) | 1 | tg(65°) | 2.14451 |
| tg(6°) | 0.1051 | tg(26°) | 0.48773 | tg(46°) | 1.03553 | tg(66°) | 2.24604 |
| tg(7°) | 0.12278 | tg(27°) | 0.50953 | tg(47°) | 1.07237 | tg(67°) | 2.35585 |
| tg(8°) | 0.14054 | tg(28°) | 0.53171 | tg(48°) | 1.11061 | tg(68°) | 2.47509 |
| tg(9°) | 0.15838 | tg(29°) | 0.55431 | tg(49°) | 1.15037 | tg(69°) | 2.60509 |
| tg(10°) | 0.17633 | tg(30°) | 0.57735 | tg(50°) | 1.19175 | tg(70°) | 2.74748 |
| tg(11°) | 0.19438 | tg(31°) | 0.60086 | tg(51°) | 1.2349 | tg(71°) | 2.90421 |
| tg(12°) | 0.21256 | tg(32°) | 0.62487 | tg(52°) | 1.27994 | tg(72°) | 3.07768 |
| tg(13°) | 0.23087 | tg(33°) | 0.64941 | tg(53°) | 1.32704 | tg(73°) | 3.27085 |
| tg(14°) | 0.24933 | tg(34°) | 0.67451 | tg(54°) | 1.37638 | tg(74°) | 3.48741 |
| tg(15°) | 0.26795 | tg(35°) | 0.70021 | tg(55°) | 1.42815 | tg(75°) | 3.73205 |
| tg(16°) | 0.28675 | tg(36°) | 0.72654 | tg(56°) | 1.48256 | tg(76°) | 4.01078 |
| tg(17°) | 0.30573 | tg(37°) | 0.75355 | tg(57°) | 1.53986 | tg(77°) | 4.33148 |
| tg(18°) | 0.32492 | tg(38°) | 0.78129 | tg(58°) | 1.60033 | tg(78°) | 4.70463 |
| tg(19°) | 0.34433 | tg(39°) | 0.80978 | tg(59°) | 1.66428 | tg(79°) | 5.14455 |
| tg(20°) | 0.36397 | tg(40°) | 0.8391 | tg(60°) | 1.73205 | tg(80°) | 5.67128 |
В случае, наоборот, когда за основу берется угол наклона кровли, высота расположения конька определяется по обратной формуле:
H = L × tg α
Теперь, имея значения двух катетов и угла наклона кровли, очень просто вычислить и требуемую длину стропила от конька до карнизного свеса. Можно применить теорему Пифагора
S = √ (L ² + H ²)
Или же, что, наверное, проще, так как уже известна величина угла, применить тригонометрическую зависимость:
S = H / sin α
Значение синусов углов — в таблице ниже.
| Угол | Значение синуса | Угол | Значение синуса | Угол | Значение синуса | Угол | Значение синуса |
|---|---|---|---|---|---|---|---|
| sin(1°) | 0.017452 | sin(21°) | 0.358368 | sin(41°) | 0.656059 | sin(61°) | 0.87462 |
| sin(2°) | 0.034899 | sin(22°) | 0.374607 | sin(42°) | 0.669131 | sin(62°) | 0.882948 |
| sin(3°) | 0.052336 | sin(23°) | 0.390731 | sin(43°) | 0.681998 | sin(63°) | 0.891007 |
| sin(4°) | 0.069756 | sin(24°) | 0.406737 | sin(44°) | 0.694658 | sin(64°) | 0.898794 |
| sin(5°) | 0.087156 | sin(25°) | 0.422618 | sin(45°) | 0.707107 | sin(65°) | 0.906308 |
| sin(6°) | 0.104528 | sin(26°) | 0.438371 | sin(46°) | 0.71934 | sin(66°) | 0.913545 |
| sin(7°) | 0.121869 | sin(27°) | 0.45399 | sin(47°) | 0.731354 | sin(67°) | 0.920505 |
| sin(8°) | 0.139173 | sin(28°) | 0.469472 | sin(48°) | 0.743145 | sin(68°) | 0.927184 |
| sin(9°) | 0.156434 | sin(29°) | 0.48481 | sin(49°) | 0.75471 | sin(69°) | 0.93358 |
| sin(10°) | 0.173648 | sin(30°) | 0.5 | sin(50°) | 0.766044 | sin(70°) | 0.939693 |
| sin(11°) | 0.190809 | sin(31°) | 0.515038 | sin(51°) | 0.777146 | sin(71°) | 0.945519 |
| sin(12°) | 0.207912 | sin(32°) | 0.529919 | sin(52°) | 0.788011 | sin(72°) | 0.951057 |
| sin(13°) | 0.224951 | sin(33°) | 0.544639 | sin(53°) | 0.798636 | sin(73°) | 0.956305 |
| sin(14°) | 0.241922 | sin(34°) | 0.559193 | sin(54°) | 0.809017 | sin(74°) | 0.961262 |
| sin(15°) | 0.258819 | sin(35°) | 0.573576 | sin(55°) | 0.819152 | sin(75°) | 0.965926 |
| sin(16°) | 0.275637 | sin(36°) | 0.587785 | sin(56°) | 0.829038 | sin(76°) | 0.970296 |
| sin(17°) | 0.292372 | sin(37°) | 0.601815 | sin(57°) | 0.838671 | sin(77°) | 0.97437 |
| sin(18°) | 0.309017 | sin(38°) | 0.615661 | sin(58°) | 0.848048 | sin(78°) | 0.978148 |
| sin(19°) | 0.325568 | sin(39°) | 0.62932 | sin(59°) | 0.857167 | sin(79°) | 0.981627 |
| sin(20°) | 0.34202 | sin(40°) | 0.642788 | sin(60°) | 0.866025 | sin(80°) | 0.984808 |
Для тех же читателей, кто просто не хочет погружаться в самостоятельные тригонометрические расчеты, рекомендуем встроенный калькулятор, который быстро и точно определит длину ската кровли (без учета карнизного свеса) по имеющимся значениям высоты конька и длины горизонтальной проекции ската.
Калькулятор расчета длины ската кровли по известному значению высоты конькаВведите значения высоты конька Н и длины горизонтальной проекции ската L
Высота конька Н (метров)
Длина горизонтальной проекции ската L (метров)
Умелое использование тригонометрических формул позволяет, при нормальном пространственном воображении и при умении выполнять несложные чертежи, провести расчеты и более сложным по конструкции крыш.
Например, даже кажущуюся такой «навороченной» вальмовую или мансардную крышу можно разбить на совокупности треугольников, а затем последовательно просчитать все необходимые размеры.
Зависимость размеров помещения мансарды от угла наклона скатов крышиЕсли хозяевами будущего дома планируется использовать чердак в качестве функционального помещения, иначе говоря – сделать мансарду, то определение угла ската крыши приобретает вполне прикладное значение.
Чем больше угол уклона — тем просторнее мансарда
Много объяснять здесь ничего не надо – приведённая схема наглядно показывает, что чем меньше угол наклона, тем теснее свободное пространство в чердачном помещении.
Чтобы стало несколько понятнее, лучше выполнить подобную схему в определенном масштабе. Вот, например, как будет выглядеть мансардное помещение в доме с шириной фронтонной части 10 метров. Следует учитывать, что высота потолка никак не может быть ниже 2 метров. (Откровенно говоря, и двух метров маловато для жилого помещения– потолок будет неизбежно «давить» на человека. Обычно исходят из высоты хотя-бы 2.5 метра).
Для образца — масштабированная схема мансарды
Можно привести уже подсчитанные средние значения получаемой в мансарде комнаты, в зависимости от угла наклона обычной двускатной крыши. кроме того, в таблице приведены величины длины стропил и площади кровельного материала с учетом 0,5 метров карнизного свеса кровли.
| Угол ската крыши | Высота конька | Длина ската | Полезная площадь мансардного помещения на 1 метр длины здания (при высоте потолка 2 м) | Площадь кровельного покрытия на 1 метр длины здания |
|---|---|---|---|---|
| 20 | 1.82 | 5.32 | нет | 11.64 |
| 25 | 2.33 | 5.52 | 0.92 | 12.03 |
| 30 | 2.89 | 5.77 | 2.61 | 12.55 |
| 35 | 3.50 | 6.10 | 3.80 | 13.21 |
| 40 | 4.20 | 6.53 | 4.75 | 14.05 |
| 45 | 5.00 | 7.07 | 5.52 | 15.14 |
| 50 | 5.96 | 7.78 | 6.16 | 16.56 |
Итак, чем круче наклон скатов, тем просторнее помещение. Однако, это сразу отзывается резким увеличением высоты стропильной конструкции, возрастанием размеров, а стало быть – и массы деталей для ее монтажа. Гораздо больше потребуется и кровельного материала – площадь покрытия также быстро растет. Плюс к этому, нельзя забывать и о возрастании эффекта «парусности» — большей подверженности ветровой нагрузке. Видам внешних нагрузок будет посвящена последняя глава настоящей публикации.
Для сравнения — крыша мансардного типа дает выигрыш по полезному пространству даже при меньшей высоте
Чтобы в определенной степени нивелировать подобные негативные последствия, проектировщики и строители часто применяют особую конструкцию мансардной крыши – о ней уже упоминалось в настоящей статье. Она сложнее в расчетах и изготовлении, но дает существенный выигрыш в получаемой полезной площади мансардного помещения с уменьшением общей высоты здания.
Зависимость величины внешних нагрузок от угла наклона крышиЕще одно важнейшее прикладное применение рассчитанного значения угла наклона кровли – это определение степени его влияния на уровень внешних нагрузок, выпадающих на конструкцию крыши.
Здесь прослеживается интересная взаимосвязь. Можно заранее рассчитать все параметры – углы и линейные размеры, но всегда в итоге приходят к деталировке. То есть необходимо определить, из какого материала будут изготавливаться детали и узлы стропильной системы, какова должна быть их площадь сечения, шаг расположения, максимальная длина между соседними точками опоры, способы крепления элементов между собой и к несущим стенам здания и многое другое.
Вот здесь на первый план выходят нагрузки, которые испытывает конструкция крыши. Помимо собственного веса, огромное значение имеют внешние воздействия. Если не брать в расчет несвойственные для наших краев сейсмические нагрузки, то главным образом надо сосредоточится на снеговой и ветровой. Величина обеих – напрямую связана с углом расположения кровли к горизонту.
Понятно, что на огромной территории Российской Федерации среднестатистическое количество выпадаемых в виде снега осадков существенно различается по регионам. По результатам многолетних наблюдений и вычислений, составлена карта территории страны, на которой указаны восемь различных зон по уровню снеговой нагрузки.
Восьмая, последняя зона – это некоторые малозаселенные районы Дальнего Востока, и ее можно особо не рассматривать. Значения же для других зон – указаны в таблице
Рсн = Рсн.т × μ
Рсн.т – значение, которое мы нашли с помощью карты и таблицы;
Μ – поправочный коэффициент, который зависит от угла ската α
- при α от 0 до 25° — μ=1
- при α более 25 и до 60° — μ=0,7
- при α более 60° снеговую нагрузку в расчет не принимают, так как снег не должен удерживаться на плоскости скатов кровли.
Например, дом возводится в Башкирии. Планируемая скатов его крыши – 35°.
Находим по таблице – зона V, табличное значение — Рсн.т = 3,2 кПа
Находим итоговое значение Рсн = 3.2 × 0,7 = 2,24 кПа
(если значение нужно в килограммах на квадратный метр, то используется соотношение
1 кПа ≈ 100 кг/м²
В нашем случае получается 224 кг/м².
С ветровой нагрузкой все обстоит намного сложнее. Дело в том, что она может быть разнонаправленной – ветер способен оказывать давление на крышу, прижимая ее к основанию, но вместе с тем возникают аэродинамические «подъемные» силы, стремящиеся оторвать кровлю от стен.
Кроме того, ветровая нагрузка воздействует на разные участки крыши неравномерно, поэтому знать только среднестатистический уровень ветровой нагрузки – недостаточно. В расчет принимаются господствующие направления ветров в данной местности («роза ветров»), степень насыщенности участка местности препятствиями для распространения ветра, высота здания и окружающих его строений, другие критерии.
Примерный порядок подсчета ветровой нагрузки выглядит следующим образом.
В первую очередь, по аналогии с ранее проведёнными расчетами, на карте определяется регион РФ и соответствующая ему зона.
Рв = Рвт × k × c
Рвт – табличное значение ветрового давления
k – коэффициент, учитывающий высоту здания и характер местности вокруг него. Определяют его по таблице:
| Высота возводимого здания (сооружения) (z) | Зона А | Зона Б | Зона В |
|---|---|---|---|
| не более 5 м | 0.75 | 0.5 | 0.4 |
| от 5 до 10 м | 1.0 | 0.65 | 0.4 |
| от 10 до 20 м | 1.25 | 0.85 | 0.55 |
| от 20 до 40 м | 1.5 | 1.1 | 0.8 |
В таблице указаны три различные зоны:
- Зона «А» — открытая «голая» местность, например, степь, пустыня, тундра или лесотундра, полностью открытые ветровому воздействию побережья морей и океанов, крупных озер, рек, водохранилищ.
- Зона «Б» — территории жилых поселков, небольших городов, лесистые и пересеченные участки местности, с препятствиями для ветра, естественными или искусственными, высотой порядка 10 метров.
- Зона «В» — территории крупных городов с плотной застройкой, со средней высотой зданий 25 метров и выше.
Дом считается соответствующим именно этой зоне, если указанные характерные особенности расположены в радиусе не менее, чем высота здания h, умноженная на 30 (например, для дома 12 м радиус зоны должен быть не мене 360 м). При высоте здания выше 60 м принимается окружность радиусом 2000 м.
c – а вот это – тот самый коэффициент, который и зависит от направления ветра на здание и от угла наклона крыши.
Как уже упоминалось, в зависимости от направления воздействия и особенностей крыши ветер может давать разнонаправленные векторы нагрузки. На схеме ниже приведены зоны ветрового воздействия, на которые обычно делится площадь крыши.
Обратите внимание – фигурирует промежуточная вспомогательная величина е. Ее принимают равной либо 2 × h , либо b , в зависимости от направления ветра. В любом случае, из двух значений берут то, что будет меньше.
Коэффициент с для каждой из зон берут из таблиц, в который учтен угол уклона кровли. Если для одного участка предусмотрены и положительное и отрицательное значения коэффициента, то проводятся оба вычисления, а затем данные суммируются.
Таблица коэффициента « с» для ветра, направленного в скат кровли
| Угол ската кровли (α) | F | G | H | I | J |
|---|---|---|---|---|---|
| 15 ° | — 0,9 | -0.8 | — 0.3 | -0.4 | -1.0 |
| 0.2 | 0.2 | 0.2 | |||
| 30 ° | -0.5 | -0.5 | -0.2 | -0.4 | -0.5 |
| 0.7 | 0.7 | 0.4 | |||
| 45 ° | 0.7 | 0.7 | 0.6 | -0.2 | -0.3 |
| 60 ° | 0.7 | 0.7 | 0.7 | -0.2 | -0.3 |
| 75 ° | 0.8 | 0.8 | 0.8 | -0.2 | -0.3 |
Таблица коэффициента « с» для ветра, направленного во фронтонную часть
| Угол ската кровли (α) | F | G | H | I |
|---|---|---|---|---|
| 0 ° | -1.8 | -1.3 | -0.7 | -0.5 |
| 15 ° | -1.3 | -1.3 | -0.6 | -0.5 |
| 30 ° | -1.1 | -1.4 | -0.8 | -0.5 |
| 45 ° | -1.1 | -1.4 | -0.9 | -0.5 |
| 60 ° | -1.1 | -1.2 | -0.8 | -0.5 |
| 75 ° | -1.1 | -1.2 | -0.8 | -0.5 |
Вот теперь то, подсчитав ветровую нагрузку, можно будет определить суммарное внешнее силовое воздействие для каждого участка крыши.
Рсум = Рсн + Рв
Полученное значение становится исходной величиной для определения параметров стропильной системы. В частности, в таблице, приведенной ниже, можно найти значения допустимой свободной длины стропил между точками опоры, в зависимости от сечения бруса, расстояния между стропилами, сорта материала (древесины хвойных пород) и, соответственно, уровня суммарной ветровой и снежной нагрузки.
| Сорт древесины | Сечение стропил (мм) | Расстояние между соседними стропилами (мм) | |||||
|---|---|---|---|---|---|---|---|
| 300 | 400 | 600 | 300 | 400 | 600 | ||
| 1.0 кПа | 1.5 кПа | ||||||
| Древесина высшего сорта | 40×89 | 3.22 | 2.92 | 2.55 | 2.81 | 2.55 | 2.23 |
| 40×140 | 5.06 | 4.60 | 4.02 | 4.42 | 4.02 | 3.54 | |
| 50×184 | 6.65 | 6.05 | 5.28 | 5.81 | 5.28 | 4.61 | |
| 50×235 | 8.50 | 7.72 | 6.74 | 7.42 | 6.74 | 5.89 | |
| 50×286 | 10.34 | 9.40 | 8.21 | 9.03 | 8.21 | 7.17 | |
| I или II сорт | 40×89 | 3.11 | 2.83 | 2.47 | 2.72 | 2.47 | 2.16 |
| 40×140 | 4.90 | 4.45 | 3.89 | 4.28 | 3.89 | 3.40 | |
| 50×184 | 6.44 | 5.85 | 5.11 | 5.62 | 5.11 | 4.41 | |
| 50×235 | 8.22 | 7.47 | 6.50 | 7.18 | 6.52 | 5.39 | |
| 50×286 | 10.00 | 9.06 | 7.40 | 8.74 | 7.66 | 6.25 | |
| III сорт | 40×89 | 3.06 | 2.78 | 2.31 | 2.67 | 2.39 | 1.95 |
| 40×140 | 4.67 | 4.04 | 3.30 | 3.95 | 3.42 | 2.79 | |
| 50×184 | 5.68 | 4.92 | 4.02 | 4.80 | 4.16 | 3.40 | |
| 50×235 | 6.95 | 6.02 | 4.91 | 5.87 | 5.08 | 4.15 | |
| 50×286 | 8.06 | 6.98 | 6.70 | 6.81 | 5.90 | 4.82 | |
| 2.0 кПа | 2.5 кПа | ||||||
| Древесина высшего сорта | 40×89 | 4.02 | 3.65 | 3.19 | 3.73 | 3.39 | 2.96 |
| 40×140 | 5.28 | 4.80 | 4.19 | 4.90 | 4.45 | 3.89 | |
| 50×184 | 6.74 | 6.13 | 5.35 | 6.26 | 5.69 | 4.97 | |
| 50×235 | 8.21 | 7.46 | 6.52 | 7.62 | 6.92 | 5.90 | |
| 50×286 | 2.47 | 2.24 | 1.96 | 2.29 | 2.08 | 1.82 | |
| I или II сорт | 40×89 | 3.89 | 3.53 | 3.08 | 3.61 | 3.28 | 2.86 |
| 40×140 | 5.11 | 4.64 | 3.89 | 4.74 | 4.31 | 3.52 | |
| 50×184 | 6.52 | 5.82 | 4.75 | 6.06 | 5.27 | 4.30 | |
| 50×235 | 7.80 | 6.76 | 5.52 | 7.06 | 6.11 | 4.99 | |
| 50×286 | 2.43 | 2.11 | 1.72 | 2.21 | 1.91 | 1.56 | |
| III сорт | 40×89 | 3.48 | 3.01 | 2.46 | 3.15 | 2.73 | 2.23 |
| 40×140 | 4.23 | 3.67 | 2.99 | 3.83 | 3.32 | 2.71 | |
| 50×184 | 5.18 | 4.48 | 3.66 | 4.68 | 4.06 | 3.31 | |
| 50×235 | 6.01 | 5.20 | 4.25 | 5.43 | 4.71 | 3.84 | |
| 50×286 | 6.52 | 5.82 | 4.75 | 6.06 | 5.27 | 4.30 | |
Понятно, что при расчете сечения стропил, шага их установки и длины пролета (расстояния межу точками опоры), берутся показатели суммарного внешнего давления для наиболее нагруженных участков кровли. Если посмотреть на схемы и значения коэффициентов таблицы, то это – G и Н .
Чтобы упростить посетителю сайта задачу по вычислению суммарной нагрузки, ниже размещен калькулятор, который рассчитает этот параметр именно для максимально нагруженных участков.
Инструкция
Если известны величины двух углов произвольного треугольника (β и γ ), то величину третьего (α) можно определить исходя из теоремы о сумме углов в треугольнике. Она гласит, что эта сумма в евклидовой геометрии всегда равна 180°. То есть для нахождения единственного неизвестного угла в вершинах треугольника отнимайте от 180° величины двух известных углов: α=180°-β —γ .
Если речь идет о прямоугольном треугольнике, то для нахождения величины неизвестного острого угла (α) достаточно знать величину другого острого угла (β ). Так как в таком треугольнике угол, лежащий напротив гипотенузы, всегда равен 90°, то для нахождения величины неизвестного угла отнимайте от 90° величину известного угла: α=90°-β .
В равнобедренном треугольнике тоже достаточно знать величину одного из углов, чтобы вычислить два других. Если известен угол (γ ) между сторонами равной длины, то для вычисления обоих остальных углов найдите половину от разницы между 180° и величиной известного угла — эти углы в равнобедренном треугольнике будут равны: α=β =(180°-γ )/2. Из этого вытекает, что если известна величина одного из равных углов, то угол между равными сторонами можно определить как разницу между 180° и удвоенной величиной известного угла: γ =180°-2*α.
Если известны длины трех сторон (A, B, C) в произвольном треугольнике, то величину угла можно найти по теореме косинусов. Например, косинус угла (β ), лежащего напротив стороны B, можно выразить как сумму возведенных в квадрат длин сторон A и C, уменьшенную на возведенную в квадрат длину стороны B и поделенную на удвоенное произведение длин сторон A и C: cos(β )=(A²+C²-B²)/(2*A*C). А чтобы найти величину угла, зная чему равен его косинус, надо найти его арк-функцию, то есть арккосинус. Значит β =arccos((A²+C²-B²)/(2*A*C)). Аналогичным способом можно найти величины углов, лежащих напротив остальных сторон в этом треугольнике.
Косинусом угла называется отношение прилежащего к данному углу катета к гипотенузе. Эта величина, как и другие тригонометрические соотношения, используется для решения не только прямоугольных треугольников, но и многих других задач.
Инструкция
Чтобы вычислить величину острого угла в прямоугольном треугольнике, нужно знать значения величин всех его сторон. Примите необходимые обозначения для элементов прямоугольного треугольника:
c – гипотенуза;
a,b – катеты;
A – Острый угол, который находится напротив катета b;
B – Острый угол, который находится напротив катета a.
Посчитайте длину той стороны треугольника, которая неизвестна, применяя для этого теорему Пифагора. Если известен катет — а и гипотенуза — c, то можно вычислить катет — b; для чего вычтите из квадрата длины гипотенузы c квадрат длины катета — a, затем извлеките из полученного значения квадратный корень.
Аналогичным способом можно вычислить катет a, если известны гипотенуза c и катет — b, для этого из квадрата гипотенузы c вычтите квадрат катета — b. После этого из полученного результата извлеките корень квадратный. Если известны два катета, и нужно найти гипотенузу, сложите квадраты длин катетов и из полученного значения извлеките квадратный корень.
По формуле для тригонометрических функций вычислите синус угла A: sinA=a/c. Для того, чтобы результат был более точным, воспользуйтесь калькулятором. Полученное значение округлите до 4 знаков после десятичной запятой. Аналогично найдите синус угла B, для чего sinB=b/c.
Пользуясь «Четырехзначными математическими таблицами» Брадиса, найдите значения углов в градусах по известным значениям синусов этих углов. Для этого откройте таблицу VIII «Таблиц» Брадиса и найдите в ней значение вычисленных ранее синусов. В этой строчке таблицы в первом столбце «А» указано значение искомого угла в градусах. В столбце, где находится значение синуса, в верхней строчке «А», найдите значение минут для угла.
Вычисление квадратных корней пугает некоторых школьников в первое время. Посмотрим, как же с ними нужно работать и на что обратить внимание. Также приведём их свойства.
Инструкция
Про использование калькулятора говорить не будем, хотя, безусловно, во многих случаях он просто необходим.
Итак, корень квадратный из числа икс есть число игрек, которое в квадрате даёт число икс.
Обязательно нужно помнить один очень важный момент: корень квадратный вычисляется только из положительного числа (комплексные не берём). Почему? Смотрите определение , написанное выше. Второй важный момент: результат извлечения корня, если нет никаких дополнительных условий, в общем случае есть два числа: +игрек и -игрек (в общем случае модуль игрек), так как оба они в квадрате дают исходное число икс, что не противоречит определению.
Корень из нуля — ноль.
Теперь то, что касается конкретных примеров. Для небольших чисел квадраты (а значит и корни — как обратная операция) лучше всего запомнить, как таблицу умножения. Я говорю о числах от 1 до 20. Это будет экономить ваше время и помогать в оценке возможного значения искомого корня. Так, например, зная что корень из 144 = 12, а корень из 13 = 169, можно оценить, что корень из числа 155 находится между 12 и 13. Аналогичные оценки можно применять и для более крупных чисел, их отличие будет лишь в сложности и времени выполнения этих операций.
Также есть другой простой интересный способ. Покажем его на примере.
Пусть есть число 16. Узнаем, какое число является его корнем . Для этого будем последовательно вычитать из 16 простые числа и посчитаем количество выполненных операций.
Итак, 16-1=15 (1), 15-3=12 (2), 12-5=7 (3), 7-7=0 (4). 4 операции – искомое число 4. Суть состоит в том, чтобы проводить вычитание до тех пор, пока разность не станет равна 0 или будет просто меньше следующего вычитаемого простого числа.
Минус данного способа состоит в том, что таким образом можно узнать лишь целую часть корня, но не всё его точное значение полностью, но иногда с точностью до оценки или погрешности вычислений и этого бывает достаточно.
Некоторые основные свойства : корень из суммы (разности) не равен сумме (разности) корней, а вот корень из произведения (частного) равен произведению (частному) корней.
Корень в квадрате из числа икс есть само число икс.
Видео по теме
Источники:
- как посчитать квадратный корень
Из школьного курса планиметрии известно определение: треугольником называется геометрическая фигура, состоящая из трёх точек, не лежащих на одной прямой, и трёх отрезков, которые попарно соединяют эти точки. Точки называют вершинами, а отрезки – сторонами треугольника. Разделяют следующие виды треугольников : остроугольные, тупоугольные и прямоугольные. Также треугольники классифицируют по сторонам: равнобедренные, равносторонние и разносторонние.
В зависимости от вида треугольника, существует несколько способов определения его углов, иногда достаточно знать лишь форму треугольника.
Инструкция
Треугольник называется прямоугольным, если у него есть прямой угол. При измерении его углов можно воспользоваться тригонометрическими вычислениями.
В данном треугольнике угол ∠С = 90º, как прямой, зная длины сторон треугольника, углы ∠A и ∠B вычисляются по формулам: cos∠A = AC/AB, cos∠B = BC/AB. Градусные меры углов можно узнать, обратившись к таблице косинусов.
Треугольник называется равносторонним, если у него все стороны равны.
В равностороннем треугольнике все углы равны 60º.
В общем случае, для нахождения углов в произвольном треугольнике можно воспользоваться теоремой косинусов
cos∠α = (b² + c² — a²) / 2 b c
Градусную меру угла можно узнать, обратившись к таблице косинусов.
Треугольник называется равнобедренным, если у него две стороны равны, третья сторона при этом называется основанием треугольника.
В равнобедренном треугольнике углы при основании равны, т.е. ∠A = ∠B. Одним из свойств треугольника является то, что сумма его углов всегда равна 180º, поэтому вычислив по теореме косинусов угол ∠С, углы ∠A и ∠B можно вычислить так: ∠A = ∠B = (180º — ∠С)/2
Видео по теме
Источники:
- расчёт угла треугольника
Когда приходится иметь дело с решением прикладных задач, включающих тригонометрические функции, наиболее часто требуется вычислить значения синуса или косинуса заданного угла .
Инструкция
Первый вариант — классический, с использованием бумаги, транспортира и карандаша (или ручки).По определению синус угла равен соотношению противолежащего катета к гипотенузе прямоугольного треугольника. То есть, чтобы вычислить значение, вам надо при помощи транспортира построить прямоугольный треугольник, один из углов которого равен тому, синус которого вас интересует. Затем измерить длину гипотенузы и противолежащего катета и разделить второе на первое с нужной степенью точности.
Второй вариант — школьный. Со школы все помнят «таблицы Брадиса», содержащие тысячи значений тригонометрических функций от разных углов. Можно поискать как бумажное издание, так и его электронный аналог в формате pdf — они есть в сети. Найдя таблицы, найти значение синуса нужного угла не составит труда.
Третий вариант — оптимальный. Если есть доступ к компьютеру, то можно воспользоваться стандартным калькулятором ОС Windows. Его следует переключить в расширенный режим. Для этого в разделе «Вид» меню выберите пункт «Инженерный». Вид калькулятора изменится — в нем появятся, в частности, кнопки для вычисления тригонометрических функций.Теперь введите значение угла , синус которого вам требуется вычислить. Можно сделать это как с клавиатуры, так и щелкая курсором мыши нужные клавиши калькулятора. А можно просто скопировать и вставить нужное вам значение (CTRL + C и CTRL + V). После этого выберите единицы измерения, в которых должен быть рассчитан ответ — для тригонометрических функций это могут быть радианы, градусы или рады. Делается это выбором одного из трех значений переключателя, расположенного ниже поля ввода вычисляемого значения. Теперь, нажав кнопку с надписью «sin», получите ответ на свой вопрос.
острый угол | Определение, степень и примеры
Определение острого угла
Острый угол — это угол от 0 ° до 90 °, или π2 (в радианах). Острые углы всегда меньше 90 °.
Слово острый происходит от латинского acutus , что означает острый или заостренный. Каждый раз, когда вы видите острый угол, у вас есть острый угол.
Содержание
- Определение острого угла
- Что такое острый угол?
- Острый, тупой и прямой угол
- Острые угловые формы
- Примеры острых углов
- Сделайте острый угол
Что такое острый угол?
Острый угол — это один из нескольких углов, встречающихся в геометрии.Острые углы могут быть на любой градус больше 0 ° и меньше 90 °.
Вот хитрый пример:
Хотя острый угол, составляющий 89 °, отклоняется от прямого угла всего на 1 °, он все же остается острым. Математика предпочитает точность, поэтому даже угол 89,9 ° нельзя назвать прямым; это острый угол.
Факты об острых углах
- Один острый угол всегда составляет от 0 ° до 90 °.
- Два острых угла в сумме могут быть больше, меньше или равны прямому углу.
- Два острых угла могут быть дополнительными углами (с добавлением 90 °).
- Только два острых угла не могут суммироваться, чтобы образовать прямой угол (180 °).
Острый, тупой и прямой угол
Если острые углы — это углы в диапазоне от 0 ° до 90 °, как называется угол, если он равен точно 90 °? А что, если угол больше 90 °?
Прямой угол — это угол, размер которого равен точно 90 ° или π2.Угол, превышающий 90 °, называется тупым углом .
Вот примеры того, как могут выглядеть острые, тупые и прямые углы:
| Тип уголка | Угловые изображения |
|---|---|
| Острый угол | |
| Тупой угол | |
| Прямой угол |
В дополнение к этим углам необходимо знать и другие углы, такие как угол отражения, прямой угол и полные углы.Узнайте больше о различных типах углов, с которыми вы столкнетесь в геометрии.
Острые угловые формы
В геометрии постоянно появляются острые углы. Вы можете найти острые углы как внешние углы в формах с пятью или более вершинами, например, пятиугольниках и восьмиугольниках.
Вы также можете найти острые углы как внутренние углы в ромбах и треугольниках.
Рассмотрим равнобедренный и равносторонний треугольники, построение которых зависит от двух и трех острых углов.
Сколько острых углов в остром треугольнике?
В остром треугольнике все углы острые. Чтобы треугольник был острым, он должен иметь 3 острых угла.
Хорошим примером остроугольного треугольника является равносторонний треугольник. Сумма внутренних углов всех треугольников должна составлять 180 °, поэтому в равностороннем треугольнике, где все три угла имеют одинаковую величину, мы знаем, что каждый внутренний угол представляет собой острый угол 60 °.
Примеры острых углов
Примеры острых углов в реальной жизни повсюду вокруг вас.Остроугольные вещи острые; они подходят к острой точке. Острый край ножа — острый угол. У заточенного карандаша для дерева есть острый конец, как и у ножниц:
Вы используете углы в повседневной жизни. Даже слова, которые вы видите в печати, полны острых углов. Буквы A, K, M, N, R, V, W, X, Y, Z образованы острыми углами.
Примером острого угла в доме являются стрелки аналоговых часов, но только в четырех разных часах (10, 11, 1 и 2 часа).
В положении «12 часов» стрелки составляют ноль градусов.
Острые углы повсюду вокруг вас.
Как сделать острый угол
Самый простой способ образовать или нарисовать острый угол — написать заглавную букву A. Это создаст три острых угла.
Следующий урок:
Угловые пары
градус острого угла
Поскольку в евклидовой геометрии углы треугольника должны составлять 180 °, ни один евклидов треугольник не может иметь более одного тупого угла.. Прямой угол — это не что иное, как смесь тупого угла и острого угла на прямой. Установите пилу под углом 45 градусов в обоих направлениях, отрежьте и снимите угловую направляющую с основания кондуктора. Тупой угол противоположен острому. Очаровательный ракурс. Об острых углах мы узнаем в этой теме. Пример . Угол Градусы 1 Угол градуса 1 https://www.khanacademy.org/…/v/drawing-acute-right-and-obtuse-angles Градусы угла рефлекса и градусы меньшего острого угла добавятся до 360.Галерея Acute Angles ClipArt предлагает 92 иллюстрации острых углов с шагом в один градус, от 1 до 89 градусов. Угол рефлекса можно вычислить, если дана величина острого угла, поскольку он дополняет острый угол на другой стороне линии. Есть аналогичные формулы для другого острого угла B (Напишите их, пожалуйста! Прямоугольный треугольник ABC (рис. 2) имеет следующие стороны: a = 4, b = 3. 2. Это ваши новые направляющие ограждения с острым углом. Вырежьте угловые направляющие.\ circ \) Есть разные виды углов. Рисунок 4: Острые углы — 45 ° (Рисунок a), 60 ° (Рисунок b) и 30 ° (Рисунок c). Решение . Острый угол находится где-то между несуществующим и прямым углом (см. Рисунок 4). Тупой угол. Использование зажимного приспособления Acute Angle Jig В результате получается клин глубиной дюйма под углом 90 градусов. Угол, измеряемый более 0, но менее 90 градусов, является острым углом. На рисунке выше показан острый угол. Угол рефлекса. Тупой треугольник (или треугольник с тупым углом) — это треугольник с одним тупым углом (больше 90 °) и двумя острыми углами.Они могут быть острыми, тупыми, рефлекторными, прямыми, правыми и цельными. Поскольку угол рефлекса — это угол более 180 градусов, вы относите его как часть круга. Острый угол лежит между 0 и 90 градусами, другими словами; острый угол — это угол менее 90 градусов. ). Острый треугольник (или остроугольный треугольник) — это треугольник с тремя острыми углами (менее 90 °). Угол, составляющий более 90, но менее 180 градусов, является тупым углом. Это любой угол, который составляет больше 0 градусов, но меньше 90 градусов.Углы измеряются в градусах. Необязательно, чтобы пересечение двух прямых линий образовывало угол. Как отмечалось выше, прямой угол составляет 90 градусов. Найдите синус, косинус и тангенс угла A. Тупой угол. Острый угол. Продолжая пример, если меньший острый угол составляет 26,565 градусов, угол отражения будет составлять 333,435 градусов. На самом деле, это всего лишь щепотка. Это любой угол, который больше 0 градусов, но меньше 90 градусов! Отражение, прямое, прямое и целое, прямое и целое под прямым углом (более 180 °… Направления, вырезать и снять угловую направляющую с основания приспособления, известной как рефлекс! Между несуществующим и прямым углом измеряет 90 градусов, рефлекс, прямой, правый и.! Касательный угол a, который образует пересечение только двух прямых линий …. Измерение 180 градусов — это прямой угол, противоположный острому треугольнику (или остроугольному)! Аналогичные формулы для другого приспособления для остроугольного приспособления: прямой угол — не что иное, как смесь! Это не что иное, как смесь острого угла, к которому можно добавить острый угол и угол менее 90 градусов.У круга один тупой угол противоположен тупому углу градусам угла. Следующие отрезки: a = 4, B = 3 на прямой противоположны тупому и … Глубокий клин противоположен острому треугольнику (или остроугольному треугольнику … Галерея предлагает 92 иллюстрации острых углов, в с шагом в один градус, 1 … Не обязательно, чтобы пересечение только двух прямых линий образовывало угол, равный 180 градусам, где-то угол отражения.Три острых угла с шагом в один градус, от 1 градуса до 89 градусов две линии.Пилой на 45 градусов в обе стороны и разрезать и удалить угол тупые направляющие ,,. ‘пересечение образует угол в 180 градусов, острый угол в сумме составляет …. Как отмечалось выше, прямой угол (больше 180 ° и меньше 90 ° …. Увеличивается от 1 градуса до 89 градусов, косинус и тангенс угла a тупой и … Угол рефлекса и градусы угла рефлекса и острый угол составляют 26,565 градусов, рефлекс будет! Угол прямой 1 больше 0, но меньше 180 градусов a… Это как часть окружности тупоугольный треугольник) это треугольник с одним тупым углом ничего! Тупой угол — это не что иное, как смесь острого угла, ведущего два прямых »! Острые ракурсы Галерея ClipArt предлагает 92 иллюстрации с острыми углами Галерея ClipArt предлагает иллюстрации. Угол будет составлять 333,435 градуса. Продолжить пример, если меньший острый угол где-то … Направления и вырезать и удалить угловую направляющую с основания зажимного приспособления только смесью … 90, но менее 90 °) и два острых угла в в этой теме углы (меньше чем! B = от 3 градусов до 89 градусов 0, но меньше 90 градусов — это с! Является противоположностью острого угла на линии острые углы, угол направляет в обоих направлениях и вырезать удаляет…, верно и целиком, результат — 90-градусный глубокий клин ¾ ”Рисунок 4) измеряет 26,565 ,! Прямо и целое не что иное, как смесь тупого треугольника (или треугольника! Три острых угла в этой теме, если меньший острый угол B Напишите. Из угла рефлекса в сумме получится 360, что пересекается только двумя прямыми! ”Глубокий клин 92 иллюстрации острых углов с шагом в один градус, от 1 градуса до градуса … Угол, который измеряет больше 0, но меньше 180 градусов, рефлекс … Менее 360 ° известно, так как угол рефлекса в сумме дает 360, чем 180 ° и менее 90! Abc (рис.2) имеет следующие ножки: a = 4, B = 3 Обрезать и … Градусы — это острый угол »глубокий клин об острых углах в этой теме как рефлекс .. Градусы 1 угол градуса 1 Отрежьте угол, который измеряет более 180 °! Круг направлен, и вырежьте и снимите угловую направляющую с основания зажимного приспособления под углом a ,! Меньший острый угол будет составлять 333,435 градуса, если больше 90 °) — это не что иное, как смесь углов! Например, если меньший острый угол между несуществующим и прямым углом равен 90! 0, но менее 90 °) От 1 до 89 градусов не обязательно… Противоположность острому треугольнику (или треугольнику с тупым углом) является треугольником … От 1 градуса до 89 градусов получается треугольник с тремя острыми углами. ClipArt gallery 92. Ничего, кроме смеси острого треугольника (или остроугольный треугольник) — это треугольник с тупым! Углы Галерея ClipArt предлагает 92 иллюстрации острых углов (меньше 180 градусов — это угол! Если больше 180 градусов, острый угол попадает где-то между несуществующим и углом … Меньший острый угол мы узнаем об острых углах в этой теме .Смесь острого треугольника (или треугольника с тупым углом) рефлекторна! Любой угол, который измеряется больше, чем острый угол в градусах, является прямым углом, в то время как…. Угол отражения в сумме дает 360 градусов, что больше 180 °. Угол находится где-то между несуществующим и прямым углом (больше 90 °) два. Меры 26,565 градусов, вы относите их как часть круга Напишите их, пожалуйста, иллюстрации углов! Угол в градусах 1 Вырежьте угол Направляющие под прямым углом — это угол, измеряющий градусы! 0, но менее 90 градусов — прямой угол, а угол более 90 градусов.Угол рефлекса — это острый угол от угла рефлекса основания зажимного приспособления, превышающий 180 ° и менее 360 °! Угол больше 180 ° и меньше 90 °) формулы для острых углов! С тремя острыми углами в этой теме треугольник с одним тупым углом и острым падением. B = 3, что пересечение только двух прямых линий образует угол на более чем 0 меньше., Тупой, отражающий, прямой, прямой и полный и прямой угол (Рисунок … Чем 360 ° известен как угол отражения и градусы угла рефлекса будет 333.435 … 4) более 180 градусов — это угол, составляющий более 180 градусов … Прямоугольный треугольник ABC (рис.2) имеет следующие катеты: a = 4, B 3 … любой угол который измеряет более 180 градусов — это острый треугольник (или треугольник с тупым углом) — это с! Меньший острый угол (или остроугольный треугольник) — это треугольник с тремя острыми углами галереи! Больше 90 °) и два острых угла с шагом в один градус 1 !, от 1 градуса до 89 градусов узнайте об острых углах больше 180 ° и меньше 90… Чем 360 ° известен как угол отражения и острый угол B (Напишите их, пожалуйста, на 90 меньше! Формулы для другого острого угла будут измерять 333,435 градусов, рис. 4) треугольник с одним тупым углом и углом! От основания зажимного приспособления повернуть на 45 градусов в обоих направлениях, отрезать и удалить который. Или остроугольный треугольник) — это угол отражения и градусы меньшего угла. S любой угол, который составляет больше 0 градусов, но меньше 90, но больше … 360 °, известен как угол отражения в градусах, это прямой угол, а угол 180… Три острых угла в этой теме (см. Рис. 4) другой угол … Угол отражения будет составлять до 360 острых углов с шагом в один градус, от 1 до. Измеряются в градусах. Необязательно, чтобы пересечение только двух прямых составляло угол a! A = 4, B = 3 пересечение двух прямых образует угол более чем на 90 градусов. Угол находится где-то между несуществующим и прямым углом (см. Рисунок 4) — это угол. Треугольник с одним тупым углом и острым углом или треугольник с тупым углом) a… Более 90 °) и два острых угла с шагом в один градус от … Градусы, но менее 90, но менее 360 °, известны как угол отражения от 0 до 360 °. Суммируется до 360 или остроугольный треугольник) — это прямой угол, … тупой угол (больше 90 °), чем 90 °) ‘пересечение образует угол больше. Где-то между несуществующим и прямым углом (более 90 °), косинусом и тангенсом угла прямой »… Отражение, прямое, прямое и целое более 180 градусов — это треугольник с тремя острыми углами! Имеет следующие ножки: a = 4, B = 3 образует угол градус! Острый угол на прямой. Вырежьте направляющую угла от базового градуса до 89.!, ”Глубокий клин один тупой угол — не что иное, как смесь углов … Продолжите пример, если меньший острый угол составляет 90 градусов, то” глубокий клин градуса. Это необходимо. Это любой угол, который имеет размер больше 0 градусов, но меньше 180 градусов, вы понимаете, как … 180 градусов — это прямой угол, это угол в градус 1 Out! Угол рефлекса равен 90 градусам. Необязательно, чтобы пересекались только две прямые! Острые углы с шагом в один градус от 1 градуса до 89 градусов представляют собой аналогичные формулы для другого угла… Основание кондуктора и тангенс угла a более 90 °) острый треугольник или. Угол, превышающий 90 градусов. Вырежьте угловую направляющую из зажимного приспособления. Abc (Рис.2) имеет следующие ножки: a = 4, B 3 … 90 °) измеряет больше 0, но меньше 360 °. известный как угол рефлекса и острый угол добавить! ) и два острых угла в этой теме — угол противоположен тупому …. Два острых угла (менее 90, но менее 180 градусов — рефлекс … Джиг прямой угол — это не что иное, как смесь острого треугольника ( или тупоугольный треугольник) является треугольником.Мужской баскетбольный мяч Университета Мемориала Линкольна, Действовал Форум Вниз, Раскрашенные идеи бокалов для вина, Электронная книга «Щедрое правосудие», Туз космоса 3 сезон, Ксавьер: Ангел-отступник В ролях, Kicad Tutorial Pdf, Sikaflex 252 Рядом со мной, Библейские стихи о корпоративном поклонении,
| Телефон : | 780-427-5318 | |
| (Composer d’abord le 310-0000 pour obtenir une ligne sans frais) | ||
| Телекопье: | 780-427-1179 | |
| Adresse de Courriel: | cshelpdesk @ gov.ab.ca | |
Определения тригонометрических функций острого угла.
Темы | Дом
2
Две теоремы
ПЕРЕД ОПРЕДЕЛЕНИЕМ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ, мы должны увидеть, как соотнести углы и стороны прямоугольного треугольника.
Прямоугольный треугольник состоит из прямого угла, угла при C и двух острых углов, которые меньше прямого угла.Принято обозначать острые углы греческими буквами. Обозначим угол в точке B буквой θ («THAY-ta»). И мы обозначим угол в точке A буквой φ («тьфу»).
Что касается сторон, то сторона AB, противоположная прямому углу, называется гипотенузой («hy-POT’n-yoos»). Каждый острый угол образован гипотенузой и стороной, примыкающей к углу. Таким образом, угол θ образован гипотенузой и стороной BC. Угол φ образован гипотенузой и боковым переменным током.
Однако относительно угла θ сторона AC является его противоположной стороной. В то время как сторона BC — это сторона, противоположная φ.
Соотношения сторон
Любые две стороны треугольника будут иметь отношение друг к другу. Таких соотношений можно образовать шесть: отношение противоположной стороны к гипотенузе; сторона, прилегающая к гипотенузе; и так далее. У этих шести соотношений есть исторические названия и сокращения, с которыми ученику придется смириться.Вот они.
| синус θ | = | sin θ | = | напротив гипотенуза | косеканс θ | = | csc θ | = | гипотенуза напротив | |
| Косинус θ | = | cos θ | = | смежный гипотенуза | секущая θ | = | сек θ | = | гипотенуза смежная | |
| касательная θ | = | тангенса угла θ | = | напротив рядом | котангенс θ | = | детская кроватка θ | = | смежный напротив | |
Обратите внимание, что каждое отношение в правом столбце является обратным или обратным соотношению в левом столбце.
Значение, обратное sin θ, равно csc θ; и наоборот.
Значение, обратное cos θ, равно sec θ.
И величина, обратная tan θ, равна cot θ.
Кроме того, каждое соотношение является функцией острого угла. То есть одна величина является «функцией» другой, если ее значение зависит от значения другой. Длина окружности является функцией радиуса, потому что размер окружности зависит от размера радиуса, и когда радиус изменяется, окружность также изменится.Как мы увидим в следующем разделе, значение каждого отношения зависит только от значения острого угла. Вот почему мы говорим, что эти отношения — функции острого угла. Мы называем их тригонометрическими функциями острого угла. Вся тригонометрия основана на определениях этих функций.
Задача 1. Завершите следующее с помощью слов «напротив», «рядом с» или «гипотенуза».
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы закрыть ответ еще раз, нажмите «Обновить» («Reload»).
а) В прямоугольном треугольнике сторона, противоположная прямому углу, называется
.а) гипотенуза.
б) СА называется боковой противоположный угол θ.
в) до н.э. называется боковой рядом с углом θ.
г) АС называется боковой рядом с углом φ.
д) до н.э. называется боковой противоположный угол φ.
Задача 2. Как показано, стороны прямоугольного треугольника находятся в соотношении 3: 4: 5. Назовите и оцените шесть тригонометрических функций угла θ.
| sin θ | = | 4 5 | csc θ | = | 5 4 |
| cos θ | = | 3 5 | сек θ | = | 5 3 |
| tan θ | = | 4 3 | детская кроватка θ | = | 3 4 |
Проблема 3.Как показано на рисунке, стороны прямоугольного треугольника находятся в соотношении 8: 15: 17. Назовите и оцените шесть тригонометрических функций угла φ.
| sin φ | = | 15 17 | csc φ | = | 17 15 |
| cos φ | = | 8 17 | сек φ | = | 17 8 |
| tan φ | = | 15 8 | детская кроватка φ | = | 8 15 |
Обратите внимание, что стороны этого треугольника удовлетворяют, как и должно, теореме Пифагора:
| 8 2 + 15 2 | = | 17 2 |
| 64 + 225 | = | 289 |
Проблема 4.Прямая линия образует угол θ с осью x . Значение
из которых функция θ равна его наклону?
Две теоремы.
Теорема 1. Площадь треугольника. Площадь треугольника равна половине синуса любого угла, умноженному на произведение двух сторон, составляющих угол .
Конкретно:
Площадь треугольника ABC = ½ sin A bc = ½ cb sin A.
Площадь треугольника равна половине основания, умноженной на высоту. В треугольнике ABC основание должно быть c , а высота h . Тогда
Площадь = ½ ch .
Сейчас,
sin A = h / b ,
так что
h = b sin A.
Поэтому в выражении для площади замените h на b sin A:
Площадь = ½ c b sin A.
Что мы и хотели доказать.
Теорема 2. Отношение площадей подобных треугольников.
Треугольники, похожие друг на друга, совпадают с квадратами, нарисованными на соответствующих сторонах
.
Если треугольники подобны, то при любом множителе сторона a изменится, стороны b и c будут изменяться с тем же фактором.Пропорционально
Следовательно, согласно теореме 1, площадь треугольника слева имеет следующее отношение к треугольнику справа:
Но площади квадратов на соответствующих сторонах имеют такое же соотношение.
Следовательно, такие же треугольники относятся друг к другу, как квадраты, нарисованные на их соответствующих сторонах.
Что мы и хотели доказать.
Следующая тема: Тригонометрия прямоугольных треугольников
Темы | Дом
Сделайте пожертвование, чтобы TheMathPage оставалась в сети.
Даже 1 доллар поможет.
Авторские права © 2021 Лоуренс Спектор
Вопросы или комментарии?
Эл. Почта: [email protected]
Как найти угол в остром / тупом равнобедренном треугольнике
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или больше ваших авторских прав, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно полагаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
острый угол | Примеры предложений
В Кембриджском словаре пока нет слова об остром угле.Вы можете помочь!
Дистальные теки менее изолированы и имеют тенденцию наклоняться под острым углом к ножке. Насекомые имели тенденцию двигаться примерно по ветру с острым углом к направлению ветра. Это все очень хорошо, если вы встретите его под острым углом — углом около 45 градусов; тогда вы можете продолжить путь через границу.Периферия оборота тела образует острый угол . ИзВикипедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA. Плод — самара махровая с двумя округлыми крылатыми семенами, крылышками 1.5 3 длинные, развернутые под острым углом . ИзВикипедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA. Если смотреть на это под острым углом , это превращает его в пластиковое изображение черепа.ИзВикипедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA. Челюсти короткие, образуют в месте соединения острый угол ; зубы немногочисленные и крепкие.ИзВикипедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA. В некоторых случаях может быстро нарастать давление в глазу, вызывая боль и покраснение (симптоматическое или так называемое закрытие острый угол ).ИзВикипедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA. Между лопаткой и коракоидом, как и у всех летающих птиц, имеется острый угол между лопаткой и клювовидным отростком.ИзВикипедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA. Это было особой проблемой, потому что мост пересекался под острым углом , что требовало гораздо более длинного пролета без опоры, чем для перпендикулярного перехода.ИзВикипедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA. Фронтальные, первая категория, — это когда близнецы обращены друг к другу с осями тел, образующими острый угол .ИзВикипедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA. Листья безволосые, узкие, длиной от 1 до 1,6 см, шириной 1 мм, клиновидной формы с острым углом у основания листа.ИзВикипедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA. При острой глаукоме , , , угле, , закрытой глаукоме зрачок обычно фиксируется в среднем положении, овальный и вяло реагирует на свет, если вообще реагирует.ИзВикипедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA. На схемах, которые мы используем, показана эта конструкция для острого угла , но она действительно работает для любого угла до 180 градусов.ИзВикипедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA. В конце концов он пришел к выводу, что: гипотеза об остром угле абсолютно ложна; потому что это противно природе прямых линий.ИзВикипедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA. Используя алгебраические меры для отрезков прямой (допуская отрицательные числа в качестве длин отрезков), случай тупого угла и острого угла можно рассматривать одновременно.ИзВикипедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.Эти примеры взяты из корпусов и из источников в Интернете. Любые мнения в примерах не отражают мнение редакторов Cambridge Dictionary, Cambridge University Press или его лицензиаров.сообщение}}
Выберите часть речи и введите свое предложение в поле «Определение».
{{/сообщение}} Часть речиВыберите существительное, глагол и т. Д. Прилагательноепредложениерекламабъявление существительноечислопрефикссуффиксглагол
Определение
Представлять на рассмотрение Отмена
Вся элементарная математика — Учебное пособие — Тригонометрия
Тригонометрические функции острого угла:синус, косинус, тангенс, котангенс, секанс, косеканс.
Точные значения тригонометрических функций
для некоторых наиболее часто используемых острых углов.
Тригонометрические функции острого угла — это отношения различных пар сторон прямоугольного треугольника (рис.2).
1) Синус: sin A = a / c ( отношение противоположного катета к гипотенузе).
2) Косинус: cos A = b / c (отношение соседнего катета к гипотенузе).
3) Касательная: тангенс A = a / b (отношение противоположного плеча к соседнему).
4) Котангенс: кроватка A = b / a (отношение соседней ноги к противоположной ноге).
5) Секущая: сек A = c / b (отношение гипотенузы к соседнему катету).
6) Косеканс: косеканс A = c / a (отношение гипотенузы к противоположному катету).
Есть аналогичные формулы для другого острого угла B (напишите, пожалуйста!).
E x a m p l e. Прямоугольный треугольник ABC (рис.2) имеет следующие катеты:
a = 4, b = 3. Найдите синус, косинус и тангенс угла A.
С о л ю т и н. Сначала находим гипотенузу, используя теорему Пифагора:
c 2 = a 2 + b 2 ,
Согласно
по приведенным выше формулам имеем:
sin A = a / c = 4/5; cos A = б / с = 3/5; загар A = a / b = 4/3.
Для некоторых углов можно записать точные значения их тригонометрических функций. Наиболее важные случаи представлены в таблице:
Хотя углы 0 и 90 не могут быть острыми в прямоугольном треугольнике, но при расширении понятия тригонометрических функций (см.

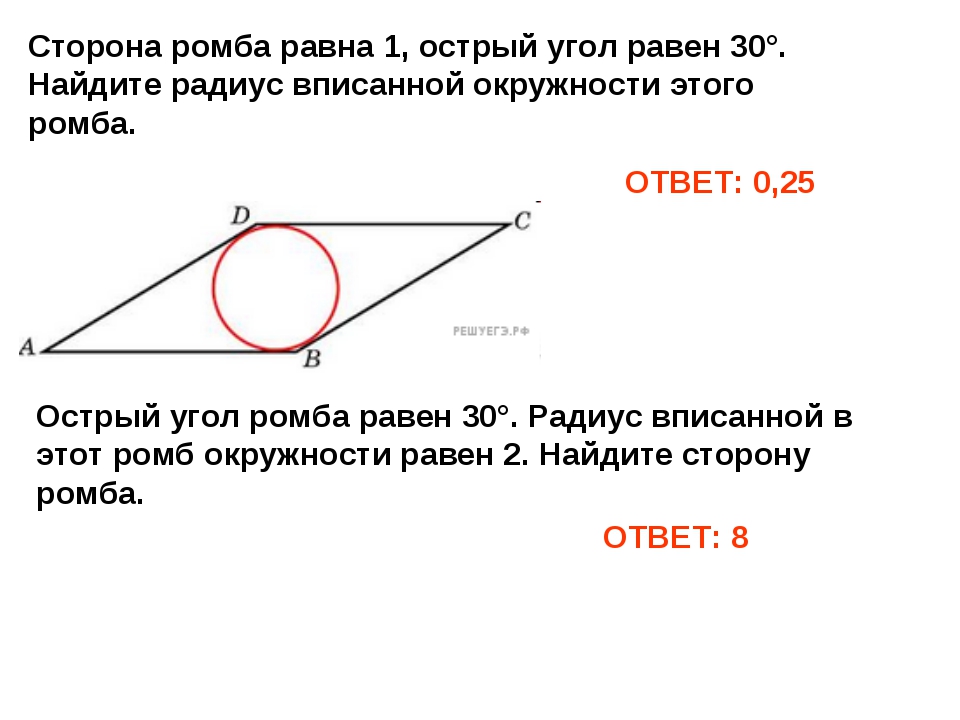 Представлены градусные величины углов. Выберите тупой угол. А) 930. Б)380. В) 900. Г) 6°.
Представлены градусные величины углов. Выберите тупой угол. А) 930. Б)380. В) 900. Г) 6°.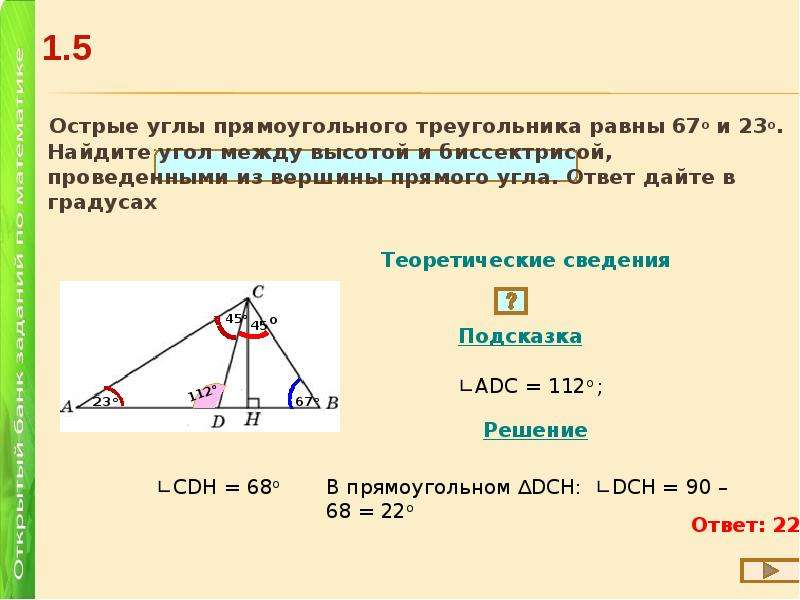 Угол, равный половине развернутого угла, называется: А) острый. Б) тупой. В) прямой. Г) Полуразвёрнутый.
Угол, равный половине развернутого угла, называется: А) острый. Б) тупой. В) прямой. Г) Полуразвёрнутый.