Острый угол — это… Что такое Острый угол?
«∠», обозначение угла в математике
Плоский у́гол — неограниченная геометрическая фигура, образованная двумя лучами (сторонами угла), выходящими из одной точки (вершины угла).
Углом также называют фигуру образованную всеми точками плоскости, заключёнными между этими лучами (Вообще говоря, двум таким лучам соответствуют два угла, так как они делят плоскость на две части. Один из этих углов условно называют внутренним, а другой — внешним.
Иногда, для краткости, углом называют угловую меру.
Угловая мера
Угол в измеряют в градусной мере (градус, минута, секунда), в оборотах — отношение длины дуги s к длине окружности L, в радианах — отношение длины дуги s к радиусу r; исторически применялась также градовая мера измерения углов, в настоящее время она почти нигде не используется.
1 оборот = 2π радианам = 360° = 400 градам.
В системе СИ принято использовать радианы.
В морской терминологии углы обозначаются румбами.
Углы на тригонометрической окружности
В математике в качестве начала отсчёта углов принято направление оси абсцисс (то есть для наблюдателя, расположенного в начале координат, — относительно направления направо), и отсчитывается против часовой стрелки.
В географии в качестве начала отсчёта углов принято направление оси ординат (то есть для наблюдателя, расположенного в начале координат, — относительно направления север (вперёд)), и отсчитывается по часовой стрелке.
Типы углов
Смежные углы — острый (a) и тупой (b). Развёрнутый угол (c)
Смежные углы — два угла с общей вершиной, одна из сторон которых — общая, а оставшиеся стороны лежат на одной прямой (не совпадая). Сумма смежных углов равна 180°.
Вертикальные углы — два угла, которые образуются при пересечении двух прямых и не имеют общих сторон. Два вертикальных угла равны.
Центральные и вписанные углы окружности.
В зависимости от величины углы разделяются на:
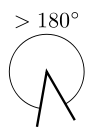
Невыпуклый угол
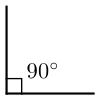
Прямой угол
Вариации и обобщения
Величиной ориентированного угла между прямыми AB и CD (обозначение: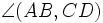 
) называбт величину угла, на который нужно повернуть против часовой стрелки прямую AB так, чтобы она стала параллельна прямой CD. При этом углы, отличающиеся на 
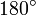или, что по нашему соглашению то же самое, 
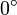). Ориентированные углы обладает следующими свойствами: а) 
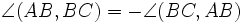; б)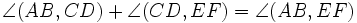 
; в) точки A,B,C,D, не лежащие на одной прямой, принадлежат одной окружности тогда и только тогда, когда 
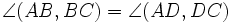.Ряд практических задач приводит к целесообразности рассматривать угол как фигуру, получающуюся при вращении фиксированного луча вокруг точки О (из которой исходит луч) до заданного положения. В этом случае угол является мерой поворота луча. Такое определение позволяет обобщить понятие угла: в зависимости от направления вращения различают положительные и отрицательные углы, рассматривают углы, большие 360°, углы, равные 0°, и т. д. В тригонометрии такое рассмотрение позволяет изучать тригонометрические функции для любых значений аргумента.
Понятие угла обобщается также на различные объекты, рассматриваемые в стереометрии (двугранный угол, многогранный угол, телесный угол).
Кроме этого, рассматривается угол между гладкими кривыми в точке касания: по определению, его величина равна величине угла между касательными к кривым.
Wikimedia Foundation. 2010.
Определение острого угла
Острый угол: определение
Определение 1
Острый угол — это угол, который меньше $90°$ в градусах или $\frac{π}{2}$ в радианах.
Помимо острых углов также существуют тупые и прямые углы. Прямой угол равен 90°, а если две прямые пересекаются под прямым углом, о них также говорят, что они перпендикулярны.
Рисунок 1. Как выглядит острый угол. Автор24 — интернет-биржа студенческих работ
Тупой угол — это любой угол больше чем $90°$, но меньше $180°$.
Для того чтобы определить, является ли угол острым или тупым, достаточно приложить любой предмет, имеющий прямой угол к данному углу так, чтобы их вершины совпадали, например, линейку.
Если прямой угол полностью вмещает в себя нарисованный — то этот угол является острым, если же наоборот нарисованный угол помещает в себя прямой — то рассматриваемый угол тупой.
Более точно угол можно измерить с помощью транспортира. Транспортир — это инструмент, состоящий из линейки и полуокружности.
Для того чтобы им воспользоваться, нужно наложить центр транспортира на вершину угла, причём так, чтобы один из образующих угол лучей совпадал с гранью линейки.
Готовые работы на аналогичную тему
Рисунок 2. Измерение острого угла. Автор24 — интернет-биржа студенческих работ
Второй же луч укажет на значение угла.
Также с помощью транспортира можно построить острый или тупой угол: для этого нужно нарисовать один из лучей, затем разместить его начало в центре транспортира, приложить линейку к необходимому числу градусов и провести по ней линию.
Особенности острых углов
- Если рассматривать 2 смежных угла, один из которых острый, то второй смежный угол обязательно будет тупым;
- В любом треугольнике есть по крайней мере один острый угол;
- Существуют треугольники, все три угла которых являются острыми. Они называются остроугольными.
Пример 1
Какой из углов не является острым?
Рисунок 3. Углы. Автор24 — интернет-биржа студенческих работ
Острым не является угол под буквой «б», так как он больше $90°$.
Определение острый угол общее значение и понятие. Что это такое острый угол
Первое, что мы собираемся сделать, прежде чем полностью войти в установление значения термина «острый угол», это узнать этимологическое происхождение двух слов, которые его формируют:
-Ангуло, во-первых, происходит от греческого. В частности, оно происходит от «ankulos», которое можно перевести как «свернутый», а затем передать на латынь как «angulus», где оно уже принимает значение «угла».
Два луча, которые имеют одну и ту же вершину в качестве исходной точки, образуют угол . В соответствии с анализируемыми характеристиками можно различать различные типы углов.
Острый угол — это угол, который измеряет более 0º и менее 90º . Это означает, что, если рассматривать только целые числа, острый угол составляет от 1 ° до 89 °.
Это определение мер острых углов позволяет утверждать, что это углы, большие нулевых углов (мера которых равна 0º), но меньшие, чем прямые углы (90º),
Следуя классификации острых углов, мы можем подчеркнуть, что они относятся к набору выпуклых углов, который охватывает все углы с измерениями больше 0 ° и меньше 180 °, в отличие от вогнутых углов (которые измеряют больше 180 ° и меньше 360º).
Можно найти острые углы у разных геометрических фигур. В прямоугольных треугольниках появляются два острых угла и прямой угол. У тупых треугольников, с другой стороны, есть два острых угла и тупой угол. В случае острых треугольников три внутренних угла фигуры являются острыми углами.
Мы также можем заметить острые углы на предметах или элементах повседневной жизни. Самый обычный способ нарезать пиццу — это треугольные порции: в каждой порции мы можем найти три острых угла.
В дополнение ко всему вышесказанному мы можем указать, что для измерения острого угла мы должны прибегнуть к использованию конвейера. Эта статья может иметь две основные формы: с полукруглой формой, чтобы можно было измерить углы максимум 180 градусов, или с круглой формой. Последний используется для измерения приблизительно любого типа угла, поскольку его максимум составляет 400 º.
Таким же образом, мы не можем игнорировать тот факт, что некоторые математические и тригонометрические операции могут быть выполнены с острыми углами в треугольниках. Таким образом, например, можно вычислить синус, который будет результатом отношения между длиной ноги, противоположной углу, и гипотенузой.
И что, не забывая, что, кроме того, вы можете приступить к вычислению косинуса, касательной, секущей, косеканс и котангенса.
Прямой, тупой, острый и развернутый углы
Давайте начнем с определения того, что такое угол. Во-первых, он является геометрической фигурой. Во-вторых, он образован двумя лучами, которые называются сторонами угла. В-третьих, последние выходят из одной точки, которую называют вершиной угла. Исходя из этих признаков, мы можем составить определение: угол — геометрическая фигура, которая состоит из двух лучей (сторон), выходящих из одной точки (вершины).
Их классифицируют по градусной величине, по расположению относительно друг друга и относительно окружности. Начнем с видов углов по их величине.
Существует несколько их разновидностей. Рассмотрим подробнее каждый вид.
Основных типов углов всего четыре — прямой, тупой, острый и развернутый угол.
Прямой
Он выглядит так:
Его градусная мера всегда составляет 90о, иначе говоря, прямой угол — это угол 90 градусов. Только они есть у таких четырехугольников, как квадрат и прямоугольник.
Тупой
Он имеет такой вид:
Градусная мера тупого угла всегда больше 90о, но меньше 180о. Он может встречаться в таких четырехугольниках, как ромб, произвольный параллелограмм, во многоугольниках.
Острый
Он выглядит так:
Градусная мера острого угла всегда меньше 90о. Он встречается во всех четырехугольниках, кроме квадрата и произвольного параллелограмма.
Развернутый
Развернутый угол имеет такой вид:
В многоугольниках он не встречается, но не менее важен, чем все остальные. Развернутый угол — это геометрическая фигура, градусная мера которой всегда равняется 180º. На нем можно построить смежные углы, проведя из его вершины один или несколько лучей в любых направлениях.
Есть еще несколько второстепенных видов углов. Их не изучают в школах, но знать хотя бы об их существовании необходимо. Второстепенных видов углов всего пять:
1. Нулевой
Он выглядит так:
Само название угла уже говорит о его величине. Его внутренняя область равняется 0о, а стороны лежат друг на друге так, как показано на рисунке.
2. Косой
Косым может быть и прямой, и тупой, и острый, и развернутый угол. Главное его условие — он не должен равняться 0о, 90о, 180о, 270о.
3. Выпуклый
Выпуклыми являются нулевой, прямой, тупой, острый и развернутый углы. Как вы уже поняли, градусная мера выпуклого угла — от 0о до 180о.
4. Невыпуклый
Невыпуклыми являются углы с градусной мерой от 181о до 359о включительно.
5. Полный
Полным является угол с градусной мерой 360о.
Это все типы углов по их величине. Теперь рассмотрим их виды по расположению на плоскости относительно друг друга.
1. Дополнительные
Это два острых угла, образовывающие один прямой, т.е. их сумма 90о.
2. Смежные
Смежные углы образуются, если через развернутый, точнее, через его вершину, провести луч в любом направлении. Их сумма равна 180о.
3. Вертикальные
Вертикальные углы образуются при пересечении двух прямых. Их градусные меры равны.
Теперь перейдем к видам углов, расположенным относительно окружности. Их всего два: центральный и вписанный.
1. Центральный
Центральным является угол с вершиной в центре окружности. Его градусная мера равна градусной мере меньшей дуги, стянутой сторонами.
2. Вписанный
Вписанным называется угол, вершина которого лежит на окружности, и стороны которого ее пересекают. Его градусная мера равна половине дуги, на которую он опирается.
Это все, что касается углов. Теперь вы знаете, что помимо наиболее известных — острого, тупого, прямого и развернутого — в геометрии существует много других их видов.
Острый угол прямоугольного треугольника: синус, косинус, тангенс, котангенс
В данной публикации мы рассмотрим соотношения катетов и гипотенузы в прямоугольном треугольнике, выраженные в виде тригонометрических функций острого угла, а также, научимся применять полученные знания на практике для решения задач.
Отношения сторон в прямоугольном треугольнике
Допустим, у нас есть треугольник (прямоугольный) со сторонами a, b, c и острым углом α.
Для него верно следующее:
- Синус угла α равен отношению противолежащего катета к гипотенузе:
sin α = b/c - Косинус угла α равен отношению прилежащего катета к гипотенузе:
cos α = a/c - Тангенс угла α равняется отношению противолежащего катета к прилежащему:
tg α = b/a - Котангенс угла α равняется отношению прилежащего катета к противолежащему:
ctg α = a/b - Секанс угла α определяется как отношение гипотенузы к прилежащему катету:
sec α = c/a - Косеканс угла α определяется как отношение гипотенузы к противолежащему катету:
cosec α = c/b
Примеры задач
Задание 1
В прямоугольном треугольнике один из катетов равен 3 см, а гипотенуза 5 см. Найдите угол, который расположен напротив заданного катета.
Решение:
Пусть неизвестный угол – это α. Применяем формулу синуса для его нахождения:
sin α = 3 см / 5 см = 0,6. Следовательно, угол α = aarcsin (0,6) ≈ 36,87°.
Задание 2
В прямоугольном один из острых углов равен 45°, а прилежащий к нему катет – 3 см. Найдите гипотенузу.
Решение:
Так как нам известен угол (α) и прилежащий катет (a), выведем длину гипотенузы из формулу косинуса (c): c = a / cos α = 3 см / cos 45° ≈ 4,24 см.
Острый, тупой, прямой и правый
Угол измеряет величину поворота
Названия углов
По мере увеличения угла название меняется:
Попробуйте сами:
В одной схемеЭта диаграмма может помочь вам запомнить: Также: Acute, Obtuse и Reflex расположены в алфавитном порядке. |
Также: буква «А» имеет острый угол.
Будьте осторожны при измерении
| Меньший угол — тупой угол , , но больший угол — угол отражения |
Поэтому при именовании углов убедитесь, что что вы знаете , какой угол просил !
Положительные и отрицательные углы
При измерении от линии:
- положительный угол идет против часовой стрелки (направление, противоположное ходу часов)
- отрицательный угол идет по часовой стрелке
Пример: −67 °
Части угла
Угловая точка угла называется вершиной
И две прямые стороны называются руками
Угол равен повороту между каждым плечом.
Как маркировать углы
Есть два основных способа маркировать углы:
1. Назовите угол, обычно строчной буквой, например a или b , или иногда греческой буквой, например α (альфа) или θ (тета)
2. или тремя буквами на фигуре, которые определяют угол, при этом средняя буква указывает на то, где на самом деле угол (его вершина).
Пример угла « a » — « BAC », а угол « θ » — « BCD »
,острый угол | Примеры предложений
В Кембриджском словаре пока нет слова об остром угле. Ты можешь помочь!
A с ответвлениямиВикипедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.Плод — самара махровая с двумя округлыми крылатыми семенами, длина крыльев 1,5 3, разложенные под острым углом . ИзВикипедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.Если смотреть на него под острым углом , это превращается в пластиковое изображение черепа. ИзВикипедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.Челюсти короткие, образуют острый угол в месте их соединения; зубы немногочисленны и крепки. ИзВикипедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.В некоторых случаях давление в глазу может быстро нарастать, вызывая боль и покраснение (симптоматическое или так называемое закрытие острый угол ). ИзВикипедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.Между лопаткой и коракоидом, как и у всех летающих птиц, имеется острый угол . ИзВикипедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.Это было особой проблемой, потому что мост пересекался под острым углом , что требовало гораздо более длинного пролета без опоры, чем для перпендикулярного перехода. ИзВикипедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.Фронтальные, первая категория, — это когда близнецы обращены друг к другу так, что оси тел образуют острый угол . ИзВикипедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.Листья безволосые, узкие, длиной от 1 до 1,6 см, шириной 1 мм, клиновидной формы с острым углом у основания листа. ИзВикипедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.При острой -угольной -закрытой глаукоме зрачок обычно фиксируется в среднем положении, овал и вяло реагирует на свет, если вообще реагирует. ИзВикипедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.На схемах, которые мы используем, показана эта конструкция для острого угла , но она действительно работает для любого угла до 180 градусов. ИзВикипедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.В конце концов он пришел к выводу, что: гипотеза об остром угле абсолютно ложна; потому что это противно природе прямых линий. ИзВикипедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.Используя алгебраические меры для отрезков прямых (с учетом отрицательных чисел в качестве длин отрезков), случай тупого угла и острого угла можно рассматривать одновременно. ИзВикипедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.Эти примеры взяты из Cambridge English Corpus и из источников в Интернете. Любые мнения в примерах не отражают мнение редакторов Cambridge Dictionary, Cambridge University Press или его лицензиаров.
острый угол еще нет в Кембриджском словаре.сообщение}}
Выберите часть речи и введите свое предложение в поле «Определение».
{{/сообщение}} Часть речиВыберите существительное, глагол и т. Д. имя прилагательное наречие восклицание существительное число префикс суффикс глагол
Определение
Отправить Отмена
,