Первый замечательный предел
Замечательных пределов существует несколько, но самыми известными являются первый и второй замечательные пределы. Замечательность этих пределов состоит в том, что они имеют широкое применение и с их помощью можно найти и другие пределы, встречающиеся в многочисленных задачах. Этим мы и будем заниматься в практической части данного урока. Для решения задач путём приведения к первому или второму замечательному пределу не нужно раскрывать содержащиеся в них неопределённости, поскольку значения этих пределов уже давно вывели великие математики.
Первым замечательным пределом называется предел отношения синуса бесконечно малой дуги к той же дуге, выраженной в радианной мере:
Приведённое выше равенство основано на эквивалентности бесконечно малых . Следовательно, верно равенство и следующего отношения:
.
Переходим к решению задач на первый замечательный предел. Заметим: если под знаком предела находится тригонометрическая функция, это почти верный признак того, что это выражение можно привести к первому замечательнному пределу.
Пример 1. Найти предел .
Решение. Подстановка вместо x нуля приводит к неопределённости:
.
В знаменателе — синус, следовательно, выражение можно привести к первому замечательному пределу. Начинаем преобразования:
.
В знаменателе — синус трёх икс, а в числителе всего лишь один икс, значит, нужно получить три икс и в числителе. Для чего? Чтобы представить 3x = a и получить выражение .
И приходим к разновидности первого замечательного предела:
,потому что неважно, какая буква (переменная) в этой формуле стоит вместо икса.
Умножаем икс на три и тут же делим:
.
В соответствии с замеченным первым замечательным пределом производим замену дробного выражения:
.
Теперь можем окончательно решить данный предел:
.
Пример 2. Найти предел .
Решение. Непосредственная подстановка вновь приводит к неопределённости «нуль делить на нуль»:
.
Чтобы получить первый замечательный предел, нужно, чтобы икс под знаком синуса в числителе и просто икс в знаменателе были с одним и тем же коэффициентом. Пусть этот коэффициент будет равен 2. Для этого представим нынешний коэффициент при иксе как и далее, производя действия с дробями, получаем:
.
Пример 3. Найти предел .
Решение. При подстановке вновь получаем неопределённость «нуль делить на нуль»:
.
Наверное, вам уже понятно, что из исходного выражения можно получить первый замечательный предел, умноженный на первый замечательный предел. Для этого раскладываем квадраты икса в числителе и синуса в знаменателе на одинаковые множители, а чтобы получить у иксов и у синуса одинаковые коэффициенты, иксы в числителе делим на 3 и тут же умножаем на 3. Получаем:
.
Пример 4. Найти предел .
Решение. Вновь получаем неопределённость «нуль делить на нуль»:
.
Можем получить отношение двух первых замечательных пределов. Делим и числитель, и знаменатель на икс. Затем, чтобы коэффициенты при синусах и при иксах совпадали, верхний икс умножаем на 2 и тут же делим на 2, а нижний икс умножаем на 3 и тут же делим на 3. Получаем:
Пример 5. Найти предел .
Решение. И вновь неопределённость «нуль делить на нуль»:
.
Помним из тригонометрии, что тангенс — это отношение синуса к косинусу, а косинус нуля равен единице. Производим преобразования и получаем:
.
Пример 6. Найти предел .
Решение. Тригонометрическая функция под знаком предела вновь наталкивает на мысль о применении первого замечательного предела. Представляем его как отношение синуса к косинусу.
.
Так как , то и
Пример 7. Найти предел .
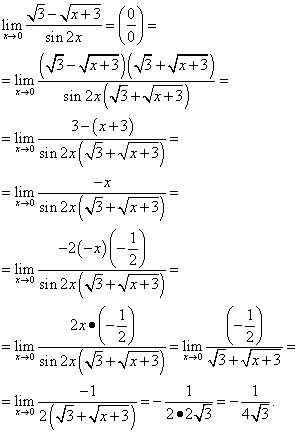
Пример 8. Найти предел .
Решение. Бороться с неопределённостью «ноль делить на ноль» будем приведением к первому замечательному пределу. Вспоминаем формулу тригонометрической единицы и подставляем её. Потом вспоминаем, что косинус в квадрате нуля и просто косинус нуля равны единице, а они у нас с противоположными знаками, значит взаимно уничтожаются. Затем умножаем числитель и знаменатель на выражение, сопряжённое знаменателю. И дальнейшие преобразования. Всё вышеописанное выглядит так:
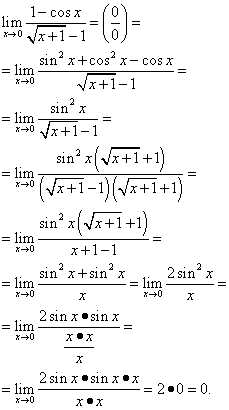
Начало темы «Предел»
Продолжение темы «Предел»
function-x.ru
Замечательные пределы и их примеры
Примеры пределов содержащие неопределенности вида ноль на ноль часто встречаются в тригонометрических функциях. Для их раскрытия используют первый замечательный предел суть которого заключается в том, что предел отношения синус функции к аргументу, когда тот стремится к нулю равен единице
На основе этой формулы можно получить ряд полезных для практики пределов
1)
2)
3)
Второй замечательный предел позволяет раскрыть неопределенности вида .
Коротко он имеет следующую запись
где –экспонента.
На основе второго замечательного предела получают следующие формулы
1)
2)
Примеры, которые сводятся к первому и второму замечательному пределу встречаются довольно редко, однако без них такие примеры не решить.
Рассмотрим некоторые примеры из сборника задач Дубовика В.П., Юрика И.И. «Высшая математика» которые приводят к применению замечательных пределов.
————————————
Пример 1. Найти пределы функций.
1) (4. 388)
2) (4. 393)
3) (4. 399)
4) (4. 432)
5) (4. 437)
6)
7)
Решение.
1) Домножим числитель и знаменатель на аргумент и сведем к первой замечательной границы
2) Разделим числитель и знаменатель на аргумент и сократим
3) Согласно разложению корня в окрестности единицы
знаменатель возможно превратить следующим образом
На основе этого и находим предел
4) Сведем к второму замечательному пределу
5) Сведем к правильной дроби выражение в скобках
и подставим в предел
Вычислим первый множитель
Второй предел равна единице
Окончательно получим
6) Сведем решение к первому замечательному пределу
7) Преобразуем показатель для применения второго замечательного предела
Подобных примеров можно привести много, они встречаются в контрольных, тестах, екзаменах. Их решения позволит закрепить Вам лучшие практические навыки поэтому пробуйте решать самостоятельно. Если в обучении вам встретятся тяжелые пределы посчитать которые Вы не в состоянии обращайтесь к нам. Мы Вам в этом поможем!
————————————
Посмотреть материалы:
yukhym.com
Первый замечательный предел. , где P(x) = a0xn + a1xn-1 +…+an,
Q(x) = b0xm + b1xm-1 +…+bm — многочлены.
Итого:
Второй замечательный предел.
Третий замечательный предел.
Часто если непосредственное нахождение предела какой – либо функции представляется сложным, то можно путем преобразования функции свести задачу к нахождению замечательных пределов.
Кроме трех, изложенных выше, пределов можно записать следующие полезные на практике соотношения:
Пример. Найти предел.
Пример. Найти предел.
Пример. Найти предел.
Пример.
Пример. Найти предел.
Пример. Найти предел .
Для нахождения этого предела разложим на множители числитель и знаменатель данной дроби.
X2 – 6X + 8 = 0; X2 – 8X + 12 = 0;
D = 36 – 32 = 4; D = 64 – 48 = 16;
X1 = (6 + 2)/2 = 4; X1 = (8 + 4)/2 = 6;
X2 = (6 – 2)/2 = 2 ; X2 = (8 – 4)/2 = 2;
Тогда
Пример. Найти предел.
домножим числитель и знаменатель дроби на сопряженное выражение: =
=.
Пример. Найти предел.
Пример. Найти предел .
Разложим числитель и знаменатель на множители.
X2 – 3X + 2 = (X – 1)(X – 2)
X3 – 6X2 + 11X – 6 = (X – 1)(X – 2)(X – 3), т. к.X3 – 6×2 + 11x – 6 x — 1
x3 – x2 x2 – 5x + 6
— 5×2 + 11x
— 5×2 + 5x
6x — 6
6x — 6 0
X2 – 5x + 6 = (x – 2)(x – 3)
Тогда
Пример. Найти предел.
Для самостоятельного решения:
1)
2)
3)
4)
5)
6)
7)
8) — не определен.
| < Предыдущая | Следующая > |
|---|
matica.org.ua
2 замечательный предел | Математика
2 замечательный предел:
где
при условии, что f(x)→∞.
2 замечательный предел, как правило, применяют в тех случаях, когда нужно найти предел степени с переменной в показателе. Рассмотрим примеры на второй замечательный предел.
Чтобы раскрыть неопределенность единица в степени бесконечность, используем 2 замечательный предел. Для этого минус уберем в знаменатель и воспользуемся рассуждениями:
Итак, имеем:
2й замечательный предел раскрывает неопределенность вида единица в степени бесконечность. Значит, неопределенность бесконечность на бесконечность в степени бесконечность необходимо привести к такому виду. Рассуждаем так:
получили неопределенность единица в степени бесконечность, и теперь можем применить второй замечательный предел:
Рассуждаем аналогично: чтобы раскрыть неопределенность бесконечность на бесконечность в степени бесконечность, нужно привести выражение к виду единица в степени бесконечность и затем применить второй 2 замечательный предел:
www.matematika.uznateshe.ru
Первый замечательный предел — Мегаобучалка
Рассмотрим следующий предел: (вместо родной буквы «хэ» я буду использовать греческую букву «альфа», это удобнее с точки зрения подачи материала).
Согласно нашему правилу нахождения пределов (см. статью Пределы. Примеры решений) пробуем подставить ноль в функцию: в числителе у нас получается ноль (синус нуля равен нулю), в знаменателе, очевидно, тоже ноль. Таким образом, мы сталкиваемся с неопределенностью вида , которую, к счастью, раскрывать не нужно. В курсе математического анализа, доказывается, что:
Данный математический факт носит название Первого замечательного предела.
Нередко в практических заданиях функции могут быть расположены по-другому, это ничего не меняет:
– тот же самый первый замечательный предел.
! Но самостоятельно переставлять числитель и знаменатель нельзя! Если дан предел в виде, то и решать его нужно в таком же виде, ничего не переставляя.
На практике в качестве параметра может выступать не только переменная , но и элементарная функция, сложная функция. Важно лишь, чтобы она стремилась к нулю.
Примеры:
, , ,
Здесь , , , , и всё гуд – первый замечательный предел применим.
А вот следующая запись – ересь:
Почему? Потому-что многочлен не стремится к нулю, он стремится к пятерке.
Кстати, вопрос на засыпку, а чему равен предел ? Ответ можно найти в конце урока.
На практике не все так гладко, почти никогда студенту не предложат решить халявный предел и получить лёгкий зачет. Все-таки «халявные» математические определения и формулы вроде лучше помнить наизусть, это может оказать неоценимую помощь на зачете, когда вопрос будет решаться между «двойкой» и «тройкой», и преподаватель решит задать студенту какой-нибудь простой вопрос или предложить решить простейший пример («а может он (а) все-таки знает чего?!»).
Переходим к рассмотрению практических примеров:
Пример 1
Найти предел
Если мы замечаем в пределе синус, то это нас сразу должно наталкивать на мысль о возможности применения первого замечательного предела.
Сначала пробуем подставить 0 в выражение под знак предела (делаем это мысленно или на черновике):
Итак, у нас есть неопределенность вида , ее обязательно указываем в оформлении решения. Выражение под знаком предела у нас похоже на первый замечательный предел, но это не совсем он, под синусом находится , а в знаменателе .
В подобных случаях первый замечательный предел нам нужно организовать самостоятельно, используя искусственный прием. Ход рассуждений может быть таким: «под синусом у нас , значит, в знаменателе нам тоже нужно получить ».
А делается это очень просто:
То есть, знаменатель искусственно умножается в данном случае на 7 и делится на ту же семерку. Теперь запись у нас приняла знакомые очертания.
Когда задание оформляется от руки, то первый замечательный предел желательно пометить простым карандашом:
Что произошло? По сути, обведенное выражение у нас превратилось в единицу и исчезло в произведении:
Теперь только осталось избавиться от трехэтажности дроби:
Готово. Окончательный ответ:
Если не хочется использовать пометки карандашом, то решение можно оформить так:
“
Используем первый замечательный предел
“
Пример 2
Найти предел
Опять мы видим в пределе дробь и синус. Пробуем подставить в числитель и знаменатель ноль:
Действительно, у нас неопределенность и, значит, нужно попытаться организовать первый замечательный предел. На уроке Пределы. Примеры решений мы рассматривали правило, что когда у нас есть неопределенность , то нужно разложить числитель и знаменатель на множители. Здесь – то же самое, степени мы представим в виде произведения (множителей):
Далее, по уже знакомой схеме организовываем первые замечательные пределы. Под синусами у нас , значит, в числителе тоже нужно получить :
Аналогично предыдущему примеру, обводим карандашом замечательные пределы (здесь их два), и указываем, что они стремятся к единице:
Собственно, ответ готов:
В следующих примерах, я не буду заниматься художествами в Пэйнте, думаю, как правильно оформлять решение в тетради – Вам уже понятно.
Пример 3
Найти предел
Подставляем ноль в выражение под знаком передела:
Получена неопределенность , которую нужно раскрывать. Если в пределе есть тангенс, то почти всегда его превращают в синус и косинус по известной тригонометрической формуле (кстати, с котангенсом делают примерно то же самое, см. методический материалГорячие тригонометрические формулы на странице Математические формулы, таблицы и справочные материалы).
В данном случае:
Косинус нуля равен единице, и от него легко избавиться (не забываем пометить, что он стремится к единице):
Таким образом, если в пределе косинус является МНОЖИТЕЛЕМ, то его, грубо говоря, нужно превратить в единицу, которая исчезает в произведении.
Дальше по накатанной схеме, организуем первый замечательный предел:
Здесь все вышло проще, без всяких домножений и делений. Первый замечательный предел тоже превращается в единицу и исчезает в произведении:
В итоге получена бесконечность, бывает и такое.
Пример 4
Найти предел
Пробуем подставить ноль в числитель и знаменатель:
Получена неопределенность (косинус нуля, как мы помним, равен единице)
Используем тригонометрическую формулу . Возьмите на заметку! Пределы с применением этой формулы почему-то встречаются очень часто.
Постоянные множители вынесем за значок предела:
Организуем первый замечательный предел:
Здесь у нас только один замечательный предел, который превращается в единицу и исчезает в произведении:
Избавимся от трехэтажности:
Предел фактически решен, указываем, что оставшийся синус стремится к нулю:
Пример 5
Найти предел
Этот пример сложнее, попробуйте разобраться самостоятельно:

megaobuchalka.ru
Примеры первого и второго замечательных пределов онлайн · Как пользоваться Контрольная Работа РУ
Некоторые пределы можно вычислить, используя первый замечательный предел, для других же потребуется применить второй замечательный предел.
Здесь мы приведём примеры таких пределов, которые используют методы замечательных пределов
. Причём данные примеры будут вычислены онлайн.
Итак, нам даны два примера:
/7*x\
11 - 11*cos|---|
\ 9 /
lim ----------------
x->0+ 2
x и
3*x
/3 + 2*x \
lim |--------|
x->oo\-2 + 2*x/
Первый предел решим с помощью первого замечательного предела, второй пример соответственно с помощью второго замечательного предела.
Для того, чтобы решить указанные примеры, откройте сервис по нахождению пределов онлайн:
и вбейте для первого примера:
(11 — 11*cos(7*x/9))/x^2
Не забудьте указать предел аргумента x, стремящегося к 0
Вы получите подробный ответ:
Возьмём предел
::
/7*x\
11 - 11*cos|---|
\ 9 /
lim ----------------
x->0+ 2
x
Используем тригонометрическую формулу
::
sin(a)^2 = (1 - cos(2*a))/2
преобразуем
::
/7*x\ /7*x\
11 - 11*cos|---| 11 - 11*cos|---|
\ 9 / \ 9 /
lim ---------------- = lim ---------------- =
x->0+ 2 x->0+ 2
x x
::
2
/ \
| /7*x\|
= | sin|---||
| \ 18/|
22*| lim --------|
\x->0+ x /
Сделаем замену
::
7*x
u = ---
18
тогда
::
/7*x\
sin|---|
\ 18/ 7*sin(u) =
lim -------- = lim --------
x->0+ x u->0+ 18*u
::
sin(u)
7* lim ------
u->0+ u
-------------
18
Предел
::
sin(u)
lim ------
u->0+ u
есть первый замечательный предел, он равен 1.
тогда
::
2
/ \ 2
| /7*x\| / sin(u)\
| sin|---|| |7* lim ------| =
| \ 18/| | u->0+ u |
22*| lim --------| = 22*|-------------|
\x->0+ x / \ 18 /
::
= 22*(7/18)^2 = 539/162
Тогда, окончательный ответ:
::
/7*x\
11 - 11*cos|---|
\ 9 / 539
lim ---------------- = ---
x->0+ 2 162
x
Для второго примера вы должны вбить в калькулятор пределов:
((3 + 2*x)/(-2 + 2*x))^(3*x)
Не забудьте указать, что аргумент x стремится к бесконечности (нужно вбить +oo)
Тогда для вбитой функции вы получите подробное решение:
Возьмём предел
::
3*x
/3 + 2*x \
lim |--------|
x->oo\-2 + 2*x/
преобразуем
::
3*x
/3 + 2*x \
lim |--------| =
x->oo\-2 + 2*x/
::
3*x
/-2 + 2*x + 5\
lim |------------| =
x->oo\ -2 + 2*x /
::
3*x
/-2 + 2*x 5 \
lim |-------- + --------| =
x->oo\-2 + 2*x -2 + 2*x/
::
3*x
/ 5 \
lim |1 + --------| =
x->oo\ -2 + 2*x/
сделаем замену
::
-2 + 2*x
u = --------
5
тогда
::
3*x
/ 5 \
lim |1 + --------| =
x->oo\ -2 + 2*x/
::
15*u
3 + ----
2
/ 1\ =
lim |1 + -|
u->oo\ u/
::
15*u
----
3 2
/ 1\ / 1\ =
lim |1 + -| *|1 + -|
u->oo\ u/ \ u/
::
15*u
----
3 2
/ 1\ / 1\ =
lim |1 + -| * lim |1 + -|
u->oo\ u/ u->oo\ u/
::
15*u
----
2
/ 1\ =
lim |1 + -|
u->oo\ u/
::
15/2
/ \
| u|
| / 1\ |
| lim |1 + -| |
\u->oo\ u/ /
Предел
::
u
/ 1\
lim |1 + -|
u->oo\ u/
есть второй замечательный предел, он равен e ~ 2.718281828459045
тогда
::
15/2
/ \
| u|
| / 1\ | 15/2
| lim |1 + -| | = e
\u->oo\ u/ /
Получаем окончательный ответ:
::
3*x
/3 + 2*x \ 15/2
lim |--------| = e
x->oo\-2 + 2*x/
Ещё раз приведу ссылку на сервис:
>> решение пределов <<
www.kontrolnaya-rabota.ru
