Взаимосвязь различных классов неорганических веществ – HIMI4KA

Рассмотрим её на нескольких примерах.
Пример 1. Взаимосвязь соединений железа.
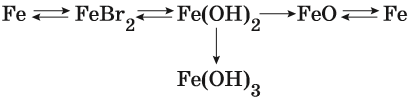
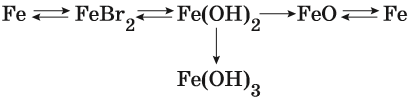
Переход из железа в бромид железа (II) возможен при реакции железа с бромоводородной кислотой:
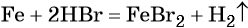
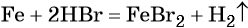
Получить из бромида железа (II) чистое железо можно при электролизе расплава:
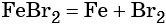
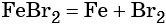
При добавлении к бромиду железа (II) щёлочи образуется гидроксид железа (II):
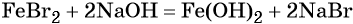
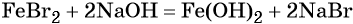
Обратный переход возможен при взаимодействии гидроксида железа (II) с бромоводородной кислотой:
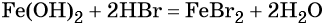
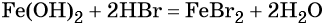
Окисление гидроксида железа (II) приводит к гидроксиду железа (III):
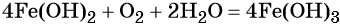
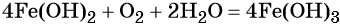
При нагревании гидроксид железа (II) теряет воду, превращаясь в оксид железа (II):
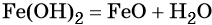
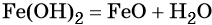
Восстановление оксида железа (II) приводит к железу:
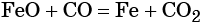
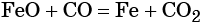
Пример 2. Взаимосвязь соединений железа.
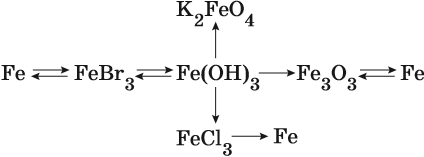

Реакция железа с бромом приводит к бромиду железа (III):
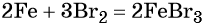
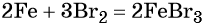
Получить из этого соединения железо можно электролизом расплава:
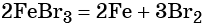
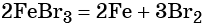
Переход из бромида железа (III) в гидроксид железа (III) возможен под действием щёлочи:
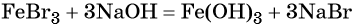
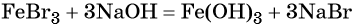
При нагревании гидроксид железа (III) теряет воду, превращаясь в оксид железа (III):
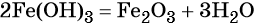
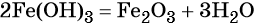
Восстановлением оксида железа (III) можно получить железо:
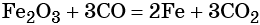
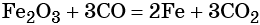
Железо в степени окисления +6 можно получить из гидроксида железа (III) по реакции:
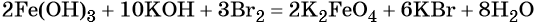
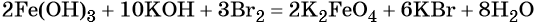
Гидроксид железа (III) под действием соляной кислоты переходит в хлорид железа (III):
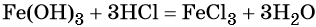
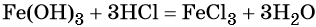
Из хлорида железа (III) электролизом можно получить железо:


Пример 3. Взаимосвязь соединений серы.
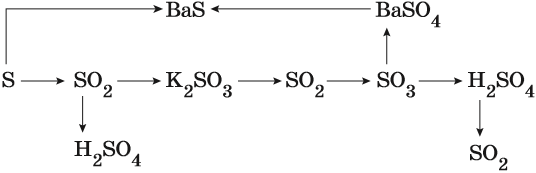

Сера окисляется кислородом воздуха до оксида серы (IV):
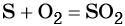
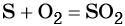
Взаимодействие серы с водородом приводит к сероводороду:
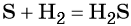
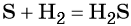
Оксид серы (IV) может вступить в окислительно-восстановительную реакцию с образованием серной кислоты или в обменную реакцию с образованием сульфита калия:
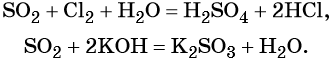
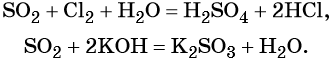
Под действием сильных кислот сульфит калия разлагается до SO2:
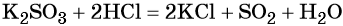
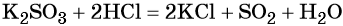
Каталитическое окисление SO2 приводит к оксиду серы (VI):
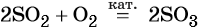
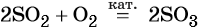
Из оксида серы (VI) можно получить как серную кислоту, так и сульфат бария:
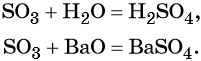
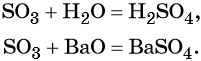
Из сульфата бария восстановлением углём можно получить сульфид бария:
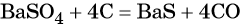
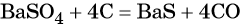
Восстановление SO2 приводит к сере:
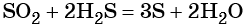
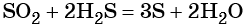
Пример 4. Осуществить следующую цепочку превращений: N2 → NH3 → (NH4)2SO4 → NH4Cl.
Азот взаимодействует с водородом при повышенной температуре в присутствии катализатора с образованием аммиака:
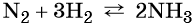
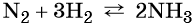
Реакция газообразного аммиака с серной кислотой приводит к сульфату аммония:
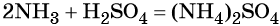
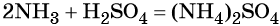
При взаимодействии водных растворов сульфата аммония и хлорида бария образуется нерастворимый сульфат бария, эта реакция идёт до конца. После отделения осадка и упаривания водного раствора можно выделить чистый хлорид аммония:
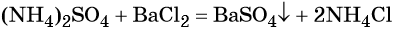
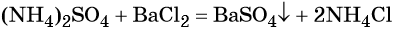
Пример 5. Осуществить следующую цепочку превращений: NO2 → HNO3 → NH4NO3 → N2O.
Оксид азота (IV) при взаимодействии с кислородом и водой даёт азотную кислоту:
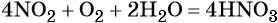
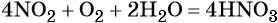
При реакции азотной кислоты с аммиаком образуется нитрат аммония:
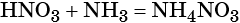
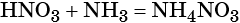
Контролируемое разложение нитрата аммония приводит к образованию оксида азота (I) и воды:
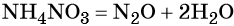
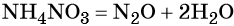
Пример 6. Осуществить следующую цепочку превращений: NaBr → NaCl → Cl2 → KClO.
Хлор способен вытеснять бром из бромидов:
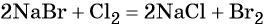
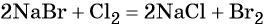
Электролиз расплава хлорида натрия приводит к образованию молекулярного хлора:
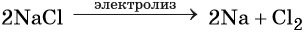
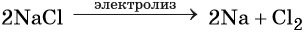
Гипохлорид калия образуется при взаимодействии газообразного хлора с водным раствором гидроксида калия при охлаждении:
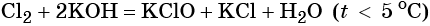
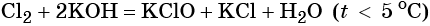
Особенностью заданий, в которых требуется определить неизвестное вещество Х как промежуточный продукт в цепочке химических превращений, является принципиальная возможность наличия нескольких правильных ответов. Вам нужно обосновать свой выбор.
Пример 7. Предложите формулы неизвестных веществ в приведённых ниже последовательностях химических превращений и обоснуйте этот выбор. Приведите уравнения химических реакций, с помощью которых эти превращения можно осуществить:
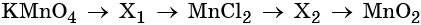
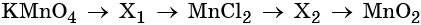
Каким же может быть вещество X1? Возможны несколько вариантов. Предположим, что марганец в этом соединении имеет степень окисления +2, тогда этим веществом будет, например, сульфат марганца (II). Почему? Из него удобно получит хлорид марганца (II) с помощью обменной реакции:
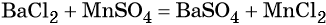
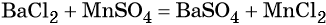
Данная реакция пойдёт до конца, потому что сульфат бария выпадет в осадок.
Перманганат калия — сильный окислитель, который при реакции с восстановителем в кислой среде может понизить свою степень окисления до +2. Чтобы получить сульфат марганца (II) из перманганата калия, можно использовать окислительно-восстановительную реакцию:
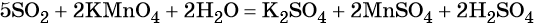
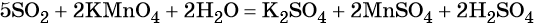
Другой вариант ответа:
Из хлорида марганца (II) можно получить нитрат марганца (II) с помощью обменной реакции с нитратом серебра. Эта реакция идёт до конца благодаря образованию нерастворимого хлорида серебра:
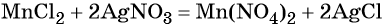
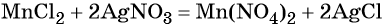
Термическое разложение нитрата марганца (II) — обычный способ получения оксида марганца (IV):
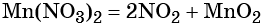
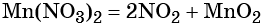
Пример 8. Предложите формулы неизвестных веществ в приведённых ниже последовательностях химических превращений и обоснуйте этот выбор. Приведите уравнения химических реакций, с помощью которых эти превращения можно осуществить:
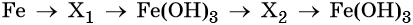
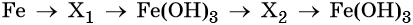
Наиболее рациональным вариантом будет следующий. Вначале железо под действием хлора окисляется до хлорида железа (III) (вещество X1), из которого по обменной реакции получают гидроксид железа (III):
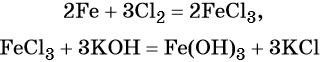
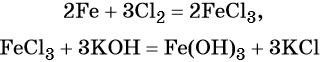
Веществом (X2) может быть любая растворимая соль железа (III), например сульфат, нитрат и т. д.:
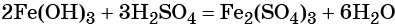
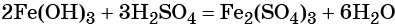
Под действием расчётного количества щёлочи в осадок выпадает гидроксид железа (III):
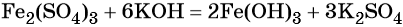
Тренировочные задания
Общее задание 1. Составьте уравнения реакций, с помощью которых можно осуществить следующие цепочки превращений:
1. Al → AlCl3 → Al(OH)3 → KAlO2 → K[Al(OH)4] → Al(OH)3.
2. Ca3(PO4)2 → P → P2O5 → → Ca(H2PO4)2 → CaHPO4 → Ca3(PO4)2.
3. FeS → H2S → S → SO2 → NaHSO3 → BaSO3 → BaSO4.
4. Cl2 → CaOCl2 → CaCO3 → CaO → → CaC2 → Ca(OH)2 → Ca(HSO3)2.
5. Ca3(PO4)2 → P → P2O5 → H3PO4.
6. NH4NO2 → N2 → NH3 → NH4NO3.
7. P → Ca3P2 → PH3 → H3PO4.
8. NH3 → N2 → Mg3N2 → NH3.
9. KNO2 → NO → NO2 → HNO3.
10. H2SO4 → SO2 → SO3 → H2SO4.
11. HCl → Cl2 → KClO3 → Cl2.
12. Cl2 → NaCl → HCl → AlCl3.
13. KCl → Cl2 → NaClO → NaClO3.
14. HBr → NaBr → Br2 → HBr.
15. KBr → Br2 → HBr → NaBr.
16. NaCl → HCl → Cl2 → KClO3.
17. Mg → Mg3N2 → NH3 → Al(OH)3.
18. Ba(NO3)2 → Fe(NO3)2 → Fe2O3 → Fe.
Общее задание 2. Предложите формулы неизвестных веществ в приведённых ниже последовательностях химических превращений и обоснуйте ваш выбор. Приведите уравнения химических реакций, с помощью которых эти превращения можно осуществить:
1. Cu(NO3)2 → X1 → CuCl2 → X2 → Cu(OH)2.
2. FeS → X1 → Fe2O3 → X2 → FeS.
3. H3PO4 → X1 → P → X2 → H3PO4.
4. SiO2 → Si → X → BaSiO3.
5. MgSO4 → X1 → MgI2 → X2 → Mg(OH)2.
6. KNO2 → X1 → NO2 → X2 → Ba(NO3)2.
Ответы


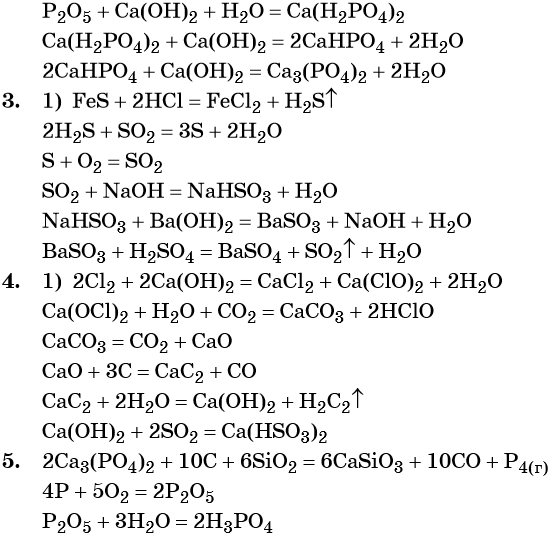
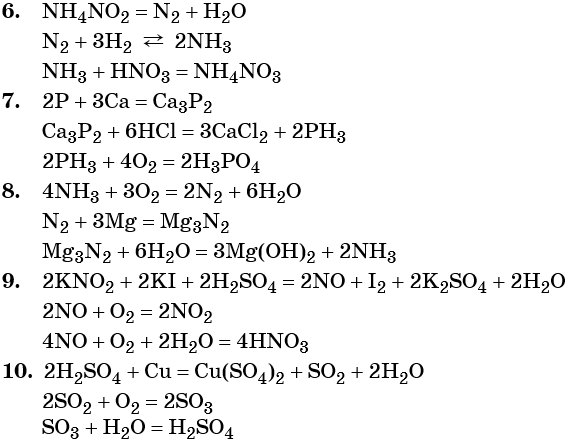
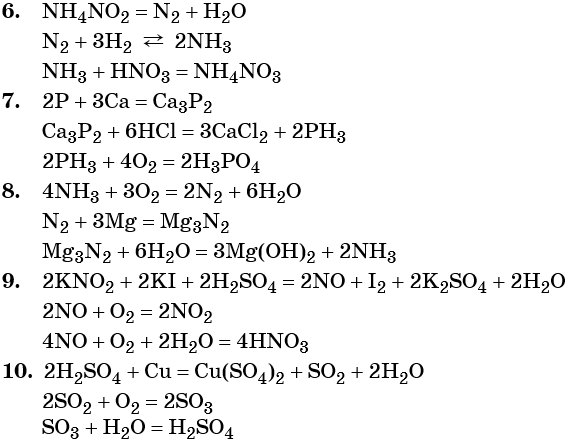


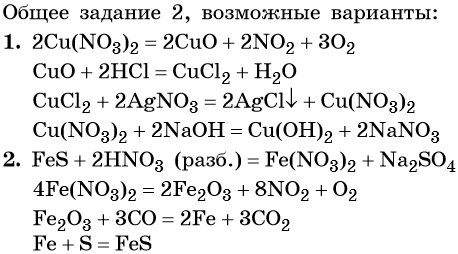
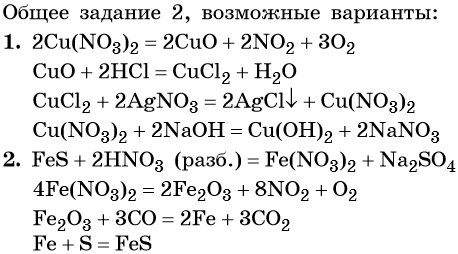
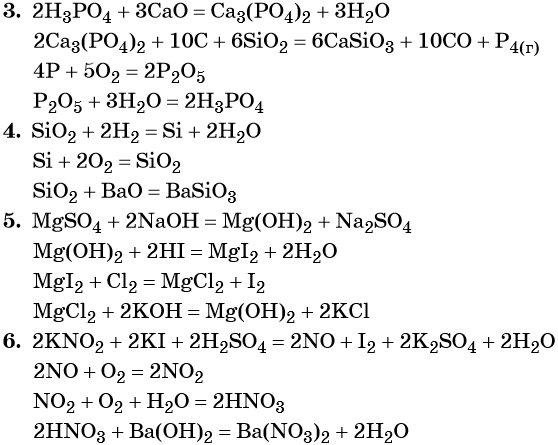
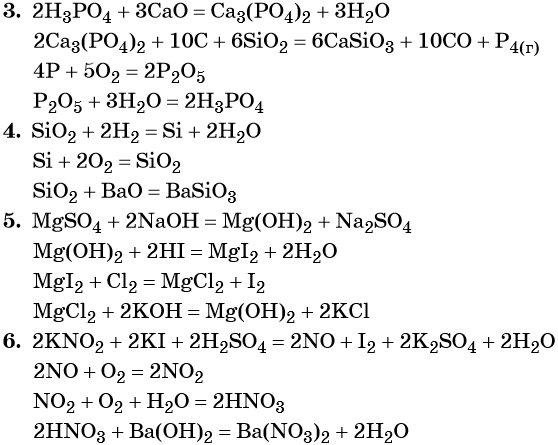
Органические цепочки из ЕГЭ с решениями (50 цепочек).
Задание №1
Напишите уравнения реакций, с помощью которых можно осуществить следующие превращения:

При написании уравнений реакций используйте структурные формулы органических веществ.
Решение1) Уравнение спиртового брожения глюкозы под действием дрожжей:

2) Этиловый спирт сернокислым раствором перманганата калия может быть окислен до уксусной кислоты:
3) Уравнение нейтрализации уксусной кислоты гидроксидом натрия:

4) Взаимодействие солей карбоновых кислот со щелочами при сплавлении приводит к образованию углеводорода с меньшим числом атомов углерода
5) Алканы вступают в реакцию нитрования с разбавленной азотной кислотой при сильном нагревании:
Задание №2
Напишите уравнения реакций, с помощью которых можно осуществить следующие превращения:

При написании уравнений реакций используйте структурные формулы органических веществ.
Решение1) При нагревании одноатомных спиртов с концентрированной серной кислотой выше 140 оС протекает внутримолекулярная дегидратация с образованием алкена:

2) Алкены вступают в реакцию соединения с бромом. При этом атомы брома присоединяются по месту двойной связи, сами двойная связь превращается в одинарную:

3) Вицинальные дигалогенпроизоводные углеводородов при нагревании с некоторыми металлами, например, цинком или магнием, образуют алкены:

4) Гидратация несимметричных алкенов протекает в соответствии с правилом Марковникова:

5) Вторичные спирты в ЕГЭ окисляем до соответствующих кетонов (углеродный скелет не рвем):
Задание №3
Напишите уравнения реакций, с помощью которых можно осуществить следующие превращения:

При написании уравнений реакций используйте структурные формулы органических веществ.
Решение1) При бромировании бутана на свету образуется преимущественно 2-бромбутан:

2) При действии на галогенпроизводные алканов спиртового раствора щелочи при нагревании образуется алкен. Реакция протекает для 2-бромбутана в соответствии с правилом Зайцева:

3) Бутен-2, реагируя с бромом, образует 2,3-дибромбутан:

4) 2,3-дибромбутан при реакции с избытком спиртового раствора щелочи образует бутин-2:

5) Гидратация алкинов с числом углеродных атомов в молекуле больше 2-х приводит к образованию кетонов:
Задание №4
Напишите уравнения реакций, с помощью которых можно осуществить следующие превращения:

При написании уравнений реакций используйте структурные формулы органических веществ.
Решениеv1) Реакция алкенов с нейтральным холодным раствором перманганата калия приводит к образованию соответствующих вицинальных диолов:
2) Взаимодействие этиленгликоля с избытком бромоводорода приводит к образованию 1,2-дибромэтана:

3) Дегидрогалогенирование вицинальных дигалогеналканов действием спиртового раствора щелочи приводит к образованию соответствующих алкинов:

4) В результате гидратации ацетилена в присутствии солей ртути образуется ацетальдегид:

5) Совместное нагревание ацетальдегида с гидроксидом меди (II) приводит к его окислению до уксусной кислоты. Гидроксид меди (II) при этом восстанавливается до оксида меди (I) (кирпично-красный осадок):

Задание №5
Напишите уравнения реакций, с помощью которых можно осуществить следующие превращения:

При написании уравнений реакций используйте структурные формулы органических веществ.
Решение
Задание №6
Напишите уравнения реакций, с помощью которых можно осуществить следующие превращения:

При написании уравнений реакций используйте структурные формулы органических веществ.
Решение
Задание №7
Напишите уравнения реакций, с помощью которых можно осуществить следующие превращения:

При написании уравнений реакций используйте структурные формулы органических веществ.
Решение
Задание №8
Напишите уравнения реакций, с помощью которых можно осуществить следующие превращения:

При написании уравнений реакций используйте структурные формулы органических веществ.
Решение
Задание №9
Напишите уравнения реакций, с помощью которых можно осуществить следующие превращения:

При написании уравнений реакций используйте структурные формулы органических веществ.
Решение
Задание №10
Напишите уравнения реакций, с помощью которых можно осуществить следующие превращения:

При написании уравнений реакций используйте структурные формулы органических веществ.
РешениеОтвет:

Задание №11
Напишите уравнения реакций, с помощью которых можно осуществить следующие превращения:

При написании уравнений реакций используйте структурные формулы органических веществ.
РешениеОтвет: 
Задание №12
Напишите уравнения реакций, с помощью которых можно осуществить следующие превращения:

При написании уравнений реакций используйте структурные формулы органических веществ.
РешениеОтвет:

Задание №13
Напишите уравнения реакций, с помощью которых можно осуществить следующие превращения:

При написании уравнений реакций используйте структурные формулы органических веществ.
РешениеОтвет:

Задание №14
Напишите уравнения реакций, с помощью которых можно осуществить следующие превращения:

При написании уравнений реакций используйте структурные формулы органических веществ.
РешениеОтвет:

Задание №15
Напишите уравнения реакций, с помощью которых можно осуществить следующие превращения:

При написании уравнений реакций используйте структурные формулы органических веществ.
РешениеОтвет:

Задание №16
Напишите уравнения реакций, с помощью которых можно осуществить следующие превращения:

При написании уравнений реакций используйте структурные формулы органических веществ.
РешениеОтвет:

Задание №17
Напишите уравнения реакций, с помощью которых можно осуществить следующие превращения:

При написании уравнений реакций используйте структурные формулы органических веществ.
РешениеОтвет:

Задание №18
Напишите уравнения реакций, с помощью которых можно осуществить следующие превращения:

При написании уравнений реакций используйте структурные формулы органических веществ.
РешениеОтвет:

Задание №19
Напишите уравнения реакций, с помощью которых можно осуществить следующие превращения:

При написании уравнений реакций используйте структурные формулы органических веществ.
РешениеОтвет:

Задание №20
Напишите уравнения реакций, с помощью которых можно осуществить следующие превращения:

При написании уравнений реакций используйте структурные формулы органических веществ.
РешениеОтвет:

Задание №21
Напишите уравнения реакций, с помощью которых можно осуществить следующие превращения:

При написании уравнений реакций используйте структурные формулы органических веществ.
РешениеОтвет:

Задание №22
Напишите уравнения реакций, с помощью которых можно осуществить следующие превращения:

При написании уравнений реакций используйте структурные формулы органических веществ.
РешениеОтвет:

Задание №23
Напишите уравнения реакций, с помощью которых можно осуществить следующие превращения:

При написании уравнений реакций используйте структурные формулы органических веществ.
РешениеОтвет:

Задание №24
Напишите уравнения реакций, с помощью которых можно осуществить следующие превращения:

При написании уравнений реакций используйте структурные формулы органических веществ.
РешениеОтвет:

Задание №25
Напишите уравнения реакций, с помощью которых можно осуществить следующие превращения:

При написании уравнений реакций используйте структурные формулы органических веществ.
РешениеОтвет:
Задание №26
Напишите уравнения реакций, с помощью которых можно осуществить следующие превращения:

При написании уравнений реакций используйте структурные формулы органических веществ.
РешениеОтвет:

Задание №27
Напишите уравнения реакций, с помощью которых можно осуществить следующие превращения:

При написании уравнений реакций используйте структурные формулы органических веществ.
РешениеОтвет:

Задание №28
Напишите уравнения реакций, с помощью которых можно осуществить следующие превращения:

При написании уравнений реакций используйте структурные формулы органических веществ.
РешениеОтвет:

Задание №29
Напишите уравнения реакций, с помощью которых можно осуществить следующие превращения:

При написании уравнений реакций используйте структурные формулы органических веществ.
РешениеОтвет:

Задание №30
Напишите уравнения реакций, с помощью которых можно осуществить следующие превращения:

При написании уравнений реакций используйте структурные формулы органических веществ.
РешениеОтвет:

Задание №31
Напишите уравнения реакций, с помощью которых можно осуществить следующие превращения: При написании уравнений реакций используйте структурные формулы органических веществ. Решение Ответ:
При написании уравнений реакций используйте структурные формулы органических веществ. Решение Ответ: 
Задание №32
Напишите уравнения реакций, с помощью которых можно осуществить следующие превращения:

При написании уравнений реакций используйте структурные формулы органических веществ.
РешениеОтвет:

Задание №33
Напишите уравнения реакций, с помощью которых можно осуществить следующие превращения:

При написании уравнений реакций используйте структурные формулы органических веществ.
РешениеОтвет:

Задание №34
Напишите уравнения реакций, с помощью которых можно осуществить следующие превращения:

При написании уравнений реакций используйте структурные формулы органических веществ.
РешениеОтвет:

Задание №35
Напишите уравнения реакций, с помощью которых можно осуществить следующие превращения:

При написании уравнений реакций используйте структурные формулы органических веществ.
РешениеОтвет:

Задание №36
Напишите уравнения реакций, с помощью которых можно осуществить следующие превращения:

При написании уравнений реакций используйте структурные формулы органических веществ.
РешениеОтвет:

Задание №37
Напишите уравнения реакций, с помощью которых можно осуществить следующие превращения:

При написании уравнений реакций используйте структурные формулы органических веществ.
РешениеОтвет:

Задание №38
Напишите уравнения реакций, с помощью которых можно осуществить следующие превращения:

При написании уравнений реакций используйте структурные формулы органических веществ.
РешениеОтвет:

Задание №39
Напишите уравнения реакций, с помощью которых можно осуществить следующие превращения:

При написании уравнений реакций используйте структурные формулы органических веществ.
РешениеОтвет:

Задание №40
Напишите уравнения реакций, с помощью которых можно осуществить следующие превращения:

При написании уравнений реакций используйте структурные формулы органических веществ.
РешениеОтвет:

Задание №41
Напишите уравнения реакций, с помощью которых можно осуществить следующие превращения:

При написании уравнений реакций используйте структурные формулы органических веществ.
РешениеОтвет:

Задание №42
Напишите уравнения реакций, с помощью которых можно осуществить следующие превращения:

При написании уравнений реакций используйте структурные формулы органических веществ.
РешениеОтвет:

Задание №43
Напишите уравнения реакций, с помощью которых можно осуществить следующие превращения:

При написании уравнений реакций используйте структурные формулы органических веществ.
РешениеОтвет:

Задание №44
Напишите уравнения реакций, с помощью которых можно осуществить следующие превращения:

При написании уравнений реакций используйте структурные формулы органических веществ.
РешениеОтвет:

Задание №45
Напишите уравнения реакций, с помощью которых можно осуществить следующие превращения:

При написании уравнений реакций используйте структурные формулы органических веществ.
РешениеОтвет:

Задание №46
Напишите уравнения реакций, с помощью которых можно осуществить следующие превращения:

При написании уравнений реакций используйте структурные формулы органических веществ.
РешениеОтвет:

Задание №47
Напишите уравнения реакций, с помощью которых можно осуществить следующие превращения:

При написании уравнений реакций используйте структурные формулы органических веществ.
РешениеОтвет:

Задание №48
Напишите уравнения реакций, с помощью которых можно осуществить следующие превращения:

При написании уравнений реакций используйте структурные формулы органических веществ.
РешениеОтвет:

Задание №49
Напишите уравнения реакций, с помощью которых можно осуществить следующие превращения:

При написании уравнений реакций используйте структурные формулы органических веществ.
РешениеОтвет:

Задание №50
Напишите уравнения реакций, с помощью которых можно осуществить следующие превращения:

При написании уравнений реакций используйте структурные формулы органических веществ.
РешениеОтвет:

«Цепочки химических превращений в органической химии»
Напишите уравнения реакций, с помощью которых можно осуществить следующие превращения:
1. ацетат калия → этан → X → этанол → диэтиловый эфир
2.CaC2→ этин → этаналь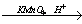 X1
X1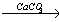 X2
X2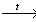 X3
X3
3.Al4C3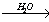 X1
X1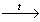
 этаналь
этаналь 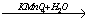 X3
X3 X1
X1 4. CaC2→этин→этаналь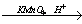 X1
X1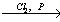 X2
X2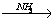 X 3
X 3
5. CaC2 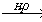 X1
X1 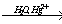 X2→ H3C–COOH
X2→ H3C–COOH  X3→ (CH3)2–C=O
X3→ (CH3)2–C=O
6. HC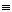 CH
CH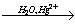 X1
X1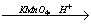
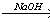 X2
X2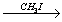 X3
X3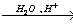 уксусная кислота
уксусная кислота 7.Метилат калия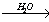 → бромметан
→ бромметан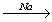 Х2
Х2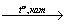 Х3
Х3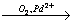
8. Ацетальдегид → ацетат калия → этановая кислота → этилацетат → ацетат кальция → ацетон
9. CH3CHO 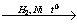 Х1
Х1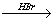 Х2→ этилен → CH3CHO
Х2→ этилен → CH3CHO 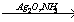 X3
X3
10. CH3COOH→ X1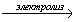 С2H6
С2H6 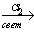
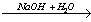 X3
X3 X4
X4 11. C2H5OH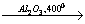 X1
X1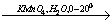 X2
X2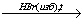 X3
X3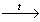
 C2H4O
C2H4O 12. CH2BrCH2CH2Br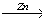 X1
X1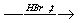 X2→ пропен
X2→ пропен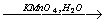 X3→ 1,2- дибромпропан
X3→ 1,2- дибромпропан
13. CH4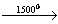 X1→ C6H6
X1→ C6H6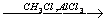
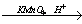 X3
X3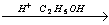 X4
X4 14. карбид алюминия 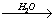 Х1
Х1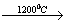 Х2
Х2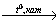 бензол
бензол 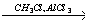
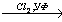 X4
X4 15. 1-хлорпропан 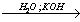 Х1
Х1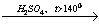 X2
X2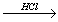 X3
X3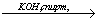 X2→ изопропилбензол
X2→ изопропилбензол
16. этен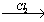 X1
X1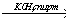
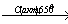 X3→толуол
X3→толуол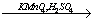 X4
X4 17. C2H4→ C2H4Cl2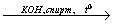 X1
X1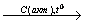 X2
X2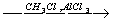 X3
X3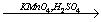
18. CH3CH2CH2OH→ X1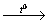 C6H14
C6H14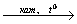 X2
X2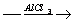 C6H5СН3→ C6H5CООН
C6H5СН3→ C6H5CООН
19. С2Н2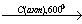 Х1→ C6H5С2Н5
Х1→ C6H5С2Н5
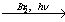 X2
X2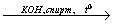 X3
X3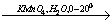 X4
X4 20. ацетилен бензол
бензол этилбензол
этилбензол 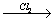 X1
X1 X2
X2 полистирол
полистирол
21. C6H6→C6H5CH3→ C6H5CООН→ C6H5CООCH3→CH3OH→(CH3)2O (укажите условия проведения реакций).
22.
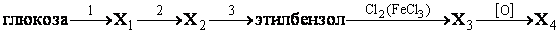
23. C2H2→X1→X2→C6H5CH3→NO2–C6H4–CH3 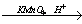 X3
X3
24. CH3-CH2-CH(CH3)-CH3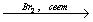 X1
X1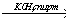 X2
X2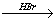 X1
X1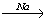 X3CO2
X3CO2
25. CH4→ HCHO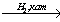 X1
X1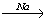 X2
X2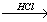 X1
X1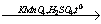 X3
X3
26. пропилацетат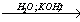 X1→ CH4
X1→ CH4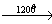 X2
X2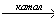 винилацетат
винилацетат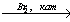 X3
X3
27. CH3-CH2-CHO 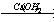 X1
X1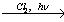 X2
X2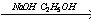 X3
X3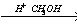 X4
X4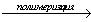 X5
X5
28. Ацетат калия 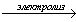 X1
X1 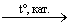 X2
X2 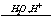 X3
X3 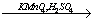 X4
X4 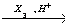 X5
X5
29. этанол 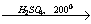 Х1
Х1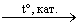 Х2
Х2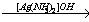 Ag2C2
Ag2C2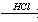 X2
X2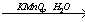 X3
X3
30. C6H6→C6H5-CH(CH3)2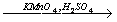 X1
X1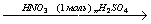 X2
X2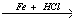 X3
X3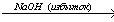 X4
X4
Ответы на задания практической части:
Задание 1
Электролиз раствора ацетата калия:
K(-) (K+) – не восстанавливается, щелочной металл
2H2O + 2ē = H2+ 2OH– | 2
А(+) 2CH3COO––2ē = CH3-CH3 + 2CO2 | 2
Суммарное уравнение:
2CH3COO– + 2H2O = H2+ 2OH– + CH3-CH3 + 2CO2
Или 2CH3COOK + 2H2O = H2+ 2KOH + CH3-CH3 + 2CO2
При нагревании этана в присутствии катализатора Ni, Pt, происходит дегидрирование, X – этен: CH3-CH3 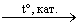 CH2=CH2 + H2
CH2=CH2 + H2
Следующая стадия – гидратация этена:
CH2=CH2 + H2O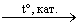 CH3-CH2OH;
CH3-CH2OH;
Перманганат калия в кислой среде – сильный окислитель и окисляет спирты до карбоновых кислот:
5C2H5OH + 4KMnO4 + 6H2SO4 = 5CH3COOH + 4MnSO4 + 2K2SO4 + 11H2O
Наконец, взаимодействие уксусной кислоты и спирта приведет к образованию сложного эфира:
CH3COOH + C2H5OH = CH3COOC2H5 + H2O
Задание 2
1) CaC2 + 2H2O → Ca(OH)2 + C2H2
2) C2H2 + H2O 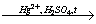 CH3СHO
CH3СHO
3) 5CH3СHO + 2KMnO4 + 3H2SO4 → 5CH3COOH + K2SO4 + 2MnSO4 + 3H2O
4) 2CH3COOH + CaCO3 → (CH3COO)2Ca + H2O + CO2
5) (CH3COO)2Ca 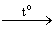 CaCO3 + (CH3)2CO
CaCO3 + (CH3)2CO
Задание 3
1) Al4C3 + 12H2O= 3CH4 + 4 Al(OH)3
2) 2 CH4C2H2 + 3H2
3) C2H2 + H2O 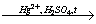 CH3СHO
CH3СHO
4) 3CH3СHO + 2KMnO4 + 3H2O → 2CH3COOK+ CH3COOH+ 2MnO2 + H2O
5) CH3COOK + KOH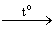 CH4 + K2CO3
CH4 + K2CO3
Задание 4
1) CaC2 + 2H2O → Ca(OH)2 + C2H2
2) C2H2 + H2O 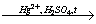 CH3СHO
CH3СHO
3) 5CH3СHO + 2KMnO4 + 3H2SO4 → 5CH3COOH + K2SO4 + 2MnSO4 + 3H2O
4) 2CH3COOH + Cl2 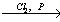 CH2ClCOOH + HCl
CH2ClCOOH + HCl
5) CH2ClCOOH + NH3 CH2(NH2)COOH + HCl
20) CaC2 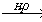 X1
X1 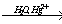 X2→ H3C–COOH
X2→ H3C–COOH  X3→ (CH3)2–C=O
X3→ (CH3)2–C=O
Задание 5
1) CaC2 + 2H2O → Ca(OH)2 + C2H2
2) Н-С≡С-Н 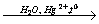 H3C – COH
H3C – COH
3) H3C–COH +2Сu(ОН)2 → H3C–COOH +Сu2О + 2Н2О
4) 2H3C–COOH + Ba(OH)2 →(СН3COO)2Ba + 2Н2О
5) (СН3COO)2Ba (к) 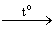 (CH3)2–C=O + BaCO3
(CH3)2–C=O + BaCO3
Задание 6
1) Н-С≡С-Н 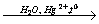 H3C – COH
H3C – COH
2) 5CH3СHO + 2KMnO4 + 3H2SO4 → 5CH3COOH + K2SO4 + 2MnSO4 + 3H2O
3) H3C–COOH + NaOH→СН3COONa + Н2О
4) СН3COONa + CH3I СН3COOCH3 + NaI
5) СН3COOCH3 + H2O 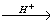 CH3COOH + CH3OH
CH3COOH + CH3OH
Задание 7
1) CH3OK+ H2O 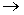 KOH + CH3OH
KOH + CH3OH
2) CH3OH + HBr 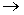 CH3Br + H2O
CH3Br + H2O
3) 2CH3Br + 2Na  С2H6 + 2NaBr
С2H6 + 2NaBr
4) С2H6 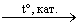 C2H4 + H2
C2H4 + H2
5) 2C2H4 + O2 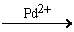 2CH3CHO
2CH3CHO
Задание 8
Ацетальдегид ацетат калия этановая кислота этилацетат ацетат кальция ацетон. Перепишем:
CH3CHO CH3COOK CH3COOH CH3COOC2H5 (CH3COO)2Ca (CH3)2CO
Тип реакции может подсказать сравнение состава исходного и получаемого веществ. Так, для первого превращения видно, что необходимо окислить альдегид в щелочной среде, например:
CH3CHO + 2KMnO4 + 3KOH CH3COOK + 2K2MnO4 + 2H2O
CH3COOK + HCl = CH3COOH + KCl
CH3COOH + C2H5OH 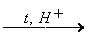 CH3COOC2H5 + H2O
CH3COOC2H5 + H2O
Чтобы из эфира получить ацетат, надо провести его гидролиз в щелочной среде, причем в качестве щелочи взять гидроксид кальция:
2CH3COOC2H5 + Ca(OH)2 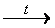 (CH3COO)2Ca + 2C2H5OH
(CH3COO)2Ca + 2C2H5OH
Особую сложность может вызвать последнее превращение, поскольку способы получения кетонов в базовом курсе химии обычно не рассматриваются. Для его осуществления проводят пиролиз (термическое разложение) ацетата кальция:
(CH3COO)2Ca 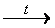 (CH3)2CO + CaCO3
(CH3)2CO + CaCO3
Задание 9
1) CH3CHO + H2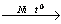 C2H5OH
C2H5OH
2) C2H5OH + HBr C2H5Br + H2O
3) C2H5Br + KOH (спирт) C2H4 + KBr + H2O
4) 2C2H4 + O2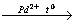 2 CH3CHO
2 CH3CHO
5) CH3CHO + Ag2O + NH3 CH3COONH4 + 2Ag
Задание 10:
1) CH3COOH + KOH CH3COOK + H2O
2) CH3COOK + 2H2O H2+ 2KOH + CH3-CH3 + 2CO2
H2+ 2KOH + CH3-CH3 + 2CO2
3) CH3-CH3 + Cl2 CH3-CH2Cl + HCl
CH3-CH2Cl + HCl
4) CH3-CH2Cl + NaOH (водн) CH3-CH2-OH +NaCl
5) 2CH3-CH2-OH H2O + CH3-CH2-O-CH2-CH3
H2O + CH3-CH2-O-CH2-CH3
Задание 11
1) C2H5OH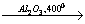 CH2=CH2 + H2O
CH2=CH2 + H2O
2) 3CH2=CH2 + 2KMnO4 + 4H2O  3CH2OH-CH2OH + 2MnO2 + 2KOH
3CH2OH-CH2OH + 2MnO2 + 2KOH
3) CH2OH-CH2OH + 2HBr CH2BrCH2Br +2H2O
CH2BrCH2Br +2H2O
4) CH2BrCH2Br +2KOH (спирт) 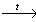 Н-С≡С-Н + 2H2O +2KBr
Н-С≡С-Н + 2H2O +2KBr
5) Н-С≡С-Н +H2O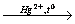
Задание 12
1) CH2BrCH2CH2Br + Zn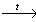 CH2=CH2CH3 + ZnCl2
CH2=CH2CH3 + ZnCl2
2) CH2=CH2CH3+ HBr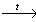 CH3-CH2BrCH3
CH3-CH2BrCH3
3) CH3-CH2BrCH3 +KOH (спирт) CH2=CH2CH3 + KBr
4) CH2=CH2CH3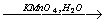 CH2(OH)-CH(OH)-CH3
CH2(OH)-CH(OH)-CH3
5) CH2(OH)-CH(OH)-CH3 + 2HBr 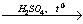 CH2BrCH2BrCH3 + 2H2O
CH2BrCH2BrCH3 + 2H2O
Задание 13
1) 2CH4 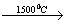 C2H2 + 3H2
C2H2 + 3H2
2) 3C2H2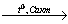 C6H6
C6H6
3) C6H6 + CH3Cl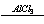 C6H5CH3 + HCl
C6H5CH3 + HCl
4) C6H5CH3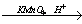 C6H5-COOH
C6H5-COOH
5) C6H5-COOH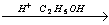 C6H5-COOC2H5 +H2O
C6H5-COOC2H5 +H2O
Задание 14
1) Al4C3 + 12H2O= 3CH4 + 4 Al(OH)3
2) 2CH4 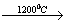 C2H2 + 3H2
C2H2 + 3H2
3) 3C2H2 C6H6
C6H6
4) C6H6 + CH
Цепочки химеческих превращений. Задачи 4
- Подробности
- Категория: Общая химия
Цепочка химических превращений
Задача 4.
С помощью каких химических реакций можно осуществить следующие цепочки превращений (напишите уравнения реакций, укажите условия их протекания и название продуктов): СаС2 → С2Н2 → С6Н6 → С6Н5-СН3 → С6Н5-СООН.
Решение:
1. СаС2 + 2Н2О = Са(ОН)2 + С2Н2↑
Карбид кальция очень энергично взаимодействует с водой с образованием газообразного ацетилена (С2Н2) и гидроксида кальция (Са(ОН)2).
2. 3С2Н2 = С6Н6
При температуре красного каления ацетилен превращается в бензол.
3. С6Н6 + СН3Сl = С6Н5-СН3 + HCl
В присутствии катализаторов — галогенидов алюминия ( AlCl3, AlBr3 и т.д.) из бензола и хлорметила можно получить гомолог бензола — метилбензол или толуол (С6Н5-СН3) и хлороводород HCl. Это реакция алкилирования.
4. С6Н5-СН3 + [O] ⇔ C6H5-COOH
При окислении метилбензола (толуола) получается бензойная кислота (C6H5-COOH). Реакция окисления характерная для алкилбензолов и не характерная для самого бензола. В качестве окислителя применяется раствор перманганата калия.
Типы химических реакций
Задача 5.
Напишите уравнения химических реакции согласно приведенной схемы:
Са → СаО → Са (ОН)2 → КОН → КС1 → НС1 → ВаСl2→ АgС1
↓
Са(Н2РО4)2 → СаНРО4 → Са3(РО4)2
Уровняйте и укажите тип каждой реакции.
Решение:
1. 2Са + О2 = 2СаО — реакция соединения;
2. СаО + Н2О = Са(ОН)2 — реакция соединения;
3. Са(ОН)2 + K2SO4 = CaSO4 + 2KOH — реакция обмена;
4. 2НСl + 2KOH = 2KCl + 2H2O — реакция нейтрализации;
5. KCl + H2SO4 = KHSO4 + 2HCl — реакция обмена;
6. Ba(OH)2 + 2HCl = BaCl2 + 2H2O — реакция нейтрализации;
7. BaCl2 + 2AgNO3 = 2AgCl↓ + Ba(NO3)2 — реакция обмена;
8. Са + 2Н3РО4 = Са(Н2РО4)2 + Н2↑ — реакция обмена
9.Ca(H2PO4)2 + Ca(OH)2 = 2CaHPO4↓ + 2H2O — реакция нейтрализации
10. 2СаНРО4 + Са(ОН)2 = Са3(РО4)2 + 2Н2О — реакция нейтрализации.
или
2CaHPO4 + CaO = Ca3(PO4)2 + H2O (спекание).
Цепное правило — подход к исчислению
7
Производная функции от функции
Цепное правило
Доказательство цепного правила
Производная функции от функции
Пусть
f ( x ) = x 5 и g ( x ) = x 2 + 1.
Если теперь мы позволим g ( x ) быть аргументом f , тогда f будет функцией g .
f ( г ( x )) = ( x 2 + 1) 5 .
(Тема 3 Precalculus.)
Что является производным от f ( g ( x ))?
Во-первых, обратите внимание, что
| d f ( x ) dx | = 5 x 4 . |
То есть: производная f по аргументу (который в данном случае составляет x ) равна 5-кратной четвертой степени аргумента.
Это означает, что если g — или любая переменная — является аргументом f , применяется та же форма :
| d f ( g ) dg | = 5 г 4 . |
| d f ( h ) dh | = 5 ч 4 . |
| d f ( v ) dv | = 5 v 4 . |
Другими словами, мы действительно можем взять производную функции от аргумента только по этому аргументу.
Следовательно, поскольку г = x 2 + 1,
| d f ( g ) dg | = 5 г 4 | = 5 ( x 2 + 1) 4 . |
Затем производная г равна 2 x . То, что называется цепным правилом, гласит следующее:
| df ( г ( x )) dx | = | df ( г ) dg | · | dg ( x ) dx |
«Если f является функцией g и g является функцией x ,
, то производная f относительно x
равна производной f ( g ) относительно g
, умноженная на производную g ( x ) относительно до x .«
Следовательно, согласно цепному правилу, производная
( x 2 + 1) 5
это
5 ( x 2 + 1) 4 · 2 x .
Примечание: In ( x 2 + 1) 5 , x 2 + 1 — это «внутри» 5-й степени, то есть «снаружи». Возьмем производную снаружи внутрь.Когда мы берем внешнюю производную, мы не меняем то, что находится внутри. Затем мы умножаем на производную того, что находится внутри.
Чтобы решить, какая функция является внешней, решает, какую из вы должны оценить, последнюю .
Оценить
( x 2 + 1) 5 ,
, вам сначала нужно оценить x 2 + 1. Затем вы должны взять его 5-ю степень.Таким образом, пятая сила находится снаружи. Вот почему мы сначала берем эту производную.
Когда мы пишем f ( g ( x )), f выходит за пределы g . Сначала возьмем производную f относительно g .
| Пример 1. f ( x ) = | . Какая его производная? |
Решение .Он имеет вид f ( g ( x )). Какая функция у f , то есть что снаружи, и что у g , что внутри?
g — это x 4 — 2, потому что это внутри функции квадратного корня, которая равна f . Производная квадратного корня приведена в примере урока 6. Для любой аргумент g функции квадратного корня,
Здесь г — это x 4 — 2.Следовательно, поскольку производная x 4 -2 равна 4 x 3 ,
| d dx | = ½ ( x 4 — 2) −½ · 4 x 3 = 2 x 3 ( x 4 — 2) −½ . |
Пример 2.Какова производная от y = sin 3 x ?
Решение . Это 3-я степень греха x . Чтобы решить, какая функция находится снаружи, как бы вы это оценили?
Сначала вы оцените sin x , а затем возьмете его 3-ю степень. sin x находится внутри третьей степени, которая находится снаружи.
Теперь производная 3-й степени — г 3 — 3 г 2 .Следовательно, если принять на данный момент, что производная sin x равна cos x (Урок 12), производная sin 3 x — снаружи внутрь — равна
.3 sin 2 x · cos x .
| Пример 3. Какая производная от | 1 x 3 + 1 | ? |
| Решение . x 3 + 1 находится внутри функции | 1 x | = x -1 , |
, производная которого равна — x −2 ; (Задача 4, Урок 4). Итак, у нас есть
| 1 x 3 + 1 | = | ( x 3 + 1) −1 | . |
Следовательно, его производная —
— ( x 3 + 1) −2 · 3 x 2
Пример 4. Предположим, что y является функцией x . y = y ( x ). Примените цепное правило к
| Решение . | dy 2 dx | = | dy 2 dy | · | dy dx | = | 2 y | dy dx | . |
y , который, как мы предполагаем, является функцией x , находится внутри функции y 2 . Производная y 2 по отношению к y равна 2 y . Что касается производной
| y относительно x , мы указываем это как | dy dx | .(См. Урок 5.) |
Задача 1. Вычислите производную от ( x 2 −3 x + 5) 9 .
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы закрыть ответ еще раз, нажмите «Обновить» («Reload»).
Сначала решите проблему сами!
9 ( x 2 −3 x + 5) 8 (2 x — 3)
Проблема 2.Вычислить производную от ( x 4 -3 x 2 + 4) 2/3 .
2/3 ( x 4 — 3 x 2 + 4) −1/3 (4 x 3 — 6 x )
Задача 3. Вычислить производную sin 5 x .
5 sin 4 x cos x
Проблема 4.Вычислить производную sin x 5 .
Внутренняя функция — x 5 — вы бы оценили это последнее. Внешняя функция sin x . (Это синус x 5 .) Следовательно, производная равна
.cos x 5 · 5 x 4 .
Задача 5. Вычислить производную sin (1 + 2).
cos (1 + 2) x −1/2 .
Задача 6. Вычислить производную
.¼ (sin x ) −3/4 cos x .
Пример 5. Более двух функций. Цепное правило может быть расширено до более чем двух функций. Например, пусть
| f ( x ) | = | . |
Внешняя функция — это квадратный корень. Внутри это (1 + 2-я степень). А внутри это sin x .
Следовательно, производная
| ½ (1 + sin 2 x ) −1/2 · 2 sin x · cos x | = | sin x cos x | . |
| Задача 7. Вычислить производную от | .
(Сравните Пример 3.)
| — [sin ( x 2 + 5)] −2 · cos ( x 2 + 5) · 2 x | = | – | 2 x cos ( x 2 + 5) sin 2 ( x 2 + 5) |
| Проблема 8.Вычислить производную от |
Проблема 9. Предположим, что y является функцией x , и применим правило цепочки, чтобы выразить каждую производную относительно x .
| а) | d dx | y 3 = | 3 y 2 | dy dx |
| б) | d dx | sin y = | cos y | dy dx |
| в) | d dx | = | ½ y −½ | dy dx |
Доказательство цепного правила
Чтобы доказать цепное правило, вернемся к основам.Пусть f является функцией g , которая, в свою очередь, является функцией x , так что у нас есть f ( g ( x )). Затем, когда значение г изменится на величину Δ г , значение f изменится на величину Δ f . У нас будет соотношение
Опять же, поскольку g является функцией x , тогда, когда x изменяется на величину Δ x , g изменится на величину Δ g .У нас будет соотношение
Но изменение x влияет на f , потому что оно зависит от g . У нас будет
| Δ f Δ x | . Это будет произведение этих соотношений: |
| Δ f Δ x | = | Δ f Δ г | · | Δ г Δ x | . |
Давайте теперь возьмем предел, поскольку Δ x приближается к 0. Тогда изменение в г ( x ) — Δ г — также приблизится к 0. Следовательно, начиная с предел продукта составляет равно произведению пределов (Урок 2) и по определению производной:
| df dx | = | df dg | · | dg dx |
Это цепное правило.
Следующий урок: правило частного
Содержание | Дом
Сделайте пожертвование, чтобы TheMathPage оставалась в сети.
Даже 1 доллар поможет.
Авторские права © 2020 Лоуренс Спектор
Вопросы или комментарии?
Эл. Почта: [email protected]
,
функций двух непрерывных случайных величин | ЛОТОС
5.2.4 Функции двух непрерывных случайных величин
До сих пор мы видели несколько примеров с участием функций случайных величин. Когда у нас есть две непрерывные случайные величины $ g (X, Y) $, идеи все те же. Во-первых, если нас просто интересует $ E [g (X, Y)] $, мы можем использовать LOTUS:LOTUS для двух непрерывных случайных величин:
\ Начать {Выравнивание} \ {метка эк: LOTUS-2D-прод} E [g (X, Y)] = \ int _ {- \ infty} ^ {\ infty} \ int _ {- \ infty} ^ {\ infty} g (x, y) f_ {XY} (x, y) \ hspace {5pt} dxdy \ hspace {40pt} (5.3 \ вправо) ды \\ \ nonumber & = \ frac {17} {72}. \ Конец {} AlignЕсли $ Z = g (X, Y) $ и нас интересует его распределение, мы можем начать с написания \ Начать {} Align \ nonumber F_Z (z) & = P (Z \ leq z) \\ \ nonumber & = P (g (X, Y) \ leq z) \\ \ nonumber & = \ iint \ limits_D f_ {XY} (x, y) \ hspace {5pt} dxdy, \ Конец {} Align где $ D = \ {(x, y) | g (x, y)
Пример
Пусть $ X $ и $ Y $ — две независимые $ Uniform (0,1) $ случайные величины, и $ Z = XY $. Найдите CDF и PDF для $ Z $.
- Решение
- Сначала обратите внимание, что $ R_Z = [0,1] $. Таким образом,
\ Начать {} Align
\ nonumber F_Z (z) & = 0, \ hspace {30pt} \ textrm {for} z \ leq 0, \\
\ nonumber F_Z (z) & = 1, \ hspace {30pt} \ textrm {for} z \ geq 1.
\ Конец {} Align
При $ 0
- Сначала обратите внимание, что $ R_Z = [0,1] $. Таким образом,
\ Начать {} Align
\ nonumber F_Z (z) & = 0, \ hspace {30pt} \ textrm {for} z \ leq 0, \\
\ nonumber F_Z (z) & = 1, \ hspace {30pt} \ textrm {for} z \ geq 1.
\ Конец {} Align
При $ 0
Метод преобразований:
Когда у нас есть функции двух или более совместно непрерывных случайных величин, мы можем использовать метод, аналогичный теоремам 4.1 и 4.2, чтобы найти результирующие PDF. В частности, можно сформулировать следующую теорему. Хотя формулировка теоремы может показаться немного запутанной, ее применение довольно простое, и мы увидим несколько примеров, чтобы проиллюстрировать методологию. Теорема
. Пусть $ X $ и $ Y $ — две совместно непрерывные случайные величины.{-1} $, т.е. $ (X, Y) = h (Z, W) = (h_1 (Z, W), h_2 (Z, W)) $. Тогда $ Z $ и $ W $ совместно непрерывны и их совместная PDF $ f_ {ZW} (z, w) $ для $ (z, w) \ in R_ {ZW} $ задается формулой
\ Начать {} Align
\ nonumber f_ {ZW} (z, w) = f_ {XY} (h_1 (z, w), h_2 (z, w)) | J |,
\ Конец {} Align
где $ J $ — якобиан $ h $, определенный формулой
\ Начать {} Align
\ nonumber J = \ det \ begin {bmatrix}
\ frac {\ partial h_1} {\ partial z} & \ frac {\ partial h_1} {\ partial w} \\
& \\
\ frac {\ partial h_2} {\ partial z} & \ frac {\ partial h_2} {\ partial w} \\
\ Конец {bmatrix}
= \ frac {\ partial h_1} {\ partial z}.\ frac {\ partial h_2} {\ partial w} — \ frac {\ partial h_2} {\ partial z} \ frac {\ partial h_1} {\ partial w}.
\ Конец {} Align
Пример
Пусть $ X $ и $ Y $ — две независимые стандартные нормальные случайные величины. Пусть также \ {Начинают уравнение} \ nonumber \ left \ { \ {Начинаются массив} {L} Z = 2X-Y \\ W = -X + Y \ end {array} \ right. \ Конец {} уравнение Найдите $ f_ {ZW} (z, w) $.
- Решение
- $ X $ и $ Y $ совместно непрерывны, и их совместная PDF определяется выражением \ {Начать выравнивание}% \ метка {} \ nonumber f_ {XY} (x, y) = f_X (x) f_Y (y) = \ frac {1} {2 \ pi} \ exp \ left \ {- \ frac {x ^ 2 + y ^ 2} { 2} \ right \}, \ hspace {30pt} \ textrm {для всех} x, y \ in \ mathbb {R}.\ Конец {} Align Здесь функция $ g $ определяется как $ (z, w) = g (x, y) = (g_1 (x, y), g_2 (x, y)) = (2x-y, -x + y) $. Решая относительно $ x $ и $ y $, получаем обратную функцию $ h $: \ {Начинают уравнение} \ nonumber \ left \ { \ {Начинаются массив} {L} х = z + w = h_1 (z, w) \\ у = г + 2w = H_2 (г, ш) \ end {array} \ right. \ Конец {} уравнение У нас есть \ Начать {} Align \ nonumber f_ {ZW} (z, w) & = f_ {XY} (h_1 (z, w), h_2 (z, w)) | J | \\ \ nonumber & = f_ {XY} (z + w, z + 2w) | J |, \ Конец {} Align где \ Начать {} Align \ nonumber J = \ det \ begin {bmatrix} \ frac {\ partial h_1} {\ partial z} & \ frac {\ partial h_1} {\ partial w} \\ & \\ \ frac {\ partial h_2} {\ partial z} & \ frac {\ partial h_2} {\ partial w} \\ \ Конец {bmatrix} = \ det \ begin {bmatrix} 1 и 1 \\ & \\ 1 и 2 \\ \ Конец {bmatrix} = 1.2 + 6zw} {2} \ право \}. \ Конец {} Align
Пример
Пусть $ X $ и $ Y $ — две случайные величины с совместной PDF $ f_ {XY} (x, y) $. Пусть $ Z = X + Y $. Найдите $ f_ {Z} (z) $.
- Решение
- Для применения теоремы 5.1 нам потребуются две случайные величины $ Z $ и $ W $. Мы можем просто определить $ W = X $. Таким образом, функция $ g $ имеет вид
\ {Начинают уравнение}
\ nonumber \ left \ {
\ {Начинаются массив} {L}
г = х + у \\
ш = х
\ end {array} \ right.
\ Конец {} уравнение
Затем мы можем найти обратное преобразование:
\ {Начинают уравнение}
\ nonumber \ left \ {
\ {Начинаются массив} {L}
х = ш \\
у = г-ш
\ end {array} \ right.2 \ Bigg).
\ Конец {} Align Мы увидим более простое доказательство теоремы 5.2, когда обсудим функции , производящие моменты . ,
Преобразования функций | Purplemath
Purplemath
Одно из определений «переводить» — «переходить из одного места, состояния, формы или внешнего вида в другое». Когда мы берем функцию и настраиваем ее правило так, чтобы ее график перемещался в другое место на системе осей, но при этом оставался узнаваемым тем же графиком, мы, как говорят, «переводим» функцию.
Обычно перевод включает в себя только перемещение графика. Сжатие или растяжение графика — это больше похоже на «преобразование» графика. Но эти две темы обычно преподаются одновременно и обычно под одним и тем же названием. Просто имейте в виду, что тема «перевода функций» часто включает в себя преобразование функций и наоборот.
MathHelp.com

Для начала давайте рассмотрим один из наиболее простых типов функций, которые вы нарисовали на графике; а именно квадратичные функции и связанные с ними параболы.
Когда вы впервые начали рисовать квадратичные графики, вы начали с основного квадратичного:
f ( x ) = x 2 :
Затем вы построили несколько связанных графиков, например:
г ( x ) = — x 2 — 4 x + 5:
h ( x ) = x 2 — 3 x — 4:
k ( x ) = ( x + 4) 2 :
В каждом из этих случаев основная параболическая форма была одинаковой.Единственная разница заключалась в том, где находилась вершина, и была ли она правой или перевернутой.
Если вы рисовали графики вручную, вы, вероятно, начали замечать некоторую взаимосвязь между уравнениями и графиками. Тема преобразования функций делает эти отношения более явными.
Движение вверх и вниз
Начнем с обозначения функции основной квадратичной:
Преобразование функции берет то, что является базовой функцией f ( x ), а затем «преобразует» (или «переводит»), что является причудливым способом сказать, что вы немного измените формулу и тем самым переместите график вокруг.
Например, график для y = x 2 + 3 выглядит так:
Это на три единицы больше, чем базовая квадратичная, f ( x ) = x 2 . То есть x 2 + 3 равно f ( x ) + 3. Мы добавили «3» вне основной функции возведения в квадрат f ( x ) = x 2 и тем самым перешел от базовой квадратичной x 2 к преобразованной функции x 2 + 3.
Это всегда верно: чтобы переместить функцию вверх, вы добавляете за пределы функции: f ( x ) + b is f ( x ) перемещено вверх на b единиц. Перемещение функции вниз работает точно так же; f ( x ) — b — f ( x ) перемещено вниз b единиц.
Учитывая г ( x ) = 4 x — 3, какая функция h ( x ) будет представлять сдвиг вниз на две единицы?
Так как исходная функция сдвигается вниз на две единицы, то новая функция является старой, с добавлением «минус два» на конце:
г ( x ) — 2 = (4 x — 3) — 2
Тогда новая функция:
Перемещение влево и вправо
С другой стороны, y = ( x + 3) 2 выглядит так:
На этом графике f ( x ) перемещено на три единицы влево: f ( x + 3) = ( x + 3) 2 is f ( x ) сместился на три единицы влево.
Это всегда верно: чтобы сдвинуть функцию влево, добавьте внутри аргумента функции: f ( x + b ) дает f ( x ) со сдвигом b единиц влево. Сдвиг вправо работает точно так же; f ( x — b ) — f ( x ) со смещением b единиц вправо.
Предупреждение. Распространенное искушение состоит в том, чтобы думать, что f ( x + 3) сдвигает f ( x ) вправо на три, потому что «+3» находится вправо.Но смещение влево-вправо происходит в обратном направлении от того, что вы могли ожидать.
Добавление перемещает вас влево; вычитание перемещает вас вправо.
Если вы заблудились, подумайте о точке на графике, где x = 0. Для f ( x + 3), что теперь должно быть x , чтобы 0 было подключено к f ? В этом случае x должно быть –3, поэтому аргумент равен –3 + 3 = 0, поэтому мне нужно сдвинуть влево на три.
Этот процесс сообщит вам, куда сместились значения x и, следовательно, график. По крайней мере, так я мог отслеживать вещи. Да, у меня тоже были проблемы с этой концепцией.
Дано f ( x ) = — x 2 + 5 x + 2, найдите выражение в терминах f для сдвига влево на пять единиц.
Чтобы сместить график из стороны в сторону, мне нужно добавить или вычесть внутри аргумента функции (то есть внутри круглых скобок). Чтобы переместиться влево, мне нужно (что противоречит интуиции) к добавить внутри скобок. Чтобы переместить пять единиц, мне нужно добавить 5 в скобках.
Тогда мой ответ:
Дано с ( t ) = 2 t + 4, найдите выражение для функции w ( t ), которая представляет сдвиг вправо на одну единицу.
Мне сказали повернуть вправо. Для этого я должен (вопреки интуиции) вычесть внутри аргумента. Мне сказали сдвинуть вправо на одну единицу, поэтому я вычитаю на 1.
Но они не сказали мне выражать новую функцию в терминах старой. Они хотят фактического выражения сдвига вправо. Так что мне нужно будет заняться алгеброй, вставив « t — 1» для каждого экземпляра « t » в исходной функции.К счастью, эта функция очень проста, поэтому:
w ( т ) = с ( т — 1)
= 2 ( т — 1) + 4
= 2 т — 2 + 4
= 2 т + 2
Тогда моя новая функция:
URL: https: // www.purplemath.com/modules/fcntrans.htm
,Исчисление III — Правило цепочки
Онлайн-заметки ПавлаНоты Быстрая навигация Скачать
- Перейти к
- Ноты
- Проблемы с практикой
- Проблемы с назначением
- Показать / Скрыть
- Показать все решения / шаги / и т. Д.
- Скрыть все решения / шаги / и т. Д.
- Разделы
- Дифференциалы
- Направленные производные
- Разделы
- Трехмерное пространство
- Приложения частичных производных
- Классы
- Алгебра
- Исчисление I
- Исчисление II
- Исчисление III
- Дифференциальные уравнения
- Дополнительно
- Алгебра и триггерный обзор
- Распространенные математические ошибки
- Праймер комплексных чисел
- Как изучать математику
- Шпаргалки и таблицы
- Разное
- Свяжитесь со мной
- Справка и настройка MathJax
- Мои студенты
- Notes Загрузки
- Полная книга
- Текущая глава
- Текущий раздел
- Practice Problems Загрузок
- Полная книга — Только проблемы
- Полная книга — Решения
- Текущая глава — Только проблемы
- Текущая глава — Решения
- Текущий раздел — Только проблемы
- Текущий раздел — Решения
- Проблемы с назначением Загрузок
- Полная книга
- Текущая глава
- Текущий раздел
- Прочие товары
- Получить URL для загружаемых элементов
- Распечатать страницу в текущем виде (по умолчанию)
- Показать все решения / шаги и распечатать страницу
- Скрыть все решения / шаги и распечатать страницу
- Дом
- Классы
- Алгебра
- Отборочные
- Целочисленные экспоненты
- Рациональные экспоненты
- Радикалы
- Полиномы
- Факторинговые многочлены
- Рациональные выражения
- Комплексные числа
- Решение уравнений и неравенств
- Решения и наборы решений
- Линейные уравнения
- Приложения линейных уравнений
- Уравнения с более чем одной переменной
- Квадратные уравнения — Часть I
- Квадратные уравнения — Часть II
- Квадратные уравнения: сводка
- Приложения квадратных уравнений
- Уравнения, сводимые к квадратичным в форме
- Уравнения с радикалами
- Линейные неравенства
- Полиномиальные неравенства
- Рациональные неравенства
- Уравнения абсолютных значений
- Неравенства абсолютных значений
- Графики и функции
- График
- Строки
- Круги
- Определение функции
- Графические функции
- Комбинирование функций
- Обратные функции
- Общие графы
- Отборочные
- Для применения теоремы 5.1 нам потребуются две случайные величины $ Z $ и $ W $. Мы можем просто определить $ W = X $. Таким образом, функция $ g $ имеет вид
\ {Начинают уравнение}
\ nonumber \ left \ {
\ {Начинаются массив} {L}
г = х + у \\
ш = х
\ end {array} \ right.
\ Конец {} уравнение
Затем мы можем найти обратное преобразование:
\ {Начинают уравнение}
\ nonumber \ left \ {
\ {Начинаются массив} {L}
х = ш \\
у = г-ш
\ end {array} \ right.2 \ Bigg).
\ Конец {} Align Мы увидим более простое доказательство теоремы 5.2, когда обсудим функции , производящие моменты . ,