Контрольные по математике | Тесты по статистике для решения
5. Статистика
69. Выберите формулы, которые отражают функциональную зависимость между
переменными:
1)
2)
3)
4)
5)
6)
.
Эталон правильного ответа: 1, 2, 3, 4.
70. Укажите доверительную вероятность, используемую в медицине:
1) 95%;
2) 68%;
3) 50%;
4) 99%;
5) 58%.
Эталон правильного ответа: 1, 4.
71. От каких параметров зависит коэффициент Стьюдента?
1) От температуры;
2) От объема выборки;
3) От надежности;
4) От доверительного интервала.
Эталон правильного ответа: 2, 3.
72. Как зависит от объема выборки коэффициент Стьюдента?
1) Прямо пропорционально;
2) Квадратично;
3) Обратно пропорционально;
4) Гиперболически.
Эталон правильного ответа: 3.
73. Как зависит коэффициент Стьюдента от надежности выборки?
1) Прямо пропорционально;
2) Обратно пропорционально;
3) Линейно;
4) Квадратично.
Эталон правильного ответа: 1.
74. Укажите формулу для нахождения коэффициента различий между средними
величинами:
1)
2)
3)
4)
5)
Эталон правильного ответа: 5.
75. Укажите формулы для нахождения характеристики распределения Стьюдента:
1)
2)
3)
4)
5)
Эталон правильного ответа: 2.
76. Укажите формулу для нахождения ошибки среднего арифметического:
1)
2)
3)
4)
5)
Эталон правильного ответа: 3.
77. Укажите верную формулу для нахождения предельной ошибки при построении
доверительного интервала:
1)
2)
3)
4)
5)
Эталон правильного ответа: 4.
78. Какой вид тесноты связи в статистике, если 0 < Ry/x < 0,3?
1) Сильная связь;
2) Нейтральная связь;
3) Слабая связь;
4) Средняя связь.
Эталон правильного ответа: 3.
79. Какой вид тесноты связи в статистике, если 0,3 ≤ Rxy< 0,7?
1) Нейтральная связь;
2) Средняя связь;
3) Сильная связь;
4) Слабая связь.
Эталон правильного ответа: 2.
80. Какой вид тесноты связи в статистике, если Rxy= 0?
1) Связь отсутствует;
2) Средняя связь;
3) Сильная связь;
4) Слабая связь.
Эталон правильного ответа : 1.
81. Какой вид тесноты связи в статистике, если 0,7≤ Rxy≤1?
1) Нейтральная связь;
2) Средняя связь;
3) Сильная связь;
4) Слабая связь.
Эталон правильного ответа: 3.
82. Укажите формулу для плотности распределения в нормальном законе
распределения:
1)
2)
3)
4)
5)
Эталон правильного ответа: 3.
83. Укажите формулу для нахождения математического ожидания в выборке:
1)
2)
3)
4)
5)
6)
84. Укажите формулу для нахождения квадратичного отклонения в выборке:
1)
2)
3)
4)
5)
6)
Эталон правильного ответа: 2.
85. Укажите формулу для нахождения дисперсии в выборке:
1)
2)
3)
4)
5)
6)
Эталон правильного ответа: 3.
86. Из предложенных формул, укажите верную для расчета коэффициента вариации:
1)
2)
3)
4)
5)
Эталон правильного ответа: 1.
87. Из предложенных формул, укажите верную для расчета коэффициента линейного
отклонения:
1)
2)
3)
4)
5)
Эталон правильного ответа: 4.
88. Из предложенных формул, укажите верную для расчета размаха вариации:
1)
2)
3)
4)
5)
89. Как зависит коэффициент Стьюдента от надежности выборки?
1) Прямо пропорционально;
2) Обратно пропорционально;
3) Линейно;
4) Квадратично.
Эталон правильного ответа: 1.
90. Что такое гистограмма?
1) Ломаная кривая, соединяющая точки, соответствующие срединным значениям
интервалов и частотам этих интервалов;
2) Зависимость между функцией и аргументом;
3) Столбиковая диаграмма.
Эталон правильного ответа: 3.
91. Что такое полигон?
1) Ломаная кривая, соединяющая точки, соответствующие срединным значениям
интервалов и частотам этих интервалов;
2) Зависимость между функцией и аргументом;
3) Способ графического представления табличных данных.
Эталон правильного ответа: 1.
92. Что такое график?
1) Ломаная кривая, соединяющая точки, соответствующие срединным значениям
интервалов и частотам этих интервалов.
2) Зависимость между функцией и аргументом.
3) Способ графического представления табличных данных.
Эталон правильного ответа: 2.
93. Какая связь называется прямой?
1) Если с ростом одного параметра растет другой;
2) Если с ростом одного параметра убывает другой;
3) Положительная;
4) Отрицательная.
Эталон правильного ответа: 1.
94. Какая связь называется обратной?
1) Если с ростом одного параметра растет другой;
2) Если с ростом одного параметра убывает другой;
3) Положительная;
4) Отрицательная.
Эталон правильного ответа: 2.
95. Назовите точечные оценки случайной величины в выборке:
1) Среднее квадратическое отклонение;
2) Плотность распределения;
3) Коэффициент Стьюдента;
4) Доверительный интервал;
5) Математическое ожидание;
6) Дисперсия.
Эталон правильного ответа: 1, 5, 6.
Эталон правильного ответа: 3.
97. Какой коэффициент определяет тесноту связи между двумя случайными
величинами?
1) Коэффициент объемного расширения;
2) Коэффициент линейной корреляции;
3) Коэффициент линейного расширения;
4) Коэффициент линейной регрессии.
Эталон правильного ответа: 2.
98. Какой коэффициент определяет силу связи между двумя случайными величинами?
1) Коэффициент объемного расширения;
2) Коэффициент линейной корреляции;
3) Коэффициент линейного расширения;
4) Коэффициент линейной регрессии.
Эталон правильного ответа: 2, 4.
Тесты
(Выберите один или несколько правильных ответов)
1.
А) частота события, которое при реализации определенного комплекса условий
произойдет непременно
Б) велицина, которая при реализации определенного комплекса условий может
принимать различные значения
В)численная мера объективной возможности появления данного события при
реализации определенного комплекса условий
2. В каких границах может находиться вероятность появления случайного
события:
А) 0< p(A) <1
Б) p(A) >1
В) 0< p(A) <1
3. Какой уровень значимости считается допустимым для большинства медико-
биологических исследований?
А) p< 0,5
Б) 0,05< p <0,01
В) p < 0,05
1. Назовите разделы медицинской статистики:
А) статистика здоровья населения
Б) статистика системы здравоохранения
В) статистика научно-практических исследований
2. Выберите определение статистики как науки:
А) наука, изучающая закономерности распространенности заболеваний и
факторов, их определяющих
Б) наука, изучающая количественные закономерности материальных явлений
в неразрывной связи с их качественной стороной
В) наука, изучающая числовые данные учетно-отчетной документации в
системе здравоохранения
Тесты
(Выберите один или несколько правильных ответов)
1.
Укажите виды научных статистических исследований в зависимости от
времени регистрации
А) сплошное
Б) текущее
В) единовременное
Г) выборочное
Д) ретроспективное
Е) проспективное
2. Пилотажное исследование проводится с целью:
А) установления корреляционной зависимости
В) оценки вариабельности признака
Г) выбора вида исследования
Д) оценки затрат
Е) оценки динамики явления
3. Укажите виды научных статистических исследований в зависимости от
степени охвата объекта исследования:
А) сплошное
Б) текущее
В) единовременное
Г) выборочное
Д) ретроспективное
Е) проспективное
4. Сколько этапов включает в себя научное статистическое исследование?
А) три
Б) четыре
В) пять
Г) шесть
Д) зависит от цели исследования
Е) зависит от вида исследования
5. Выберите правильное определение статистической совокупности
А) группа отдельных единичных наблюдений, объединенных исследователем
Б) группа относительно одноролных элементов, взятых вместе в известных
границах времени и пространства
В) объект наблюдения статистического научно-практического исследования
ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ВАРИАЦИОННОГО РЯДА:
1).
Показатели, характеризующие центральную тенденцию (central tendency) или
уровень ряда: средние величины или меры расположения (собственно средние и
структурные средние).
2). Показатели, характеризующие разнообразие (рассеяние, вариацию, разброс)
(spread) признака: стандартное отклонение, дисперсия, размах.
Выбор характеристик центральной тенденции и разнообразия признака прежде
всего зависит от вида распределения. В случае нормального распределения
используют показатели параметрической статистики, в случае распределения,
отличного от нормального и при неизвестном виде распределения применяют
показатели непараметрической статистики.
Средние величины
Средняя величина — обобщающий коэффициент, который характеризует
наиболее типичный размер определенного признака в целом для совокупности или
для отдельных ее частей. Расчет средних величин имеет смысл только для
качественно однородной совокупности, в связи с этим в одной совокупности может
быть столько средних, на сколько однородных групп она может быть разбита.
Виды средних величин
Средняя арифметическая(mean) — применяется, если варианты возрастают
(убывают) в арифметической прогрессии.
х — средняя арифметическая;
xi — варианта;
р — частота встречаемости варианты;
n — число наблюдений
Структурные средние
Мода (Мо) (mode)- наиболее часто встречающаяся в вариационном
ряду варианта.
Мода используется:
— при малом числе наблюдений, когда велико влияние состава совокупности
на среднюю ;
— для характеристики центральной тенденции при ассиметричных распределениях,
когда велико влияние на среднюю
крайних вариант;
—
Медиана (Me)(median) — варианта, которая делит вариационный ряд на две равные
части.
Медиана используется:
— при необходимости знать, какая часть вариант лежит выше и ниже средин
ного значения ;
— для характеристики центральной тенденции при ассиметричных распределениях.
Характеристики разнообразия вариационного ряда
1.
Размах вариации (амплитуда) (range): А = Хmах — Xmin
2. Стандартное отклонение (среднее квадратическое отклонение) (standard
deviation, SD)
— приблизительный расчет стандартного отклонения по амплитуде:
где К — коэффициент Ермолаева, рассчитывается по специальной таблице с
учетом числа наблюдений.
При числе наблюдений больше 30:
Стандартное отклонение наиболее часто используется при определении нормы и
патологии, в основе которого лежит «правило трех сигм», справедливое только для
нормального распределения.
«Правило трех сигм»
68.3 % всех вариант отклоняются от своей средней не более, чем на σ
95.4% вариант находятся в пределах X ± 2σ
99.7% вариант находятся в пределах X ± 3σ
35
Отклонение параметра от его средней арифметической в пределах σ
расценивается как норма, субнормальным считается отклонение в пределах ± 2σ и
патологическим — сверх этого предела, т. е. > ± 2σ» (рис.
)
3. Дисперсия (варианса) (variance)
При распределении Пуассона дисперсия равна средней: σ2 = х .
4. Коэффициент вариации (variation coefficient):
Вариационный ряд считается однородным при Cv <10 % , обладающим средней
вариабельностью (разнообразием) при Сv =10-15% и обладающим значительной
вариабельностью при Cv >15% .
Коэффициент вариации используется при сравнении вариационных рядов,
имеющих различную размерность, или одной размерности, но обладающими резкими
различиями в своих значениях, затрудняющими их сопоставление.
несколько правильных ответов)
1. Модой называется:
А. Варианта с наибольшей частотой
Б. Варианта с наименьшей частотой
В. Варианта, находящаяся в середине ряда
Г. Выскакивающая варианта
Ответ: А
2. Медианой называется:
А. Варианта с наибольшей частотой
Б. Варианта с наименьшей частотой
В. Варианта, находящаяся в середине ряда
Г.
Выскакивающая варианта
Ответ: В
3. Какая зависимость между степенью разнообразия вариационного ряда и значением
среднего квадратического отклонения:
А. Прямая
Б. Обратная
Ответ: А
4. Коэффициент вариации применяется в целях:
А. Определения разности между наибольшей и наименьшей вариант
Б. Определения частоты вариант в вариационном ряду
В. Сравнения признаков, выраженных в разных единицах измерения
Ответ: В
5. Средняя арифметическая величина применяется для:
А. Обобщения качественных признаков
Б. Обобщения числовых значений варьирующего признака
В. Выявления взаимосвязи между явлениями
Ответ: Б
6. Из всех видов распределения в медико-биологических исследованиях наиболее часто
встречается:
А. Биномиальные
Б. Нормальное
В. Пуассена
Г. Альтернативное
Д. Все вышеперечисленные встречаются с одинаковой частотой
Ответ: Б
7.
Основным условием применения параметрических методов анализа является:
41
А. Формирование случайной выборки
Б. Наличие двух независимых выборок
В. Корреляционная связь между признаками
Г. Невозможность применения непараметрических методов
Д. Нормальное распределение признака
Ответ: Д
8. Вариационный ряд состоит из:
А. Набора вариант
Б. Набора ошибок репрезентативности
В. Набора частот
Г. Набора отклонений
Ответ: А, В
9. Укажите виды вариационных рядов:
А. Непрерывный
Б. Частотный
В. Полный
Г. Прерывный (дискретный)
Д. Интервальный (сгруппированный)
Ответ: А, Г, Д
10. К показателям разнообразия вариационного ряда относятся
А. Размах (амплитуда)
Б. Мода
В. Медиана
Г. Среднее квадратическое отклонение
Д. Коэффициент вариации
Ответ: А, Г, Д
11. Укажите виды средних арифметических величин:
А.
Простая
Б. Взвешенная
В. Алгебраическая
Г. По способу моментов
Д. Квадратическая
Ответ: А, Б, Г
12. Для графического изображения структурных показателей следует применять:
А. Столбиковые диаграммы
Б. Секторные диаграммы
В. Линейные графики
Г. Внутристолбиковые диаграммы
Д. Диаграммы рассеивания
Ответ: Б, Г
13. Для графического изображения динамики изучаемого явления следует применять:
А. Линейные графики
Б. Радиальные графики
В. Секторные диаграммы
Г. Внутристолбиковые диаграммы
Д. Все вышеперечисленное
Ответ: А, Б
14. Статистические таблицы:
А. Являются рациональной формой представления сводных количественных данных
Б. Должны иметь четкое и краткое заглавие, отражающее содержание статистического
материала
В. Не требуют итоговых граф/строк
Г. Используются для группировки материалов статистического наблюдения
Д.
Содержат только абсолютные величины
Ответ: А, Б, Г
15. К статистической таблице можно отнести:
А. Таблицу умножения
42
Б. Таблицу, содержащую показатели заболеваемости населения
В. Таблицу «Периодическая система элементов Д. И. Менделеева»
Г. Таблицу, характеризующую численность населения по полу и возрасту
Д. Табличную форму анкеты
Ответ: Б, Г
16. Перцентилями называют значения изучаемого количественного признака:
А. Повторяющиеся в вариационному ряду с наибольшей частотой
Б. Делящие вариационный ряд на десять равных частей
В. Находящиеся в центре вариационного ряда
Г. Делящие вариационный ряд на сто равных частей
Д. Делящие вариационный ряд на четыре равновеликие части
Ответ: Г
17. Квартили это значения изучаемого количественного признака:
А. Повторяющиеся в вариационному ряду с наибольшей частотой
Б. Делящие вариационный ряд на десять равных частей
В.
Находящиеся в центре вариационного ряда
Г. Делящие вариационный ряд на сто равных частей
Д. Делящие вариационный ряд на четыре равновеликие части
Ответ: Д
18. Децили – это значения изучаемого количественного признака:
А. Повторяющиеся в вариационному ряду с наибольшей частотой
Б. Делящие вариационный ряд на десять равных частей
В. Находящиеся в центре вариационного ряда
Г. Делящие вариационный ряд на сто равных частей
Д. Делящие вариационный ряд на четыре равновеликие части
Ответ: Б
Выборочное наблюдение — вид несплошного наблюдения, при котором отбор
подлежащих обследованию единиц наблюдения из генеральной
совокупности(population) осуществляется случайно, отобранная часть (выборка)
(sample)подвергается обследованию, после чего результаты распространяются на всю
исходную совокупность.
Репрезентативность — это способность выборочной совокупности как
количественно, так и качественно отражать свойства генеральной совокупности.
Количественная репрезентативность достигается достаточностью числа наблюдений,
качественная — соответствием признаков единиц наблюдения в выборочной и генеральной
совокупностях.
1. Какое из приведенных ниже требований к выборочной совокупности является основным:
А. Однородность
Б. Типичность
В. Репрезентативность
Г. Достаточность количества наблюдений
Д. Качественность
Ответ: В
2. Для большинства медико-биологических исследований оптимальной является
вероятность безошибочного прогноза:
А. 60,0%
Б. 68,3%
В. 95,5%
Г. 99,7%
Д. 100%
Ответ: В
3. В основе выборочного метода исследования лежит закон:
50
А. Нормального распределения
Б. Бесконечности пространства
В. Больших чисел
Ответ: В
4. Главным свойством выборки является:
А. Вариабельность
Б. Достоверность
В. Репрезентативность
Ответ: В
5.
Главным требованием к формированию выборки является:
А. Направленность отборки
Б. Случайность отбора
В. Точность отбора
Ответ: Б
6. Под количественной репрезентативностью понимается:
А. Охват всех возможных единиц наблюдений
Б. Количественное соотношение изучаемых признаков
В. Достаточное число наблюдений
Ответ: В
7. Под качественной репрезентативностью понимается:
А. Качественная полноценность выборочной совокупности
Б. Соответствие признаков единиц наблюдения в выборочной и генеральной
совокупностях
В. Наличие качественных признаков в выборочной совокупности
Ответ: Б
8. Ошибка репрезентативности показывает:
А. Степень разнообразия изучаемого признака
Б. На сколько отличаются показатели выборочной и генеральной совокупностей
В. Уровень вероятности безошибочного прогноза
Ответ: Б
9. Что такое малая выборка?
А. n ≤ 100
Б. n ≤ 50
В.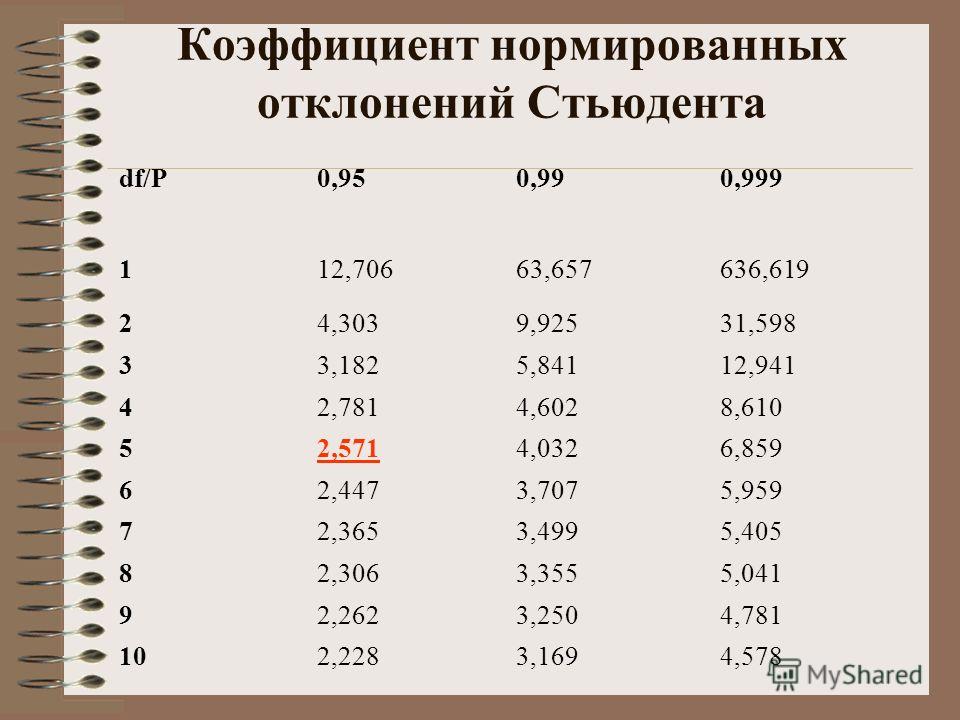
n ≤ 30
Ответ: В
10. Под доверительным интервалом понимают:
А. Пределы возможных колебаний показателя в генеральной совокупности
Б. Интервал, в пределах которого колеблется средняя арифметическая в вариационном
ряду
В. Доверительный коэффициент
Ответ: А
11. Репрезентативность выборки должна быть:
А. Качественной
Б. Количественной
В. Полной
Г. Случайной
Д. Характеризуется всеми вышеперечисленными признаками
Ответ: А, Б
12. Величина доверительного коэффициента (t) определяется:
А. Уровнем вероятности
Б. Разнообразием
В. Способом расчета показателя
Г. Всем вышеперечисленным
51
Д. Ничем из вышеперечисленного
Ответ: А
13. Что устанавливает закон больших чисел?
А. Распределение случайных величин с заданной достоверностью
Б. Тенденцию показателя выборочной совокупности при увеличении числа наблюдений
максимально приближаться к генеральной совокупности
В.
Закономерную устойчивость некоторых средних в массовых случайных явлениях
Г. Все вышеперечисленное
Ответ: Б
14. Основными методами формирования выборки являются:
А. Типологический
Б. Механический
В. Качественный
Г. Случайный
Д. Серийно-гнездовой
Ответ: А, Б, Г, Д
1. Разность между сравниваемыми величинами при n>30 считается существенной
(достоверной) если:
А. t = 2
Б. t ≥ 2
В. 1 ≤ t ≤ 2
Г. t = 0
Ответ: Б
2. Оценка достоверности полученного значения критерия t для малых выборок проводится
по:
А. Специальной формуле
Б. По принципу t ≥ 2
В. По таблице Стьюдента
66
Г. Все вышеперечисленное возможно
Ответ: В
3. Что устанавливает закон больших чисел?
А. Распределение случайных величин с заданной достоверностью
Б. Тенденцию показателя выборочной совокупности при увеличении числа наблюдений
максимально приближаться к генеральной совокупности
В.
Закономерную устойчивость некоторых средних в массовых случайных явлениях
Г. Все вышеперечисленное
Ответ: Б
4. Непараметрические методы оценки достоверности различий характеризуются тем, что:
А. Требуют предварительного знания характера распределения признака в совокупности
Б. Позволяют проводить оценку по качественным признакам
В. Дают более точные результаты, чем параметрические методы
Г. Обычно применяются для малых выборок
Д. Просты в применении
Ответ: Б, Г, Д
5. К непараметрическим критериям в статистике относят:
А. Критерий Стьюдента
Б. Критерий Вилкоксона
В. Критерий Манна-Уитни
Г. Критерий Колмогорова-Смирнова
Ответ: Б, В, Г
1. Регрессионный анализ позволяет:
А. Установить достоверность различия между показателями
Б. Устранить неоднородность сравниваемых групп
В. Определить взаимосвязь между признаками без измерения ее величины
Г. Дать количественную оценку взаимосвязи между признаками
Д.
Оценить динамику явления
Ответ: Г
2. Корреляционный анализ устанавливает:
А. Наличие связи
Б. Силу связи
В. Длительность связи
Г. Направление связи
Д. Все вышеперечисленное
Ответ: А, Б, Г
3. Укажите способы представления корреляционной связи:
78
А. Корреляционная таблица
Б. Корреляционный ряд
В. Корреляционное поле
Г. Коэффициент корреляции
Д. Все вышеперечисленное
Ответ: А, В, Г
4. Укажите методы расчета коэффициента корреляции:
А. Метод квадратов (Пирсона)
Б. Метод Фишера
В. Метод рангов (Спирмена)
Г. Все вышеперечисленное
Д. Ничего из вышеперечисленного
Ответ: А, В
5. Под корреляцией понимается:
А. Взаимосвязь между изучаемыми признаками
Б. Взаимопроникновение изучаемых признаков
В. Изучение изменения явления во времени
Ответ: А
6. Какие значения может принимать коэффициент корреляции:
А.
-1 ÷ +1
Б. 0 ÷ +1
В. 0 ÷ -1
Г. 0 ÷ +3
Д. 0 ÷ ∞
Ответ: А
Критерий Фишера и критерий Стьюдента в эконометрике
С помощью критерия Фишера оценивают качество регрессионной модели в целом и по параметрам.
Для этого выполняется сравнение полученного значения F и табличного F значения. F-критерия Фишера. F фактический определяется из отношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы:
где n — число наблюдений;
m — число параметров при факторе х.
F табличный — это максимальное значение критерия под влиянием случайных факторов при текущих степенях свободы и уровне значимости а.
Уровень значимости а — вероятность не принять гипотезу при условии, что она верна. Как правило а принимается равной 0,05 или 0,01.
Если Fтабл > Fфакт то признается статистическая незначимость модели, ненадежность уравнения регрессии.
Таблицы по нахождению критерия Фишера и Стьюдента
Таблицы значений F-критерия Фишера и t-критерия Стьюдента Вы можете посмотреть здесь.
Табличное значение критерия Фишера вычисляют следующим образом:
- Определяют k1, которое равно количеству факторов (Х). Например, в однофакторной модели (модели парной регрессии) k1=1, в двухфакторной k=2.
- Определяют k2, которое определяется по формуле n — m — 1, где n — число наблюдений, m — количество факторов. Например, в однофакторной модели k2 = n — 2.
- На пересечении столбца k1 и строки k2 находят значение критерия Фишера
Для нахождения табличного значения критерия Стьюдента определяют число степеней свободы, которое определяется по формуле n — m — 1 и находят его значение при определенном уровне значимости (0,10, 0,05, 0,01).
Критерии Стьюдента
Для оценки статистической значимости модели по параметрам рассчитывают t-критерии Стьюдента.
Оценка значимости модели с помощью критерия Стьюдента проводится путем сравнения их значений с величиной случайной ошибки:
Случайные ошибки коэффициентов линейной регрессии и коэффициента корреляции определяются по формулам:
Сравнивая фактическое и табличное значения t-статистики и принимается или отвергается гипотеза о значимости модели по параметрам.
Зависимость между критерием Фишера и значением t-статистики Стьюдента определяется так
Как и в случае с оценкой значимости уравнения модели в целом, модель считается ненадежной если tтабл > tфакт
Видео лекциий по расчету критериев Фишера и Стьюдента
Для более подробного изучения расчетов критериев Фишера и Стьюдента советуем посмотреть это видео
Лекция 1. Критерии и Гипотезы
Лекция 2. Критерии и Гипотезы
Лекция 3. Критерии и Гипотезы
Определение доверительных интервалов
Для построения доверительного интервала определяется предельная ошибка А для обоих показателей:
Формулы для нахождения доверительных интервалов выглядят так
Прогнозное значение у определяется с помощью подстановки в
уравнение регрессии прогнозного значения х.
Вычисляется средняя стандартная ошибка прогноза
и находится доверительный интервал
Задача регрессионного анализа в предмете эконометрика состоит в анализе дисперсии изучаемого показателя y:
общая сумма квадратов отклонений (TSS)
сумма квадратов отклонений, обусловленная регрессией (RSS)
остаточная сумма квадратов отклонений (ESS)
Долю дисперсии, обусловленную регрессией, в общей дисперсии показателя у характеризует коэффициент детерминации R, который должен превышать 50% (R2 > 0,5). В контрольных по эконометрике в ВУЗах этот показатель рассчитывается всегда.
Коэффициент детерминации: Обзор
По
Эндрю Блументаль
Полная биография
Эндрю Блументаль имеет более чем 20-летний опыт работы редактором в качестве финансового журналиста и автора статей по маркетингу финансовых услуг.
Узнайте о нашем редакционная политика
Обновлено 10 октября 2021 г.
Рассмотрено
Маргарет Джеймс
Рассмотрено Маргарет Джеймс
Полная биография
Пегги Джеймс — дипломированный бухгалтер с более чем 9многолетний опыт работы в области бухгалтерского учета и финансов, включая корпоративные, некоммерческие и личные финансы. Последнее время она работала в Университете Дьюка и является владельцем Peggy James, CPA, PLLC, обслуживающей малый бизнес, некоммерческие организации, индивидуальных предпринимателей, фрилансеров и частных лиц.
Узнайте о нашем Совет финансового контроля
Факт проверен
Сюзанна Квилхауг
Факт проверен Сюзанна Квилхауг
Полная биография
Сюзанна — исследователь, писатель и специалист по проверке фактов.
Она имеет степень бакалавра финансов в государственном университете Бриджуотер и работала над печатным контентом для владельцев бизнеса, национальных брендов и крупных изданий.
Узнайте о нашем редакционная политика
Что такое коэффициент детерминации?
Коэффициент детерминации — это статистическое измерение, которое исследует, как различия в одной переменной могут быть объяснены различием во второй переменной при прогнозировании исхода данного события. Другими словами, этот коэффициент, более известный как R-квадрат (или R 2 ), оценивает, насколько сильна линейная связь между двумя переменными, и на него в значительной степени полагаются исследователи при проведении анализа тенденций. Чтобы привести пример его применения, этот коэффициент может рассматривать следующий вопрос: если женщина забеременеет в определенный день, какова вероятность того, что она родит ребенка в определенный день в будущем? В этом сценарии эта метрика предназначена для расчета корреляции между двумя связанными событиями: зачатием и рождением.
R-квадрат
Ключевые выводы
- Коэффициент детерминации — это комплексная идея, основанная на статистическом анализе моделей данных.
- Коэффициент детерминации используется для объяснения того, насколько изменчивость одного фактора может быть вызвана его связью с другим фактором.
- Этот коэффициент широко известен как R-квадрат (или R 2 ) и иногда упоминается как «качество соответствия».
- Этот показатель представлен значением от 0,0 до 1,0, где значение 1,0 указывает на идеальное соответствие и, таким образом, является высоконадежной моделью для будущих прогнозов, а значение 0,0 указывает на то, что модель не может точно смоделировать данные вообще.
Понимание коэффициента детерминации
Коэффициент детерминации — это мера, используемая для объяснения того, насколько изменчивость одного фактора может быть вызвана его связью с другим родственным фактором. Эта корреляция, известная как «степень соответствия», представлена как значение от 0,0 до 1,0.
Значение 1,0 указывает на идеальное соответствие и, таким образом, является очень надежной моделью для будущих прогнозов, тогда как значение 0,0 указывает на то, что расчет вообще не может точно смоделировать данные. Но значение 0,20, например, предполагает, что 20 % зависимой переменной предсказывается независимой переменной, а значение 0,50 предполагает, что 50 % зависимой переменной предсказывается независимой переменной, и так далее.
График коэффициента детерминации
На графике качество подгонки измеряет расстояние между подобранной линией и всеми точками данных, разбросанными по всей диаграмме. Плотный набор данных будет иметь линию регрессии, расположенную близко к точкам и имеющую высокий уровень соответствия, что означает, что расстояние между линией и данными невелико. Хотя хорошее соответствие имеет R 2 , близкое к 1,0, само по себе это число не может определить, являются ли точки данных или прогнозы смещенными. Это также не говорит аналитикам, является ли значение коэффициента детерминации хорошим или плохим по своей сути.
Пользователь может по своему усмотрению оценить значение этой корреляции и то, как ее можно применять в контексте анализа будущих тенденций.
Коэффициент вариации в статистике
Коэффициент вариации (CV) является относительной мерой изменчивости, которая указывает размер стандартного отклонения по отношению к его среднему значению. Это стандартизированная безразмерная мера, позволяющая сравнивать изменчивость между разрозненными группами и характеристиками. Он также известен как относительное стандартное отклонение (RSD).
В этом посте вы узнаете о коэффициенте вариации, как его рассчитать, когда он особенно полезен, а когда его следует избегать.
Как рассчитать коэффициент вариации
Для расчета коэффициента вариации используется простое соотношение. Просто возьмите стандартное отклонение и разделите его на среднее значение.
Более высокие значения указывают на то, что стандартное отклонение относительно велико по сравнению со средним значением.
Например, пиццерия измеряет время доставки в минутах. Среднее время доставки составляет 20 минут, а стандартное отклонение — 5 минут.
Интерпретация коэффициента вариации
В примере с доставкой пиццы коэффициент вариации равен 0,25. Это значение говорит вам об относительном размере стандартного отклонения по сравнению со средним значением. Аналитики часто сообщают коэффициент вариации в процентах. В этом примере стандартное отклонение составляет 25% размера среднего.
Если значение равно единице или 100 %, стандартное отклонение равно среднему значению. Значения меньше единицы указывают на то, что стандартное отклонение меньше среднего (типичное), тогда как значения больше единицы возникают, когда С.Д. больше среднего.
Как правило, более высокие значения представляют большую степень относительной изменчивости.
Абсолютные и относительные меры вариабельности
В другом посте я рассказываю о стандартном отклонении, межквартильном диапазоне и диапазоне.
Эти статистические данные являются абсолютными мерами изменчивости. Они используют единицу измерения переменной для описания изменчивости.
Для пятиминутного стандартного отклонения в примере с доставкой пиццы мы знаем, что типичная доставка происходит на пять минут раньше или позже среднего времени доставки.
Очень полезная информация! Он сообщает нам о изменчивости наших данных, удобно используя исходные единицы измерения. Мы можем сравнить эту изменчивость времени доставки с другой пиццерией.
Для получения дополнительной информации прочитайте мой пост о стандартном отклонении и других абсолютных мерах изменчивости.
С другой стороны, относительные измерения используют процесс стандартизации, который удаляет исходные единицы измерения. В коэффициенте CV и стандартное отклонение, и среднее значение используют одни и те же единицы измерения, что уравновешивает их и дает безразмерную статистику.
Когда вы хотите использовать коэффициент вариации? Его безразмерный характер дает ему некоторые преимущества.
В частности, коэффициент вариации облегчает содержательные сравнения в сценариях, где абсолютные меры не могут этого сделать.
Используйте коэффициент вариации, если вы хотите сравнить изменчивость между:
- группами, которые имеют очень разные средние величины.
- Характеристики, использующие разные единицы измерения.
В этих двух случаях абсолютные измерения могут быть проблематичными. Давайте узнаем больше!
Использование коэффициента вариации, когда средние значения сильно различаются
Когда вы измеряете характеристику, которая имеет широкий диапазон значений, вы часто ожидаете, что среднее значение и стандартное отклонение будут изменяться одновременно. Это явление часто встречается в данных поперечного сечения. В этих случаях вы хотите знать, как стандартное отклонение сравнивает 90 101 относительно 90 102 с совершенно разными средними значениями.
Предположим, вы измеряете расходы домохозяйств и хотите сравнить изменчивость расходов домохозяйств с высоким и низким доходом.
Эти данные вымышлены.
| Расходы | Высокий доход | Низкий доход |
| Среднее | 500 000 долларов США | 40 000 долларов США |
| Стандартное отклонение | 125 000 долларов США | 10 000 долларов США |
Эти значения используют одну и ту же единицу измерения (доллары США), что позволяет сравнивать стандартные отклонения. Изменчивость расходов домохозяйств с высоким доходом намного больше, чем у домохозяйств с низким доходом (125 000 долларов США против 10 000 долларов США). Впрочем, учитывая огромную разницу в средних расходах, это неудивительно.
Однако, если вы хотите сравнить изменчивость при учете разрозненных средних значений, вам необходимо использовать относительную меру изменчивости, такую как коэффициент вариации. В приведенной ниже таблице показано, что при учете различий в расходах группа с низким доходом фактически имеет одинаковую изменчивость.
| Коэффициент вариации | Высокий доход | Низкий доход |
| 25% | 25% |
Примеры из реальной жизни
Аналитики часто используют коэффициент изменчивости, когда их набор данных имеет широкий диапазон средних значений, как показано в предыдущем примере.
Исследователи используют CV для оценки неравенства доходов в разных странах. Средние доходы по странам сильно различаются. Есть богатые страны и бедные страны. Для учета неравенства внутри каждой страны при учете совершенно разных средних доходов аналитики используют коэффициент вариации. В этом контексте, когда страна имеет более высокий коэффициент изменчивости, она представляет собой более высокую степень неравенства в доходах.
Точно так же финансовые аналитики используют коэффициент изменчивости для оценки волатильности доходности финансовых вложений в широком диапазоне оценок.
В этом контексте более высокие коэффициенты указывают на более значительный риск.
Коэффициент вариации особенно полезен, когда данные подчиняются логнормальному распределению. В этих распределениях стандартное отклонение изменяется в зависимости от оцениваемой части распределения. Однако коэффициент вариации остается постоянным в пределах логарифмически нормального распределения.
Использование коэффициента вариации для сравнения измерений, в которых используются разные единицы измерения
Когда в измерениях используются разные шкалы, их нельзя сравнивать напрямую. Предположим, вы хотите сравнить вариабельность результатов SAT с оценками ACT? Хотя эти вступительные экзамены в колледжи схожи по своему характеру и цели, они используют разные шкалы. Следовательно, вы не можете напрямую сравнивать их стандартные отклонения.
Однако коэффициент вариации стандартизирует необработанные данные, что означает, что вы можете сравнить относительную изменчивость результатов SAT и ACT.
Кроме того, каждый раз, когда вы хотите оценить изменчивость изначально различных характеристик, вам нужно будет использовать относительную меру изменчивости, такую как коэффициент изменчивости. Например, вы можете захотеть оценить изменчивость рабочей температуры и скорости ракет. Или сравнить изменчивость веса и прочности образцов материалов. Вы не можете осмысленно сравнивать стандартные отклонения, которые используют разные единицы измерения, такие как килограммы для веса и мегапаскали для силы!
Однако, если ваша переменная килограммы имеет более высокий коэффициент изменчивости, чем мегапаскали, то вы знаете, что вес относительно более изменчив, чем сила.
В этих примерах измеряются совершенно разные характеристики с использованием разных единиц измерения. Однако вы можете использовать коэффициент вариации, чтобы сравнить их относительную изменчивость!
Предупреждения о том, когда не следует использовать коэффициент вариации
Хотя коэффициент вариабельности чрезвычайно полезен в некоторых случаях, в некоторых случаях его использовать не следует.
Не использовать, когда среднее значение близко к нулю
Если среднее значение равно нулю, знаменатель отношения равен нулю, что проблематично! К счастью, у вас вряд ли будет среднее значение, точно равное нулю. Но когда среднее значение близко к нулю, коэффициент вариации может приближаться к бесконечности, и его значение чувствительно к небольшим изменениям среднего!
Не использовать с шкалами интервалов
Используйте коэффициент вариации, только если в ваших данных используется шкала отношений. Не используйте его для интервальных шкал.
Шкалы отношения имеют абсолютный ноль, что представляет собой полное отсутствие характеристики. Например, нулевой вес (в имперской или метрической системе) указывает на полное отсутствие веса. Вес — это шкала отношений.
Тем не менее, температуры в градусах Фаренгейта и Цельсия являются интервальными шкалами. Эти системы измерения имеют нулевое значение, но эти нули не указывают на отсутствие температуры.
(Кельвин имеет абсолютный ноль, который представляет собой отсутствие температуры. Кельвин — это шкала отношений.)
Интервальные шкалы не позволяют осмысленно разделить измерения. Например, 10°С — это не 1/3 температуры 30°С! Поскольку коэффициент вариации включает деление, эта статистика не имеет смысла для интервальных шкал.
Давайте рассмотрим пример проблемы, возникающей при использовании коэффициента вариации с интервальными шкалами!
В таблице ниже показаны пары эквивалентных температур. Вы ожидаете, что их коэффициенты вариации будут равными. Давай проверим!
Резюме совсем другое! Это происходит потому, что мы оцениваем интервальные шкалы.
Используйте коэффициент вариации только тогда, когда у вас есть истинный абсолютный ноль на шкале отношений!
Абсолютные и относительные показатели в других статистических контекстах
Необходимость выбора между использованием абсолютного показателя (например, стандартного отклонения) и относительного, стандартизированного показателя (например, коэффициента вариабельности) возникает в других областях статистики.