5. Определение синуса и косинуса; тангенса и котангенса на единичной окружности.
Определение. Рассмотрим окружность единичного радиуса с центром в начале координат. Пусть точка на окружности, начав движение в точке М0 (1, 0), прошла по окружности дугу величиной х радиан, или же соответствующий этой точке луч, отрезок, вектор) повернулся на угол х радиан. Пусть Мх – положение точки на окружности в конце движения. Эта точка полностью описывается ее координатами, поэтому для них вводят специальные обозначения.
Ординату точки Мх (или проекцию точки на ось ординат) называют синусом числа х, а абсциссу (или проекцию на ось абсцисс)– косинусом числа х.
Элемент математической культуры как компетенция
ЭМК
Работа с определением
Основная цель работы с определением –
выделить существенные признаки
определяемого понятия.
Задание
Задание
Найдите значения синуса и косинуса для углов 0; 2; ; /2; 3/2. и результаты отразите в таблице
Значения синуса и косинуса в характерных точках окружности
Число функция | 0 | 2 | | /2 | 3/2 |
Синус | |||||
Косинус |
Организация записей как компетенция
Систематизируйте информацию в виде
таблицы.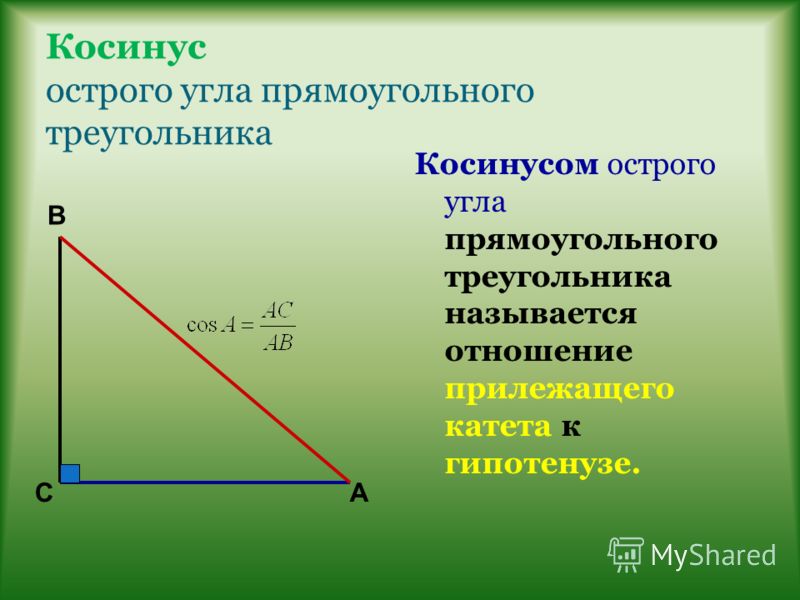 Заголовок таблицы должен
отражать название системы, название
1-ой строки и 1-го столбца – ее основные
характеристики.
Заголовок таблицы должен
отражать название системы, название
1-ой строки и 1-го столбца – ее основные
характеристики.
Определение. Тангенсом числа х называется отношение синуса данного числа к его косинусу. Котангенсом числа х называется отношение косинуса данного числа к его синусу.
; .
6. Определение синуса и косинуса; тангенса и котангенса в прямоугольном треугольнике.
Р ассмотрим тригонометрические функции в прямоугольном треугольнике.
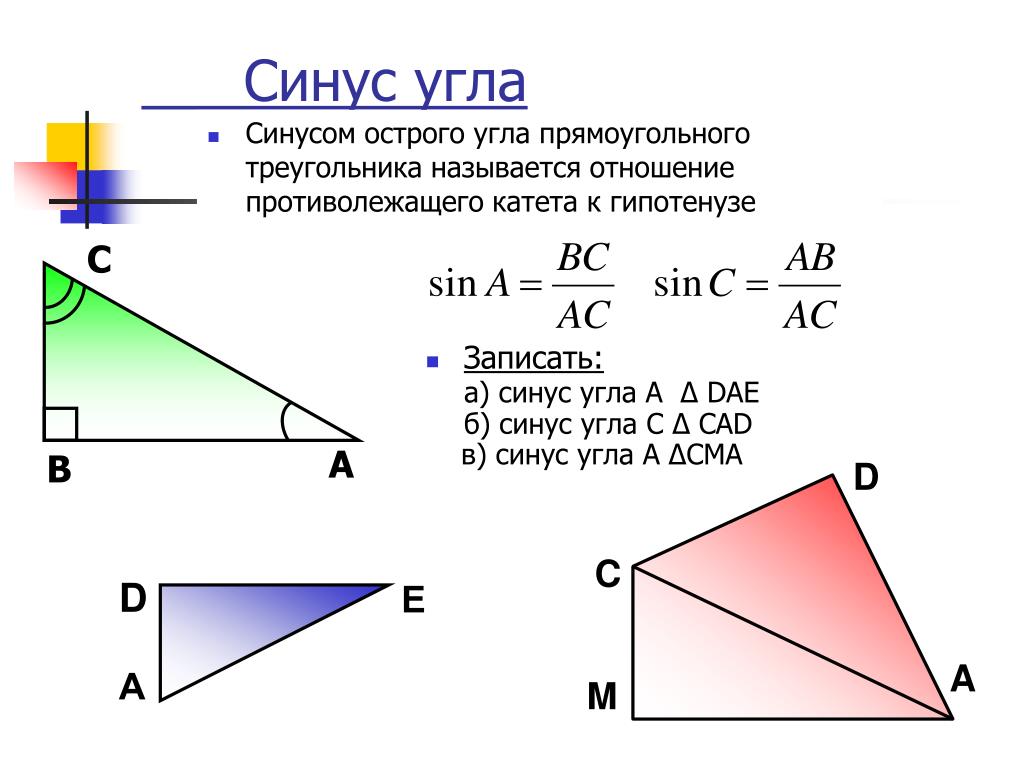
Синусом острого угла прямоугольного треугольника называют отношение противолежащего катета к гипотенузе: sinA =
Косинусом острого угла прямоугольного треугольника называют отношение прилежащего катета к гипотенузе: cos
Задание
Найдите значения синуса и косинуса для углов /6; /4; /3 и результаты отразите в таблице
(
прием
Шаталова с демонстрацией прямоугольного
треугольника с помощью рук).
______________________________________________________________
_______ __________ | /6 | /4 | /3 |
Синус | |||
Косинус |
Проверка организации записей как компетенции
Дайте название таблице и ее основных характеристик
Тангенсом острого угла прямоугольного треугольника называют отношение противолежащего катета к прилежащему: tg A = .
Котангенсом острого угла прямоугольного
треугольника называют отношение
прилежащего катета к противолежащему:
ctg A = .
II Основные тригонометрические тождества (группы тождеств, способы доказательства).
Определение основных тригонометрических функций. | Образовательный портал. Решение задач по физике, математике, химии. Справочник физико-химических величин. Онлайн-учебники.
синус угла косинус угла тангенс угла котангенс угла cеканс угла косеканс угла
Введем основные тригонометрические функции.
Пусть радиус-вектор $\vec{r} = \bar{OM}$ точки $M$ образует угол $\alpha$ с осью $Ox$ (рис.), причем $x$ и $y$ соответственно абсцисса и ордината конца $M$ вектора, $r$ — его модуль, а величина угла $\alpha$ измеряется в градусах или в радианах.
1. Синусом угла $\alpha$ (обозначение: $\sin \alpha$) называется отношение ординаты $y$ (см.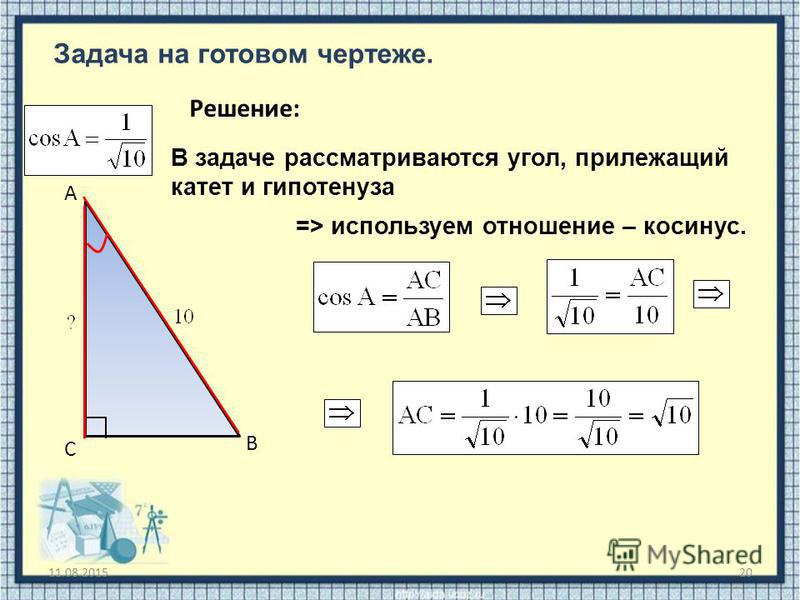 рис.) к длине $r$ радиуса-вектора $\bar {OM}$:
рис.) к длине $r$ радиуса-вектора $\bar {OM}$:
$\sin \alpha = \frac{y}{r}$. (1)
2. Косинусом угла $\alpha$ (обозначение: $\cos \alpha$) называется отношение абсциссы $x$ к длине $r$ радиуса-вектора $\bar {OM}$:
$\cos \alpha = \frac{x}{r}$. (2)
Ниже (замечание 1) мы покажем, что $\sin \alpha$ и $\cos \alpha$, определенные равенствами (1) и (2), действительно зависят лишь от угла $\alpha$ (но не от радиуса окружности $r$).
3. Тангенсом угла $\alpha$ (обозначение: $tg \alpha$) называется отношение синуса угла $\alpha$ к косинусу этого угла:
$tg \alpha = \frac {\sin \alpha}{\cos \alpha}$. (3)
4. Котангенсом угла $\alpha$ (обозначение: $ctg \alpha$) называется отношение косинуса угла $\alpha$ к синусу этого угла:
$ctg \alpha = \frac {\cos \alpha}{\sin \alpha}$. (4)
5. Секансом угла $\alpha$ (обозначение: $sec \alpha$) называется величина, обратная $\cos \alpha$:
Секансом угла $\alpha$ (обозначение: $sec \alpha$) называется величина, обратная $\cos \alpha$:
$sec \alpha = \frac{1}{ \cos \alpha}$. (5)
6. Косекансом угла $\alpha$ (обозначение: $cosec \alpha$) называется величина, обратная $\sin \alpha$:
$cosec \alpha = \frac{1}{ \sin \alpha}$ (6)
Замечание 1. Тригонометрические функции (1) — (6) действительно являются функциями только угла $\alpha$, т. е. не зависят от длины подвижного радиуса-вектора. Для того чтобы в этом убедиться, достаточно доказать, что если подвижный радиус-вектор $\vec{r}$ образует с осью абсцисс данный угол $\alpha$, то отношения $\frac{х}{r}$ и $\frac{у}{r}$ не зависят от длины радиуса-вектора.
Замечание 2. Из определения $tg \alpha$ и $ctg \alpha$ следует, что
$tg \alpha = \frac{y}{x}$, (7)
$ctg \alpha = \frac{x}{y}$. (8)
Соотношения (7) и (8) можно было бы принять в качестве определений для $tg \alpha$ и $ctg \alpha$.
Замечание 3. Аналогично получаем
$sec \alpha = \frac{r}{x}$,(9)
$cosec \alpha = \frac{r}{y}$ (10).
Соотношения (9) и (10) можно было бы также принять в качестве определений для $sec \alpha$ и $\cosec \alpha$.
Замечание 4. Во всех определениях (1) — (6) предполагаем, что соответствующие отношения существуют (имеют смысл). Например, $tg \alpha$ имеет смысл, если $\cos \alpha \neq 0, ctg \alpha$ имеет смысл, если $\sin \alpha \neq 0$, и т.д. Поскольку (замечание 1) тригонометрические функции (1) — (6) угла $\alpha$ не зависят от длины подвижного радиуса-вектора, то в качестве радиуса-вектора можно брать вектор с длиной, равной единице $(| \vec{r}| = r = 1)$. Такой вектор называют единичным радиусом-вектором. В случае единичного радиуса-вектора формулы для основных тригонометрических функций запишутся так (рис.):
$\begin{cases} \sin \alpha = y, \cos \alpha = x \\ tg \alpha = \frac{y}{x}, ctg \alpha = \frac{x}{y} \\ sec \alpha = \frac{1}{x}, cosec \alpha = \frac{1}{y} \end{cases}$. {\circ}$ опишет окружность, называемую единичной окружностью (рис.). Для геометрического истолкования тангенса и котангенса вводят понятия оси тангенсов и оси котангенсов. Осью тангенсов называется перпендикуляр, восставленный в точке $A$ к неподвижному радиусу-вектору $\bar{OA}$. Положительное и отрицательное направления на оси тангенсов выбирают так, чтобы они совпадали с соответствующими направлениями оси ординат (рис.). Рассмотрим угол $\alpha = \angle AOM$ и введем понятие соответствующей точки оси тангенсов.
{\circ}$ опишет окружность, называемую единичной окружностью (рис.). Для геометрического истолкования тангенса и котангенса вводят понятия оси тангенсов и оси котангенсов. Осью тангенсов называется перпендикуляр, восставленный в точке $A$ к неподвижному радиусу-вектору $\bar{OA}$. Положительное и отрицательное направления на оси тангенсов выбирают так, чтобы они совпадали с соответствующими направлениями оси ординат (рис.). Рассмотрим угол $\alpha = \angle AOM$ и введем понятие соответствующей точки оси тангенсов.
а) Если точка $M$ единичной окружности лежит справа от оси ординат, то соответствующей ей точкой оси тангенсов назовем точку $M_{1}$ (точку пересечения продолжения $MO$ с осью тангенсов, рис а.
б) Если точка $M$ единичной окружности лежит слева от оси ординат, то соответствующей ей точкой сси тангенсов назовем точку $M_{1}$ (точку пересечения продолжения $MO$ с ссыо тангенсов, рис. б.
Заметим, что тангенс угла а численно равен ординате $y_{1}$ (рис.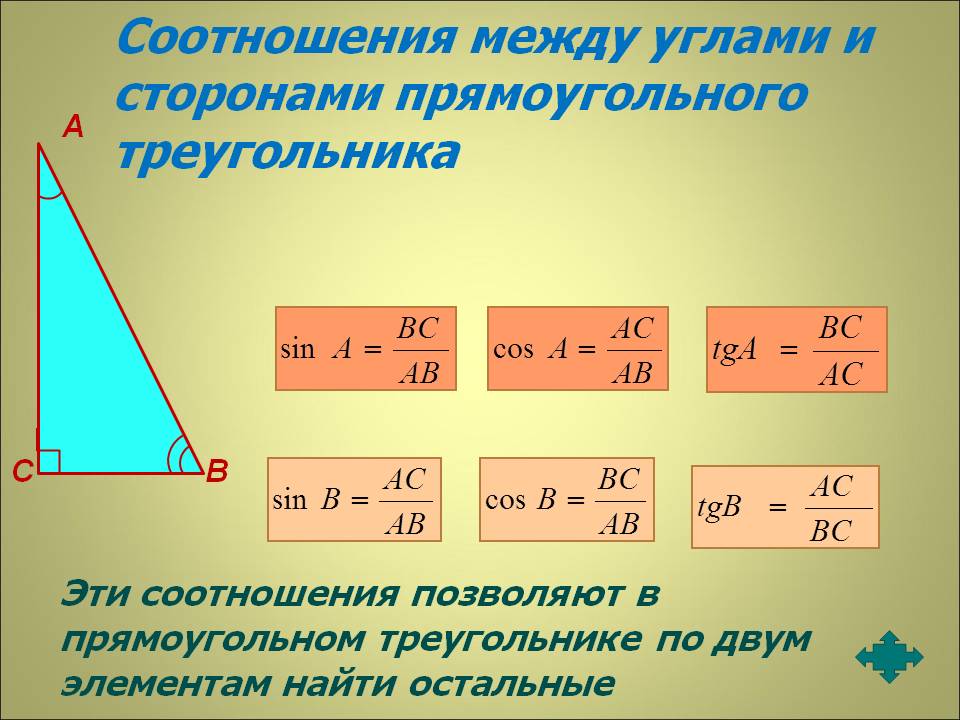
Урок: Косинусное отношение | Нагва
Портал деактивирован. Обратитесь к администратору портала.
- оценок
- Порталы
- Руководство пользователя
В этом уроке мы научимся находить недостающие длины и углы в треугольнике, используя соотношения косинусов.
План урока
- использовать прямоугольные треугольники для нахождения косинусных соотношений,
- использовать специальные прямоугольные треугольники для нахождения косинусных соотношений для углов 45∘, 30∘ и 60∘,
- использовать косинусное отношение для нахождения недостающих длин в прямоугольных треугольников,
- используют отношение арккосинуса для нахождения отсутствующих мер угла в прямоугольных треугольниках,
- решают более сложные задачи, такие как использование соотношения косинуса или арккосинуса в сочетании с теоремой Пифагора, простыми свойствами 2D-формы или координатой геометрия.

Видео урока
12:44
Плейлист урока
05:11
02:45
Рабочий лист урока
Q1:
𝐴𝐵𝐶 — прямоугольный треугольник в точке 𝐵, где
𝐴𝐵=26см
и 𝑚∠𝐴=64∘. Найдите длину 𝐴𝐶 с точностью до двух знаков после запятой.
Найдите длину 𝐴𝐶 с точностью до двух знаков после запятой.
Q2:
Найдите длину 𝐴𝐵 с точностью до двух знаков после запятой.
Q3:
𝐴𝐵𝐶𝐷 — прямоугольник, диагональ которого 𝐴𝐶=4см, а 𝑚∠𝐴𝐶𝐵=27∘. Найдите длину 𝐵𝐶 с точностью до двух знаков после запятой.
Коэффициент косинуса | Мир математики Пасси
Источник изображения: http://rekkerd.org
В этом уроке мы еще раз займемся тригонометрией.
Источник изображения: Google Images
Выше показаны некоторые основные звуковые волны «синусоидальной» формы.
Наше ухо улавливает их при воспроизведении музыки.
Различные «гитарные педали» или «педали» могут использоваться для изменения этих основных звуковых волн для создания новых и интересных звуков.
Математика этих кривых волн включает в себя тригонометрию прямоугольных треугольников.
Эти криволинейные волны формируются путем графического отображения всех значений десятичной тригонометрии, которые могут быть образованы прямоугольными треугольниками различной формы.
Это прекрасно иллюстрирует следующая диаграмма:
Изображение использовано с разрешения Рассела Кайтли
Искаженный Тяжелый звук гитары возникает, когда гладкие синусоидальные волны математически преобразуются в волны квадратной, пилообразной и треугольной формы.
Это показано на анимации ниже:
Источник изображения: Google Images
Математика изменения формы волны работает для создания широкого спектра звуков электрогитары.
Image Copyright 2013 by Passy’s World of Mathematics
Guitar Mathematics
Image Copyright 2013 by Passy’s World of Mathematics
Здесь, в Passy’s World, мы любим играть на гитаре.
Если вы хотите узнать больше о математике игры на гитаре, ознакомьтесь с нашим уроком по этой ссылке:
Guitar Mathematics
чрезвычайно важно в областях, связанных с волнами, такими как Звук, Свет, Электричество и Океанография.
В этом уроке мы рассмотрим тригонометрическую функцию, известную как «Косинус».
Косинусное отношение
Существует три основных тригонометрических отношения: синус, косинус и тангенс.
Трудно пытаться выучить все три сразу, поэтому в этом уроке рассматривается только отношение косинуса.
В Passy’s World мы обнаружили, что пытаться выучить все три коэффициента одновременно — все равно, что пытаться научиться водить, чиповать и патт — и все это за один урок гольфа.
Это сложно, запутанно и неприятно.
Мы предпочитаем изучать отношение синуса, а затем отдельно отношение косинуса, прежде чем пытаться работать со всеми тремя коэффициентами срабатывания.
Прежде чем приступить к этому уроку по косинусам, важно, чтобы вы знали, как обозначить стороны прямоугольного треугольника как «гипотенуза», «противоположная» и «прилежащая».
Если вам нужно узнать, как обозначить прямоугольный треугольник, нажмите на ссылку ниже:
The Sine Ratio
Также важно, чтобы вы уже изучили отношение синусов в нашем предыдущем уроке по ссылке ниже: Стороны гипотенузы прямоугольного треугольника выглядят следующим образом:
Image Copyright 2013 by Passy’s World of Mathematics
Отношение косинуса будет одинаковым для любого прямоугольного треугольника, в котором содержится определенное значение угла.
На приведенной ниже диаграмме показано это для трех прямоугольных треугольников разного размера с углами 37 градусов.
Image Copyright 2013 by Passy’s World of Mathematics
Косинусный треугольник – сводка формул
Вот четыре формулы, которые мы используем при работе с косинусными треугольниками.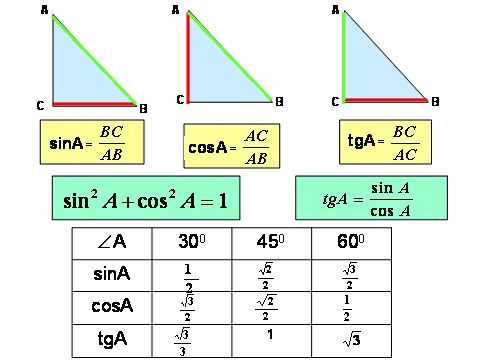
Image Copyright 2013 by Passy’s World of Mathematics
Использование калькулятора косинуса треугольников
Если нам дан угол и нам нужно определить его десятичное значение косинуса, мы можем сделать это на калькуляторе, как показано ниже :
Image Copyright 2013 by Passy’s World of Mathematics
Если нам даны смежная область и гипотенуза, и нам нужно определить опорное значение угла, мы можем сделать это на калькуляторе, как показано ниже:
Image Copyright 2013 by Passy’s World of Mathematics
Вышеупомянутая функция иногда также называется поиском «ArcCos» или «ACos».
Онлайн-калькулятор тригонометрии
Если вы хотите использовать онлайн-калькулятор для определения значений Cos или угла, то он есть по следующей ссылке:
Онлайн-калькулятор коэффициентов срабатывания
Обратите внимание, что вам нужно будет установить этот калькулятор на 4 десятичных разряда для значений Sin.
Косинусный треугольник – этапы разработки
Если мы работаем над прямоугольным треугольником, который включает в себя прилежащую сторону и гипотенузу, то вот шаги, которые нам необходимо выполнить.
Image Copyright 2013 by Passy’s World of Mathematics
Выполните описанные выше шаги, чтобы ответить на все вопросы для косинусных треугольников.
Примеры треугольников косинуса
Следующие примеры показывают, как мы применяем наши формулы треугольника косинуса к вопросам для определения неизвестных значений прямоугольных треугольников.
В этом первом примере нас просят найти значение «Смежной» стороны.
Image Copyright 2013 by Passy’s World of Mathematics
В следующем примере показано, как найти значение «гипотенузы» для косинусного треугольника.
Image Copyright 2013 by Passy’s World of Mathematics
В нашем следующем примере мы используем функцию обратного косинуса, чтобы найти неизвестный угол.
Image Copyright 2013 by Passy’s World of Mathematics
В этом последнем примере нам даны смежная и гипотенуза, и нас просят уточнить десятичное значение косинуса.
Важно внимательно читать вопросы, а не сразу предполагать, что это пример «Найти угол», как в примере 3.
Image Copyright 2013 by Passy’s World of Mathematics
Рабочий лист на косинусное отношение
Следующий рабочий лист содержит несколько типов вопросов на косинусное отношение и включает ответы в конце листа.
Щелкните следующую ссылку, чтобы получить доступ к этой рабочей таблице косинусных отношений:
Рабочий лист косинусных отношений
Связанные элементы
Синусное отношение
Обозначение тригонометрических треугольников и треугольников
0085 Классификация треугольников
Пифагор и прямоугольные треугольники
Конгруэнтные треугольники
Высокие здания и большие плотины
Подобные формы и подобные треугольники
Геометрия в животном мире наш сайт.
После этого вы сможете получать уведомления о новых страницах прямо на свой адрес электронной почты.
Перейдите в область подписки на правой боковой панели, введите свой адрес электронной почты и нажмите кнопку «Подписаться».
Чтобы точно узнать, как работает бесплатная подписка, нажмите на следующую ссылку:
Как работает бесплатная подписка
Если вы хотите предложить идею для статьи или стать приглашенным автором на нашем веб-сайте, напишите нам по адресу адрес горячей почты, показанный в правой части этой страницы.
Если вы являетесь подписчиком Passy’s World of Mathematics и хотели бы получить бесплатную версию этого урока в PowerPoint, которая на 100 % бесплатна для вас как подписчика, напишите нам по следующему адресу:
Пожалуйста, укажите в своем электронном письме, что вы хотите получить бесплатную подписную копию Powerpoint «Косинусное отношение».
Не стесняйтесь размещать ссылки на любые наши уроки, делиться ими в социальных сетях или использовать их в системах управления обучением в школах.
Нравится нам на Facebook
На нашей странице Facebook есть много дополнительных элементов, которые не размещены на этом сайте.
Сюда входят материалы, представляющие математический интерес, забавные математические картинки и мультфильмы, а также случайные зарисовки из личной жизни «Пасси».
Проверьте это по следующей ссылке:
https://www.facebook.com/PassysWorldOfMathematics
Пока вы там, ставьте лайк странице, чтобы вы могли получать наши обновления FB в своей ленте новостей Facebook.
Помогите Passy’s World расти
Каждый день Passy’s World предоставляет сотням людей бесплатные уроки математики.
Помогите нам поддерживать этот бесплатный сервис и поддерживать его рост.
Пожертвуйте любую сумму от $2 и выше через PayPal, щелкнув изображение PayPal ниже. Благодарю вас!
PayPal принимает кредитные карты, но вам нужно будет указать адрес электронной почты и пароль, чтобы PayPal мог создать для вас учетную запись PayPal для обработки транзакции. За это действие с вас не будет взиматься плата за обработку, так как PayPal вычитает комиссию из вашего пожертвования до того, как оно попадет в Passy’s World.
За это действие с вас не будет взиматься плата за обработку, так как PayPal вычитает комиссию из вашего пожертвования до того, как оно попадет в Passy’s World.
Наслаждайтесь,
Passy
Эта запись была размещена в Треугольники, Тригонометрия и помечена смежной формулой, отношение косинуса, косинус, угол косинуса, примеры косинуса, формула косинуса, косинус на калькуляторе, отношение косинуса, рабочий лист отношения косинуса, косинус треугольник, нахождение угла, нахождение значений косинуса, как сделать косинус, как выполнить тригонометрические вычисления, как найти гипотенузу, как научить коэффициенту косинуса, как научить тригонометрическому соотношению, гипотенуза, формула гипотенузы, арккосинус, арккосинус, Online Trig Калькулятор соотношений, прямоугольные треугольники, математика треугольников, тригонометрия, расчеты триггеров, калькулятор триггеров, формулы триггеров, функция триггеров, рабочий лист соотношений тригонометров, тригонометрия, что такое косинус.

