Деление многочлена на двучлен по схеме Горнера
Деление многочлена на двучлен по схеме Горнера
Рассмотрим частный случай деления многочленов – деление многочлена на двучлен вида x — b0. Алгоритм деления для этого случая называется схемой Горнера или методом сокращенного деления многочлена на двучлен.Пусть требуется поделить многочлен
a(x)= an*xn + an-1*xn-1 + an-2*xn-2 + … + a1*x + a0
на двучлен b(x)= x — b0, то есть требуется представить многочлен a(x) в виде
a(x)=b(x)*c(x) + r(x), где степень частного c(x) равна n-1, а степень остатка r(x) равна 0. Пусть
c(x)= cn-1*xn-1 + cn-2*xn-2 + … + c1*x + c0,
r(x)=r0.
То есть a(x) = (x — b0)*(cn-1*xn-1 + cn-2*xn-2 + . .. + c1*x + c0) + r0
.. + c1*x + c0) + r0
Перемножим x — b0 и c(x), сложим с r0 и приравняем коэффициенты многочленов при одинаковых степенях x в левой и правой частях равенства. Получим рекуррентные формулы для определения значений ci и остатка r0.
cn-1=a0,
cn-2=a1 + cn-1*b0,
…
c1=an-2 + c2*b0,
c0=an-1 + c1*b0,
r0=an + c0*b0. Для удобства вычислений по этим формулам создается таблица, заполняемая слева направо.
В первой строке записываются коэффициенты делимого в порядке убывания степеней x и число b0.
Во второй строке — соответствующие значения выражений сi*b0 (первое число 0, так как cn=0).
Числа в первой строке складываются с числами во второй и записываются в третью строку.
Заполняют эту таблицу в таком порядке:
Сначала заполняют первую строку. Под первым числом первой строки пишем 0.
Складываем числа в первом столбце, и результат будет первым числом третьей строки.
Затем первое число третьей строки cn-1 умножаем на последнее число первой строки b0, результат записываем на второе место второй строки.
Складываем числа второго столбца и получаем второе число третьей строки cn-2.
Это число опять умножаем на последнее число первой строки b0, результат записываем на третье место во второй строке.
Складываем числа третьего столбца, и получаем третье число третьей строки и т.д.
Хотя объяснение выглядит довольно громоздким, но выполнять деление с помощью схемы Горнера очень просто и удобно. Рассмотрим применение схемы Горнера на примерах.
Калькуляторы для решение примеров и задач по математике
Лучшие математические приложения для школьников и их родителей, студентов и учителей. Подробнее …
Подробнее …
Пример 1. Разделить многочлен x4 — 3x3 — 3x2 + 7x + 6 на двучлен x-3 используя схему Горнера.
Решение.
Делимое a(x)=x4 — 3x3 — 3x2 + 7x + 6, b0=3. В соответствии со схемой Горнера заполняем таблицу
Таким образом, остаток r (это последнее число в третьей строке) равен нулю. Значит, многочлен x4 — 3x3 — 3x2 + 7x + 6 разделился на x — 3 нацело. Частное с(x)=1*x3 + 0*x2 — 3x — 2.
Ответ: x4 — 3x3 — 3x2 + 7x + 6=(x3 — 3x — 2)*(x — 3).
Пример 2. Разделить многочлен 2x5 + 5x4 — 4x3 + 612 на двучлен x + 4 используя схему Горнера.
Решение.
Делимое a(x)= 2x5 + 5x4 — 4x3 + 612, b0=-4. В соответствии со схемой Горнера заполняем таблицу
Остаток r = 100 — это последнее число в третьей строке. Частное с(x)=2*x4 — 3*x3 — 8*x2 — 32*x + 128.
Частное с(x)=2*x4 — 3*x3 — 8*x2 — 32*x + 128.
Ответ: 2x5 + 5x4 — 4x3 + 612 = (2x4 — 3x3 — 8x2 — 32x + 128)*(x + 4) + 100.
Деление многочлена a(x) на двучлен вида b1 x — b0 легко сводится к случаю деления на x — b0.
Пусть a(x) = (b1x — b0)* c(x) + r0, можно преобразовать это выражение
Анализ последнего выражения показывает, что остаток от деления a(x) на b1x — b0 тот же самый, что и остаток от деления a(x) на x — b0/b1, а коэффициенты частного c(x) получаются из коэффициентов частного от деления на x — b0/b1 делением их на b1.
Пример 3. Разделить многочлен x3 — 6x2 + 5x + 2 на двучлен 2x + 1 используя схему Горнера.
Решение.
Так как 2x + 1=2(x + 1/2), с помощью схемы Горнера будем делить исходный многочлен на x + 1/2, затем полученные коэффициенты частного разделим на 2.
Остаток r0 = -17/8. Коэффициенты частного получим, разделив коэффициенты в третьей строке таблицы на 2. Таким образом, частное от деления исходного многочлена на 2x + 1
Ответ:
Пример 4. Разделить многочлен x5 — x3 + 2x — 1 на двучлен 3 — 2x.
Решение.
Так как 3 — 2x = — 2(x — 3/2), с помощью схемы Горнера будем делить исходный многочлен на x — 3/2, затем полученные коэффициенты частного разделим на -2.
Остаток r0 = 199/32. Коэффициенты частного получим, разделив коэффициенты в третьей строке таблицы на -2. Таким образом, частное от деления исходного многочлена на 3 — 2x
Ответ:
Использование схемы Горнера для разложения многочлена по степеням двучлена
Рассмотрим еще одно применение схемы Горнера – разложение многочлена по степеням двучлена. Для любого многочлена
где и для любого числа b0 можно написать разложение a(x) по степеням x — b0:
Как видно из этой формулы, чтобы вычислить p0, необходимо разделить многочлен a(x) на x — b0 и найти остаток r = p0 . В частном мы получим многочлен
В частном мы получим многочлен
Теперь, чтобы вычислить p1, необходимо разделить многочлен d1 (x) на x — b0 и найти остаток r=p1. В частном получим многочлен
Далее продолжаем деление до тех пор, пока в частном не получится число. Полученный на последнем шаге остаток будет равен pn-1, а частное d n=pn.
На каждом шаге деление на x — b0 будем проводить с помощью схемы Горнера. При этом очень удобно результаты вычислений записывать в одну общую таблицу. Рассмотрим соответствующие примеры.
Пример 5. Разложить многочлен 2x4 + x3 — 5x + 3 по степеням двучлена x + 1.
Решение.
Все вычисления проведем, последовательно заполняя таблицу в соответствии с алгоритмом.
Таким образом, получаем, что остаток от деления исходного многочлена на x+1 равен 9, коэффициенты частного 2,-7,9,-10.
Ответ:
2x4 + x3 — 5x + 3 = 2(x + 1)4 — 7(x + 1)3 + 9(x + 1)2 — 10(x + 1) + 9.
Вычисление значения многочлена в заданной точке с помощью схемы Горнера
Еще одна задача, которую можно решать с помощью схемы Горнера – вычисление значения многочлена в заданной точке. Пусть многочлен a(x) делится на двучлен x — b
Если в это равенство подставить значение x=b0, получим a(b0)=r0. Таким образом, мы доказали теорему Безу.
Теорема Безу. Если x0 — произвольное число, то при делении многочлена a(x) на двучлен x-x0 получается остаток, равный значению многочлена при x=x0, то есть r0= a(x0).
Таким образом, с помощью схемы Горнера можно находить значение многочлена при заданном значении x=x0 как остаток от деления этого многочлена на двучлен x-x0. Иногда это сделать гораздо проще, чем подставлять x0 в исходный многочлен.
У теоремы Безу есть очень важное следствие.
Следствие. Число x0 является корнем многочлена a(x) тогда и только тогда, когда многочлен a(x) делится нацело на двучлен x-x 0.
Это следствие позволяет проверять, является ли число x0 корнем многочлена, вычисляя остаток от деления многочлена на двучлен x-x0.
Пример 6. Вычислить значение многочлена 2x6 + 6x5 + x4 — 4x3 + 3x2 — x — 1 при x=-3.
Решение.
Вычислить значение многочлена при x=-3 равносильно найти остаток при делении этого многочлена на x+3. Для этого воспользуемся схемой Горнера
Остаток r (это последнее число в третьей строке) равен 218.
(Частное с(x)=2x5 + x3 — 7x2 + 24x — 73;
2x6 + 6x5 + x4 — 4x3 + 3x2 — x — 1=(2x5 + x3 — 7x2 + 24x — 73)*(x+3)+218).
Ответ: 218.
Разложение полинома по степеням : Чулан (М)
Сообщения без ответов | Активные темы | Избранное
Правила форума

| guranvir |
| ||
27/01/10 |
| ||
| |||
| Joker_vD |
| |||
09/09/10 |
| |||
| ||||
| мат-ламер |
| |||
30/01/09 |
| |||
| ||||
| svv |
| |||
23/07/08 |
| |||
| ||||
| nnosipov |
| |||
20/12/10 |
| |||
| ||||
| VAL |
| |||
27/06/08 |
| |||
| ||||
| Mitrius_Math |
| ||
22/05/09 |
| ||
| |||
| Joker_vD |
| |||
09/09/10 |
| |||
| ||||
| VAL |
| |||
27/06/08 |
| |||
| ||||
| Mitrius_Math |
| ||
22/05/09 |
| ||
| |||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 10 ] |
Модераторы: Модераторы Математики, Супермодераторы
Кто сейчас на конференции |
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
| Найти: |
 Повторно примените метод для $x=-1$. Последнее число в каждой строке даст вам следующий коэффициент, начиная с наименьшей степени.
\begin{массив}{|с|с|с|с|с|с|}
\hline
& 1 & 2 & -3 & -4 & 1 \\\hline
-1 и 1& 1& -4 & 0 & 1 \стрелка вправо a_0\\ \hline
-1 и 1 и 0& -4 и 4 \стрелка вправо a_1\\ \hline
-1 & 1 & -1& -3 \rightarrow a_2\\ \hline
\конец{массив}
и так далее.
Повторно примените метод для $x=-1$. Последнее число в каждой строке даст вам следующий коэффициент, начиная с наименьшей степени.
\begin{массив}{|с|с|с|с|с|с|}
\hline
& 1 & 2 & -3 & -4 & 1 \\\hline
-1 и 1& 1& -4 & 0 & 1 \стрелка вправо a_0\\ \hline
-1 и 1 и 0& -4 и 4 \стрелка вправо a_1\\ \hline
-1 & 1 & -1& -3 \rightarrow a_2\\ \hline
\конец{массив}
и так далее.$\endgroup$
1 92+\цвет{синий}{4}(x+1)+\цвет{синий}{1}$$
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.

 04.2011, 20:09
04.2011, 20:09 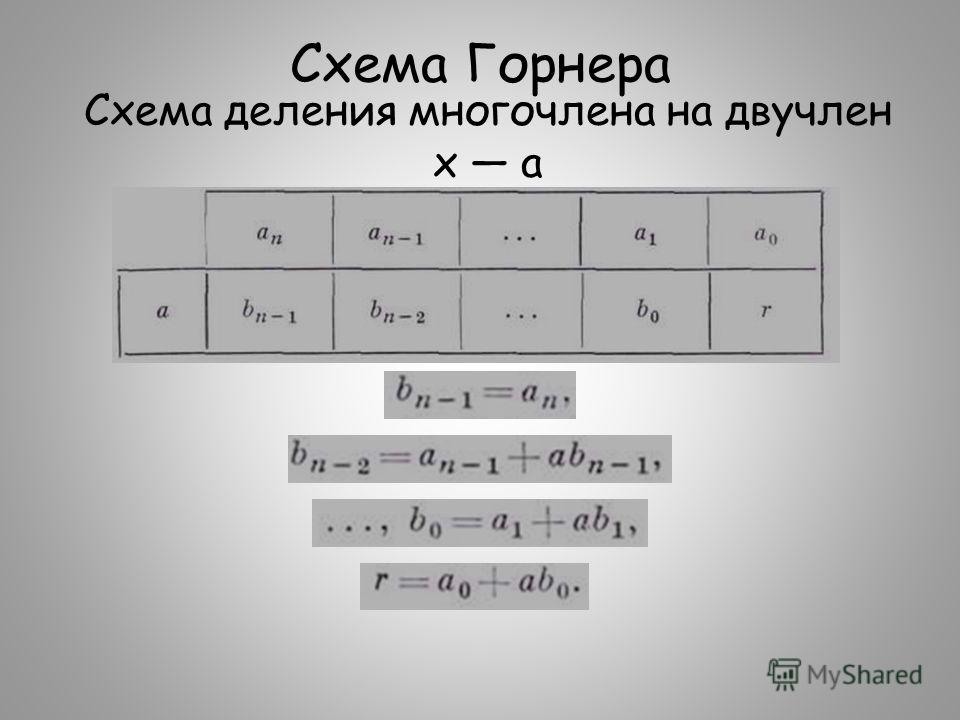 04.2011, 20:16
04.2011, 20:16  04.2011, 20:19
04.2011, 20:19  04.2011, 20:45
04.2011, 20:45 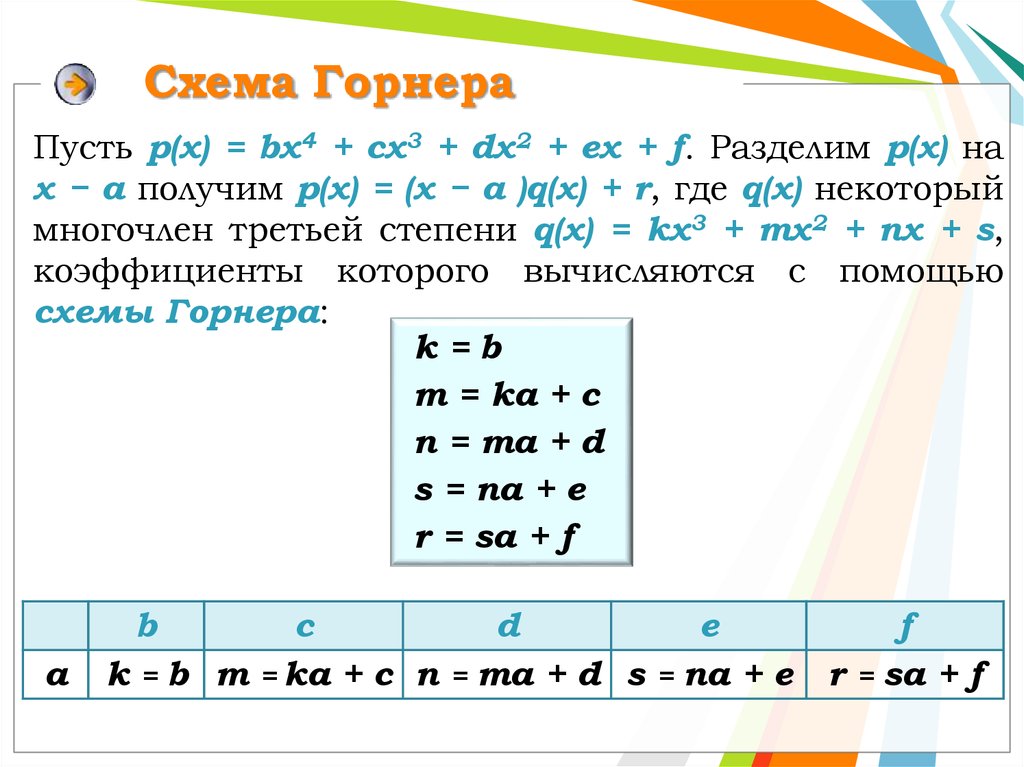 04.2011, 20:55
04.2011, 20:55  04.2011, 21:01
04.2011, 21:01  04.2011, 21:12
04.2011, 21:12  04.2011, 21:38
04.2011, 21:38  04.2011, 21:40
04.2011, 21:40