Изображение отношений между множествами с помощью кругов Эйлера. — Мегаобучалка
Понятие множества. Способы задания множеств.
Множество – совокупность объектов, рассматривая как одно целое. Понятие множества принимается за основное, т.к. не сводится к другим понятиям. Объекты, составляющие данное множество, называются его элементами. Множества бывают конечные и бесконечные (натуральные, целые, рациональные, действительные числа). Множества принято обозначать: А,В,С; Элементы множества принято обозначать а,б,с…Есть и пустое множество( ноль перечеркнутый) Способы задания множества:
Перечисление объектов, и характеристическое свойство множества-свойством, которым обладает каждый элемент этого множества, и не имеет ни один элемент не принадлежащий элементу не входящего в это множество.
Отношения между множествами: пересечение, подмножество, равенство.
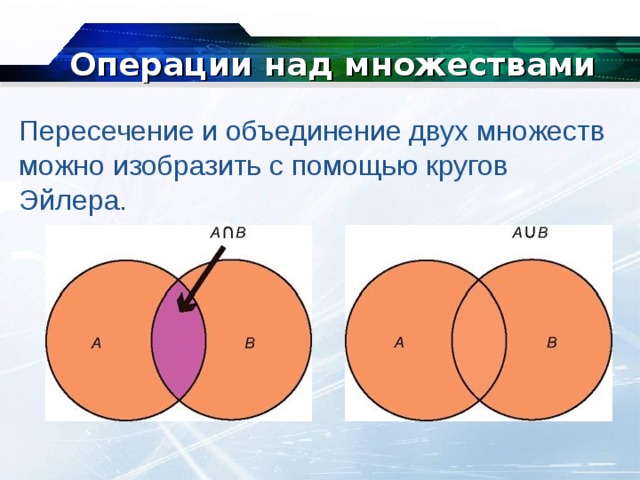
Если множества А и В имеют общие элементы, т.е. элементы принадлежащие одновременно А и В, то говорят, что эти множества пересекаются.
Множество В называют подмножеством А, если каждый элемент множества В является также элементом множества А. (Пустое множество является подмножеством любого множества, любое множество является подмножеством самого себя, количество подмножеств равно числу 2 в степени равной количеству элементов во множестве).
Множества А и В называются равными(А=В), если А принадлежит В, а В принадлежит А.
Операции над множествами: объединение, пересечение, дополнение,вычитание.
Пересечением множеств А и В называют множество, содержащее те и только те элементы, которые принадлежат множеству А и В (два способа нахождения элементов пересечения, (перечисление элементов, характерический способ) ( более сильная операция и выполняется первой перед объединением, если нет скобок.)
Объединением множества А и В называется множество, содержащее те и только те элементы, которые принадлежат множеству А или множеству В.
Свойства объединения и пересечения.
1) Переместительно или коммуникативное.
2) Сочетательное или ассоциативное.
3) Распределительное или дистрибутивное
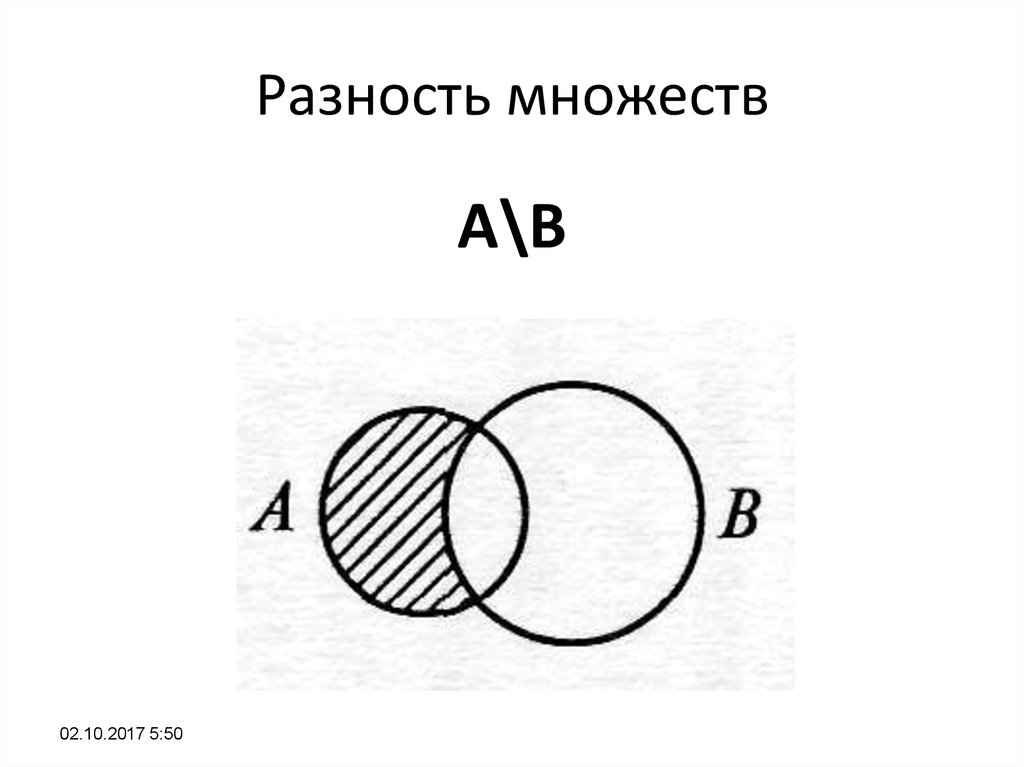
Разностью множества А и В называют множество, содержащее те и только те элементы, которые принадлежат множеству А и не принадлежат множеству В. (два способа нахождения элементов пересечения, (перечисление элементов, характерический способ) А/В.
Пусть В ( А .Дополнением подмножества в ДО множества А называют множество, содержащие те и только те элементы множества А, которые не принадлежат множеству В.
| Разность |
| Пересечение |
| Объединение |
Изображение отношений между множествами с помощью кругов Эйлера.
Круги эйлера используются для того, чтобы показать отношения между множествами.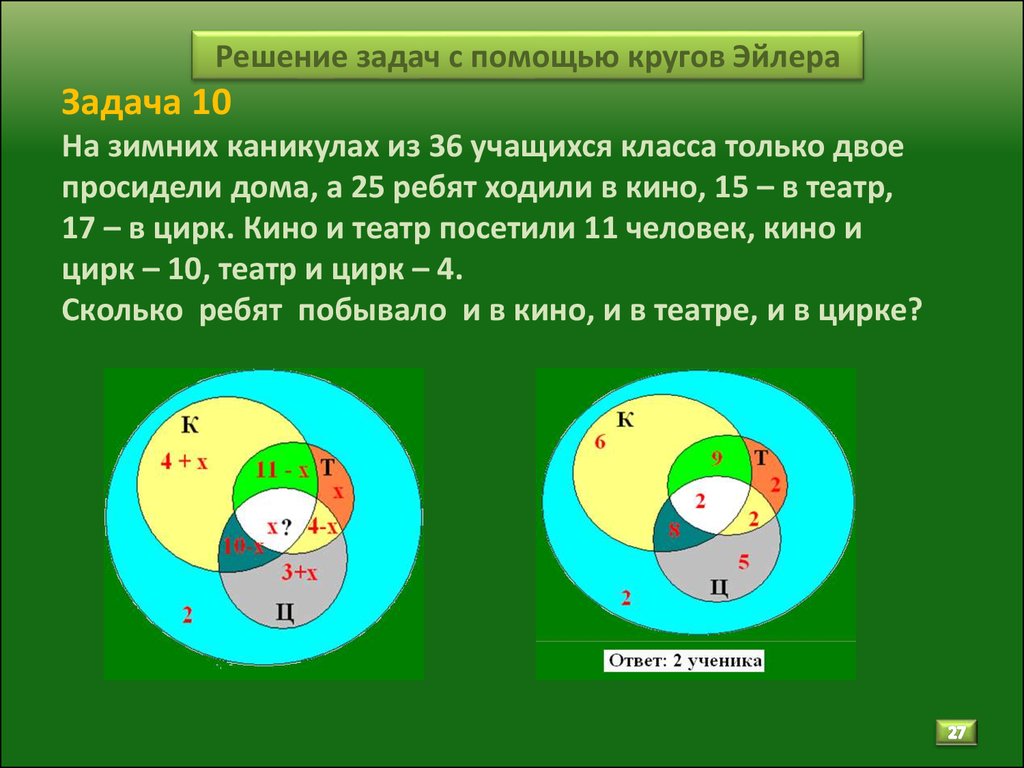 Существуют следующие отношения: Пересечением множеств А и называют множество, содержащее те и только те элементы, которые принадлежат множеству А и В (два способа нахождения элементов пересечения, (перечисление элементов, характерический способ) ( более сильная операция)
Существуют следующие отношения: Пересечением множеств А и называют множество, содержащее те и только те элементы, которые принадлежат множеству А и В (два способа нахождения элементов пересечения, (перечисление элементов, характерический способ) ( более сильная операция)
Пусть В ( А .Дополнением подмножества в ДО множества А называют мнржество, содержащие те и только те элементы множества А, которые не принадлежат множеству В.
Разностью множества А и В называют множество, содержащее те и только те элементы, которые принадлежат множеству А и не принадлежат множеству В. (два способа нахождения элементов пересечения, (перечисление элементов, характерический способ) А/В.
Объединением множества А и В называется множество, содержащее те и только те элементы, которые принадлежат множеству А или множеству В.
Решение задач с помощью кругов Эйлера
Пояснительная записка Очень часто решение задачи помогает найти рисунок.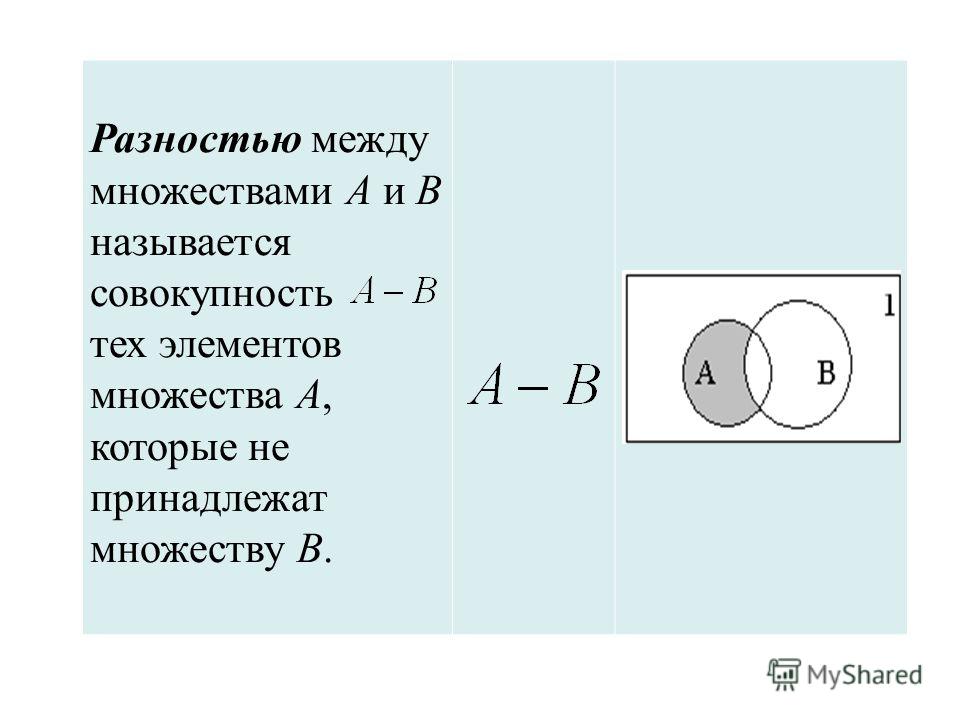 Использование рисунка делает решение простым и наглядным.
Использование рисунка делает решение простым и наглядным.
В данной разработке приведены примеры решения задач с помощью кругов Эйлера. Это не просто занимательная и интересная штука, но и весьма полезный метод решения задач. Они помогают быстро и просто решить даже достаточно сложные или просто запутанные на первый взгляд задачи.
С данным способом решения задач учащихся можно познакомить как на уроках, так и на кружковых занятиях.
Главной целью этой работы является помощь учителям математики для подготовки учащихся к олимпиадам, а также к экзаменам.
Основные понятия Понятие множества − одно из первичных в математике. Поэтому очень трудно дать ему какое-либо определение, которое бы не заменяло слово «множество» каким-нибудь равнозначным выражением, например, совокупность, собрание элементов и т.д. Элементы множества − это то, из чего это множество состоит, например, каждый ученик вашего класса есть элемент множества школьников.
Пересечение множеств в теории множеств — это множество, которому принадлежат те и только те элементы, которые одновременно принадлежат всем данным множествам.
Круги Эйлера — геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления. Изобретены Леонардом Эйлером. Используется в математике, логике, менеджменте и других прикладных направлениях.
2. Решение задач с помощью кругов Эйлера2.1. «Обитаемый остров» и «Стиляги»Некоторые ребята из нашего класса любят ходить в кино. Известно, что 15 ребят смотрели фильм «Обитаемый остров», 11 человек — фильм «Стиляги», из них 6 смотрели и «Обитаемый остров», и «Стиляги». Сколько человек смотрели только фильм «Стиляги»?
Решение:
Чертим два множества таким образом:
6 человек, которые смотрели фильмы «Обитаемый остров» и «Стиляги», помещаем в пересечение множеств.
1. 15 — 6 = 9 — человек, которые смотрели только «Обитаемый остров»,
2. 11- 6 = 5 — человек, которые смотрели только «Стиляги».
Получаем:
Ответ: 5 человек.
2.2. Задача про библиотекиКаждый из 35 шестиклассников является читателем, по крайней мере, одной из двух библиотек: школьной и районной. Из них 25 человек берут книги в школьной библиотеке, 20 — в районной.
Сколько шестиклассников:
- Являются читателями обеих библиотек;
- Не являются читателями районной библиотеки;
- Не являются читателями школьной библиотеки;
- Являются читателями только районной библиотеки;
- Являются читателями только школьной библиотеки?
Решение:
Чертим два множества таким образом:
1) 20+ 25 — 35 = 10 (человек) — являются читателями обеих библиотек.
2) 35 — 20 = 15 (человек) — не являются читателями районной библиотеки,
3) 35 — 25 = 10 (человек) — не являются читателями школьной библиотеки,
4) 35- 20 = 10 (человек) — являются читателями только районной библиотеки,
5) 35- 20 = 15 (человек) — являются читателями только школьной библиотеки.
Очевидно, что вопросы 2 и 5, а также 3 и 4 — равнозначны и ответы на них совпадают.
Ответ: 10 человек; 15 человек; 10 человек; 10 человек; 15 человек.
2.3. Гарри Поттер, Рон и Гермиона На полке стояло 26 волшебных книг по заклинаниям, все они были прочитаны. Из них 4 прочитал и Гарри Поттер, и Рон.
Решение:
Учитывая условия задачи, сделаем чертеж:
Так как Гарри Поттер всего прочитал 11 книг, из них 4 книги читал Рон и 2 книги — Гермиона, то 11 — 4 — 2 = 5 — книг прочитал только Гарри.
Следовательно, 26 — 7 — 2 — 5 — 4 = 8 — книг прочитал только Рон.
Ответ: 8 книг.
2.4. Задача про любимые мультфильмы Шестиклассники заполняли анкету с вопросами об их любимых мультфильмах. Оказалось, что большинству из них нравятся «Белоснежка и семь гномов», «Губка Боб Квадратные Штаны» и «Волк и теленок». В классе 38 учеников. «Белоснежка и семь гномов» нравится 21 ученику. Причем трем среди них нравятся еще и «Волк и теленок», шестерым — «Губка Боб Квадратные Штаны», а один ребенок одинаково любит все три мультфильма.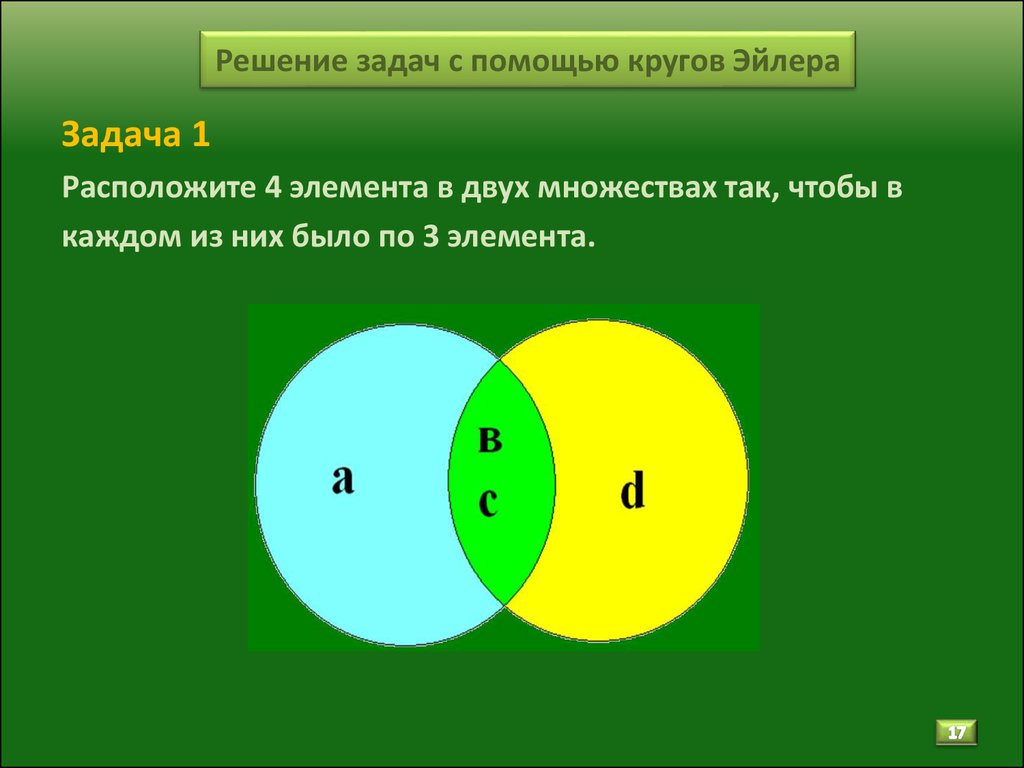
Решение:
Чертим три круга, таким образом:
Из условия знаем, что трем ученикам нравиться и «Белоснежка и семь гномов», и «Волк и теленок», шестерым — «Белоснежка и семь гномов» и «Губка Боб Квадратные Штаны», а один ребенок одинаково любит все три мультфильма.
Мы помним, что по условиям задачи среди фанатов мультфильма «Волк и теленок» пятеро ребят выбрали два мультфильма сразу, т.е. 5 — 3 = 2 — ученика выбрали «Волк и теленок» и «Губка Боб Квадратные Штаны».
1) 21 — 3 — 1 — 6 = 11 — учеников выбрали только «Белоснежка и семь гномов»,
2) 13 — 3 — 1 — 2 = 7 — учеников выбрали — «Волк и теленок»,
3) 38 — (11 + 3 + 1 + 2 + 6 + 7) = 8 — ребят выбрали «Губка Боб Квадратные Штаны».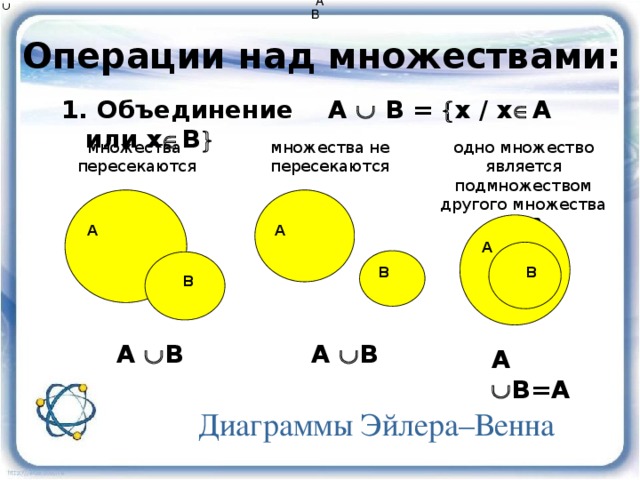
4) 8 + 2 + 1 + 6 = 17 — человек выбрали мультик «Губка Боб Квадратные Штаны».
Ответ: 17 учеников.
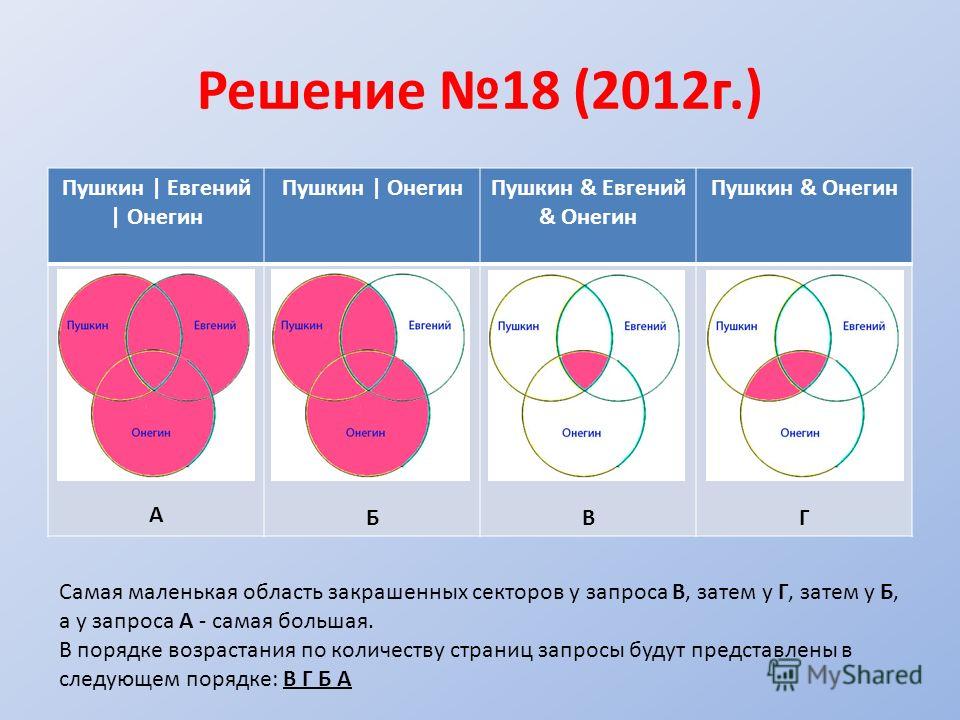
2.5. Задача про Крейсер и ЛинкорВ таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети интернет.
Запрос | Найдено страниц, тыс. |
Крейсер и Линкор | 7000 |
Крейсер | 4800 |
Линкор | 4500 |
Какое количество страниц (в тысячах) будет найдено по запросу Крейсер и Линкор? (Считается, что все вопросы выполняются практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.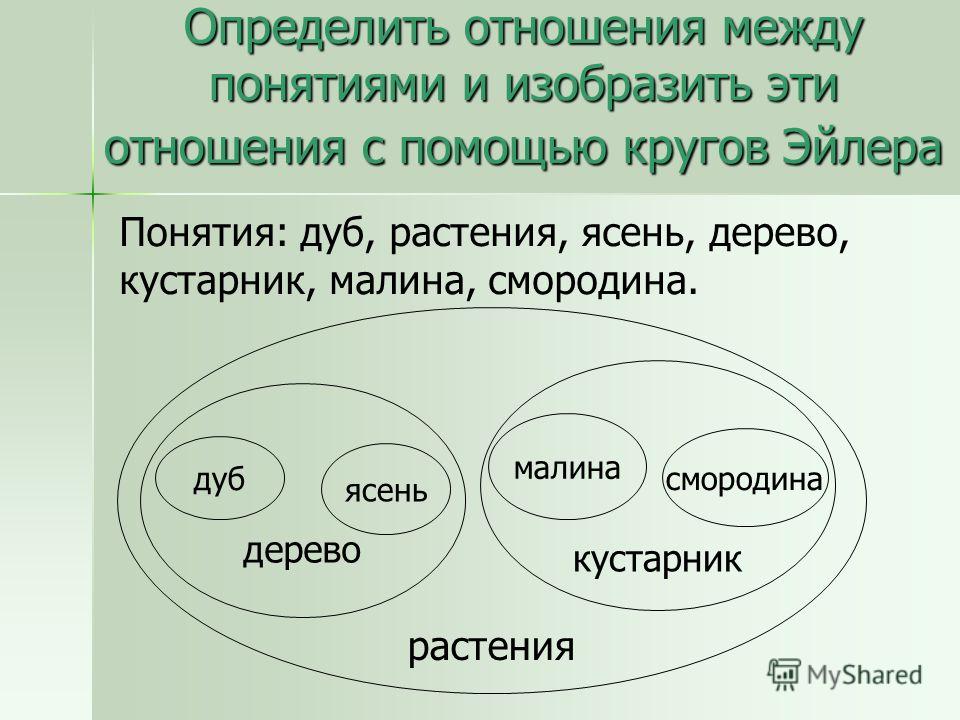 )
)
Решение:
При помощи кругов Эйлера изобразим условия задачи.
1) 4800 + 4500 — 7000 = 2300 (тыс. страниц) — найдено по запросу Крейсер и Линкор,
2) 4800 — 2300 = 2500 (тыс. страниц) — найдено по запросу Крейсер,
3) 4500 — 2300 = 2200 (тыс. страниц) — найдено по запросу Линкор.
Ответ: 2300 тыс. страниц.
2.6. Задача про блондинокКаждый ученик класса — либо девочка, либо блондин, либо любит математику. В классе 20 девочек, из них 12 блондинок, но одна блондинка любит математику. Всего в классе 24 ученика — блондина, математику из них любят 12, а всего учеников (мальчиков и девочек), которые любят математику, 17, из них 6 девочек. Сколько учеников в данном классе?
Решение:
Изобразим с помощью кругов Эйлера данные из задачи:
1) 12 — 1 = 11 (учеников) — девочек блондинок,
2) 12 — 1 = 11 (учеников) — блондины и любят математику,
3) 6 — 1 = 5 (учеников) — девочек, которые любят математику,
4) 20 — 11 — 1 — 5 = 3 (ученика) — девочки,
5) 24 — 11 — 1 — 11 = 1 (ученик) — блондин,
6) 17- 5 — 1 — 11 = 0 (учеников) — любят математику,
7) 3 + 1 + 0 + 5 + 11 + 11 + 1 = 32 (ученика) — всего в классе.
Ответ: 32 ученика.
2.7. Задача про кружкиВ трёх седьмых классах 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют в хоре, не увлекаются спортом и не занимаются в драмкружке? Сколько ребят заняты только спортом?
Решение:
Учитывая условия задачи, сделаем чертеж:
1) 10 — 3 = 7 (ребят) — посещают драмкружок и хор,
2) 6 — 3 = 3 (ребят) — поют в хоре и занимаются спортом,
3) 8 — 3 = 5 (ребят) — занимаются спортом и посещают драмкружок,
4) 27 — 7 — 3 — 5 = 12 (ребят) — посещают драмкружок,
5) 32 — 7 3 — 3 = 19 (ребят) — поют в хоре,
6) 22 — 5 — 3 — 3 = 11 (ребят) — увлекаются спортом,
7) 70 — (12 + 19 + 11 + 5+ 7 + 3 + 3) = 10 (ребят) — не поют в хоре, не увлекаются спортом и не занимаются в драмкружке.
Ответ: 10 человек и 11 человек.
Задачи для самостоятельного решения1. На фирме работают 67 человек. Из них 47 знают английский язык, 35 — немецкий язык, а 23 — оба языка. Сколько человек фирмы не знают ни английского, ни немецкого языков?
2. Из 40 учащихся нашего класса 32 любят молоко, 21 — лимонад, а 15 — и молоко, и лимонад. Сколько ребят в нашем классе не любят ни молоко, ни лимонад?
3. 12 моих одноклассников любят читать детективы, 18 — фантастику, трое с удовольствием читают и то, и другое, а один вообще ничего не читает. Сколько учеников в нашем классе?
4. Из тех 18 моих одноклассников, которые любят смотреть триллеры, только 12 не прочь посмотреть и мультфильмы. Сколько моих одноклассников смотрят одни «мультики», если всего в нашем классе 25 учеников, каждый из которых любит смотреть или триллеры, или мультфильмы, или и то и другое?
5. Из 29 мальчишек нашего двора только двое не занимаются спортом, а остальные посещают футбольную или теннисную секции, а то и обе. Футболом занимается 17 мальчишек, а теннисом — 19. Сколько футболистов играет в теннис? Сколько теннисистов играет в футбол?
Футболом занимается 17 мальчишек, а теннисом — 19. Сколько футболистов играет в теннис? Сколько теннисистов играет в футбол?
6. В одном классе 25 учеников. Из них 7 любят груши, 11 — черешню. Двое любят груши и черешню; 6 — груши и яблоки; 5 — яблоки и черешню. Но есть в классе два ученика, которые любят все и четверо таких, что не любят фруктов вообще. Сколько учеников этого класса любят яблоки?
7. В конкурсе красоты участвовали 22 девушки. Из них 10 было красивых, 12 — умных и 9 — добрых. Только 2 девушки были и красивыми, и умными; 6 девушек были умными и одновременно добрыми. Определите, сколько было красивых и в то же время добрых девушек, если я скажу вам, что среди участниц не оказалось ни одной умной, доброй и вместе с тем красивой девушки?
8. В нашем классе 35 учеников. За первую четверть пятерки по русскому языку имели 14 учеников; по математике — 12; по истории — 23. По русскому и математике — 4; по математике и истории — 9; по русскому языку и истории — 5. Сколько учеников имеют пятерки по всем трем предметам, если в классе нет ни одного ученика, не имеющего пятерки хотя бы по одному из этих предметов?
Сколько учеников имеют пятерки по всем трем предметам, если в классе нет ни одного ученика, не имеющего пятерки хотя бы по одному из этих предметов?
9. Из 100 человек 85 знают английский язык, 80 — испанский, 75 — немецкий. Все владеют, по крайней мере, одним иностранным языком. Среди них нет таких, которые знают два иностранных языка, но есть владеющие тремя языками. Сколько человек из этих 100 знают три языка?
10. Из сотрудников фирмы 16 побывали во Франции, 10 — в Италии, 6 — в Англии; в Англии и Италии — 5; в Англии и Франции — 6; во всех трех странах — 5 сотрудников. Сколько человек посетили и Италию, и Францию, если всего в фирме работают 19 человек, и каждый из них побывал хотя бы в одной из названных стран?
Список использованных источников
1. Баженов И.И, Порошкин А.Г., Тимофеев А.Ю., Яковлев В.Д. Задачи для школьных математических кружков: учеб. пособие / Сыктывкар: Сыктывкарский университет, 2006.
2. Марков И.С. Новые олимпиады по математике — Ростов н/Д: Феникс, 2005.
Марков И.С. Новые олимпиады по математике — Ростов н/Д: Феникс, 2005.
3. https://ru.wikipedia.org/wiki/
4. http://logika.vobrazovanie.ru
5. http://www.otvet-prost.ru/load/diskretnaja_matematika/na_krugi_ehjlera/zadacha_na_krugi_ehjlera/18-1-0-22
6. http://urok.1sept.ru/articles/550092/
7. http://www.tutoronline.ru/blog/reshit-zadachu-pomogut-krugi-jejlera
диаграмм Венна и Эйлера | Поговорим о науке
Диаграммы Венна и Эйлера (Поговорим о науке)
Диаграммы Венна и Эйлера (Поговорим о науке)
Поговорим о науке
Диаграммы Венна
Иногда мы используем картинки для рисования наборов. Один тип изображения называется диаграммой Венна . Диаграммы Венна помогают наглядно показать отношения между множествами. Обычно диаграммы Венна имеют две перекрывающиеся окружности. Но вы можете рисовать диаграммы Венна с тремя или более перекрывающимися замкнутыми кривыми. Диаграммы Венна не всегда показывают, что именно находится в наборе. Например, на картинке ниже показаны наборы K и L:
Диаграммы Венна не всегда показывают, что именно находится в наборе. Например, на картинке ниже показаны наборы K и L:
Каждый кружок представляет все элементы набора. Имея только картинку, вы можете задавать вопросы о подмножествах , пересечении и объединении .
Является ли K ⊆ L (находится ли K внутри L)? НЕТ.
Является ли L ⊆ K (L внутри K)? НЕТ.
Вопросы 1: Что такое K ∩ L? (Какая область находится внутри обоих наборов?) Нарисуйте изображение, а затем заштрихуйте его. Ответы даны внизу страницы.
Диаграмма Венна множеств K и L (© Let’s Talk Science, 2021). Вопросы 2: Что такое K ∪ L? (Какова общая площадь набора K, набора L или обоих?) Заштрихуйте картинку, чтобы показать свой ответ.
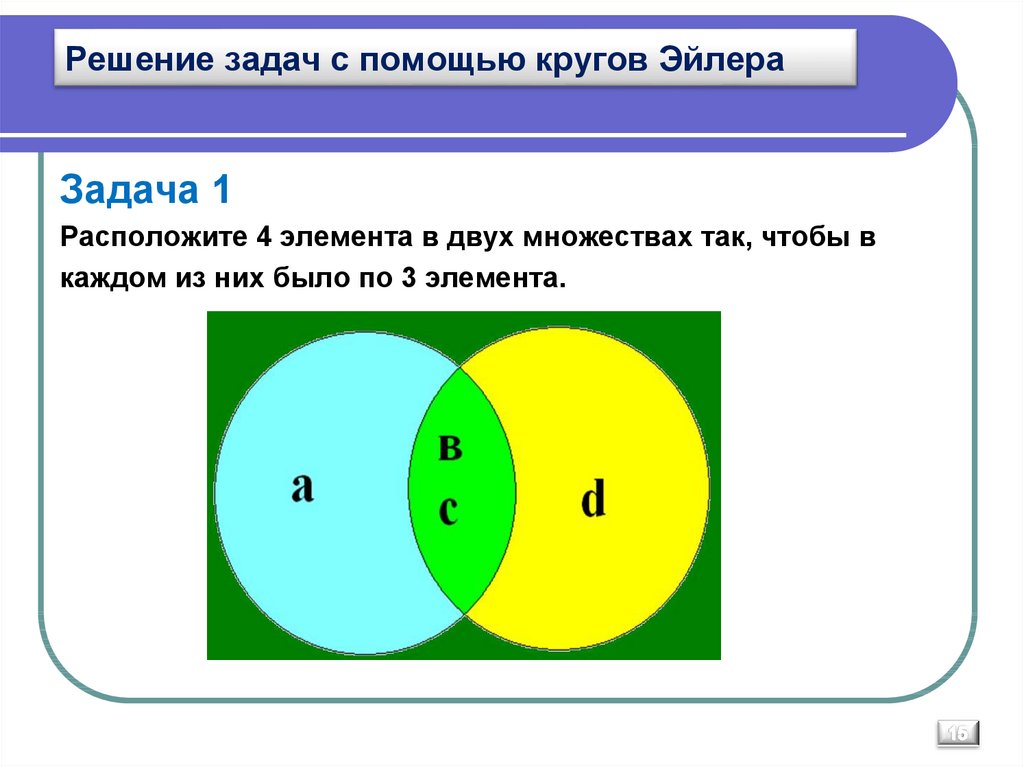
Попробуйте с наборами:
E = {1, 3, 8, 9, 14, 17}
F = {0, 14, 3, 5, 10, 20}
3 90 вопросов 3 : Используйте диаграмму Венна, чтобы показать наборы E и F .
Что такое E ∩ F ?
Что такое E ∪ F ?
Кто такой Венн?
Джон Венн (1834-1923) был английским логиком . Логик — это тот, кто изучает способы логического мышления. Его помнят за то, что он изобрел диаграмму, названную в его честь — диаграмму Венна.
Венна воспитывал его отец, который был преподобным англиканской церкви. Его мать умерла, когда он был очень молод. Он поступил в Кембриджский университет, где на втором курсе получил стипендию по математике. Несмотря на то, что в школе он действительно хорошо разбирался в математике, после окончания школы он стал преподобным, как его отец и дед.
Венн никогда не переставал думать о математике. После нескольких лет религиозной работы он вернулся в Кембридж, где преподавал логику и вероятность. В 1867 году он женился и имел сына — Иоанна. Его сын Джон в конце концов стал президентом Королевского колледжа в Кембриджском университете, где он вместе с отцом занимался важными исследовательскими проектами.
Диаграммы Венна были впервые опубликованы в 1880 году в статье под названием «О диаграммном и механическом представлении предложений и рассуждений». в «Философском журнале и научном журнале».
Диаграммы Эйлера
Еще один способ показать наборы и их взаимосвязи — использовать диаграмму Эйлера . Эти диаграммы похожи на диаграммы Венна, но имеют тенденцию быть более сложными. Они часто показывают подмножества, а также пересечение и объединение. В диаграмме Эйлера размер и форма кругов/овалов не важны. Важно то, как они перекрываются или не перекрываются.
Пример диаграммы Эйлера для множеств M, N, P, Q и R (© Let’s Talk Science, 2021).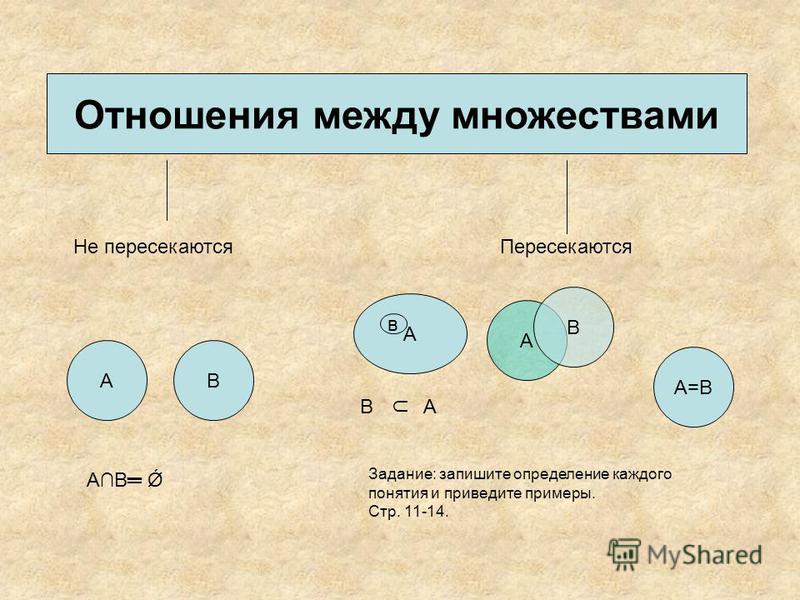
Вопрос 4:
Является ли какое-либо множество подмножеством (⊆) другого?
Если да, то какой?
Вопрос 5:
A) Затенить N ∪ Q
Пример диаграммы Эйлера для множеств M, N, P, Q и R (© Let’s Talk Science, 2021).B) Оттенок M ∩ R
Пример диаграммы Эйлера для множеств M, N, P, Q и R (© Let’s Talk Science, 2021).C) Оттенок P ∩ N ∩ Q
Пример диаграммы Эйлера для множеств M, N, P, Q и R (© Let’s Talk Science, 2021).D) Оттенок M ∪ P ∪ R
Пример диаграммы Эйлера для множеств M, N, P, Q и R (© Let’s Talk Science, 2021).
Возможно ли N ∩ R ? Нет! N и R не пересекаются. В теории множеств мы называем это нулевым набором или пустым набором , потому что он ничего не содержит. Символ нулевого множества — ∅ .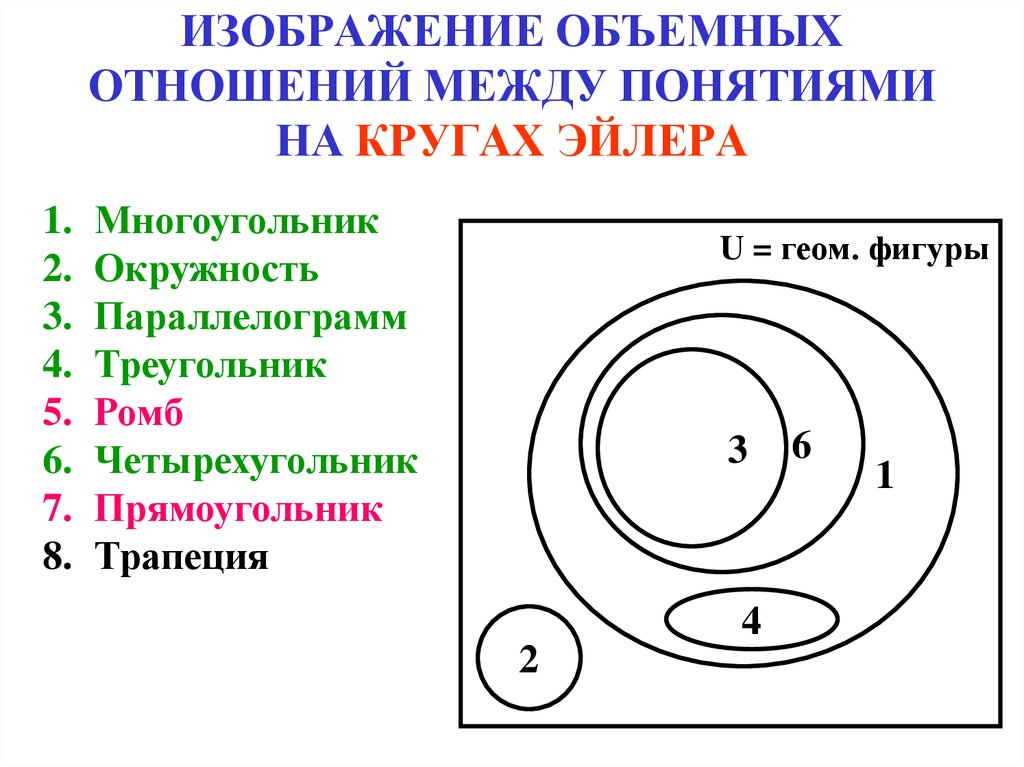 Вот еще один пример нулевого набора:
Вот еще один пример нулевого набора:
G — количество жирафов в классе миссис Браун. В = {} = ∅
Применение диаграмм Венна и Эйлера
Диаграммы Венна и Эйлера полезны в различных контекстах. Оба типа диаграмм помогают нам визуализировать концепции и отношения. Это может помочь нам легче понять сложную информацию. Эти диаграммы используют одну и ту же структуру для представления различных типов контента.
Например, диаграммы Венна часто используются для решения математических задач. Представление вопроса в виде диаграммы Венна часто может облегчить его понимание и решение. Предприятия часто используют диаграммы Венна для сравнения продуктов, анализа конкурентов и принятия решений. Диаграммы Венна представляют многие другие типы практической информации, от химии до географии. Их можно даже использовать для юмора или для представления сложных философских вопросов. Диаграммы Венна и Эйлера — это простой способ представления всех видов информации.
Вопрос 1:
Что такое K ∩ L? (Какая область находится внутри обоих наборов?) Заштрихуйте картинку, чтобы показать свой ответ.
Пересечение множеств K и L (© Let’s Talk Science, 2021).
Вопрос 2:
Что такое К ∪ Л? (Какова общая площадь набора K, набора L или обоих?) Заштрихуйте картинку, чтобы показать свой ответ.
Объединение множеств K и L (© 2021 Let’s Talk Science).
Вопрос 3:
Используйте диаграмму Венна, чтобы показать наборы E и F .
Пересечение и объединение множеств E и F (© Let’s Talk Science, 2021).E ∩ F = {3, 14}
E ∪ F = {0, 1, 3, 5, 8, 9, 10, 14, 17, 20}
3 900 Вопрос :
Является ли какое-либо множество подмножеством (⊆) другого?
Если да, то какой?
Да, R является частью P ( R ⊆ P )
Вопрос 5:
A) Оттенок N ∪ Q 3
N ∪ Q (© 2021 Let’s Talk Science). B) Оттенок M ∩ R C) Затенить P ∩ N ∩ Q D) Оттенок M ∪ P ∪ R Перекрывающиеся определения и сложные иерархии часто классифицируют с помощью диаграмм, которые могут ясно показать взаимосвязь между различными множествами. Одной из таких моделей является диаграмма Эйлера, которая часто используется для различения наборов, чтобы понять соответствующие отношения между ними. В этой статье мы рассмотрим, что определяет диаграмму Эйлера и как ее построить. Диаграмма Эйлера — это визуальное представление отношений между различными множествами, которое используется для понимания сложных иерархий и проверки аргументов. Диаграмма используется для представления связей между наборами с помощью форм. Диаграммы Эйлера изображают замкнутые формы с использованием двумерной плоскости, каждая из которых показывает категорию. Перекрытие этих форм демонстрирует взаимосвязь между множествами. Диаграммы Эйлера используются в различных областях, таких как бизнес-анализ и концептуальное моделирование, математика, биология и т. д. Использование диаграммы Эйлера приписывается Леонарду Эйлеру, Швейцарский математик 18 века. Он считается одним из величайших математиков, которые когда-либо жили. Эйлер внес вклад в области математики, механики, оптики, астрономии и гидродинамики. Ему приписывают первое использование круговых диаграмм для объяснения отношений, которые Эйлер использовал для иллюстрации силлогистических рассуждений с помощью замкнутых кривых. Существует множество применений диаграммы Эйлера в различных областях. Некоторые из распространенных причин использования диаграмм Эйлера упомянуты ниже. Диаграммы Эйлера важны для объяснения сложных иерархий и перекрывающихся определений. Используя диаграмму Эйлера, вы можете представлять наборы и отображать соответствующую информацию в виде отношений между наборами. Диаграммы Эйлера могут помочь визуально организовать информацию для анализа и изучения, поскольку наборы могут быть четко дифференцированы в диаграммной форме. Диаграммы Эйлера могут помочь организовать и визуализировать релевантную информацию, чтобы помочь лучше понять и сравнить ее. Следуя приведенному ниже примеру, вы можете построить диаграмму Эйлера. Мы нарисуем диаграмму Эйлера, чтобы представить это утверждение: В этом примере диаграммы Эйлера мы построим 3 круга для представления 3 категорий (камни, кролики и неодушевленные предметы). Прочитайте приведенное выше утверждение и переместите кружки соответствующим образом. Поскольку «все камни неодушевленные», это означает, что весь круг камней должен находиться внутри неодушевленного круга. Прочитайте второе утверждение и затем переместите соответствующий кружок, чтобы представить информацию. Поскольку «кролики не камни», это означает, что весь круг кроликов будет вне круга камней. Прочитайте последнее утверждение и переместите кружок соответствующим образом. Поскольку «никакие камни не являются кроликами», весь круг кроликов должен находиться за пределами неодушевленного круга. Поскольку эта окружность уже находится снаружи, мы правильно построили диаграмму Эйлера. Хотя диаграммы Венна и Эйлера могут показаться похожими, между ними есть ряд различий. Наиболее существенное различие между диаграммами Венна и Эйлера заключается в том, что диаграмма Венна представляет все возможные отношения между множествами. Диаграмма Венна становится намного сложнее, чем диаграмма Эйлера за пределами трех наборов. Это связано с представлением всех возможных отношений на диаграмме Венна, в отличие от диаграммы Эйлера, которая фокусируется только на соответствующих отношениях. На диаграмме Эйлера представлены только непустые пересечения. Однако на диаграмме Венна представлено каждое пересечение между каждым набором. Чтобы лучше понять использование диаграмм Эйлера, давайте рассмотрим несколько реальных приложений и примеров. Диаграммы Эйлера используются для анализа и проверки аргументов. Это, пожалуй, самая распространенная причина использования диаграмм Эйлера. Используя дедуктивное рассуждение с помощью диаграммы Эйлера, вы можете проверить аргумент, выполнив несколько простых шагов. Как упоминалось ранее, одним из приложений диаграмм Эйлера является концептуальное моделирование. Концептуальная модель — это представление системы, в котором концепции используются для понимания и моделирования объектов, связанных с моделью. Например, диаграммы Эйлера могут помочь бизнес-аналитикам понять сложность различных взаимосвязей между различными концепциями. Поскольку диаграммы Эйлера имеют математическое применение, они также широко используются в обучении учащихся, например, для решения математических задач или для упрощенного отображения отношений между множествами. Объяснение сложных иерархий с помощью простого схематического представления. Диаграммы Эйлера настолько просты в построении, что для их построения можно использовать ряд инструментов. Если вы умеете пользоваться сложными приложениями, такими как Adobe Photoshop или Adobe Illustrator, вы можете легко построить диаграмму Эйлера. Поскольку оба программного обеспечения используют слои, можно также легко перемещаться по фигурам, когда вы пытаетесь проверить аргумент или найти отношения между наборами. Inkscape — известное кроссплатформенное приложение для создания масштабируемых векторных изображений. Вы также можете использовать Inkscape для рисования диаграмм. Inkscape также позволяет преобразовывать фигуры путем их перемещения, масштабирования или вращения. Хотя Inkscape — сложный инструмент, при определенных навыках он может помочь вам создавать визуально привлекательные диаграммы Эйлера. Помимо Windows и Mac, приложение также доступно для Linux и FreeBSD. Одним из самых простых способов создания диаграммы Эйлера является использование фигур в Microsoft Paint. Приложение для рисования Google, доступное на Google Диске, может быть еще одним хорошим вариантом для рисования диаграммы Эйлера. Приложение для рисования может быть особенно полезным для людей, которые хорошо умеют рисовать в произвольной форме. Вы также можете экспортировать свои рисунки в форматах PNG, JPG, SVG и PDF. Если вам сложно создавать диаграммы Эйлера самостоятельно, вы также можете использовать готовые шаблоны PowerPoint или фигуры в PowerPoint или Google Slides для построения диаграммы. Поскольку обе платформы чрезвычайно просты в использовании и позволяют перемещать объекты слайдов, вы также можете проверить аргументы, находя отношения между наборами с помощью слайда презентации.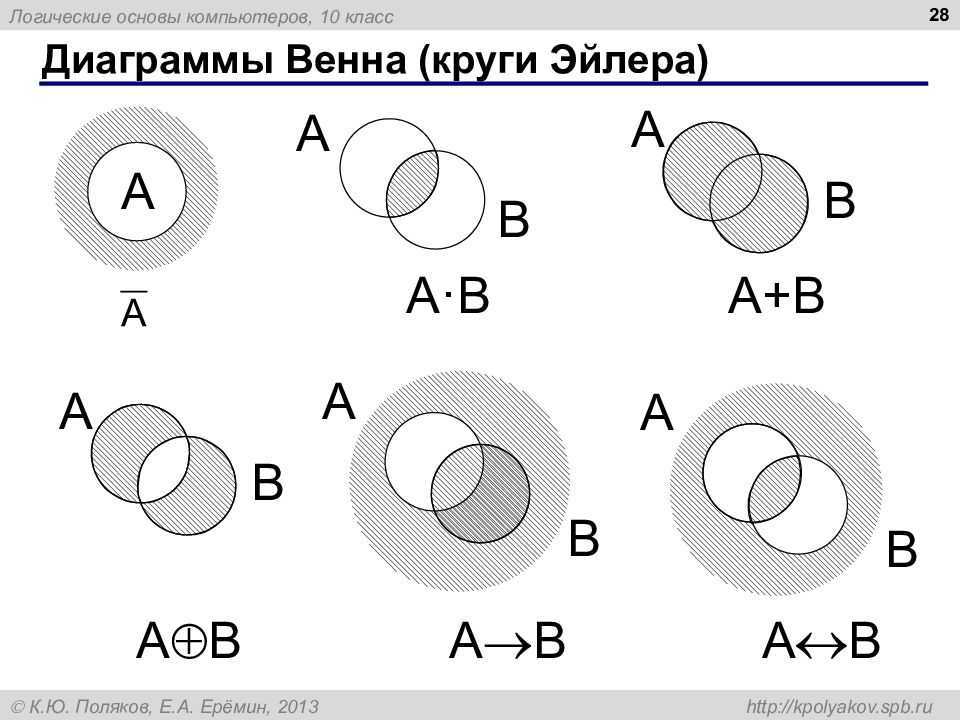
Что такое диаграмма Эйлера и как ее составить: пошаговое руководство
Что такое диаграмма Эйлера?
 Она похожа на диаграмму Венна. Однако, в отличие от диаграммы Венна, она показывает только релевантные отношения между множествами. Диаграмма Эйлера обеспечивает отличный способ объяснения сложных иерархий и перекрывающихся определений, представляя только релевантную информацию.
Она похожа на диаграмму Венна. Однако, в отличие от диаграммы Венна, она показывает только релевантные отношения между множествами. Диаграмма Эйлера обеспечивает отличный способ объяснения сложных иерархий и перекрывающихся определений, представляя только релевантную информацию. История диаграммы Эйлера
 В 20 -м -м веке диаграммы Эйлера и Венна были включены в Соединенные Штаты как часть инструкций по теории множеств в 1960-х годах.
В 20 -м -м веке диаграммы Эйлера и Венна были включены в Соединенные Штаты как часть инструкций по теории множеств в 1960-х годах. Зачем использовать диаграммы Эйлера?
Объяснение сложных иерархий
Визуальная организация информации
Сравнение релевантной информации
 Такая диаграмма может позволить разбить информацию, чтобы определить, где наборы пересекаются и перекрываются.
Такая диаграмма может позволить разбить информацию, чтобы определить, где наборы пересекаются и перекрываются. Пример построения диаграммы Эйлера
Шаг 1. Представление 3 категорий
Шаг 2. Переместите соответствующий кружок в соответствии с первым утверждением
Шаг 3.
 Переместите соответствующий кружок в соответствии со вторым утверждением
Переместите соответствующий кружок в соответствии со вторым утверждением Шаг 4. Переместите соответствующий кружок в соответствии с третьим утверждением
Различия между диаграммами Эйлера и диаграммами Венна
Различие в представлении отношений между множествами
 Однако диаграмма Эйлера показывает только релевантные отношения.
Однако диаграмма Эйлера показывает только релевантные отношения. Сложность визуального представления
Требования к пересечениям
Использование диаграмм Эйлера (применение в реальном мире + примеры)
Анализ аргументов с помощью диаграмм Эйлера
 Помимо упомянутого ранее примера диаграммы Эйлера, в приведенном ниже видео представлено несколько дополнительных примеров того, как вы можете проверить аргумент, построив диаграмму Эйлера.
Помимо упомянутого ранее примера диаграммы Эйлера, в приведенном ниже видео представлено несколько дополнительных примеров того, как вы можете проверить аргумент, построив диаграмму Эйлера. Диаграмма Эйлера для концептуального моделирования
Диаграммы Эйлера в образовании
Инструменты для создания диаграммы Эйлера
 Существует ряд доступных кросс-платформенных и веб-приложений, которые могут помочь вам в создании диаграмм Эйлера.
Существует ряд доступных кросс-платформенных и веб-приложений, которые могут помочь вам в создании диаграмм Эйлера. Adobe Photoshop/Illustrator
Inkscape
Microsoft Paint
 Поскольку диаграммы Эйлера обычно строятся с использованием кругов, вы можете выбрать форму круга в MS Paint, чтобы создать диаграмму Эйлера и пометить ее текстом. Однако, поскольку перемещение фигур невозможно с помощью слоев в MS Paint, вам может быть сложнее его использовать.
Поскольку диаграммы Эйлера обычно строятся с использованием кругов, вы можете выбрать форму круга в MS Paint, чтобы создать диаграмму Эйлера и пометить ее текстом. Однако, поскольку перемещение фигур невозможно с помощью слоев в MS Paint, вам может быть сложнее его использовать. Google Drawings
Google Slides и PowerPoint

