Отрезок соединяющий середины двух сторон треугольника называется: Средняя линия — урок. Геометрия, 8 класс.

Свойства треугольников, формулы и примеры

Онлайн калькуляторы

На нашем сайте собрано более 100 бесплатных онлайн калькуляторов по математике, геометрии и физике.

Справочник

Основные формулы, таблицы и теоремы для учащихся. Все что нужно, чтобы сделать домашнее задание!

Заказать решение

Не можете решить контрольную?!
Мы поможем! Более 20 000 авторов выполнят вашу работу от 100 руб!

Главная Справочник Свойства Свойства треугольников

Все свойства треугольников

В любом треугольнике три угла и три стороны.

Сумма углов любого треугольника равна .

Против большего угла треугольника лежит большая сторона.

Треугольники бывают остроугольными (если все его углы острые), тупоугольными (если один из его углов тупой), прямоугольными (если один из его углов прямой).

Основные линии треугольника

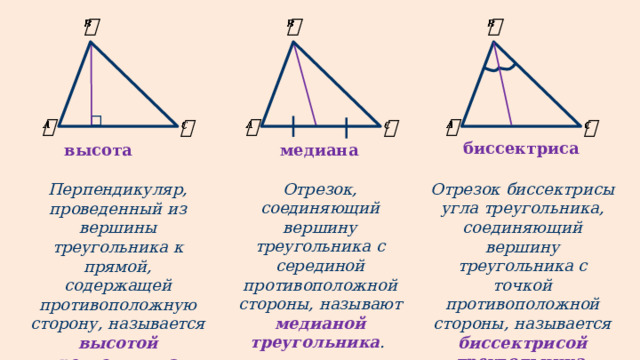
Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

Биссектрисой угла треугольника называется луч, исходящий из вершины треугольника и делящий его пополам.

Высотой треугольника называется перпендикуляр, опущенный из вершины треугольника на противоположную сторону (или ее продолжение).

Средняя линия треугольника – это отрезок, соединяющий середины двух сторон треугольника и параллельный третьей стороне.

В любой треугольник можно вписать окружность и около любого треугольника можно описать окружность.

Два треугольника называются равными, если у них равны соответствующие стороны и соответствующие углы.

Признаки равенства треугольников

I признак. Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

II признак. Если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны.

III признак. Если три стороны одного треугольника равны трем сторонам другого треугольника, то такие треугольники равны.

Треугольники называются подобными, если их стороны пропорциональны.

Признаки подобия треугольников

1. Если два угла одного треугольника раны двум углам другого треугольника, то такие треугольники подобны.
2. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, и углы, образованные этими сторонами, равны, то такие треугольники подобны.
3. Если три стороны одного треугольника пропорциональны двум сторонам другого треугольника, то такие треугольники подобны.

Теорема косинусов. Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:

   

Подробнее про теорему косинусов по ссылке.

Теорема синусов. Стороны треугольника пропорциональны синусам противолежащих углов.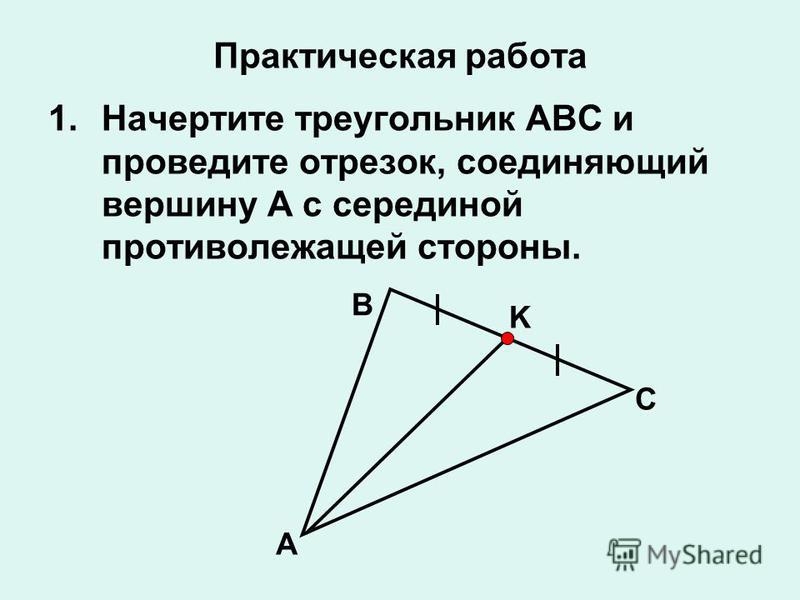 Коэффициент пропорциональности равен диаметру описанной окружности (обобщенная теорема синусов):

   

Подробнее про теорему синусов по ссылке.

Площадь треугольника можно вычислить по формулам

1. Через высоту и основание

   

2. По двум сторонам и углу между ними

   

3. По формуле Герона

   

где – полупериметр треугольника

4. Через радиусы вписанной и описанной окружностей

   

где – полупериметр треугольника, – радиус вписанной окружности;

   

– радиус описанной окружности.

Примеры решения задач

Понравился сайт? Расскажи друзьям!

Как найти среднюю длину треугольника. Средняя линия треугольника

Как найти среднюю длину треугольника. Средняя линия треугольника

Видеокурс «Получи пятерку» включает все темы, необходимые для успешной сдачи ЕГЭ по математике на 60-65 баллов.

Полностью все задачи 1-13 Профильного ЕГЭ по математике. Подходит также для сдачи Базового ЕГЭ по математике. Если вы хотите сдать ЕГЭ на 90-100 баллов, вам надо решать часть 1 за 30 минут и без ошибок!

Курс подготовки к ЕГЭ для 10-11 класса, а также для преподавателей. Все необходимое, чтобы решить часть 1 ЕГЭ по математике (первые 12 задач) и задачу 13 (тригонометрия). А это более 70 баллов на ЕГЭ, и без них не обойтись ни стобалльнику, ни гуманитарию.

Вся необходимая теория. Быстрые способы решения, ловушки и секреты ЕГЭ. Разобраны все актуальные задания части 1 из Банка заданий ФИПИ. Курс полностью соответствует требованиям ЕГЭ-2018.

Курс содержит 5 больших тем, по 2,5 часа каждая. Каждая тема дается с нуля, просто и понятно.

Сотни заданий ЕГЭ. Текстовые задачи и теория вероятностей. Простые и легко запоминаемые алгоритмы решения задач. Геометрия. Теория, справочный материал, разбор всех типов заданий ЕГЭ. Стереометрия. Хитрые приемы решения, полезные шпаргалки, развитие пространственного воображения.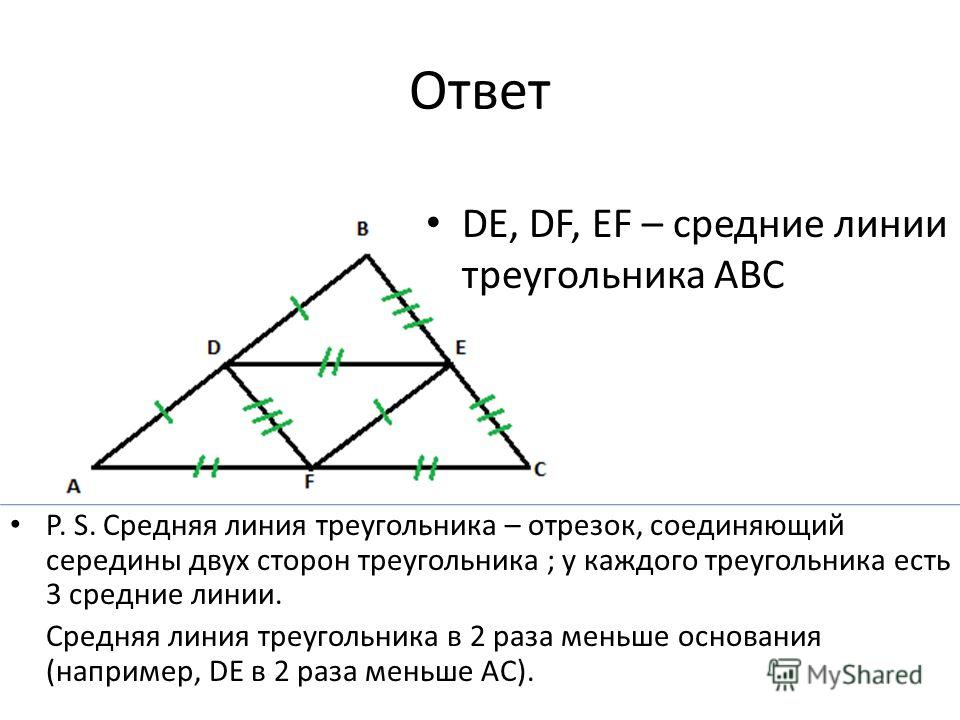

Тригонометрия с нуля — до задачи 13. Понимание вместо зубрежки. Наглядное объяснение сложных понятий. Алгебра. Корни, степени и логарифмы, функция и производная. База для решения сложных задач 2 части ЕГЭ.

\[{\Large{\text{Подобие треугольников}}}\]

Определения

Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого
(стороны называются сходственными, если они лежат напротив равных углов).

Коэффициент подобия (подобных) треугольников – это число, равное отношению сходственных сторон этих треугольников.

Определение

Периметр треугольника – это сумма длин всех его сторон.

Теорема

Отношение периметров двух подобных треугольников равно коэффициенту подобия.

Доказательство

Рассмотрим треугольники \(ABC\) и \(A_1B_1C_1\) со сторонами \(a,b,c\) и \(a_1, b_1, c_1\) соответственно (см. рисунок выше).

Тогда \(P_{ABC}=a+b+c=ka_1+kb_1+kc_1=k(a_1+b_1+c_1)=k\cdot P_{A_1B_1C_1}\)

Теорема

Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.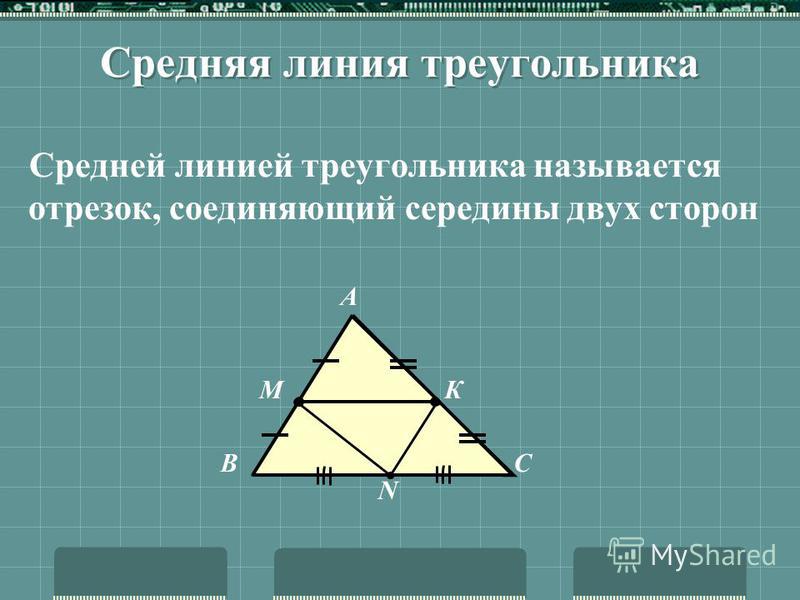 \circ — \angle A_1 — \angle B_1 = \angle C_1\) , то есть углы треугольника \(ABC\) соответственно равны углам треугольника \(A_1B_1C_1\) .

Так как \(\angle A = \angle A_1\) и \(\angle B = \angle B_1\) , то \(\dfrac{S_{ABC}}{S_{A_1B_1C_1}} = \dfrac{AB\cdot AC}{A_1B_1\cdot A_1C_1}\) и \(\dfrac{S_{ABC}}{S_{A_1B_1C_1}} = \dfrac{AB\cdot BC}{A_1B_1\cdot B_1C_1}\) .

Из этих равенств следует, что \(\dfrac{AC}{A_1C_1} = \dfrac{BC}{B_1C_1}\) .

Аналогично доказывается, что \(\dfrac{AC}{A_1C_1} = \dfrac{AB}{A_1B_1}\) (используя равенства \(\angle B = \angle B_1\) , \(\angle C = \angle C_1\) ).

В итоге, стороны треугольника \(ABC\) пропорциональны сходственным сторонам треугольника \(A_1B_1C_1\) , что и требовалось доказать.

Теорема (второй признак подобия треугольников)

Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.

Доказательство

Рассмотрим два треугольника \(ABC\) и \(A»B»C»\) , таких что \(\dfrac{AB}{A»B»}=\dfrac{AC}{A»C»}\) , \(\angle BAC = \angle A»\) . Докажем, что треугольники \(ABC\) и \(A»B»C»\) – подобны. Учитывая первый признак подобия треугольников, достаточно показать, что \(\angle B = \angle B»\) .

Рассмотрим треугольник \(ABC»»\) , у которого \(\angle 1 = \angle A»\) , \(\angle 2 = \angle B»\) . Треугольники \(ABC»»\) и \(A»B»C»\) подобны по первому признаку подобия треугольников, тогда \(\dfrac{AB}{A»B»} = \dfrac{AC»»}{A»C»}\) .

С другой стороны, по условию \(\dfrac{AB}{A»B»} = \dfrac{AC}{A»C»}\) . Из последних двух равенств следует, что \(AC = AC»»\) .

Треугольники \(ABC\) и \(ABC»»\) равны по двум сторонам и углу между ними, следовательно, \(\angle B = \angle 2 = \angle B»\) .

Теорема (третий признак подобия треугольников)

Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.

Доказательство

Пусть стороны треугольников \(ABC\) и \(A»B»C»\) пропорциональны: \(\dfrac{AB}{A»B»} = \dfrac{AC}{A»C»} = \dfrac{BC}{B»C»}\) . Докажем, что треугольники \(ABC\) и \(A»B»C»\) подобны.

Для этого, учитывая второй признак подобия треугольников, достаточно доказать, что \(\angle BAC = \angle A»\) .

Рассмотрим треугольник \(ABC»»\) , у которого \(\angle 1 = \angle A»\) , \(\angle 2 = \angle B»\) .

Треугольники \(ABC»»\) и \(A»B»C»\) подобны по первому признаку подобия треугольников, следовательно, \(\dfrac{AB}{A»B»} = \dfrac{BC»»}{B»C»} = \dfrac{C»»A}{C»A»}\) .

Из последней цепочки равенств и условия \(\dfrac{AB}{A»B»} = \dfrac{AC}{A»C»} = \dfrac{BC}{B»C»}\) вытекает, что \(BC = BC»»\) , \(CA = C»»A\) .

Треугольники \(ABC\) и \(ABC»»\) равны по трем сторонам, следовательно, \(\angle BAC = \angle 1 = \angle A»\) .

\[{\Large{\text{Теорема Фалеса}}}\]

Теорема

Если на одной из сторон угла отметить равные между собой отрезки и через их концы провести параллельные прямые, то эти прямые отсекут на второй стороне также равные между собой отрезки.

Доказательство

Докажем сначала лемму: Если в \(\triangle OBB_1\) через середину \(A\) стороны \(OB\) проведена прямая \(a\parallel BB_1\) , то она пересечет сторону \(OB_1\) также в середине.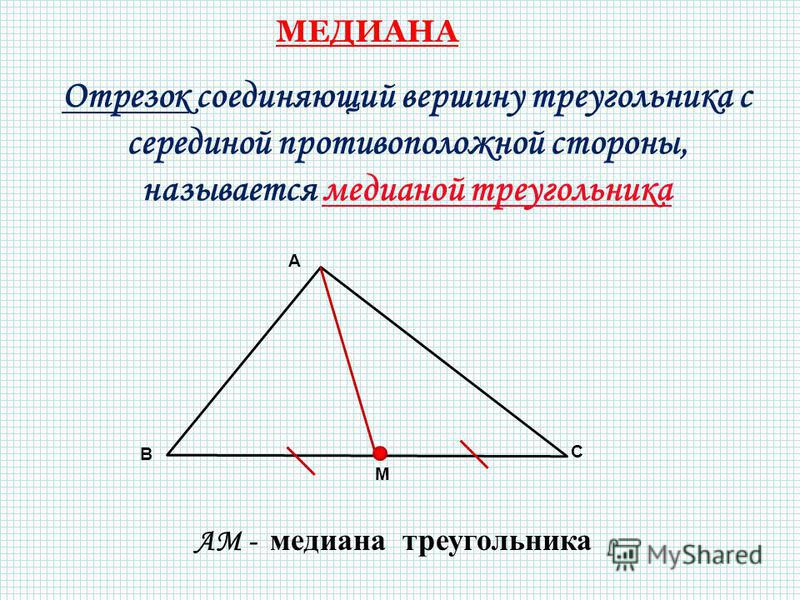

Через точку \(B_1\) проведем \(l\parallel OB\) . Пусть \(l\cap a=K\) . Тогда \(ABB_1K\) — параллелограмм, следовательно, \(B_1K=AB=OA\) и \(\angle A_1KB_1=\angle ABB_1=\angle OAA_1\) ; \(\angle AA_1O=\angle KA_1B_1\) как вертикальные. Значит, по второму признаку \(\triangle OAA_1=\triangle B_1KA_1 \Rightarrow OA_1=A_1B_1\) . Лемма доказана.

Перейдем к доказательству теоремы. Пусть \(OA=AB=BC\) , \(a\parallel b\parallel c\) и нужно доказать, что \(OA_1=A_1B_1=B_1C_1\) .

Таким образом, по данной лемме \(OA_1=A_1B_1\) . Докажем, что \(A_1B_1=B_1C_1\) . Проведем через точку \(B_1\) прямую \(d\parallel OC\) , причем пусть \(d\cap a=D_1, d\cap c=D_2\) . Тогда \(ABB_1D_1, BCD_2B_1\) — параллелограммы, следовательно, \(D_1B_1=AB=BC=B_1D_2\) . Таким образом, \(\angle A_1B_1D_1=\angle C_1B_1D_2\) как вертикальные, \(\angle A_1D_1B_1=\angle C_1D_2B_1\) как накрест лежащие, и, значит, по второму признаку \(\triangle A_1B_1D_1=\triangle C_1B_1D_2 \Rightarrow A_1B_1=B_1C_1\) .

Теорема Фалеса

Параллельные прямые отсекают на сторонах угла пропорциональные отрезки.

Доказательство

Пусть параллельные прямые \(p\parallel q\parallel r\parallel s\) разбили одну из прямых на отрезки \(a, b, c, d\) . Тогда вторую прямую эти прямые должны разбить на отрезки \(ka, kb, kc, kd\) соответственно, где \(k\) – некоторое число, тот самый коэффициент пропорциональности отрезков.

Проведем через точку \(A_1\) прямую \(p\parallel OD\) (\(ABB_2A_1\) — параллелограмм, следовательно, \(AB=A_1B_2\) ). Тогда \(\triangle OAA_1 \sim \triangle A_1B_1B_2\) по двум углам. Следовательно, \(\dfrac{OA}{A_1B_2}=\dfrac{OA_1}{A_1B_1} \Rightarrow A_1B_1=kb\) .

Аналогично проведем через \(B_1\) прямую \(q\parallel OD \Rightarrow \triangle OBB_1\sim \triangle B_1C_1C_2 \Rightarrow B_1C_1=kc\) и т.д.

\[{\Large{\text{Средняя линия треугольника}}}\]

Определение

Средняя линия треугольника – это отрезок, соединяющий середины любых двух сторон треугольника.

Теорема

Средняя линия треугольника параллельна третьей стороне и равна ее половине.

Доказательство

1) Параллельность средней линию основанию следует из доказанной выше леммы .

2) Докажем, что \(MN=\dfrac12 AC\) .

Через точку \(N\) проведем прямую параллельно \(AB\) . Пусть эта прямая пересекла сторону \(AC\) в точке \(K\) . Тогда \(AMNK\) — параллелограмм (\(AM\parallel NK, MN\parallel AK\) по предыдущему пункту). Значит, \(MN=AK\) .

Т.к. \(NK\parallel AB\) и \(N\) – середина \(BC\) , то по теореме Фалеса \(K\) – середина \(AC\) . Следовательно, \(MN=AK=KC=\dfrac12 AC\) .

Следствие

Средняя линия треугольника отсекает от него треугольник, подобный данному с коэффициентом \(\frac12\) .

Как найти середину треугольника: задачка по геометрии. Основные элементарные задачи по Евклидовой геометрии пришли к нам из античности. В них заключается сама первичная сущность и необходимые базовые знания о восприятии человеком пространственных форм. Одной из таких задач является проблема нахождения середины треугольника. Сегодня эта задачка рассматривается как учебный прием развития интеллектуальных способностей школьников. В древнем же мире, знание того, как найти середину треугольника, применялось и на практике: в землеустройстве, при изготовлении разнообразных механизмов и т.д. В чем же состоит сущность этого геометрического ребуса?

Что такое медиана? Перед решением задачи необходимо ознакомиться с простейшей геометрической терминологией, касающейся треугольников. Прежде всего, у каждого треугольника есть три вершины, три стороны и три угла, от чего и происходит название данной геометрической фигуры. Важно знать, как называются линии, соединяющие вершины с противоположными сторонами: высота, биссектриса и медиана.

Высота − линия перпендикулярная стороне, противоположной вершине, из которой она проводится; биссектриса − делит угол пополам; медиана же делит противоположную исходящей вершине сторону пополам. Для решения этой задачи нужно знать, как найти координаты середины отрезка, ведь именно точка пересечения медиан треугольника и является его серединой.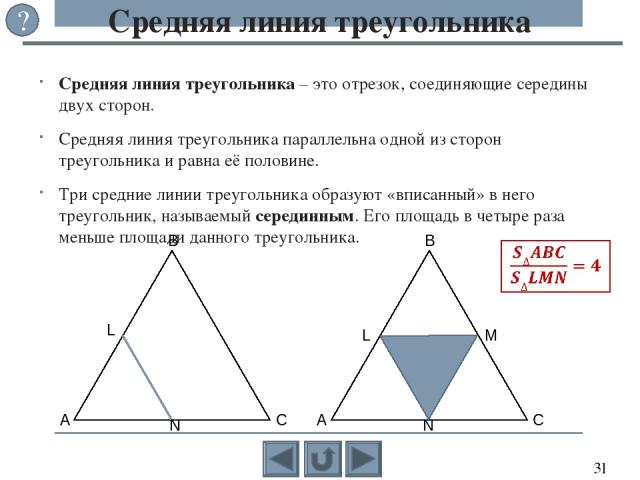

Находим середины сторон треугольника. Нахождение середины отрезка тоже является классической геометрической задачей, для решения которой понадобится циркуль и линейка без делений. Ставим иглу циркуля в точку окончания отрезка и чертим полукруг, больший половины отрезка в середине последнего. Проделываем то же самое с другой стороны отрезка. Полученные полуокружности обязательно пересекутся в двух точках, ведь их радиусы больше половины исходного отрезка.

Соединяем две точки пересечения окружности прямой линией при помощи линейки. Эта линия пересекает исходный отрезок точно в его середине. Теперь, зная то, как найти середину отрезка, проделываем это с каждой стороной треугольника. После нахождения всех середин сторон треугольника всё готово для построения его собственной середины.

Строим середину треугольника. Соединив прямыми линиями вершины треугольника с серединами противоположных им сторон, получаем три медианы. Может кого-то это и удивит, но одним из законов гармонии этой геометрической фигуры является то, что все три медианы всегда пересекаются в одной точке.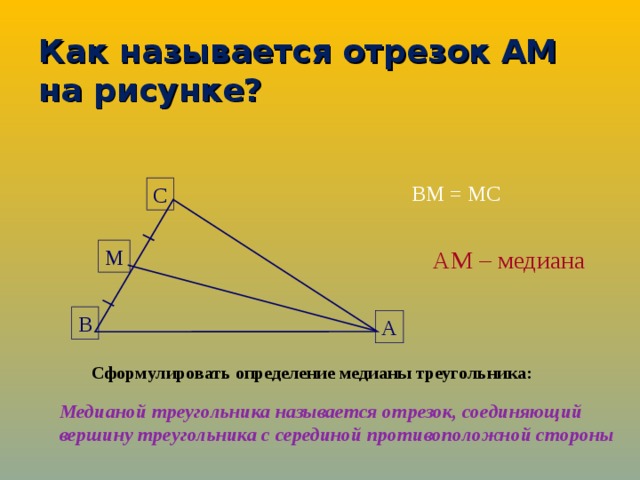 Именно эта точка и будет искомой серединой треугольника, которую не так трудно найти, если знать;как построить середину отрезка.

Интересно и то, что точка пересечения медиан представляет собой не только геометрическую, но и «физическую» середину треугольника. То есть, если, к примеру, вырезать треугольник из фанеры, найти его середину и поместить эту точку на кончик иглы, то в идеале такая фигура будет балансировать и не упадет. Элементарная геометрия несет в себе множество подобных захватывающих «тайн», знание которых помогает постигать гармонию окружающего мира и природу более сложных вещей.

Порой темы, которые объясняют в школе, могут быть не всегда понятны с первого раза. Особенно это касается такого предмета, как математика. Но все становится намного сложнее, когда эта наука начинает подразделяться на две части: алгебру и геометрию.

Каждый ученик может обладать способностью к одному из двух направлений, но особенно в начальных классах важно понять базу и алгебры, и геометрии. В геометрии одной из главных тем принято считать раздел о треугольниках.

Как находить среднюю линию треугольника? Давайте разбираться.

Основные понятия

Для начала чтобы разобраться, как находить среднюю линию треугольника, важно понимать, что же это.

Для проведения средней линии нет ограничений: треугольник может быть любым (равнобедренным, равносторонним, прямоугольным). И все свойства, которые относятся к средней линии, будут действовать.

Средняя линия треугольника является отрезком, соединяющим середины 2-х его сторон. Следовательно, любой треугольник может иметь 3 таких линии.

Свойства

Чтобы знать, как находить среднюю линию треугольника, обозначим ее свойства, которые необходимо запомнить, иначе без них будет невозможным решение задач с необходимостью обозначить длину средней линии, поскольку все полученные данные необходимо обосновать и аргументировать теоремами, аксиомами или свойствами.

Таким образом, чтобы ответить на вопрос: «Как найти среднюю линию треугольника АВС?», достаточно знать одну из сторон треугольника.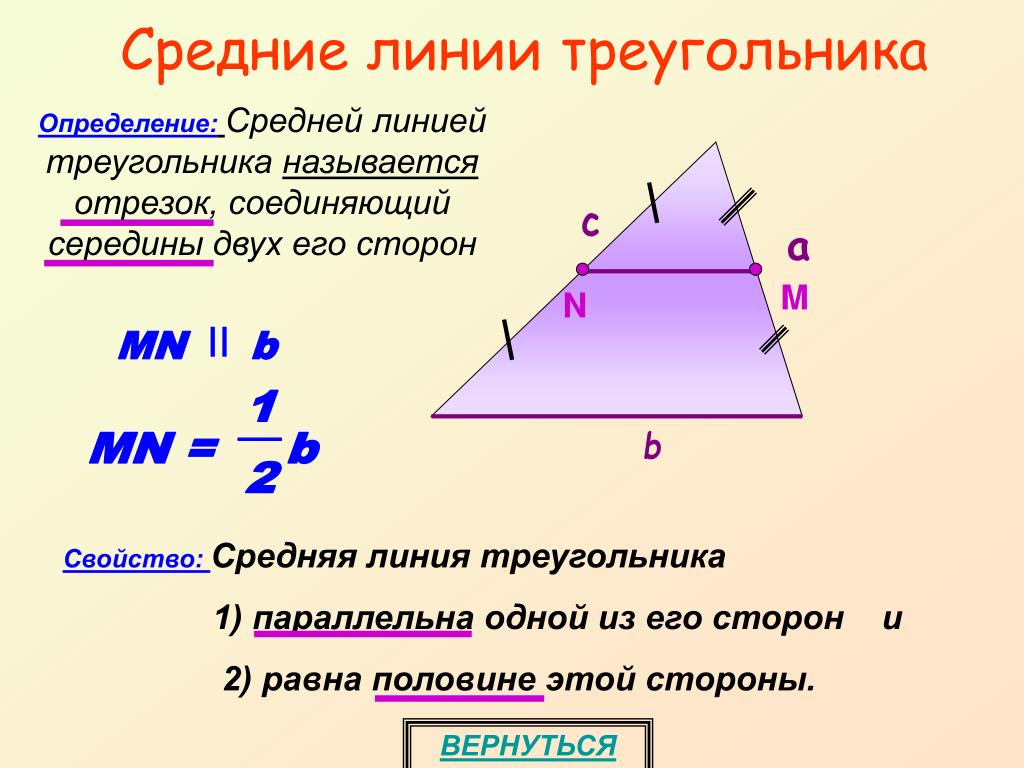

Приведем пример

Взгляните на рисунок. На нем представлен треугольник ABC со средней линией DE. Обратим внимание, что она параллельна основанию AC в треугольнике. Следовательно, каким бы ни было значение AC, средняя линия DE будет в два раза меньше. К примеру, AC=20, значит DE=10 и т. д.

Вот такими несложными способами можно понять, как находить среднюю линию треугольника. Запомните ее основные свойства и определение, и тогда у вас никогда не возникнет проблем с нахождением ее значения.

Четырёхугольник, у которого только две стороны параллельны называются трапецией .

Параллельные стороны трапеции называются её основаниями , а те стороны, которые не параллельны, называются боковыми сторонами . Если боковые стороны равны, то такая трапеция является равнобедренной. Расстояние между основаниями называется высотой трапеции.

Средняя Линия Трапеции

Средняя линия — это отрезок, соединяющий середины боковых сторон трапеции.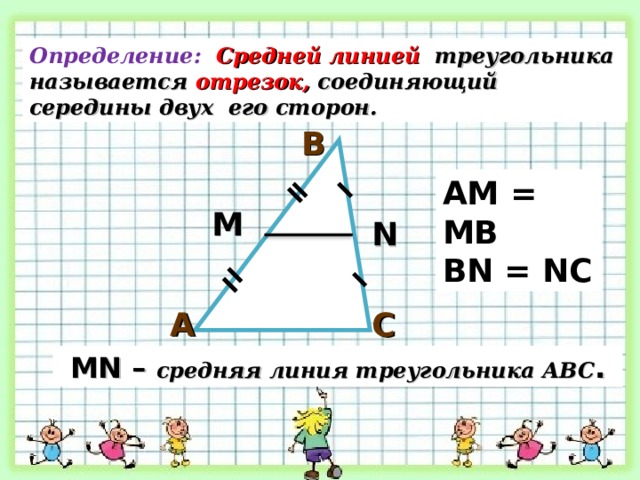 Средняя линия трапеции параллельна её основаниям.

Теорема:

Если прямая, пересекающая середину одной боковой стороны, параллельна основаниям трапеции, то она делит пополам вторую боковую сторону трапеции.

Теорема:

Длина средней линии равна среднему арифметическому длин её оснований

MN || AB || DC
AM = MD; BN = NC

MN средняя линия, AB и CD — основания, AD и BC — боковые стороны

MN = (AB + DC)/2

Теорема:

Длина средней линии трапеции равна среднему арифметическому длин её оснований.

Основная задача : Доказать, что средняя линия трапеции делит пополам отрезок, концы которого лежат в середине оснований трапеции.

Средняя Линия Треугольника

Отрезок, соединяющий середины двух сторон треугольника, называется средней линией треугольника. Она параллельна третьей стороне и её длина равна половине длины третьей стороны.
Теорема : Если прямая, пересекающая середину одной стороны треугольника, параллельна другой стороне данного треугольника, то она делит третью сторону пополам.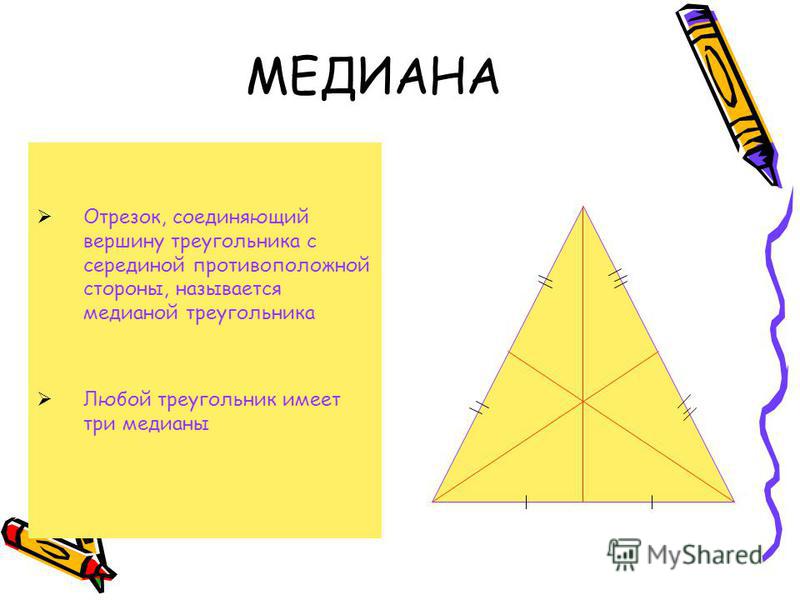

AM = MC and BN = NC =>

Применение свойств средней линии треугольника и трапеции

Деление отрезка на определённое количество равных частей.
Задача: Разделить отрезок AB на 5 равных частей.
Решение:
Пусть p это случайный луч, у которого начало это точка А, и который не лежит на прямой AB. Мы последовательно откладываем 5 равных сегментов на p AA 1 = A 1 A 2 = A 2 A 3 = A 3 A 4 = A 4 A 5
Мы соединяем A 5 с B и проводим такие прямые через A 4 , A 3 , A 2 и A 1 , которые параллельны A 5 B. Они пересекают AB соответственно в точках B 4 , B 3 , B 2 и B 1 . Эти точки делят отрезок AB на 5 равных частей. Действительно, из трапеции BB 3 A 3 A 5 мы видим, что BB 4 = B 4 B 3 . Таким же образом, из трапеции B 4 B 2 A 2 A 4 получаем B 4 B 3 = B 3 B 2

В то время как из трапеции B 3 B 1 A 1 A 3 , B 3 B 2 = B 2 B 1 .
Тогда из B 2 AA 2 следует, что B 2 B 1 = B 1 A. В заключении получаем:
AB 1 = B 1 B 2 = B 2 B 3 = B 3 B 4 = B 4 B
Ясно, что для разделения отрезка AB на другое количество равных частей, нам нужно проецировать то же самое количество равных сегментов на луч p.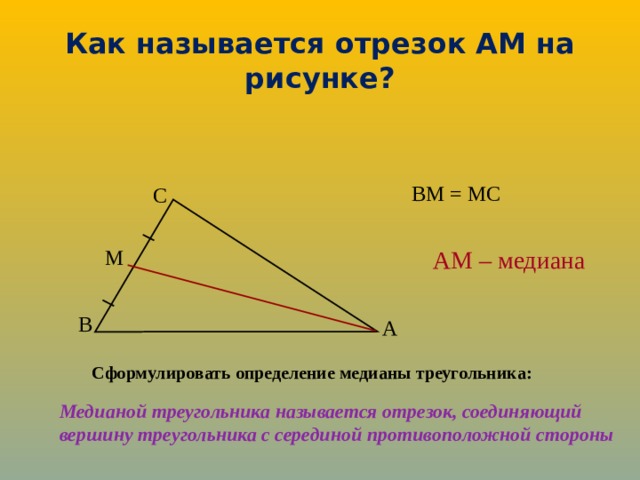 И далее продолжать вышеописанным способом.

Теорема о средней линии: построение и нахождение длин

Ключевые понятия

• Теорема о средней линии.
• Теорема о средней линии для нахождения длин.
• Размещение фигуры на координатной плоскости

Введение 

На предыдущем занятии мы узнали о свойствах треугольников, а на предыдущих занятиях узнали о нахождении расстояний, упрощении выражений, решении уравнений и неравенств.

Теперь мы узнаем о теореме о средней линии и доказательстве координат.

Вы слышали о теореме о средней линии?

Вы имеете представление о сегментах?

Теорема о средней линии 

Треугольник имеет три стороны.

Отрезок, соединяющий середины двух сторон треугольника, называется средним сегментом треугольника.

Теорема о средней линии утверждает, что средняя линия двух сторон треугольника параллельна третьей стороне, а длина средней части равна половине длины третьей стороны.

Рисование среднего сегмента 

Как нарисовать средний сегмент?

Посмотрим на это.

Шаг 1:  

Сначала нарисуйте треугольник, сохранив все свойства треугольника.

Шаг 2:  

Затем найдите середины любых двух сторон треугольника.

Шаг 3:  

Теперь соедините эти средние точки отрезком.

Этот сегмент называется средним сегментом.

Нахождение длин

Теперь воспользуемся теоремой о средних отрезках, чтобы найти длины.

Давайте посмотрим на пример.

Пример: 

Дан треугольник BCD, где GF, GE, ED — средние сегменты.

Найдите значение GF, если BD = 24 дюйма.

Если

∠GFE=35, тогда ∠GFE=35°, найдите ∠FED.

Объяснение:

Из теоремы о среднем отрезке

GF является средним отрезком BD, поэтому GF = половина длины BD = ½ * 24 = 12 дюймов

∠GFE=35

▀

BD GF, аналогично EF  

Итак, n∠FED = 35°

Размещение фигуры на координатной плоскости

Как разместить фигуру на координатной плоскости?

Объяснение: 

Мы можем разместить фигуру на координатной плоскости, рассматривая первый квадрант координатной плоскости.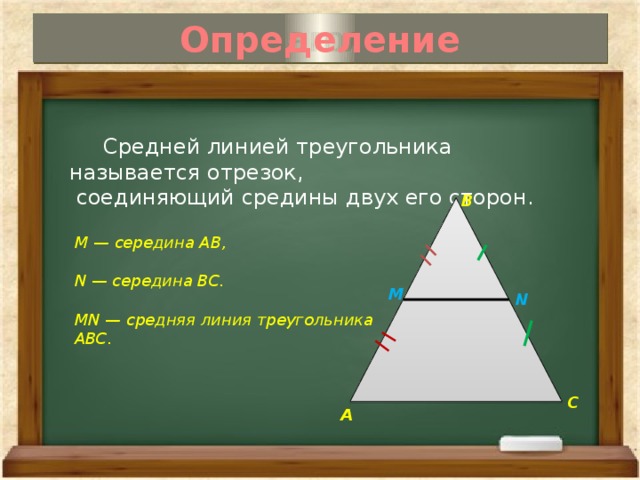

Длину легко найти, если рассматривать начало координат как одну вершину и

разместить одну вершину по оси x и еще одну по оси y.

Посмотрим какие-нибудь фигуры на координатной плоскости.

Пример 1: 

Как нарисовать прямоугольник на координатной плоскости?

Объяснение: 

Мы рассматриваем начало координат как одну вершину.

Длина составляет 12 единиц, что отложено по оси X.

Ширина 9 единиц, которая отложена по оси Y.

Другой вершиной будет (12, 9) 

Теперь проведем линии, соединяющие все вершины, таким образом, получится прямоугольник.

Пример 2:

Как нарисовать треугольник на координатной плоскости?

Объяснение: 

Мы рассматриваем начало координат как одну вершину.

Мы рассматриваем 15 на оси Y,

Другая вершина как (10, 8).

Теперь мы рисуем линии, соединяющие все вершины.

Таким образом, полученная фигура представляет собой треугольник.

Построение средней линии на координатной плоскости

Сначала мы построим треугольник на координатной плоскости.

(см. график)

Вершины (0, 0) (0, 15) (10, 8) 

Затем мы проводим средние сегменты этого треугольника, находя середины.

Средние точки будут

(0+102,15+82), (0+102,0+82)

= (5, 11,5) (5, 4)

Теперь мы соединяем эти две средние точки, чтобы сформировать средний сегмент.

Средняя линия параллельна основанию треугольника.

Применение переменных координат 

Если равнобедренный прямоугольный треугольник с длиной основания k единиц поместить в координатную плоскость,  

найти гипотенузу и середину гипотенузы.

Объяснение: 

Мы рассматриваем начало координат как одну вершину.

Мы рассматриваем k единиц по оси Y, 

Мы рассматриваем k единиц по оси x.

Затем мы строим треугольник,

Теперь длина гипотенузы равна расстоянию от (0, K)

(K, 0).

Гипотенуза = √(0−K) ² +(K−0) ²

= √K ² +K ²  

=√K ²

Используя формулу середины, находим середину гипотенузы

Середина = (0 + K/2, K + 0/2)

(K/2, K/2) )

Теорема о средней линии и ее доказательство

На предыдущих слайдах мы сформулировали теорему о средней линии, теперь проверим ее координатное доказательство

Теорема о средней линии:  

Средняя линия двух сторон треугольника параллельна третьей стороне, длина среднего сегмента равна половине длины третьей стороны.

Доказательство:

Учитывая, что AB является серединой ΔXYZ,

нам нужно доказать, что AB ‖ YZ и AB = ½ YZ

мы видим график для ΔXYZ

AB ‖ ‖0YZ координаты 90-0YZ:

координаты 90-0YZ: A и B одинаковы, поэтому наклон одинаков.

Точно так же координаты x Y и Z находятся на оси y, где x = 0, поэтому наклоны AB и YZ одинаковы.

Так как наклоны одинаковые AB ‖ YZ

AB = ½ YZ:

X (2x, 2z) Y (0, 2y), Z (0, 0) — вершины треугольника XYZ.

A является серединой XY

Мы находим A, используя формулу средней точки.

A = (0+2x/2 ,2y+2z/2)

=(x, y+z)

Следовательно, A =(x, y+z)

B — середина XZ

We найти B по формуле средней точки.

B = (0+2x/2, 0+2z/2)

=(x, z)

Следовательно, B =(x, z)

Теперь

YZ = √(0−0) ² + (0−2y) ²

  (по формуле расстояния)

= √ (2y) ²

= 2y

AB = √ (x — x) ² + (y + z — z) ²

4 (на расстоянии расстояния)

4 (на расстоянии расстояния)

4 (на расстоянии)

4 (на расстоянии)

4 (на расстоянии)

(на расстоянии)

4 (на расстоянии. √(y) ²

=y

AB = ½ YZ: 

AB = yAB = y

= 1/2(2y)

=1/2(YZ)

5 Следовательно .

Отсюда доказано.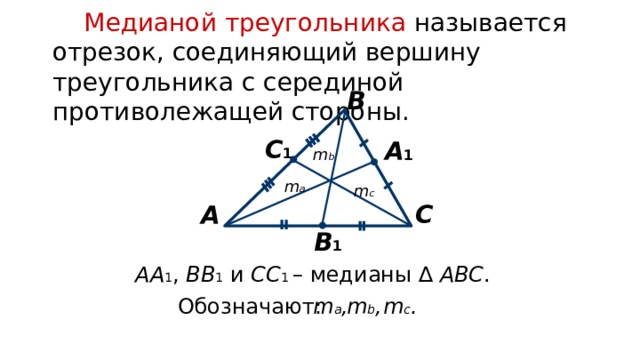

Расширение теоремы о средней линии

Мы можем расширить теорему о средней линии, доказав теорему о средней линии для всех сторон треугольника.

Мы можем доказать как свойство параллельности, так и свойство половины длины для всех трех сторон треугольника, если мы доказали это для одной стороны.

Пример из реальной жизни (диско-шар)  

Дан диско-шар, если в его AD ≅ DB, AE ≅ EC, докажите, что DE ‖ BC.

Объяснение: 

Дан дискотечный шар, если в его AD ≅ DB, AE ≅ EC

Нам нужно доказать, что DE ‖ BC.

Из предоставленной информации D — середина AB, а E — середина AC.

Таким образом, DE образует средний сегмент.

Итак, DE ‖ BC из теоремы о середине отрезка.

Упражнение

• Если DE = 5 дюймов — средняя линия треугольника ABC, найдите длину BC.

• Расположенные ниже рисунки удобно расположите на координатной плоскости.
• Прямоугольник длиной x единиц и шириной y единиц.
• Прямоугольный равнобедренный треугольник длиной 9 единиц, найдите гипотенузу.
• Поместите треугольник двумя разными способами на координатную плоскость, найдите гипотенузу в обоих случаях. Проверьте, одинаково ли значение гипотенузы в обоих случаях.
• Найдите длину и наклон треугольника с вершинами (a, 0), (0, 0) (a, b). В треугольнике ABC-D, E, F являются серединами.

• Если AB = 3x + 15, DE = 5x + 4, какова длина AB?
• Если DF = 9y + 4, BC = 3y + 13, какова длина DF?
• Если середины каждой стороны треугольника равны (4, 0) (5, 8) (9, 12), найдите периметр треугольника, образованного средними сегментами.
• Если середины каждой стороны треугольника равны (5, 2) (12, 4) (9, 9), найдите периметр треугольника, образованного средними отрезками.
• Если середины каждой стороны треугольника равны (5, 2) (12, 4) (9, 9) и образуют треугольник. Найдите исходный треугольник.
• В классе установлен проектор для объяснения средних сегментов, между проектором и стеной, на которую производится проекция, стоит ученик ростом 4 фута. Край света проектора достигает макушки его головы. Какова высота его тени?

Концептуальная карта

Что мы узнали

• Теорема о средней линии.
• Середина отрезка Теорема для нахождения длин.
• Размещение фигуры на координатной плоскости.

Mideegment трапециевого рабочего листа. Показать …

www.neshaminy.org › cms › lib › Centricity › Домен › практика_6_…

Практическое занятие 6-6. Рабочий лист. Решение средних сегментов трапеций. Показать все работы. Трапеция со средним сегментом. 4y= 20. X = 34-2=58. 34 = 60. 8=20.

[PDF] Решение средних сегментов трапеций. Показать все работы.

www.neshaminy.org › cms › lib › Centricity › Domain › практика_6_…

Практика 6-6 Рабочий лист – Решение средних сегментов трапеций. Показать все работы. Имя. 1. Трапеция со средним сегментом. 2. Равнобедренная трапеция со средней частью.

Рабочий лист для урока: Теорема о среднем сегменте трапеции — Нагва

www. nagwa.com › рабочие листы

В этом рабочем листе мы потренируемся находить неизвестные длины трапеций, используя теорему о середине трапеции.

[PDF] Трапеции — отсканированный документ

msschum.weebly.com › загрузки › gcc_9-4_notes

Найдите каждое отсутствующее значение на трапециях ниже. Помните: … Средняя часть трапеции соединяет середины катетов: Если EF является средней линией …

[PDF] HW Трапеции 8.5.ks-ig

www.lcps.org › cms › lib4 › Centricity › Domain › HW Trapezoids 8

Рабочий лист от Kuta Software LLC. Геометрия… Найдите длину середины каждой трапеции. … Ответы на HW Трапеции.

[PDF] Нахождение середины трапеции. Рабочий лист — Math Monks

mathmonks.com ). 12 м. МН = 18 м. W. X = … Ответы. 1 Найдите середину данной трапеции а). Х а). М. Н. Дата:.

[PDF] 6.6 Трапезии

www.anderson1.org ›lib04› Центричность ›Домен› Трейпезоид WS

P 2 Tallylz Qrbimghhtdsvesv 5rueSelrtrnh.