Может ли математическое ожидание быть отрицательным числом
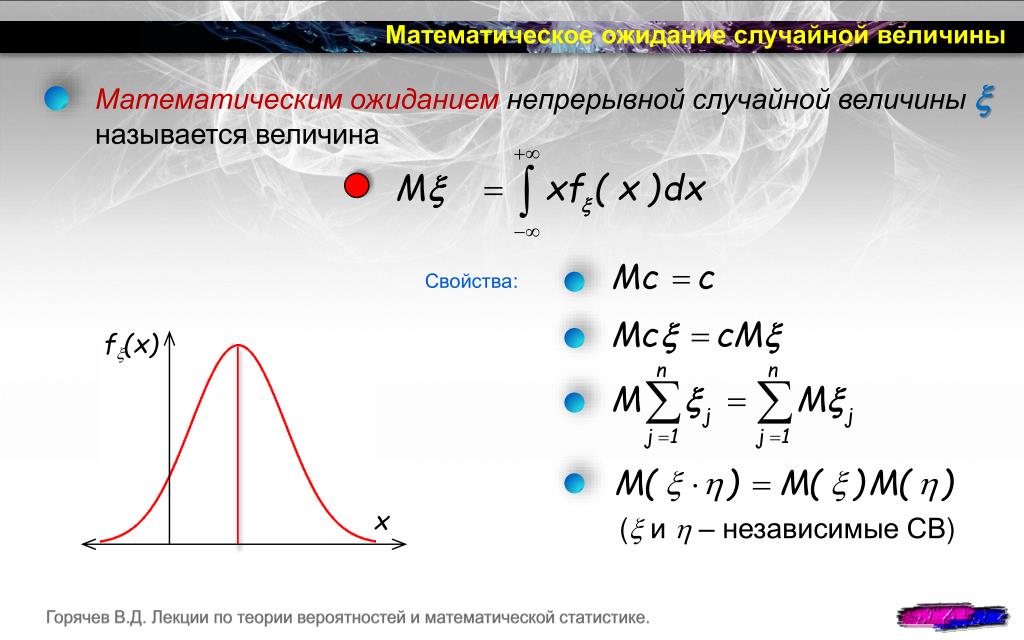
Математическим ожиданием (МО) случайной величины называют ее среднее значение, определяемое по следующим формулам.
Для случайных дискретных величин МО равно
, где – частное значение случайной дискретной величины; – вероятность ее появления.
Для случайной непрерывной величины МО определяется выражением
, где x – частное значение случайной непрерывной величины; f(x)dx – элемент вероятности.
Математическое ожидание случайной величины представляет собой центр, около которого группируются частные значения ее.
Свойства математического ожидания:
а) математическое ожидание случайной величины может быть положительным и отрицательным, целым и дробным, и обладает размерностью случайной величины;
б) не все случайные величины имеют МО. Случайные величины не имеют МО, если или ;
в) математическое ожидание постоянной величины равно самой постоянной величине, т. е. .
е. .
г) постоянную величину можно выносить за знак математического ожидания, т.е.
.
Частный случай математического ожидания. Пусть случайная величина X может принимать только два частных значения . Тогда вероятности появления этих частных значений будут равны
.
Откуда математическое ожидание .
Следовательно, математическое ожидание такой случайной величины равна вероятности того, что случайная величина примет значение равное единице.
Пример 1: В технической системе имеется n элементов. Вероятность выхода из строя элемента в течении N часов работы равна p. Требуется определить математическое ожидание числа отказавших элементов в течении N часов работы.
Обозначим через X – случайную величину числа отказавших элементов, а через M[X] – математическое ожидание этого числа.
Для использования формулы математического ожидания определяем из условия задачи, что случайная величина X принимает частные значения , причем .
Тогда математическое ожидание числа отказавших элементов будет равно
.
Отсюда следует, что если случайная величина X подчиняется биномиальному закону, то ее МО равно произведению числа опытов на вероятность появления события в одном опыте.
Часто происходит так, что после продолжительной серии успешных ставок беттор вдруг начинает «сыпаться». Та стратегия игры, которая давала результат вчера, сегодня приносит лишь одни убытки. Одна из основных ошибок бетторов состоит в том, что они полностью полагаются на свой успех в прогнозировании, при этом не рассчитывая реальные вероятности прохода тех или иных рынков.
Возьмем обычный пример, чтобы посмотреть, как себя ведут различные типы игроков.
К примеру, в теннисной игре встречаются Джокович и Вавринка. Букмекер дает на Джоковича коэффициент 1.3, а на Вавринку 3.70.
Как размышляет обычный игрок:
- Джокович сильнее Вавринки;
- У Джоковича хорошая форма;
- Джокович победит.

После этого делается ставка на победу серба.
Как размышляет опытный беттор:
- У Джоковича превосходство в личных встречах;
- Джокович – универсал, поэтому сила Вавринки на харде не сыграет большого значения;
- С учетом погоды, мотивации, формы и других факторов вероятность победы Джоковича равна 70%.
После этого делается ставка на серба.
Как размышляет профессиональный гандикапер:
- Так же, как и опытный беттор, но так как вероятность победы Джоковича равна 70%, то минимальный коэффициент безубыточности должен быть равен 1.43. Поэтому ставка на коэффициент 1.30 будет невыгодным вложением средств;
- Вероятность победы Вавринки составляет не менее 30%. В этом случае коэффициент 3.34 уже на дистанции даст возврат средств, а так как на Вавринку дают коэффициент 3.70, то делается ставка именно на него.
Допустим, что Джокович все же победил Вавринку в трех сетах. В этом случае первый игрок порадуется «легким» деньгам, опытный беттор оценит свое умение анализировать, а профессионал даже не обратит внимания на исход данного противостояния.
Дело в том, что по логике двух первых игроков ставка сделана верно, так как она прошла. При этом они не учитывают, того, что в 70% случаев эта ставка должна быть выигрышной и поэтому на дистанции у них не будет преимущества над линией. Если вероятность составляет 75%, а букмекер дает коэффициент, который равносилен 70% вероятности, то такая ставка будет с отрицательным математическим ожиданием. Можно получить от данных ставок сиюминутную прибыль, но со временем депозит будет проигран.
Вывод
При анализе вы должны не указать победителя предстоящей игры, а правильно оценить шансы соперников. Сопоставив шансы с коэффициентами букмекеров, можно понять, насколько такая ставка будет выгодна на дистанции.
При размещении ставок любого типа всегда существует определенная вероятность получения прибыли и риск потерпеть неудачу. Положительный исход сделки, и риск потерять деньги неразрывно связаны с математическим ожиданием. В данной статье мы подробно остановимся на этих двух аспектах трейдинга.

Математическое ожидание —среднее значениеслучайной величины при количестве выборок или количества её измерений (иногда говорят — количества испытаний) стремящимся к бесконечности.
Смысл в том, что положительное математическое ожидание ведет к положительной (с повышением прибыли) торговле, а нулевое или отрицательное математическое ожидание означают, что не нужно торговать вообще.
Что бы было легче разобраться в данном вопросе, давайте рассмотрим понятие математического ожидания при игре в рулетку. Пример с рулеткой очень прост для понимания.
Рулетка —азартная игра ( Крупье запускает шарик в противоположную сторону вращения колеса, с того номера на какой шарик упал в предыдущий раз, который должен упасть в одну из пронумерованных ячеек, сделав не менее трёх полных оборотов по колесу.
Ячейки, пронумерованные числами от 1 до 36, окрашены в чёрный и красный цвета. Номера расположены не по порядку, хотя цвета ячеек строго чередуются, начиная с 1 — красного цвета. Ячейка, обозначенная цифрой 0, окрашена в зелёный цвет и называется зеро
Ячейка, обозначенная цифрой 0, окрашена в зелёный цвет и называется зеро
Рулетка- это игра с отрицательным математическим ожиданием. Все из-за поля зеро.«0», которое не является ни черным, ни красным.
Поскольку (в общем случае) если не применять изменение ставки, игрок теряет 1$ за каждые 37 вращений колеса (при ставке 1$ за раз), что приводит к линейному убытку на уровне -2,7%, который увеличивается по мере роста числа ставок (в среднем).
Конечно у игрока на интервале , к примеру, в 1000 игр, могут случаться серии побед, и человек может начать ошибочно считать, что он может зарабатывать, обыгрывая казино, так и серии поражений. Серия побед в таком случае может увеличить капитал игрока на большее значение, чем у него было изначально, в таком случае, если у игрока была 1000$, после 10 игр по 1$ у него в среднем должно остаться 973$. Но если в таком сценарии у игрока окажется денег меньше или больше, мы будем называть такую разницу между текущим капиталом дисперсией.
Зарабатывать на игре в рулетку можно только в рамках дисперсии.Если игрок продолжит следовать этой стратегии, в конечном счете человек останется без денег, а казино заработает.
Второй пример — знаменитые бинарные опционы. Вам дают сделать ставку, при удачном исходе вы забираете аж 90 процентов сверху от своей ставки, а при неудачном- теряете все 100. И дальше владельцам БО достаточно просто ждать, рынок и отрицательное мат ожидание сделают свое дело. А временная дисперсия даст надежду трейдеру бинарных опционов, что на данном рынке можно зарабатывать. Но это временно.
В чем же плюс криптовалютного трейдинга ( как и трейдинга на фондовом рынке) ?Человек сам может создать для себя систему. Сам может ограничить свой риск, и стараться забрать с рынка максимум возможной прибыли. (Причем если со вторым ситуация довольно спорная, то риск нужно контролировать очень четко.)
Чтобы понимать в каком направлении вас ведёт ваша стратегия необходимо ведение статистики.
- Количество своих трейдов. Чем больше количество трейдов по заданной стратегии, тем точнее будет математическое ожидание
- Частота удачных входов. (Вероятность) (R)
- Свой профит по каждой положительной сделке.
- Смещение (коэффициент прибыльных сделок) (B)
- Средний размер вашей ставки (стоп ордер) (S)
Математическое ожидание (Е) = B * R – (1 – B) = B * (1 + R) –1
Чтобы примерно узнать свой итоговый заработок или убыток на счете (EE), к примеру, на дистанции в 1000 трейдов, воспользуемся формулой.
Где N — количество трейдов, которые мы планируем исполнить.
Для примера возмем начальные данные:
стоп лосс — 30 долларов.
профит — 100 долларов.
Количество сделок 30
Математическое ожидание отрицательное только при соотношении прибыльных и убыточных сделок (R) 20%/80% или хуже В остальных случаях положительное.
Пусть теперь профит будет 150. Тогда отрицательным мат ожидание будет при соотношении 16%/84%. Или ниже.
Или ниже.
Что с этим делать? Начните вести статистику, если еще не начинали. Проверьте свои трейды, определите Ваше мат ожидание. Найдите то, что можно улучшить ( количество верных входов, добор профита, урезание убытков)
Игра с отрицательным мат. ожиданием
Это жизненно важная концепция для всех спекулянтов, это концепция, на которой строится система веры, но сама концепция не может быть построена на вере. Казино не работают на вере. Они оперируют, управляют своим бизнесом, основываясь на чистой математике. Они знают, что, в конечном счете, законы рулетки или игры в кости возьмут верх. Поэтому они не дают игре останавливаться. Они не против того, чтобы подождать, но они не останавливаются. Они играют круглые сутки также не без причины чем дольше вы играете в их игру отрицательного математического ожидания, тем больше они уверены, что получат ваши деньги. [c.193]В отношении управления капиталом очень важно понимать, что при игре с отрицательным ожиданием нет схемы управления деньгами, которая может сделать вас победителем.
Эта аксиома верна не только для игры с отрицательным ожиданием, она истинна также для игры с равными шансами. Поэтому единственный случай, когда у вас есть шанс выиграть в долгосрочной перспективе, — это игра с положительным математическим ожиданием. Кроме того, вы можете выиграть только в двух случаях. Во-первых, при использовании ставки одинакового размера, во-вторых, используя ставки при f, меньшем значения f, соответствующего точке, в которой среднее геометрическое HPR становится равным или меньшим 1. [c.25]
Эта аксиома истинна только при отсутствии верхнего поглощающего барьера. Например, азартный игрок, который начинает со 100 долларов, прекратит играть, если его счет вырастет до 101 доллара. Эта верхняя цель (101 доллар) называется поглощающим барьером. Допустим, игрок всегда ставит 1 доллар на красный цвет рулетки. Таким образом, у него небольшое отрицательное математическое ожидание. У игрока больше шансов увидеть, как его счет вырастет до 101 доллара и он прекратит играть, чем то, что его счет уменьшится до нуля, и он будет вынужден прекратить играть. Если он будет повторять этот процесс снова и снова, то окажется в отрицательном математическом ожидании. Если сыграть в такую игру только раз, то аксиома неизбежного банкротства, конечно же, не применима. Различие между отрицательным ожиданием и положительным ожиданием — это различие между жизнью и смертью. Не имеет значения, насколько положительное или насколько отрицательное ожидание важно только то, положительное оно или
[c.25]
У игрока больше шансов увидеть, как его счет вырастет до 101 доллара и он прекратит играть, чем то, что его счет уменьшится до нуля, и он будет вынужден прекратить играть. Если он будет повторять этот процесс снова и снова, то окажется в отрицательном математическом ожидании. Если сыграть в такую игру только раз, то аксиома неизбежного банкротства, конечно же, не применима. Различие между отрицательным ожиданием и положительным ожиданием — это различие между жизнью и смертью. Не имеет значения, насколько положительное или насколько отрицательное ожидание важно только то, положительное оно или
[c.25]
Допустим, вы начинаете игру с одного доллара, выигрываете при первом броске и зарабатываете два доллара. При следующем броске вы также ставите весь счет (3 доллара), однако на этот раз проигрываете и теряете 3 доллара. Вы проиграли первоначальную сумму в 1 доллар и 2 доллара, которые ранее выиграли. Если вы выигрываете при последнем броске, то зарабатываете 6 долларов, так как сделали 3 ставки по 1 доллару.
 Дело в том, что если вы используете 100% счета, то выйдете из игры, как только столкнетесь с проигрышем, что является неизбежным событием. Если бы мы могли переиграть предыдущий сценарий и вы делали бы ставки без реинвестирования, то выиграли бы 2 доллара при первой ставке и проиграли 1 доллар при второй. Теперь ваша чистая прибыль 1 доллар, а счет равен 2 долларам. Где-то между этими двумя сценариями находится оптимальный выбор ставок при положительном ожидании. Однако сначала мы должны рассмотреть оптимальную стратегию ставок для игры с отрицательным ожиданием. Когда вы знаете, что игра имеет отрицательное математическое ожидание, то лучшей ставкой будет отсутствие ставки. Помните, что нет стратегии управления деньгами, которая может превратить проигрышную игру в выигрышную. Однако если вы должны сделать ставку в игре с отрицательным ожиданием, то наилучшей стратегией будет стратегия максимальной смелости. Другими словами, вам надо сделать как можно меньше ставок (в противоположность игре с положительным ожиданием, где следует ставить как можно чаще).
Дело в том, что если вы используете 100% счета, то выйдете из игры, как только столкнетесь с проигрышем, что является неизбежным событием. Если бы мы могли переиграть предыдущий сценарий и вы делали бы ставки без реинвестирования, то выиграли бы 2 доллара при первой ставке и проиграли 1 доллар при второй. Теперь ваша чистая прибыль 1 доллар, а счет равен 2 долларам. Где-то между этими двумя сценариями находится оптимальный выбор ставок при положительном ожидании. Однако сначала мы должны рассмотреть оптимальную стратегию ставок для игры с отрицательным ожиданием. Когда вы знаете, что игра имеет отрицательное математическое ожидание, то лучшей ставкой будет отсутствие ставки. Помните, что нет стратегии управления деньгами, которая может превратить проигрышную игру в выигрышную. Однако если вы должны сделать ставку в игре с отрицательным ожиданием, то наилучшей стратегией будет стратегия максимальной смелости. Другими словами, вам надо сделать как можно меньше ставок (в противоположность игре с положительным ожиданием, где следует ставить как можно чаще). Чем больше попыток, тем больше вероятность, что при отрицательном ожидании вы проиграете. Поэтому при отрицательном ожидании меньше возможности для проигрыша, если длина игры укорачивается (то есть когда число попыток приближается к 1). Если вы играете в игру, где есть шанс 49% выиграть 1 доллар и 51% проиграть 1 доллар, то лучше всего сделать только одну попытку. Чем больше ставок вы будете делать, тем больше вероятность, что вы проиграете (с вероятностью проигрыша, приближающейся к уверенности, когда игра приближается к бесконечности). Это не означает, что вы достигаете
[c.31]
Чем больше попыток, тем больше вероятность, что при отрицательном ожидании вы проиграете. Поэтому при отрицательном ожидании меньше возможности для проигрыша, если длина игры укорачивается (то есть когда число попыток приближается к 1). Если вы играете в игру, где есть шанс 49% выиграть 1 доллар и 51% проиграть 1 доллар, то лучше всего сделать только одну попытку. Чем больше ставок вы будете делать, тем больше вероятность, что вы проиграете (с вероятностью проигрыша, приближающейся к уверенности, когда игра приближается к бесконечности). Это не означает, что вы достигаете
[c.31] Необходимо отметить, что залог под открытые позиции не имеет ничего общего с тем, какое математически оптимальное количество контрактов надо открывать. Залог не так важен, поскольку размеры отдельных прибылей и убытков не являются продуктом залоговых средств. Прибыли и убытки зависят от выигрыша и убытка в расчете на одну открытую единицу (один фьючерсный контракт). Для управления деньгами залог не имеет значения, так как размер убытка не ограничивается только залоговыми средствами.
 Многие ошибочно полагают, что f является линейной функцией, и чем большей суммой рисковать, тем больше можно выиграть, так как по мнению сторонников такого подхода положительное математическое ожидание является зеркальным отражением отрицательного ожидания, то есть если увеличение общего оборота в игре с отрицательным ожиданием в результате приносит более быстрый проигрыш, то увеличение общего оборота в игре с положительным ожиданием в результате принесет более быстрый выигрыш. Это неправильно. В некоторой точке в ситуации с положительным ожиданием дальнейшее увеличение общего оборота работает против вас. Эта точка является функцией как прибыльности системы, так и ее стабильности (то есть ее средним геометрическим), так как вы реинвестируете прибыли обратно в систему. Когда два человека сталкиваются с одной и той же последовательностью благоприятных ставок или сделок, и один использует оптимальное f, а другой использует любую другую систему управления деньгами, математическим фактом является то, что отношение счета держащего пари на
[c.
Многие ошибочно полагают, что f является линейной функцией, и чем большей суммой рисковать, тем больше можно выиграть, так как по мнению сторонников такого подхода положительное математическое ожидание является зеркальным отражением отрицательного ожидания, то есть если увеличение общего оборота в игре с отрицательным ожиданием в результате приносит более быстрый проигрыш, то увеличение общего оборота в игре с положительным ожиданием в результате принесет более быстрый выигрыш. Это неправильно. В некоторой точке в ситуации с положительным ожиданием дальнейшее увеличение общего оборота работает против вас. Эта точка является функцией как прибыльности системы, так и ее стабильности (то есть ее средним геометрическим), так как вы реинвестируете прибыли обратно в систему. Когда два человека сталкиваются с одной и той же последовательностью благоприятных ставок или сделок, и один использует оптимальное f, а другой использует любую другую систему управления деньгами, математическим фактом является то, что отношение счета держащего пари на
[c. 35]
35]Я подозреваю, что большинство теорий, основанных на эффекте нескольких следующих друг за другом выигрышных и/или проигрышных сделок, проникло в мир торговли из азартных игр. Азартная игра основана на теории полос. Любой профессиональный игрок скажет вам, что невозможно обратить неблагоприятную ситуацию в свою пользу. Таким образом, схемы управления капиталом, которые используют азартные игроки, берут свое начало в сфере управления полосами удач и неудач. Вспомним пример с подбрасыванием монеты и пари с отрицательным ожиданием. В некоторых ситуациях [c.147]
Приведем интересный сценарии. Я все время напоминаю, что никакой метод управления капиталом не может превратить отрицательное ожидание в положительное. Это абсолютно верное замечание. Математических доказательств этому утверждению нет. Однако это не означает, что такое не может произойти. В азартных играх участник может выйти на полосу выигрышей и просто прекратить игру. Такой человек оказывается победителем. Торговлю с использованием скользящей средней капитала нельзя сравнивать с азартной игрой. Но в некоторых ситуациях использование этого метода может дать положительные результаты, даже если система и/или метод приводят к убыткам по всем сделкам. Трейдеры стараются не торговать на некоторых рынках и избегают некоторых методов, потому что опасаются потерять деньги. При этом ожидания могут быть вполне положительными. Независимо оттого, насколько положительными могут быть ожидания, используемый метод или система не всегда следуют одному и тому же правилу. Рассмотрим следующий торговый поток [c.163]
Но в некоторых ситуациях использование этого метода может дать положительные результаты, даже если система и/или метод приводят к убыткам по всем сделкам. Трейдеры стараются не торговать на некоторых рынках и избегают некоторых методов, потому что опасаются потерять деньги. При этом ожидания могут быть вполне положительными. Независимо оттого, насколько положительными могут быть ожидания, используемый метод или система не всегда следуют одному и тому же правилу. Рассмотрим следующий торговый поток [c.163]
Трейдеру необходимо иметь понятие о математическом ожидании. В зависимости от того, у кого математическое преимущество в игре, оно называется либо преимуществом игрока — положительное ожидание, либо преимуществом игорного дома — отрицательное ожидание. Допустим, мы играем с вами в орла-или-решку. Ни у вас, ни у меня нет преимущества у каждого 50% шансов на выигрыш. Но если мы перенесем эту игру в казино, которое снимает 10% с каждого кона, то вы выиграете только 90 центов на каждый проигранный доллар. Это преимущество игорного дома оборачивается для вас как игрока отрицательным математическим ожиданием. И ни одна система контроля над капиталом не может одолеть игру с отрицательным ожиданием.
[c.278]
Это преимущество игорного дома оборачивается для вас как игрока отрицательным математическим ожиданием. И ни одна система контроля над капиталом не может одолеть игру с отрицательным ожиданием.
[c.278]
Кстати, игры с нулевым математическим ожиданием обладают отрицательным ожиданием полезности, так как полезность прироста меньше ущерба от возможного убытка аналогичной суммы. Это будет хорошо видно в материале главы, посвященной психологии. [c.125]
Для красных PL = 0,04, a AL = 3 поэтому PL xAL = 0,04 х 3 = 0,12. Сложив их, получим 0,5 + 0,2 + 0,12 = 0,82. Это сумма всех отрицательных ожиданий игры. [c.159]
И наконец, общее ожидание для игры равно разности этих двух сумм. Мы найдем эту разность, вычтя сумму отрицательных ожиданий (0,82) из суммы положительных ожиданий (1,6). Ответ равен 0,78. Таким образом, в этой игре в результате многих извлечений шаров вы можете ожидать выигрыша, равного 78 центам на каждый вложенный в игру доллар или на каждый доллар риска. Отметим, что эта игра почти в четыре раза более прибыльна, чем первая игра.
[c.159]
Отметим, что эта игра почти в четыре раза более прибыльна, чем первая игра.
[c.159]
Большинство полагает, что основное назначение входных сигналов состоит в том, чтобы улучшить выбор подходящего момента для открытия позиций и тем самым повысить надежность вашей системы. По моей оценке, не менее 95% людей, пытающихся изобрести системы трейдинга, просто пытаются найти замечательный входной сигнал. Фактически трейдеры почти всегда говорят мне о своих краткосрочных системах, имеющих коэффициент надежности не менее 60%. Но при этом их удивляет, почему они не зарабатывают денег. Если вы начали читать книгу не с этой главы, то должны знать, что система с высоким процентом выигрышей может все же иметь отрицательное ожидание. Ключ к зарабатыванию денег состоит в том, чтобы иметь систему с высоким положительным ожиданием, и в том, чтобы использовать такую модель установления размера позиции, которая при данном показателе ожидания позволит вам все же не выходить из игры. Вход составляет лишь малую часть игры в зарабатывание денег на рынке. И все же следует затратить определенную энергию, чтобы найти такие входы (правила входа), которые отвечают вашим целям. Для решения этой задачи существует два подхода.
[c.217]
И все же следует затратить определенную энергию, чтобы найти такие входы (правила входа), которые отвечают вашим целям. Для решения этой задачи существует два подхода.
[c.217]
Не один раз краткосрочные трейдеры звонили мне по телефону с заявлениями типа Я дэй-трейдер. Вхожу в рынок и выхожу из него по нескольку раз в день. И почти каждый день зарабатываю деньги. Это замечательно Но за один вчерашний день я потерял почти годовую прибыль и очень этим расстроен . Это явно психологическая проблема. Такие ошибки возникают в результате грубых промахов при трейдинге либо психологических просчетов, связанных с игрой при отрицательном ожидании. В такой игре выигрыши идут почти посто- [c.305]
Важно помнить, что исторически ваш проигрыш может быть такой же большой, как и процент f (в смысле возможного уменьшения баланса). В действительности вам следует ожидать, что в будущем он будет выше, чем данное значение. Это означает, что комбинация двух рыночных систем, даже если они имеют отрицательную корреляцию, может привести к уменьшению баланса на 44%. Это больше, чем в системе с положительным математическим ожиданием, в которой оптимальное f= 0,25, и поэтому максимальный исторический проигрыш уменьшит баланс только на 25%. Мораль такова диверсификация, если она произведена правильно, является методом, который повышает прибыли. Она не обязательно уменьшает проигрыши худшего случая, что абсолютно противоречит популярному представлению. Диверсификация смягчает многие мелкие проигрыши, но она не уменьшает проигрыши худшего случая. При оптимальном f максимальные проигрыши могут быть существенно больше, чем думают многие. Поэтому, даже если вы хорошо диверсифицировали портфель, следует быть готовым к значительным уменьшениям баланса. Однако давайте вернемся и посмотрим на результаты, когда коэффициент корреляции между двумя играми равен 0. В такой ситуации, какими бы ни были результаты одного броска, они не влияют на результаты другого броска. Таким образом, есть четыре возможных результата [c.49]
Это больше, чем в системе с положительным математическим ожиданием, в которой оптимальное f= 0,25, и поэтому максимальный исторический проигрыш уменьшит баланс только на 25%. Мораль такова диверсификация, если она произведена правильно, является методом, который повышает прибыли. Она не обязательно уменьшает проигрыши худшего случая, что абсолютно противоречит популярному представлению. Диверсификация смягчает многие мелкие проигрыши, но она не уменьшает проигрыши худшего случая. При оптимальном f максимальные проигрыши могут быть существенно больше, чем думают многие. Поэтому, даже если вы хорошо диверсифицировали портфель, следует быть готовым к значительным уменьшениям баланса. Однако давайте вернемся и посмотрим на результаты, когда коэффициент корреляции между двумя играми равен 0. В такой ситуации, какими бы ни были результаты одного броска, они не влияют на результаты другого броска. Таким образом, есть четыре возможных результата [c.49]
Отметьте, что в этом примере ставки как после выигрышей, так и после проигрышей все еще имеют положительное математическое ожидание. Что произойдет, если после проигрыша вероятность выигрыша будет равна 0,3 В таком случае математическое ожидание имеет отрицательное значение и оптимального f не существует, таким образом, вам не следует использовать эту игру (1.03) МО=(0,3 2)+(0,7 -1) =0,6-0,7 =-0,1
[c.64]
Что произойдет, если после проигрыша вероятность выигрыша будет равна 0,3 В таком случае математическое ожидание имеет отрицательное значение и оптимального f не существует, таким образом, вам не следует использовать эту игру (1.03) МО=(0,3 2)+(0,7 -1) =0,6-0,7 =-0,1
[c.64]
Как мы уже знаем (см. главу 2), добавление рыночных систем увеличивает среднее геометрическое по портфелю в целом. Однако возникает проблема каждая следующая рыночная система вносит все меньший и меньший вклад в среднее геометрическое и все больше ухудшает его, понижая эффективность из-за одновременных, а не последовательных результатов. Поэтому не следует торговать слишком большим числом рыночных систем. Более того, реальное применение теоретически оптимальных портфелей осложняется из-за залоговых требований. Другими словами, вам лучше торговать 3 рыночными системами при полном оптимальном f, чем 300 рыночными системами при значительно пониженных уровнях, согласно уравнению (8.08). Скорее всего вы придете к выводу, что оптимальное число рыночных систем для торговли должно быть невелико. Особенно это обстоятельство важно, когда у вас много ордеров к исполнению и увеличивается вероятность ошибок. Если одна или несколько рыночных систем в портфеле имеют оптимальные веса больше единицы, может возникнуть еще одна проблема. Рассмотрим рыночную систему с оптимальным f=0,8 и наибольшим проигрышем, составляющим 4000 долларов. Для этой рыночной системы f = 5000 долларов. Давайте предположим, что оптимальный вес данного компонента в портфеле равен 1,25, поэтому вы будете торговать одной единицей компонента на каждые 4000 долларов ( 5000/1,25) баланса счета. Как только компонент столкнется с наибольшим проигрышем, весь активный баланс на счете будет обнулен, если прибылей в других рыночных системах не хватит для сохранения активного баланса. Рассмотренная проблема наиболее актуальна для систем, которые редко генерируют сделки. Если бы у нас были две рыночные системы с отрицательной корреляцией и положительным ожиданием, необходимо было бы открывать бесконечное количество контрактов на рынке.
Особенно это обстоятельство важно, когда у вас много ордеров к исполнению и увеличивается вероятность ошибок. Если одна или несколько рыночных систем в портфеле имеют оптимальные веса больше единицы, может возникнуть еще одна проблема. Рассмотрим рыночную систему с оптимальным f=0,8 и наибольшим проигрышем, составляющим 4000 долларов. Для этой рыночной системы f = 5000 долларов. Давайте предположим, что оптимальный вес данного компонента в портфеле равен 1,25, поэтому вы будете торговать одной единицей компонента на каждые 4000 долларов ( 5000/1,25) баланса счета. Как только компонент столкнется с наибольшим проигрышем, весь активный баланс на счете будет обнулен, если прибылей в других рыночных системах не хватит для сохранения активного баланса. Рассмотренная проблема наиболее актуальна для систем, которые редко генерируют сделки. Если бы у нас были две рыночные системы с отрицательной корреляцией и положительным ожиданием, необходимо было бы открывать бесконечное количество контрактов на рынке. Когда один из компонентов проигрывает, другой выигрывает равную или большую сумму. Таким образом, мы получаем прибыль в каждой игре, однако только в том случае, когда рыночные системы ведут игру одновременно. Рассматриваемая же торговля аналогична гипотетической ситуации, когда один из компонентов в игре не активен, но используется другая рыночная система с бесконечным числом контрактов. Проигрыш может быть катастрофическим. Проблему можно решить следующим образом разделите единицу на наибольший вес компонента портфеля и используйте полученное значение в качестве верхней границы активного баланса, если оно меньше, чем значение, найденное из уравнения (8.08). В таком случае, если в будущем произойдет проигрыш той же величины, что и наибольший проигрыш (на основе которого рассчитано f), мы не потеряем все деньги. Например, наибольший вес компонента в нашем портфеле составляет 1,25. Если значение из уравнения (8.08) будет больше 1 / 1,25 = 0,8, следует использовать 0,8 в качестве верхней границы для доли активного баланса.
Когда один из компонентов проигрывает, другой выигрывает равную или большую сумму. Таким образом, мы получаем прибыль в каждой игре, однако только в том случае, когда рыночные системы ведут игру одновременно. Рассматриваемая же торговля аналогична гипотетической ситуации, когда один из компонентов в игре не активен, но используется другая рыночная система с бесконечным числом контрактов. Проигрыш может быть катастрофическим. Проблему можно решить следующим образом разделите единицу на наибольший вес компонента портфеля и используйте полученное значение в качестве верхней границы активного баланса, если оно меньше, чем значение, найденное из уравнения (8.08). В таком случае, если в будущем произойдет проигрыш той же величины, что и наибольший проигрыш (на основе которого рассчитано f), мы не потеряем все деньги. Например, наибольший вес компонента в нашем портфеле составляет 1,25. Если значение из уравнения (8.08) будет больше 1 / 1,25 = 0,8, следует использовать 0,8 в качестве верхней границы для доли активного баланса. Если первоначальная доля активного баланса небольшая, вышеописанная проблема может и не возникнуть, однако более агрессивному трейдеру следует всегда принимать ее во внимание. Альтернативное решение состоит в введении дополнительных ограничений в матрице портфеля (например, для каждой рыночной системы можно ограничить максимальные веса единицей и ввести дополнительные ограничения по залоговым средствам). Подобные дополнительные ограничения
[c.241]
Если первоначальная доля активного баланса небольшая, вышеописанная проблема может и не возникнуть, однако более агрессивному трейдеру следует всегда принимать ее во внимание. Альтернативное решение состоит в введении дополнительных ограничений в матрице портфеля (например, для каждой рыночной системы можно ограничить максимальные веса единицей и ввести дополнительные ограничения по залоговым средствам). Подобные дополнительные ограничения
[c.241]
Заметьте, что оптимальное /, доставляющее максимум роста, одинаково для всех конов игры, хотя и является функцией того, как долго вы будете играть. Если вы собираетесь остановиться после первого кона, то оптимальное / максимизирует среднее арифметическое HPR (для игры с положительным математическим ожиданием это/всегда равно 1,0, а игры с отрицательным математическим ожиданием — 0,0). Для игры с положительным математическим ожиданием оптимальное/убывает по мере увеличения времени до остановки (асимптотически убывает для бесконечной игры) и максимизирует среднее геометрическое HPR. Для игры с отрицательным математическим ожиданием оптимальное / всегда остается нулевым.
[c.106]
Для игры с отрицательным математическим ожиданием оптимальное / всегда остается нулевым.
[c.106]
Это — классический пример азартной игры, где участники пытаются воспользоваться сериями. Единственный случай, который приводит их к проигрышу при таком подходе, — это когда в серии наблюдается 6 одинаковых выпадений подряд. Тем не менее здесь все же не обеспечивается положительное математическое ожидание. С математической точки зрения мы обсудим серии несколько позже. Сейчас же, как я думаю, будет достаточно рассказать вам о том, каким образом повела себя следующая серия, состоящая из 100 подбрасываний. У меня получилось 9 серий из 3 орлов или решек подряд. Однако только четыре из них дали противоположный результат при четвертом подбрасывании. В этих 4 сериях выигрыши составили 16 долларов. Только одна серия дала противоположный результат после пятого подбрасывания монеты. Она добавила еще 3 доллара выигрыша, общая сумма которого составила 19 долларов. Две серии закончились после шести одинаковых выпадений подряд и обеспечили еще по 1 доллару, что привело к совокупному итогу в 21 доллар. Были также еще две серии, которые давали подряд 6 орлов или решек. В результате каждая из этих двух серий принесла убыток в размере 35 долларов. Это привело к тому, что общая сумма выигрыша по итогу второй группы серий была отрицательной (49 долларов), и общий результат после двух
[c.27]
Были также еще две серии, которые давали подряд 6 орлов или решек. В результате каждая из этих двух серий принесла убыток в размере 35 долларов. Это привело к тому, что общая сумма выигрыша по итогу второй группы серий была отрицательной (49 долларов), и общий результат после двух
[c.27]
Может показаться, что эта тема является неуместной в книге по управлению капиталом. Тем не менее косвенным образом она тесно связана с вопросами, рассматриваемыми в этом издании. Управление капиталом без метода или системы торговли попросту бесполезно. Помимо этого, использование в торговле метода с отрицательным математическим ожиданием тоже бесполезно. Таким образом, метод или торговая система должны давать деньги для того, чтобы в игру вступили факторы роста, ведущие происхождение от управления капиталом и позволяющие получить хорошие конечные результаты. Откройте любой журнал по торговле и вы найдете там больше торговых систем и методов, чем сумеете опробовать. Все они кажутся великолепными, и большинство из них, как утверждается, являются самыми лучшими способами создания денег. Помимо всего прочего, основой для большинства таких утверждений являются гипотетические результаты. Как-то раз я получил «рассылку», автор которой утверждал, что он «превратил» 200 долларов в 18.000.000 долларов (здесь нет ошибки — в 18 миллионов долларов) за какие-то несколько лет. Там же говорилось, что вы тоже сумеете это сделать, приобретя книгу за 39,95 доллара и прочитав о невероятном методе, описанном в ней. (За небольшую плату я скажу вам, что собой представляет эта книга). Дело в том, что большинство этих гипотетических результатов появляется только после проведения значительного оптимизационного тестирования представляемого метода. Если управление капиталом сложным образом связано с системой или методами, используемыми в торговле, то гипотетические результаты становятся особенно важны в момент принятия решения о том, стоит ли пользоваться данным методом или системой.
[c.188]
Помимо всего прочего, основой для большинства таких утверждений являются гипотетические результаты. Как-то раз я получил «рассылку», автор которой утверждал, что он «превратил» 200 долларов в 18.000.000 долларов (здесь нет ошибки — в 18 миллионов долларов) за какие-то несколько лет. Там же говорилось, что вы тоже сумеете это сделать, приобретя книгу за 39,95 доллара и прочитав о невероятном методе, описанном в ней. (За небольшую плату я скажу вам, что собой представляет эта книга). Дело в том, что большинство этих гипотетических результатов появляется только после проведения значительного оптимизационного тестирования представляемого метода. Если управление капиталом сложным образом связано с системой или методами, используемыми в торговле, то гипотетические результаты становятся особенно важны в момент принятия решения о том, стоит ли пользоваться данным методом или системой.
[c.188]
Большинство игроков погибают от одной из двух пуль от невежества или от эмоций. Любители играют по интуиции и заключают такие сделки, которые не следует заключать никогда из-за отрицательного математического ожидания. Те, кто переживает стадию исходного невежества, начинает строить более приемлемые системы игры. Когда они становятся более уверенными, они высовывают голову из окопа, и вторая пуля поражает их Уверенность делает их жадными, они рискуют слишком большой суммой в одной сделке, и короткая череда неудач выметает их с рынка.
[c.149]
Те, кто переживает стадию исходного невежества, начинает строить более приемлемые системы игры. Когда они становятся более уверенными, они высовывают голову из окопа, и вторая пуля поражает их Уверенность делает их жадными, они рискуют слишком большой суммой в одной сделке, и короткая череда неудач выметает их с рынка.
[c.149]
Система удвоения выглядит беспроигрышной до того момента, когда вы сообразите, что длинная полоса неудач разорит любого игрока, сколь бы богат он ни был. Игрок, начавший с 1 доллара и проигравший 46 раз, должен поставить 47-ю ставку в 70 триллионов долларов, а это больше, чем стоимость всего мира (примерно 50 триллионов). Ясно, что намного раньше у него кончатся деньги или он упрется в ограничения казино. Система удвоения бесполезна, если у вас отрицательное или нулевое математическое ожидание. Она самоубийственна, если у вас хорошая система игры и положительное математическое ожидание. [c.150]
Игра с отрицательным математическим ожиданием
[c. 164]
164]
Дополнительно к этому отметим, что неприглядная роль спрэда усугубляется еще и тем, что из-за него не только возникает неблагоприятное соотношение вероятностей успеха и неудачи , но и становится отрицательным средний итог игры, т.е. математическое ожидание результата. [c.122]
В бесконечном продолжении такая игра является бесперспективной (потому что математическое ожидание имеет отрицательное значение). Но при ограниченном числе серий вероятность выйти победителем достаточно убедительна (вероятность достижения 0,79). [c.126]
Большинство трейдеров гибнут от одной из двух пуль это незнание и эмоции. Профаны играют по наитию, ввязываясь в сделки, которые им — вследствие отрицательного математического ожидания — следовало бы пропустить. Если они выживают, то, подучившись, начинают разрабатывать системы поумнее. Затем, уверившись в себе, они высовывают голову из окопа — и попадают под вторую пулю От самонадеянности они ставят слишком много на одну сделку и вылетают из игры после короткой вереницы потерь. [c.281]
[c.281]
Здесь мы видим, что математическое ожидание игры в рулетку при игры на красное-черное отрицательное и равно -0.0526. Данную игру, таким образом, можно назвать невыгодной. Произошло это по причине наличия среди игровых полей двух зеро, при выпадении которых наш жетон забирает в свою пользу казино. В принципе, именно зеро и является прямым доходом казино во всех играх в рулетку. [c.172]
В играх с отрицательным математическим ожиданием не имеется никакой схемы управления деньгами, которая сделает вас победителем [c.172]
Эмоциональность оказывает самое непосредственное влияние на финансовый результат, получаемый инвестором н в большей степени игроком от финансовых спекуляций. И чем эмоциональней поведение человека, тем значительней будет отклонение математического ожидания финансовых результатов его торговли от реальности. Для азартных игр, обладающих отрицательным математическим ожиданием финансовые результаты, полученные под влиянием эмоций, будут выглядеть как это показано на нижеприведенном рисунке. [c.263]
[c.263]
У вас может возникнуть закономерный вопрос а каково математическое ожидание финансовых игр С одной стороны, эти игры обладают всеми внешними атрибутами азартных игр — спрэд и комиссионные являются своеобразными аналогами зеро рулетки. Это дает основание говорить об отрицательном математическом ожидании. Однако финансовые игры имеют одно кардинальное отличие от азартных игр — главным действующим лицом в них является не господин случай, а человек. Если поведение человека прогнозируемо и подчиняется определенным закономерностям, то и рынок может быть прогнозируемым. [c.113]
Из этого раздела можно сделать два вывода. Первый состоит в том, что при одновременных ставках или торговле портфелем существует небольшая потеря эффективности, вызванная невозможностью рекапитализировать счет после каждой отдельной игры. Второй заключается в том, что комбинирование рыночных систем, при условии, что они имеют положительные математические ожидания (даже если они положительно коррелированы), никогда не уменьшит ваш общий рост за определенный период времени. Однако когда вы продолжаете добавлять все больше и больше рыночных систем, эффективность уменьшается. Если у вас есть, скажем, 10 рыночных систем, и все они одновременно несут убытки, совокупный убыток может уничтожить весь счет, так как вы не сможете уменьшить размер каждого проигрыша, как в случае последовательных сделок. Таким образом, при добавлении новой рыночной системы в портфель польза будет только в двух случаях когда рыночная система имеет коэффициент корреляции меньше 1 и положительное математическое ожидание или же когда система имеет отрицательное ожидание, но достаточно низкую корреляцию с другими составляющими портфеля, чтобы компенсировать отрицательное ожидание. Каждая добавленная рыночная система вносит постепенно уменьшающийся вклад в среднее геометрическое. То есть каждая новая рыночная система улучшает среднее геометрическое все в меньшей и меньшей степени. Более того, когда вы добавляете новую рыночную систему, теряется общая эффективность из-за одновременных, а не последовательных результатов.
Однако когда вы продолжаете добавлять все больше и больше рыночных систем, эффективность уменьшается. Если у вас есть, скажем, 10 рыночных систем, и все они одновременно несут убытки, совокупный убыток может уничтожить весь счет, так как вы не сможете уменьшить размер каждого проигрыша, как в случае последовательных сделок. Таким образом, при добавлении новой рыночной системы в портфель польза будет только в двух случаях когда рыночная система имеет коэффициент корреляции меньше 1 и положительное математическое ожидание или же когда система имеет отрицательное ожидание, но достаточно низкую корреляцию с другими составляющими портфеля, чтобы компенсировать отрицательное ожидание. Каждая добавленная рыночная система вносит постепенно уменьшающийся вклад в среднее геометрическое. То есть каждая новая рыночная система улучшает среднее геометрическое все в меньшей и меньшей степени. Более того, когда вы добавляете новую рыночную систему, теряется общая эффективность из-за одновременных, а не последовательных результатов. В некоторой точке добавление еще одной рыночной системы принесет больше вреда, чем пользы.
[c.67]
В некоторой точке добавление еще одной рыночной системы принесет больше вреда, чем пользы.
[c.67]
Согласно этому методу, по мере уменьшения суммы счета размер последующей торговли увеличивается. Базовая концепция метода Мартингейл строится на том, что по мере уменьшения суммы в результате убытков возможность компенсации потерь либо увеличивается, либо остается прежней. Это популярный тип управления капиталом для игроков в азартные игры. Как сказано во второй главе, никакой тип управления капиталом не может превратить сценарий с «отрицательным ожиданием» в сценарий с «положительным ожиданием». Поэтому игроки не пытаются изменить шансы, они стараются воспользоваться сериями. Рассмотрим следующий пример. [c.26]
В случае ожидания резкого скачкообразного изменения курса валюты несбалансированность спроса и предложения на нее в любом случае будет вызвана нормальными операциями по покрытию рисков продажа поступлений и отсутствие сделок по покупке валюты, в отношении которой ожидаются обесценение, хеджирование риска вложений в этой валюте. Опережения и задержки ( лидз энд лэгз ) по валютным расчетам и валютным сделкам достигают миллиардных сумм и вызывают огромное давление на курс. Спекулятивные валютные сделки могут многократно усилить такие воздействия. Игра на повышение и понижение курса валют дезорганизует валютный рынок, нарушает равновесие между спросом и предложением валюты, отрицательно влияет на валютно-экономическое положение соответствующих стран и мировую валютную систему.
[c.360]
Опережения и задержки ( лидз энд лэгз ) по валютным расчетам и валютным сделкам достигают миллиардных сумм и вызывают огромное давление на курс. Спекулятивные валютные сделки могут многократно усилить такие воздействия. Игра на повышение и понижение курса валют дезорганизует валютный рынок, нарушает равновесие между спросом и предложением валюты, отрицательно влияет на валютно-экономическое положение соответствующих стран и мировую валютную систему.
[c.360]
Normal Distribution — нормальное распределение распределение вероятностей случайной величины X, возникающее обычно, когда X представляет собой сумм большого числа независимых случайных величин, каждая из которых играет в образовании всей суммы незначительную роль. Нормальное распределение унимодально, описывается колоколообразной кривой его средняя (математическое ожидание) совпадает с модой. Н.р. широко используется в математической статистике. Предпосылка Н.р. учитывается в большинстве критериев статистической проверки гипотез. Математики считают, что Н.р. в экономике во многих случаях неприменимо например, вряд ли можно себе представить его в модели ценообразования, тогда в нее вошли бы также отрицательные цены.
[c.35]
Математики считают, что Н.р. в экономике во многих случаях неприменимо например, вряд ли можно себе представить его в модели ценообразования, тогда в нее вошли бы также отрицательные цены.
[c.35]
По отношению к личности группа может играть как положительную, так и отрицательную роль. Если группа обеспечивает удовлетворение потребностей личности, а установленный группой статус соответствует ожиданиям личности, это можно считать положительным моментом в ее развитии (профессиональном, социальном, культурном, физическом и т. д.). Если этого не наблюдается, возможна деградация личности, искажение развития, конфликт между личностью и группой. Это отмечали немецкие ученые В. Зигерт и Л. Ланг, особенно для личности, находящейся на стадии удовлетворения потребностей в уважении и самореализации. [c.112]
У игроков в рулетку математическое ожидание отрицательное. На колесе американской рулетки 38 ячеек, на европейском — 37, но в обоих случаях в игре участвует только 36. Одну или две ячейки оставляет за собой казино. Поскольку одна ячейка — это примерно 2,7% колеса рулетки, именно такой процент хозяева казино кладут себе в карман в среднем с каждой сделки, медленно выкачивая деньги из клиентов. Есть примитивная система управления капиталом, называемая мартингал (martingale) игрок начинает с минимальной ставки, обычно с 1 доллара, и после каждого проигрыша удваивает ставку. Теоретически он рано или поздно должен выиграть и тогда получит обратно все проигранное плюс один доллар. После этого он опять может сделать минимальную ставку и начать сначала. В реальной жизни системой мартингал воспользоваться нельзя, так как казино ограничивают максимальную ставку. Как только
[c.236]
Поскольку одна ячейка — это примерно 2,7% колеса рулетки, именно такой процент хозяева казино кладут себе в карман в среднем с каждой сделки, медленно выкачивая деньги из клиентов. Есть примитивная система управления капиталом, называемая мартингал (martingale) игрок начинает с минимальной ставки, обычно с 1 доллара, и после каждого проигрыша удваивает ставку. Теоретически он рано или поздно должен выиграть и тогда получит обратно все проигранное плюс один доллар. После этого он опять может сделать минимальную ставку и начать сначала. В реальной жизни системой мартингал воспользоваться нельзя, так как казино ограничивают максимальную ставку. Как только
[c.236]
Эта интерпретация U — U (7) как полезности, приписываемой конкретному риску, непосредственно соотносится с вопросом, которому фон Нейман и Моргенштерн и комментаторы их работы уделили много внимания, а именно, вопросу, может ли человек распознавать полезность (положительную или отрицательную) простого акта риска», азартной игры, ведь полезность не учитывается при использовании математического ожидания (von Neumann and Morgenstern. Op. it. P. 28 рус. изд. С. 58). С нашей точки зрения, гипотезу лучше интерпретировать как довольно нестандартное объяснение того, почему азартные игры имеют для потребительской единицы полезность или вредность, и ее лучше интерпретировать как дающую конкретную меру полезности или вредности, чем как отрицание того, что азартные игры имеют полезность (см. там же, стр. 28, 629—632 рус. изд. С. 58, 626—630).
[c.225]
Op. it. P. 28 рус. изд. С. 58). С нашей точки зрения, гипотезу лучше интерпретировать как довольно нестандартное объяснение того, почему азартные игры имеют для потребительской единицы полезность или вредность, и ее лучше интерпретировать как дающую конкретную меру полезности или вредности, чем как отрицание того, что азартные игры имеют полезность (см. там же, стр. 28, 629—632 рус. изд. С. 58, 626—630).
[c.225]
Например. Так, рассчитаем математическое ожидание игры в рулетку, если играть только на красное-черное . Прн это задано, что всего 38 игровых полей — 36 цифр (по 18 красных и черных полей), а также два зеро . Таким образом, вероятность выигрыша при ставке на красное или черное составляет приблизительно 0.4737 (18/38). В случае положительного исхода ставки мы получаем 1 жетон, а в случае неудачи теряем один жетон. Отсюда имеем отрицательное матожндание [c.172]
Как правило, любые игры с денежным выигрышем, будь это лотерея, ставки на ипподроме и в букмекерских конторах, игральные автоматы и т. п., являются играми с отрицательным математическим ожиданием. Поэтому участие в любой из них нельзя расценивать как источник стабильного дохода.
[c.172]
п., являются играми с отрицательным математическим ожиданием. Поэтому участие в любой из них нельзя расценивать как источник стабильного дохода.
[c.172]
Ответ мы найдем у тех же рыночных участников. В любой сделке неизменно участвуют две стороны — покупатель н продавец. То, что хорошо для покупателя, как правило, ие хорошо для продавца и наоборот. Я здесь не рассматриваю случаи вынужденной продажи, к которой могут прибегать инвесторы, нуждающиеся в деньгах, импортеры и экспортеры в другой валюте, хеджеры в конкретном товаре и т.д. Тогда можно рассчитать, что максимальное положительное математическое ожидание покупателя на уровне поддержки является максимальным отрицательным матожиданием для продавца. Вряд ли вы найдете много таких продавцов. Скорее всего это будут или недальновидные игроки, или вынужденные рыночные участники. Таким образом, наибольшие объемы сделок действительно будут находиться в зонах, где матожидания прибыли покупателей н продавцов будут как можно больше совпадать.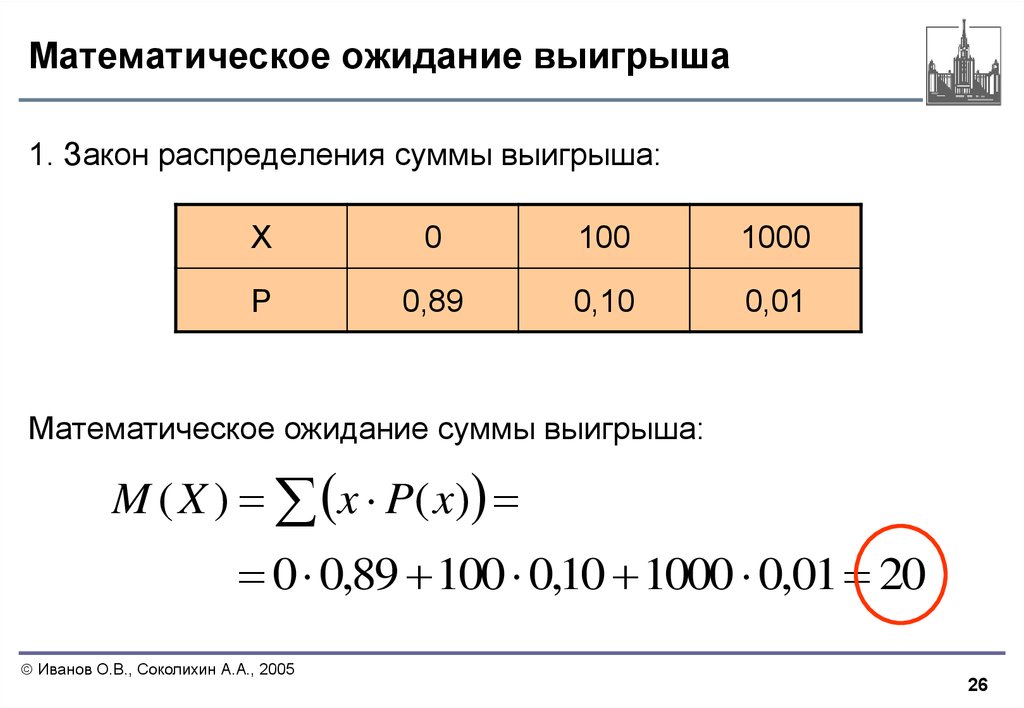 Небольшую подвижку в значениях матожиданий будет играть разница в оценках уровней сопротивления и поддержки, присущая разным рыночным участникам.
[c.176]
Небольшую подвижку в значениях матожиданий будет играть разница в оценках уровней сопротивления и поддержки, присущая разным рыночным участникам.
[c.176]
Отрицательное математическое ожидание и теория вероятности в трейдинге = стратегия «Светофор» — Екатерина Игоревна Шевченко на vc.ru
В трейдинге надо осознать, что ваша стратегия не так важна, как вы думаете. Чертовски большое значение имеет ваше управление рисками.
355 просмотров
Вы можете думать, что вложения в акции или монеты — это тот самый ключ к славе и богатству. Но ниже я расскажу вам, почему это не так и почему вы должны больше заботиться не о входе в актив, а о сбережении прибыли, которая у вас уже есть на данный момент.
Вы можете ошибиться независимо от того, насколько хороши вы или ваши сигналы при выборе компаний, которые изменят мир через пять лет. И вы будете часто ошибаться. Вам придётся переживать периоды потери денег (так называемые просадки). Забудьте про стабильность: рынок не будет платить вам зарплату.
На рынке действует правило отрицательного математического ожидания. Биржи существуют за счет проигравших. Зачем же тогда так много людей стремятся на ней заработать. Изобретают индикаторы, выстраивают стратегии. В конечном итоге все-таки зарабатывают.
Тут начинается теория вероятностей.
Теория вероятностей зародилась в XVII веке, когда Гэмблер (профессиональный игрок в азартные игры) и писатель Антуан Гомбо начал терять деньги и обратился за советом к блестящему французскому математику Блейзу Паскалю. Гомбо зарабатывал на игре в кости и любил называть себя шевалье де Мере. Вскоре жадность взяла над ним верх. Он решил, что сможет заработать больше, если удвоит ставки. И оказался неправ. Так описали этот случай:
Внезапно он потерял деньги! Де Мере был ошеломлён. Он рассуждал, что вероятность получить две «единицы» в двух бросках — 1/6 от вероятности получить одну в одном броске. Чтобы компенсировать эту меньшую вероятность, две кости должны быть брошены шесть раз. Наконец, чтобы достичь вероятности одной «единицы» в четырёх бросках, количество бросков должно быть увеличено в четыре раза.
Наконец, чтобы достичь вероятности одной «единицы» в четырёх бросках, количество бросков должно быть увеличено в четыре раза.
Дальше идёт более сложная математика, которая, по сути, сводится к тому, что он увеличил риск и уменьшил шансы на победу, выбрав два кубика и увеличив количество бросков. Де Мере не понимал математику игры.
«Не фокусируйтесь на увеличении прибыли; фокусируйтесь на сохранении того, что у вас есть». Задумайтесь об этом на секунду.
Вы слышали о диверсификации активов («не кладите все яйца в одну корзину»), которая поможет справиться с просадкой. Ведь если риски слишком большие, вы можете обесценить весь свой портфель, и игра для вас закончится.
Я не буду углубляется в математику и расскажу о стратегии, которую я создала из своего собственного понимания теории вероятности и отрицательного математического ожидания.
Во-первых, у рынка есть только три постоянных состояния. Движение вниз, движение вверх или флет это когда цена практически не куда не двигается. Цена на актив; валютная пара, акция, индексы, криптовалюта, сырьевые активы, металлы. Цена всегда находится в этих трех состояниях. Это константа.
Цена на актив; валютная пара, акция, индексы, криптовалюта, сырьевые активы, металлы. Цена всегда находится в этих трех состояниях. Это константа.
Во-вторых, все индикаторы, которые есть всегда дают серию ложных сигналов и серию правдивых сигналов. Это серии могут длится очень долго.
В-третьих, нужно учитывать объёмы нет больших объёмов нет качественного движения актива в одну сторону вверх или вниз.
В-четвертых, используя тот или иной индикатор мы его должны использовать так, как его задумал автор Болинжер, Вильямс и др. При этом мы не понимаем до самого конца и мельчайших деталях всю его работу, и поэтому ошибаемся даже тогда, когда используем 3 индикатора сразу. Не понимая и не учитывая какие-либо иные факторы новостные, например, или внезапного импульсного движения. Так не лучше ли создать свою стратегию на основе своего понимания рынка его движения и работе индикатора.
Моя стратегия называется «Светофор»
Для построения графика я использую простую и понятную для начиняющих и мощную для экспертов в тех. анализе платформу TradingView, располагает всеми инструментами для создания и просмотра торговых идей. Котировки в реальном времени и графики в браузере позволяю делать прогнозы и следить за рынками. Валютная пара EURCAD.
анализе платформу TradingView, располагает всеми инструментами для создания и просмотра торговых идей. Котировки в реальном времени и графики в браузере позволяю делать прогнозы и следить за рынками. Валютная пара EURCAD.
График Trading View Екатерина Шевченко
Как видно на графике сначала идет полнейший флет (отмечен прямоугольником) потом цена двинулась вниз потом вверх. Многие это использую и заходят в сделку. Не плохой момент сам по себе для входа в рынок, но дальше выстраивается коридор, по которому движется цена, индикатор даёт серию ложных сигналов (отмечены красным дислайком) как красный сигнал светофора.
Увеличенное изображение.
График Trading View Екатерина Шевченко
На индикаторе Светофор, на TradingView он называется Tabajara traffic lights все точки одновременно становятся красными. Но последующая после свеча противоположного цвета. Объёмы при этом возрастают. Появляется желтый сигнал светофора при этом свеча которая дала этот сигнал, и свеча, которая идет после нее, того же самого цвета. Это и есть тот же самый желтый сигнал при его повторении выстраивании всех точек одного цвета, я и захожу в сделку после повтора этого сигнала. и получаю профит (отмечено зеленым флажком). Это и есть зеленый сингал светофора.
Это и есть тот же самый желтый сигнал при его повторении выстраивании всех точек одного цвета, я и захожу в сделку после повтора этого сигнала. и получаю профит (отмечено зеленым флажком). Это и есть зеленый сингал светофора.
Таймфрейм ( время формирования свечи) я использую 1минуту, 5 минут, 15 минут. 30 минут или час.
Сделки я открываю на Alpari, кто не знает старейший брокер на российском рынке 22 года он работает в России.
Торговый счет можно пополнить несколькими способами Интернет-банк Альфа Клик, Промсвязьбанк, Русский Стандарт, Neteller . Perfeсt money, ADVcash , Монета ру, B2BinPay , WebMoney , Криптовалюты. Вывести деньги можно на Skrill, VLoad , ADVcash , WebMoney, Neteller . Я использую ADVcash самый удобный способ на полонение без комиссии пополнение счета осуществляется через ваш E — mail комиссия есть, но небольшая, можно пополнить там счет и без комиссии через европейский банк SEPA . Есть реферальная программа.
График Alpari Екатерина Шевченко
На графиках Аlpari нет возможности рисовать на графике, так что сделала как смогла для того что показать идентичность графиков, на простой рисовалке в скриншоте.
Логично при этом что после серии ложных сигналов пойдут качественные правдивые сигналы. Это не всегда означает что они пойдут друг за другом, поэтому для повторного входа в рынок во избежание повторения серии ложных сигналов лучше подождать еще одного желтого сигнала светофора.
Часто они идут и сериями, это зависит от настроения рынка.
На данном графике пары EURUSD рынок не стоял на месте он был в движении. В этом случает не будет серии из 5,6,7,10 можно сигналов есть небольшая проторговка из всего трех красных дизлайков. интервал между ними очень маленький, далее желтый сигнал светофора и можно открываться. Получаем профит. Скриншоты ниже.
График Trading View Екатерина Шевченко
Также сделки открываю на Alpari. Напомню рисовалок там нет, так что не судите строго)).
График Alpari Екатерина Шевченко
Вот и вся стратегия на мой взгляд заработать в принцепи на любом рынке могут терпеливые! Ваш враг в этом деле — эмоции мы теряем только тогда, когда не можем дождаться нужного сигнала или думает, что за серией ложных сигналов пойдет серия непременно правдивых сигналов подряд. Нужно смотреть за ситуацией, которая складывается на рынке в данный момент.
Нужно смотреть за ситуацией, которая складывается на рынке в данный момент.
Также удобно эту стратегию использовать на одной из самых популярных бирж криптовалют Kraken. Она находится на первом месте по объёму торгов в паре BTC/EUR.Для построения графиков используется интерфейс TradingView. Это значит, что у вас всегда будет доступ к широкому набору инструментов технического анализа. График открывается в дополнительном окне, которое вы можете перемещать и изменять по своему усмотрению. Кроме того, у Kraken есть неплохое мобильное приложение, которое на сегодняшний день доступно только для пользователей iOS.Завести фиат на биржу можно только при помощи банковского перевода. Помимо фиата для пополнения счёта можно использовать криптоваюты.
Математическое ожидание в трейдинге. Риски и вероятность выигрыша :Blog Siwitpro
В трейдинге достаточно много нюансов, которые, не являясь значительными в принципе, существенно влияют на конечный результат. К примеру, математическое ожидание. Примечательно, что, даже хорошо владея фундаментальным и техническим анализом, трейдер, чья торговая система показывает отрицательное математическое ожидание, не добьётся успеха и сольёт депозит в долгосрочной перспективе. В этой статье мы постараемся максимально просто объяснить, что такое математическое ожидание в трейдинге, каким оно бывает и как сказывается на торговле. Также мы обсудим, что можно сделать, чтобы повысить мат. ожидание по сделкам.
Примечательно, что, даже хорошо владея фундаментальным и техническим анализом, трейдер, чья торговая система показывает отрицательное математическое ожидание, не добьётся успеха и сольёт депозит в долгосрочной перспективе. В этой статье мы постараемся максимально просто объяснить, что такое математическое ожидание в трейдинге, каким оно бывает и как сказывается на торговле. Также мы обсудим, что можно сделать, чтобы повысить мат. ожидание по сделкам.
Если говорить просто, то математическое ожидание – это усреднённый статистический показатель, дающий представление о прибыльности торговой системы или стратегии. Расчёт математического ожидания позволяет трейдеру увидеть, что превалирует в его торговле – убыток или прибыль.
Казалось бы, чтобы это понять, достаточно просто подбить процент прибыльных и убыточных сделок по итогу какого-то периода – недели, месяца и т. п. Но такая статистика не всегда будет объективна, ведь на прибыльность сделок в этот период могли влиять самые разные факторы, не имеющие отношения к эффективности торговой системы.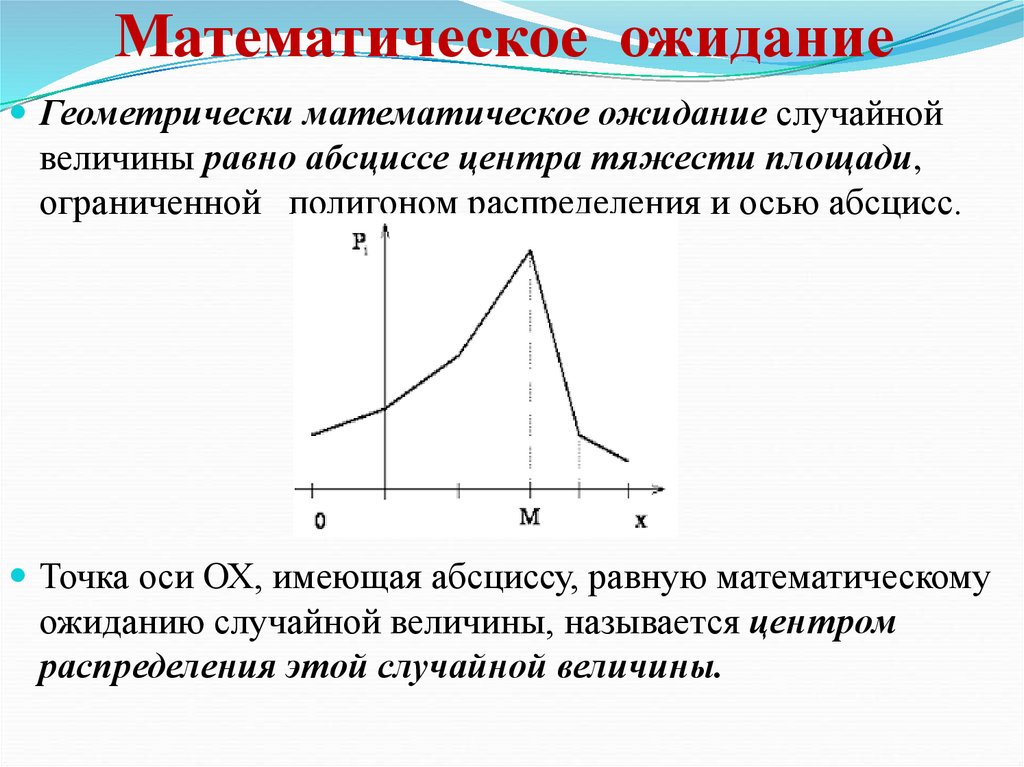
Для расчёта же математического ожидания берётся как минимум, 100 сделок. Расчёт происходит по простой формуле: От процента успешных сделок торговой системы, умноженного на прибыль в средней прибыльной сделке, отнимается процент убыточных сделок, умноженный на средний убыток в такой сделке. Статистические данные для расчёта можно без труда выгрузить из торгового терминала.
Каким бывает математическое ожидание и что это даёт?Математическое ожидание бывает положительным и отрицательным. То есть, если после расчёта по вышеприведённой формуле у Вас получилась цифра от 0 и выше, мат. ожидание положительное. Если же получилась цифра со знаком «минус» — оно отрицательное. Что это даёт трейдеру?
Положительное мат. ожидание означает, что доход от прибыльных сделок способен перекрыть потери от убыточных. Следовательно, торговая система работает хорошо, трейдер всегда в плюсе, даже несмотря на периодические неудачи. Поэтому, в долгосрочной перспективе можно рассчитывать на рост депозита.
Отрицательное значение математического ожидания – плохая новость для трейдера. Это означает, что торговая система работает не так, как должна, а убытки превышают прибыль. Даже если на данном этапе процент прибыльных сделок превышает процент убыточных, но имеет место отрицательное математическое ожидание, в долгосрочной перспективе трейдер уйдёт в минус и неизбежно сольёт депозит. Как такое возможно?
Тут всё достаточно просто. К примеру, у трейдера 70% прибыльных сделок. Это хороший показатель. Но при этом, математическое ожидание показывает минус. Это значит, что общая сумма прибыли от этих 70% не перекроет сумму убытков от оставшихся 30% убыточных.
Поясним на примере. Допустим, трейдер заключил 100 сделок. Из них было 70 прибыльных и 30 убыточных. На прибыльных он заработал в сумме 1000 долларов, а на убыточных потерял 1200 долларов. В итоге, убытки на 200 долларов превысили доход, хотя прибыльных сделок и было больше. В чём причина? Скорее всего, прибыльными оказались более мелкие позиции, а убыточными оказались крупные.
По сути, именно такую вероятность развития событий прогнозирует отрицательное математическое ожидание, даже если на момент расчёта убытки ещё не превышают прибыль.
Итак, что даёт трейдеру расчёт мат. ожидания? По сути, возможность оценить эффективность своей торговой системы в перспективе. Либо по результатам расчётов он ещё раз убедится, что делает всё правильно, либо заметит риск слива депозита и поймёт, что необходимо пересмотреть систему и стратегию, и то-то поменять. В каком-то смысле, расчёт математического ожидания – как система раннего оповещения о потере депозита (если он отрицательный).
Мат. ожидание в минусе. Всё плохо?Если говорить откровенно, то да, перспективы у трейдера с отрицательным математическим ожиданием не радужные. Но это лишь в том случае, если он не захочет ничего предпринять. А что можно сделать, чтобы повысить математическое ожидание?
Один из самых эффективных вариантов – повысить соотношение между стоп-лоссом и тейк-профитом. Вероятнее всего, математическое ожидание показало минус, потому что соотношение между стопом и тейком сейчас 1:1 или 1:2. При соотношении 1:1 убытки почти гарантированы, поскольку на бирже взымают комиссионные, что уже лишает это соотношение равенства. Соотношение 1:2 уже лучше, но если трейдеру предстоит пройти через череду неудач, этот показатель его не спасёт.
Вероятнее всего, математическое ожидание показало минус, потому что соотношение между стопом и тейком сейчас 1:1 или 1:2. При соотношении 1:1 убытки почти гарантированы, поскольку на бирже взымают комиссионные, что уже лишает это соотношение равенства. Соотношение 1:2 уже лучше, но если трейдеру предстоит пройти через череду неудач, этот показатель его не спасёт.
Многие считают, что оптимальное соотношение стопа к тейку – 1:3 или 1:4. В этом действительно есть смысл, ведь при таких соотношениях прибыль сможет перекрыть убытки даже в трудные времена для трейдера.
Однако стоит понимать, что чем больше это соотношение, тем больше риск, что цена попросту не дойдёт до отметки тейка. Тут нужно сохранять уравновешенность – вероятность, что цена пройдёт путь до тейка при соотношении 1:3 гораздо выше, чем, что она пройдёт этот путь при соотношении 1:10. Таковы уж рыночные условия – редко можно наблюдать такую волатильность достаточно долго, чтобы она сорвала тейк.
Итак, как видно, математическое ожидание в трейдинге – полезный показатель для оценки эффективности своей торговли в перспективе. Он позволяет вовремя заметить проблему и успеть предпринять меры для её решения до того, как трейдер окажется в минусе.
Он позволяет вовремя заметить проблему и успеть предпринять меры для её решения до того, как трейдер окажется в минусе.
Помочь создать эффективную торговую систему с положительным математическим ожиданием может обучение в Школе трейдинга Александра Пурнова у опытного наставника. А полезные материалы на тему трейдинга из нашего блога будут доступны Вам в полном объёме после подписки.
# каким бывает математическое ожидание в трейдинге, мат ожидание в трейдинге, математическое ожидание в трейдинге
Положительное математическое ожидание — Большая Энциклопедия Нефти и Газа, статья, страница 1
Cтраница 1
Положительное математическое ожидание — рациональная система игры — вот залог вашей победы. Игра по наитию кончается крахом. Но многие трейдеры напоминают полупьяных посетителей казино: они шатаются по залу, ввязываясь то в одну игру, то в другую. Играющие наобум разоряются из-за глупых решений, проскальзывания и комиссионных. [1]
[1]
Вычислим теперь положительное математическое ожидание для Павла. [2]
Разработав систему игры с положительным математическим ожиданием, вам необходимо установить правила управления капиталом. Соблюдайте их, как будто от этого зависит ваша жизнь. Тот, кто теряет деньги, умирает как трейдер. [3]
Отметьте, что в этом примере ставки как после выигрышей, так и после проигрышей все еще имеют положительное математическое ожидание. [4]
Для процесса зависимых испытаний, как и для процесса независимых испытаний, ставка части вашего общего счета также максимально использует положительное математическое ожидание. [5]
Скорость изменения между двумя функциями: уменьшением премии с течением времени и расширением окна X стандартных отклонений, может создать положительное математическое ожидание для длинной позиции по опциону. Это ожидание имеет наибольшее значение в момент открытия позиции и после этого понижается с уменьшающейся скоростью. Таким образом, справедливо оцененный опцион ( на основе вышеизложенных моделей) может иметь положительное математическое ожидание, если позицию по нему закрыть в начале периода падения премии.
[6]
Таким образом, справедливо оцененный опцион ( на основе вышеизложенных моделей) может иметь положительное математическое ожидание, если позицию по нему закрыть в начале периода падения премии.
[6]
Теперь у нас есть математический метод, с помощью которого можно выходить из позиции по опциону и покупать опцион при положительном математическом ожидании. Если мы выйдем из позиции в день, когда среднее геометрическое максимально и оно больше 1 0, то следует покупать число контрактов, исходя из оптимального f, которое соответствует наивысшему среднему геометрическому. Математическое ожидание, о котором мы говорим, — это геометрическое ожидание. [7]
Мы наметили, таким образом, широко применимый метод перевода результатов, касающихся случайного блуждания с ц 0, в результаты для случайных блужданий с положительным математическим ожиданием и обратно. [8]
Таким же образом, вам лучше не торговать, пока не будет убедительных доказательств того, что рыночная система, по которой вы собираетесь торговать, прибыльна, то есть пока вы не будете уверены, что рыночная система имеет положительное математическое ожидание. Математическое ожидание является суммой, которую вы можете заработать или проиграть, в среднем, по каждой ставке.
[9]
Математическое ожидание является суммой, которую вы можете заработать или проиграть, в среднем, по каждой ставке.
[9]
Заметьте, что оптимальное /, доставляющее максимум роста, одинаково для всех конов игры, хотя и является функцией того, как долго вы будете играть. Для игры с положительным математическим ожиданием оптимальное / убывает по мере увеличения времени до остановки ( асимптотически убывает для бесконечной игры) и максимизирует среднее геометрическое HPR. Для игры с отрицательным математическим ожиданием оптимальное / всегда остается нулевым. [10]
Заметьте, что оптимальное /, доставляющее максимум роста, одинаково для всех конов игры, хотя и является функцией того, как долго вы будете играть. Для игры с положительным математическим ожиданием оптимальное / убывает по мере увеличения времени до остановки ( асимптотически убывает для бесконечной игры) и максимизирует среднее геометрическое HPR. Для игры с отрицательным математическим ожиданием оптимальное / всегда остается нулевым. [11]
[11]
Для игроков важно понятие математического ожидания. Оно называется долей игрока ( положительное математическое ожидание) или долей заведения ( отрицательное математическое ожидание), смотря по тому, на чьей стороне больше шансов. [12]
Хорошая система дает вам преимущество перед конкурентами. Выражаясь техническим языком, она создает положительное математическое ожидание в длинном ряде сделок. Это значит, что система при большом числе сделок делает выигрыш более вероятным, чем проигрыш. Если ваша система это обеспечивает, к ней необходимо добавить методы управления капиталом. [13]
В конечном итоге наиболее продуктивной формой функции предпочтения полезности в смысле максимизации капитала является прямая, устремленная вверх с понижающейся абсолютной величиной и постоянной относительной величиной неприятия риска и почти индифферентная к справедливой азартной игре. То есть мы индифферентны к азартной игре, не имеющей хотя бы самого минимального положительного математического ожидания. Если ваша кривая хоть в чем-то хуже этого, то, возможно, пришло время подумать над тем, к чему и зачем вы стремитесь, и, быть может, провести некоторую самокоррекцию.
[14]
Если ваша кривая хоть в чем-то хуже этого, то, возможно, пришло время подумать над тем, к чему и зачем вы стремитесь, и, быть может, провести некоторую самокоррекцию.
[14]
Эта аксиома верна не только для игры с отрицательным ожиданием, она истинна также для игры с равными шансами. Поэтому единственный случай, когда у вас есть шанс выиграть в долгосрочной перспективе, — это игра с положительным математическим ожиданием. [15]
Страницы: 1 2 3
Мат.ожидание или «Теория казино»
Принято считать, что основной товар в казино — это адреналин. Часто мы слышим, что казино предлагает вытянуть «счастливый билет», много реже говорят что казино продает сервис. На самом же деле, основной товар казино — это азарт от возможности выигрыша. В этой статье мы рассмотрим основные принципы, на которых организована работа игорных домов, обоснование прибыли заведения, и какую роль в ее деятельности играет «госпожа удача».
А начнем обзор с рассмотрения основных математических законов, на которых построены азартные игры. Как связаны математика и казино? Ведь все игры в казино были придуманы и разработаны именно математиками. Можно ли использовать их же оружие для получения преимущества в игорном доме?
Математика игр казино
Рассмотрим процессы, происходящие в азартных играх, с точки зрения теории вероятности, и попробуем определить, подчиняются ли игры казино математике.
Бросая монету, можно утверждать, что любая из ее сторон может выпасть с одинаковой вероятностью. Есть всего две возможности — выпадет либо орел, либо решка. Вероятность того, что при бросании монеты выпадет решка равна? (50%), то есть мы вправе ожидать, что в половине случаев будет выпадать решка. Часто говоря о вероятности употребляют слово шанс. Шанс на то, что при броске монеты она упадет решкой вверх, равен 50%
Вероятность показывает, как часто ожидаемый нами результат может быть достигнут, и может быть представлена как отношение ожидаемых исходов к общему количеству всех возможных исходов за достаточно продолжительный период времени при большом количестве повторений.
Математическое ожидание при игре в рулетку
Рассчитаем математическое ожидание при игре в рулетку (американская версия с двумя секторами «зеро» ноль и двойной ноль) при ставке 5$ на цвет (черное): 18\38 х (+5$) + 20\38 х (-5$) = -0,263
Как вы уже наверное заметили, в обоих приведенных примерах, величина математического ожидания имеет знак «-», что характерно для большинства ставок казино. Отрицательное математическое ожидание на практике означает, что, чем дольше длится игра, тем больше вероятность проигрыша для игрока.
Перевес казино (House Edge) [доля заведения] – величина, противоположная математическому ожиданию игрока и показывающая, какой процент от ставок, сделанных в процессе игры за определенный промежуток времени, удерживается в пользу казино.Сейчас мы будем рассматривать самый популярный вид игры в казино, знаете какой? Самая популярная игра казино во всем мире — это игра в рулетку.Перевес казино в европейской рулетке составляет 1 — 36/37 = 2,7%, в американской рулетке уже 1 — 36/38 = 5,26% (за счет двух зеро). Это означает, что, если вы, играя в рулетку, за определенное время поставили в общей сложности 1000 долларов, то велика вероятность, что в конечном итоге около 27$ (европейская рулетка) и 54$ (американская рулетка) пойдет в доход игорному заведению. В настольных играх перевес казино меньше (Баккара, Блэкджек или Крэпс), поэтому шансы выиграть в них выше.
Это означает, что, если вы, играя в рулетку, за определенное время поставили в общей сложности 1000 долларов, то велика вероятность, что в конечном итоге около 27$ (европейская рулетка) и 54$ (американская рулетка) пойдет в доход игорному заведению. В настольных играх перевес казино меньше (Баккара, Блэкджек или Крэпс), поэтому шансы выиграть в них выше.
В качестве примера посчитаем, каковы наши шансы в казино при игре в американскую версию рулетки, игровое колесо которой, напомню, насчитывает 38 секторов (1-36 цифры + 2 сектора зеро). Предположим, что мы поставили на число. Оплата выигрыша, в этом случае производится в соотношении 1 к 36
Вероятность выиграть в этом случае 1\38 или 2,63%
Возможный выигрыш игрока (в процентах к ставке): 1/38 х 36х100 = 94.74%
Процент казино: 100 – 94,7 = 5.26 %
Математическое ожидание: [(1\38) х 36 (+1)] + [(37\38) x (-1)] = -0,0263
То есть, с каждого поставленного вами доллара, игорный дом надеется заработать 2,63 цента. Другими словами математическое ожидание выигрыша игрока при игре в американскую рулетку в казино составляет -2.6% от каждой вашей ставки.
Другими словами математическое ожидание выигрыша игрока при игре в американскую рулетку в казино составляет -2.6% от каждой вашей ставки.
Выводы:
Не надо быть великим математиком, чтобы играть в казино. Можно даже не считать математическое ожидание и дисперсию — это сделали до вас и можно пользоваться готовыми результатами. Главное понимать, что игры, имеющие большую величину математического ожидания, выгоднее для игрока, так как в них преимущество казино перед вами меньше и, соответственно, время вашей игры и возможная сумма выигрыша увеличивается. Ищите игры, в которых реализовано преимущество игрока, только в этом случае вы можете рассчитывать на выигрыш в достаточно долгой игре.
При выборе рулетки отдавайте предпочтение европейскому варианту (с одним «зеро») так как в ней преимущество казино будет 2,7%, в отличии от американской версии (с двумя «зеро»), в котором перевес игорного заведения равен уже 5,26%.
Но, рассуждая о положительных и отрицательных математических ожиданиях, вы не должны забывать и о том, что существует дисперсия. И чем она выше, тем больше вас будет «лихорадить» в игре. Вы будете проигрывать в играх с преимуществом игрока, и, в то же время, можете выиграть там, где казино имеет значительный перевес математического ожидания. Помните, что вся математика азартных игр казино корректно работает только в случае, когда число попыток велико и, поэтому, достигнуть на практике расчетных ожидаемых величин достаточно сложно из-за ограниченности бюджета игрока, величины ставок или времени игры.
И чем она выше, тем больше вас будет «лихорадить» в игре. Вы будете проигрывать в играх с преимуществом игрока, и, в то же время, можете выиграть там, где казино имеет значительный перевес математического ожидания. Помните, что вся математика азартных игр казино корректно работает только в случае, когда число попыток велико и, поэтому, достигнуть на практике расчетных ожидаемых величин достаточно сложно из-за ограниченности бюджета игрока, величины ставок или времени игры.
Источник[1];
Отдельная благодарность Алексею Маркову и его книге «Хулиномика».
Именно из за него и его творения побудилась идея создания данной статьи.
Может ли ожидаемое значение быть отрицательным? (3 вещи, которые нужно знать) – JDM Educational
Ожидаемое значение (также называемое средним) часто используется в теории вероятностей и статистике, чтобы помочь описать наборы данных или предсказать результаты. Однако это поднимает вопрос о том, какие типы значений мы можем получить в качестве ожидаемого значения.
Итак, может ли математическое ожидание быть отрицательным? Ожидаемое значение может быть отрицательным. Однако отрицательное ожидаемое значение возможно только в том случае, если некоторые данные или результаты имеют отрицательные значения. Это потому, что вероятности никогда не бывают отрицательными.
Конечно, математическое ожидание также может быть положительным или нулевым. Независимо от знака ожидаемая стоимость является инструментом и не всегда указывает на возможный или вероятный результат.
В этой статье мы поговорим об отрицательном ожидаемом значении и о том, что это значит. Мы также приведем несколько примеров отрицательного ожидаемого значения, чтобы пролить свет на эту идею.
Начнем.
Может ли ожидаемое значение быть отрицательным?
В некоторых случаях ожидаемое значение может быть отрицательным. Однако для этого требуется, чтобы по крайней мере некоторые данные или результаты имели отрицательные значения.
Причина в том, что вероятности никогда не бывают отрицательными, а математическое ожидание получается путем сложения произведений вероятностей и исходов. (Кроме того, вероятность никогда не превышает 1 — вы можете узнать больше в моей статье здесь).
Помните, что ожидаемое значение также называется средним — это одно и то же. Однако наиболее распространенный тип среднего, с которым мы знакомы (среднее арифметическое), не всегда является правильным способом расчета ожидаемого значения.
Могут ли KPI быть отрицательными?
Пожалуйста, включите JavaScript
Могут ли KPI быть отрицательными?
На самом деле среднее арифметическое — это средневзвешенное значение, которое предполагает равный вес для всех точек данных. Другими словами, среднее арифметическое предполагает одинаковую вероятность для каждого возможного результата (мы суммируем все значения и делим на количество значений — неявный вес или вероятность 1/n для каждой из n точек данных).
Давайте рассмотрим несколько примеров, чтобы проиллюстрировать, как могут возникать отрицательные ожидаемые значения (и когда они не могут возникать).
Пример 1: Отрицательное ожидаемое значение
RazeFunding, Inc. — технологическая компания, которая недавно провела IPO. Вы можете купить акцию этой компании за 100 долларов.
Ожидаемая стоимость — это инструмент, который может помочь вам решить, стоит ли инвестировать или предпринять другие действия, сопряженные с риском и вознаграждением.Вы хотите найти ожидаемую доходность этой акции через год. Вы полагаете, что есть две возможности для стоимости акции в течение одного года:
- 1.) Стоимость вырастет до 300 долларов, то есть увеличится на 200 долларов (это маловероятно, поскольку вероятность такой большой прибыли составляет всего 10 %). ).
- 2.) Значение падает до 10 долларов, снижение на 90 долларов (это очень вероятно, с ошеломляющей 90% вероятностью такого падения).

Помните, что для того, чтобы найти ожидаемую стоимость вашей прибыли на акцию, вы умножаете долларовую стоимость (прибыль или убыток) для результата и вероятность этого результата. Затем суммируем все эти результаты.
Приведенные ниже расчеты и таблица помогут разобраться.
Результат 1: стоимость акции увеличивается на 200 долларов. Вероятность того, что это произойдет, составляет 10% (0,10 в десятичном выражении), поэтому мы вычисляем:
(+200$)*(0,10) = + 20$ .
Результат 2: стоимость акции уменьшается на 90 долларов. Вероятность этого составляет 90% (0,90 в десятичном выражении), поэтому мы вычисляем:
(-90 долларов США) * (0,9) = — 81 долларов США .
Сложив эти два результата вместе, мы получаем 20 – 81 доллар = -61 доллар.
Итак, ожидаемая стоимость вашего дохода через год, если вы купите акцию, составляет -61 доллар.
| Событие | Значение | Вероятность | Продукт |
|---|---|---|---|
| Акции До $ 300 | +200 | 10% (0,10) | +20 |
Ар. | -81 | ||
| Всего | NA | 100% (1,00) | -61 (Exp. Значение) |
| Event | Value | Probability | Product |
|---|---|---|---|
| Roll 6 | +18 | 1/6 | +3 |
| Roll 1, 2, 3, 4, 5, или 6 | -6 | 5/6 | -5 |
| Всего | NA | 6/6 | -2 |
в правом нижнем углу.

Итак, каким должен быть ваш выигрыш при выпадении 6, чтобы эта игра была «честной», поэтому ожидаемая ценность игры равна 0 долларов для нас обоих? Назовем значение X.
Затем мы хотим найти ожидаемое значение = 0 или:
(X)(1/6) + (-6)(5/6) = 0
X/6 – 6 = 0
X/6 = 6
X = 36
Итак, вам нужно будет выиграть 36 долларов, если выпадет 6, чтобы игра была честной (математическое ожидание равно нулю). Если бы мы играли в эту игру много раз подряд, мы оба должны были бы рассчитывать на безубыточность (или близко к этому).
Может ли среднее значение нормального распределения быть отрицательным?
Среднее значение нормального распределения может быть отрицательным. Это может произойти, если некоторые или все точки данных имеют отрицательные значения.
Например, предположим, что изменение веса человека в течение года имеет нормальное распределение. Если средний человек теряет вес, то среднее (ожидаемое значение) может составлять -2 фунта, а стандартное отклонение может составлять 4 фунта.
Хотя некоторые люди набирают вес, больше людей теряют вес.
Вы можете узнать больше о том, когда нормальное распределение является отрицательным (и какой параметр не может быть!) в моей статье здесь.
Что означает отрицательное ожидаемое значение?
Отрицательное ожидаемое значение означает, что вы можете ожидать потери (отрицательное значение), если будете продолжать одно и то же испытание (или использовать одну и ту же возможность) снова и снова.
Вспомним прежнюю технологическую компанию: допустим, существует 1000 таких компаний с одинаковой текущей стоимостью, потенциальными результатами и профилем риска.
Если вы инвестируете по 100 долларов в каждую из этих 1000 компаний, то вы ожидаете, что потеряете 61 доллар с каждой инвестиции (поскольку ожидаемая стоимость равна -61 доллару). Это означает, что ваши инвестиции в размере 100 000 долларов США через год сократятся до 39 000 долларов США (прибыль -61%).
Как это происходит? Давайте посмотрим на цифры.
Вы инвестируете по 100 долларов в каждую из 1000 компаний, общая сумма инвестиций составляет 100 000 долларов.
Для 1000 компаний мы ожидаем, что 10% из них (100 из 1000 компаний) добьются успеха. Это означает, что цена акций этих 100 компаний увеличится до 300 долларов. Общая стоимость этих акций составит (300 долларов США) * (100 компаний) = 30 000 долларов США.
Для остальных 90% (900 из 1000 компаний) цена акций уменьшится до 10 долларов. Общая стоимость этих акций составит (10 долларов США) * (900 компаний) = 9000 долларов США.
Сложив эти значения вместе, ваш инвестиционный портфель стоит 30 000 долларов США + 9 000 долларов США = 39 000 долларов США. Не знаю, как вы, а я не хочу терять 61% любого портфеля — и уж точно не за один год!
Заключение
Теперь вы немного больше знаете об отрицательном ожидаемом значении и о том, как это может произойти. Вы также точно знаете, что означает отрицательное математическое ожидание и как этот инструмент может помочь нам принимать лучшие решения.
Вы можете узнать больше о среднем (ожидаемом значении) и медиане в моей статье здесь.
Вы можете узнать больше об использовании математического ожидания в моей статье здесь.
Надеюсь, эта статья оказалась вам полезной. Если это так, пожалуйста, поделитесь ею с теми, кто может использовать эту информацию.
Не забудьте подписаться на мой канал YouTube и получать обновления о новых математических видео!
Подпишитесь на мой канал на YouTube!
~Джонатон
вероятность — Математическое ожидаемое значение?
спросил
Изменено 8 лет, 10 месяцев назад
Просмотрено 6к раз
$\begingroup$
Мы делаем игру в казино, и нам нужно определить математическое ожидание, чтобы увидеть, будем ли мы прибыльными. Мой учитель говорит, что наше математическое ожидание должно быть небольшим положительным числом, чтобы оно было справедливым и чтобы казино зарабатывало деньги.
Мой учитель говорит, что наше математическое ожидание должно быть небольшим положительным числом, чтобы оно было справедливым и чтобы казино зарабатывало деньги.
ОДНАКО, если бы вам нужно было рассчитать ожидаемое значение, например, бросив кубик, при условии, что выпадение 1 приведет к потере 5 очков, а все остальное не дает очков. Поэтому ожидаемое значение будет отрицательным. Следовательно, это означает, что вы ПОТЕРЯЕТЕ деньги, а дом должен заработать деньги.
Значит, отрицательное математическое ожидание не должно быть лучше для казино?
Заранее спасибо!
вероятность
$\endgroup$
$\begingroup$
Вы рассматриваете ожидаемое значение с точки зрения игрока, в то время как ваш учитель рассматривает ожидаемое значение с точки зрения казино. Два ожидаемых значения будут иметь одинаковую величину, но различаться по знаку. Используя вашу терминологию, отрицательное математическое ожидание действительно было бы лучше для казино (игрок «ожидал бы» потерять немного денег, поэтому казино выиграло бы деньги).
$\endgroup$
2
$\begingroup$
Ваш вопрос не имеет большого смысла, потому что вы недостаточно точно определили свою проблему. С точки зрения казино вам нужно небольшое положительное математическое ожидание, если случайная величина отслеживает выигрыш в долларах, и вы хотите, чтобы точка зрения игрока была отрицательной.
Предположим, что случайная величина $X$ отслеживает прибыль, полученную от выплаты 2 долларов за игру в подбрасывание монеты, где если выпадет решка, вы заработаете два доллара, а если выпадет решка, то ничего не получите. Тогда $X = 0$, если H, и $X = -2$, если T. Таким образом, математическое ожидание для игрока отрицательно, он в среднем теряет деньги, играя в эту игру. Но для казино, если $X$ отслеживает прибыль, полученную от разрешения игроку играть в эту игру, тогда $X = 0$, если H, и $X = 2$, если T. В этом случае казино имеет положительное математическое ожидание от позволяя игроку играть в эту игру, казино в среднем зарабатывает деньги.
В этом случае казино имеет положительное математическое ожидание от позволяя игроку играть в эту игру, казино в среднем зарабатывает деньги.
$\endgroup$
$\begingroup$
Это зависит от того, как на это посмотреть. Ваш учитель, вероятно, попросил ожидаемые деньги, которые получит дом: это должно быть небольшим плюсом. Но ожидаемые деньги, которые должны заработать такие бедняки, как мы, должны быть небольшим минусом. Или ожидаемая сумма денег, которую должны потерять такие бедняки, как мы, должна быть небольшой положительной и т. д.
$\endgroup$
2
$\begingroup$
Вы можете думать об ожидаемом значении одним из двух способов:
1) С точки зрения Игрока.
2) С точки зрения казино.
Например, если игрок ставит $\$1$ и его шансы на выигрыш составляют $0,49$, то его математическое ожидание равно $\$0,98$.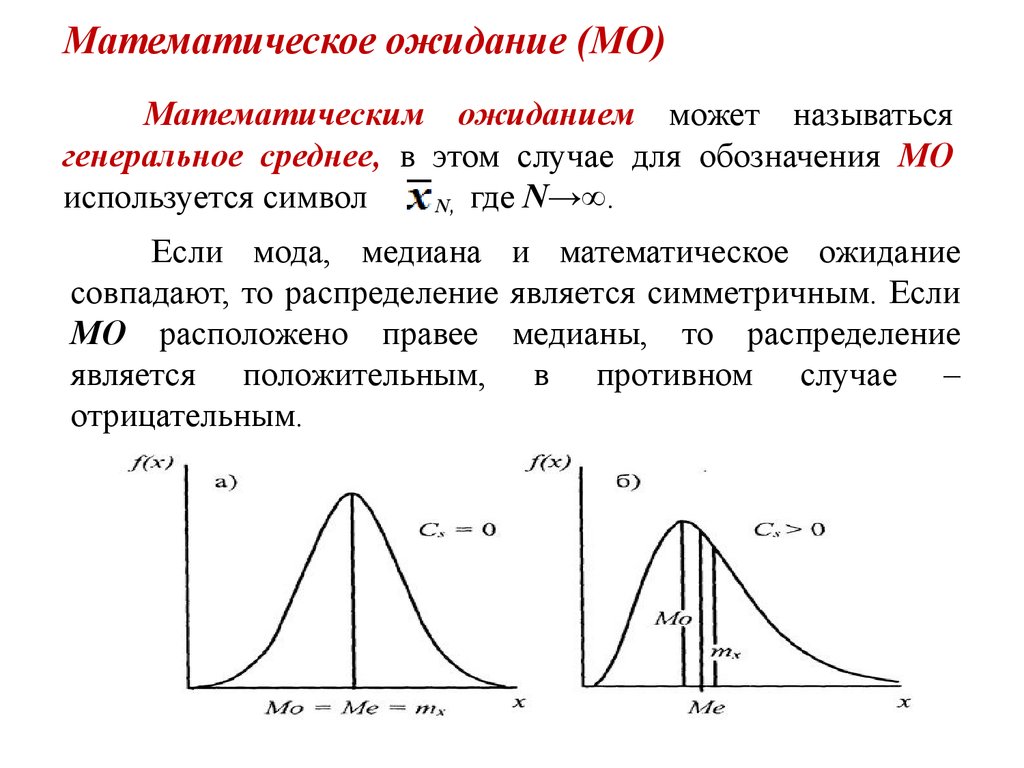 Но шансы казино на выигрыш составляют $0,51$, поэтому ожидаемая стоимость казино составляет $\$1,02$!
Но шансы казино на выигрыш составляют $0,51$, поэтому ожидаемая стоимость казино составляет $\$1,02$!
Обратите внимание, что у Игрока и Казино есть свои владеет стопками денег.
$\endgroup$
3
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
11 фактов о математическом ожидании и случайной величине — Lambda Geeks
Математическое ожидание и случайная величина статей Теперь, после обсуждения различных распределений и типов распределений, в следующей статье мы познакомимся с некоторыми более продвинутыми свойствами математического ожидания.
Мы знаем, что математическое ожидание случайной величины дискретной природы равно
, а непрерывной равно
теперь для случайной величины X и Y, если дискретно, то с совместной функцией массы вероятности p(x ,y)
математическое ожидание функции случайной величины X и Y будет равно
и если непрерывно, то с совместной функцией плотности вероятности f(x, y) математическое ожидание функции случайной величины X и Y будет равно
если g является суммированием этих двух случайных величин в непрерывной форме
и если для случайных величин X и Y мы имеем
X>Y
тогда математическое ожидание также
Пример A Covid-19 больница равномерно распределена по дороге длиной L в точке X, транспортное средство, перевозящее кислород для пациентов, находится в месте Y, которое также равномерно распределено по дороге. Найдите ожидаемое расстояние между больницей Covid-19 и транспортным средством, перевозящим кислород. если они независимы.
Найдите ожидаемое расстояние между больницей Covid-19 и транспортным средством, перевозящим кислород. если они независимы.
Решение:
Чтобы найти ожидаемое расстояние между X и Y, мы должны вычислить E { | XY | }
Теперь функция совместной плотности X и Y будет
, так как
, следуя этому, мы получим
, теперь значение интеграла будет
Таким образом, ожидаемое расстояние между этими двумя точками будет
Ожидание Выборочное среднееКак выборочное среднее последовательности случайных величин X 1 , X 2 , ………, X n с функцией распределения F и ожидаемым значением каждого из них, поскольку μ равно
, поэтому математическое ожидание среднего значения этой выборки будет равно
, что показывает, что ожидаемое значение среднего значения выборки также равно μ.
Неравенство БуляНеравенство Буля можно получить с помощью свойств ожиданий, предположим, что случайная величина X определена как
, где
здесь A i , представляет возникновение количества событий A i и другая случайная величина Y как
явно
X>=Y
E[X] >= E[Y]
и поэтому
теперь, если мы возьмем значение случайной величины X и Y эти ожидание будет
и
. Подставив эти ожидания в приведенное выше неравенство, мы получим неравенство Буля как
Подставив эти ожидания в приведенное выше неравенство, мы получим неравенство Буля как
Мы знаем, что биномиальная случайная величина — это случайная величина, которая показывает количество успехов в n независимых испытаниях с вероятностью успеха как p и неудачей как q=1-p, поэтому, если
X=X 1 + X 2 + …….+ X n
Где
здесь эти X i это ожидание Бернулли 3 из X будет Пусть случайная величина X представляет количество испытаний, необходимых для получения r успешных результатов, тогда такая случайная величина называется отрицательной биномиальной случайной величиной и может быть выражена как здесь каждый X i обозначает количество испытаний, необходимых после (i-1)-го успеха, чтобы получить общее количество успехов i. Поскольку каждый из этих X i представляет собой геометрическую случайную величину, и мы знаем, что математическое ожидание для геометрической случайной величины равно , то есть , что является ожиданием отрицательной биномиальной случайной величины. Математическое ожидание или среднее значение гипергеометрической случайной величины мы получим с помощью простого примера из реальной жизни, если n книг случайно выбрано с полки, содержащей N книг, m из которых по математике, затем найти ожидаемую количество книг по математике пусть X обозначает количество выбранных книг по математике, тогда мы можем записать X как , где , поэтому =n/N , что дает , что является средним значением такой гипергеометрической случайной величины. Это очень популярная задача, связанная с ожиданием, предположим, что в комнате есть N человек, которые бросают свои шляпы в середину комнаты, и все шляпы перемешиваются после этого каждый человек случайным образом выбрать одну шляпу, затем ожидаемое количество людей, которые выберут свою собственную шляпу, мы можем получить, если X будет количеством совпадений, поэтому Где , поскольку каждый человек имеет равные возможности выбрать любую шляпу из N шляп, затем , поэтому означает, что в среднем ровно один человек выбирает себе шляпу. Получим вероятность объединения событий с помощью матожидания так для событий A i при этом принимаем поэтому матожидание этого будет и расширится с использованием свойства ожидания как , так как у нас есть и , поэтому отсюда следует вероятность объединения как нижняя граница для этого m по математическому ожиданию f(s), где s — любой случайный элемент S, математическое ожидание которого мы можем вычислить, поэтому здесь мы получаем математическое ожидание как нижнюю границу максимального значения Максимум Минимальная идентичность — это максимум набора чисел, равный минимумам подмножеств этих чисел, то есть для любых чисел x i Чтобы показать это, ограничим x i интервалом [0 ,1], предположим равномерную случайную величину U на интервале (0,1) и события A i , так как равномерная переменная U меньше, чем x i , то есть , так как хотя бы одно из перечисленных событий произошло поскольку U меньше единицы, значение x i и Ясно, что мы знаем , и все события произойдут, если U меньше, чем все переменные и вероятность дает мы имеем результат вероятности объединения как после этого исключения включения формула для вероятности рассмотрим это дает так как что означает принимая ожидание мы можем найти ожидаемые значения максимума и частичного минимума как Ожидание с точки зрения различного распределения и корреляции ожидания с некоторыми концепциями теории вероятностей было в центре внимания этой статьи, которая показывает использование ожидания в качестве инструмента для получения ожидаемых значений различного рода. Дополнительные статьи по математике см. на нашей странице по математике. https://en.wikipedia.org/wiki/Ожидание Первый курс теории вероятностей Шелдона Росса Очерки вероятности и статистики Шаума Введение в вероятность и статистику РОХАТГИ и САЛЕХа Последнее обновление: 30 мая 2022 г. Этот вопрос время от времени задают наши эксперты. Теперь у нас есть полное подробное объяснение и ответ для всех, кто заинтересован! Автор вопроса: Alphonso Franecki Оценка: 4,6/5
(25 голосов) Математическое ожидание квадрата оператора импульса не может быть отрицательным . Ожидаемое значение — это среднее значение случайной величины по большому числу экспериментов. Ожидаемое значение равно вероятности, умноженной на значение каждого исхода . Например, 50-процентный шанс выиграть 100 долларов стоит для вас 50 долларов (если вы не возражаете против риска). … Стоимость для вас одного из этих билетов составляет 1 доллар (0,0000001 x 10 000 000), но стоит вам 10 долларов, поэтому ожидаемая стоимость отрицательна. Аналогичная наблюдаемая включает энергию, которая зависит от выбранной нами нулевой точки. Однако оператор вида , такой как «числовой» оператор , является положительно полуопределенным. Итак, ожидаемые значения всегда неотрицательны . ОДНАКО, если бы вы рассчитали ожидаемое значение, например, бросив кубик, предполагая, что приземление на 1 отнимет 5 очков, а все остальное не даст вам очков. Найдено 24 связанных вопроса ожидаемое значение любого эксперимента может быть равно нулю но это не означает, что его реальный результат будет равен нулю. Рассмотрим пример: Рассмотрим рискованный… , и вы можете видеть, что точно соответствует ожидаемому значению . Ожидание — это среднее значение или среднее значение случайной величины, а не распределение вероятностей. В квантовой механике ожидаемое значение равно вероятностному ожидаемому значению результата (измерения) эксперимента . Нет. не может быть больше 1 . Ожидаемая стоимость (EV) — это ожидаемая стоимость инвестиций в какой-то момент в будущем. В статистике и вероятностном анализе ожидаемое значение равно 9.0648 рассчитывается путем умножения каждого из возможных исходов на вероятность возникновения каждого исхода и последующего суммирования всех этих значений . В ставках ожидаемое значение (EV) является мерой того, что игрок может ожидать, чтобы выиграть или проиграть в каждой ставке, сделанной с одними и теми же коэффициентами снова и снова. Положительное математическое ожидание (+EV) подразумевает прибыли с течением времени , а отрицательное значение (-EV) подразумевает убыток с течением времени. Базовая формула ожидаемого значения представляет собой вероятность события, умноженную на количество раз, когда это событие произошло: (P(x) * n). Мы можем рассчитать среднее (или ожидаемое значение) дискретной случайной величины как средневзвешенное значение всех результатов этой случайной величины на основе их вероятностей. Мы интерпретируем ожидаемое значение как 90 648 прогнозируемого среднего результата, если рассматривать эту случайную величину в бесконечном числе испытаний 9.0649 . Существуют разные типы ожиданий, основанные на различных контекстах — личных (семья или отношения) или профессиональных (экономика, доходность или успех в карьере) . Это могут быть реалистичные ожидания, такие как получение хорошо оплачиваемой работы, или нереалистичные ожидания, такие как успех без тяжелой работы. Негативные ожидания: « Я не буду достаточно хорош . Я подведу свою команду, потому что не буду знать ни одного ответа. Я буду выглядеть дураком. Все увидят, какой я глупый». прилагательное. Что-то вроде цели или задачи, которая является реалистичной, можно разумно ожидать для достижения . Примеры параметров распределения: ожидаемое значение одномерного вероятностного распределения. его стандартное отклонение. его дисперсия. Как вычислить математическое ожидаемое значение? Расчет математического ожидания заключается в умножении вероятности выигрыша на множитель ставки (в случае выигрыша) . Математическое ожидание обычно рассчитывается для ставки в 1 единицу. Умножьте вероятность выигрыша на размер ставки, чтобы узнать ожидаемый выигрыш. Ожидаемое значение суммы выборки равно размер выборки, умноженный на совокупность, означает (среднее число чисел в рамке). … Ожидаемое значение среднего значения выборки — это среднее значение генеральной совокупности, а SE среднего значения выборки — это стандартное отклонение совокупности, деленное на квадратный корень из размера выборки. Ожидаемые значения операторов изменяются во времени из-за их изменения во времени . Потому что этот интеграл не может зависеть от времени. Математическое ожидание оператора равно среднему значению соответствующей наблюдаемой [2, p7] . Это важная часть квантовой механики, поскольку она является одним из основных связующих звеньев между квантовой механикой и классической физикой. Гамильтониан равен ˆH(x,ℏ∂22m∂x2). Чтобы получить ожидаемое значение, мне нужно проинтегрировать это: ∫ψ∗ˆHψdx. В то время как среднее значение представляет собой простое среднее всех значений, ожидаемое значение ожидания представляет собой среднее значение случайной величины, которая является взвешенной по вероятности . Среднее значение или «Среднее значение» и «Ожидаемое значение» отличаются только своим применением, однако оба они концептуально одинаковы. Ожидаемое значение используется в случае случайных переменных (или, другими словами, вероятностных распределений). Поскольку среднее значение определяется как сумма всех элементов, деленная на сумму их частот. Ожидаемое значение часто называют «долгосрочной» средней или средней . Это означает, что в течение длительного времени, проводя эксперимент снова и снова, вы должны ожидать этого среднего значения. Вы слышали о сложных процентах, верно? А вы слышали, что Эйнштейн сказал, что сложные проценты — самая мощная сила во Вселенной? Ожидание в азартных играх похоже на сложные проценты на стероидах. В этом посте я объясню разницу между азартными играми с отрицательным и положительным ожиданием и то, что это означает для ваших финансов в долгосрочной перспективе. Если я поставлю четвертак на то, что вы подбросите монету и она выпадет орлом, вероятность вашего выигрыша составит 50%. Я бы тоже. В краткосрочной перспективе — по этой единственной ставке — один из нас выиграет, а другой проиграет. Если мы сделаем эту ставку дважды подряд, произойдет одно из следующих событий: Но в конечном счете, в течение сотен или тысяч подбрасываний монеты, если бы мы с вами ставили равные деньги, мы оба были бы безубыточными. Это ставка с нулевым математическим ожиданием. Даже деньги просто означают, что каждый из нас выигрывает или проигрывает одинаковую сумму. Но если мы изменим это уравнение так, что я выиграю 50 центов, когда выиграю, а вы выиграете только четверть, когда выиграете, у меня положительное математическое ожидание, а у вас отрицательное математическое ожидание. Так, кстати, работают почти все азартные игры. Кто-то почти всегда имеет математическое преимущество над кем-то другим. Фактически, именно так казино и букмекерские конторы остаются в бизнесе. Но насколько велико это математическое ожидание? Преимущество казино — это статистический способ измерения того, сколько в среднем в долгосрочной перспективе вы ожидаете потерять в среднем на ставке против казино. В приведенном выше примере с подбрасыванием монеты это легко вычислить. Предположим, что вы рискуете 200 долларами, чтобы выиграть 100 долларов, и у вас есть статистически точные ожидаемые результаты при двух подбрасываниях монеты. Вы выигрываете 100 долларов, но теряете 200 долларов, то есть чистый убыток составляет 100 долларов. Очевидно, вы были бы дураком, если бы сделали такую ставку, но это математический принцип, применимый ко всем ставкам в казино. В большинстве случаев у вас никогда не будет математического преимущества перед казино. В большинстве игр просто нет возможности использовать какую-либо стратегию, чтобы получить такое математическое преимущество. Но если бы вы нашли игру, в которой вы могли бы получить преимущество, вы могли бы применить правило 72 к своему преимуществу, чтобы вычислить, сколько времени вам потребуется, чтобы удвоить свой банкролл, если вы будете реинвестировать все свои выигрыши через какое-то время. В конце концов, преимущество, которое вы имеете над казино, заключается в возврате инвестиций, а правило 72 применяется к возврату инвестиций. Только вместо того, чтобы смотреть на рентабельность инвестиций в годовом исчислении, вы смотрите на рентабельность инвестиций на основе каждой ставки. Это сложные проценты в действии, ребята. Допустим, вы нашли ситуацию в казино, где вы можете получить преимущество в 1% над казино. Применяя к этому правило 72, можно подумать, что потребуется 72 года, чтобы удвоить ваши деньги. Но поскольку вы видите, что в среднем на каждую ставку возвращается 1%, вам потребуется всего 72 ставки, чтобы удвоить свои деньги. Самые надежные известные мне способы получить преимущество в 1% в азартных играх — это считать карты в блэкджеке, играть в покер на профессиональном уровне и ставить спортивные гандикапы лучше, чем в букмекерских конторах. Если вы хотите выяснить, как максимизировать рентабельность инвестиций, вы должны начать думать о том, сколько ставок вы можете делать в час. Если вы играете в блэкджек, вы можете делать больше ставок в час, чем в покере или спортивных ставках. Я видел разные оценки. Я видел, как некоторые авторы утверждали, что вы можете играть 350 рук в час один на один с дилером, но я видел, как другие авторы использовали число 200 рук в час. Я думаю, что разница заключается в том, сколько рук вы играете. Если вы единственный игрок за столом, вы можете разыгрывать две руки одновременно. Если вы делаете это, цифра 350 раздач в час имеет смысл. С другой стороны, если вы сидите за столом с шестью другими игроками, вы рассчитываете примерно на 50 или 60 раздач в час. Вроде того, да. Допустим, вы начинаете со ставок по $5 за руку с преимуществом в 1%. Если все пойдет хорошо, вы сможете удвоить свой банкролл в казино в течение часа или двух. В этот момент вы можете удвоить размер своей ставки до 10 долларов на руку. Когда вы удваиваете свой средний размер ставки, вам не нужно много времени, чтобы получить огромный банкролл. Вы даже можете разориться с положительным ожиданием, если попадете в достаточно длинную полосу неудач. Секрет в том, чтобы иметь достаточно большой банкролл, чтобы противостоять капризам удачи. Вы хотите свести к минимуму риск разорения. Большинство счетчиков карт думают о наличии определенного количества единиц ставок. Имея около 2000 долларов, вы можете играть в блэкджек по 5 долларов за руку с минимальным риском разориться. Считать карты не так сложно, как вы думаете. Это работает, потому что колода карт имеет своего рода память — после того, как карта была сдана, ее нельзя сдать снова, пока колода не будет перетасована. Это меняет вероятности почти всего, что связано с игрой. А поскольку карты расположены случайным образом, иногда колода будет относительно богата картами, выгодными для игрока, а в других случаях колода будет относительно богата картами, выгодными для казино. Что это за карты? Так как натуральная рука — комбинация из 2 карт, равная 21 — оплачивается 3 к 2, выгоднее иметь большую вероятность получения естественной. А поскольку единственными картами, которые могут составить такую руку, являются десятки и тузы, игроку выгодна колода с относительно большим количеством десяток и тузов. Когда вы можете определить такую ситуацию, вы повышаете размер своих ставок. Вот как вы получаете преимущество в блэкджеке при подсчете карт. Чем лучше счет, тем больше ваша ставка. Это так же просто, как вычитать 1 из текущего счета каждый раз, когда вы видите 10 или туз, и прибавлять 1 к текущему счету каждый раз, когда вы видите 2, 3, 4, 5 или 6. Когда счет ноль или минус, ставьте минимум. По мере увеличения счета увеличивайте размер ставок пропорционально счету. Это немного сложнее, чем это, но ненамного. Не все хотят зарабатывать на жизнь играми в казино. Другие люди хотят зарабатывать на жизнь, внося свой вклад в общество. Вы не можете винить их за это. Кроме того, не у всех есть решимость, дисциплина и сосредоточенность, необходимые для подсчета карт в казино. Не забудьте. Казино не одобряют подсчет карт, и если они вас поймают, то остановят. Подсчет карт не является незаконным, но казино может запретить вам играть за столами для игры в блэкджек. На самом деле, они могут полностью запретить вам вход в помещение, если решат, что это то, что нужно. Сила азартных игр с положительным ожиданием должна быть очевидной. Казино делают ставки с положительным матожиданием почти в 100% случаев, и посмотрите, сколько у них денег. Если вы научитесь делать ставки с положительным ожиданием, вы сможете многократно удвоить свои деньги и разбогатеть. И подсчет карт — только один пример того, как это делать. Содержание: Посмотрите это видео для быстрого объяснения формул ожидаемого значения: Формула ожидаемого значения Посмотрите это видео на YouTube. Видео не видно? Кликните сюда. Например, если вы пройдете тест с множественным выбором из 20 вопросов с ответами A, B, C, D и угадаете все «A», то вы можете рассчитывать на 25% правильных ответов (5 из 20). . математика за таким ожидаемым значением: * Вместо этого вы можете увидеть это как X. Этот тип ожидаемого значения называется ожидаемое значение для биномиальной случайной величины. Это биномиальный эксперимент, потому что есть только два возможных исхода: вы даете правильный ответ или получаете неправильный ответ. Базовая формула ожидаемого значения представляет собой вероятность события, умноженную на количество раз, когда это событие произойдет: Формула немного меняется в зависимости от того, какие события происходят . Формула ожидаемого значения для биномиальной случайной величины: Совет: Рассчитайте ожидаемое значение биномиальных случайных величин (включая ожидаемое значение для нескольких событий), используя этот онлайн-калькулятор ожидаемого значения. Конечно, расчет математического ожидания (EV) в реальной жизни усложняется. Например, Вы покупаете один лотерейный билет за 10 долларов на новый автомобиль стоимостью 15 000 долларов. Продано две тысячи билетов. E(X) = ΣX * P(X) Уравнение в основном такое же, но здесь вы добавляете сумму всех выигрышей, умноженных на их индивидуальные вероятности, вместо одной вероятности. Две приведенные выше формулы являются двумя наиболее распространенными формами формул ожидаемого значения, которые вы увидите в статистике AP или элементарной статистике. Однако в более строгих или продвинутых классах статистики (таких как эти) вы можете встретить формулы ожидаемого значения для непрерывных случайных величин или для ожидаемого значения произвольной функции . Ожидаемое значение случайной величины равно означает случайной величины. Вы можете рассчитать EV непрерывной случайной величины, используя эту формулу: Где f(x) — функция плотности вероятности, которая представляет собой функцию для кривой плотности. Если событие представлено функцией случайной величины (g(x)), то эта функция подставляется в EV для формулы непрерывной случайной величины, чтобы получить: Как найти ожидаемое значение Посмотрите это видео на YouTube. Видео не видно? Кликните сюда. В этом разделе объясняется, как определить ожидаемую стоимость одного предмета (например, при покупке одного лотерейного билета) и что делать, если у вас несколько предметов . Если у вас есть дискретная случайная величина, прочтите Ожидаемое значение для дискретной случайной величины. Пример вопроса: Вы покупаете один лотерейный билет за 10 долларов на новый автомобиль стоимостью 15 000 долларов. Шаг 1: Создайте диаграмму вероятностей (см.: Как построить распределение вероятностей). Поместите «Выигрыш (X)» и «Вероятность P (X)» в качестве заголовков строк и «Выигрыш/Проигрыш» в качестве заголовков столбцов. Шаг 2: Подсчитайте, сколько вы можете выиграть и потерять . В нашем примере, если бы мы выиграли, мы бы выиграли 15 000 долларов (за вычетом стоимости лотерейного билета в 10 долларов). Если вы проиграете, вы потеряете 10 долларов. Заполните данные (здесь я использую Excel, поэтому отрицательные значения отображаются красным цветом). Шаг 3: В нижней строке укажите свои шансы на победу или проигрыш. Учитывая, что было продано 2000 билетов, у вас есть шанс на победу 1/2000. И у вас также есть вероятность проигрыша 1999/2000. Шаг 4: Умножьте прибыль (X) в верхней строке на Вероятность (P) в нижней строке . Шаг 5. Сложите два значения вместе: Вот и все! Выполните шаги точно так же, как указано выше. Составьте диаграмму вероятностей, за исключением того, что у вас будет больше элементов: Затем умножьте/сложите вероятности, как в шаге 4: 14 990 * (1/200) + 100 * (1/200) + 200 * (1/200) + -10 долл. США * (197/200). Теперь вы заметите, что поскольку у вас есть 3 приза, у вас есть 3 шанса на победу, поэтому ваш шанс проиграть уменьшается до 197/200. Примечание к формуле: Фактическая формула для ожидаемой прибыли: E(X)=∑X*P(X) (это также одна из формул AP Statistics). Нравится объяснение? Прочтите «Руководство по статистике практического мошенничества», в котором есть еще сотни пошаговых объяснений, таких как это! В начало Готово Ожидаемое значение можно представить как среднее или среднее для распределения вероятностей Дискретная случайная величина — это случайная величина, которая может принимать только определенное количество значений . Например, если вы бросали кубик, он может иметь только набор чисел {1,2,3,4,5,6}. По сути, все, что формула говорит вам, это найти среднее значение путем сложения вероятностей. Среднее значение и ожидаемое значение настолько тесно связаны, что в основном представляют собой одно и то же. Вам нужно будет сделать это немного по-разному в зависимости от того, есть ли у вас набор значений, набор вероятностей или формула. Пример задачи №1: Вес (X) пациентов в клинике (в фунтах): 108, 110, 123, 134, 135, 145, 167, 187, 199. Предположим, что один из пациентов выбраны наугад. Что такое ЭВ? Шаг 1: Найдите среднее значение. Среднее значение: Пример задачи №2. Вы подбрасываете правильную монету три раза. Шаг 2: Выясните вероятность получения каждого значения X. Возможно, вам потребуется использовать выборочное пространство (примерное пространство для этой задачи: {HHH TTT TTH THT HTT HHT HTH THH}). Вероятности: 1/8 для 0 орлов, 3/8 для 1 орла, 3/8 для двух орлов и 1/8 для 3 орлов. Шаг 3: Умножьте ваши значения X на шаге 1 на вероятности из шага 2. EV 3/2. Пример задачи №3. Вы подбрасываете монету, пока не выпадет решка. Функция плотности вероятности равна f(x) = ½ x . Что такое ЭВ? Шаг 2: Сложите значения из шага 1: Примечание: Здесь вы ищете число, к которому сходится ряд (т. е. заданное число, к которому приближаются значения). В этом случае значения приближаются к 2, так что это ваше EV. Совет : Вы можете использовать формулу дискретной случайной величины ожидаемого значения только в том случае, если ваша функция сходится абсолютно. Другими словами, функция должна остановиться на определенном значении. Если не сходится, то EV нет. Вернуться к началу Ожидаемые значения для биномиальных случайных величин (т. е. когда у вас есть две переменные), вероятно, являются самым простым типом ожидаемых значений. В реальной жизни вы, вероятно, столкнетесь с более сложными ожидаемыми значениями, которые имеют более двух возможных значений. Например, вы можете купить лотерейный билет со скидкой с призами в 1000 долларов, 10 долларов и 1 доллар. Допустим, ваша школа разыгрывает абонемент в местный тематический парк стоимостью 200 долларов. Если школа продаст тысячу билетов по 10 долларов, каждый, кто купит билет, потеряет 9,80 долларов, за исключением того, кто выиграет сезонный абонемент. Это проигрышное предложение для вас (хотя школа его загребет). Возможно, вы захотите сэкономить! Вот математика, стоящая за этим: Вот этот сценарий в таблице: Петербургский парадокс веками ставил в тупик математиков. Речь идет об игре со ставками, в которой вы можете выиграть и всегда . Но, несмотря на это, люди не готовы платить большие деньги, чтобы играть в нее. Он называется Санкт-Петербург Парадокс из-за того, где он появился в печати: в 1738 году Известия Императорской Академии наук Санкт-Петербурга . Парадокс заключается в следующем: есть простая игра со ставками, в которой ваш выигрыш равен 9.1007 всегда будет больше, чем сумма денег, которую вы ставите. Представьте себе покупку лотерейного билета со скидкой, где ожидаемая стоимость (то есть сумма, которую вы можете ожидать выиграть) всегда выше, чем сумма, которую вы платите за билет. Вы можете купить билет за 1 доллар, 10 долларов или миллион долларов. Если предположить, что игра не сфальсифицирована, вам, вероятно, следует играть в . Но парадокс в том, что большинство людей не захотят делать ставки на подобную игру больше, чем на несколько долларов. Итак, почему это? Есть несколько возможных объяснений: Короткий ответ: люди рациональны (по большей части), они готовы расстаться со своими деньгами (по большей части). И в игре нет абсолютно ничего плохого. Если вы запутались в этом месте — вот почему это называется парадоксом. Сколько бы вы поставили, если бы всегда могли выигрывать? Первоначальный парадокс был не о лотерейных билетах (в 1738 году их не существовало). Если вы вычислите ожидаемое значение (ожидаемый выигрыш) для этой игры, ваши потенциальные выигрыши будут бесконечны. Например, при первом броске у вас есть 50% шанс выиграть 2 доллара. Кроме того, вы можете снова подбросить монету, поэтому у вас также есть 25% шанс выиграть 4 доллара, плюс 12,5% шанс выиграть 8 долларов и так далее. Если вы делаете ставки снова и снова, ваш ожидаемый выигрыш (выигрыш) составляет 1 доллар каждый раз, когда вы играете, как показано в следующей таблице. Вы не можете потерять деньги. Тем не менее, несмотря на то, что математическое ожидание бесконечно велико, большинство людей не захотят раскошелиться больше, чем на несколько долларов, чтобы поиграть в эту игру. Петербургский парадокс обсуждался математиками почти три столетия. Почему люди не рискуют большими деньгами, если шансы определенно в их пользу? Пока никто не нашел удовлетворительного ответа на этот парадокс. Как заявляет Майкл Кларк: «[Парадокс Санкт-Петербурга] кажется одним из тех парадоксов, которые мы должны проглотить». Пара решений, которые были представлены, но не дали удовлетворительного ответа: Далее: Ожидаемое значение Powerball Кларк, Майкл, 2002 г., «Парадокс Санкт-Петербурга», в книге «Парадоксы от А до Я», Лондон: Routledge, стр. 174–177. Статьи по теме: НАЗВАТЬ ЭТО КАК: ————————————————— ————————- Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на ваши вопросы от эксперта в данной области.

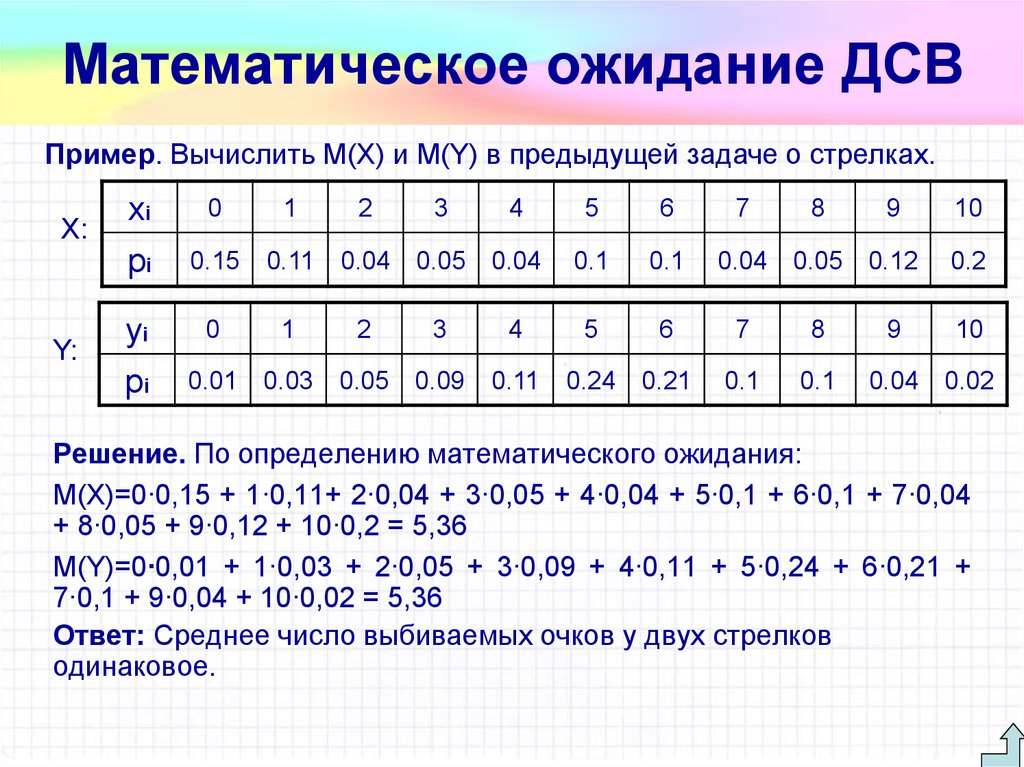 случайных величин, если вам требуется дальнейшее чтение, прочитайте книги ниже.
случайных величин, если вам требуется дальнейшее чтение, прочитайте книги ниже. Может ли математическое ожидание быть отрицательным? Разъяснено в блоге часто задаваемых вопросов
Могут ли ожидания быть отрицательными?
 … Поскольку ожидаемое значение охватывает действительные числа, оно обычно делится на числа с отрицательным, нейтральным и положительным значением.
… Поскольку ожидаемое значение охватывает действительные числа, оно обычно делится на числа с отрицательным, нейтральным и положительным значением. Что означает отрицательное ожидаемое значение?
Всегда ли математическое ожидание положительно?
Ожидаемое значение всегда отрицательное?
 Поэтому ваше ожидаемое значение будет отрицательным . Следовательно, это означает, что вы ПОТЕРЯЕТЕ деньги, а дом должен заработать деньги.
Поэтому ваше ожидаемое значение будет отрицательным . Следовательно, это означает, что вы ПОТЕРЯЕТЕ деньги, а дом должен заработать деньги. Может ли стоимость предприятия быть отрицательной? Как насчет стоимости капитала?
Может ли математическое ожидание быть равным нулю?
Равно ли математическое ожидание среднему?
Что такое физическое математическое ожидание?
 … Это фундаментальная концепция во всех областях квантовой физики.
… Это фундаментальная концепция во всех областях квантовой физики. Может ли ожидаемое значение быть меньше 1?
Что такое математическое ожидание вероятности?
Что означает положительное ожидаемое значение?
Какова формула ожидаемой стоимости?

Как вы интерпретируете ожидаемое значение?
Какие существуют два типа ожиданий?
Какие плохие ожидания?

Каковы реалистичные ожидания?
Является ли ожидаемое значение параметром?
Как рассчитать ожидаемый выигрыш?
Влияет ли размер выборки на ожидаемое значение?

Изменяется ли ожидаемое значение со временем?
Что подразумевается под ожидаемой ценностью оператора?
Каково математическое ожидание оператора Гамильтона?
В чем разница между средним и ожидаемым значением?
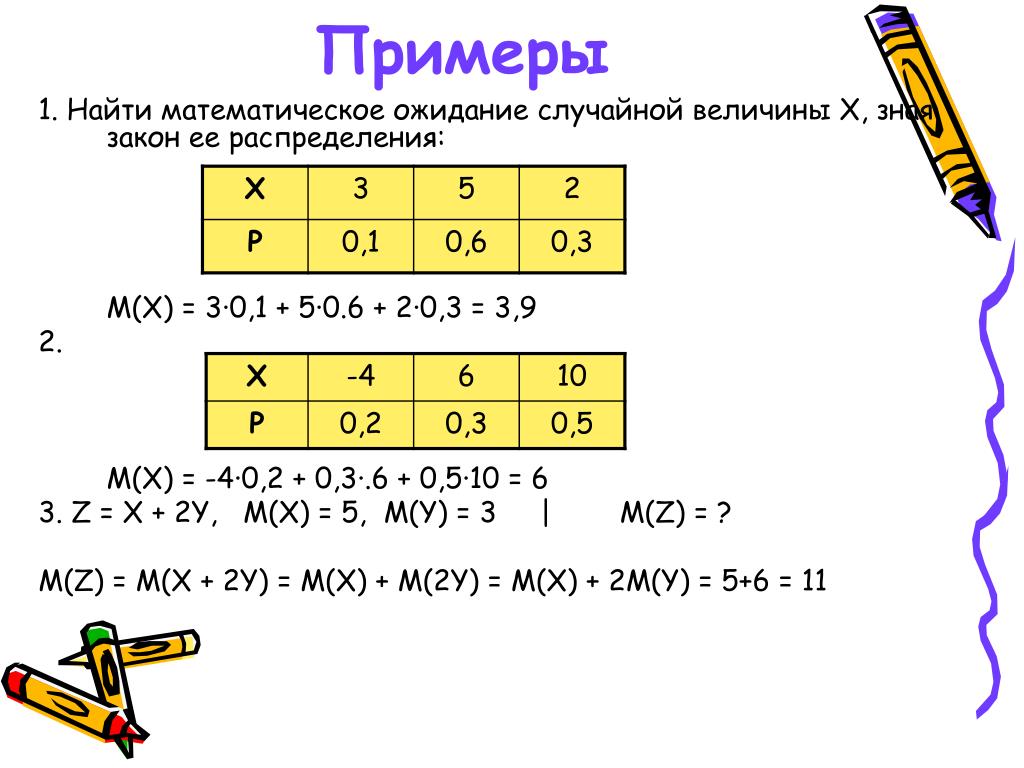 … В то время как среднее значение не учитывает вероятность, ожидание учитывает вероятность и взвешивается с учетом вероятности.
… В то время как среднее значение не учитывает вероятность, ожидание учитывает вероятность и взвешивается с учетом вероятности. В чем разница между средним и ожидаемым значением?
Ожидаемое значение совпадает со средним и средним?
Положительные и отрицательные ожидания в азартных играх

Каждая ставка имеет ожидаемое значение, даже если оно равно нулю

Концепция дома Edge
 За два подбрасывания монеты в среднем проигрывается 50 долларов на ставку. Поскольку 50 долларов составляют 50% от 100 долларов, мы бы сказали, что эта ставка имеет преимущество казино в 50%.
За два подбрасывания монеты в среднем проигрывается 50 долларов на ставку. Поскольку 50 долларов составляют 50% от 100 долларов, мы бы сказали, что эта ставка имеет преимущество казино в 50%. Что делать, если у вас есть преимущество перед казино?

Где можно получить преимущество в 1% над казино?
 Количество раздач в час, которые вы получаете в блэкджеке, зависит от количества игроков за столом. Если вы играете один на один с дилером, вы, очевидно, будете получать больше рук в час, чем если бы вы сидели за полным столом с шестью другими игроками в блэкджек.
Количество раздач в час, которые вы получаете в блэкджеке, зависит от количества игроков за столом. Если вы играете один на один с дилером, вы, очевидно, будете получать больше рук в час, чем если бы вы сидели за полным столом с шестью другими игроками в блэкджек. Значит ли это, что я могу разбогатеть, считая карты?

Как получить преимущество в блэкджеке?

Если все это правда, то почему не все разбогатеют на азартных играх?
 Некоторым людям — верьте или нет — не нравится играть в блэкджек. А некоторым любителям блэкджека не нравится строгость подсчета карт.
Некоторым людям — верьте или нет — не нравится играть в блэкджек. А некоторым любителям блэкджека не нравится строгость подсчета карт. Заключение

Ожидаемое значение в статистике: определение и расчеты
Ожидаемое значение — это именно то, что вы могли бы подумать, что оно означает интуитивно: возврат , который вы можете ожидать для какого-то действия , например, сколько вопросов вы можете ответить правильно, если угадаете в тесте с множественным выбором.
Вероятность (P) ответить на вопрос правильно, если вы угадаете: 0,25
Количество вопросов в тесте (n)*: 20
P x n = 0,25 x 20 = 5
(P(x) * n) . Для большинства простых событий вы будете использовать либо формулу ожидаемого значения биномиальной случайной переменной, либо формулу ожидаемого значения для нескольких событий.
Для большинства простых событий вы будете использовать либо формулу ожидаемого значения биномиальной случайной переменной, либо формулу ожидаемого значения для нескольких событий.
P(x) * X .
X — количество попыток, а P(x) — вероятность успеха. Например, если вы подбрасываете монету десять раз, вероятность выпадения орла в каждом испытании равна 1/2, поэтому ожидаемое значение (количество орлов, которое вы можете ожидать при 10 подбрасываниях монеты) равно:
P(x) * X = 0,5 * 10 = 5 Каково EV вашего выигрыша? Формула для расчета EV при наличии кратных вероятностей :
Каково EV вашего выигрыша? Формула для расчета EV при наличии кратных вероятностей :
Где Σ — обозначение суммирования. Другие формулы ожидаемого значения
Формула ожидаемого значения для произвольной функции
Формула ожидаемого значения для непрерывных случайных величин.
Символ «∫» называется интегралом, и он эквивалентен нахождению площади под кривой.
Формула ожидаемого значения для произвольной функции.
Вернуться к началу
Посмотрите видео для примера:  Продано две тысячи билетов. Какова ожидаемая стоимость вашего выигрыша?
Продано две тысячи билетов. Какова ожидаемая стоимость вашего выигрыша?
14 990 долл. США * 1/2000 = 7,495 долл. США,
(-10 долл. США) * (1 999/2 000) = -9,995 долл. США
7,495 долл. США + -9,995 долл. США = -2,5 долл. США.
Примечание по нескольким предметам : например, что если вы покупаете билет за 10 долларов, продано 200 билетов, и помимо автомобиля у вас есть дополнительные призы в виде проигрывателя компакт-дисков и набора багажа? Это означает (на английском языке): «Ожидаемое значение — это сумма всех выигрышей, умноженная на их индивидуальные вероятности».
Это означает (на английском языке): «Ожидаемое значение — это сумма всех выигрышей, умноженная на их индивидуальные вероятности».
Шаг 1: Введите значения в два столбца в Excel («x» в одном столбце и «f(x)» в другом.
Шаг 2: Щелкните пустую ячейку.
Шаг 3: Введите =СУММПРОИЗВ(A2:A6,B2:B6) в ячейку, где A2:A6 — фактическое расположение ваших переменных x, а f(x) — фактическое расположение ваших переменных f(x).
Шаг 4: Нажмите Enter
Вернуться к началу Формула ожидаемого значения для дискретной случайной величины:
Формула ожидаемого значения для дискретной случайной величины: Ожидаемое значение Дискретная случайная величина (дан список).
108 + 110 + 123 + 134 + 135 + 145 + 167 + 187 + 199 = 145,333.
Вот оно! Ожидаемое значение Дискретная случайная величина (дан «X»).
 Х — количество выпавших голов. Что такое ЭВ?
Х — количество выпавших голов. Что такое ЭВ?
Шаг 1: Определите возможные значения X. При подбрасывании трех монет вы можете получить от 0 до 3 решек. Таким образом, ваши значения для X равны 0, 1, 2 и 3.
E(X) = 0(1/8) + 1(3/8) + 2(3/8) + 3(1/ 8) = 3/2. Ожидаемое значение Дискретная случайная величина (данная формула f(x)).
Шаг 1. Вставьте значения «x» в первые несколько значений формулы одно за другим. Для этой конкретной формулы вы получите: 9.
= 1 + 1/2 + 1/4 + 1/8 + 1/16 + 1/32 = 1,96875. Возможно, вы захотите узнать, какой будет выплата, если вы пойдете вперед и потратите 1, 5 или даже 25 долларов.
Возможно, вы захотите узнать, какой будет выплата, если вы пойдете вперед и потратите 1, 5 или даже 25 долларов.
Что такое петербургский парадокс?
 Вы будете всегда впереди. Вы бы играли?
Вы будете всегда впереди. Вы бы играли? Игра «Парадокс Санкт-Петербурга».
 Речь шла об игре с подбрасыванием монеты. Предположим, друг попросил вас сыграть в игру с подбрасыванием монеты за 2 доллара. Предположим, что монета честная (т. е. не взвешенная). Вы подбрасываете монету до тех пор, пока не выпадет первая решка, после чего вы заработаете 2 $ n и игра закончится. Другими словами, если при первом броске выпадет решка, вы выиграете 2 9 долларов.1194 1 = 2 доллара. Если при третьем подбрасывании выпадет решка, вы выиграете 2 3 = 8 долларов. А если бы у вас была серия и при 20-м подбрасывании выпала решка, вы бы выиграли 2 20 = 1 048 576 долларов.
Речь шла об игре с подбрасыванием монеты. Предположим, друг попросил вас сыграть в игру с подбрасыванием монеты за 2 доллара. Предположим, что монета честная (т. е. не взвешенная). Вы подбрасываете монету до тех пор, пока не выпадет первая решка, после чего вы заработаете 2 $ n и игра закончится. Другими словами, если при первом броске выпадет решка, вы выиграете 2 9 долларов.1194 1 = 2 доллара. Если при третьем подбрасывании выпадет решка, вы выиграете 2 3 = 8 долларов. А если бы у вас была серия и при 20-м подбрасывании выпала решка, вы бы выиграли 2 20 = 1 048 576 долларов.
Р( и ) Премия Ожидаемый
выигрыш 1 1/2 $2 $1 2 1/4 $4 $1 3 1/8 $8 $1 4 1/16 $16 $1 5 1/32 $32 $1 6 1/64 64 $ $1 7 1/128 $128 $1 8 1/256 256 долларов $1 9 1/512 $512 $1 10 1/1024 $1024 $1 
 Вы не можете применить это правило к игре «Парадокс Санкт-Петербурга», потому что там равно без риска.
Вы не можете применить это правило к игре «Парадокс Санкт-Петербурга», потому что там равно без риска. Ссылки
Папулис, А. «Ожидаемая стоимость; дисперсия; Моменты». §5-4 в книге Вероятность, случайные величины и случайные процессы, 2-е изд. Нью-Йорк: McGraw-Hill, стр. 139-152, 1984.
Онлайн-калькулятор ожидаемой стоимости.
Стефани Глен . «Ожидаемое значение в статистике: определение и расчет» От StatisticsHowTo.com : Элементарная статистика для всех нас! https://www.statisticshowto.com/probability-and-statistics/expected-value/


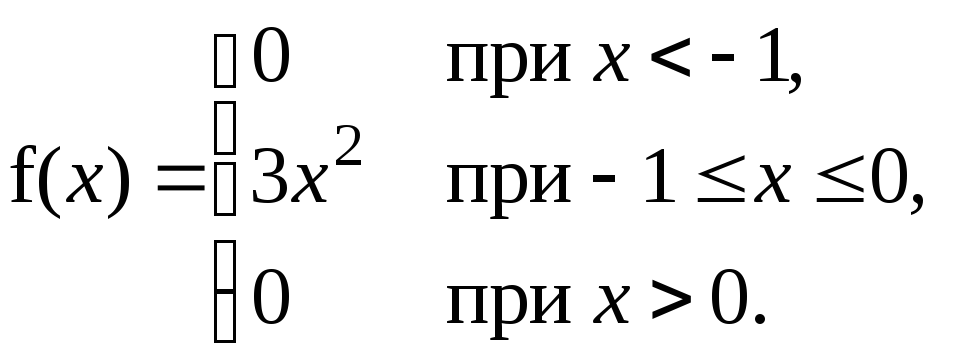


 Иногда вы можете выигрывать, но в целом вы потеряете больше, чем приобретете.
Иногда вы можете выигрывать, но в целом вы потеряете больше, чем приобретете.