На рисунке изображены графики функций f(x) = 3x + 3 и g(x) = ax2 + bх + с, которые пересекаются в точках А(–1; 0) и В(х0; у0). Найдите у0.
Источник: Ященко ЕГЭ 2022 (36 вар)
Решение:
f(x) = ах2 + bх + с – графиком, является парабола:
Коэффициент с равен координате у точки пересечения с осью у, т.е. с = –3.
Подставим координаты точек принадлежащих параболе в функцию (f(x) = ах2 + bх + с): (–4; –3) – в 1-е уравнение, (–2; 1)
Cложим уравнения:
0 + 4 = –8а + 4а + 2b – 2b
4 = –4a
a = 4/(–4) = –1
Подставим а = –1 во 2-е уравнение системы, найдём b:
1 = (–1)·(–2)2 + b·(–2) – 3
1 = – 4 – 3 –2b
–2b = 8
b = 8/(–2) = –4
Функция параболы имеет вид:
g(x) = –1·x2 – 4·x – 3
Найдём координаты абсцисс (х) точек пересечения функций:
f(x) = g(x)
–1·x2 – 4·x – 3 = 3x
–x2 – 4x – 3 – 3x – 3 = 0
–x2 – 7x – 6 = 0
D = (–7)2 – 4·(–1)·(–6) = 25 = 52
x_{1}=\frac{7+5}{2\cdot (–1)}=\frac{12}{–2}=-6\\x_{2}=\frac{7–5}{2\cdot (–1)}=\frac{2}{–2}=-1
У точки А координата х = –1, значит у точки В координата х0 = –6.
Подставим х0 = –6 точки В в функцию f(x) = 3x + 3, найдём y0:
y0 = 3·(–6) + 3 = –18 + 3 = –15
Ответ: –15.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4 / 5. Количество оценок: 32
Оценок пока нет. Поставь оценку первым.
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
- Запись опубликована:01.12.2021
- Рубрика записи10. Функции и их свойства
- Автор записи:Andrei Maniakin
Пошаговое решение :
Шаг 1 :
Уравнение в конце шага 1 :
((0 - 3x 2 ) + 30x) - 74 = 0
Шаг 2:
Шаг 3:
Вытягивая, как Условия:
3.
1. Вытягивание, как факторы:
-3x 2 + 30x — 74 = -1 • (3x 2 — 30x + 74).
Попытка факторинга путем разделения среднего члена
3.2 Факторизация 3x 2 — 30x + 74
Первый член равен 3x 2 , его коэффициент равен 3 .
Средний член равен -30x, его коэффициент равен -30.
Последний член, «константа», равен +74
Шаг-1: умножьте коэффициент первого члена на константу 3 • 74 = 222
Шаг-2: найдите два множителя 222, сумма которых равна коэффициенту среднего срока, что составляет -30 .
| -222 | + | -1 | = | -223 | |||||
| -111 | + | -2 | = | -113 | |||||
| -74 | + | -3 | = | -77 | |||||
| -37 | + | -6 | = | -43 | |||||
| -6 | + | -37 | = | -43 | |||||
| -3 | + | -74 | = | -77 | |||||
| -2 | + | -111 | = | -113 | |||||
| -1 | + | -222 | = | -223 | |||||
| 1 | + | 222 | = | 223 | |||||
| 2 | + | 111 | = | 113 | |||||
| 3 | + | 74 | = | 77 | |||||
| 6 | + | 37 | = | 43 | |||||
| 37 | + | 6 | = | 43 | |||||
| 74 | + | 3 | = | 77 | |||||
| 111 | + | 2 | = | 113 | |||||
| 222 | + | 1 | = | 223 | 1 | = | 223 9. 0048 |
Наблюдение: Невозможно найти два таких фактора !!
Вывод: Трехчлен нельзя разложить на множители
Уравнение в конце шага 3 :
-3x 2 + 30x - 74 = 0
Шаг 4 :
Парабола, нахождение вершины :
4.1 Найдите вершину y = -3x 2 +30x-74
Параболы имеют наивысшую или низшую точку, называемую вершиной. Наша парабола открывается вниз и, соответственно, имеет наивысшую точку (также известную как абсолютный максимум). Мы знаем это еще до того, как начертили «у», потому что коэффициент первого члена, -3 , отрицательный (меньше нуля).
Каждая парабола имеет вертикальную линию симметрии, проходящую через ее вершину. Из-за этой симметрии линия симметрии, например, будет проходить через середину двух точек пересечения x (корней или решений) параболы. То есть, если парабола действительно имеет два действительных решения.
Параболы могут моделировать многие ситуации из реальной жизни, такие как высота над землей объекта, брошенного вверх через некоторый период времени.
Вершина параболы может предоставить нам такую информацию, как максимальная высота, на которую может подняться объект, брошенный вверх. По этой причине мы хотим иметь возможность найти координаты вершины.
Для любой параболы, Ax 2 +Bx+C, x координата вершины определяется как -B/(2A) . В нашем случае x координата составляет 5,0000
Подключение к формуле параболы 5.0000 для x Мы можем рассчитать y -координату:
Y = -3,0 * 5,00 * 5,00 + 30,0 * 5,00 -74,0
или Y = 1,000
Parabola, 74,0
или Y = 1,000
, парабола, 74,0
или Y = 1,000
. Графические вершины и точки пересечения X:
Корневой график для: y = -3x 2 +30x-74
Ось симметрии (пунктирная) {x}={ 5,00}
Вершина в {x,y} = { 5,00, 1,00}
x -Отсечения (корни) :
Корень 1 при {x,y} = { 5,58, 0,00}
Корень 2 при {x,y} = { 4,42, 0,00}
Решите квадратное уравнение, заполнив квадрат
4.2 Решение -3x 2 +30x-74 = 0 путем заполнения квадрата.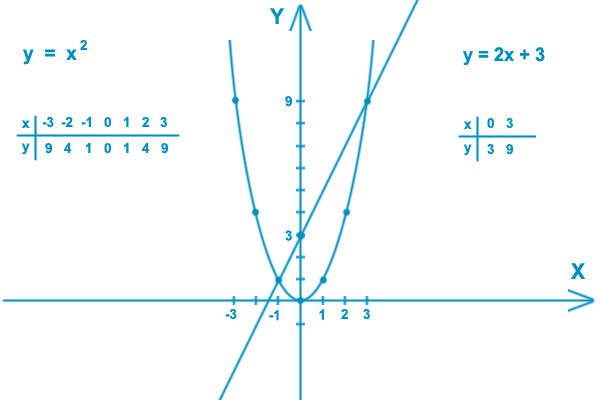
Умножьте обе части уравнения на (-1) , чтобы получить положительный коэффициент для первого члена:
3x 2 -30x+74 = 0 Поделите обе части уравнения на 3 , чтобы получить 1 в качестве коэффициента первого члена срок :
x 2 -10x+(74/3) = 0
Вычтите 74/3 из обеих частей уравнения:
x 2 -10x = -74/3
х, что равно 10, разделить на два, получится 5, и, наконец, возвести в квадрат, получится 25
. Прибавьте 25 к обеим частям уравнения: 74/3)+(25/1)
Общий знаменатель двух дробей равен 3 Добавление (-74/3)+(75/3) дает 1/3
Таким образом, прибавив к обеим сторонам, мы окончательно получим :
x 2 -10x+25 = 1/3
Добавление 25 дополнит левую часть до полного квадрата:
x 2 -10x+25 (5 = 9 002 x-5) • (x-5) =
(x-5) 2
Вещи, равные одной и той же вещи, также равны друг другу. Поскольку
x 2 -10x+25 = 1/3 и
x 2 -10x+25 = (x-5) 2
, то по закону транзитивности
(x-5) 2 = 1/3
Мы будем называть это уравнение уравнением #4.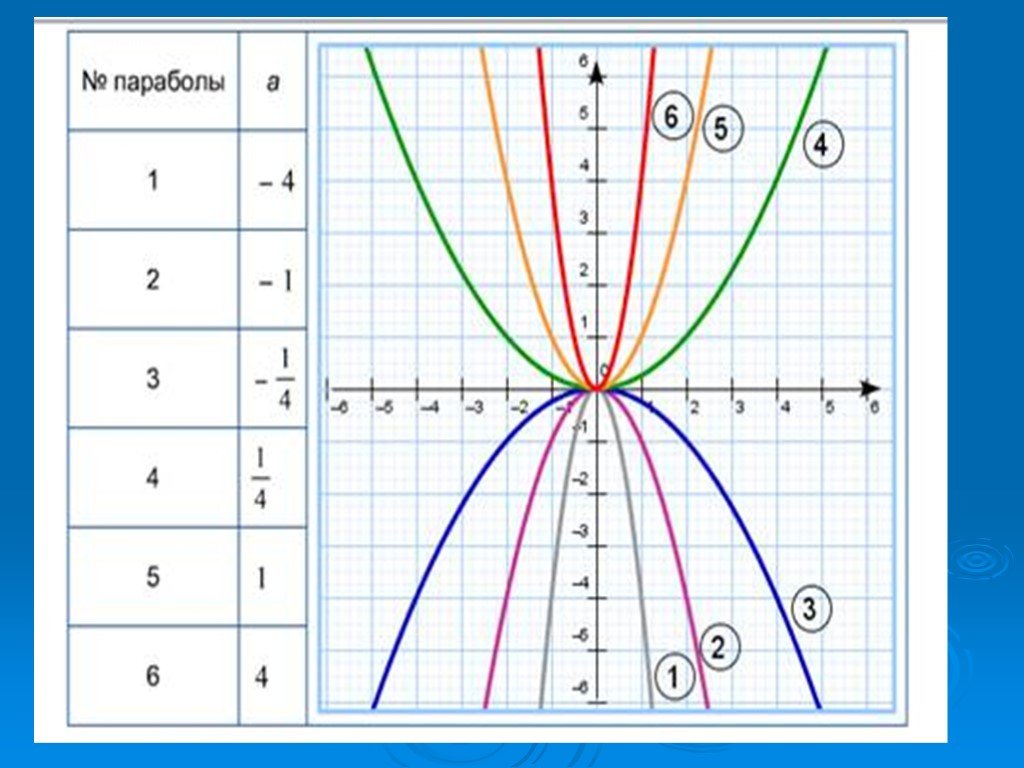
2.1
Принцип квадратного корня гласит, что когда две вещи равны, их квадратные корни равны.
Обратите внимание, что квадратный корень из
(x-5) 2 равен
(x-5) 2/2 =
(x-5) 1 = 9018 10x-5, применяя Принцип квадратного корня в уравнении #4.2.1 получаем:
x-5 = √ 1/3
Добавьте 5 к обеим сторонам, чтобы получить:
x = 5 + √ 1/3
Так как квадратный корень имеет два значения, одно положительное, а другое отрицательное
x 2 — 10x + (74/3) = 0
имеет два решения:
x = 5 + √ 1/3
или
x = 5 — √ 1/3
Обратите внимание, что √ 1/3 можно записать как
√ 1 / √ 3 , что равно 1/√ 3
. Обычно принято упрощать до тех пор, пока знаменатель не станет свободным от радикалов.
Здесь этого можно добиться, умножив числитель и знаменатель на √ 3
После этого умножения числовое значение 1 /√ 3 остается неизменным, так как оно умножается на √ 3 / √ 3 , что равно 1
Хорошо, давайте сделаем это:
1 • √ 3 1 • √ 3
—— ——————————— = ———————————
√ 3 • √ 3 3
Решение квадратного уравнения с помощью формулы квадратного уравнения
4.
3 Решение -3x 2 +30x-74 = 0 по квадратичной формуле.
Согласно квадратичной формуле, x , решение для Ax 2 +bx +c = 0, где A, B и C являются числами, часто называемыми коэффициентами, определяются как:
-B ± √ B 2 -4AC
x = ———————————————— ——
2A
В нашем случае A = -3
B = 30
C = -74
Соответственно, B 2 -4AC =
900 -888 =
12
Применение формулы квадрата:
-30 ± √ 12
x = ——————
– 2 √
можно упростить?
Да! Разложение числа 12 на простые множители – это
2•2•3
. Чтобы можно было удалить что-то из-под радикала, должно быть 2 этих экземпляра (потому что мы берем квадрат, т.е. второй корень).
√ 12 = √ 2•2•3 =
± 2 • √ 3
√ 3 , округленное до 4 десятичных знаков, равно 1,7321
Теперь мы рассматриваем:
x = ( -30 ± 2 • 1,732 ) / -6
Два действительных решения:
x = (-30+√12)/-6=5-1/3√ 3 = 4,423
или:
x = (-30-√12)/-6=5+1/3√ 3 = 5,577
Было найдено два решения:
- x = (-30-√12)/ -6=5+1/3√ 3 = 5,577
- x =(-30+√12)/-6=5-1/3√ 3 = 4,423
Parabolas — Xcelerate Math
Перед просмотром этой страницы, было бы полезно просмотреть следующие веб-страницы:
- Линейные графики
- Решение квадратных выражений путем факторизации
- Решение квадратных уравнений по формуле
Существует 4 графика, которые образуются при разрезании конуса плоской поверхностью.
- Парабола
- Круг
- Эллипс
- Гипербола
Параболические уравнения
U-образный график квадратного уравнения в виде y = ax 2 + bx + c называется параболой .
Примеры парабол включают:
- параболические зеркала, которые собирают и фокусируют солнечный свет для солнечного нагрева
- радиотелескопы, собирающие радиоволны от далеких звезд
- метание копья
- пинать футбольный мяч через стойки ворот
- запуск ракеты
корней уравнения являются точками, где парабола пересекает ось x . Эти решений, найденных с помощью факторизации или использования квадратичной формулы . Корней может быть два, один или вообще не быть.
Точка поворота — это точка поворота графика. The formula to find its x-value is:
| –b | |
| 2a |
Example One — Graph of y = x
2| x | – 3 | –2 | –1 | 0 | 1 | 2 | 3 |
| y = x 2 | 9 | 4 | 1 | 0 | 1 | 4 | 9 |
Example Two — Graph of y = 2x
2| x | –3 | –2 | –1 | 0 | 1 | 2 | 3 |
| y = 2x 2 | 18 | 8 | 2 | 0 | 2 | 8 | 18 |
Example Three — Graph of y = 3x
2| x | –3 | –2 | –1 | 0 | 1 | 2 | 3 |
| y = 3x 2 | 27 | 12 | 3 | 0 | 3 | 12 | 27 |
Вопрос
Посмотрите на крутизну графиков в примерах 1, 2 и 3.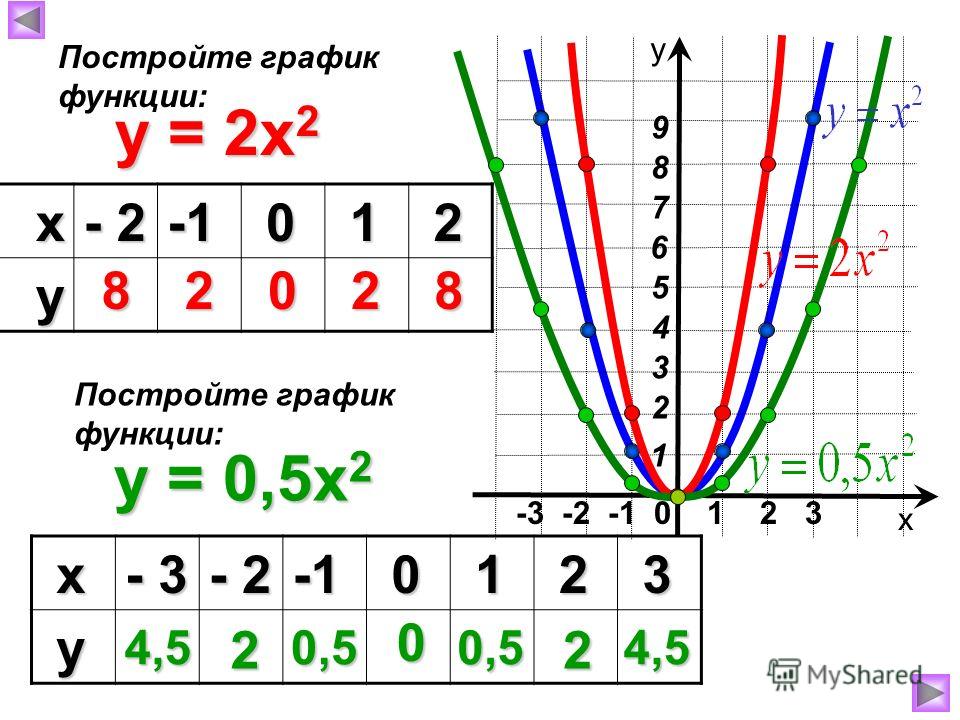
Как влияет коэффициент x 2 на крутизну параболы?
Example Four — Graph of y = –x
2| x | –3 | –2 | –1 | 0 | 1 | 2 | 3 |
| y = – х 2 | –9 | –4 | –1 | 0 | –1 | –4 | –9 |
Example Five — Graph of y = –2x
2| x | –3 | –2 | – 1 | 0 | 1 | 2 | 3 |
| y = –2x 2 | –18 | –8 | –2 | 0 | –2 | –8 | – 18 |
Пример 6. График y = –3x
2| x | –3 | –2 | –1 | 0 | 1 | 2 | 3 |
| y = –3x 2 | –27 | – 12 | –3 | 0 | –3 | –12 | –27 |
Вопрос
Просмотр на крутой эффект.
-эффективность x 2 имеют форму параболы?
Example Seven — Graph of y = x
2 + 3| x | –3 | –2 | –1 | 0 | 1 | 2 | 3 |
| y = X 2 + 3 | 12 | 7 | 4 | 3 | 4 | 7 | 12 |
Пример. Пример. Пример. Пример. Пример. Пример. Пример. Пример. Пример. Пример. Пример. Пример. Пример. Пример. Пример. Пример. Пример. Пример. Пример. Пример. Пример. Пример. Пример. Пример. Пример. Пример. Пример. Пример. Пример. Пример. Пример. Пример. Пример. Пример. Пример. Пример. Пример. Пример. Пример.0003
| x | –3 | –2 | –1 | 0 | 1 | 2 | 3 |
| y = x 2 – 4 | 5 | 0 | – 1 | –4 | –1 | 0 | 5 |
Вопрос
Посмотрите на круту или –3) иметь на позиции параболы?
Example Nine — Graph of y = x
2 – 6x + 8| x | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| y = x 2 – 6x + 8 | 8 | 3 | 0 | –1 | 0 | 3 | 8 |
Questions
ROOTS
При решении квадратного уравнения у = х 2 – 6x + 8 = 0 по факторизации или по формуле, x = 2 или 4.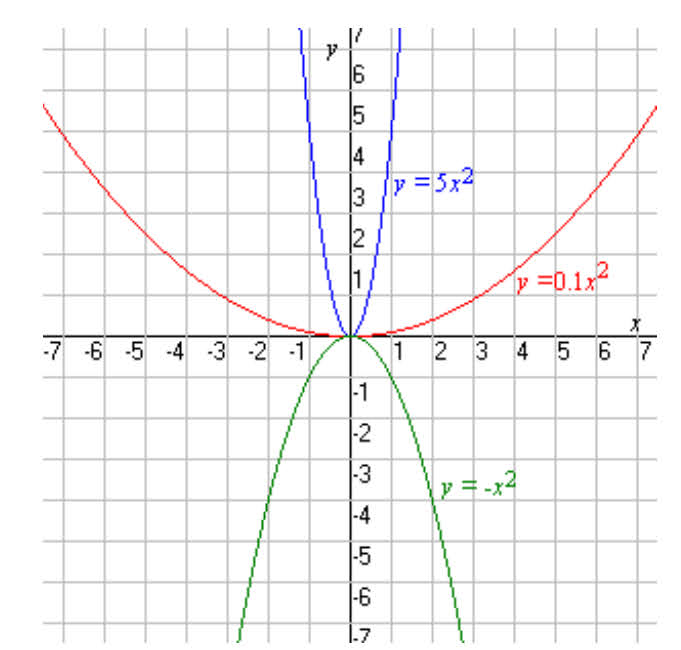
Это 2 корня уравнения.
Что вы заметили в этих корнях и точках, в которых парабола пересекает ось X?
ПОВОРОТ
Формула для нахождения значения x точки поворота параболы: x = –b/2a.
Используйте эту формулу, чтобы найти значение x, при котором график поворачивается. Подставьте это значение x в уравнение y = x 2 – 6x + 8, чтобы найти значение y точки поворота.
Что ты заметил?
Знаете ли вы, что…?
S.K.A. (массив квадратных километров) радиотелескопов в Австралии, Новой Зеландии и Южной Африке состоит из многочисленных параболических радиотелескопов , вместе с площадью сбора 1 квадратный километр. Когда в 2020 году Вселенная заработает, ее можно будет наблюдать в десять тысяч раз быстрее, чем это возможно в настоящее время.
Учтите, что когда мы смотрим на звезды, мы оглядываемся назад во времени. Свет далеких звезд покинул звезду и уже давно путешествует по космосу.
Например, свет от нашего Солнца достигает Земли за 8 минут.