Сообщество экспертов Автор24
Автор этой статьи Дата последнего обновления статьи: 09.12.2021
Выполнение любых типов работ по математике
Решение задач по комбинаторике на заказ Решение задачи Коши онлайн Математика для заочников Контрольная работа на тему числовые неравенства и их свойства Контрольная работа на тему умножение и деление рациональных чисел Контрольная работа на тему действия с рациональными числами Дипломная работа на тему числа Курсовая работа на тему дифференциальные уравнения Контрольная работа на тему приближенные вычисления Решение задач с инвариантами
Подбор готовых материалов по теме
Дипломные работы Курсовые работы Выпускные квалификационные работы Рефераты Сочинения Доклады Эссе Отчеты по практике Решения задач Контрольные работы
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия
| Справочник по математике | Алгебра | Координатная плоскость |
| Парабола на координатной плоскости |
| Решение квадратных неравенств |
Парабола на координатной плоскости
Определение 1. Параболой называют график функции
Параболой называют график функции
| y = a x2 , | (1) |
где a – любое число, не равное нулю. Точку О (0;0) называют вершиной параболы (1).
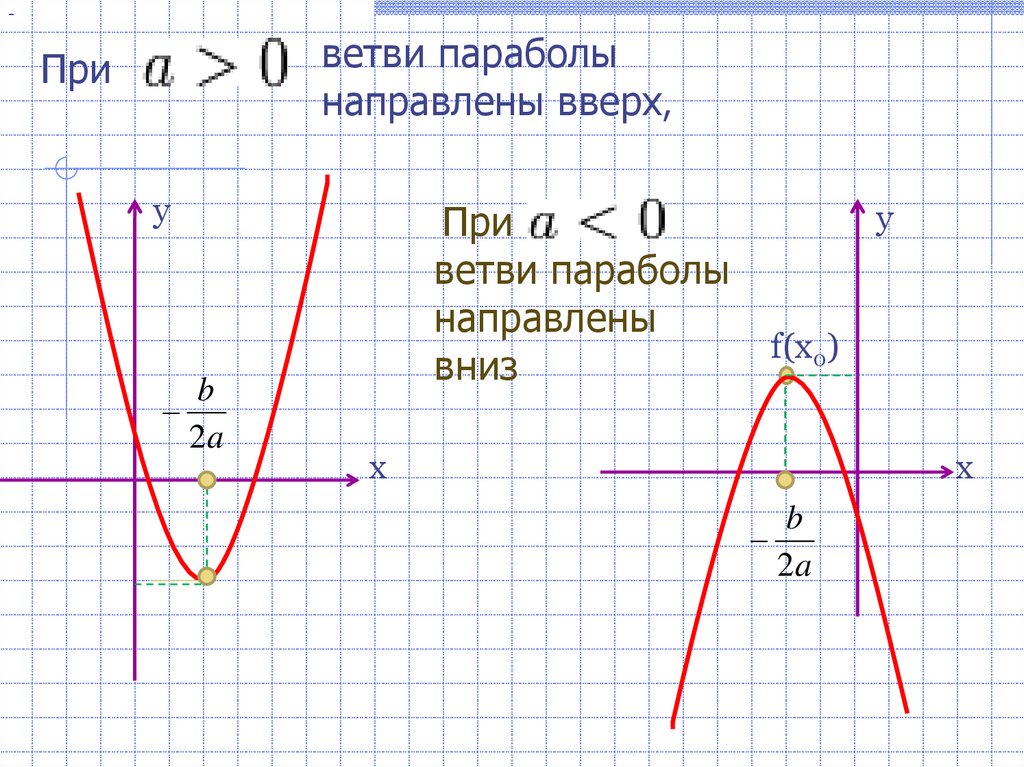
При a > 0 и a < 0 график функции (1) изображён на рисунках 1 и 2 соответственно.
| Рис.1 |
| Рис.2 |
| Рис.1 |
| Рис.2 |
Функция (1) обладает следующими свойствами:
- областью определения функции функции (1) является вся числовая ось;
- функция (1) является четной функцией, поскольку для всех значений аргумента выполнено равенство
- при a > 0 функция (1) убывает на интервале и возрастает на интервале ;
при a < 0 функция (1) возрастает на интервале и убывает на интервале ; - при a > 0 у функции (1) существует единственный минимум на всей области определения, который достигается в точке x = 0 ;
- при a < 0 у функции (1) существует единственный максимум на всей области определения, который достигается в точке x = 0 ;
- при a > 0 ветви параболы (1) направлены вверх;
- при a < 0 ветви параболы (1) направлены вниз;
- и при a > 0, и при a < 0 вершиной параболы (1) является начало координат;
- и при a > 0, и при a < 0 осью симметрии параболы (1) является ось ординат.

y (x) = y (– x) ;
Рассмотрим теперь функцию, заданную формулой
| y = a x2 + b x + c , | (2) |
где a, b, c – любые числа, но число a не равно нулю.
Поскольку выражение, стоящее в правой части формулы (2), является квадратным трёхчленом, то, в соответствии с материалом, изложенным в разделе «Квадратные уравнения», формулу (2) можно переписать в виде
| (3) |
Из формулы (3) вытекает, что график функции (2) может быть получен из графиков, изображенных на рисунках 1 или 2 (в зависимости от знака числа a) при помощи параллельного переноса, в результате которого вершина параболы (1) передвигается из начала координат в точку V (рис. 3, 4) с координатами
| (4) |
Рис.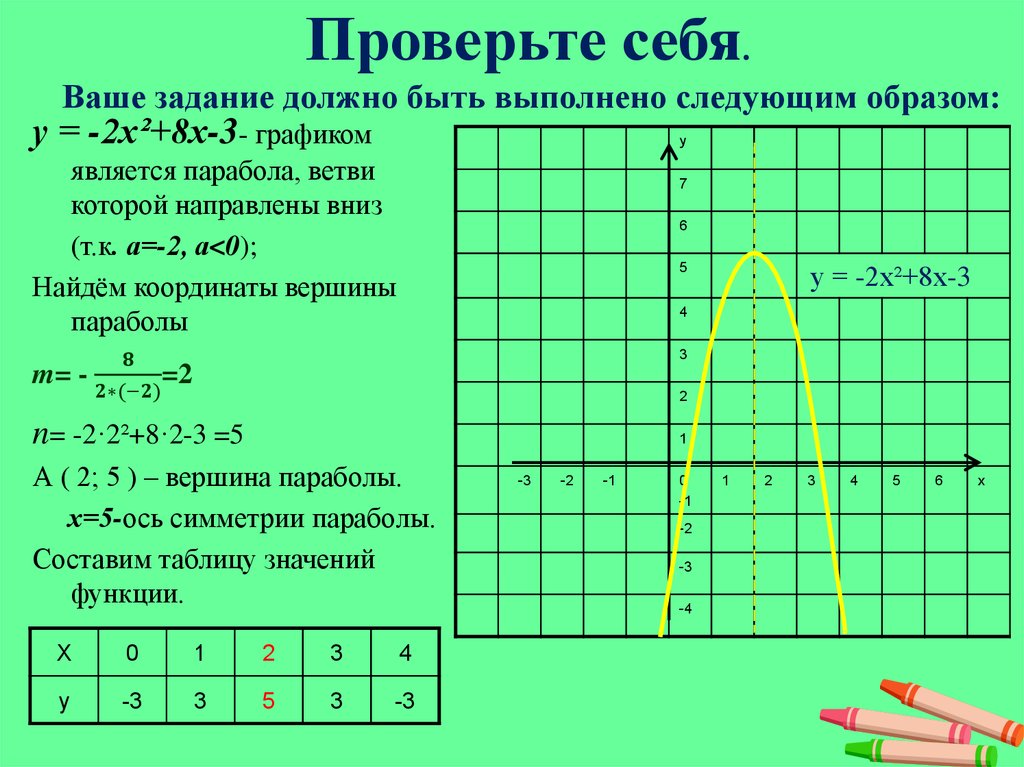 3 3 | Рис.4 |
| Рис.3 |
| Рис.4 |
| Рис.3 |
| Рис.4 |
Поскольку дискриминант квадратного трёхчлена вычисляется по формуле
| D = b2 – 4ac , | (5) |
то координаты вершины параболы (3), определяемые по формуле (4), можно записать так:
| (6) |
Замечание. При a > 0 ветви параболы (2) направлены вверх, при a < 0 ветви параболы (2) направлены вниз. Парабола (2) пересекает ось ординат в точке с координатами (0; c).
Решение квадратных неравенств
Зная расположение параболы (2) на координатной плоскости, можно, в частности, решать квадратные неравенства
как показано в следующей таблице.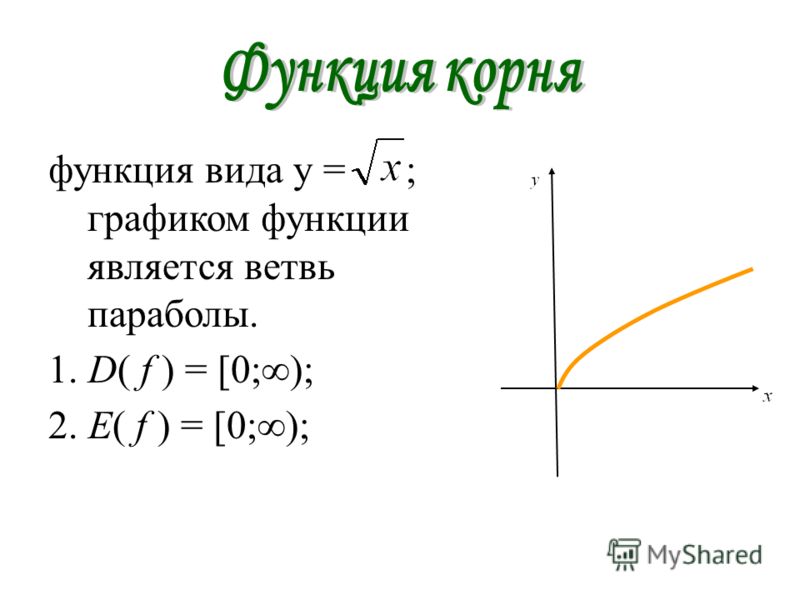
| ||||||||||||||||
| ||||||||||||||||
| ||||||||||||||||
| ||||||||||||||||
| ||||||||||||||||
|
| Знаки чисел a и D: a > 0, D > 0 |
| Корни уравнения a x2 + b x + c = 0 : |
| два различных корня: x1 и x2 |
| Расположение вершины: |
| под осью Ox |
| Пересечения с осью Ox : |
| Решение неравенства a x2 + b x + c > 0 : |
| Решение неравенства : |
| Решение неравенства a x2 + b x + c < 0 : |
| Решение неравенства : |
| Знаки чисел a и D: a > 0, D = 0 |
| Корни уравнения a x2 + b x + c = 0 : |
| два совпавших корня: x1 = x2 |
| Расположение вершины: |
| лежит на оси Ox |
| Пересечения с осью Ox : |
| касается в точке x1 |
| Решение неравенства a x2 + b x + c > 0 : |
| Решение неравенства : |
| Решение неравенства a x2 + b x + c < 0 : |
| Решение неравенства : |
| x = x1 |
| Знаки чисел a и D: a > 0, D < 0 |
| Корни уравнения a x2 + b x + c = 0 : |
| корней нет |
| Расположение вершины: |
| над осью Ox |
| Пересечения с осью Ox : |
| не пересекает |
| Решение неравенства a x2 + b x + c > 0 : |
| Решение неравенства : |
| Решение неравенства a x2 + b x + c < 0 : |
| Решение неравенства : |
| Знаки чисел a и D: a < 0, D > 0 |
| Корни уравнения a x2 + b x + c = 0 : |
| два различных корня: x1 и x2 |
| Расположение вершины: |
| над осью Ox |
| Пересечения с осью Ox : |
| в точках x1 и x2 |
| Решение неравенства a x2 + b x + c > 0 : |
| Решение неравенства : |
| Решение неравенства a x2 + b x + c < 0 : |
| Решение неравенства |
| Знаки чисел a и D: a < 0, D = 0 |
| Корни уравнения a x2 + b x + c = 0 : |
| два совпавших корня: x1 = x2 |
| Расположение вершины: |
| лежит на оси Ox |
| Пересечения с осью Ox : |
| касается в точке x1 |
| Решение неравенства a x2 + b x + c > 0 : |
| Решение неравенства : |
| x = x1 |
| Решение неравенства a x2 + b x + c < 0 : |
| Решение неравенства |
| Знаки чисел a и D: a < 0, D < 0 |
| Корни уравнения a x2 + b x + c = 0 : |
| корней нет |
| Расположение вершины: |
| под осью Ox |
| Пересечения с осью Ox : |
| не пересекает |
| Решение неравенства a x2 + b x + c > 0 : |
| Решение неравенства : |
| Решение неравенства a x2 + b x + c < 0 : |
| Решение неравенства : |
На нашем сайте можно также ознакомиться нашимиучебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Как построить параболу — Криста Кинг Математика
Завершите квадрат, чтобы преобразовать стандартную форму в вершинную
В этом уроке мы научимся определять характеристики параболы и переходить от алгебраической формы к графической.
Привет! Я Криста.
Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.
Квадратные уравнения создают параболы при отображении на графике, поэтому они являются нелинейными функциями. Есть две формы, которые особенно полезны, когда вы хотите что-то узнать о параболе.
Как преобразовать Стандартную форму в Вершинную:
Чтобы преобразовать Стандартную форму в Вершинную, заполните квадрат
Чтобы преобразовать Вершинную форму в Стандартную, разверните квадрат, затем распределите и упростите
Давайте поговорим о различных частях параболы.
Как в стандартной, так и в вершинной форме, если ???a>0???, парабола открывается вверх и вершина имеет минимальное значение.
Как в стандартной, так и в вершинной форме, если ???a<0??? парабола открывается вниз, а вершина имеет максимальное значение.
Как построить параболу
92+3x-\frac{1}{2}???Получить доступ к полному курсу Алгебра 2
Начать
Изучение математикиКриста Кинг математика, изучение онлайн, онлайн-курс, онлайн-математика, алгебра, алгебра 2, алгебра II, построение графиков, параболы, построение графиков парабол, квадратика, квадратичные функции, форма вершины, стандартная форма, форма вершины парабола, стандартная форма параболы
0 лайковКак найти фокус параболы.
 Простое руководство
Простое руководствоКак найти фокус параболы. Простое руководство
Шарлотта Тейлор
17 февраля 2021 г.
Математика
Если вы хотите знать, как найти фокус параболы, вам сначала нужно определить, что такое парабола. Парабола — это изогнутая фигура, в которой любая точка на кривой находится на равном расстоянии от фиксированной точки (называемой фокусом) и фиксированной прямой линии (называемой директрисой).
Определим части параболической функции. На приведенном выше графике вы видите заданную линию, пересекающую директрису под углом 90 градусов. Эта прямая называется осью симметрии. Точка, отмеченная C , обозначающая, где открывается парабола, называется вершиной. Вершина всегда находится посередине между фокусом и директрисой параболы.
Уравнение параболы
Приведенный выше график является базовым представлением параболы с координатами вершины (0,0). Когда вы проводите ось симметрии через вершину параболы, вы видите, что эта вертикальная линия идеально совпадает с осью Y графика. Эта парабола представлена уравнением
Эта парабола представлена уравнением
Если эту параболу повернуть на 90 градусов вправо, то фиксированная линия, представляющая ось симметрии, будет располагаться вдоль оси x. Уравнение параболы теперь .
Стандартная форма уравнения параболы, где коническая форма параболы формируется вдоль оси y, . Коэффициенты h и k представляют точки вершины. Коэффициент p представляет собой расстояние от вершины до фокуса, равное расстоянию от вершины до директрисы.
Как найти фокус параболы
Чтобы найти фокус параболы, вы должны знать, что уравнение параболы в вершинной форме имеет вид y=a(x−h)2+k, где a представляет наклон уравнения. Из формулы видно, что координаты фокуса параболы равны (h, k+1/4a).
Итак, теперь давайте решим для фокуса параболы ниже:
Когда мы используем вышеуказанные координаты, уравнение параболы выше . Мы можем подключиться к a и (0,0) для вершины. Теперь найдем координату y фокуса:
Мы определили, что точки фокуса равны (0,2).