Кубическая парабола
Кубическая парабола задается функцией . Вот знакомый со школы чертеж:
Перечислим основные свойства функции
Область определения – любое действительное число: .
Область значений – любое действительное число: .
Функция является нечётной. Если функция является нечётной, то ее график симметричен относительно начала координат. Аналитически нечётность функции выражается условием . Выполним проверку для кубической функции, для этого вместо «икс» подставим «минус икс»: , значит, функция является нечетной.
Функция не ограничена. На языке пределов функции это можно записать так: , Кубическую параболу тоже эффективнее строить с помощью Анфисы Чеховой алгоритма «челнока»:
Наверняка,
вы заметили, в чем ещё проявляется
нечетность функции. Если мы нашли, что
,
то при вычислении
уже
не нужно ничего считать, автоматом
записываем, что
.
Теперь немного поговорим о графиках многочленов.
График любого многочлена третьей степени ( ) принципиально имеет следующий вид:
В этом примере коэффициент при старшей степени , поэтому график развёрнут «наоборот». Принципиально такой же вид имеют графики многочленов 5-ой, 7-ой, 9-ой и других нечетных степеней. Чем выше степень, тем больше промежуточных «загибулин».
Многочлены 4-ой, 6-ой и других четных степеней имеют график принципиально следующего вида:
Эти знания полезны при исследовании графиков функций.
График функции
Выполним чертеж:
Основные свойства функции :
Область определения: .
Область значений: .
То есть, график функции полностью находится в первой координатной четверти.
Функция
не
ограничена сверху.
Или с помощью предела:
При построении простейших графиков с корнями также уместен поточечный способ построения, при этом выгодно подбирать такие значения «икс», чтобы корень извлекался нацело:
На самом деле хочется разобрать еще примеры с корнями, например, , но они встречаются значительно реже. Я ориентируюсь на более распространенные случаи, и, как показывает практика, что-нибудь вроде приходиться строить значительно чаще. Если возникнет необходимость выяснить, как выглядят графики с другими корнями, то, рекомендую заглянуть в школьный учебник или математический справочник.
График гиперболы
Опять же вспоминаем тривиальную «школьную» гиперболу .
Выполним чертеж: Основные свойства функции :
Область значений: .
Запись обозначает: «любое действительное число, исключая ноль»
В
точке
функция
терпит бесконечный разрыв.
Или с
помощью одностороннихпределов:
,
.
Немного поговорим об односторонних
пределах. Запись
обозначает,
что мы бесконечно
близко приближаемся
по оси
к
нулю слева.
Как при этом ведёт себя график? Он уходит
вниз на минус бесконечность, бесконечно
близко приближаясь
к оси
.
Именно этот факт и записывается
пределом
.
Аналогично, запись
обозначает,
что мы бесконечно
близко приближаемся
по оси
к
нулю справа.
При этом ветвь гиперболы уходит вверх
на плюс бесконечность,бесконечно
близко приближаясь
к оси
.
Или коротко:
.
В данном случае ось является вертикальной асимптотой для графика гиперболы при .
Будет
ГРУБОЙ ошибкой, если при оформлении
чертежа по небрежности допустить
пересечение графика с асимптотой.
Также односторонние пределы , говорят нам о том, что гипербола не ограничена сверху и не ограничена снизу.
Исследуем функцию на бесконечности: , то есть, если мы начнем уходить по оси влево (или вправо) на бесконечность, то «игреки» стройным шагом будут бесконечно близко приближаться к нулю, и, соответственно, ветви гиперболы бесконечно близкоприближаться к оси .
Функция является нечётной, а, значит, гипербола симметрична относительно начала координат. Данный факт очевиден из чертежа, кроме того, легко проверяется аналитически: .
График
функции вида ( )
представляют собой две ветви гиперболы.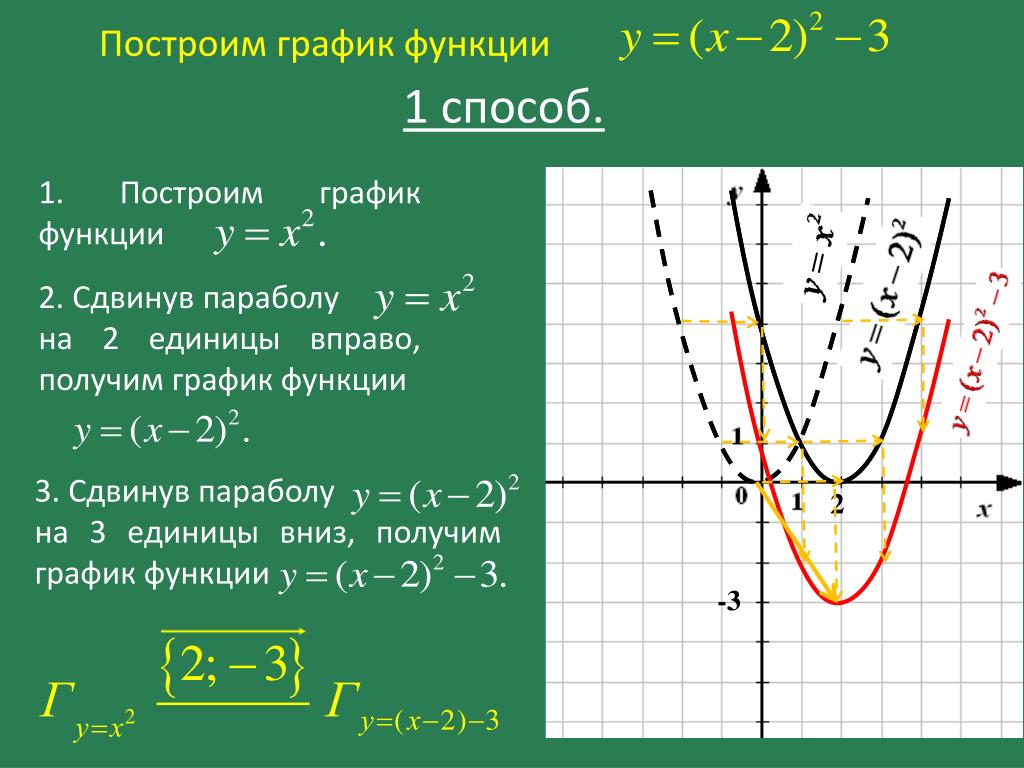
Если , то гипербола расположена в первой и третьей координатных четвертях(см. рисунок выше).
Если , то гипербола расположена во второй и четвертой координатных четвертях.
Пример 3
Построить правую ветвь гиперболы
Используем поточечный метод построения, при этом, значения выгодно подбирать так, чтобы делилось нацело:
Выполним чертеж:
Не составит труда построить и левую ветвь гиперболы, здесь как раз поможет нечетность функции. Грубо говоря, в таблице поточечного построения мысленно добавляем к каждому числу минус, ставим соответствующие точки и прочерчиваем вторую ветвь.
Что означает c в параболе. Построение графика квадратичной функции. Визуальный гид (2019)
Как построить параболу? Существует несколько способов построения графика квадратичной функции.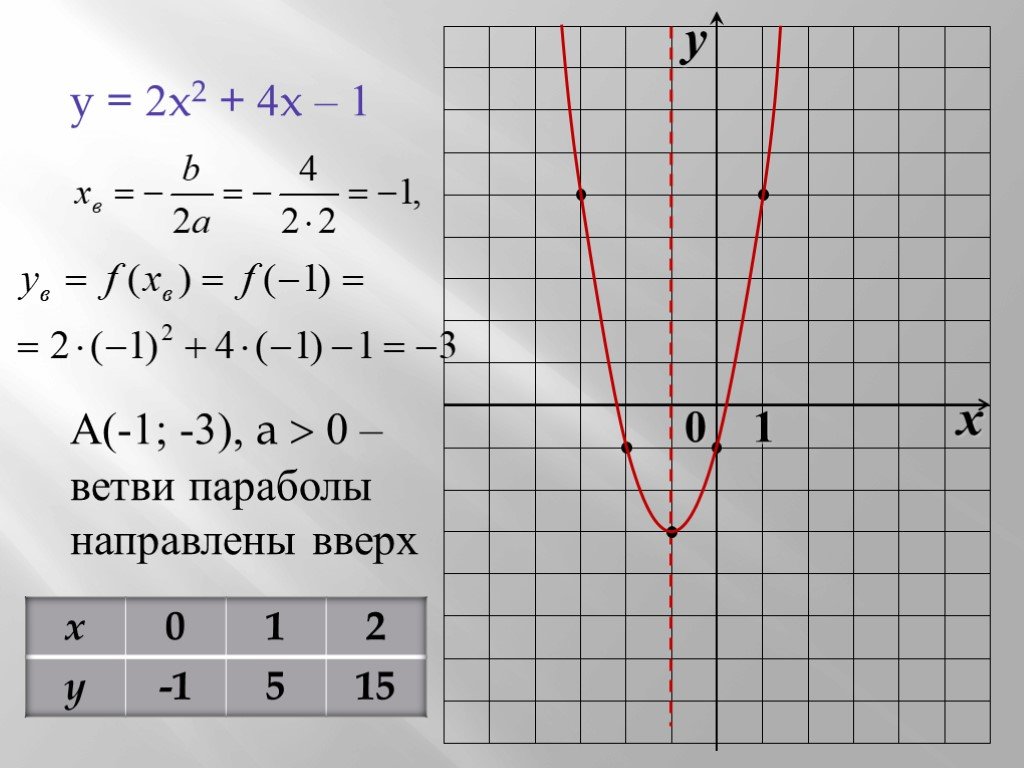
Каждый из них имеет свои плюсы и минусы. Рассмотрим два способа.
Начнём с построения графика квадратичной функции вида y=x²+bx+c и y= -x²+bx+c.
Пример.
Построить график функции y=x²+2x-3.
Решение:
y=x²+2x-3 — квадратичная функция. График — парабола ветвями вверх. Координаты вершины параболы
От вершины (-1;-4) строим график параболы y=x²(как от начала координат. Вместо (0;0) — вершина (-1;-4). От (-1;-4) идём вправо на 1 единицу и вверх на 1 единицу, затем влево на 1 и вверх на 1; далее: 2 — вправо, 4 — вверх, 2- влево, 4 — вверх; 3 — вправо, 9 — вверх, 3 — влево, 9 — вверх. Если этих 7 точек недостаточно, далее — 4 вправо, 16 — вверх и т. д.).
График квадратичной функции y= -x²+bx+c — парабола, ветви которой направлены вниз. Для построения графика ищем координаты вершины и от неё строим параболу y= -x².
Пример.
Построить график функции y= -x²+2x+8.
Решение:
y= -x²+2x+8 — квадратичная функция.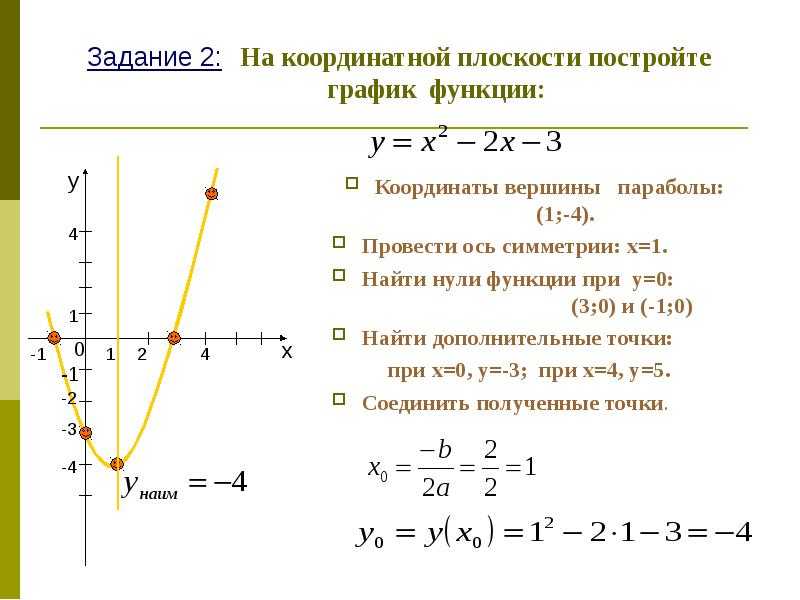
График — парабола ветвями вниз. Координаты вершины параболы
От вершины строим параболу y= -x² (1 — вправо, 1- вниз; 1 — влево, 1 — вниз; 2 — вправо, 4 — вниз; 2 — влево, 4 — вниз и т. д.):
Этот способ позволяет построить параболу быстро и не вызывает затруднений, если вы умеете строить графики функций y=x² и y= -x². Недостаток: если координаты вершины — дробные числа, строить график не очень удобно. Если требуется знать точные значения точек пересечения графика с осью Ох, придется дополнительно решить уравнение x²+bx+c=0 (или —x²+bx+c=0), даже если эти точки непосредственно можно определить по рисунку.
Другой способ построения параболы — по точкам, то есть можно найти несколько точек графика и через них провести параболу (с учетом того, что прямая x=хₒ является её осью симметрии). Обычно для этого берут вершину параболы, точки пересечения графика с осями координат и 1-2 дополнительные точки.
Построить график функции y=x²+5x+4.
Решение:
y=x²+5x+4 — квадратичная функция.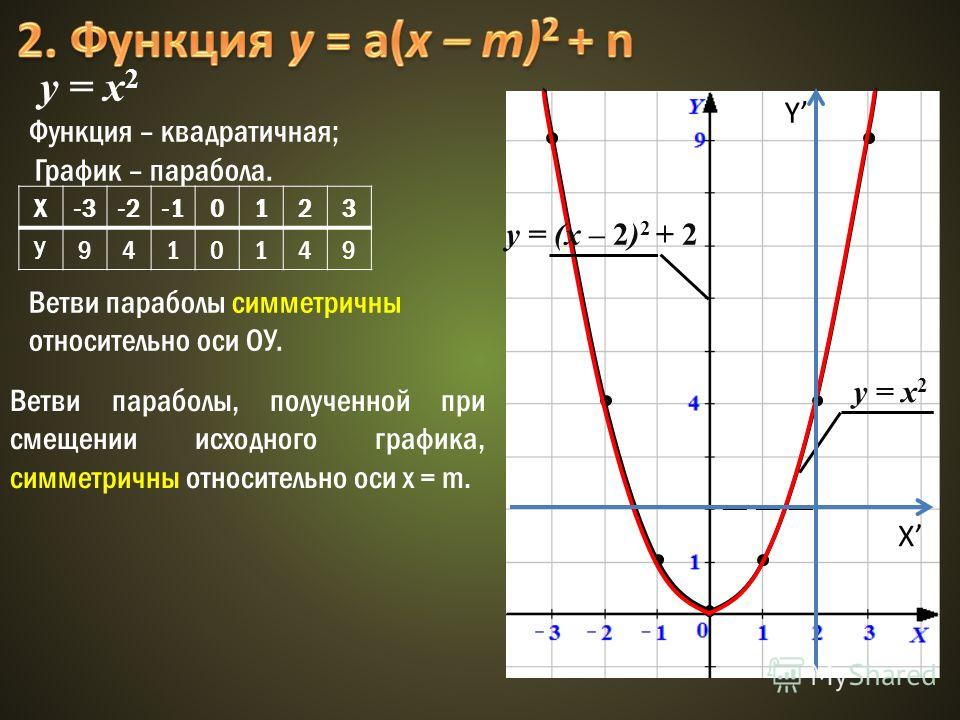
то есть вершина параболы — точка (-2,5; -2,25).
Ищем . В точке пересечения с осью Ох y=0: x²+5x+4=0. Корни квадратного уравнения х1=-1, х2=-4, то есть получили две точки графике (-1; 0) и (-4; 0).
В точке пересечения графика с осью Оy х=0: y=0²+5∙0+4=4. Получили точку (0; 4).
Для уточнения графика можно найти дополнительную точку. Возьмем х=1, тогда y=1²+5∙1+4=10, то есть еще одна точка графика — (1; 10). Отмечаем эти точки на координатной плоскости. С учетом симметрии параболы относительно прямой, проходящей через её вершину, отметим еще две точки: (-5; 6) и (-6; 10) и проведем через них параболу:
Построить график функции y= -x²-3x.
Решение:
y= -x²-3x — квадратичная функция. График — парабола ветвями вниз. Координаты вершины параболы
Вершина (-1,5; 2,25) — первая точка параболы.
В точках пересечения графика с осью абсцисс y=0, то есть решаем уравнение -x²-3x=0.
При х=1 y=-1²-3∙1=-4, то есть (1; -4) — дополнительная точка для построения графика.
Построение параболы по точкам — более трудоёмкий, по сравнению с первым, способ. Если парабола не пересекает ось Oх, дополнительных точек потребуется больше.
Прежде чем продолжить построение графиков квадратичных функций вида y=ax²+bx+c, рассмотрим построение графиков функций с помощью геометрических преобразований. Графики функций вида y=x²+c также удобнее всего строить, используя одно из таких преобразований — параллельный перенос.
Рубрика: |Как сделать параболическую тарелку для микрофона
Видеооператоры знают, что правило номер один для записи высококачественного звука — расположить микрофон как можно ближе к объекту съемки. В большинстве случаев это означает размещение звукоснимателя в нескольких дюймах от источника звука.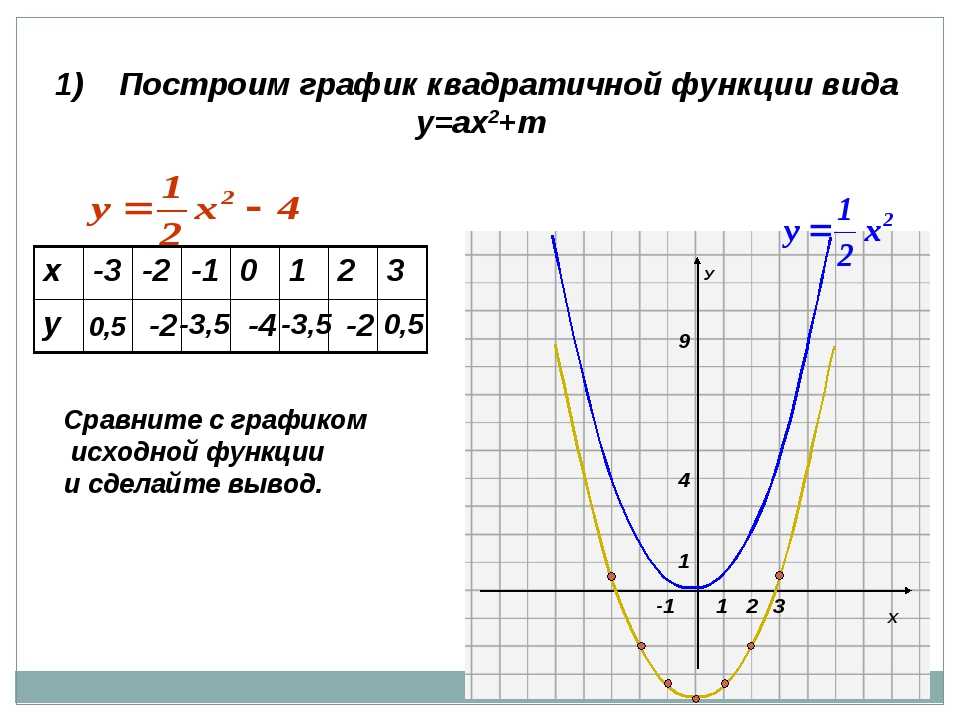
Мы можем пойти на многое, чтобы расположить наши микрофоны как можно ближе к объектам съемки. Но иногда это не выход. Бывают случаи, когда вы просто не можете расположить микрофон близко к объекту съемки. Введите параболический микрофон.
Возможно, вам нужно запечатлеть крики койотов или песни пересмешников. Может быть, вы хотите записать темп квотербека (без захвата себя). Или, может быть, вам нужно потихоньку обезопасить свой звук, как шпион, для вашего шоу со скрытой камерой и криминалом. Иногда для производства требуется, чтобы вы приблизили этот микрофон, но это может поставить под угрозу вашу жизнь, повредить ваше оборудование или раскрыть ваше прикрытие. Параболическая антенна для микрофона может быть самым звуковым решением.
Микрофон Para-what-ic?
Параболическая тарелка — это математическое чудо, которое собирает и фокусирует световые и звуковые волны в одной точке. Они используются в фарах, солнечных плитах и приемниках спутникового телевидения. Параболическая тарелка микрофона использует геометрию, чтобы превратить обычный микрофон в сверхнаправленный микрофон-монстр.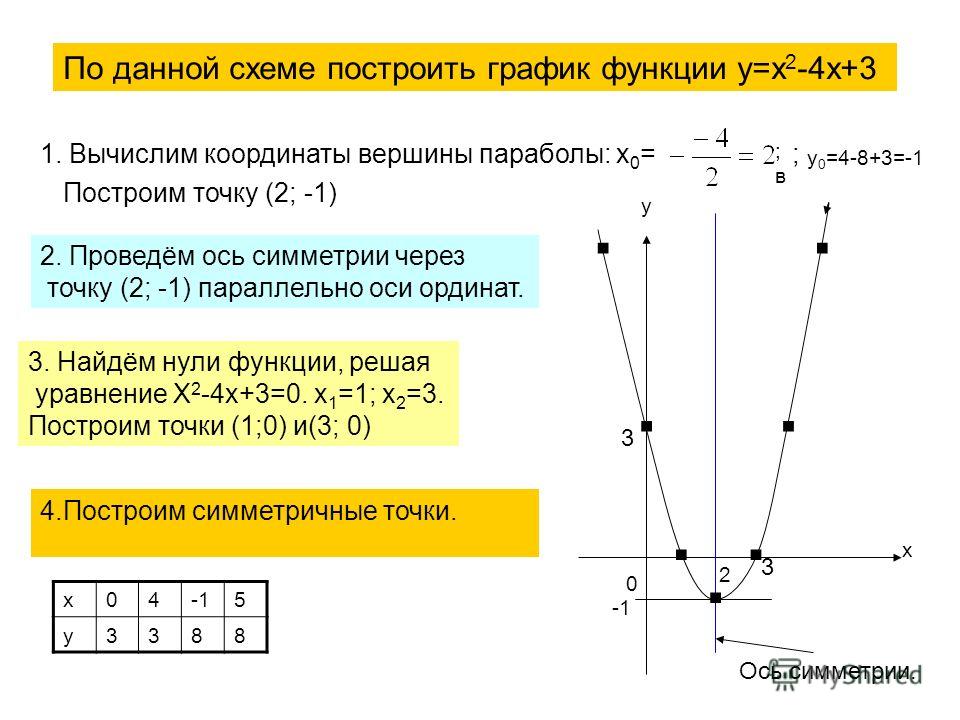
Это позволяет записывать чистый звук на расстоянии нескольких сотен футов. Если вы не снимаете видео о спорте или дикой природе, вы можете использовать параболическую установку только в редких случаях.
Реклама
Если вы не готовы инвестировать в профессиональную параболу, вы можете сделать свою собственную параболическую антенну для микрофона. Для этого потребуется всего несколько простых инструментов и материалов, которые у вас уже могут быть. Ваша самодельная параболическая тарелка может работать не так хорошо, как профессионально изготовленная модель. Это решение значительно улучшит вашу способность улавливать звуковые волны и может обеспечить всю необходимую вам мощность. Перед началом сборки важно знать, как работает параболическая антенна для микрофона.
Параболический микрофон наука
Параболического микрофона не существует. Когда мы говорим о параболическом микрофоне, мы на самом деле имеем в виду запись звука с помощью обычного микрофона, усиленного параболической тарелкой.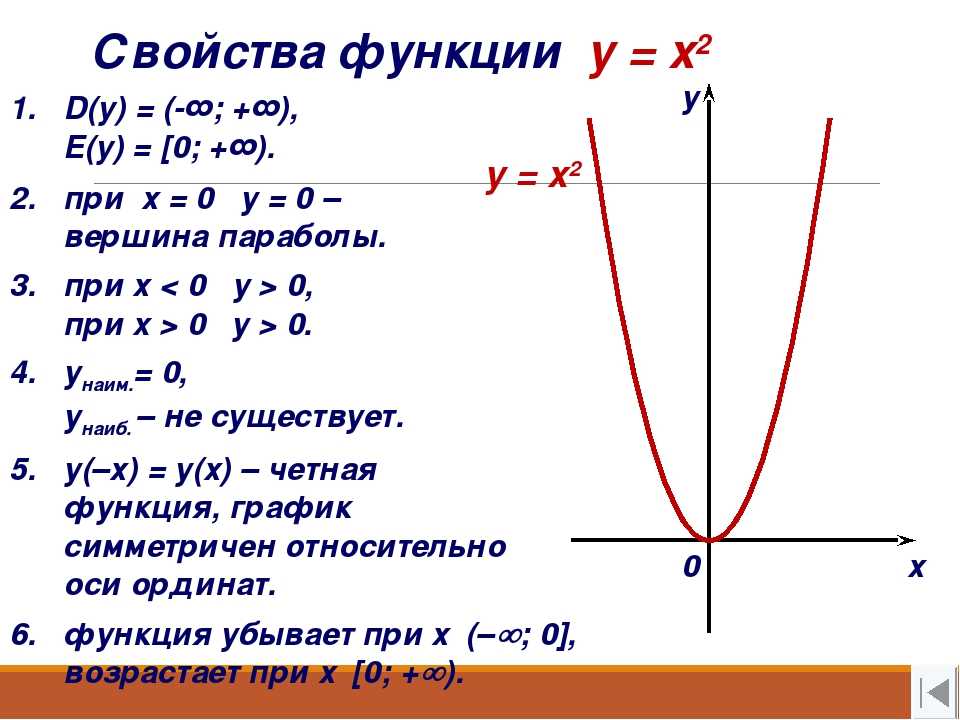
Парабола — это определенная геометрическая кривая, обладающая определенным математическим свойством. Когда прямая линия достигает какой-либо точки на внутренней поверхности параболической кривой, она отражается от склона в единую общую точку с центром перед кривой. Это положение является фокусом параболы.
С точки зрения звука это означает, что когда несколько звуковых волн от источника звука ударяются о наклонную внутреннюю стенку тарелки, они отражаются обратно в сфокусированное положение перед диском. Когда шквал звуковых волн попадает на параболическую тарелку, волны собираются вместе в фокусе. Обычный микрофон в правильном положении может зафиксировать удивительное аналоговое усиление источника звука.
Выбор микрофона
Производительность и функциональность параболической антенной тарелки в большей степени зависят от формы и конструкции, чем от качества самого микрофона. Однако наличие хорошего микрофона не помешает.
Передатчик с беспроводным микрофоном лежит на столе рядом с параболической тарелкой, сделанной своими руками.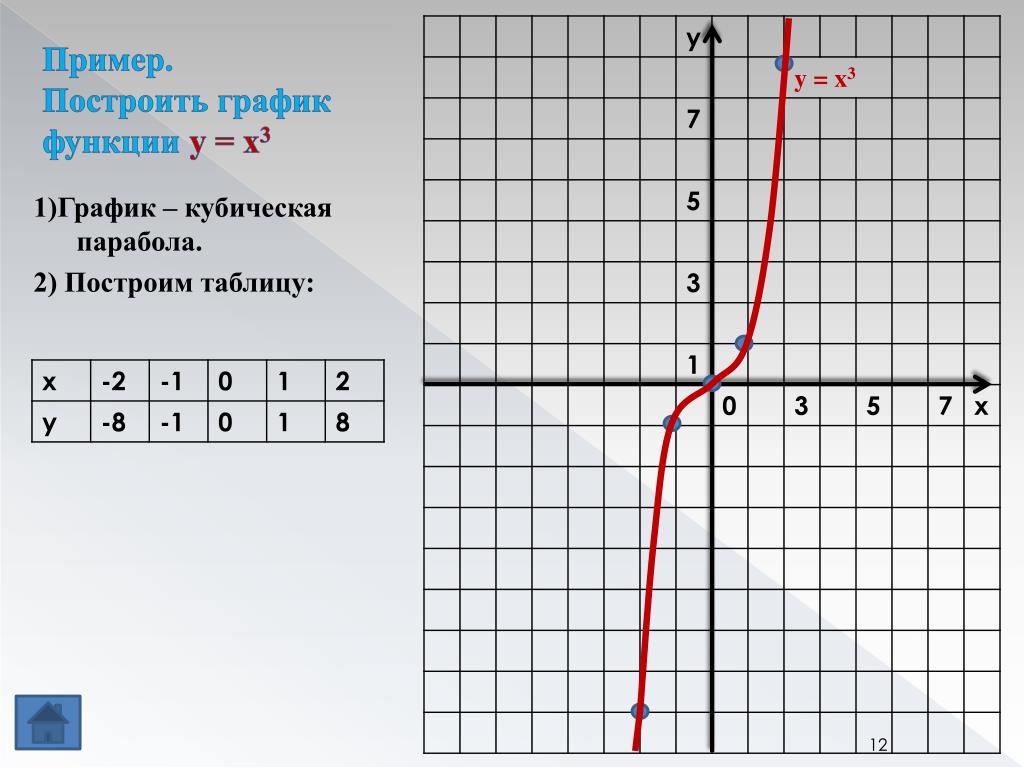
Для записи звука с параболической антенны подойдет любой обычный микрофон. Обычно с параболической тарелкой используются два типа микрофонов. Одним из вариантов является микрофон с направленной кардиоидной диаграммой направленности, такой как ручной микрофон. Другой вариант — использовать небольшой микрофон, например, петличный, со всенаправленной диаграммой направленности. В любом случае микрофон обычно крепится на кронштейне, который подвешивает его в фокусе тарелки. Элемент звукоснимателя обращен в чашу параболы. Мы решили использовать меньший по размеру и легкий беспроводной петличный микрофон.
Снимок параболической антенны для микрофона, сделанной своими руками, с дюбелем, проклеенным поперек, и крышкой молочного кувшина, сидящей на микрофоне, прикрепленном к металлической опоре. Из-за всенаправленной схемы звукоснимателя мы добавили небольшую круглую заднюю пластину. Это поможет сфокусировать петлич на записи отраженного источника звука. Для записи звука мы подключили нашу беспроводную петличку к входу XLR нашей видеокамеры.
Вы можете использовать любой портативный диктофон, если хотите.
Положение микрофона
Ключом к записи наилучшего звука с вашей параболической тарелки является расположение микрофона прямо в фокусе отражения перед параболой. Сладкое пятно варьируется от блюда к блюду в зависимости от его глубины и диаметра. Мы хотели попробовать разные блюда. Мы установили наш петличный браслет на кронштейн C-образной стойки, чтобы мы могли легко перемещать его. Во время прослушивания в наушниках мы определили идеальное место для каждой тарелки. После того, как вы определили точку фокуса параболической антенны, выполните измерение и прикрепите опорный кронштейн, чтобы использовать его в качестве постоянного крепления для микрофона.
Выбор параболического микрофона
Самой важной частью параболического микрофона является антенна. Параболическая антенна для микрофона работает не как воронка или мегафон, а как отражатель звуковых волн. Размер, форма и материал чаши влияют на ее отражательную способность.
Во многих конструкциях, сделанных своими руками, используются зонтики, сковороды, крышки для воков и другие инструменты для приготовления пищи. Вы можете использовать любой из них для создания параболической антенны для микрофона, которая улучшит характеристики вашего микрофона на большом расстоянии. Некоторые варианты лучше других. Как правило, вы хотите, чтобы блюдо имело баланс трех свойств: твердой поверхности, большого размера и правильной кривизны.
Параболическая тарелка использует геометрию, чтобы превратить обычный микрофон в сверхнаправленного монстра, способного записывать чистый звук на расстоянии нескольких сотен футов.
Кривая:
Поскольку истинная парабола представляет собой особую геометрическую кривую, немногие домашние блюда имеют полностью параболические характеристики. Хитрость заключается в том, чтобы найти тарелку, которая точно соответствует форме настоящей параболы. Если у вас есть доступ к старой спутниковой антенне, у вас есть отличный вариант.
Хотя эти приемники имеют внеосевой фокус, они представляют собой функционирующую параболу. Тем не менее, тарелка любой формы будет в определенной степени улавливать звуковые волны. Для достижения наилучших результатов выберите ту, у которой плавно изогнутое дно, а не плоское.
Материал:
Идеальный материал для параболической антенны микрофона должен быть жестким и толстым, но легким. Пластиковая, акриловая и металлическая посуда обладает высокой отражающей способностью. Они не пропускают звуковые волны, что делает их более предпочтительным выбором. Посуда с отверстиями, например дуршлаг, не является хорошим отражателем, даже если она имеет правильную форму. При тщательном осмотре тонкостенная металлическая посуда может вызвать небольшой металлический звон. Блюдо из толстого пластика или подобного материала может быть лучшим выбором.
Размер:
Звук, записанный с параболических микрофонных тарелок, обычно имеет низкочастотную характеристику. Это связано с наукой о звуковых волнах. Маленькие параболические тарелки просто не способны записывать весь спектр звука, необходимый для записи звука с полной точностью. Однако наука о звуковых волнах предполагает, что если все остальные аспекты тарелки идентичны. Большая парабола могла бы захватить низкие частоты. Так что больше на самом деле лучше. Тем не менее, тарелка, скорее всего, будет непрактично большой, прежде чем в этом случае можно будет записать хороший низкокачественный звук.
Лучший способ найти тарелку, которая одинаково хорошо отвечает всем трем критериям, — это купить настоящую параболическую тарелку у дилера. Профессиональные параболические тарелки легко доступны, но они могут быть дорогостоящими. Если вам нужна высококачественная параболическая тарелка для создания серьезного звука, обратите внимание на JonyShot от JonyJib. (1250 долларов США; микрофон не входит в комплект). Он включает в себя 24-дюймовую тарелку с ручками, монтажную пластину для штатива и изолированное крепление для микрофона. В качестве более доступного варианта вы можете приобрести тарелку дальнего радиуса действия Sound Shark SS1. При этом используется стандартный петличный за 285 долларов.
Использование параболической тарелки
Крупный план видеооператора в наушниках.Единственный способ убедиться, что вы записываете сильный и четкий сигнал, — это надеть наушники, чтобы вы могли контролировать источник звука и вносить коррективы во время записи. В зависимости от того, насколько далеко вы находитесь от объекта, даже небольшой поворот тарелки может сместить микрофон с цели, поэтому для записи требуется активный и внимательный оператор.
Тесты параболической микрофонной тарелки
Набор тестовых устройств: чаша для попкорна, зонт, сковорода, параболическая отражающая тарелка и крышка мусорного бака.Для нашего проекта мы протестировали пять вариантов домотканых тарелок, чтобы определить, какой из них лучше всего построить:
- 6-дюймовая сковорода для омлета
- 10,5-дюймовый алюминиевый кожух для освещения магазина
- 12-дюймовая пластиковая чаша для попкорна
- 22-дюймовая пластиковая крышка мусорного бака
- 45-дюймовый зонт для гольфа
Наши тесты проводились путем воспроизведения двух разных саундтреков, циклического стрекотания сверчков, а затем музыкальной кровати на расстоянии примерно 30 футов. Мы прикрепили проверенный ручной кардиоидный микрофон и петличный микрофон к стойке C-стойки, направленной на наши тарелки, и слушали через наушники. Мы записали образцы, используя каждую чашку, а затем вернулись в монтажный отсек, чтобы проанализировать наши выводы. Хотя сложно оценить сравнительное качество во время записи, мы заметили явную разницу в частотной характеристике после загрузки клипов в наше приложение для редактирования и воспроизведения их на студийных мониторах.
На основе наших тестов мы определили, что наша 22-дюймовая крышка мусорного бака работает лучше всего. Его большой диаметр, равномерный изгиб и пластиковая конструкция помогли превзойти по производительности другие протестированные нами блюда. В этом тесте мы также узнали, где должен располагаться наш микрофон, поэтому обратите внимание на это во время тестов.
Сборка микрофона
Выбрав тарелку, пришло время собрать параболический микрофон своими руками. Вот что вам понадобится для тарелки, предназначенной для петличного микрофона. Мы выбрали этот вариант, так как он был легким и беспроводным. Если бы мы выбрали кардиоидный микрофон, нам бы понадобилось амортизирующее крепление, очень похожее на микрофон-пушку.
Материалы
- 22 дюйма пластик 32 гал. крышка мусорного ведра
- 6-дюймовая полоса гибкого металлического ремня шириной 1/2 дюйма
- деревянный дюбель 24 дюйма x 1/4 дюйма
- крышка молочного кувшина
инструменты
- ножницы по металлу 6’120 ленточная пила
В дополнение к желаемому размеру и форме крышки, которую мы выбрали, мы обнаружили, что ее ручки идеально подходят для захвата; поэтому не было необходимости добавлять ручки. Нам просто нужно было построить перекладину и крепление для микрофона.
Сборка
Во-первых, с помощью ножовки мы вырезаем кусок 1/4-дюймового дюбеля, примерно такого же диаметра, как крышка мусорного бака, чтобы он плотно входил в пазы на внутренней стороне ручки. Затем мы использовали клейкую ленту, чтобы закрепить его на месте. Поперечный стержень упал чуть южнее центра нашей крышки, охватывая нашу тарелку на 1 1/4 дюйма от средней линии.
Затем с помощью ножниц по металлу мы отрезаем 6-дюймовый кусок гибкого плоского металлического ремня, который будет служить нашим центральным удлинением. держать петличный микрофон. Мы обернули один конец ремня вокруг центра дюбеля и закрепили его клейкой лентой. Затем мы придали ей небольшую кривую, наклонив ее вверх и наружу, чтобы она совпадала с центром нашей тарелки. Примерно в восьми дюймах от его нижней центральной точки, лежа на спине, мы прикрепили элемент звукоснимателя беспроводного петличного петлителя к нашему креплению. Закрепив шнур вдоль дюбеля и вокруг задней части тарелки скотчем, мы оставили достаточно провода, чтобы передатчик можно было закрепить на ремне оператора. Наконец, мы прикрепили 2-дюймовую крышку от молочного кувшина к задней части крепления микрофона. Это поможет направить всенаправленную схему захвата петличного микрофона обратно в тарелку.
Результаты
В то время как наше исследование заняло несколько часов, сама сборка заняла менее 30 минут. Общая стоимость проекта, за вычетом крышки от мусорного ведра, которая была у нас под рукой, но включая молоко, составила менее 25 долларов. Так что попробуйте. Если у вас нет крышки от мусорного ведра, которую можно было бы посвятить, используйте любую посуду, с которой вы можете справиться, или найдите профессионально сформированную параболу. Проявив немного творчества и немного простых научных данных, вы сможете использовать самодельный параболический параболический микрофон уже через час или около того.
Параболические микрофоны и футбол
Наиболее заметное место, где можно увидеть профессиональную параболическую микрофонную тарелку, находится в кулуарах футбольного матча NFL или NCAA. Просто включайте телевизор практически в любой уик-энд с сентября по январь и наблюдайте за операторами, которые держат в руках крутые составные тарелки. Хотя беспроводные микрофоны распространены на поле, еще несколько лет назад NCAA использовала в основном параболические микрофоны, чтобы слышать судей. Fox Sports использует шесть параболических микрофонов на каждой игре НФЛ, которую они освещают: по два на каждой боковой линии и по одному в каждой из конечных зон. Fox Sports выбрала параболическую антенну Klover MiK 26 (2250 долларов США; микрофон продается отдельно).
Чак Питерс — писатель и продюсер, трехкратный обладатель премии «Эмми». Он независимый продюсер и медиа-консультант.
Преобразования параболических функций — Алгебра II
Все ресурсы по Алгебре II
10 Диагностических тестов 630 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 3 Следующая →
Алгебра II Помощь » Функции и графики » Квадратичные функции » Параболические функции » Преобразования параболических функций
Рассмотрим следующие две функции:
и
Как сдвинута функция по сравнению с ?
Возможные ответы:
Единицы справа, единицы вниз
Слева единиц, единицы вниз
Слева, единицы
Слева, единицы вниз
Единицы Право, единицы вниз
Правильный ответ: 2
единиц осталось, единиц осталось
Объяснение:
Часть приводит к смещению графика на 3 единицы влево, а приводит к смещению графика на шесть единиц вниз. Вертикальные сдвиги имеют тот же знак, что и число вне круглых скобок, а горизонтальные сдвиги — это ПРОТИВОПОЛОЖНОЕ направление, как и знак внутри круглых скобок, связанный с .
Сообщить об ошибке
Если здесь изображена функция, какие графики выбора ответа?
Возможные ответы:
Ни один из этих графиков не является правильным.
Правильный ответ:
Объяснение:
Функция сдвигает функцию на f(x) единиц влево. И наоборот, сдвигает функцию f(x) вправо на единицу. В этом вопросе мы переводим график на две единицы влево.
Для перемещения по оси Y мы используем функцию или .
Сообщить об ошибке
Выберите функцию, которая точно соответствует показанному графику.
Возможные ответы:
Правильный ответ:
Объяснение:
Родительская функция параболы — где находятся вершины.
Исходный график параболической (квадратичной) функции имеет вершину в точке (0,0) и сдвигается влево или вправо на h единиц и вверх или вниз на k единиц.
.
Затем эта функция сдвигает на 1 единицу влево и на 4 единицы вниз, а минус перед квадрата члена обозначает поворот вокруг оси x.
Правильный ответ:
Отчет о ошибке
Установите вершину следующей параболы
Возможные ответы:
Правильный ответ:
. Объяснение:
Не делая много работы или манипулируя функцией, мы можем использовать наши знания о вершинной форме квадратичных функций, которая равна
с координатами вершины. Зная это, мы можем проанализировать нашу функцию, чтобы найти вершину… vertex: .
Примечание. Эта функция представляет собой простое преобразование функции
Сообщить об ошибке
Преобразуйте следующую параболу: .
Сдвиг вверх и влево.
Возможные ответы:
Правильный ответ:
Объяснение:
При преобразовании парабол, чтобы перевести вверх, прибавьте к уравнению (или прибавьте к Y).
Чтобы перевести влево, прибавьте к X.
Не забывайте, что если прибавлять к X, то, поскольку X возводится в квадрат, прибавление к X тоже должно быть возведено в квадрат.
со сдвигом вверх на 5 становится: .
Теперь прибавляя сдвиг влево получаем:
.
Сообщить об ошибке
Преобразуйте следующую параболу.
Переместить единиц влево.
Переместить единицу вниз.
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы переместить единицу вниз, вычтите из Y (или из всего уравнения) , таким образом, вычтите 1. также должен возвести в квадрат сложение).
При движении вниз наше уравнение принимает вид: .
Теперь, чтобы переместить его влево, мы получаем .
Сообщить об ошибке
Какая функция соответствует сдвигу влево?
Возможные ответы:
Правильный ответ:
Объяснение:
Родительская функция для параболической функции где – центр параболы. Чтобы сдвинуть параболу слева направо, значение h изменяется. Поскольку в родительской функции есть отрицательный знак, положительное значение перемещает параболу влево, а отрицательное значение перемещает ее вправо.
Сообщить об ошибке
Преобразования параболических функций
Учитывая функцию:
напишите уравнение новой функции, которая была перенесена на 2 пробела вправо и на 4 пробела вверх.
Возможные ответы:
Правильный ответ:
Объяснение:
Переводы, влияющие на x, должны быть напрямую связаны с x в функции и также должны менять знак. Поэтому, когда функция была переведена вправо на два пробела, должно быть связано со значением x в функции.
Перевод этого эффекта y должен быть напрямую связан с константой в функции, поэтому, когда функция была переведена вверх на 4 пробела, к (-5) в исходной функции нужно добавить +4.
Когда оба эти события происходят в функции, новая функция должна стать:
Сообщить об ошибке
Перечислить преобразования следующей функции:
Возможные ответы:
3
Горизонтальный сдвиг влево на 2 единицы
Вертикальный сдвиг вниз на 5 единиц
Растянут в 3 раза
Горизонтальный сдвиг вправо на 5 единиц
Вертикальный сдвиг вверх на 2 единицы
3 коэффициент из 3
Горизонтальное перемещение вправо 2 единицы
Вертикальное перемещение вверх 5 единиц
Сжато в 3 раза
Горизонтальное перемещение влево 2 единицы
Vertical translation up 5 units
Stretched by a factor of 3
Horizontal translation to the left 2 units
Vertical translation up 5 units
Correct answer:
Compressed by a factor of 3
Горизонтальное перемещение влево 2 единицы
Вертикальное перемещение вверх 5 единиц
Объяснение:
Поскольку родительской функцией является , мы можем записать общую форму как:
.