Параллельный перенос графика функции вдоль оси ординат. Построение графика квадратичной функции. Визуальный гид (2020). Построение графика функции вида y = f(-x)
, Конкурс «Презентация к уроку»
Презентация к уроку
Назад
Вперёд
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Цели урока:
Образовательная: исследовать смещение графика квадратичной функции, определить положение графика в зависимости от значений коэффициентов b, c .
Воспитательная: умение работать в группе, организованности.
Развивающая : навыки исследовательской работы, умение выдвигать гипотезы, анализировать полученные результаты, систематизировать полученные данные.
Структура урока
- Организационный момент – 3 минуты.

- Исследовательская работа – 20 минут.
- Закрепление изученного материала – 15 минут.
- Рефлексия – 2 минут.
- Итог урока – 3 минуты.
- Домашнее задание – 2 минуты.
Ход урока
1. Организационный момент.
Цель урока провести исследовательскую работу. Объектом исследования будут квадратичные функции разного вида. Вам предстоит определить, как влияют коэффициенты b, c на график функций вида y=x 2 +с, y=(x-b) 2 , y=(x-b) 2 +c.
Для выполнения задания необходимо разделиться на группы (4 группы по 5 человек, одна группа “эксперты” наиболее подготовленные ученики).
Каждая группа получает план исследования , лист формата А3 для оформления результатов.
2. Исследовательская работа
.
Две группы (уровень А) исследуют функции вида y= x 2 +с,
одна группа (уровень В) исследует функцию вида
y=(x-b) 2 , одна группа (уровень С) исследует
функцию y=(x-b) 2 +c.
| Функция | Результат | ||
| 1 группа | у=x 2 +3; | ||
| 2 группа | у=x 2 -5; | ||
| 3 группа | у=(х-4) 2 ; | ||
| 4 группа | у=(х-2) 2 +3. |
План работы
- Для того чтобы выдвинуть гипотезу сделайте предположение, как может выглядеть ваша функция.
- Постройте график исследуемых функций (определите вершину параболы (х 0 , y 0), задайте таблицей 4 точки).
- Сравните получившийся график с контрольным
образцом y=x 2 .

- Сделайте вывод (как изменилось положение графика вашей функции относительно контрольного образца).
- Результаты оформите на листе формата А3 и представьте “экспертной” группе.
“Экспертная” группа сверяет результаты свои с результатами остальных групп, систематизирует и обобщает результаты, выступает с выводами. В случае неточностей или ошибок учитель вносит коррекционные замечания.
Сверка полученных результатов со слайдами №2-5.
Любую квадратичную функцию y=ax 2 +bx+c, можно записать в виде y=a(x-x 0) 2 +y 0, где x 0 и y 0 выражаются через коэффициенты a, b, c. Таким образом, ваши коэффициенты b=x 0 , c=y 0 являются координатами вершины параболы.
3. Закрепление изученного материала.
Фронтальная работа с классом.
1. Найти ошибку в графиках функций (Слайды№6-9).
Коэффициент b | Нет ошибки |
Рисунок 1 | Рисунок 2 |
| у=(х+5) 2 -1 | у=(х-2) 2 +2 |
| Коэффициент b и с | Коэффициент b |
| Рисунок 3 | Рисунок 4 |
Преобразование графиков функций
В этой статье я познакомлю вас с линейными преобразованиями графиков функций и покажу, как с помощью этих преобразований из графика функции получить график функции
Линейным преобразованием функции называется преобразование самой функции и/или ее аргумента к виду , а также преобразование, содержащее модуль аргумента и/или функции.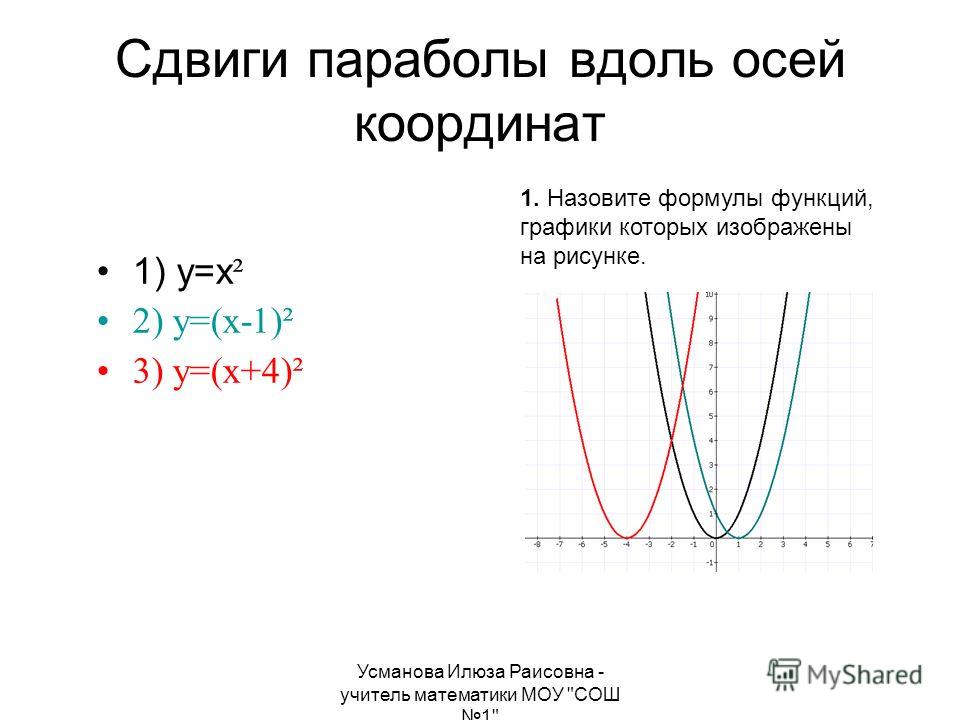
Наибольшие затруднения при построении графиков с помощью линейных преобразований вызывают следующие действия:
- Вычленение базовой функции, собственно, график которой мы и преобразовываем.
- Определения порядка преобразований.
И менно на этих моментах мы и остановимся подробнее.
Рассмотрим внимательно функцию
В ее основе лежит функция . Назовем ее базовой функцией .
При построении графика функции мы совершаем преобразования графика базовой функции .
Если бы мы совершали преобразования функции в том же порядке, в каком находили ее значение при определенном значении аргумента, то
Рассмотрим какие виды линейных преобразований аргумента и функции существуют, и как их выполнять.
Преобразования аргумента.
1. f(x) f(x+b)1. Строим график фунции
2. Сдвигаем график фунции вдоль оси ОХ на |b| единиц
- влево, если b>0
- вправо, если b
Построим график функции
1. Строим график функции
Строим график функции
2. Сдвигаем его на 2 единицы вправо:
2. f(x) f(kx)
1. Строим график фунции
2. Абсциссы точек графика делим на к, ординаты точек оставляем без изменений.
Построим график функции .
1. Строим график функции
2. Все абсциссы точек графика делим на 2, ординаты оставляем без изменений:
3. f(x) f(-x)
1. Строим график фунции
2. Отображаем его симметрично относительно оси OY.
Построим график функции .
1. Строим график функции
2. Отображаем его симметрично относительно оси OY:
4. f(x) f(|x|)
1. Строим график функции
2. Часть графика, расположенную левее оси ОY стираем, часть графика, расположенную правее оси ОY Достраиваем симметрично относительно оси OY:
График функции выглядит так:
Построим график функции
1. Строим график функции (это график функции , смещенный вдоль оси ОХ на 2 единицы влево):
2. Часть графика, расположенную левее оси OY (x
Часть графика, расположенную левее оси OY (x
3. Часть графика, расположенную правее оси OY (x>0) достраиваем симметрично относительно оси OY:
Важно! Два главных правила преобразования аргумента.
1. Все преобразования аргумента совершаются вдоль оси ОХ
2. Все преобразования аргумента совершаются «наоборот» и «в обратном порядке».
Например, в функции последовательность преобразований аргумента такая:
1. Берем модуль от х.
2. К модулю х прибавляем число 2.
Но построение графика мы совершали в обратном порядке:
Сначала выполнили преобразование 2. — сместили график на 2 единицы влево (то есть абсциссы точек уменьшили на 2, как бы «наоборот»)
Затем выполнили преобразование f(x) f(|x|).
Коротко последовательность преобразований записывается так:
Теперь поговорим о преобразовании функции . Преобразования совершаются
1. Вдоль оси OY.
2. В той же последовательности, в какой выполняются действия.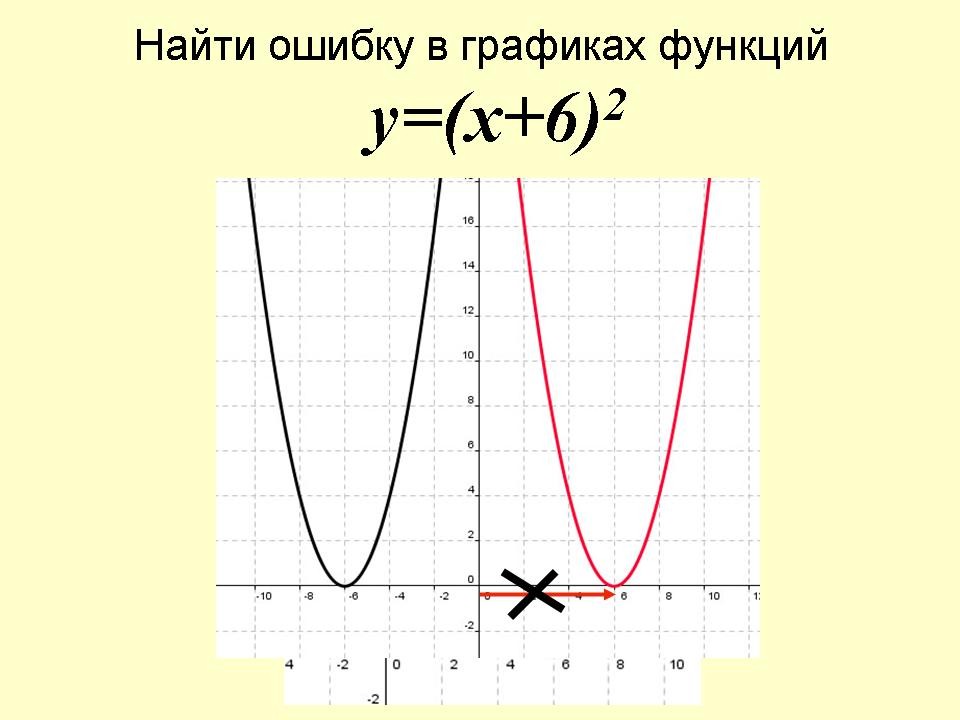
Вот эти преобразования:
1. f(x)f(x)+D
2. Смещаем его вдоль оси OY на |D| единиц
- вверх, если D>0
- вниз, если D
Построим график функции
1. Строим график функции
2. Смещаем его вдоль оси OY на 2 единицы вверх:
2. f(x)Af(x)
1. Строим график функции y=f(x)
2. Ординаты всех точек графика умножаем на А, абсциссы оставляем без изменений.
Построим график функции
1. Построим график функции
2. Ординаты всех точек графика умножим на 2:
3. f(x)-f(x)
1. Строим график функции y=f(x)
Построим график функции .
1. Строим график функции .
2. Отображаем его симметрично относительно оси ОХ.
4. f(x)|f(x)|
1. Строим график функции y=f(x)
2. Часть графика, расположенную выше оси ОХ оставляем без изменений, часть графика, расположенную ниже оси OX, отображаем симметрично относительно этой оси.
Построим график функции
1. Строим график функции . Он получается смещением графика функции вдоль оси OY на 2 единицы вниз:
2. Теперь часть графика, расположенную ниже оси ОХ, отобразим симметрично относительно этой оси:
И последнее преобразование, которое, строго говоря, нельзя назвать преобразованием функции, поскольку результат этого преобразования функцией уже не является:
|y|=f(x)
1. Строим график функции y=f(x)
2. Часть графика, расположенную ниже оси ОХ стираем, затем часть графика, расположенную выше оси ОХ достраиваем симметрично относительно этой оси.
Построим график уравнения
1. Строим график функции :
2. Часть графика, расположенную ниже оси ОХ стираем:
3. Часть графика, расположенную выше оси ОХ достраиваем симметрично относительно этой оси.
И, наконец, предлагаю вам посмотреть ВИДЕОУРОК в котором я показываю пошаговый алгоритм построения графика функции
График этой функции выглядит так:
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.

- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.

- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
, Конкурс «Презентация к уроку»
Презентация к уроку
Назад
Вперёд
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Цели урока:
Образовательная: исследовать смещение графика квадратичной функции, определить положение графика в зависимости от значений коэффициентов b, c .
Воспитательная: умение работать в группе, организованности.
Развивающая : навыки исследовательской работы, умение выдвигать гипотезы, анализировать полученные результаты, систематизировать полученные данные.
Структура урока
- Организационный момент – 3 минуты.
- Исследовательская работа – 20 минут.
- Закрепление изученного материала – 15 минут.
- Рефлексия – 2 минут.
- Итог урока – 3 минуты.
- Домашнее задание – 2 минуты.
Ход урока
1. Организационный момент.
Цель урока провести исследовательскую работу.
Объектом исследования будут квадратичные
функции разного вида. Вам предстоит определить,
как влияют коэффициенты b, c на график
функций вида y=x 2 +с, y=(x-b) 2 , y=(x-b) 2 +c.
Для выполнения задания необходимо разделиться на группы (4 группы по 5 человек, одна группа “эксперты” наиболее подготовленные ученики).
Каждая группа получает план исследования , лист формата А3 для оформления результатов.
2. Исследовательская работа
.
Две группы (уровень А) исследуют функции вида y= x 2 +с, одна группа (уровень В) исследует функцию вида y=(x-b) 2 , одна группа (уровень С) исследует функцию y=(x-b) 2 +c. Группа “Экспертов” исследует все функции.
| Функция | Результат | ||
| 1 группа | у=x 2 +3; | ||
| 2 группа | у=x 2 -5; | ||
| 3 группа | у=(х-4) 2 ; | ||
| 4 группа | у=(х-2) 2 +3. |
План работы
- Для того чтобы выдвинуть гипотезу сделайте предположение, как может выглядеть ваша функция.
- Постройте график исследуемых функций (определите вершину параболы (х 0 , y 0), задайте таблицей 4 точки).
- Сравните получившийся график с контрольным образцом y=x 2 .
- Сделайте вывод (как изменилось положение графика вашей функции относительно контрольного образца).
- Результаты оформите на листе формата А3 и представьте “экспертной” группе.
“Экспертная” группа сверяет результаты свои с результатами остальных групп, систематизирует и обобщает результаты, выступает с выводами. В случае неточностей или ошибок учитель вносит коррекционные замечания.
Сверка полученных результатов со слайдами №2-5.
Любую квадратичную функцию y=ax 2 +bx+c, можно
записать в виде y=a(x-x 0) 2 +y 0, где x 0
и y 0 выражаются через коэффициенты a, b, c. Таким образом, ваши коэффициенты b=x 0 , c=y 0
являются координатами вершины параболы.
Таким образом, ваши коэффициенты b=x 0 , c=y 0
являются координатами вершины параболы.
3. Закрепление изученного материала.
Фронтальная работа с классом.
1. Найти ошибку в графиках функций (Слайды№6-9).
Коэффициент b | Нет ошибки |
Рисунок 1 | Рисунок 2 |
| у=(х+5) 2 -1 | у=(х-2) 2 +2 |
| Коэффициент b и с | Коэффициент b |
| Рисунок 3 | Рисунок 4 |
Результаты
Какой коэффициент вам помог найти ошибку?
2. Соотнесите графики функций согласно цветам (слайд
№10) .
Соотнесите графики функций согласно цветам (слайд
№10) .
Рисунок 5
4. Рефлексия.
Группа “Экспертов” отвечают на вопросы:
– Какие ошибки допустили группы?
– Достигнута ли цель занятия?
– Соответствуют ли полученные результаты исследования поставленной гипотезе?
5. Итог урока (слайд №11)
:
На положение графика функции y=(x-b) 2 +c влияют коэффициенты b и c,
“+b” парабола сдвинута вправо по оси абсцисс на b единичных отрезков,
“–b” парабола сдвинута влево по оси абсцисс на b единичных отрезков,
“+с” парабола сдвинута вверх по оси ординат на с единичных отрезков,
“-с” парабола сдвинута вниз по оси ординат на с единичных отрезков.
6. Домашнее задание
- Построить график квадратичной функции, имеющую вершину в точке А(1;-2), коэффициент a=1.
- Подумайте, в какой области можно использовать
знания по данной теме (практическое применение).

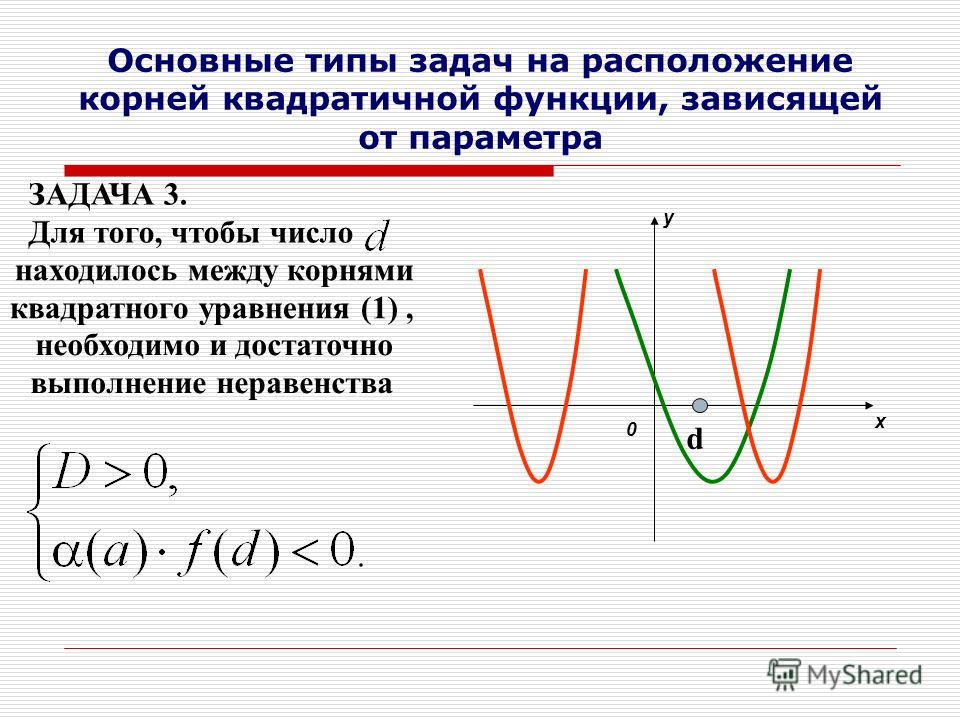
Графиком данного уравнения является окружность на координатной плоскости x Oy с центром в точке O(a;b) и радиусом r (r>0).
График данного уравнения нельзя назвать графиком функции, т.к. нарушается определение функции: каждому значению x соответствует единственное значение y.
где l — заданное положительное число, нужно сдвинуть график функции y=f(x) вдоль оси x на l единиц масштаба влево.
Чтобы построить график функции
где l — заданное положительное число, нужно сдвинуть график функции y=f(x) вдоль оси x на l единиц масштаба вправо.
Чтобы построить график функции
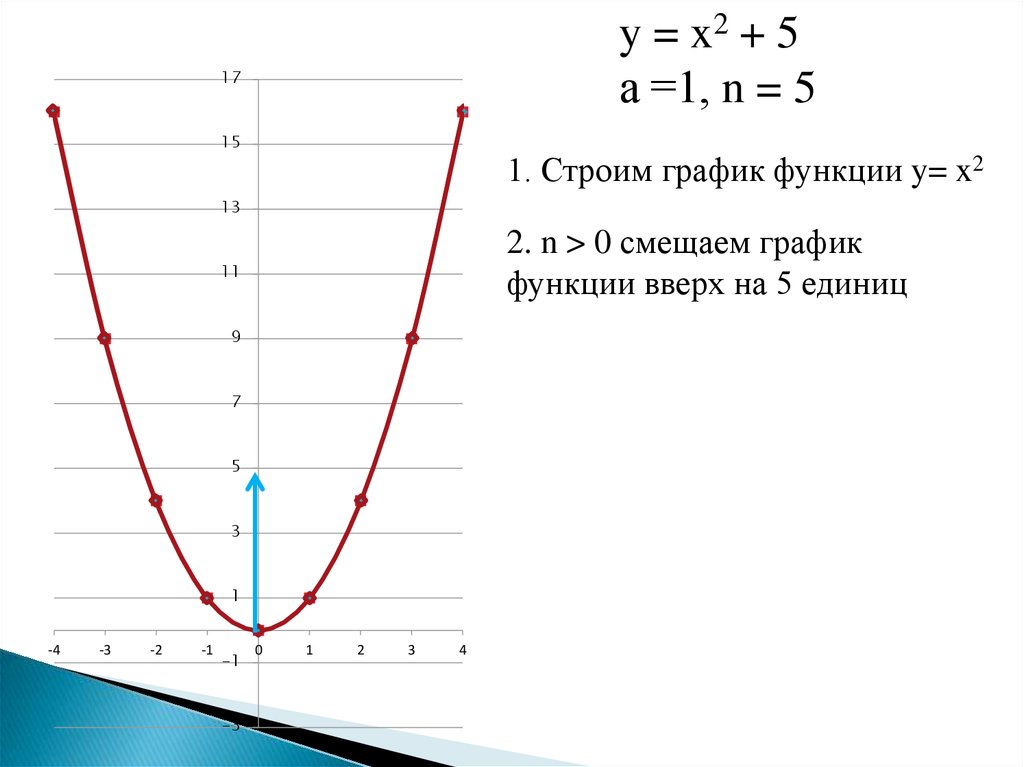
где m — заданное положительное число, надо сдвинуть график функции y=f(x) вдоль оси y на m единиц масштаба вверх.
Чтобы построить график функции y=f(x)-m, где m — заданное положительное число, надо сдвинуть график функции y=f(x) вдоль оси y на m единиц масштаба вниз.
Алгоритм 1 построения графика функции y=f(x+l)+m:
- 1. Построить график функции y=f(x).
- 2.
 Осуществить параллельный перенос графика y=f(x) вдоль оси x на единиц масштаба влево, если l>0, и вправо, если l
Осуществить параллельный перенос графика y=f(x) вдоль оси x на единиц масштаба влево, если l>0, и вправо, если l - 3. Осуществить параллельный перенос полученного на втором шаге графика вдоль оси y на единиц масштаба вверх, если
Алгоритм 2 построения графика функции y=f(x+l)+m:
- 1. Перейти к вспомогательной системе координат, проведя пунктиром вспомогательные прямые x=-l, y=m, т.е. выбрав в качестве начала новой системы координат точку (-l;m).
- 2. Новой системе координат привязать график функции y=f(x).
«Сдвиг графика квадратичной функции вдоль координатных осей»
С амостоятельная работа «Сдвиг графика функции y=ax2 вдоль осей координат» Вариант1
1. Укажите формулу функции, сдвинутой вдоль оси ОУ:
а) ; в) ;
б) у = 2(х + 5)2 ; г) у = 3х.
2. Укажите формулу функции, сдвинутой вдоль оси ОХ:
а) ; в) ;
б) у = 2(х + 5)2 ; г) у = 3х 0.
3. Укажите вершину параболы у = — 10х2+ 1
4. Постройте график функции у = (х+1)2-2
5. Постройте график функции y = x2 +8x + 5
Самостоятельная работа «Сдвиг графика функции y=ax2 вдоль осей координат» Вариант 2
1. Укажите формулу функции, сдвинутой вдоль оси ОУ:
а) ; в) ;
б) у = -3(х — 4)2 ; г) у = 2х³.
2. Укажите формулу функции, сдвинутой вдоль оси ОХ:
а) ; в) ;
б) у = -3(х — 4)2 ; г) у = 2х³ + 6.
3. Укажите вершину параболы у = 2х2 — 4
4. Постройте график функции у = 2(х-3)2+1
5. Постройте график функции y = x2 — 4x + 7
С амостоятельная работа «Сдвиг графика функции y=ax2 вдоль осей координат» Вариант1
1. Укажите формулу функции, сдвинутой вдоль оси ОУ:
а) ; в) ;
б) у = 2(х + 5)2 ; г) у = 3х.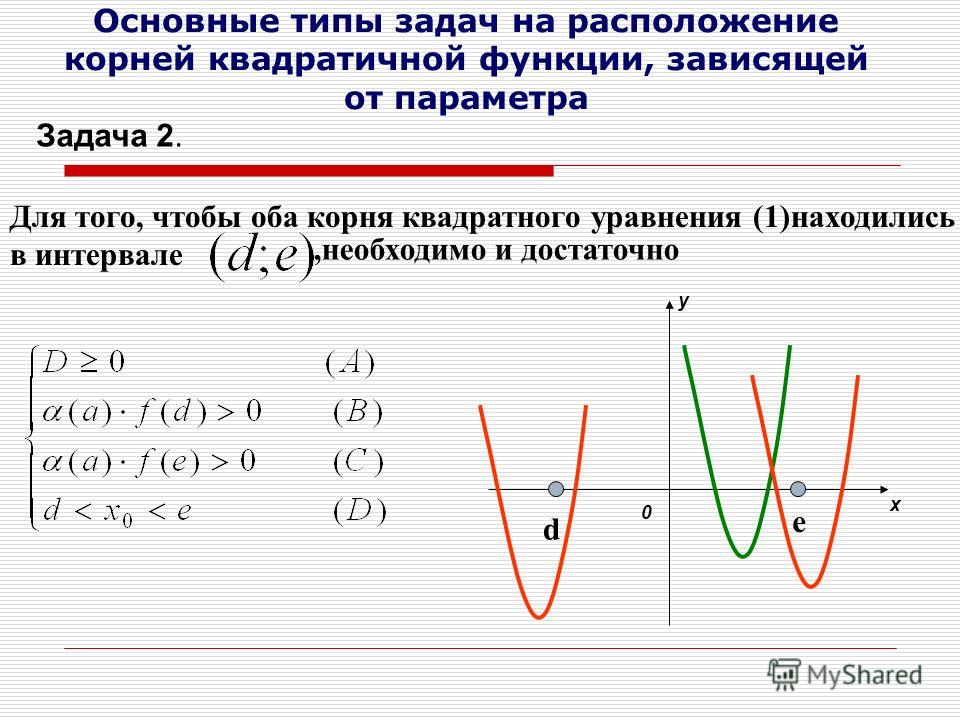
2. Укажите формулу функции, сдвинутой вдоль оси ОХ:
а) ; в) ;
б) у = 2(х + 5)2 ; г) у = 3х 0.
3. Укажите вершину параболы у = — 10х2+ 1
4. Постройте график функции у = (х+1)2-2
5. Постройте график функции y = x2 +8x + 5
Самостоятельная работа «Сдвиг графика функции y=ax2 вдоль осей координат» Вариант 2
1. Укажите формулу функции, сдвинутой вдоль оси ОУ:
а) ; в) ;
б) у = -3(х — 4)2 ; г) у = 2х³.
2. Укажите формулу функции, сдвинутой вдоль оси ОХ:
а) ; в) ;
б) у = -3(х — 4)2 ; г) у = 2х³ + 6.
3. Укажите вершину параболы у = 2х2 — 4
4. Постройте график функции у = 2(х-3)2+1
5. Постройте график функции y = x2 — 4x + 7
Самостоятельная работа «Сдвиг графика функции y=ax2 вдоль осей координат» Вариант1
1. Укажите формулу функции, сдвинутой вдоль оси ОУ:
Укажите формулу функции, сдвинутой вдоль оси ОУ:
а) ; в) ;
б) у = 2(х + 5)2 ; г) у = 3х.
2. Укажите формулу функции, сдвинутой вдоль оси ОХ:
а) ; в) ;
б) у = 2(х + 5)2 ; г) у = 3х 0.
3. Укажите вершину параболы у = — 10х2+ 1
4. Постройте график функции у = (х+1)2-2
5. Постройте график функции y = x2 +8x + 5
Самостоятельная работа «Сдвиг графика функции y=ax2 вдоль осей координат» Вариант 2
1. Укажите формулу функции, сдвинутой вдоль оси ОУ:
а) ; в) ;
б) у = -3(х — 4)2 ; г) у = 2х³.
2. Укажите формулу функции, сдвинутой вдоль оси ОХ:
а) ; в) ;
б) у = -3(х — 4)2 ; г) у = 2х³ + 6.
3. Укажите вершину параболы у = 2х2 — 4
4. Постройте график функции у = 2(х-3)2+1
5. Постройте график функции y = x2 — 4x + 7
Постройте график функции y = x2 — 4x + 7
Как решать квадратичные задачи о движении снаряда
Общие словесные задачиЗадачи на максимум/минимум
Purplemath
Исчисление включает множество задач по нахождению максимумов, минимумов и нулей. Вы почувствуете это с квадратичными задачами. На самом деле, если/когда вы дойдете до исчисления, вы обнаружите, что некоторые из домашних упражнений будут идентичны тем, которые вы делаете сейчас; просто у вас будут новые инструменты для поиска ответов.
Содержание продолжается ниже
MathHelp.com
Основная категория текстовых задач с квадратными уравнениями связана с так называемым движением снаряда. Для наших целей снаряд — это любой объект, который бросают, стреляют или бросают. Почти всегда в этом контексте объект изначально движется прямо вверх или прямо вниз. (Если он начинает движение вверх, то, естественно, позже он снова пойдет вниз.) Эта начальная скорость движения и есть скорость.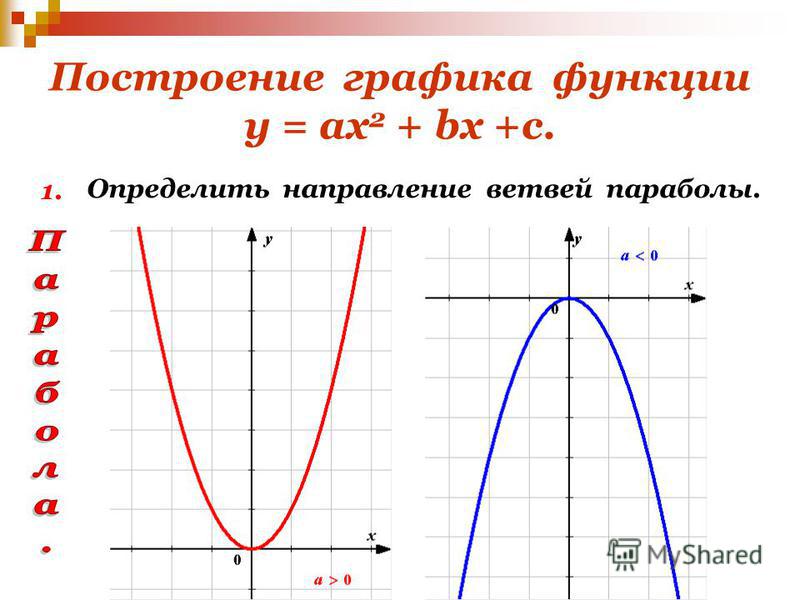
В упражнениях с движением снаряда объект, который высвобождается (выстреливается, падает или что-то еще
Что говорит об объекте знак скорости?
Начальная скорость объекта в этих упражнениях говорит нам, как объект был освобожден. Начальное значение скорости будет либо нулевым (значит, объект был только что брошен), либо положительным (значит, он был брошен или выстрелен вверх), либо отрицательным (значит, предмет был брошен вниз).
Что означает «
г «?В упражнениях на движение снаряда коэффициент при квадрате члена равен −½ г . г означает постоянную силы тяжести (на Земле), которая составляет -9,8 метра в секунду в квадрате (то есть метров в секунду в секунду) в метрических единицах или -32 фута в секунду в квадрате в имперских единицах. Знаки «минус» отражают тот факт, что гравитация Земли тянет нас и рассматриваемый объект вниз.
Что означает «за секунду в квадрате»?
Ускорение (являющееся изменением скорости, а не самой скоростью) измеряется с точки зрения того, насколько скорость изменяется в единицу времени. Итак, если скорость объекта измеряется в футах в секунду, то ускорение этого объекта говорит о том, насколько эта скорость изменяется в единицу времени; то есть ускорение измеряет, насколько футы в секунду изменяются в секунду. И это дубликат «в секунду» — это то, как мы получаем «секунду в квадрате». Это из физики ситуации.
Итак, если скорость объекта измеряется в футах в секунду, то ускорение этого объекта говорит о том, насколько эта скорость изменяется в единицу времени; то есть ускорение измеряет, насколько футы в секунду изменяются в секунду. И это дубликат «в секунду» — это то, как мы получаем «секунду в квадрате». Это из физики ситуации.
Какое значение следует использовать для гравитации?
Если упражнение по движению снаряда выражено в футах, милях или других имперских единицах, тогда используйте −32 для гравитации; если единицами измерения являются метры, сантиметры или другие метрические единицы, используйте −9,8 для силы тяжести.
Что такое уравнение движения снаряда?
Уравнение движения снаряда имеет вид0022 + h 0 , где g — гравитационная постоянная, v 0 — начальная скорость (т. — начальная высота объекта (то есть высота объекта at t = 0, время выпуска).
Да, вам нужно следить за всеми этими вещами при работе с движением снаряда.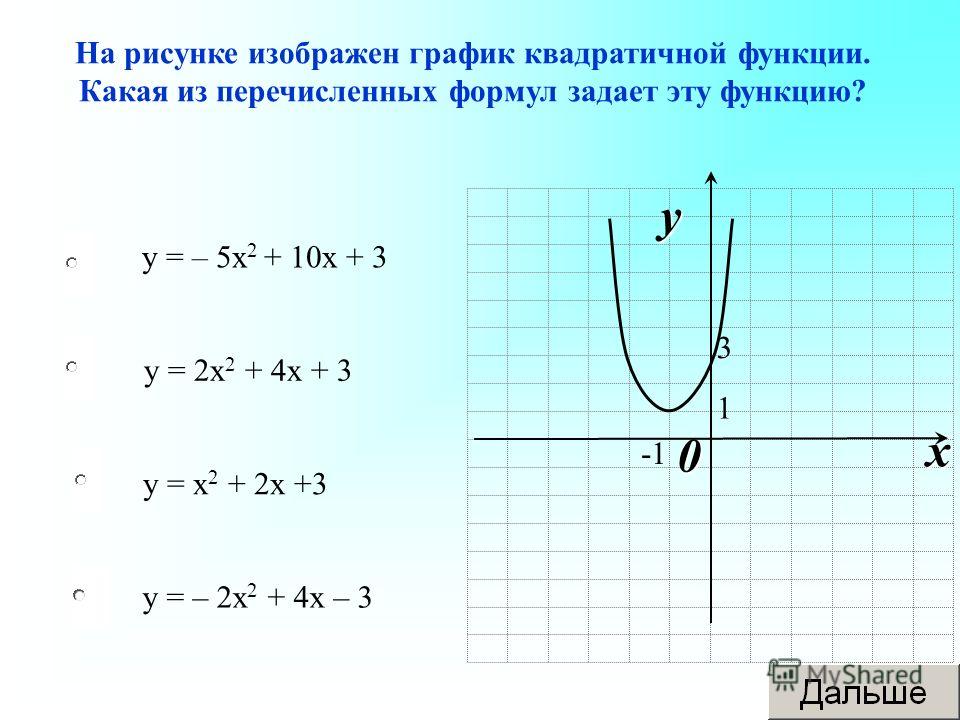
- Объект запущен в 190,6 метра в секунду (м/с) с платформы высотой 58,8 метра. Уравнение для высоты объекта S во время T секунд после запуска составляет S ( T ) = -4,9 T 2 +19,6 T +58,8,8, где S 22222221 T +58,8, где S 2222222 2 T +58,8,8, где S 222222 2 T +58,8,8, где S 222221 . Когда предмет ударяется о землю?
На какой высоте (над уровнем земли) объект врезается в землю? Ну, очевидно же, ноль. Так что я ищу время, когда высота s = 0. Я приравняю s к нулю и решу:
0 = −4,9 t 2 + 19,6 t + 58,8
0 = t 2 − 4 t − 12
0 = ( t — 6)( t + 2)
Тогда t = 6 или t = -2. Второе решение — за две секунды до запуска, что не имеет смысла в данном контексте. (Это имеет смысл на графике, потому что линия пересекает x -ось на -2, но отрицательное время не будет работать в этой задаче со словами.) Таким образом, « t = -2″ является посторонним решением, и я его проигнорирую.
(Это имеет смысл на графике, потому что линия пересекает x -ось на -2, но отрицательное время не будет работать в этой задаче со словами.) Таким образом, « t = -2″ является посторонним решением, и я его проигнорирую.
Вместо этого мой ответ на это упражнение (то есть правильный ответ в контексте) — это другое значение решения. Они спросили меня о времени, а время здесь измеряется в секундах, так что мой ответ:
Объект ударяется о землю через шесть секунд после запуска.
Обратите внимание на построение уравнения высоты в приведенной выше задаче. (Да, мы обсуждали это в начале, но вам действительно понадобится эта информация, поэтому мы вернемся к ней.)
Начальная высота пуска была 58,8 метра, а постоянный срок был «58,8». Начальная скорость (или стартовая скорость) составляла 19,6 м/с, а коэффициент при линейном члене равнялся «19,6». Это всегда верно для этих проблем с движением снаряда вверх/вниз. (Если у вас есть упражнение с боковым движением, уравнение будет иметь другую форму, но они всегда дадут вам это уравнение. ) Начальная скорость — это коэффициент для среднего члена, а начальная высота — постоянный член. .
) Начальная скорость — это коэффициент для среднего члена, а начальная высота — постоянный член. .
А коэффициент при старшем члене получается от силы тяжести. Этот коэффициент отрицательный, так как гравитация тянет вниз, и значение будет либо «−4,9» (если ваши единицы измерения «метры»), либо «–16» (если ваши единицы измерения — «футы»). Да, эти значения составляют половину значений гравитационной постоянной, перечисленных в начале этой страницы; они умножили ½.
В общем, формат уравнения движения снаряда следующий:
с ( t ) = − gt 2 + v 0 t + h 0
…где « g» получено из «6» или «6» здесь. сила тяжести (технически это сила тяжести на Земле ), « v 0 » («ни-ноль» или «ни-ниже нуля») — начальная скорость, а « h 0 «(«aitch-naught» или «aitch-sub-zero») — начальная высота.
Запомните это уравнение (или хотя бы его значение), потому что оно может понадобиться вам на тесте.
- Объект запущен прямо вверх со скоростью 64 фута в секунду (фут/с) с платформы высотой 80 футов. Какова будет максимальная высота объекта? Когда он достигнет этой высоты?
Хм… На этот раз мне не дали уравнение. Но это нормально, потому что я могу составить уравнение из информации, которую мне дали . Начальная высота составляет 80 футов над землей, а начальная скорость — 64 фута/с вверх. Поскольку моими единицами измерения являются футы, то число для силы тяжести будет равно −16, и мое уравнение:
s ( t ) = −16 t 2 + 64 t + 80
Они хотят, чтобы я нашел максимальную высоту. Для такого отрицательного квадратичного уравнения максимум будет в вершине перевернутой параболы. Так что они действительно хотят, чтобы я нашел вершину. Из графика я знаю, как найти вершину; в этом случае вершина находится в точке ( h , k ) = (2, 144):
h = − b / 2 a = −(64)/2(−16) = −64/−32 = 2
k = с (2) = −16(2) 2 + 64(2) + 80 = -16(4) + 128 + 80 = 208 — 64 = 144
Но что говорят мне координаты этой вершины? Согласно моему уравнению, я подставляю значения времени и извлекаю значения высоты, поэтому ввод 2 — это время, а вывод 144 — высота.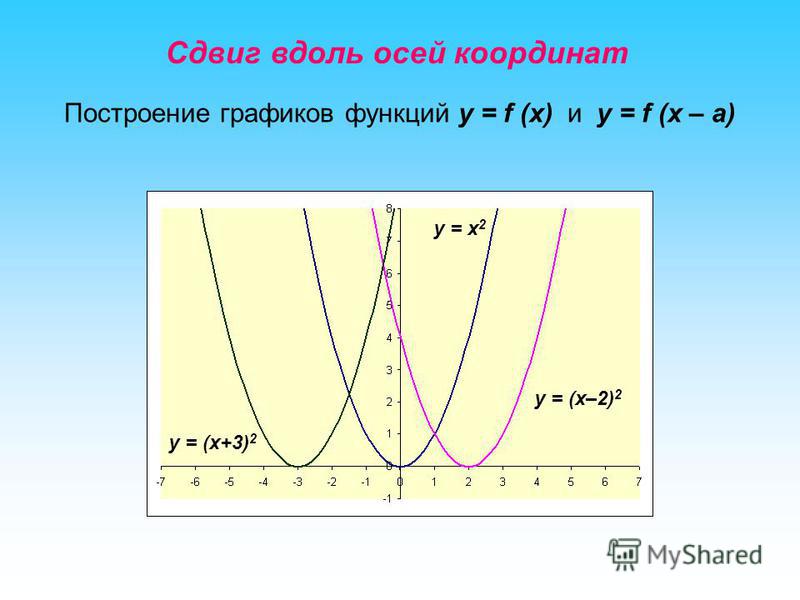
Требуется две секунды, чтобы достичь максимальной высоты в 144 фута.
Пока вы четко маркируете, вам не нужно полное предложение (как я использовал выше) для вашего ответа. Таким образом, вы также можете дать ответ: «время: 2 секунды; высота: 144 фута».
- Объект запускается с земли прямо вверх со скоростью 39,2 м/с. Как долго объект находится на высоте 34,3 метра или выше?
На этот раз я использую метры, поэтому гравитационное число будет −4,9. Так как объект начинался на уровне земли, начальная высота была равна 0. Тогда мое уравнение: квадратичный, то график представляет собой перевернутую параболу. Я могу найти два случая, когда высота объекта составляет ровно 34,3 метра, и я знаю, что объект будет выше 34,3 метра все время между ними.
Почему «два раза» и как узнать, что период времени находится между этими двумя временами? Потому что первый раз будет, когда объект пройдет высоту 34,3 метра на пути к своей максимальной высоте, а второй раз, когда он преодолеет 34,3 метра, падая обратно на землю. Итак, я должен решить следующее:
Итак, я должен решить следующее:
-4,9 t 2 + 39,2 t = 34,3
t 2 — 8 2 t ( t − 7)( t − 1) = 0
Два решения: в моменты времени t = 1 и t = 7. Таким образом, объект находится на высоте 34,3 м через одну секунду после запуска (подъем вверх). ) и снова через семь секунд после запуска (спуск). Вычитая, чтобы найти разницу, я обнаружил, что:
Объект находится на высоте 34,3 метра или выше в течение шести секунд.
Опять же, технически вам не нужно полное предложение для вашего прямого ответа; сказать «6 секунд», вероятно, достаточно. Но обязательно включите в свой ответ единицу измерения «секунды».
Не удивляйтесь, если многие из ваших упражнений сработают так же «аккуратно», как и в приведенных выше примерах. Многие учебники до сих пор тщательно разрабатывают свои упражнения, чтобы вы могли решать их с помощью факторизации (то есть, быстро выполняя алгебраические операции).
Однако (справедливое предупреждение!), сильная зависимость от калькуляторов приводит к тому, что больше текстов приводит к созданию «интересных» (то есть излишне сложных) упражнений, поэтому некоторые (или все) ваши упражнения могут включать гораздо более беспорядочные вычисления, чем здесь отображались. Если это так, внимательно изучите эти «хорошие» примеры, пока не будете уверены, что следуете рассуждениям.
- По окончании семестра вы обнаруживаете, что математический факультет (снова) изменил учебники, поэтому книжный магазин не выкупит вашу почти новую книгу. Вы и ваш друг Герман решаете проявить творческий подход. Вы идете на крышу двенадцатиэтажного здания и смотрите через край на отражающий бассейн в 160 футах ниже. Вы бросаете свою книгу через край в тот самый момент, когда Герман бросает свою книгу прямо вниз со скоростью 48 футов в секунду. На сколько секунд его книга опережает вашу? (Округлите ответ до двух знаков после запятой.)
Наши начальные высоты запуска будут одинаковыми: мы оба запускаем с высоты 160 футов над землей. А гравитационное число, поскольку мы работаем в футах, будет −16. Моя начальная скорость равна нулю, так как я только что уронил свою книгу, но скорость моего приятеля Германа равна минус 48, отрицательная величина возникает из-за того, что он бросил свою книгу вниз , а не вверх. Таким образом, наши уравнения «высоты»:0021 т
А гравитационное число, поскольку мы работаем в футах, будет −16. Моя начальная скорость равна нулю, так как я только что уронил свою книгу, но скорость моего приятеля Германа равна минус 48, отрицательная величина возникает из-за того, что он бросил свою книгу вниз , а не вверх. Таким образом, наши уравнения «высоты»:0021 т
его: с ( t ) = −16 t 2 − 48 t + 160
В каждом случае мне нужно найти время, за которое книги достигнут нулевой высоты (высоты нулевое «уровень земли»), так:
шахта: 0 = −16 T 2 + 160
T 2 — 10 = 0
T =
± SQRT (T =
°5 ( 10)
его: 0 = −16 T 2 — 48 T + 160
T 2 + 3 T — 10 = 0
( T + 5) ( T ° 2) = 09000 =22 + 5) ( T ‘2) = 2) = 2) = 2) = 2) = 2) = 2). t = −5, +2
t = −5, +2
Я буду игнорировать отрицательные значения времени, поскольку они не имеют значения в данном контексте. (В какой-то момент в каком-то упражнении может возникнуть случай, когда отрицательное значение оказывается полезным в данном контексте, поэтому мне нужно помнить, что нужно думать о значениях и контексте, а не рефлекторно отбрасывать любые и все отрицательные решения.)
Книга Германа падает в воду через две секунды, а моя — через
sqrt (10) секунд, или примерно через 3,16 секунды. То есть:
Книга Германа падает на воду примерно на 1,16 секунды раньше, чем моя.
Время от времени они будут хитрить и помещать «снарядную» проблему в другую среду. Уравнение останется прежним по структуре, но вам, возможно, придется учитывать другое значение гравитации.
- Международное космическое агентство наконец посадило робота-исследователя на внесолнечную планету.
 Некоторые зонды выдвигаются из корпуса спускаемого аппарата для проведения различных тестов. Чтобы продемонстрировать сокрушительный вес гравитации на этой планете, камера посадочного модуля направлена на порт выброса зонда на уровне земли, и порт запускает бейсбольный мяч прямо вверх со скоростью 147 футов в секунду (фут/с), что примерно соответствует максимальной скорости профессиональный кувшин. Сила гравитации на этой планете составляет 98 фут/с 2 . Если предположить, что ветра нет и что зонд может вовремя уйти в сторону, сколько времени потребуется, чтобы шар снова врезался в поверхность?
Некоторые зонды выдвигаются из корпуса спускаемого аппарата для проведения различных тестов. Чтобы продемонстрировать сокрушительный вес гравитации на этой планете, камера посадочного модуля направлена на порт выброса зонда на уровне земли, и порт запускает бейсбольный мяч прямо вверх со скоростью 147 футов в секунду (фут/с), что примерно соответствует максимальной скорости профессиональный кувшин. Сила гравитации на этой планете составляет 98 фут/с 2 . Если предположить, что ветра нет и что зонд может вовремя уйти в сторону, сколько времени потребуется, чтобы шар снова врезался в поверхность?
Чтобы составить уравнение для этого упражнения, мне нужно иметь в виду, что значение коэффициента g из приведенного выше уравнения движения снаряда составляет половину значения силы гравитации в данном месте. .
В физике существует «универсальная гравитационная постоянная» G , представляющая собой гравитационное притяжение, присущее нашей Вселенной (или, по крайней мере, нашей ее области). Каждый объект оказывает свою гравитационную силу, которая связана с его собственной массой и универсальной постоянной 9.0021 Г . В формуле «движения снаряда» « г » — это половина значения гравитационной силы для этого конкретного тела. Например, гравитационная сила на Земле направлена вниз со скоростью 32 фута/с 2 , но мы использовали 16 в уравнении.
Каждый объект оказывает свою гравитационную силу, которая связана с его собственной массой и универсальной постоянной 9.0021 Г . В формуле «движения снаряда» « г » — это половина значения гравитационной силы для этого конкретного тела. Например, гравитационная сила на Земле направлена вниз со скоростью 32 фута/с 2 , но мы использовали 16 в уравнении.
Итак, г для моего уравнения на этот раз будет на 98 ÷ 2 = 49 футов в секунду в квадрате. Тогда:
с = −49 t 2 + 147 t
0 = −49 т 2 + 147 т
0 = t 2 − 3 t
0 = t ( t − 3)
Тогда t = 0 или t = 3. Первое решение представляет момент запуска мяча, поэтому мне нужно второе решение.
Чтобы мяч коснулся земли, требуется три секунды.
Примечание: на Земле мячу потребовалось бы немногим более девяти секунд, чтобы упасть на землю.
. в этом разделе вы сможете:
- Задайте положение, перемещение и пройденное расстояние.
- Вычислите общее перемещение с заданным положением как функцию времени.
- Определите общее пройденное расстояние.
- Рассчитайте среднюю скорость, зная перемещение и прошедшее время.
Когда вы в движении, основные вопросы, которые нужно задать: Где вы находитесь? Куда ты идешь? Как быстро вы туда добираетесь? Ответы на эти вопросы требуют, чтобы вы указали ваше положение, ваше перемещение и вашу среднюю скорость — термины, которые мы определяем в этом разделе.
Позиция
Чтобы описать движение объекта, вы должны сначала уметь описать его положение ( x ): где в любой момент времени . Точнее, нам нужно указать его положение относительно удобной системы отсчета. Система отсчета — это произвольный набор осей, от которых описывается положение и движение объекта. Земля часто используется в качестве системы отсчета, и мы часто описываем положение объекта по отношению к неподвижным объектам на Земле. Например, запуск ракеты можно описать с точки зрения положения ракеты относительно Земли в целом, тогда как положение велосипедиста можно описать с точки зрения того, где он находится по отношению к зданиям, которые он проезжает (рис. 3.2). В других случаях мы используем системы отсчета, которые не стационарны, а движутся относительно Земли. Например, чтобы описать положение человека в самолете, мы используем в качестве системы отсчета самолет, а не Землю. Для описания положения объекта, совершающего одномерное движение, часто используется переменная х . Далее в этой главе, при обсуждении свободного падения, мы используем переменную y .
Земля часто используется в качестве системы отсчета, и мы часто описываем положение объекта по отношению к неподвижным объектам на Земле. Например, запуск ракеты можно описать с точки зрения положения ракеты относительно Земли в целом, тогда как положение велосипедиста можно описать с точки зрения того, где он находится по отношению к зданиям, которые он проезжает (рис. 3.2). В других случаях мы используем системы отсчета, которые не стационарны, а движутся относительно Земли. Например, чтобы описать положение человека в самолете, мы используем в качестве системы отсчета самолет, а не Землю. Для описания положения объекта, совершающего одномерное движение, часто используется переменная х . Далее в этой главе, при обсуждении свободного падения, мы используем переменную y .
Рисунок
3.2
Этих велосипедистов во Вьетнаме можно описать по их положению относительно зданий или канала. Их движение можно описать изменением их положения или перемещением в системе отсчета. (кредит: модификация работы Сьюзан Блэк)
(кредит: модификация работы Сьюзан Блэк)
Смещение
Если объект перемещается относительно системы отсчета, например, если профессор перемещается вправо относительно доски (рис. 3.3), положение объекта изменяется. Это изменение положения называется смещением. Слово смещение подразумевает, что объект переместился или был смещен. Хотя положение является числовым значением x вдоль прямой линии, где может быть расположен объект, смещение дает изменение положения вдоль этой линии. Поскольку смещение указывает направление, это вектор, который может быть как положительным, так и отрицательным, в зависимости от выбора положительного направления. Кроме того, в анализ движения может быть включено множество смещений. Если правое положительное и объект перемещается на 2 м вправо, затем на 4 м влево, отдельные смещения составляют 2 м и -4-4 м соответственно.
Рисунок
3. 3
Профессор ходит влево и вправо во время лекции. Ее положение относительно Земли определяется как x . Смещение профессора относительно Земли на +2,0 м показано стрелкой, указывающей вправо.
3
Профессор ходит влево и вправо во время лекции. Ее положение относительно Земли определяется как x . Смещение профессора относительно Земли на +2,0 м показано стрелкой, указывающей вправо.
смещение
Перемещение ΔxΔx — изменение положения объекта:
Δx=xf−x0,Δx=xf−x0,
3.1
где ΔxΔx — смещение, xfxf — конечное положение, x0x0 — начальное положение.
Мы используем заглавную греческую букву дельта (Δ) для обозначения «изменения» любой величины, следующей за ней; таким образом, ΔxΔx означает изменение положения (конечное положение минус начальное положение). Мы всегда находим смещение, вычитая начальную позицию x0x0 из конечной позиции xfxf. Обратите внимание, что единицей СИ для перемещения является метр, но иногда мы используем километры или другие единицы длины. Имейте в виду, что когда в задаче используются единицы измерения, отличные от метров, вам может потребоваться преобразовать их в метры, чтобы завершить расчет (см.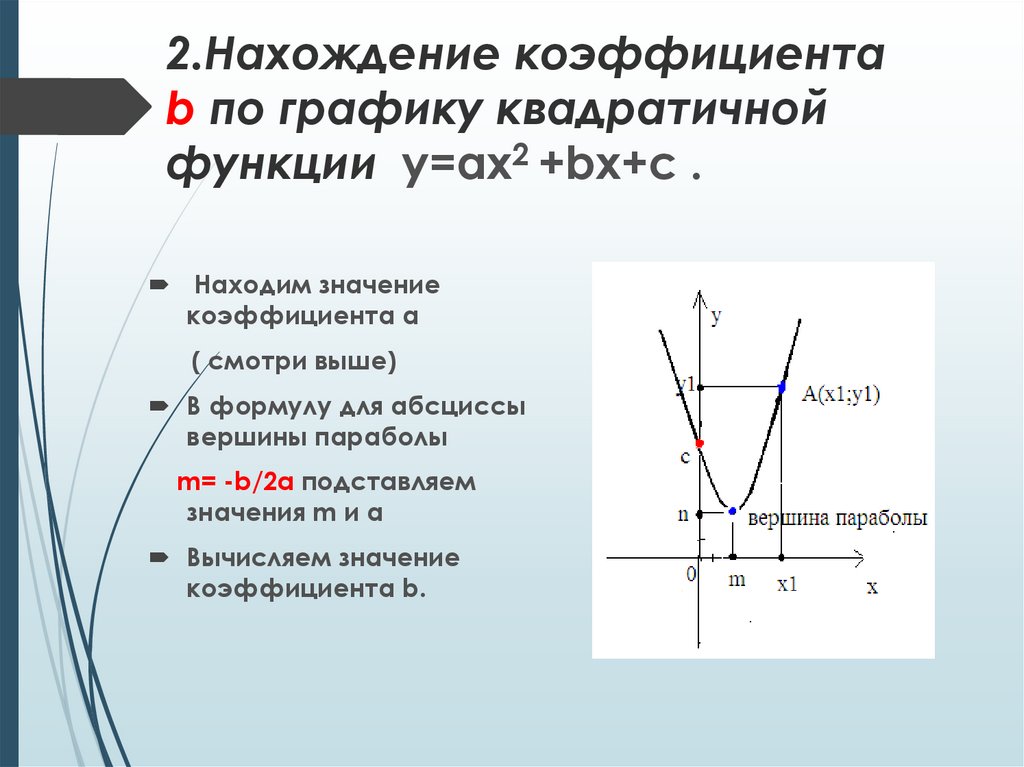 Приложение B).
Приложение B).
Объекты в движении также могут иметь ряд перемещений. В предыдущем примере с профессором стимуляции индивидуальные смещения составляют 2 м и -4-4 м, что дает общее смещение -2 м. Мы определяем общее перемещение ΔxTotalΔxTotal как сумму индивидуальных перемещений и выражаем это математически уравнением
ΔxTotal=∑Δxi,ΔxTotal=∑Δxi,
3,2
, где ΔxiΔxi — индивидуальные перемещения. В предыдущем примере
Δx1=x1−x0=2−0=2m.Δx1=x1−x0=2−0=2m.
Аналогично,
Δx2=x2−x1=−2−(2)=−4m.Δx2=x2−x1=−2−(2)=−4m.
Таким образом,
ΔxTotal=Δx1+Δx2=2−4=−2m.ΔxTotal=Δx1+Δx2=2−4=−2m.
Полное перемещение равно 2 − 4 = −2 м вдоль оси x . Также полезно рассчитать величину смещения или его размер. Величина смещения всегда положительна. Это абсолютное значение смещения, потому что смещение является вектором и не может иметь отрицательное значение величины. В нашем примере величина полного смещения равна 2 м, а величина отдельных перемещений равна 2 м и 4 м.
В нашем примере величина полного смещения равна 2 м, а величина отдельных перемещений равна 2 м и 4 м.
Величину полного смещения не следует путать с пройденным расстоянием. Пройденное расстояние xTotalxTotal — это общая длина пути, пройденного между двумя позициями. В предыдущей задаче пройденное расстояние равно сумме величин отдельных перемещений:
xTotal=|Δx1|+|Δx2|=2+4=6m.xTotal=|Δx1|+|Δx2|=2+4=6m.
Средняя скорость
Для вычисления других физических величин в кинематике мы должны ввести переменную времени. Переменная времени позволяет нам не только указать, где находится объект (его положение) во время его движения, но и как быстро он движется. Насколько быстро движется объект, определяется скоростью, с которой его положение меняется со временем.
Для каждой позиции xixi мы назначаем определенное время titi. Если детали движения в каждый момент времени не важны, скорость обычно выражают как среднюю скорость v–v–. Эта векторная величина представляет собой просто общее перемещение между двумя точками, деленное на время, затрачиваемое на перемещение между ними.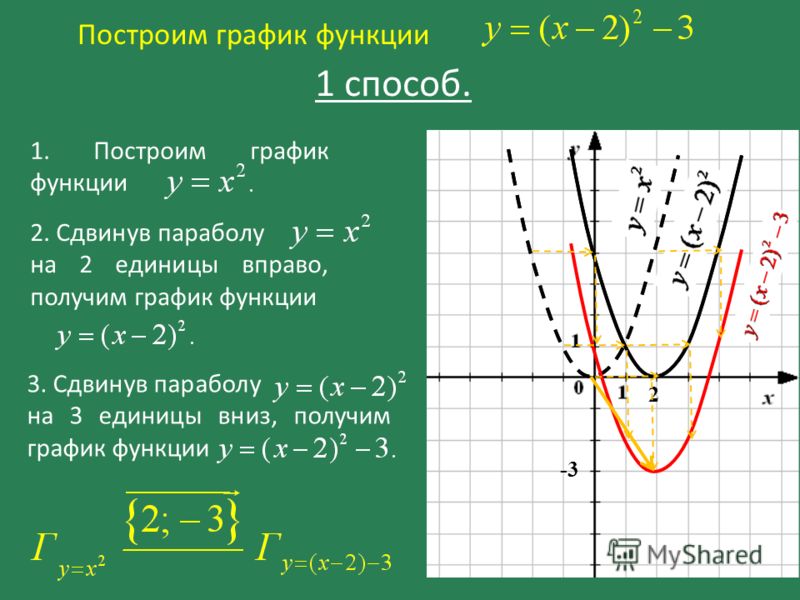 Время, необходимое для перемещения между двумя точками, называется истекшим временем ΔtΔt.
Время, необходимое для перемещения между двумя точками, называется истекшим временем ΔtΔt.
Средняя скорость
Если x1x1 и x2x2 — положения объекта в моменты времени t1t1 и t2t2 соответственно, то
Средняя скорость=v–=Смещение между двумя точкамиВремя, необходимое для выполнения смещенияv–=ΔxΔt=x2−x1t2−t1. Средняя скорость=v–=Смещение между двумя точкамиВремя, необходимое для выполнения смещенияv–=ΔxΔt=x2−x1t2− т1.
3,3
Важно отметить, что средняя скорость является вектором и может быть отрицательной, в зависимости от положений x1x1 и x2x2.
Пример 3.1
Доставка листовок
Джилл выходит из своего дома, чтобы доставить листовки для распродажи во дворе, путешествуя прямо на восток по своей улице, застроенной домами. На 0,5-0,5 км и 9Через несколько минут у нее заканчиваются листовки, и ей приходится возвращаться к дому, чтобы получить еще.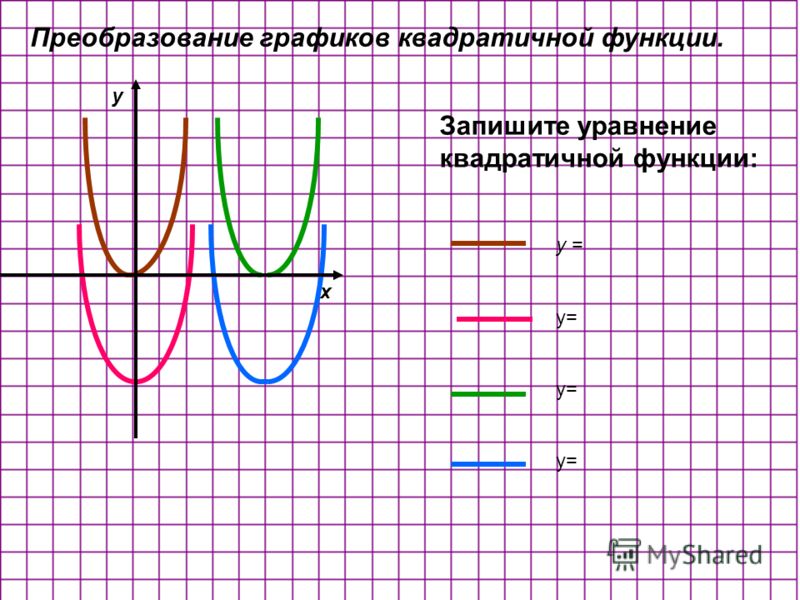 Это занимает еще 9 минут. Собрав больше листовок, она снова отправляется по тому же пути, продолжая с того места, где остановилась, и оказывается в 1,0 км от своего дома. Этот третий этап ее путешествия занимает 1515 минут. В этот момент она поворачивает обратно к своему дому, направляясь на запад. Через 1.751,75 км и 2525 минут она останавливается на отдых.
Это занимает еще 9 минут. Собрав больше листовок, она снова отправляется по тому же пути, продолжая с того места, где остановилась, и оказывается в 1,0 км от своего дома. Этот третий этап ее путешествия занимает 1515 минут. В этот момент она поворачивает обратно к своему дому, направляясь на запад. Через 1.751,75 км и 2525 минут она останавливается на отдых.
- Каково полное перемещение Джилл до точки, где она останавливается для отдыха?
- Какова величина окончательного смещения?
- Какова средняя скорость во время всего путешествия?
- Каково общее пройденное расстояние?
- Постройте график зависимости положения от времени.
Набросок движений Джилл показан на рис. 3.4.
Рисунок 3.4 Хронология движений Джилл.
Стратегия
Задача содержит данные о различных этапах пути Джилл, поэтому было бы полезно составить таблицу физических величин.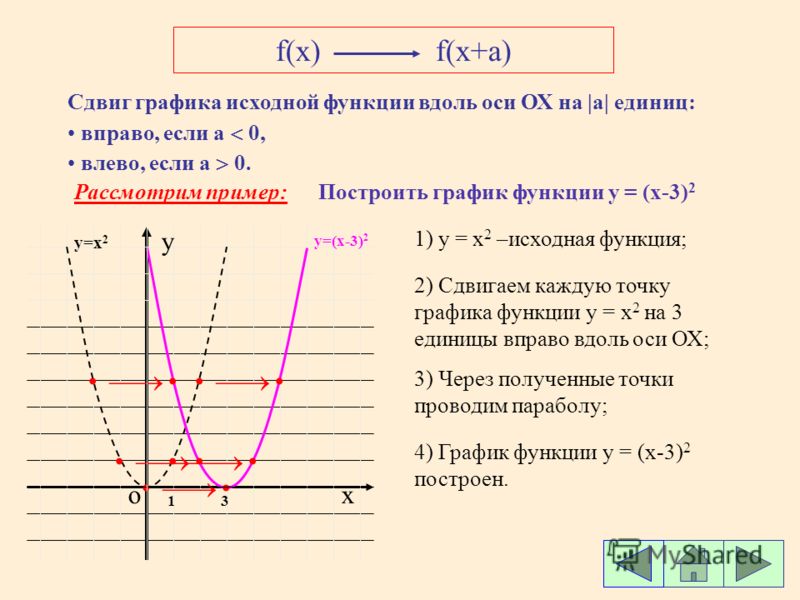 Нам даны положение и время в формулировке задачи, поэтому мы можем рассчитать смещения и затраченное время. Мы берем восток, чтобы быть положительным направлением. Из этой информации мы можем найти полное перемещение и среднюю скорость. Дом Джилл является отправной точкой x0x0. В следующей таблице указано время и положение Джилл в первых двух столбцах, а смещения рассчитаны в третьем столбце.
Нам даны положение и время в формулировке задачи, поэтому мы можем рассчитать смещения и затраченное время. Мы берем восток, чтобы быть положительным направлением. Из этой информации мы можем найти полное перемещение и среднюю скорость. Дом Джилл является отправной точкой x0x0. В следующей таблице указано время и положение Джилл в первых двух столбцах, а смещения рассчитаны в третьем столбце.
| Время t i (мин) | Местоположение xixi (км) | Водоизмещение ΔxiΔxi (км) |
|---|---|---|
| t0=0t0=0 | х0=0х0=0 | Δx0=0Δx0=0 |
| т1=9т1=9 | х1=0,5х1=0,5 | Δx1=x1−x0=0,5Δx1=x1−x0=0,5 |
| т2=18т2=18 | х2=0х2=0 | Δx2=x2−x1=−0,5Δx2=x2−x1=−0,5 |
| t3=33t3=33 | х3=1,0х3=1,0 | Δx3=x3−x2=1,0 Δx3=x3−x2=1,0 |
| т4=58т4=58 | x4=-0,75×4=-0,75 | Δx4=x4−x3=−1,75Δx4=x4−x3=−1,75 |
Решение
- Из приведенной выше таблицы общий рабочий объем равен
∑Δxi=0,5−0,5+1,0−1,75 км=−0,75 км.
 ∑Δxi=0,5−0,5+1,0−1,75 км=−0,75 км.
∑Δxi=0,5−0,5+1,0−1,75 км=−0,75 км. - Величина полного смещения равна |−0,75|км=0,75км|−0,75|км=0,75км.
- Средняя скорость = TotaldisplacementElapsedtime=v–=−0,75 км58мин=−0,013 км/мин0099
- Общее пройденное расстояние (сумма величин отдельных перемещений) равно xTotal=∑|Δxi|=0,5+0,5+1,0+1,75 км=3,75 кмxTotal=∑|Δxi|=0,5+0,5+1,0+1,75 км=3,75 км.
- Мы можем построить график положения Джилл в зависимости от времени, чтобы увидеть движение; график показан на рис. 3.5.
Рисунок 3,5 На этом графике показано положение Джилл в зависимости от времени. Средняя скорость — это наклон линии, соединяющей начальную и конечную точки.
Значение
Полное перемещение Джилл составляет −0,75 км, что означает, что в конце путешествия она окажется на расстоянии 0,75 км — 0,75 км к западу от своего дома. Средняя скорость означает, что если кто-то пойдет прямо на запад со скоростью 0,0130,013 км/мин, начиная с того же момента, когда Джилл вышла из дома, они оба прибудут к конечной точке остановки в одно и то же время.


 Осуществить параллельный перенос графика y=f(x) вдоль оси x на единиц масштаба влево, если l>0, и вправо, если l
Осуществить параллельный перенос графика y=f(x) вдоль оси x на единиц масштаба влево, если l>0, и вправо, если l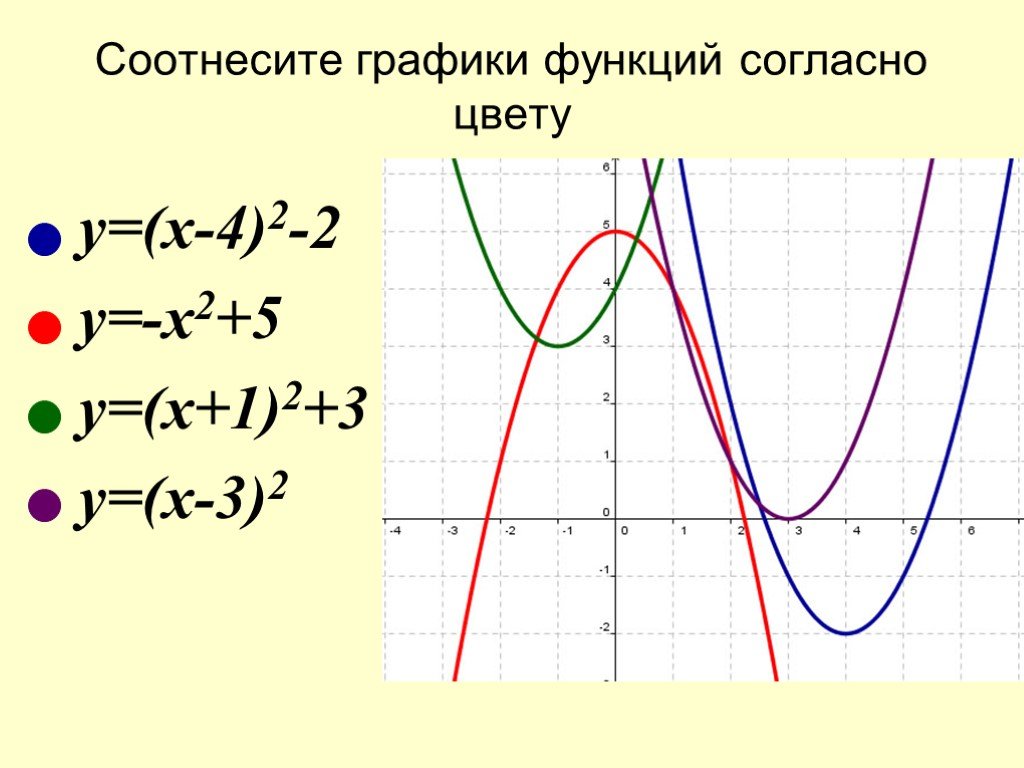 Некоторые зонды выдвигаются из корпуса спускаемого аппарата для проведения различных тестов. Чтобы продемонстрировать сокрушительный вес гравитации на этой планете, камера посадочного модуля направлена на порт выброса зонда на уровне земли, и порт запускает бейсбольный мяч прямо вверх со скоростью 147 футов в секунду (фут/с), что примерно соответствует максимальной скорости профессиональный кувшин. Сила гравитации на этой планете составляет 98 фут/с 2 . Если предположить, что ветра нет и что зонд может вовремя уйти в сторону, сколько времени потребуется, чтобы шар снова врезался в поверхность?
Некоторые зонды выдвигаются из корпуса спускаемого аппарата для проведения различных тестов. Чтобы продемонстрировать сокрушительный вес гравитации на этой планете, камера посадочного модуля направлена на порт выброса зонда на уровне земли, и порт запускает бейсбольный мяч прямо вверх со скоростью 147 футов в секунду (фут/с), что примерно соответствует максимальной скорости профессиональный кувшин. Сила гравитации на этой планете составляет 98 фут/с 2 . Если предположить, что ветра нет и что зонд может вовремя уйти в сторону, сколько времени потребуется, чтобы шар снова врезался в поверхность? ∑Δxi=0,5−0,5+1,0−1,75 км=−0,75 км.
∑Δxi=0,5−0,5+1,0−1,75 км=−0,75 км.