Решение высшей математики онлайн
‹— Назад
В школьном курсе математики достаточно подробно изучалась парабола, которая, по определению, являлась графиком квадратного трехчлена. Здесь мы дадим другое (геометрическое) определение параболы.
Определение 12.7 Параболой называется геометрическое место точек плоскости, для каждой из которых расстояние до фиксированной точки этой плоскости, называемой фокусом, равно расстоянию до фиксированной прямой, лежащей в той же плоскости и называемой директрисой параболы.
Чтобы получить уравнение кривой, соответствующей этому определению, введем подходящую систему координат. Для этого из фокуса опустим перпендикуляр на директрису . Начало координат расположим на середине отрезка , ось направим вдоль отрезка так, чтобы ее направление совпадало с направлением вектора . Ось проведем перпендикулярно оси (рис. 12.15).
Ось проведем перпендикулярно оси (рис. 12.15).
Рис.12.15.
Теорема 12.4 Пусть расстояние между фокусом и директрисой параболы равно . Тогда в выбранной системе координат парабола имеет уравнение
| (12.10) |
Доказательство. В выбранной системе координат фокусом параболы служит точка , а директриса имеет уравнение (рис. 12.15).
Пусть — текущая точка параболы. Тогда по формуле (10.4) для плоского случая находим
Расстоянием от точки до директрисы служит длина перпендикуляра , опущенного на директрису из точки . Из рисунка 12.15 очевидно, что . Тогда по определению параболы , то есть
Тогда по определению параболы , то есть
Возведем обе части последнего уравнения в квадрат:
откуда
После приведения подобных членов получим уравнение (12.10).
Уравнение (12.10) называется каноническим уравнением параболы.
Предложение 12.4 Парабола обладает осью симметрии. Если парабола задана каноническим уравнением, то ось симметрии совпадает с осью .
Доказательство. Проводится так же, как и доказательство (предложения 12.1).
Точка пересечения оси симметрии с параболой называется вершиной параболы.
Если переобозначить переменные , , то уравнение (12.10) можно записать в виде
который совпадает с обычным уравнением параболы в школьном курсе математики. Поэтому параболу нарисуем без дополнительных исследований (рис. 12.16).
12.16).
Рис.12.16.Парабола
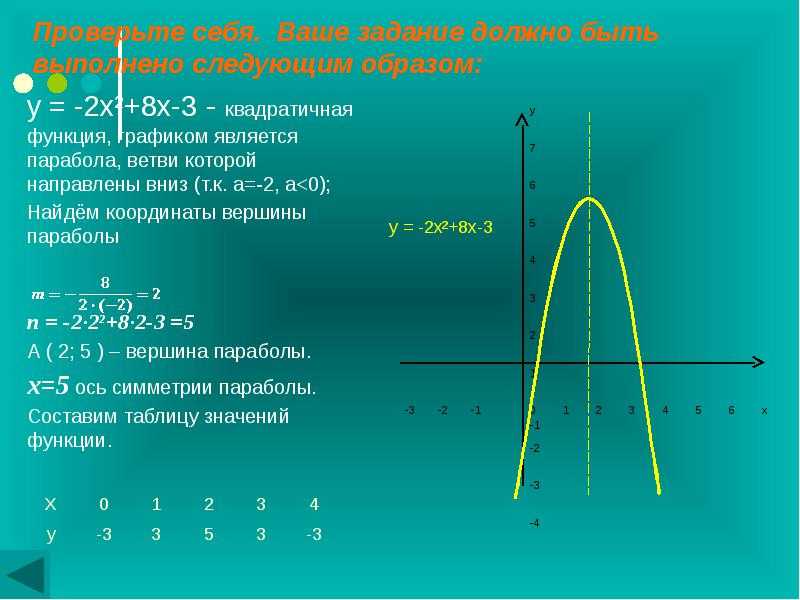
Пример 12.6 Постройте параболу . Найдите ее фокус и директрису.
Решение. Уравнение является каноническим уравнением параболы, , . Осью параболы служит ось , вершина находится в начале координат, ветви параболы направлены вдоль оси . Для построения найдем несколько точек параболы. Для этого придаем значения переменному и находим значения . Возьмем точки , , . Учитывая симметрию относительно оси , рисуем кривую (рис. 12.17)
Рис.12.17.Парабола, заданная уравнением
Фокус лежит на оси на расстоянии от вершины, то есть имеет координаты . Директриса имеет уравнение , то есть .
Парабола так же, как и эллипс, обладает свойством, связанным с отражением света (рис. 12.18). Свойство сформулируем опять без доказательства.
Предложение 12.5 Пусть — фокус параболы, — произвольная точка параболы, — луч с началом в точке параллельный оси параболы. Тогда нормаль к параболе в точке делит угол, образованный отрезком и лучом , пополам.
Рис.12.18.Отражение светового луча от параболы
Это свойство означает, что луч света, вышедший из фокуса , отразившись от параболы, дальше пойдет параллельно оси этой параболы. И наоборот, все лучи, приходящие из бесконечности и параллельные оси параболы, сойдутся в ее фокусе. Это свойство широко используется в технике. В прожекторах обычно ставят зеркало, поверхность которого получается при вращении параболы вокруг ее оси симметрии (параболическое зеркало). Источник света в прожекторах помещают в фокусе параболы. В результате прожектор дает пучок почти параллельных лучей света. Это же свойство используется и в приемных антеннах космической связи и в зеркалах телескопов, которые собирают поток параллельных лучей радиоволн или поток параллельных лучей света и концентрируют его в фокусе зеркала.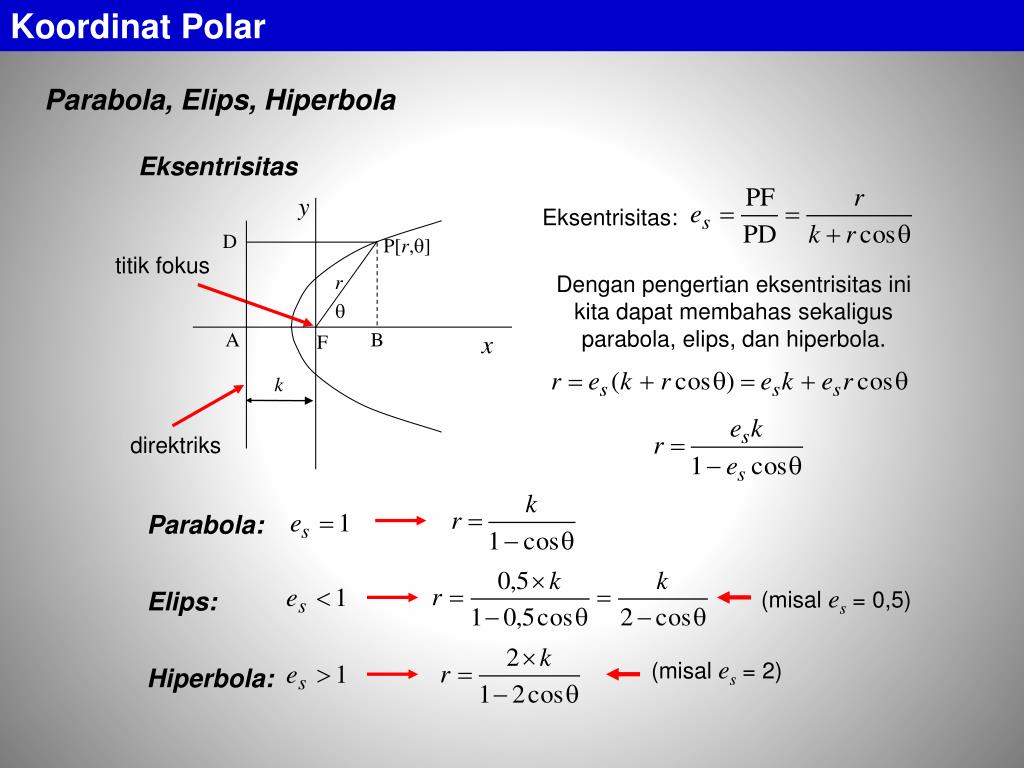
Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции
Титта Руффо — Парабола моей жизни читать онлайн
12 3 4 5 6 7 …102
ТИТТА РУФФО И ЕГО ВОСПОМИНАНИЯ
Перевод с итальянского и вступительная статья А. БУШЕН
БУШЕН
Книга воспоминаний Титта Руффо, названная им «Парабола моей жизни»,— правдивое описание нелегкого жизненного и творческого пути одного из величайших вокалистов-баритонов первой половины XX века. Мемуары эти, занимательные и поучительные, привлекательны своей искренностью, прямотой и бесхитростной откровенностью.
Жизнь знаменитого артиста с самого начала и до конца складывалась не гладко.. На его долю выпали жизненные и творческие конфликты, требовавшие от него активного участия и немедленного разрешения. Такой уж он был человек и такая была у него судьба.
У многих прославленных итальянских певцов и голос и актерские способности в какой-то степени «прорезывались» с детства. Будущие артисты мальчиками пели в церковных хорах, а иногда выступали и на сценах. Так или иначе приобщаясь к музыке, они в той или иной форме тренировали слух и память. Ничего подобного нет в детстве Титта Руффо. Суровым и безрадостным было его детство. Да и было ли оно у прославившегося на весь мир певца? С восьми лет малыш уже работал, раздувая мехи в кузнице, и начал он работать по собственной инициативе, из какого-то удивительного для ребенка горячего желания во что бы то ни стало помочь нуждавшейся семье.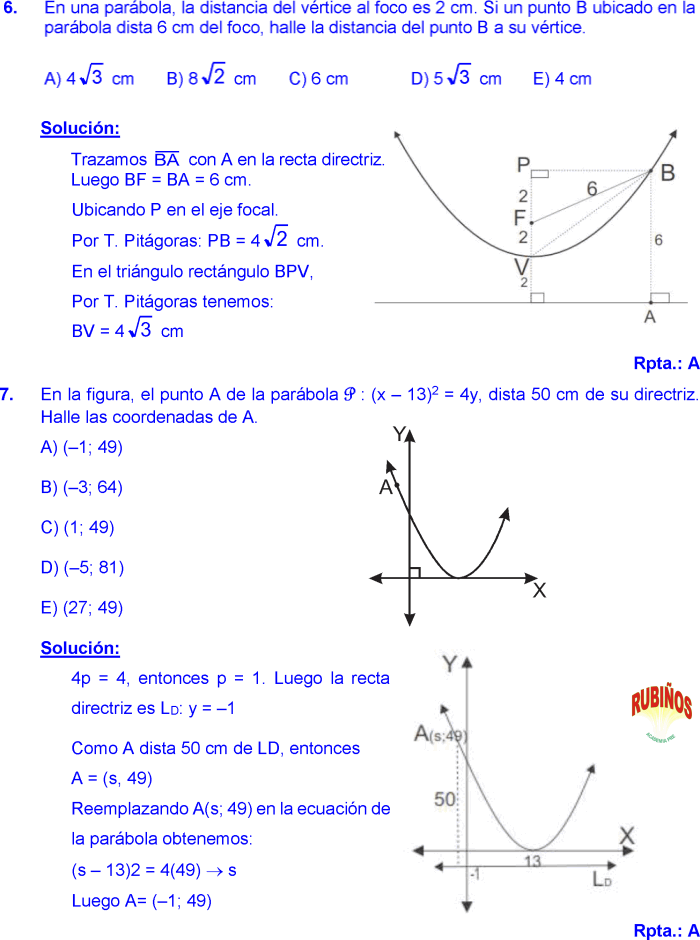 Вот уже с какого времени наметились отличительные черты характера этого незаурядного человека — неукротимая работоспособность, желание жить собственным тРУДОм.
Вот уже с какого времени наметились отличительные черты характера этого незаурядного человека — неукротимая работоспособность, желание жить собственным тРУДОм.
На первый взгляд кажется, что ничто в ребенке не свидетельствовало о его творческих способностях. Но так кажется только на первый взгляд. Правда, никаких воспоминаний об изобретательных играх или хотя бы выдумках, живо отображающих детское мировосприятие, у него не сохранилось. На работе он, несомненно, уставал. Иначе и быть не могло. Во всяком случае даже в воскресный день ему не хочется побегать и порезвиться. Он предпочитает оставаться дома, сидеть с мамой у окна и подчас засыпать у нее на коленях. Но вот что характерно: хотя ему не рассказывают сказок, не читают интересных историй и даже грамоте его не учат, у этого ребенка какая-то необыкновенно повышенная душевная чувствительность, не по возрасту обостренная наблюдательность, особое, почти художественное восприятие внешнего облика людей, легко воспламеняющееся богатое воображение. И все эти особенности характера и душевной организации сыграют впоследствии свою роль в формировании выдающегося дарования певца-актера. Слуховые впечатления раннего детства Титта Руффо также не способствовали развитию у ребенка музыкальных навыков. Резкие звуки ударов молота по наковальне, лязг железа, разные звоны, шумы и стуки кузнечной мастерской — вот чем с самых первых дней жизни питается нежное детское ухо. О благозвучных музыкальных впечатлениях Титта Руффо не упоминает. Возможно, что их и не было. Он не знает даже, что у него отличный слух музыканта и безотказная память. Но когда при переезде в Рим он слышит песенку «О Кароли», которую напевает хозяин гостиницы, мелодия, как он сам пишет, входит в его сознание и он запоминает ее на всю жизнь.
И все эти особенности характера и душевной организации сыграют впоследствии свою роль в формировании выдающегося дарования певца-актера. Слуховые впечатления раннего детства Титта Руффо также не способствовали развитию у ребенка музыкальных навыков. Резкие звуки ударов молота по наковальне, лязг железа, разные звоны, шумы и стуки кузнечной мастерской — вот чем с самых первых дней жизни питается нежное детское ухо. О благозвучных музыкальных впечатлениях Титта Руффо не упоминает. Возможно, что их и не было. Он не знает даже, что у него отличный слух музыканта и безотказная память. Но когда при переезде в Рим он слышит песенку «О Кароли», которую напевает хозяин гостиницы, мелодия, как он сам пишет, входит в его сознание и он запоминает ее на всю жизнь.
Растет будущий певец в весьма неблагополучной семейной обстановке. Мало того, что семья живет чуть ли не впроголодь и между отцом и матерью нет доброго согласия, отец Руффо, человек мятежный, не лишенный таланта, но уязвленный в своих художественных стремлениях, озлобленный засасывающей нуждой, вложил все свои мечты и надежды в старшего сына, красивого белокурого Этторе. Мальчика и балуют, и учат, и стараются получше одеть. А от младшего, внешне ничем не примечательного Руффо, отец не ждет ничего хорошего. Он заставляет его почти бесплатно работать в своей мастерской, не учит ничему, кроме ремесла, жесток с ним, несправедливо придирчив и, наконец, повздорив с сыном, гонит тринадцатилетнего мальчугана вон из дома. И мальчик бесстрашно пускается в неизвестность, не имея в кармане ни одного сольдо, и начинает самостоятельную жизнь с того, что ночует в Альбано на кладбище, устроившись в заброшенной гробнице. Конечно же, маленькому путешественнику могло взгрустнуться, ему было и холодно и неуютно — все это естественно. Но достаточно слова прохожего, назвавшего конусообразный памятник могилой Горациев и Куриациев*, чтобы детская фантазия заработала вовсю. Будущий артист в сонном забытьи видит себя в некоем театральном аспекте, взрослым человеком в костюме римского воина с золотым шлемом на голове, в пурпурной мантии, с мечом в руке…
Мальчика и балуют, и учат, и стараются получше одеть. А от младшего, внешне ничем не примечательного Руффо, отец не ждет ничего хорошего. Он заставляет его почти бесплатно работать в своей мастерской, не учит ничему, кроме ремесла, жесток с ним, несправедливо придирчив и, наконец, повздорив с сыном, гонит тринадцатилетнего мальчугана вон из дома. И мальчик бесстрашно пускается в неизвестность, не имея в кармане ни одного сольдо, и начинает самостоятельную жизнь с того, что ночует в Альбано на кладбище, устроившись в заброшенной гробнице. Конечно же, маленькому путешественнику могло взгрустнуться, ему было и холодно и неуютно — все это естественно. Но достаточно слова прохожего, назвавшего конусообразный памятник могилой Горациев и Куриациев*, чтобы детская фантазия заработала вовсю. Будущий артист в сонном забытьи видит себя в некоем театральном аспекте, взрослым человеком в костюме римского воина с золотым шлемом на голове, в пурпурной мантии, с мечом в руке…
Сурова жизнь тринадцатилетнего человека, живущего самостоятельно, в полном одиночестве, в разлуке с семьей. Но и в этот период в нем теплится еще никем не осознанная, чисто инстинктивная тяга к искусству. Он не может удовлетвориться одной только грубой работой в кузнечной мастерской. Проявляя изобретательность и фантазию, он в свободное время выделывает из железа занятные вещицы: выковывает распустившуюся розу с бутоном и листьями, изящный рог изобилия. А когда он выучился читать и в руки ему попала растрепанная книжонка — «Граф Монте-Кристо» Дюма, он с особым, взволнованным любопытством вглядывается в картинки, на которых изображены действующие лица увлекательного романа.
Но и в этот период в нем теплится еще никем не осознанная, чисто инстинктивная тяга к искусству. Он не может удовлетвориться одной только грубой работой в кузнечной мастерской. Проявляя изобретательность и фантазию, он в свободное время выделывает из железа занятные вещицы: выковывает распустившуюся розу с бутоном и листьями, изящный рог изобилия. А когда он выучился читать и в руки ему попала растрепанная книжонка — «Граф Монте-Кристо» Дюма, он с особым, взволнованным любопытством вглядывается в картинки, на которых изображены действующие лица увлекательного романа.
* Мифические герои древнеримской легенды, жившие якобы в VII в.
Оживленные его пылкой фантазией, они в своих живописных, кажущихся театральными, костюмах точно сходят со страниц книги, и мальчик, с замиранием сердца переживая вместе с ними все перипетии их бурной жизни, по-актерски перевоплощается поочередно в каждого из них. Тут же в изгнании, вне дома и семьи, он приобретает непоколебимую трудовую дисциплину и самообладание, которым будет подчинена впоследствии вся его творческая деятельность.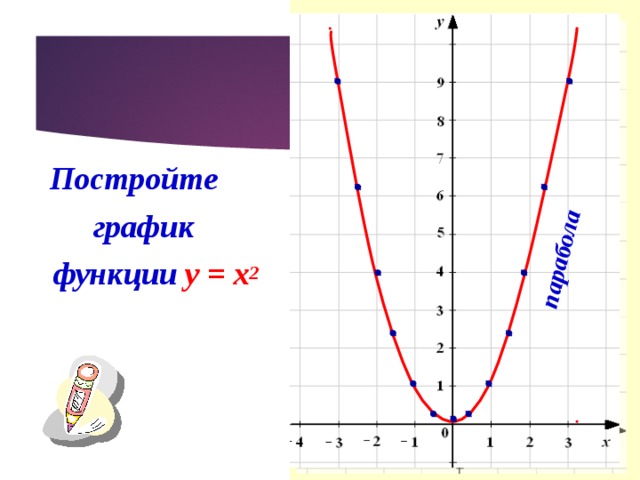
Когда он, возвратившись домой, застает брата студентом двух учебных заведений — академии св. Луки и римской консерватории Санта Чечилия, Руффо, вынужденный снова стучать по железу в невыносимой для него обстановке отцовской мастерской, поначалу мало интересуется занятиями брата. Но однажды, когда Этторе тщательно выдувает на флейте мелодию из «Сельской чести» Масканьи, Руффо с волнением прислушивается к ней. Ему не приходит в голову подпевать, о нет. Он только слушает и с наслаждением читает текст либретто: «О Лола, ты как жизнь…»
Ему идет семнадцатый год, когда он в первый раз попадает в оперу. В первый раз слышит симфонический оркестр. В первый раз воспринимает голоса замечательных певцов. Брат пригласил его в театр Костанци. Идет «Сельская честь» с Бел-линчиони и Станьо в главных ролях. Нельзя без волнения читать, как он пишет об этом. Музыка обрушивается на него с силой катаклизма. Он потрясен до глубины души, сражен неслыханной им доселе красотой искусства. Он почти теряет сознание от восторга.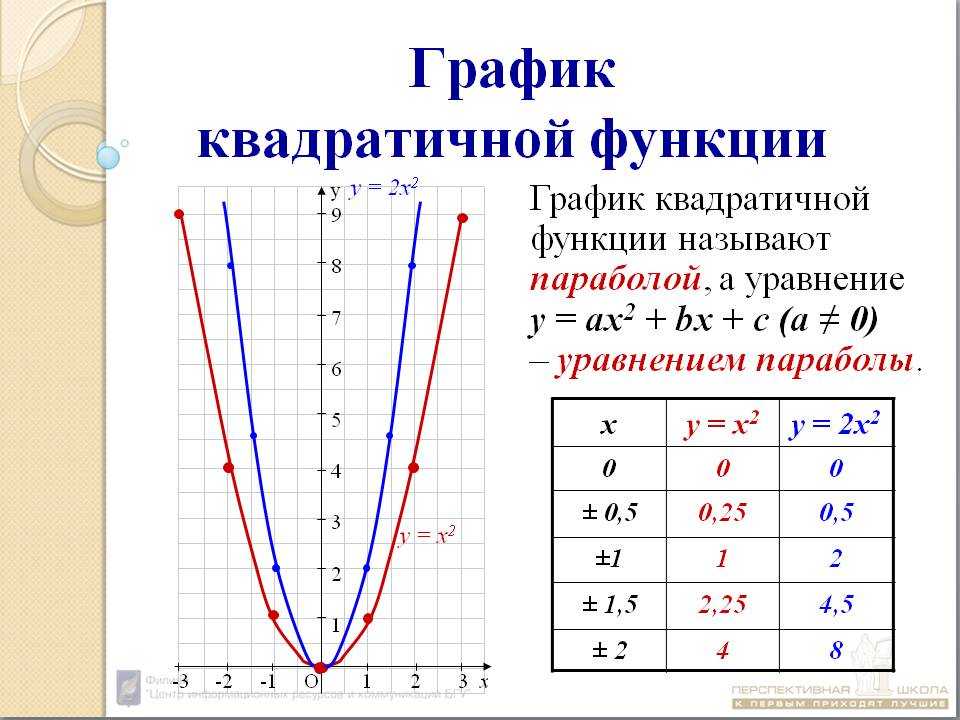 .. Трудно понять это нам, людям, с детства привыкшим к музыке, несущейся из радиоточек, телевизоров, патефонов, радиол. Но для юноши с нетронутой, так сказать, целинной музыкальной организацией, а таким и был Титта Руффо,— открытие музыки в симфонической форме, да еще впервые на семнадцатом году жизни, было не только необыкновенно значительным, но и ошеломляющим событием. Он пережил почти экстатическую радость, захлебнулся ею, как мог бы захлебнуться красотой мира внезапно прозревший слепорожденный.
.. Трудно понять это нам, людям, с детства привыкшим к музыке, несущейся из радиоточек, телевизоров, патефонов, радиол. Но для юноши с нетронутой, так сказать, целинной музыкальной организацией, а таким и был Титта Руффо,— открытие музыки в симфонической форме, да еще впервые на семнадцатом году жизни, было не только необыкновенно значительным, но и ошеломляющим событием. Он пережил почти экстатическую радость, захлебнулся ею, как мог бы захлебнуться красотой мира внезапно прозревший слепорожденный.
Читать дальше
12 3 4 5 6 7 …102
Читать онлайн «Парабола замысла» — Кончаловский Андрей Сергеевич — RuLit
Андрей Михалков-Кончаловский.
Парабола замысла.
М.,”Искусство”. 1977г
Книга посвящена профессии режиссера, его работе над фильмом – от замысла до встречи со зрителем.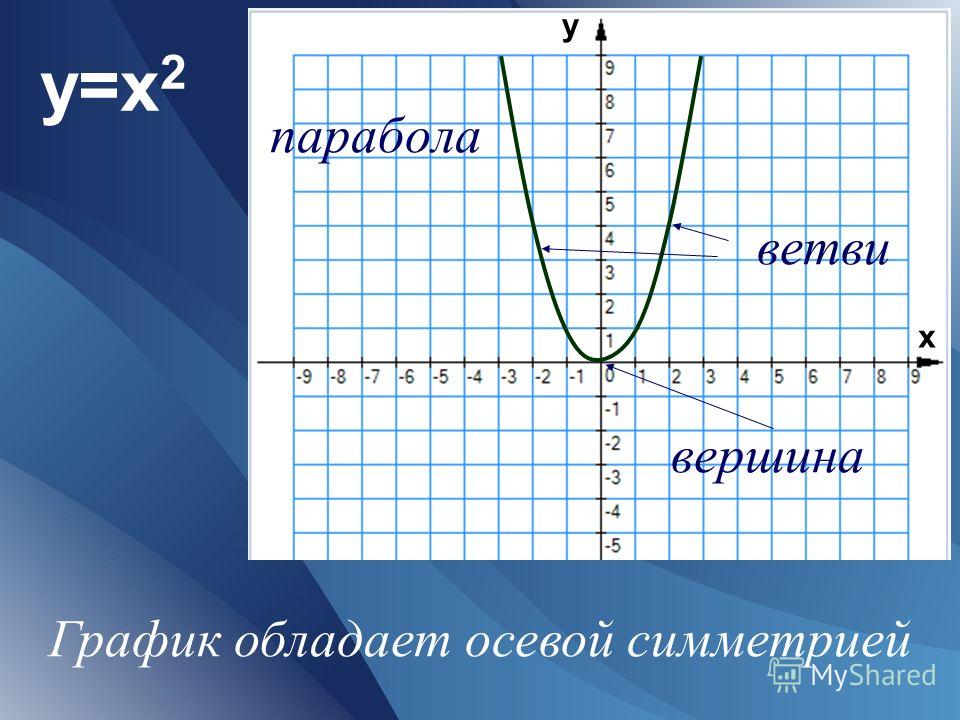 Привлекая богатый материал своих постановок – “Романс о влюбленных”, “Первый учитель”, “Дворянское гнездо”, “Дядя Ваня”,- автор рассматривает широкий круг дискуссионных вопросов современной теории и практики. Книга дает интересный материал для размышлений как профессионалам кинематографистам, так и любителям киноискусства.
Привлекая богатый материал своих постановок – “Романс о влюбленных”, “Первый учитель”, “Дворянское гнездо”, “Дядя Ваня”,- автор рассматривает широкий круг дискуссионных вопросов современной теории и практики. Книга дает интересный материал для размышлений как профессионалам кинематографистам, так и любителям киноискусства.
Содержание
Вступление. 4
Сценарий. 8
“Кинематографичность” и кинематографичность. 8
“Романс о влюбленных”. Первое потрясение. 10
Сценарный ход. 15
Начало параболы.. 16
С точки зрения зрителя. 18
Мир. 21
“Как в жизни” и “как в искусстве”. 21
Кстати, о Шекспире. 24
За “синей птицей”. 26
“Кирпичики” мира. 30
Сотворение мира. Подготовка. 33
Изображение. 33
Художник. Искажение мира.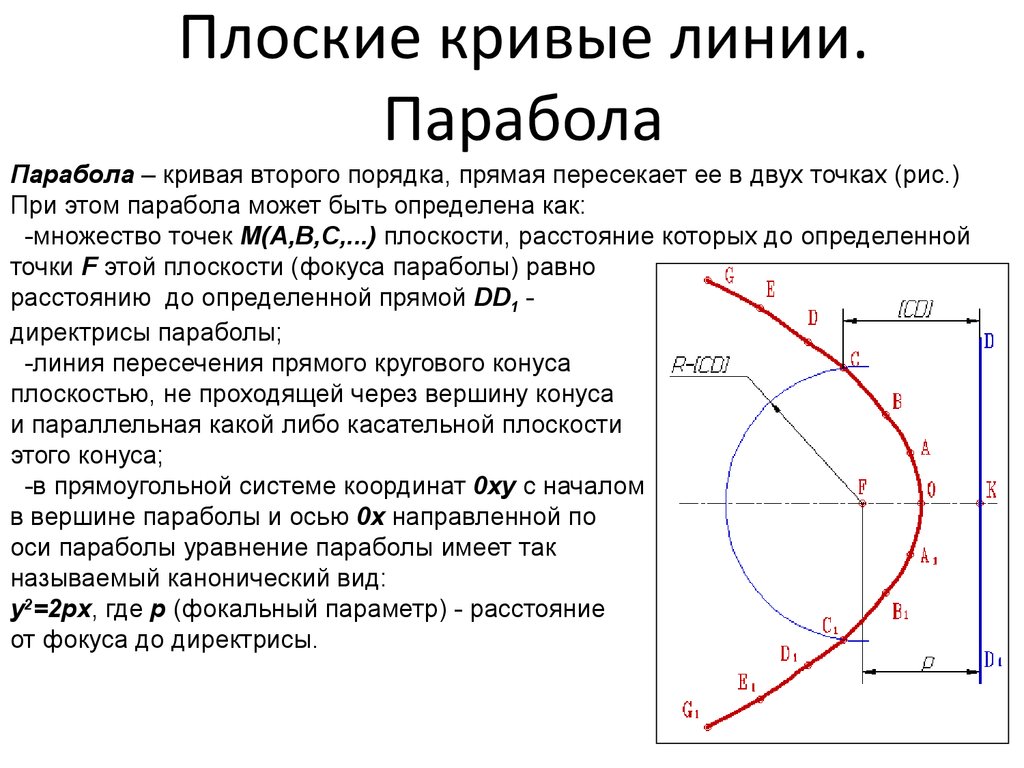 35
35
Немного о костюме. 38
Несколько слов об еще одной существенной частности. 40
Поиски актеров. 41
Пробы.. 42
Герои. 43
Сочинение биографий. 46
Актеры на эпизоды.. 48
Второй план. 50
Композитор. 52
Режиссерский сценарий. 53
ОТСТУПЛЕНИЕ О ПРАВДЕ ЭКРАНА. 57
Похвала документалистике. 57
Метод съемки. 58
Импровизация. 61
Барьер подсознания. 63
О профессионализме и профессионалах. 66
Жанр. 70
За рамкой кадра. 72
Субъективная камера. 74
СОТВОРЕНИЕ МИРА. СЪЕМКА.. 76
Образ целого. 76
Ростки правды.. 77
Будь проклято это кино. 78
Момент условности. 81
Торт на третье. 85
Издержки риска. 87
Пробуждение на бетонном полу. 89
89
Ангел пролетел. 93
Сотворение мира. Монтаж.. 95
Силовые поля. 95
Высшее из искусств. 96
Ритм.. 99
Текучесть формы.. 101
Зритель. 106
Пятое рождение. 106
Дилемма. 107
Странности любви. 108
Пирамида восприятия. 110
Почему?. 110
Зритель и критик. 111
Куда ж нам плыть?. 113
Вместо заключения. 115
Вступление
Мысль написать эту книгу возникла у меня во время беседы с космонавтом Феоктистовым, организованной “Литературной газетой”. Тогда по ходу диалога невольно пришла мысль сравнить две траектории — фильма и космического корабля. Тут есть общее даже в производственной терминологии: “запуск фильма” — “запуск ракеты”. Правда, на стороне техники пока что явные преимущества. Траектория космического корабля контролируется точными, способными делать миллионы операций в секунду вычислительными машинами.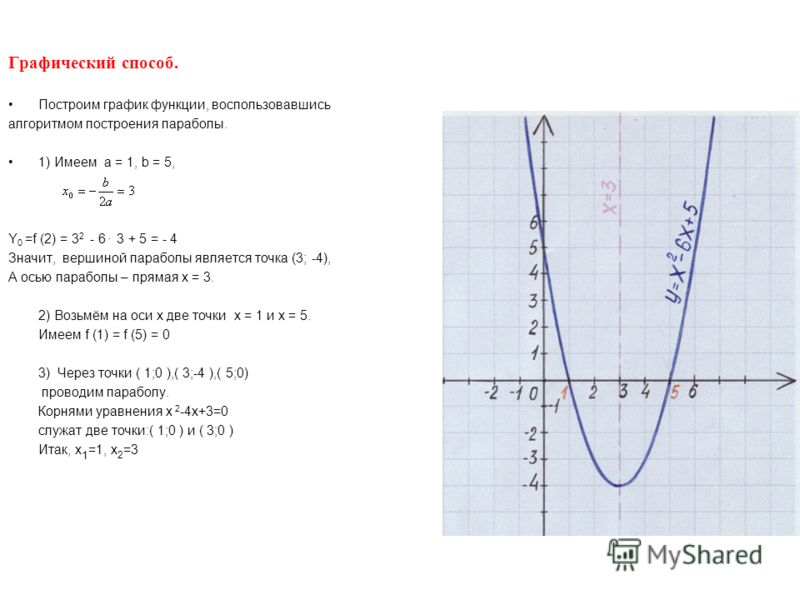 Любое внезапное отклонение от намеченного курса — помехи, ошибки, непредвиденные случайности — ЭВМ может тут же учесть, внести соответствующие коррективы, вернуть корабль на заданную траекторию. Но ведь и путь, который проходит фильм от момента запуска (даже еще раньше — от рождения сценарного замысла), испытывает влияние тысячи разных отклоняющих воздействий: объективных, не зависящих от нас; субъективных, проистекающих уже по нашей воле, ибо по ходу работы приходят новые решения, открываются новые возможности. А помимо всего прочего режиссеру невольно порой приходится производить тысячу дипломатических ухищрений: обещать редакторам и руководству студии очередной шедевр, что-то утаивать от автора сценария, доказывать актерам, что жаждешь делать то, чего делать совсем не намерен.
Любое внезапное отклонение от намеченного курса — помехи, ошибки, непредвиденные случайности — ЭВМ может тут же учесть, внести соответствующие коррективы, вернуть корабль на заданную траекторию. Но ведь и путь, который проходит фильм от момента запуска (даже еще раньше — от рождения сценарного замысла), испытывает влияние тысячи разных отклоняющих воздействий: объективных, не зависящих от нас; субъективных, проистекающих уже по нашей воле, ибо по ходу работы приходят новые решения, открываются новые возможности. А помимо всего прочего режиссеру невольно порой приходится производить тысячу дипломатических ухищрений: обещать редакторам и руководству студии очередной шедевр, что-то утаивать от автора сценария, доказывать актерам, что жаждешь делать то, чего делать совсем не намерен.
Вся режиссура в кино — сплошной компромисс. Да, и в театре, я думаю, тоже. Все время приходится искать решения из всех возможных наиболее приемлемые — иногда даже самые вынужденные, скоропалительные, от отчаяния и безысходности, занят в театре актер, — приходится снимать другого.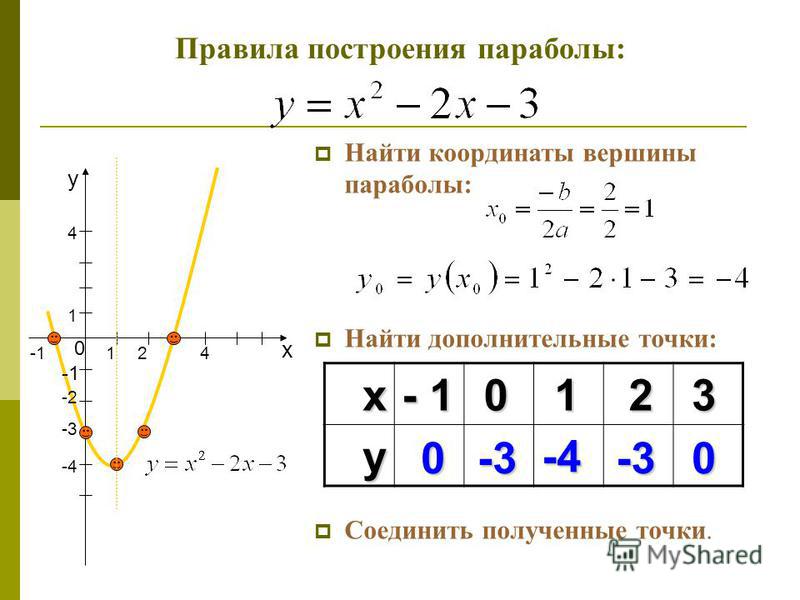
Процесс создания фильма, на мой взгляд, точнее всего было бы уподобить траектории летящего снаряда. Чтобы накрыть цель, артиллерист заведомо берет прицел с превышением: он знает, что снаряд не полетит по прямой — ветер, гравитация, сопротивление воздуха окажут свое воздействие, выгнут первоначальную прямую в дугу параболы.
Как найти вершину параболы онлайн
Расчет вершины параболы
Парабола — это геометрическое место точек на плоскости, равноудалённых от прямой и данной точки.
Формула расчета вершины параболы:
y = ax 2 + bx + c
yв = -(b 2 — 4ac) / 4a
xв — значение x вершины параболы;
yв — значение y вершины параболы;
a, b, c — параметры функции.
Быстро выполнить эту простейшую математическую операцию можно с помощью нашей онлайн программы. Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.
На этой странице представлен самый простой онлайн калькулятор расчета вершины параболы по простой математической формуле в зависимости от значения аргументов. С помощью этого калькулятора вы в один клик сможете вычислить вершины параболы.
Как найти вершину параболы — методы, формулы и примеры вычислений
Парабола — кривая, состоящая из равноудаленных точек от заданной точки (вершина) и прямой. Последняя называется директрисой. График функции имеет ось симметрии, которая проходит по определенной траектории и зависит от функции кривой (рис. 1). Ее вершина находится в центре координат.
1). Ее вершина находится в центре координат.
Рисунок 1. График квадратичной функции с вершиной в начале координат.
Однако существуют и другие случаи прохождения кривой. Она может пересекать оси абсцисс или ординат. В некоторых случаях ее ветви направлены вниз. При вращении вокруг оси симметрии получается поверхность, которая используется в различных устройствах. По этому принципу изготовлены фары автомобиля, зеркала в телескопах и т. д. Кроме того, парабола — это квадратичная зависимость переменных друг от друга. Парабола имеет некоторые свойства:
- Парабола — кривая второго порядка.
- Ось симметрии перпендикулярна директрисе и проходит через фокус и вершины.
- Оптическое свойство отражения.
- Отрезок, который соединяет середину любой хорды параболы и точку пересечения касательных прямых, является перпендикуляром относительно директрисы.
- Подобность всех парабол.
- Траектория фокуса, которая катится по произвольной прямой — цепная молния.

Следует отметить, что оптическое свойство — это способность отражать свет от источника. Если пучок лучей, которые являются параллельными ее оси, отражаются в параболе, то они собираются в фокусе кривой. При нахождении источника света в фокусе происходит отражение параллельного пучка лучей относительно ее оси.
Уравнения квадратичной функции
Параболу можно описать несколькими способами. Каждый из них нужно применять в конкретных случаях для удобства вычислений. Существует три формы описания кривой:
- Каноническая.
- Квадратичная.
- Общая.
В первой форме она имеет следующий вид: y 2 = 2px. Если поменять местами оси декартовой системы, то получится следующий вид: x 2 = 2yp. Коэффициент p — фокальный параметр. Он соответствует расстоянию между фокусом и директрисой. Кроме того, его значение всегда больше нуля. Вершина лежит всегда между фокусом и директрисой кривой на расстоянии, равном p/2 (рис.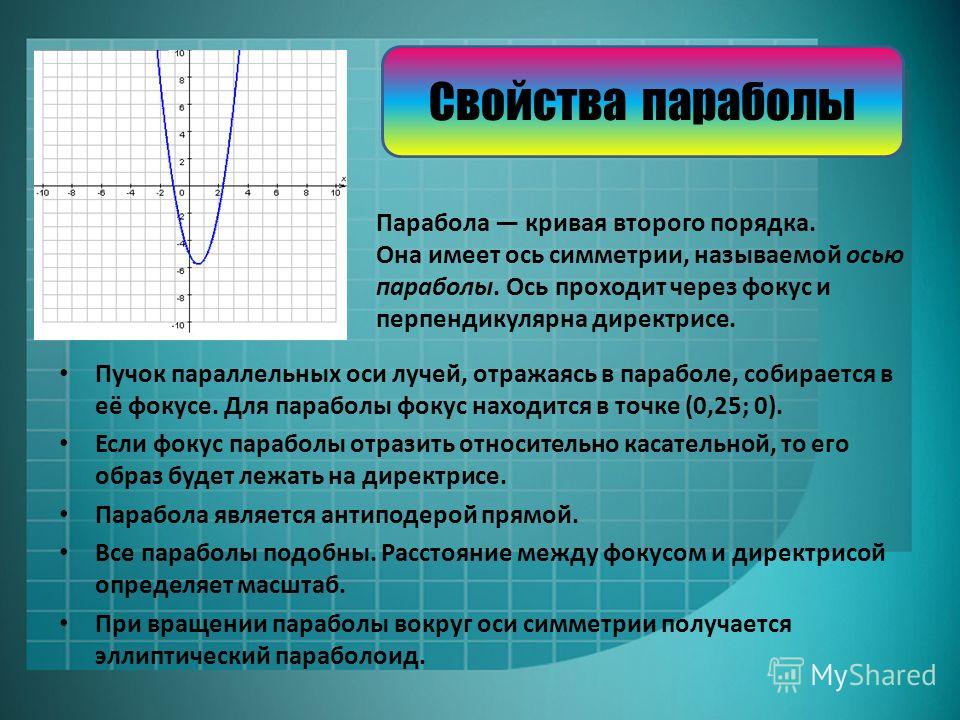 0.5. При возведении в квадрат и приведении подобных слагаемых, получается искомое уравнение параболы (y 2 = 2px).
0.5. При возведении в квадрат и приведении подобных слагаемых, получается искомое уравнение параболы (y 2 = 2px).
Парабола может задаваться квадратичной функцией. Она имеет такой вид: y = ax 2 + bx + c. Следует учитывать, что коэффициент «a» не должен быть равен 0. Если a=1, b = 0 и с = 0, функция принимает такой вид: y = ax 2 . В этом случае формула нахождения вершины параболы выглядит таким образом:
- Абсцисса вершины параболы: xa = -b / 2a.
- Координата «игрек» по оси ординат: yb = — D / 2a.
В последней формуле переменная D является дискриминантом квадратного уравнения искомой функции. Он вычисляется с помощью такого соотношения: D = b 2 — 4ac. При а>0 фокус лежит на оси, и находится над вершиной. Ось симметрии параллельна оси ординат. Кроме того, она проходит через вершину кривой. Расстояние до нее равно ¼ величины «а». Если а<0, то ось ее симметрии параллельна оси абсцисс. Расстояние до фокуса также равно ¼а. Уравнение y = a (x — xa)^2 + ya — функция, определяющая кривую II порядка, как параболу.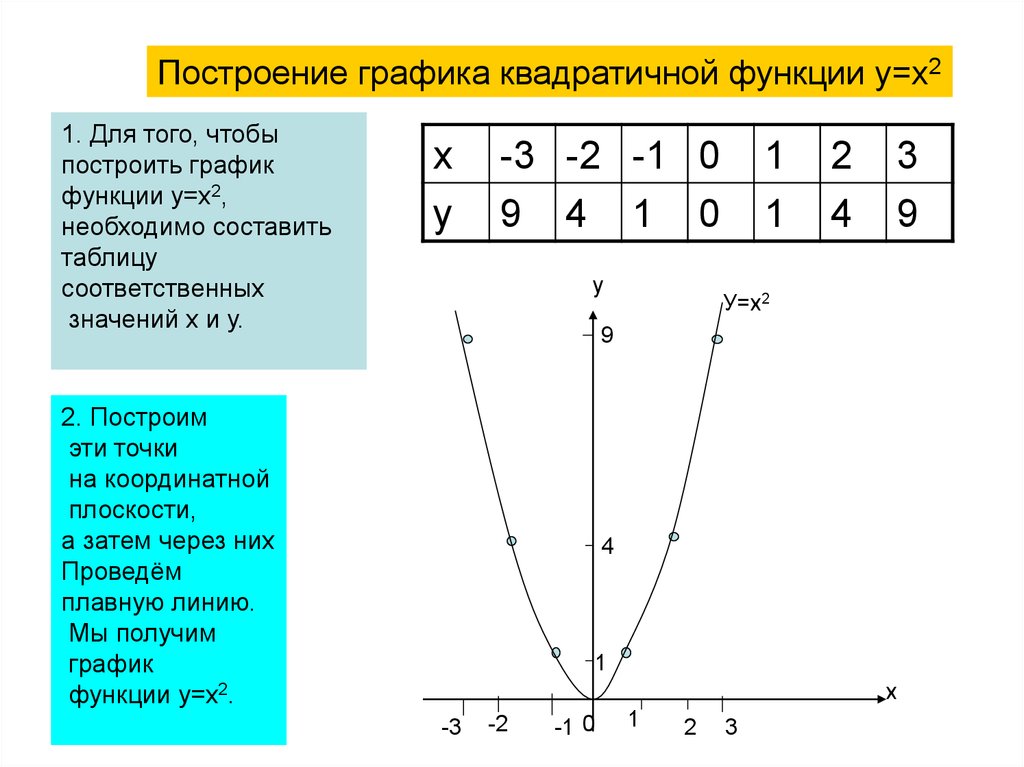
Поскольку искомую функцию можно назвать кривой второго порядка, то ее уравнение может быть записано в виде квадратного многочлена в декартовой системе координат. Вид его имеет такой вид: Ax 2 + Bxy + Cy 2 + Dx + Ey + F = 0. Дискриминант равен нулю (при старших членах).
В полярной системе координат с осями p и v уравнение квадратичной функции имеет такой вид: p (1 + cos (v)) = p. Расстояние от фокуса до директрисы обозначается фокальным коэффициентом p. Кроме того, p соответствует удвоенной длине отрезка, проведенного от фокуса до вершины.
Методы нахождения вершины
В математике есть три способа нахождения координат точки вершины кривой: по формуле, выделением полного квадрата и нахождением производной. Следует отметить, что первый способ не подойдет в том случае, когда функция отличается от вида y = ax 2 + bx + c. Первый способ — расчет по формуле вершины параболы квадратичной функции. Координата x0 вычисляется таким образом: x0 = -b / 2a. Для нахождения координаты y0 следует подставить в функцию найденное значение x0.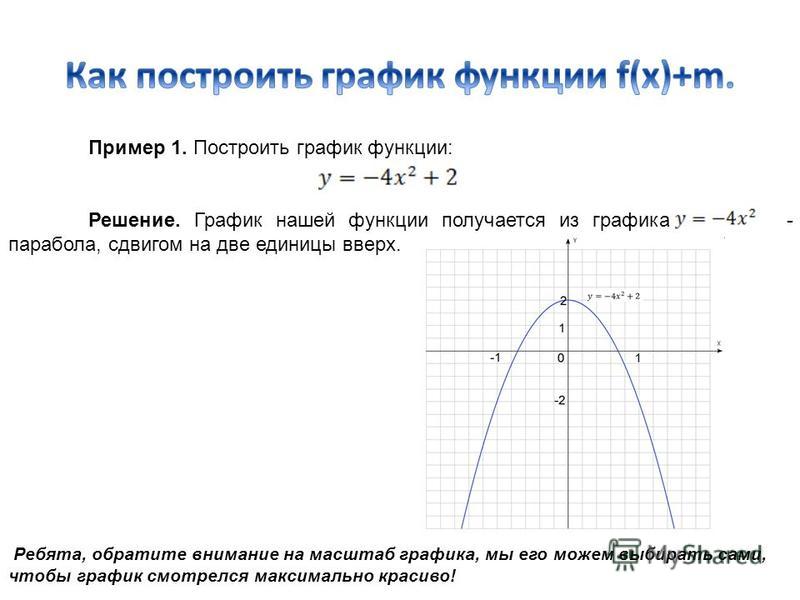 2 = 0. Следовательно, x = -2.
2 = 0. Следовательно, x = -2.
При изображении графика вершину нужно сместить в точку (-2;2). Третий способ позволяет узнать координаты вершины с помощью определения производной. Находить ее следует от заданной функции. Для вычисления координат вершины нужно действовать по следующему алгоритму:
- Найти производную и приравнять ее к нулю: f'(x) = (ax 2 + bx + c)’ = 2ax + b.
- Выразить х: х = -b / (2a).
- Подставить в функцию для вычисления y.
- Записать координаты точки.
Однако эти все три метода относятся к ручному вычислению. Автоматизация действий осуществляется с помощью специализированного программного обеспечения. Для этой цели подойдет онлайн-калькулятор, поддерживающий функцию нахождения точек вершины квадратичной кривой. Программы рекомендуется применять только для проверки решения, поскольку очень важно знать методы нахождения этой точки.
Алгоритм построения
В различных задачах нужно выполнить построение графика функции. В некоторых случаях даются координаты вершины, а в других — их следует искать, используя какой-либо метод. Чтобы построить квадратичную функцию, нужно воспользоваться таким алгоритмом:
- Если вершина не задана, то нужно найти ее любым из методов.
- Определить точки пересечения с осями декартовой системы координат.
- Построить таблицу зависимости ординаты от абсциссы. Для этой цели нужно выделить минимум 3 значения «х». Вершина должна находиться по центру таблицы.
- Выполнить построение, соединив точки.
Если необходим более точный график, то необходимо брать больше точек. Значения рассчитываются при подстановке значений «х» в функцию. Когда парабола задана функцией y = x 2 + c, нет смысла брать разные значения. Нужно использовать для построения искомой таблицы числа с противоположными знаками. Например, x1 = 2 и x2 = -2.
Специалисты-математики настоятельно рекомендуют не усложнять вычисления.
Возможно, в школьных программах и рассматриваются различные случаи. Однако в высших учебных заведениях основной аспект изучения дисциплин с физико-математическим уклоном сводится к оптимизации процесса решения задачи.
Примеры решений
В математике существует определенная классификация заданий на простые и сложные типы. Все они считаются однотипными, но отличаются только объемами вычислений и необходимостью построения графиков. Для решения нужно воспользоваться рекомендуемыми алгоритмами, которые существенно оптимизируют вычисления.
«Корень» трудностей при расчете — отсутствие систематизации вычислений. Не все ими пользуются. В результате простая задача становится очень сложной, поскольку в ней присутствует много ненужных вычислений. Кроме того, как отмечалось выше, рекомендуется «набить руку» на ручных вычислениях, ведь не всегда можно будет воспользоваться программами.
Упрощенная задача
Простым примером задания является следующий: необходимо вычислить координаты вершины точки параболы y = x 2 + 3x — 18.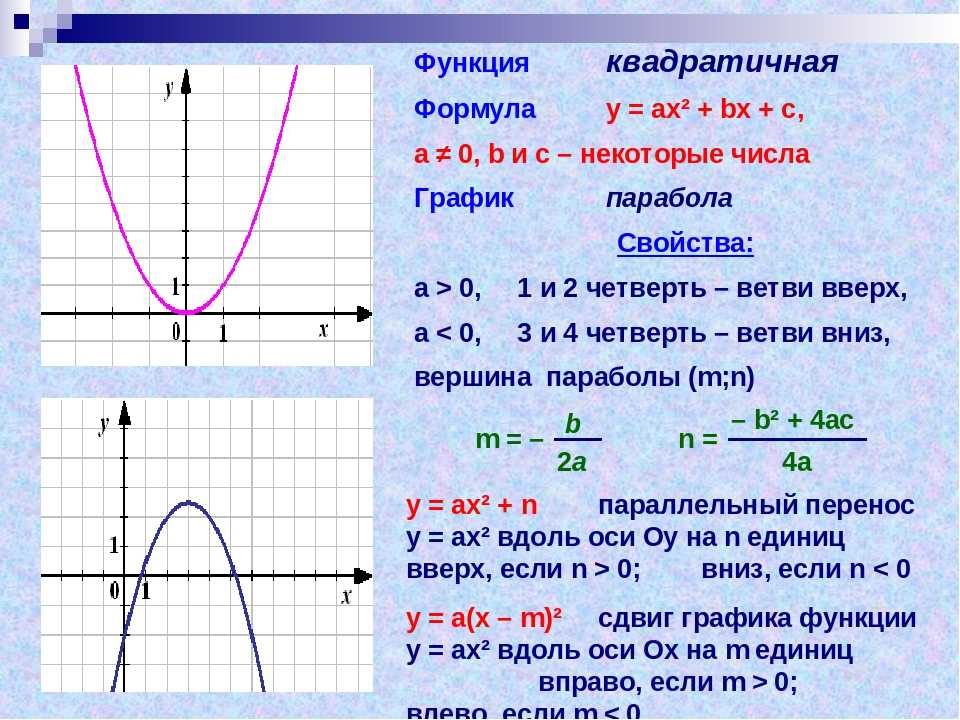 2 = 20,25.
2 = 20,25.
Для решения третьим методом следует найти производную: y’ = (x 2 + 3x — 18)’ = 2x + 3. Затем нужно приравнять ее к нулю: 2х + 3 = 0. Уравнение является простым, а его переменная легко находится: x = -3 / 2 = -1,5. После этого необходимо подставить абсциссу в функцию, приравняв ее к 0: y = 20,25.
Повышенная сложность
Задания повышенной сложности сводятся к вычислению нескольких значений. Кроме того, в некоторых случаях следует построить график параболы y = x 2 — 7x +10. Необходимо выполнить такие действия:
- Пересечение с осями.
- Вычислить экстремум (вершину) всеми методами.
- Выполнить графический эскиз (график).
Точек пересечения по ОУ нет. Они есть по оси абсцисс. Следует приравнять функцию к 0. Нахождение корней выполняется по теореме Виета: x1 = 2 и x2 = 5.
Для нахождения вершины необходимо воспользоваться тремя методами. При решении первым способом находится координата x0 = 7 / (2 * 1) = 3,5. 2 = 2,25.
2 = 2,25.
Для следующего метода нужно найти производную: y’ = (x 2 — 7x +10)’ = 2x — 7. Далее нужно приравнять y’ к нулю: 2x — 7 = 0. Значение по оси абсцисс равно х0 = 3,5, а y0 = -2,25. Далее нужно заполнить таблицу зависимостей ординаты от переменной.
| y | 4 | 0 | -2 | -2,25 | -2 | 0 | 4 |
| x | 1 | 2 | 3 | 3,5 | 4 | 5 | 6 |
Таблица 1. Зависимость y от x.
После заполнения таблицы следует построить график искомой функции (рис. 3). Таблица состоит из следующих элементов: вершины, точек пересечения с осью абсцисс и 4 произвольных значений.
Рисунок 3. График функции.
Математики рекомендуют использовать для построения графика полученные значения при расчетах, поскольку подстановка и вычисление произвольных х существенно снижает скорость вычислений.
Таким образом, нахождение координат вершины параболы является довольно простой задачей, поскольку существует несколько методов.
Из них можно выбрать оптимальный, который подходит в конкретной ситуации.
Координаты вершины параболы онлайн
Причем, в зависимости от знака коэффициента , ветви параболы направлены вверх (если ) или вниз (если ).
В школьном курсе алгебры возникает задача нахождения координат вершины параболы. Их можно найти по формулам:
Вершина параболы, отмечена оранжевой точкой на приведённом выше графике.
Наш онлайн калькулятор позволяет найти координаты вершины параболы с описанием подробного хода решения на русском языке. Для работы калькулятора, необходимо ввести уравнение параболы и указать её переменную. Уравнение параболы можно вводить в различных форматах, а коэффициентами могут быть не только числа или дроби, но и параметры. Нажмите на кнопку «Примеры», расположенную на панели калькулятора, чтобы посмотреть различные форматы ввода.
Парабола — mathcracker.com
Алгебра Учебники
Парабола является геометрическим местом точек на координатных осях, которые имеют свойство, которое они равны с фиксированной точкой (называемой фокусом) и строкой (называемой Directrix). 2\) Предавляет собой парабалу?
Конечно, это поможет.И вы можете думать «Почему вы не сказали мне от самого начала, что Parabola это функционирует?».
2\) Предавляет собой парабалу?
Конечно, это поможет.И вы можете думать «Почему вы не сказали мне от самого начала, что Parabola это функционирует?».
Потому что нет парабола, есть бесконечное число их.И парабола даже не должна быть представлена функцией.Да, некоторые отношения — параболы, как мы увидим.
Одно важно упомянуть: использование функций и отношений, есть параболы, которые «открываются» вдоль __xxyz_a __-оси, и есть параболы, которые «открываются» вдоль оси \(x\).
В конце концов, симметрией, легко осознавать, что эти параболы, которые «открываются» вдоль оси Y имеют ту же структуру, что и те, которые «открываются» вдоль оси X, поэтому достаточно учиться, какобрабатывать один тип.
Общее уравнение парабола
Существуют простые производства для получения уравнения параболы на основе расположения Directrix и фокусировки, но мы пропустим деривацию в этом введении.
Проверьте график ниже.Нам нужно определить некоторые важные элементы парабола: у нас есть вершина, фокус и Directrix.
Мы не будем гораздо подробно, но мы скажем уравнение общей параболы с вершиной в начале происхождения, с фокусом \((0, a)\) и Directrix, равным \(y = -a\)
Эта парабола — это парабола, которая открывается вдоль оси Y.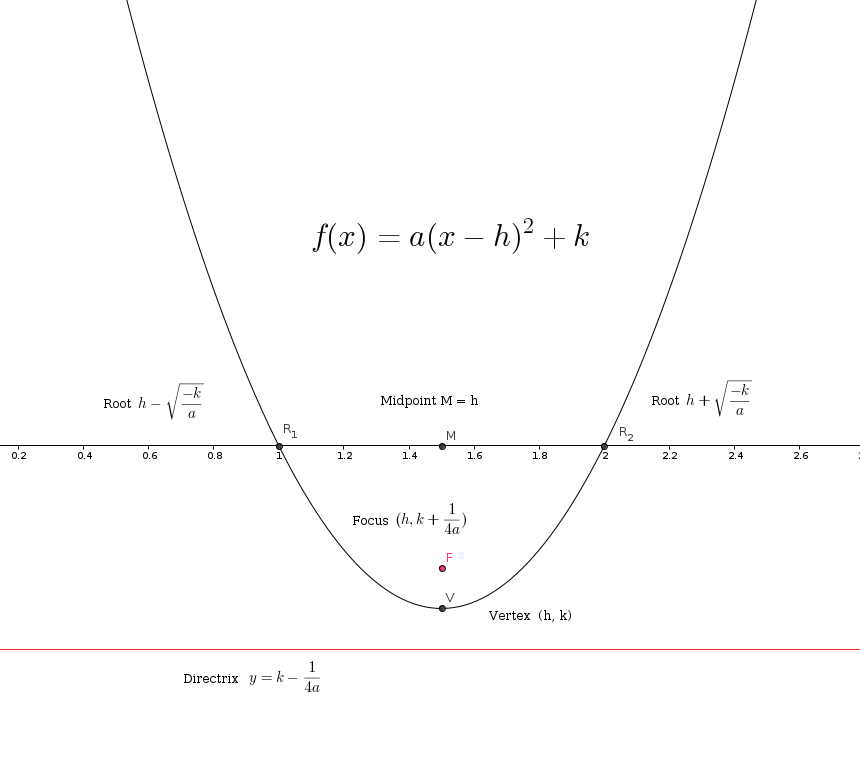
Теперь, что происходит, когда вместо того, чтобы иметь вершину в начале происхождения, мы хотим иметь вершину в данной точке \((k,h)\)?
Ну, это волшебство работы с системой координат, и все, что нам нужно сделать перевод по точке точки \((k,h)\)?Но как вы делаете перевод на \((k,h)\)?
Простой!Везде, где у вас есть \(x\), вы замените его \(x-k\), и куда у вас есть \(y\), вы замените его \(x-h\).
Следовательно, делать перевод, уравнение общей параболы с вершиной в точке \((k,h)\), с фокусом \((k, h+a)\) и Directrix, равным \(y = h-a\)
\[\large y-h = 4a(x-k)^2\]который можно записать как
\[\large \boxed{ y = 4a(x-k)^2 + h }\]Что происходит с параболами, которые открываются вдоль оси X?
Симметрией, это просто получено путем замены ролей \(x\) и \(y\) в уравнении Параболы, у нас уже есть.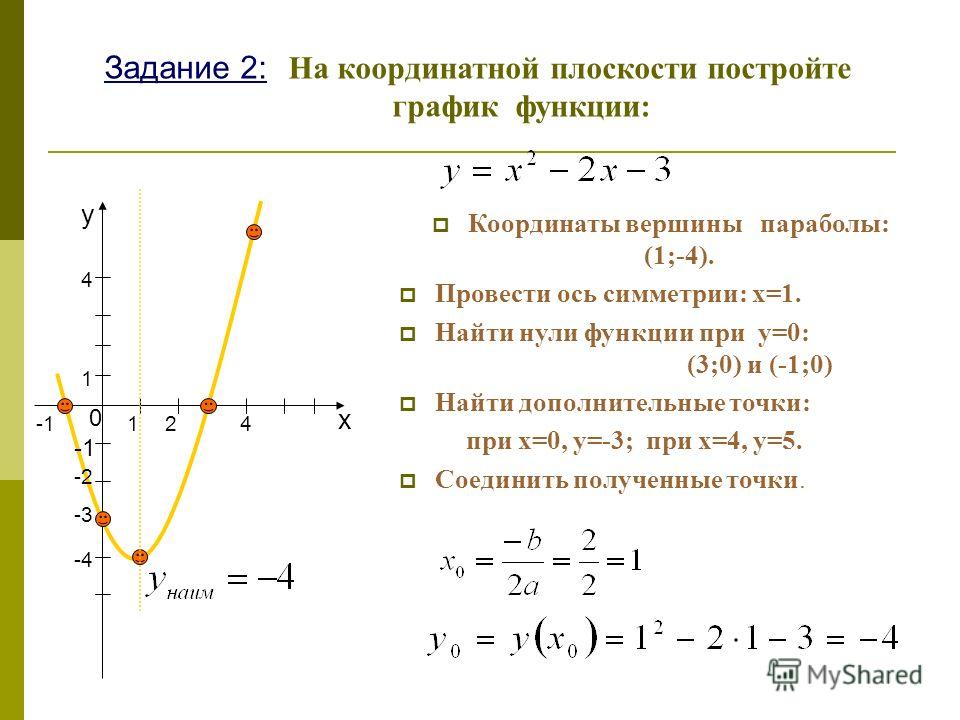 2 + h }\]
2 + h }\]
Обратите внимание на разницу:
Когда Parabola имеет Directrix из формы __xxyz_a__, то PARABOLA открывается вдоль оси Y (вверх или вниз, в зависимости от того, является ли фокусировка выше или ниже Directrix).
Когда парабола имеет Directrix из формы \(x = -a\), то парабола открывается вдоль оси X (влево или вправо в зависимости от того, находится ли фокус влево или вправо от Directrix).
Пример 1.
Найдите уравнение парабола, имеющего Directrix _ Xyz _ _ и фокус _ xyz_b _.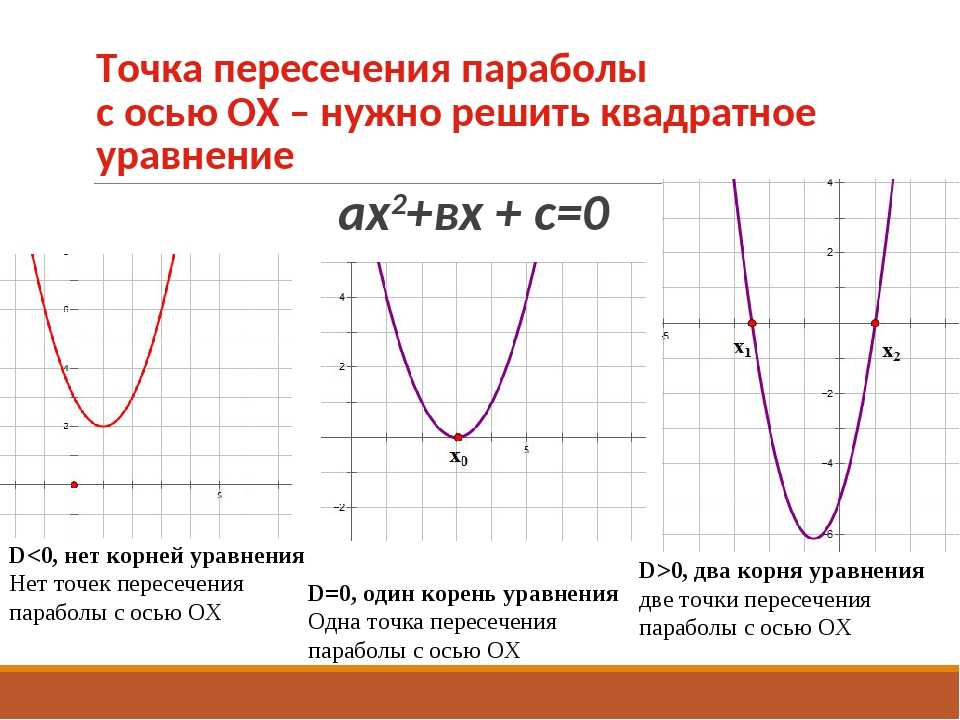 2 + 1 \]
2 + 1 \]
Приравнивая это к общему уравнению, мы обнаруживаем, что вершина находится в точке \((1, 1)\), а также у нас есть что \(4a = 8\), поэтому \(a = 2\), следовательно, Directrix __xxyz_d__ и фокус \((k, h + a) = (1, 1+2) = (1, 3)\).
Графически:
Парабола и общие конические разделы
Как можно странно, парабола плотно связана с конусом.Как бы вы сказали?Греческие математики по имени Аполлоний, доверившись с помощью современной версии, используя систему координат, конических разделов.
Аполлоний и другие математики обнаружили, что когда вы разрезаете конус с плоским, в зависимости от относительного угла конуса и плоскости, конус разрезан таким образом, что разрез имеет разные формы.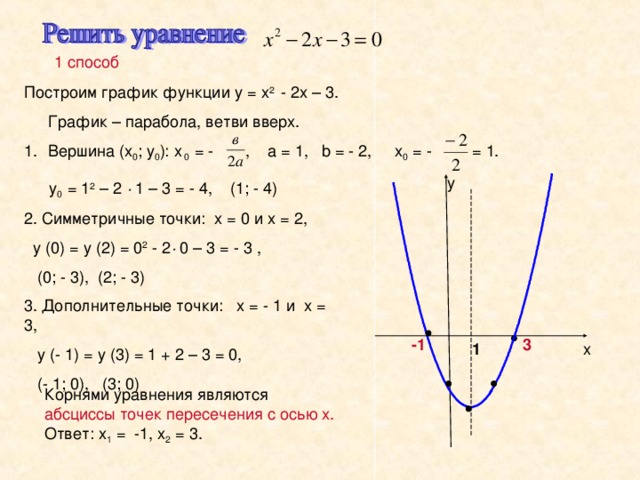 2\).
2\).
Затем общая вершина может быть получена путем нанесения перевода в данную точку \((k, h)\).
Приложения
Парабола обладает бесчисленными применениями в области физики, из-за того, как действует гравитационная сила и законы Ньютона, траектория большинства организмов, которые выброшены, будут следовать параболической траектории.
Кроме того, алгебраически говоря, параболы появляются в алгебре все время, потому что все квадратичные функции имеют параболический график, а квадратные функции появляются много в алгебре.
Также параболы появляются в исчислении при нахождении минимумов и максимумов. Оказывается, многие задачи максимизации и минимизации имеют квадратичную функцию для максимизации и геометрически, максимальный или минимум (в зависимости от того, если открывается парабола вверх или вниз), достигается на вершине.
Оказывается, многие задачи максимизации и минимизации имеют квадратичную функцию для максимизации и геометрически, максимальный или минимум (в зависимости от того, если открывается парабола вверх или вниз), достигается на вершине.
Другие конические разделы, которые вы можете быть заинтересованы в изучении Эллипс , то Гипербола. и то Круг Отказ
Учебники алгебры Учебные пособия Секции конических Уравнение Параболы Общее уравнение Параболы Парабола
Калькулятор параболы
Создано Богной Шик и Войцехом Сас, кандидатом наук
Отредактировано Стивеном Вудингом и Джеком Боуотером
Последнее обновление: 18 января 2022 г.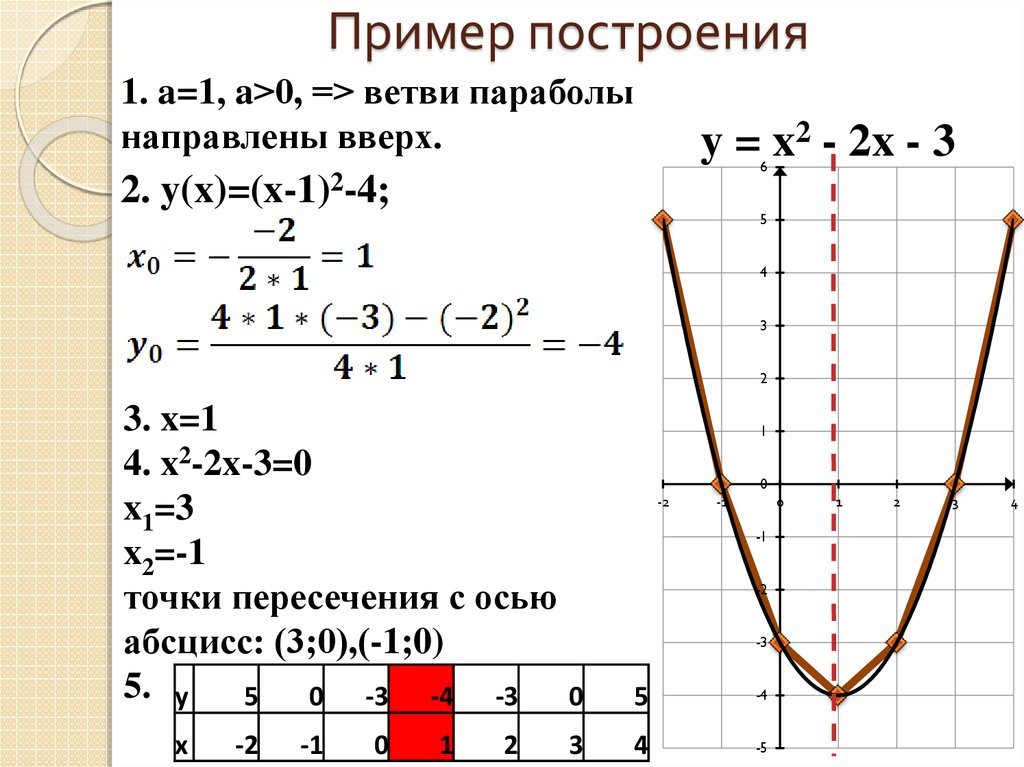
- Что такое парабола?
- Уравнение параболы в вершинной форме
- Фокус параболы и директриса
- Как использовать калькулятор уравнения параболы: пример калькулятор параболы, чтобы быть идеальным инструментом для вас. Он не только предоставит вам уравнение параболы как в стандартной форме , так и в форме вершины , но также вычислить для вас вершину параболы, фокус и директрису.
Что такое парабола?
источник: Wikimedia Парабола — это U-образная симметричная кривая . Его основное свойство состоит в том, что каждая точка, лежащая на параболе, равноудалена как от некоторой точки, называемой фокусом параболы, так и от прямой, называемой ее директрисой. Это также кривая, соответствующая квадратным уравнениям.
Ось симметрии параболы всегда перпендикулярна директрисе и проходит через точку фокусировки. Вершина параболы — это точка, в которой парабола делает самый крутой поворот; он находится на полпути между фокусом и директрисой.

Реальным примером параболы является траектория, прочерченная объектом, движущимся снарядом.
Уравнение параболы в форме вершины
Стандартная форма квадратного уравнения:
y = ax² + bx + c. Вы можете использовать этот калькулятор вершин, чтобы преобразовать это уравнение в вершинную форму, которая позволит вам найти важные точки параболы — ее вершину и фокус.Уравнение параболы в его вершинной форме имеет вид
y = a(x - h)² + k, где:- a — То же, что и коэффициент a в стандартной форме;
- h — x-координата вершины параболы; и
- k — координата y вершины параболы.
Вы можете рассчитать значения h и k из следующих уравнений:
h = - b/(2a)k = c - b²/(4a)Фокус и директриса параболы
Калькулятор формы вершины параболы также находит фокус и директрису параболы.
 Все, что вам нужно сделать, это использовать следующие уравнения:
Все, что вам нужно сделать, это использовать следующие уравнения:- Координата x фокуса:
x₀ = - b/(2a); - Координата Y фокуса:
y₀ = c - (b² - 1)/(4a); и - Уравнение директрисы:
y = c - (b² + 1)/(4a).
Как пользоваться калькулятором уравнения параболы: пример
Введите коэффициенты a, b и c стандартной формы вашего квадратного уравнения. Предположим, что уравнение
y = 2x² + 3x - 4, что означает, что a = 2, b = 3 и c = -4.Рассчитайте координаты вершины, используя приведенные выше формулы:
ч = - б/(2а) = -3/4 = -0,75k = c - b²/(4a) = -4 - 9/8 = -5,125Найдите координаты фокуса параболы. Координата x фокуса такая же, как у вершины (x₀ = -0,75), а координата y:
y₀ = c - (b² - 1)/(4a) = -4 - (9-1)/8 = -5Найдите директрису параболы.
 Вы можете использовать калькулятор параболы, чтобы сделать это за вас, или вы можете использовать уравнение:
Вы можете использовать калькулятор параболы, чтобы сделать это за вас, или вы можете использовать уравнение:y = c - (b² + 1)/(4a) = -4 - (9+1)/8 = -5,25
Если вы хотите узнать больше о понятиях координатной геометрии, мы рекомендуем проверить калькулятор средней скорости изменения и калькулятор прямой кишки.
Часто задаваемые вопросы
Что такое парабола?
Парабола представляет собой симметричную U-образную кривую, каждая точка которой равноудалена от директрисы и фокуса.
Как определить параболу?
Парабола определяется уравнением, которому удовлетворяет каждая точка кривой. Математически
y = ax² + bx + c.Как вычислить вершину параболы?
Для вычисления вершины параболы, заданной координатами (x, y):
Найдите координату x, используя формулу оси симметрии:
х₀ = - б/(2а)Найдите координату y, используя уравнение параболы:
y₀ = c - (b² - 1)/(4a)
Как рассчитать фокус параболы?
Чтобы вычислить фокус параболы, заданной координатами (x, y):
- Найдите координату y по формуле
y = c - (b² + 1)/(4a) - Найдите координату x, используя уравнение параболы.

Богна Шик и Войцех Сас, кандидат наук
Что вводить?
Ориентация по параболе
Стандартная форма: y = ax² + bx + c Результаты
Показать результаты с использованием дробей?
Ознакомьтесь с 38 похожими калькуляторами координатной геометрии 📈
Средняя скорость измененияБилинейная интерполяцияКатенарная кривая… Еще 35
Калькулятор параболы + онлайн-решатель с бесплатными шагами
Калькулятор параболы вычисляет различные свойства параболы (фокус, вершина и т. д.) и строит ее, используя уравнение параболы в качестве входных данных. Парабола визуально представляет собой U-образную зеркально-симметричную открытую плоскую кривую.
Калькулятор поддерживает двумерные параболы с осью симметрии вдоль оси x или y. Он не предназначен для обобщенных парабол и не будет работать для трехмерных параболических форм (не парабол), таких как параболические цилиндры или параболоиды.
 2}{b}$ и тому подобное, калькулятор для него не подойдет.
2}{b}$ и тому подобное, калькулятор для него не подойдет.Что такое калькулятор параболы?
Калькулятор параболы — это онлайн-инструмент, который использует уравнение параболы для описания ее свойств: фокуса, фокального параметра, вершины, директрисы, эксцентриситета и длины полуоси. Кроме того, он также рисует графики параболы.
Интерфейс калькулятора состоит из одного текстового поля с надписью «Введите уравнение параболы». Это говорит само за себя; Вы просто вводите уравнение параболы здесь. Он может быть любой формы, если он изображает параболу в двух измерениях. 92+4х+4”. Здесь также можно использовать математические константы и стандартные функции, такие как абсолютные значения, введя «абс», $\pi$ с «пи» и т. д.
Результаты
Результаты отображаются в новом всплывающем окне, содержащем три раздела:
- Ввод: Входное уравнение, как его понимает калькулятор, в формате LaTeX. Вы можете использовать его, чтобы убедиться, что калькулятор правильно интерпретировал входное уравнение или если была какая-либо ошибка.

- Геометрическая фигура: Тип геометрии, описываемой уравнением. Если это парабола, здесь также проявятся ее свойства. В противном случае отображается только имя геометрии. У вас также есть возможность скрыть свойства, если хотите.
- Графики: Два 2D графика с нарисованной параболой. Разница между графиками заключается в диапазоне по оси x: первый показывает увеличенный вид для удобного более внимательного изучения, а второй — уменьшенный вид для анализа того, как в конечном итоге раскрывается парабола.
Как работает калькулятор параболы?
Калькулятор параболы работает, определяя свойства параболы путем анализа уравнения и преобразования его в стандартную форму параболы. Оттуда он использует известные уравнения, чтобы найти значения различных свойств.
Что касается построения графика, калькулятор просто решает предоставленное уравнение в диапазоне значений x (если парабола y-симметрична) или y (если парабола x-симметрична) и отображает результаты.

Определение
Парабола — это набор точек на плоскости, изображающий незамкнутую зеркально-симметричную U-образную плоскую кривую. Параболу можно определить несколькими способами, но наиболее распространены два из них:
- Коническое сечение: Пересечение трехмерного конуса с плоскостью, при котором трехмерный конус представляет собой прямоугольную коническую поверхность, а плоскость параллельна к другой плоскости, касательной к конической поверхности. Тогда парабола представляет сечение конуса.
- Геометрическое место точки и линии: Это более алгебраическое описание. В нем говорится, что парабола — это набор точек на плоскости, каждая точка которых равноудалена от прямой, называемой директрисой, и точки, не лежащей на директрисе, называемой фокусом. Такое множество описываемых точек называется геометрическим местом.
Помните о втором описании для следующих разделов.
Свойства парабол
Чтобы лучше понять, как работает калькулятор, нам сначала нужно более подробно узнать о свойствах параболы:
- Ось симметрии (AoS): Линия, делящая параболу пополам на две симметричные половины.
 Он проходит через вершину и может быть параллелен оси x или y при определенных условиях.
Он проходит через вершину и может быть параллелен оси x или y при определенных условиях. - Вершина: Самая высокая (если парабола направлена вниз) или самая низкая (если парабола направлена вверх) точка параболы. Более конкретное определение — это точка, в которой производная параболы равна нулю.
- Директриса: Линия, перпендикулярная оси симметрии, такая, что любая точка параболы равноудалена от нее и точки фокуса.
- Фокус: Точка на оси симметрии, такая, что любая точка на параболе равноудалена от нее и директрисы. Точка фокусировки не лежит на параболе или директрисе.
- Длина полуоси: Расстояние от вершины до фокуса. Также называется фокусным расстоянием. Для парабол это равно расстоянию от вершины до директрисы. Следовательно, длина полуоси составляет половину значения фокального параметра. Обозначается как $f = \frac{p}{2}$.
- Фокус Параметр: Расстояние от фокуса и соответствующей директрисы.
 Иногда также называется полуширокой прямой кишкой. Для парабол это удвоенное значение полуоси/фокусного расстояния. Обозначается как p = 2f.
Иногда также называется полуширокой прямой кишкой. Для парабол это удвоенное значение полуоси/фокусного расстояния. Обозначается как p = 2f. - Эксцентриситет: Отношение расстояния между вершиной и фокусом к расстоянию между вершиной и директрисой. Он определяет тип коники (гипербола, эллипс, парабола и т. д.). Для параболы эксцентриситет e = 1, 92 + k \]
ось симметрии (AoS) для параболы, описанной в стандартной форме, параллельна оси неквадратного члена в уравнении. В приведенном выше случае это ось Y. Мы найдем точное уравнение линии, когда у нас будет вершина.
Направление, в котором раскрывается парабола, — к положительному концу AoS, если a > 0 . Если a < 0 , парабола открывается к отрицательному концу AoS.
Значения 92 \]
Вы можете видеть, что h и k представляют смещения по осям x и y. Когда оба равны нулю, вершина находится в (0, 0).
 В противном случае это (h, k) . Поскольку AoS проходит через вершину, и мы знаем, что она параллельна либо оси x, либо оси y, мы можем сказать, что AoS: y=k для x-симметричных парабол и AoS: x=h для y-симметричных парабол.
В противном случае это (h, k) . Поскольку AoS проходит через вершину, и мы знаем, что она параллельна либо оси x, либо оси y, мы можем сказать, что AoS: y=k для x-симметричных парабол и AoS: x=h для y-симметричных парабол.Длина полуоси определяется выражением $f = \frac{1}{4a}$. Тогда фокальный параметр равен p = 2f. 9Значения фокуса 0194 F и директрисы D зависят от оси симметрии и направления раскрытия параболы. Для параболы с вершиной (h. k):
\[ F = \left\{ \begin{array}{rl} \text{x-симметричный:} & \left\{ \begin{array}{rcl} (h-f,\, k) & \text{for} & a < 0 \\ (h + f,\, k) & \text{for} & a > 0 \end{array} \right. \\ \text{y-симметричный:} & \left\{ \begin{array}{rcl} (h,\, k-f) & \text{for} & a < 0 \\ (h,\, k+f ) & \text{for} & a > 0 \end{массив} \right. \end{массив} \right. \]
\[ D = \left\{ \begin{array}{rl} \text{x-симметричный:} & \left\{ \begin{array}{rcl} y=h+f & \text{for} & a < 0 \\ y = h-f & \text{for} & a > 0 \end{array} \right.
 2 + 15x + 220 \] 92 + k \]
2 + 15x + 220 \] 92 + k \]\[ \Rightarrow a > 0 = \frac{1}{4}, h= -30, k = -5 \]
\[ \text{vertex} = (h, k) = (-30, -5) \]
Ось симметрии параллельна оси y. Так как а > 0, парабола направлена вверх. Полуось/фокусное расстояние:
\[ f = \frac{1}{4a} = 1 \]
\[ \text{Focus :} \,\, (-30,\, -5+ f) = \mathbf{(-30,\, 4)} \]
Директриса перпендикулярна AoS и, следовательно, представляет собой горизонтальную линию:
\[ \text{Направляющая :} \,\, y = -5 -f = \mathbf{-6} \]
Длина полуширочайшей прямой кишки равна фокальному параметру:
\[ \text{Focal Param :} \,\, p = 2f = \mathbf{2} \]
Вы можете визуально проверить результаты в Рис. 1 ниже.
Рисунок 1
Все графики/изображения были созданы с помощью GeoGebra.
Список математических калькуляторов
Калькулятор параболы — Решите уравнение параболы
Онлайн-калькулятор параболы находит стандартные и вершинные параболические уравнения и вычисляет фокус, направление, вершину и важные точки параболы.
Что такое парабола? Кроме того, графограф параболы отображает график для данного уравнения.
Кроме того, графограф параболы отображает график для данного уравнения.Он определяется как особая кривая, имеющая форму арки. Это один из видов конических сечений. Эта симметричная плоская кривая образована пересечением прямого кругового конуса с плоской поверхностью. Эта U-образная кривая обладает некоторыми особыми свойствами. Короче говоря, можно сделать вывод, что любая точка на этой кривой находится на равном расстоянии от:
- Фиксированная точка называется фокусом.
- Неподвижная прямая линия известна как директриса параболы. 92+1} {(4а)}\)
- Ось симметрии \( \frac {-b}{(2a)} \) и решить точку пересечения y, сохранив \( x = 0 \) в уравнении.
- Выполните эти математические операции, чтобы получить требуемые значения.
Однако онлайн-калькулятор дискриминанта помогает вычислить дискриминант квадратного многочлена, а также многочленов более высоких степеней.
Пример:Найти ось симметрии, точку пересечения y, точку пересечения x, директрису, фокус и вершину уравнения параболы \( x = 11y^2 + 10y + 16 \)? 92 + 4x + 10$$
$$Нет точки пересечения по оси x.
 $$
$$ Однако онлайн-калькулятор гиперболы поможет вам определить центр, эксцентриситет, фокусный параметр, главную и асимптоту для заданных значений в уравнение гиперболы.
Как найти директрису параболы?Возьмем стандартную форму уравнения параболы: \( (x – h)2 = 4p (y – k) \)
- В этом уравнении основное внимание уделяется: \( (h, k + p)\)
- Принимая во внимание, что направляющая \( y = k – p \).
Если мы повернем параболу, то ее вершина будет: \( (h,k) \). Однако ось симметрии параллельна оси x, и ее уравнение будет таким: \( (y – k)2 = 4p (x – h)\) ,
- Теперь фокус: \( (h + р, к)\)
- Направляющая параболы равна \( x = h – p \).
Кроме того, директриса параболы также может быть рассчитана с помощью простого уравнения: \(y = c – \frac{(b² + 1)}{(4a)}\) .
Как работает калькулятор параболы?Калькулятор уравнения параболы делает расчет быстрее и без ошибок, поскольку он использует математическое уравнение параболы.
Ввод: Для удобства вам необходимо выполнить следующие шаги:
Для удобства вам необходимо выполнить следующие шаги:- Сначала выберите уравнение параболы из раскрывающегося списка. Вы можете выбрать стандартную форму, форму вершины, три точки или вершину и точки для ввода.
- Теперь будет отображаться выбранное уравнение для параболы. Поэтому просто введите значения в данные поля соответственно.
- Нажмите кнопку расчета.
Калькулятор уравнения параболы вычисляет:
- Уравнение параболы в стандартной форме.
- Уравнение параболы в вершинной форме.
- Все параметры, такие как вершина, фокус, эксцентриситет, директриса, широкая прямая кишка, ось симметрии, пересечение по оси x, пересечение по оси y.
- Приведите пошаговые расчеты, когда парабола проходит через разные точки.
- Наряду со всеми этими математическими значениями, этот графограф параболы отображает график параболы в конце.

Всякий раз, когда расстояние между фокусом и директрисой параболы увеличивается, |a| уменьшится. Это означает, что парабола расширяется с увеличением расстояния между двумя ее параметрами.
Как построить параболу?Для быстрых и простых расчетов вы можете использовать онлайн-график парабол, который строит графическое представление данного уравнения параболы. Однако для ручного построения графика параболы необходимо выполнить несколько шагов:
- Прежде всего, найдите следующие параметры:
- y-перехват.
- x-перехватов.
- Ищите дополнительные точки, чтобы иметь не менее пяти точек для построения графика.
- Теперь просто нанесите точки и нарисуйте график параболы.
Первый тип преобразования известен как преобразование.
 Он перемещает узел из одного положения в другое вместе с одной из осей, связанных с его начальным положением.
Он перемещает узел из одного положения в другое вместе с одной из осей, связанных с его начальным положением.Второй тип — вращение. Он перемещает узел по кругу вокруг точки вращения.
Как вы описываете преобразование параболы?Вертикальное перемещение параболы дает возможность построить новую параболу. Это будет то же самое, что и основная парабола. Таким же образом можно перевести параболу по горизонтали.
Вывод:Калькулятор параболы используется для получения быстрых результатов и построения графика для любого заданного параболического уравнения. Этот поиск уравнения параболы делает ваш расчет быстрее и проще, решая все связанные свойства параболического уравнения. Это также позволяет вам понять, как поместить значения в формулу параболы. Итак, этот инструмент всегда готов предоставить свои услуги всем в мгновение ока и без каких-либо затрат.
Каталожные номера:Из источника Википедии: Декартова система координат, Сходство с единичной параболой, Положение фокуса.

Из источника онлайн-заметок Пола: Параболы, Зарисовка парабол, Направление оси.
Из источника ООР Услуги: Графики парабол с вершинами в начале координат, Стандартные формы парабол с вершинами, Ось x как ось симметрии.
Другие языки: Parabol Hesaplama, Kalkulator Parabola, Kalkulator Paraboli, Parabel Rechner, 放物線 計算.
Математика 1010 онлайн — Параболы
Математика 1010 онлайн — ПараболыКафедра математики — Колледж науки — Университет Юты
График .
Рисунок 1. Параболаграфик уравнения с участием и представляет собой множество всех точки в декартова координатная плоскость координаты которого удовлетворяют уравнению. график функции – это график уравнения Например, на рис.
Этот конкретный график является примером параболы . Обратите внимание, что это симметричен относительно -оси, которая называется его осью или линией симметрии . Самая нижняя точка параболы (которая в данном случае является началом координат) называется его вершиной . 1 показан график уравнения
1 показан график уравненияМы будем использовать этот график и уравнение, чтобы проиллюстрировать некоторые идеи, которые имеют гораздо более широкое применение. Давайте подумаем о том, чтобы сделать некоторые изменения:
Изменение масштаба
Предположим, мы умножаем значение на константу. Давайте назовем это . Таким образом, мы получаем новое уравнение
Если это то же уравнение, что и раньше. Рассмотрим некоторые другие однако возможности:- В этом случае мы увеличиваем значение и поэтому стрейч график по вертикали.
- В этом случае мы уменьшаем значение и так компресс график по вертикали.
- Заменяем на .
 Геометрически результат
отражение графика через -ось.
Геометрически результат
отражение графика через -ось. - В этом случае отражение сочетается с вертикальное сжатие.
- В этом случае отражение сочетается с вертикальное растяжение.
Рисунок 2. Несколько параболНа рис. 2 представлены графики этих уравнений для
Графики могут быть аналогичным образом отображены, растянуты или сжаты в горизонтальное направление путем умножения на константу. Однако, в настоящем простом примере этот эффект эквивалентен масштабирование по вертикали с куда .
Переводы
Рассмотрим теперь эффект вычитания константы из :
Это эквивалентно
так и есть эффект поднятие графика на единицы. Конечно, если есть отрицательный, график опущен на (по единицам).Вычитание константы из дает тот же эффект в горизонтальное направление. Рассмотрим уравнение
а также сравните его с исходным уравнением. Как в , никогда не бывает отрицательным. Он принимает свое минимальное значение () при .
Таким образом, график представляет собой график сдвинутых единиц на
право. Если отрицательный, график сдвигается на единицу
слева.
Он принимает свое минимальное значение () при .
Таким образом, график представляет собой график сдвинутых единиц на
право. Если отрицательный, график сдвигается на единицу
слева.
Рис. 3. Смещенные параболыГоризонтальные и вертикальные сдвиги можно комбинировать, и любой такой комбинация называется переводом . Общая форма перевод, примененный к, дается
который часто пишут как перевод не меняет форма или ориентация графика. Он только меняет свой расположение. На рис. 3 показаны переводы графика сЗаполненная квадратная форма
Полная квадратная форма квадратичной функции равна
Его график представляет собой параболу с вершиной . Если открывается вверх, если открывается вниз. (Если график представляет собой горизонтальную линию, которую вы можете считать вырожденной парабола.) Вертикальная линия ось или линия симметрия параболы.
Ясно, как общий квадратичный многочлен
можно преобразовать в стандартную форму. Просто заполните квадрат, как проиллюстрировано в следующем примере:График этого конкретного уравнения приведен на рисунке 4. Полученная парабола имеет и вершину (. Это получается из стандартной параболы путем ее тщательного отражения -ось, растянув ее по вертикали и переведя на 1 единицу в влево и 8 единиц вверх. Обратите внимание, что все эти свойства могут быть немедленно прочитать уравнение
Рис. 4. Еще одна параболаМасштабирование и преобразование графиков
Проиллюстрированные здесь принципы применимы к любому уравнению, поэтому давайте переформулируйте их:
- Комбинация горизонтальных и вертикальных сдвигов перевод графика, сочетание горизонтального и вертикальное сжатие и растяжение — это масштабирование график.
- Добавление константы для смещения единиц измерения графика
вправо, если положительно, и влево, если
отрицательный.

- Добавление константы для смещения единиц графика вверх если положительный, и вниз, если отрицательный.
- Умножение на положительную константу сжимает график по горизонтали, если и растягивает его по горизонтали, если . Если отрицательный, эти эффекты сочетаются с отражением через ось.
- Умножение на положительную константу сжимает график по вертикали, если и растягивает его по вертикали, если . Если отрицательный, эти эффекты сочетаются с отражением через ось.
Как обычно, я рекомендую вам не запоминать эти факты. Скорее подумайте о том, что происходит с точки зрения взаимодействия между график и уравнение, и выяснить влияние того, что вы делать или что вам нужно сделать, а не полагаться на запоминание тайные факты.
Алгебра — Параболы
Показать мобильное уведомление Показать все примечания Скрыть все примечания
Мобильное уведомление
Похоже, вы находитесь на устройстве с «узкой» шириной экрана ( т.
 е. вы, вероятно, на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
е. вы, вероятно, на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.Раздел 4-2: Параболы
В этом разделе мы хотим посмотреть на график квадратичной функции. Наиболее общая форма квадратичной функции: 92} + Ьх + с\]
Графики квадратичных функций называются параболами . Вот несколько примеров парабол.
Все параболы имеют неопределенную форму буквы «U», и у них будет самая высокая или самая низкая точка, которая называется вершиной . Параболы могут открываться вверх или вниз, могут иметь или не иметь \(x\)-пересечения, и они всегда будут иметь одиночное \(y\)-пересечение.
Также обратите внимание, что парабола, которая открывается вниз, всегда будет открываться вниз, а парабола, которая открывается вверх, всегда будет открываться вниз.
 Другими словами, парабола не развернется вдруг и не начнет раскрываться, если она уже начала раскрываться вниз. Точно так же, если он уже начал открываться, он не развернется и не начнет открываться внезапно.
Другими словами, парабола не развернется вдруг и не начнет раскрываться, если она уже начала раскрываться вниз. Точно так же, если он уже начал открываться, он не развернется и не начнет открываться внезапно.Пунктирная линия с каждой из этих парабол называется осью симметрии . Каждая парабола имеет ось симметрии, и, как показывает график, график по обе стороны от оси симметрии является зеркальным отражением другой стороны. Это означает, что если мы знаем точку на одной стороне параболы, мы также будем знать точку на другой стороне на основе оси симметрии. Мы увидим, как найти эту точку, как только мы перейдем к некоторым примерам.
Нам, вероятно, следует быстро просмотреть перехваченные сообщения, прежде чем идти дальше. Точки пересечения — это точки пересечения графика с осью \(x\) или \(y\). Мы также видели график в разделе, где мы ввели точки пересечения, где точки пересечения просто касались оси, фактически не пересекая ее.
Поиск перехватов — довольно простой процесс.
 Чтобы найти \(y\)-перехват функции \(y = f\left( x \right)\), все, что нам нужно сделать, это установить \(x = 0\) и вычислить, чтобы найти \(y\ ) координата. Другими словами, \(y\)-перехват — это точка \(\left( {0,f\left( 0 \right)} \right)\). Мы находим \(x\)-перехваты примерно таким же образом. Положим \(y = 0\) и решим полученное уравнение относительно координат \(x\). Итак, нам нужно будет решить уравнение,
Чтобы найти \(y\)-перехват функции \(y = f\left( x \right)\), все, что нам нужно сделать, это установить \(x = 0\) и вычислить, чтобы найти \(y\ ) координата. Другими словами, \(y\)-перехват — это точка \(\left( {0,f\left( 0 \right)} \right)\). Мы находим \(x\)-перехваты примерно таким же образом. Положим \(y = 0\) и решим полученное уравнение относительно координат \(x\). Итак, нам нужно будет решить уравнение,\[е\влево( х \вправо) = 0\]
Теперь вернемся к параболам. Существует базовый процесс, который мы всегда можем использовать, чтобы получить довольно хороший набросок параболы. Вот.
Рисование парабол
- Найдите вершину. Мы обсудим, как найти это в ближайшее время. Это довольно просто, но есть несколько способов его найти, поэтому мы обсудим их отдельно.
- Найдите точку пересечения \(y\), \(\left( {0,f\left( 0 \right)} \right)\).
- Решите \(f\left( x \right) = 0\), чтобы найти \(x\) координаты \(x\)-перехватов, если они существуют.
 Как мы увидим в наших примерах, у нас может быть 0, 1 или 2 \(x\)-перехвата.
Как мы увидим в наших примерах, у нас может быть 0, 1 или 2 \(x\)-перехвата. - Убедитесь, что у вас есть хотя бы одна точка по обе стороны от вершины. Это делается для того, чтобы убедиться, что мы получаем достаточно точный набросок. Если парабола имеет две \(x\)-пересечения, то эти точки уже есть. Если у него есть 0 или 1 точка пересечения \(x\), мы можем либо просто подставить другое значение \(x\), либо использовать точку пересечения \(y\) и ось симметрии, чтобы получить вторую точку.
- Нарисуйте график. На данный момент мы получили достаточно точек, чтобы получить довольно приличное представление о том, как будет выглядеть парабола.
Теперь мы рассмотрим две формы параболы. Эта первая форма сделает графическое построение парабол очень простым. К сожалению, большинство парабол не имеют такой формы. Вторая форма является более распространенной и потребует немного (и только немного) больше работы, чтобы нарисовать график параболы.
 2} + к \]
2} + к \]Есть две части информации о параболе, которые мы можем мгновенно получить из этой функции. Во-первых, если \(а\) положительна, то парабола откроется вверх, а если \(а\) отрицательна, то парабола развернется вниз. Во-вторых, вершиной параболы является точка \(\left( {h,k} \right)\). Будьте очень осторожны со знаками при получении вершины здесь.
Итак, когда нам посчастливилось получить эту форму параболы, мы получили вершину бесплатно.
Давайте посмотрим здесь на пару примеров. 92} — 8\) Показать решение
Сначала нам нужно найти вершину. Однако нам нужно быть осторожными со знаками. Сравнивая наше уравнение с формой выше, мы видим, что мы должны иметь \(h = — 3\) и \(k = — 8\), так как это единственный способ получить правильные знаки в нашей функции. Следовательно, вершина этой параболы равна
. \[\влево( { — 3, — 8} \вправо)\]
Теперь найдем \(y\)-перехват.
 Это не что иное, как быстрая оценка функции. 92} — 8 = 2 \ влево ( 9 \ вправо) — 8 = 10 \ hspace {0,25 дюйма} y — {\ mbox {перехват: }} \ влево ( {{\ mbox {0,10}}} \ вправо) \]
Это не что иное, как быстрая оценка функции. 92} — 8 = 2 \ влево ( 9 \ вправо) — 8 = 10 \ hspace {0,25 дюйма} y — {\ mbox {перехват: }} \ влево ( {{\ mbox {0,10}}} \ вправо) \]Далее нам нужно найти \(x\)-перехваты. Это означает, что нам нужно решить уравнение. Однако прежде чем мы это сделаем, мы можем сказать, будут ли они у нас, еще до того, как мы начнем решать уравнение.
В этом случае у нас есть \(а = 2\), что положительно, и поэтому мы знаем, что парабола раскрывается. Также вершина — это точка ниже оси \(x\). Итак, мы знаем, что парабола будет иметь хотя бы несколько точек ниже оси \(х\) и она развернется. Следовательно, поскольку парабола, начавшая раскрываться, будет продолжать раскрываться, в конце концов нам придется пересечь ось \(x\). Другими словами, у этой параболы есть \(x\)-перехваты. 92} & = 4\\ x + 3 & = \pm \sqrt 4 = \pm 2\\ x & = — 3 \pm 2\hspace{0.25in} \Rightarrow \hspace{0.25in}x = — 1, \,\,х = — 5\конец{выравнивание*}\]
Две точки пересечения x равны
\[\left( { — 5,0} \right)\hspace{0.
 25in}{\mbox{and}}\hspace{0.25in}\left( {- 1,0} \right)\]
25in}{\mbox{and}}\hspace{0.25in}\left( {- 1,0} \right)\]Теперь у нас есть точки по обе стороны от вершины, так что мы официально закончили с поиском точек. Однако давайте немного поговорим о том, как найти вторую точку, используя точку пересечения \(y\) и ось симметрии, так как в конечном итоге нам это понадобится.
Во-первых, обратите внимание, что \(y\)-перехват имеет координату \(x\) 0, а вершина имеет координату \(x\) -3. Это означает, что \(y\)-отрезок находится на расстоянии 3 справа от оси симметрии, поскольку он будет двигаться прямо вверх от вершины.
Теперь левая часть графика будет зеркальным отражением правой части графика. Таким образом, поскольку существует точка \(y = 10\), которая находится на расстоянии 3 правее от оси симметрии, должна быть также точка \(y = 10\), которая находится на расстоянии 3 от оси симметрии. слева от оси симметрии. 92} — 1\) Показать решение
Ладно, не будем вдаваться в подробности.
 2} — 1 = — 4 — 1 = — 5\]
2} — 1 = — 4 — 1 = — 5\]Тогда \(y\)-отрезок равен \(\left( {0, — 5} \right)\).
Теперь мы знаем, что вершина начинается ниже оси \(x\) и парабола раскрывается вниз. Это означает, что не может быть \(x\)-пересечений, так как ось \(x\) находится выше вершины, и парабола всегда будет открываться вниз. Это означает, что в общем случае нет причин проходить через процесс решения, чтобы найти то, чего не будет.
Тем не менее, давайте сделаем это. Это покажет нам, что искать, если мы сразу не поймаем, что их не будет из вершины и направления, в котором раскрывается парабола. Нам нужно решить, 92} & = — 1\\ x — 2 & = \pm \,i\\ x & = 2 \pm \,i\end{align*}\]
Итак, мы получили комплексные решения. Комплексные решения всегда будут указывать на отсутствие \(x\)-перехватов.
Теперь нам нужны точки по обе стороны от вершины, поэтому воспользуемся точкой пересечения \(y\) и осью симметрии, чтобы получить вторую точку. Точка пересечения \(y\) находится на расстоянии двух левее оси симметрии и находится в точке \(y = — 5\), поэтому должна быть вторая точка только с тем же значением \(y\) на расстоянии 2 вправо от оси симметрии.
 Тогда координаты этой точки должны быть \(\left( {4, — 5} \right)\). 92} + 4\) Показать решение
Тогда координаты этой точки должны быть \(\left( {4, — 5} \right)\). 92} + 4\) Показать решениеЭто на самом деле довольно просто для построения графика. Сначала мы заметим, что он откроется вверх.
Вершина, вероятно, та точка, где у большинства учеников возникают проблемы. Поскольку у нас есть x 2 само по себе, это означает, что мы должны иметь \(h = 0\), и поэтому вершина равна \(\left({0,4} \right)\).
Обратите внимание, что это означает, что не будет никаких \(x\)-пересечений с этой параболой, так как вершина находится над осью \(x\) и парабола открывается вверх. 92} + 4 = 4\hspace{0,25 дюйма}y — {\mbox{перехват:}}\left({0,4} \right)\]
Пересечение \(y\) точно такое же, как вершина. Это будет происходить время от времени, поэтому мы не должны слишком беспокоиться об этом, когда это произойдет. Хотя это будет означать, что на этот раз мы не сможем использовать \(y\)-перехват, чтобы найти вторую точку по другую сторону вершины.
 На самом деле, у нас еще даже нет точки, которая не была бы вершиной!
На самом деле, у нас еще даже нет точки, которая не была бы вершиной!Итак, нам нужно найти точки по обе стороны от вершины. В данном случае, поскольку функция не так уж и плоха, мы просто добавим пару точек. 92} + 4 = 8\hspace{0,25 дюйма} \стрелка вправо \hspace{0,25 дюйма}\left( {2,8} \right)\end{align*}\]
Обратите внимание, что мы могли бы получить здесь вторую точку, используя ось симметрии, если бы захотели.
Вот набросок графика.
Итак, мы рассмотрели несколько примеров этой формы параболы. Однако, как отмечалось ранее, большинство парабол не даются в такой форме. Итак, нам нужно взглянуть на то, как построить график параболы в общем виде.
92} + Ьх + с\]В этой форме знак \(a\) будет определять, будет ли парабола открываться вверх или вниз, как это было в предыдущем наборе примеров. В отличие от предыдущей формы, на этот раз мы не получим вершину бесплатно. Тем не менее, это будет легко найти. Вот вершина параболы в общем виде.
 2} + 4x + 4\) Показать решение
92} + 4\влево( { — 2} \вправо) + 4 = 0\конец{выравнивание*}\]
2} + 4x + 4\) Показать решение
92} + 4\влево( { — 2} \вправо) + 4 = 0\конец{выравнивание*}\]Итак, вершина равна \(\left( { — 2,0} \right)\). Обратите внимание, что поскольку координата \(y\) этой точки равна нулю, она также является точкой пересечения \(x\). Фактически это будет единственный \(x\)-перехват для этого графа. Это имеет смысл, если принять во внимание тот факт, что вершина в данном случае является самой нижней точкой графа, и поэтому граф просто не может касаться оси \(x\) где-либо еще.
Тот факт, что эта парабола имеет только одну \(x\)-пересечение, можно проверить, решая, как мы это делали в других примерах до этого момента. 92}\hspace{0,25 дюйма} \Rightarrow \hspace{0,25 дюйма}x = — 2\end{align*}\]
Конечно, есть только один \(x\)-перехват. Обратите внимание, что это будет означать, что в этом случае нам придется использовать ось симметрии, чтобы получить вторую точку от точки пересечения \(y\).
Говоря об этом, \(y\)-перехват в данном случае равен \(\left( {0,4} \right)\).
 Это означает, что вторая точка равна \(\left( { — 4,4} \right)\).
Это означает, что вторая точка равна \(\left( { — 4,4} \right)\).Вот набросок графика. 92} — 6x + \frac{3}{2}} \right)\]
Обратите внимание, что это часто приводит к тому, что дроби становятся проблемой, с которой нам нужно иметь дело. Также обратите внимание, что если нам посчастливилось получить коэффициент 1 для члена x 2 , нам не нужно будет делать этот шаг.
Теперь процесс действительно начинает отличаться от того, что мы видели до сих пор. Мы по-прежнему берем половину коэффициента \(х\) и возводим его в квадрат. Однако вместо того, чтобы добавлять это к обеим сторонам, мы делаем с ним следующее. 92} — 6x + 9 — 9 + \frac{3}{2}} \right)\]
Мы складываем и вычитаем это количество внутри скобок, как показано. Обратите внимание, что все, что мы на самом деле здесь делаем, это добавляем ноль, поскольку 9-9=0! Порядок, указанный здесь, важен. Мы ДОЛЖНЫ сначала сложить, а затем вычесть.
 2} — \ frac {{15}}{2}} \right)\]
92} + 24\конец{выравнивание*}\]
2} — \ frac {{15}}{2}} \right)\]
92} + 24\конец{выравнивание*}\]Калькулятор построения графика параболы онлайн
Что говорят наши клиенты…
Тысячи пользователей используют наше программное обеспечение, чтобы справиться со своими домашними заданиями по алгебре. Вот некоторые из их опытов:
Это более интуитивно понятно. И даже «взял» мои негативные научные аннотации и показал мне, как упростить! Спасибо!!!
Джеймс Мур, Мичиган
Какой замечательный дружелюбный интерфейс, полный цветов, ведь с программным обеспечением Algebrator легко работать, а также с ним так легко работать, вам не нужно каждый раз прерывать поток мыслей вам нужно взаимодействовать с программой.
B.C., Malta-EU
Я только что купил это программное обеспечение и после нескольких дней использования понял, что оно стоит тех денег, которые я за него заплатил. Я люблю влезать в свои собственные проблемы; программное обеспечение охватывает все аспекты вопросов по алгебре, которые можно получить на экзамене.

Дженнифер, Огайо.
Мои родители очень счастливы. Вчера я принес домой свою первую пятерку по математике и знаю, что не смог бы сделать это без Алгебратора.
Шон О’Коннор
Если у вас возникли проблемы со сложными алгебраическими уравнениями, у меня есть для вас два слова: Алгебратор! Попробуйте, я гарантирую, что вы увидите результаты в своей математической производительности. Это помогло мне и моим друзьям пройти сложный курс математики для первокурсников.
Адалия Томс, OK
Поисковые фразы, использованные 21 февраля 2008 г.:
Студенты, борющиеся со всевозможными задачами по алгебре, узнают, что наше программное обеспечение может спасти им жизнь. Вот поисковые фразы, которые сегодняшние поисковики использовали, чтобы найти наш сайт. Сможете ли вы найти среди них свою?
- упражнения на радикальные выражения
- Математическая головоломка
- «Анализ с введением в доказательство» решения упражнений
- алгебра, проценты, уравнения
- Программа аппроксимации суммы Римана для графического калькулятора TI 84
- добавление целых десятков рабочих листов
- алгебра 1 читы
- добавление рабочего листа вычитания целых чисел
- Коды доступа учителей McDougal
- решить неоднородное волновое уравнение
- полный идентификационный лист тригонометрии
- Триганометрический стол
- упростить выражения, содержащие скобки
- VB 6 Математическая викторина
- как посчитать проценты с помощью калькулятора ti 83
- работает ли Кумон
- Какие упорядоченные дроби
- практических вопросов по бинарным операциям NY math A
- график х в квадрате плюс один
- наименьшее общее кратное с переменными и показателями
- ответы на домашнее задание по математике
- спросить Джибеса, как решить двухшаговые уравнения
- Вопросы по уравнениям баланса 8 класса
- приложений логарифмических функций с графической таблицей
- радикальный онлайн калькулятор математика
- игр с целыми числами
- gre список формул
- как преобразовать целые числа в проценты
- ti 83 нахождение квадратных корней
- листы перестановок с ответами
- Печатные формы четвертого класса
- расстояние между двумя точками на декартовой плоскости калькулятор в радикальной форме
- ти-83 плюс конвертировать в дробь
- бесплатный лист по математике, сравнение и заказ
- Калькулятор преобразования десятичных знаков в дроби
- Калькулятор инструкций ТИ-86 «Заказной список»
- Написание квадратного уравнения в форме вершин
- стихотворение о математическом неравенстве
- Рабочие листы 4 класса сбалансированных уравнений
- Таблица полярных формул
- формула параболы
- изменить базу программы ti 89
- мультипликация и деление
- решение радикалов в кубе
- бесплатная электронная книга по производственному учету
- TI калькулятор скачать компьютер бесплатно
- как найти квадратный корень в кубе
- упрощенные радикалы
- алгебраические графы
- Булева алгебра Учебник и руководства
- десятичных знаков как смешанные числа
- рабочих листов в стиле кумон
- практика для теста Гаусса 8 класса
- Лист преобразования геометрии для печати
- решатель алгебры онлайн
- онлайн трехчленный калькулятор
- glencoe алгебра 1 книга ответов
- простых вероятностных игр
- деление на упрощенные квадраты
- неравенства сложения и вычитания покажи свою работу
- Решатель квадратных уравнений полный квадрат
- программа алгебры
- вершинная форма линейного уравнения
- Калькулятор квадратичного факторинга
- перевести дробь в десятичную
- бесплатно скачать книгу учета затрат
- возведение в квадрат калькулятор квадратного уравнения
- Таблицы функций для пятого класса
- преобразовать десятичную дробь в ближайшую целую дробь
- Скачать шрифт Boca Raton
- скачать тест способностей
- пример вероятности TI-83 плюс ключевой колледж
- математический ответ ключ бесплатно gr 6 канадский
- сравнение дробей от наименьшей к наибольшей
- ti-83 плюс лог-инструкции
- mcdougal littell алгебра 2 практических теста
- макдугал литтел ответ ключ алгебра 2
- напиши дроби на моем калькуляторе
- решатель неопределенного интегрального уравнения первообразной
- добавление целых чисел бесплатно рабочий лист
- онлайн-калькуляторы для преобразования дробей в десятичные
- бесплатных онлайн игр по алгебре
- основные уравнения обучения алгебре
- работа по математике
- онлайн калькулятор полиномиальное деление
- Бесплатная помощь и ответы по алгебре 2
- c Учебники по программированию Lamguage.


 Из них можно выбрать оптимальный, который подходит в конкретной ситуации.
Из них можно выбрать оптимальный, который подходит в конкретной ситуации.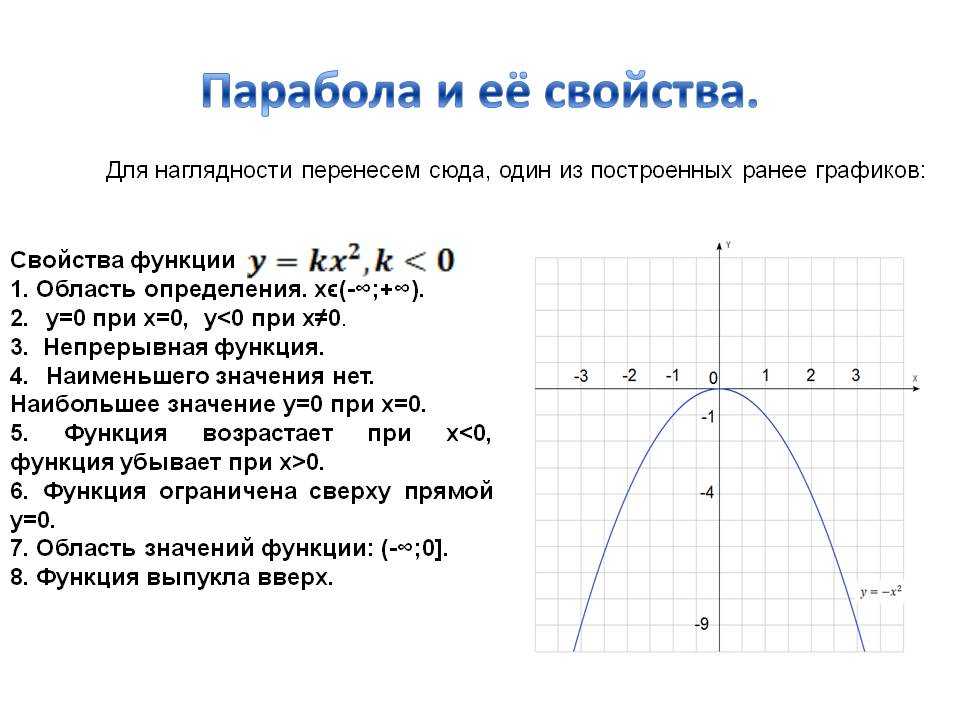
 Все, что вам нужно сделать, это использовать следующие уравнения:
Все, что вам нужно сделать, это использовать следующие уравнения: Вы можете использовать калькулятор параболы, чтобы сделать это за вас, или вы можете использовать уравнение:
Вы можете использовать калькулятор параболы, чтобы сделать это за вас, или вы можете использовать уравнение: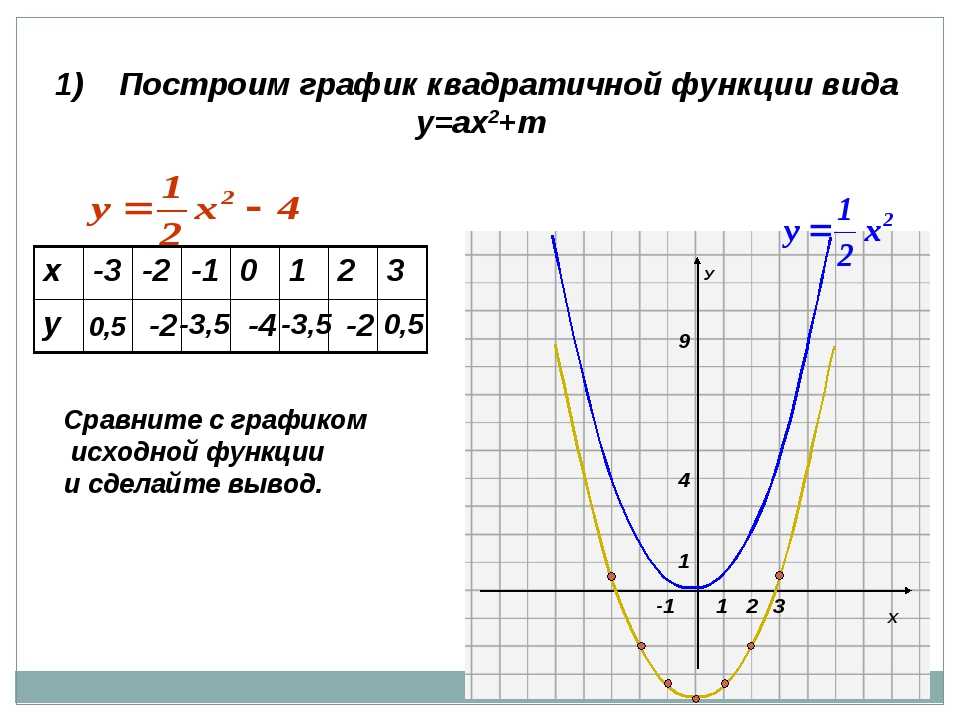
 2}{b}$ и тому подобное, калькулятор для него не подойдет.
2}{b}$ и тому подобное, калькулятор для него не подойдет.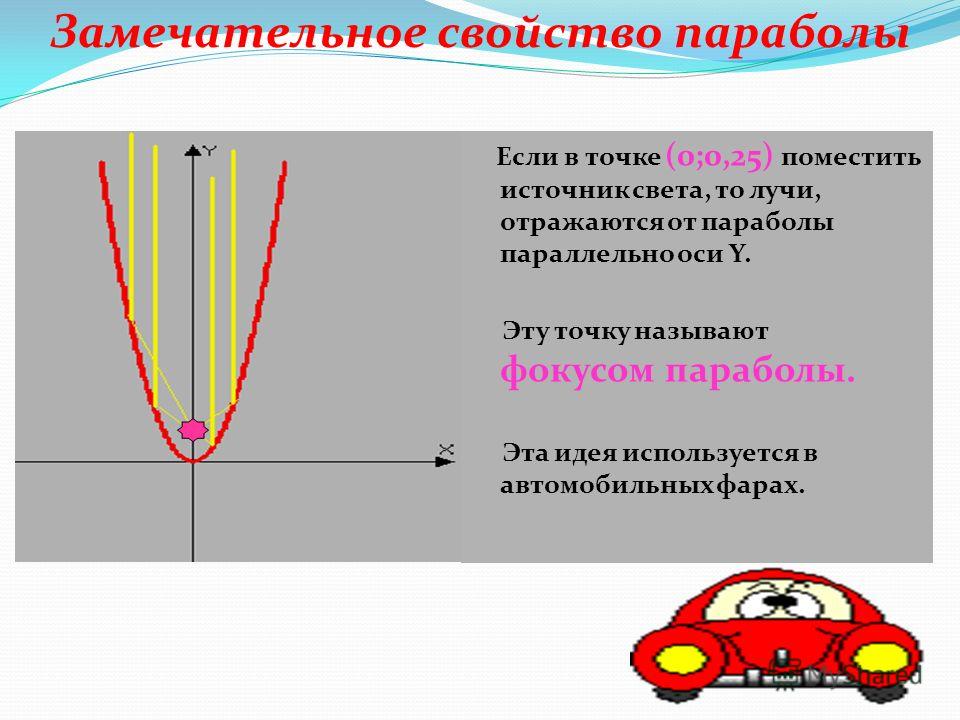
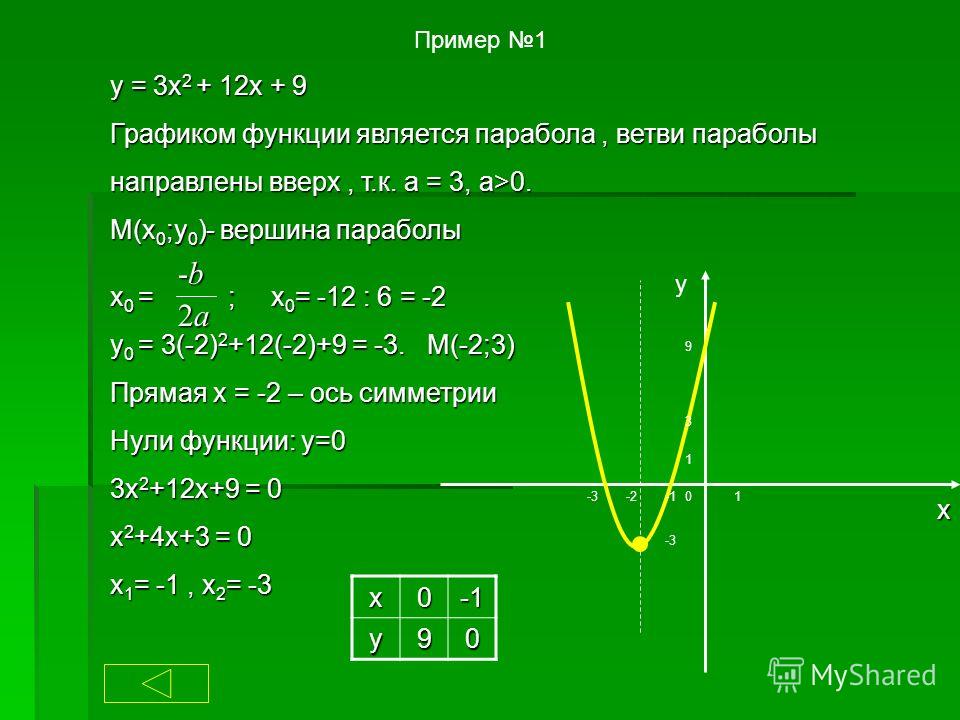
 Он проходит через вершину и может быть параллелен оси x или y при определенных условиях.
Он проходит через вершину и может быть параллелен оси x или y при определенных условиях. Иногда также называется полуширокой прямой кишкой. Для парабол это удвоенное значение полуоси/фокусного расстояния. Обозначается как p = 2f.
Иногда также называется полуширокой прямой кишкой. Для парабол это удвоенное значение полуоси/фокусного расстояния. Обозначается как p = 2f. 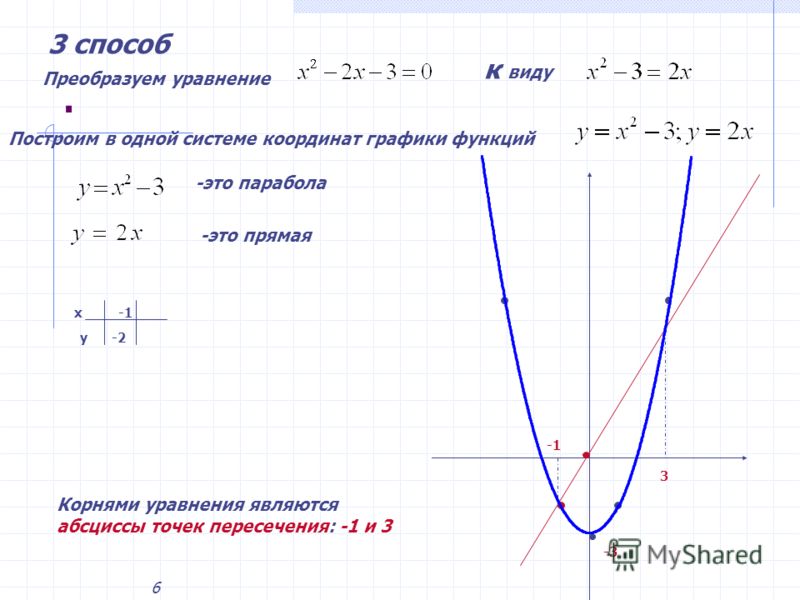 В противном случае это (h, k) . Поскольку AoS проходит через вершину, и мы знаем, что она параллельна либо оси x, либо оси y, мы можем сказать, что AoS: y=k для x-симметричных парабол и AoS: x=h для y-симметричных парабол.
В противном случае это (h, k) . Поскольку AoS проходит через вершину, и мы знаем, что она параллельна либо оси x, либо оси y, мы можем сказать, что AoS: y=k для x-симметричных парабол и AoS: x=h для y-симметричных парабол.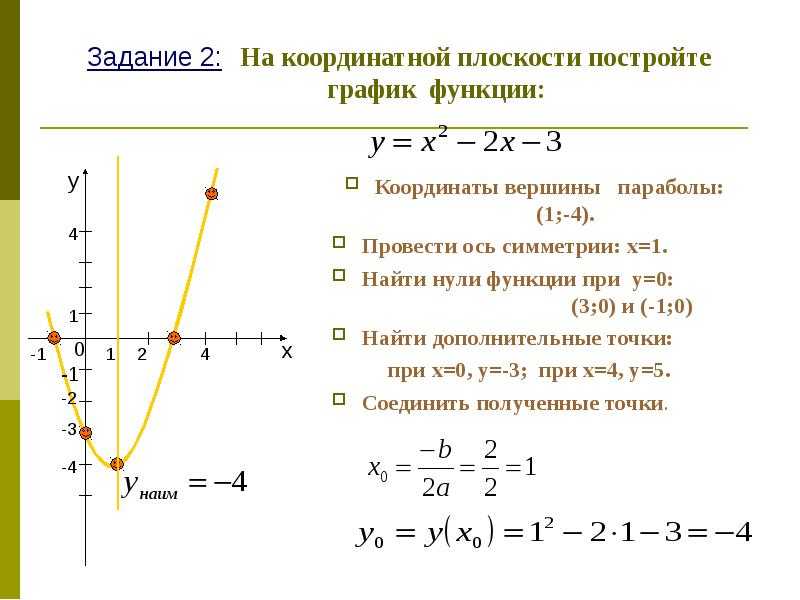 2 + 15x + 220 \] 92 + k \]
2 + 15x + 220 \] 92 + k \]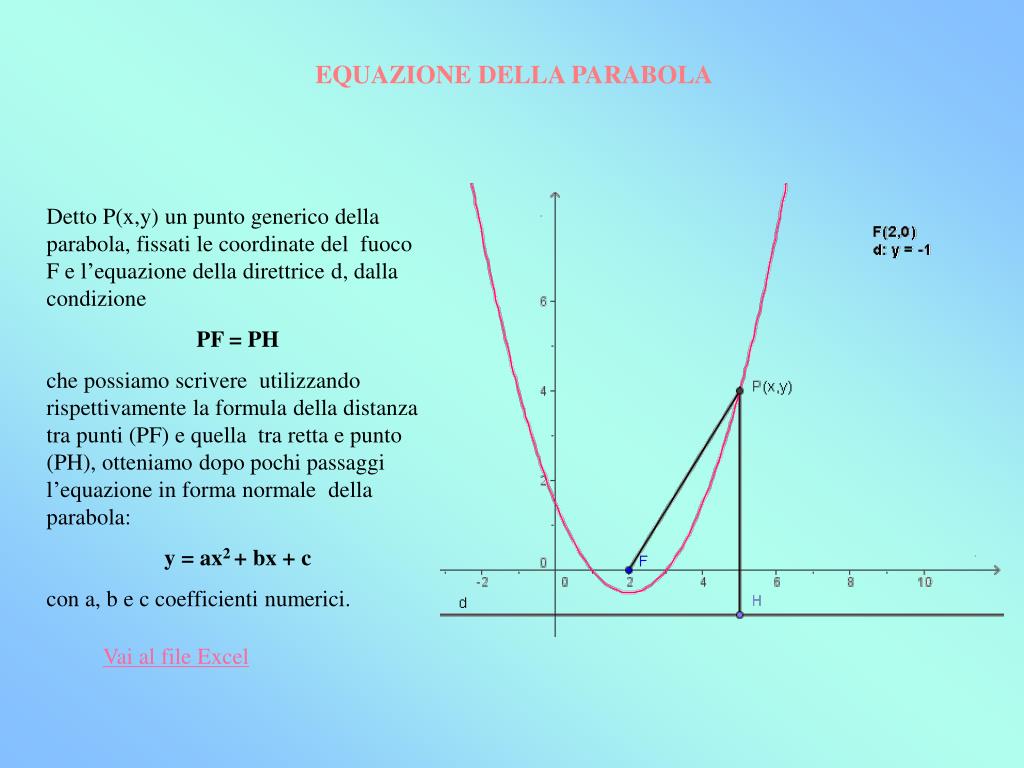 $$
$$ 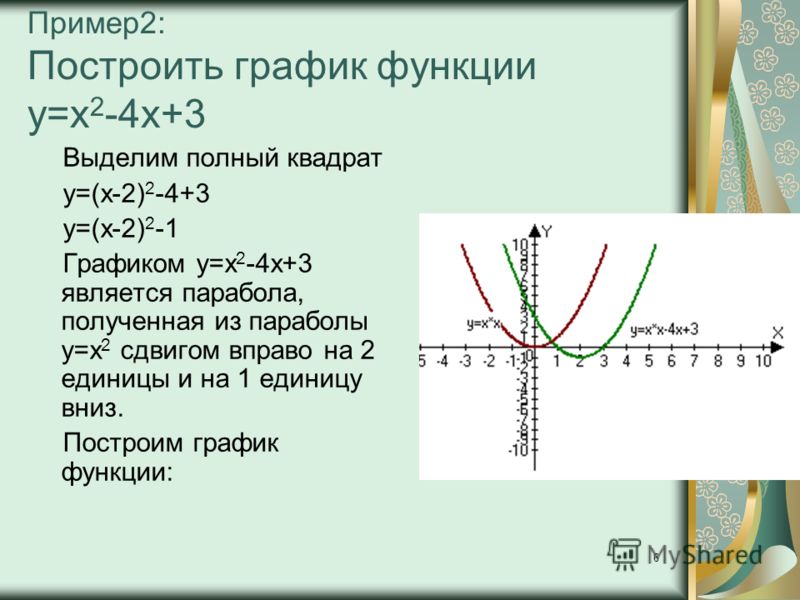 Для удобства вам необходимо выполнить следующие шаги:
Для удобства вам необходимо выполнить следующие шаги:
 Он перемещает узел из одного положения в другое вместе с одной из осей, связанных с его начальным положением.
Он перемещает узел из одного положения в другое вместе с одной из осей, связанных с его начальным положением.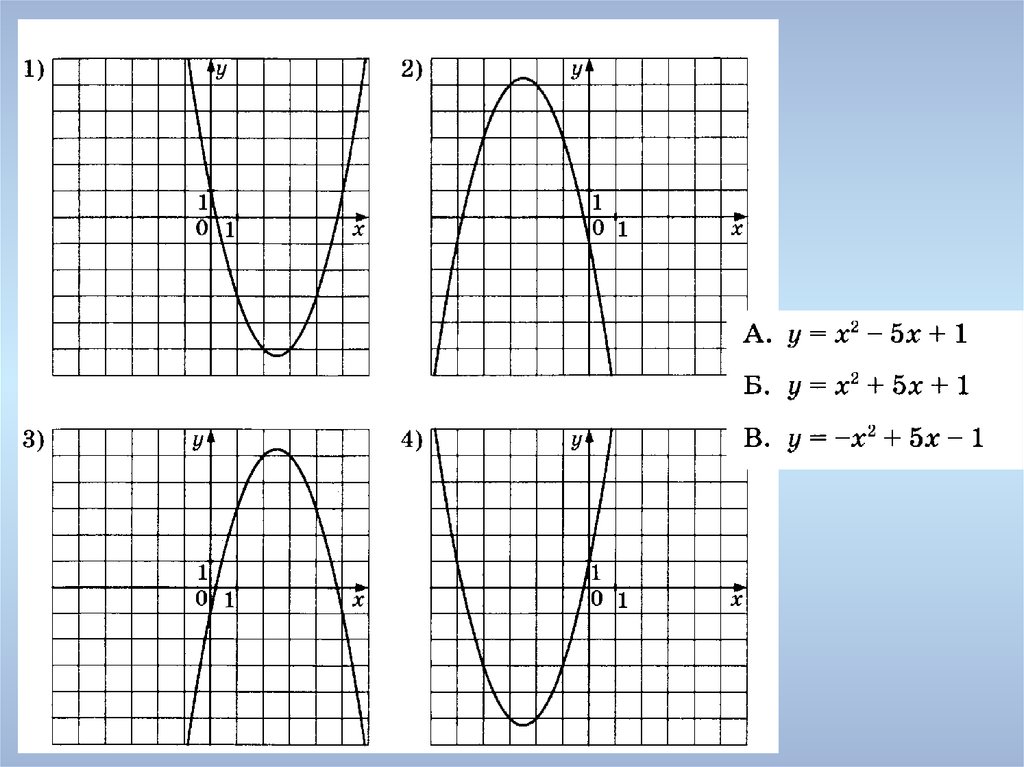
 1 показан график уравнения
1 показан график уравнения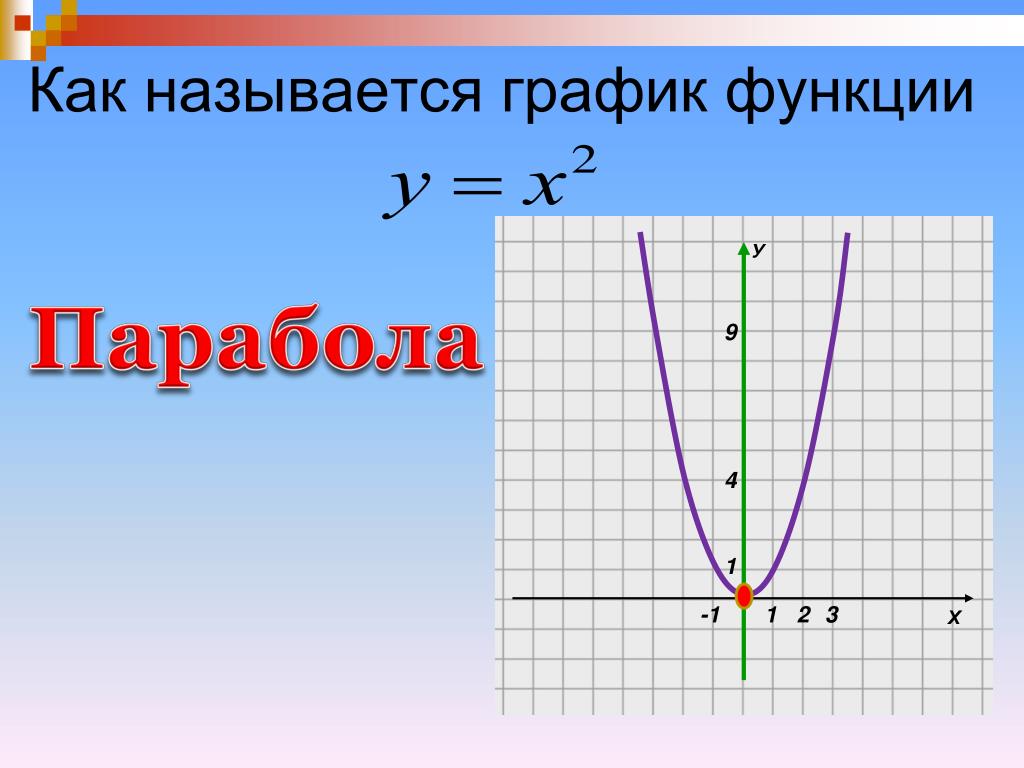 Геометрически результат
отражение графика через -ось.
Геометрически результат
отражение графика через -ось. Он принимает свое минимальное значение () при .
Таким образом, график представляет собой график сдвинутых единиц на
право. Если отрицательный, график сдвигается на единицу
слева.
Он принимает свое минимальное значение () при .
Таким образом, график представляет собой график сдвинутых единиц на
право. Если отрицательный, график сдвигается на единицу
слева.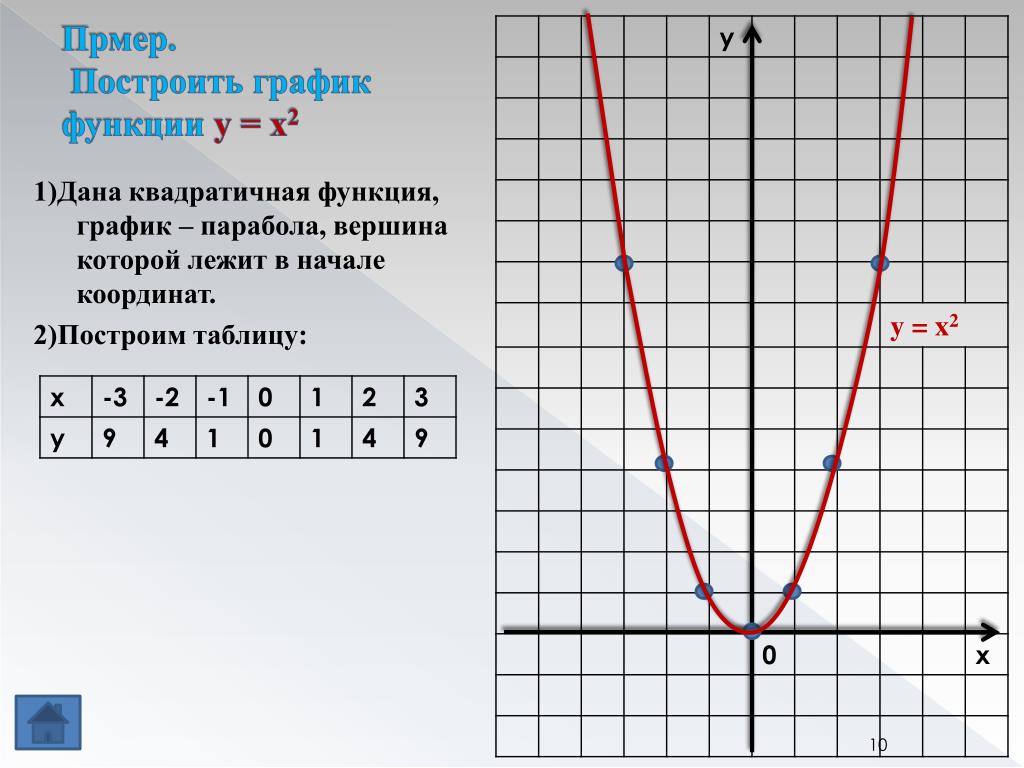

 е. вы, вероятно, на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
е. вы, вероятно, на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана. Другими словами, парабола не развернется вдруг и не начнет раскрываться, если она уже начала раскрываться вниз. Точно так же, если он уже начал открываться, он не развернется и не начнет открываться внезапно.
Другими словами, парабола не развернется вдруг и не начнет раскрываться, если она уже начала раскрываться вниз. Точно так же, если он уже начал открываться, он не развернется и не начнет открываться внезапно.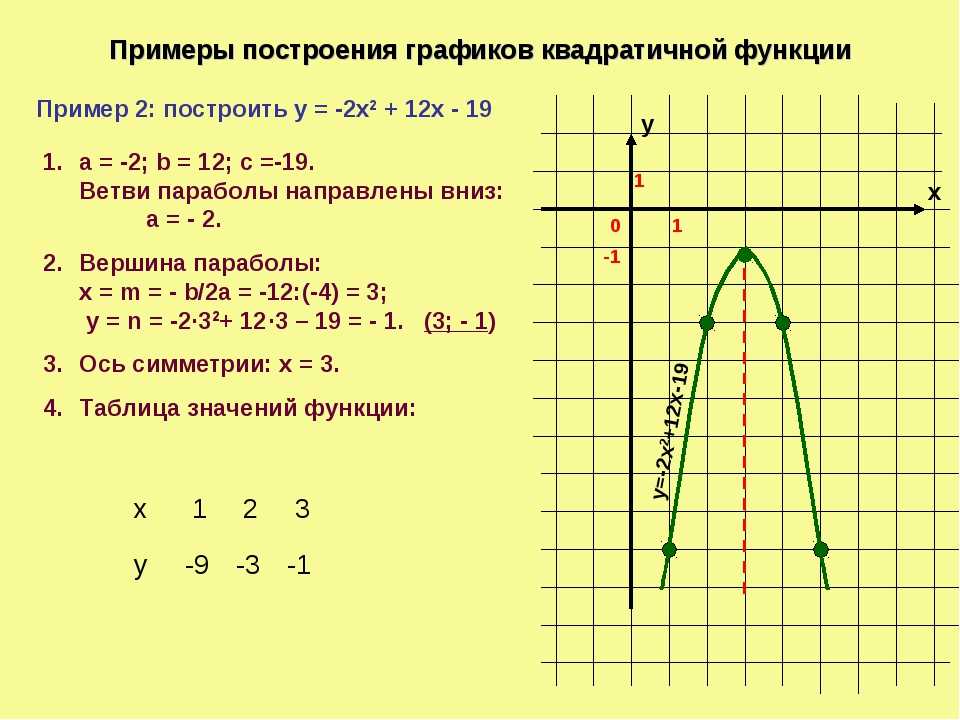 Чтобы найти \(y\)-перехват функции \(y = f\left( x \right)\), все, что нам нужно сделать, это установить \(x = 0\) и вычислить, чтобы найти \(y\ ) координата. Другими словами, \(y\)-перехват — это точка \(\left( {0,f\left( 0 \right)} \right)\). Мы находим \(x\)-перехваты примерно таким же образом. Положим \(y = 0\) и решим полученное уравнение относительно координат \(x\). Итак, нам нужно будет решить уравнение,
Чтобы найти \(y\)-перехват функции \(y = f\left( x \right)\), все, что нам нужно сделать, это установить \(x = 0\) и вычислить, чтобы найти \(y\ ) координата. Другими словами, \(y\)-перехват — это точка \(\left( {0,f\left( 0 \right)} \right)\). Мы находим \(x\)-перехваты примерно таким же образом. Положим \(y = 0\) и решим полученное уравнение относительно координат \(x\). Итак, нам нужно будет решить уравнение,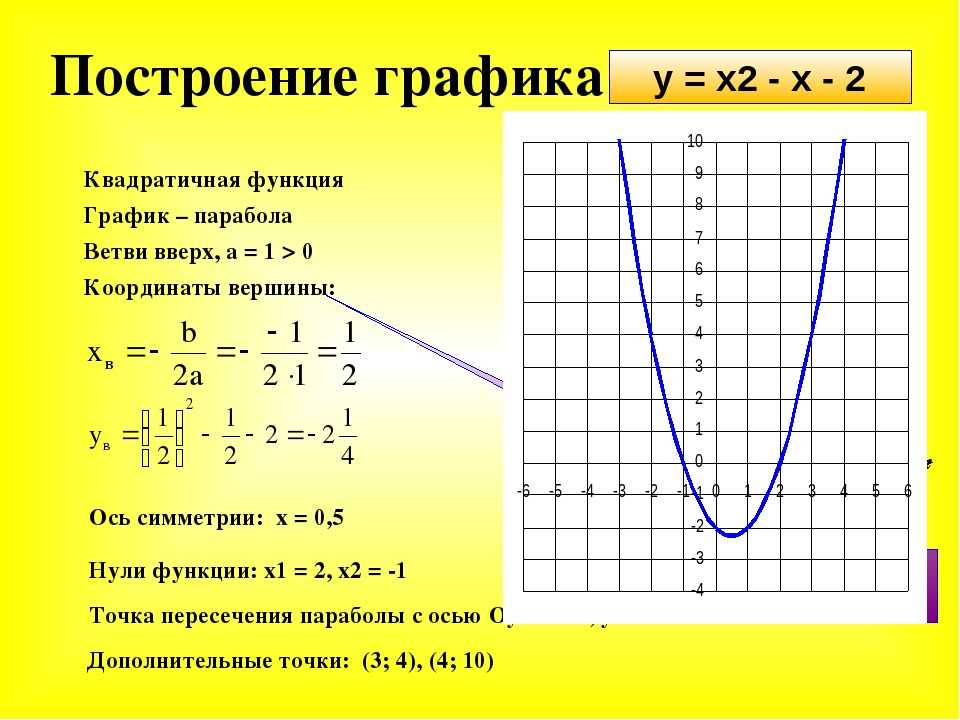 Как мы увидим в наших примерах, у нас может быть 0, 1 или 2 \(x\)-перехвата.
Как мы увидим в наших примерах, у нас может быть 0, 1 или 2 \(x\)-перехвата. 2} + к \]
2} + к \]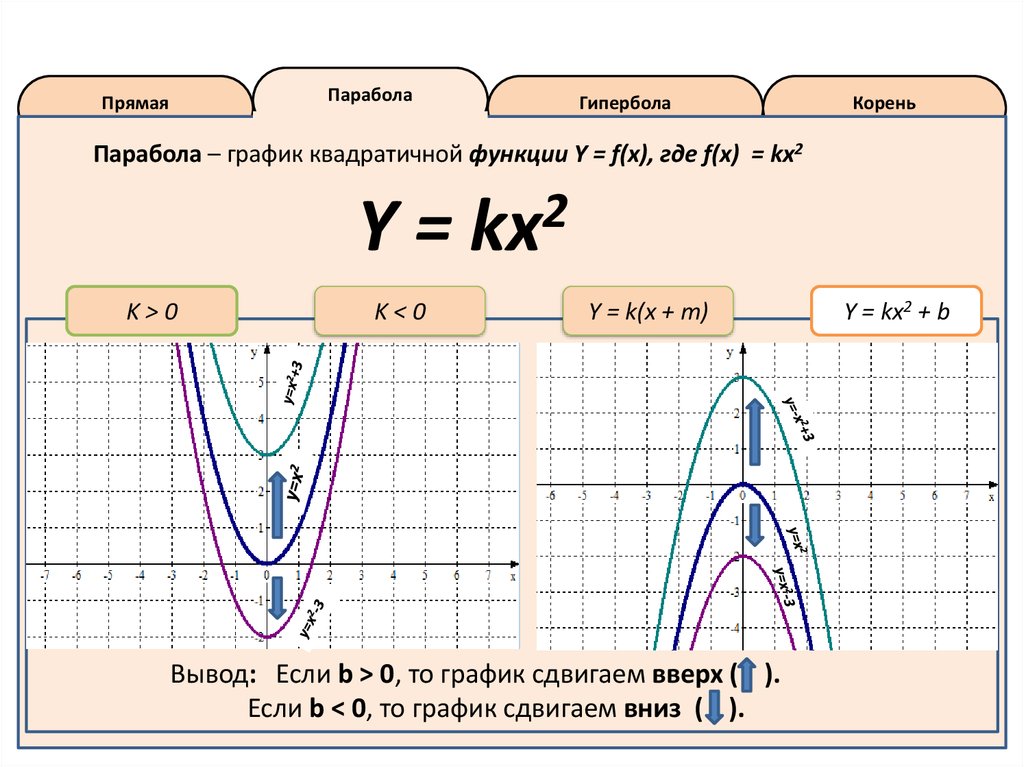 Это не что иное, как быстрая оценка функции. 92} — 8 = 2 \ влево ( 9 \ вправо) — 8 = 10 \ hspace {0,25 дюйма} y — {\ mbox {перехват: }} \ влево ( {{\ mbox {0,10}}} \ вправо) \]
Это не что иное, как быстрая оценка функции. 92} — 8 = 2 \ влево ( 9 \ вправо) — 8 = 10 \ hspace {0,25 дюйма} y — {\ mbox {перехват: }} \ влево ( {{\ mbox {0,10}}} \ вправо) \]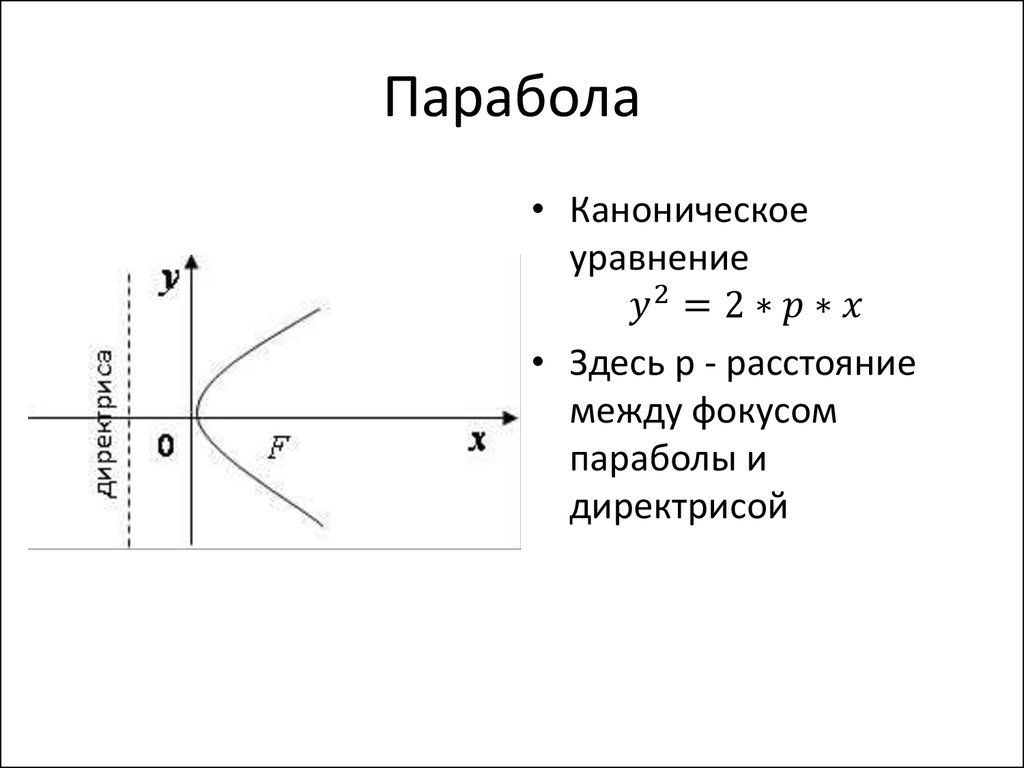 25in}{\mbox{and}}\hspace{0.25in}\left( {- 1,0} \right)\]
25in}{\mbox{and}}\hspace{0.25in}\left( {- 1,0} \right)\]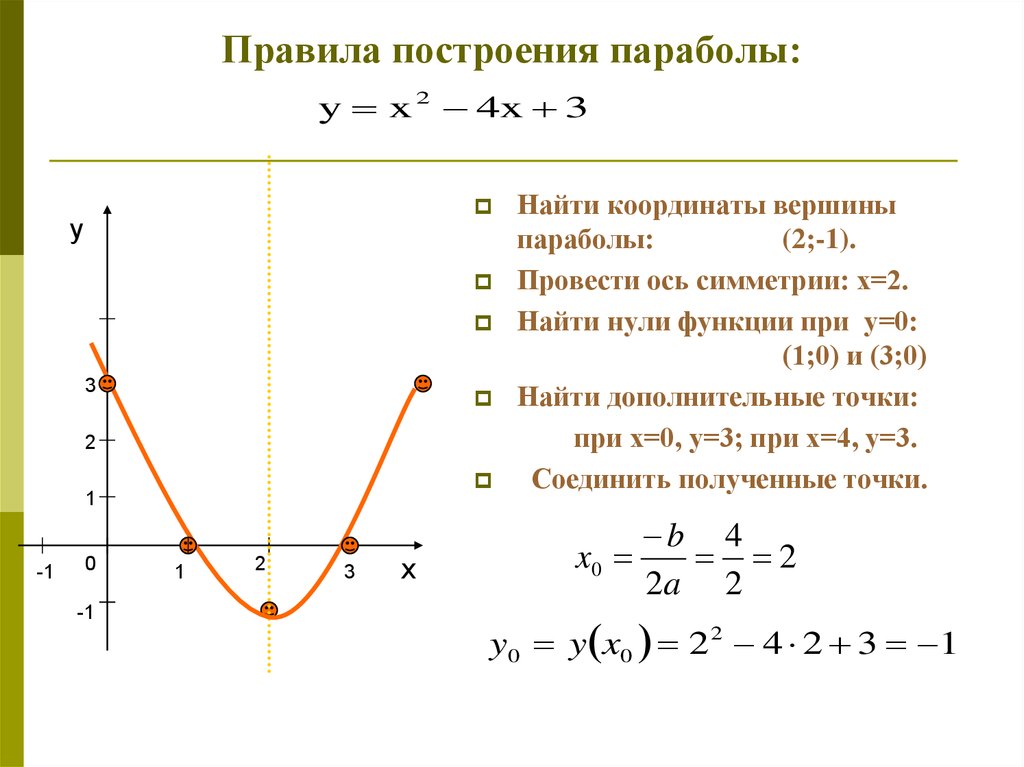 2} — 1 = — 4 — 1 = — 5\]
2} — 1 = — 4 — 1 = — 5\]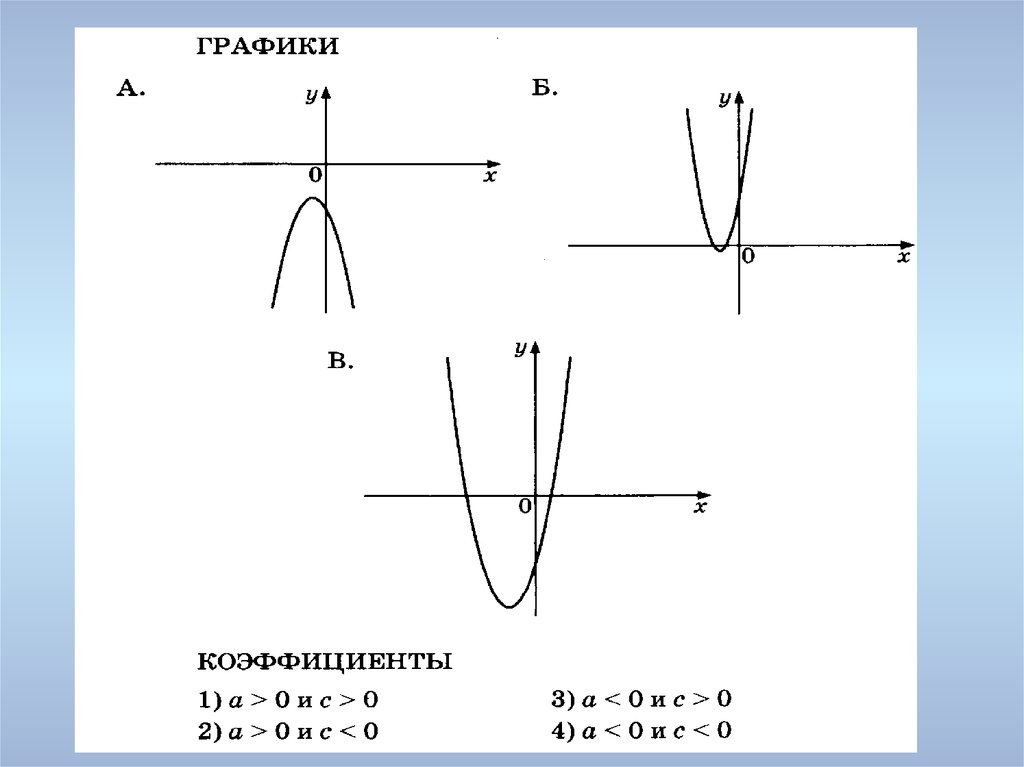 Тогда координаты этой точки должны быть \(\left( {4, — 5} \right)\). 92} + 4\) Показать решение
Тогда координаты этой точки должны быть \(\left( {4, — 5} \right)\). 92} + 4\) Показать решение На самом деле, у нас еще даже нет точки, которая не была бы вершиной!
На самом деле, у нас еще даже нет точки, которая не была бы вершиной!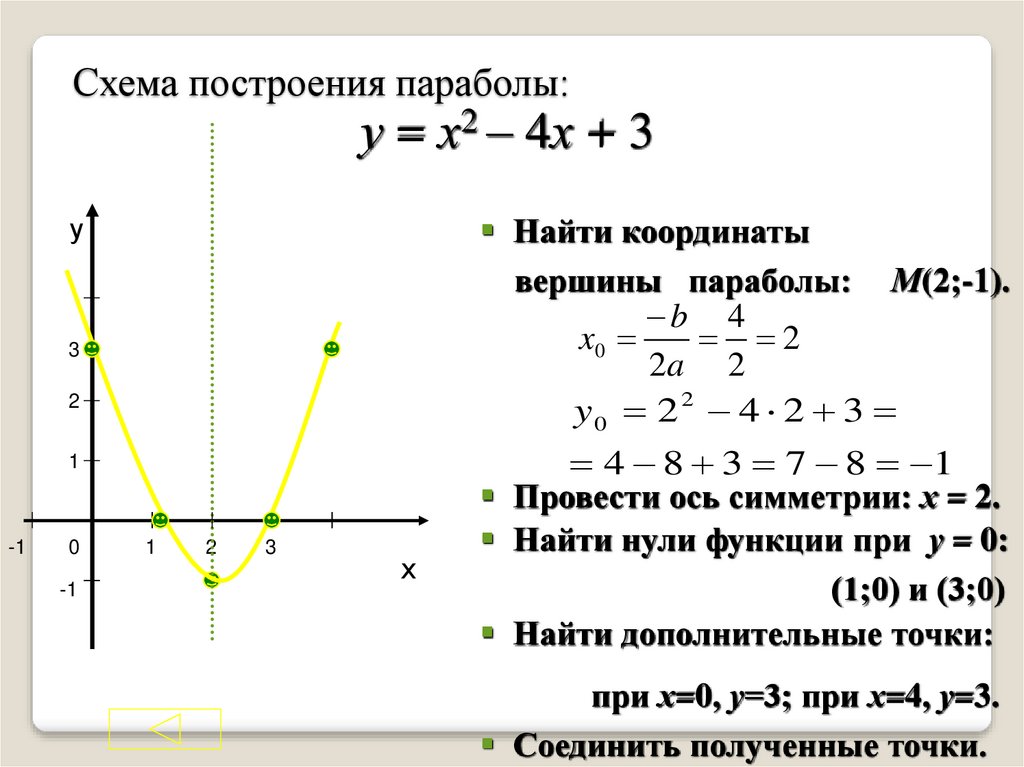 2} + 4x + 4\) Показать решение
92} + 4\влево( { — 2} \вправо) + 4 = 0\конец{выравнивание*}\]
2} + 4x + 4\) Показать решение
92} + 4\влево( { — 2} \вправо) + 4 = 0\конец{выравнивание*}\]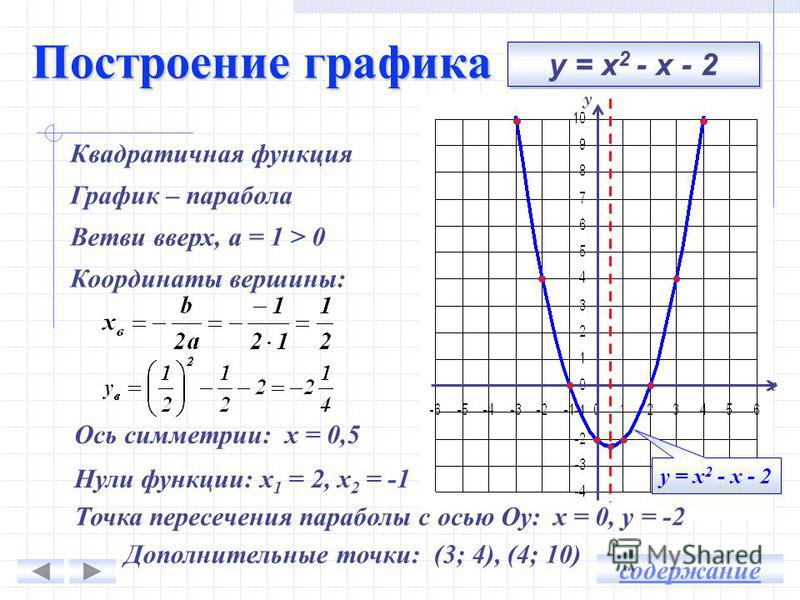 Это означает, что вторая точка равна \(\left( { — 4,4} \right)\).
Это означает, что вторая точка равна \(\left( { — 4,4} \right)\).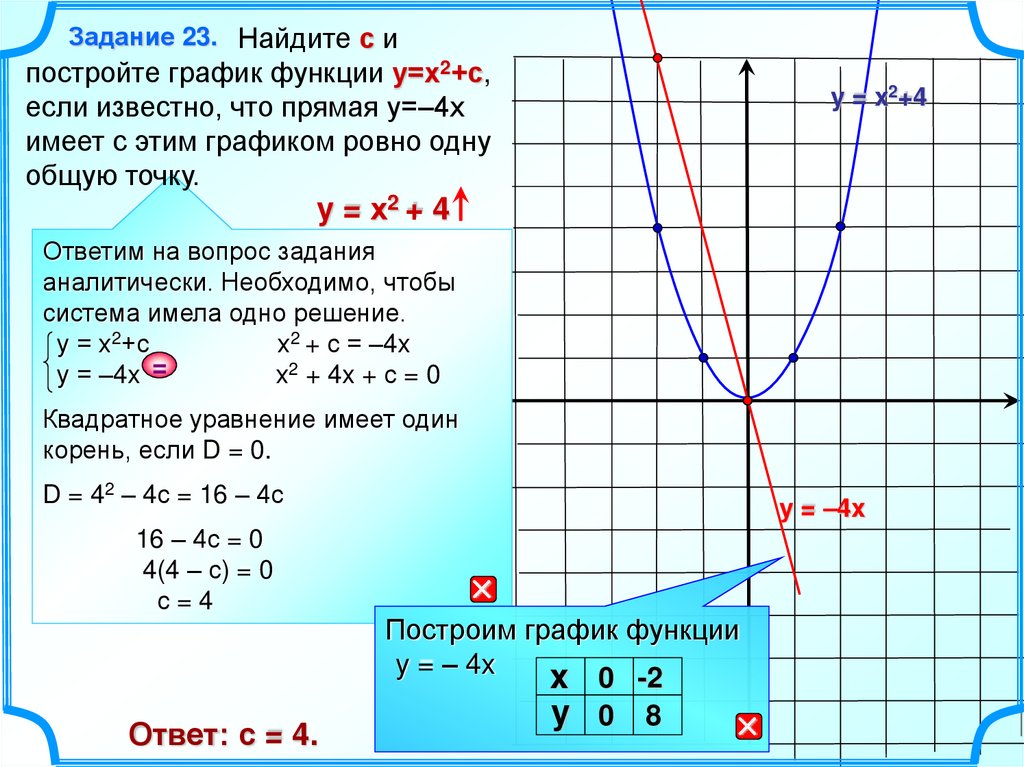 2} — \ frac {{15}}{2}} \right)\]
92} + 24\конец{выравнивание*}\]
2} — \ frac {{15}}{2}} \right)\]
92} + 24\конец{выравнивание*}\]