Парабола онлайн построение: Точки разрыва функции онлайн

Построение графика квадратичной функции — презентация онлайн

Похожие презентации:

Построение графика квадратичной функции

Построение графика квадратичной функции

График квадратичной функции. Построение графика квадратичной функци

Еще один способ построения графика квадратичной функции

Квадратичная функция, ее график и свойства

Задачи ОГЭ №11, №23. Функции и их графики. Построение графика сложной функции

Построение графика квадратичной функции

Квадратичная функция и её график

Построение графика квадратичной функции. (9 класс)

Построение графиков квадратичной функции

1. Цели урока:

ТЕМА УРОКА:
Построение графика
квадратичной функции
ЦЕЛИ УРОКА:
Сформулировать алгоритм построения
графика квадратичной функции, т. е. функции
вида
y = ax2+bx+c ( у=а(х- n)2 + m)
Научиться строить график квадратичной
функции по алгоритму.
Нет ни одной области
математики, как бы
абстрактна она ни была,
которая когда-нибудь не
окажется применимой к
явлениям действительного
мира.
Н.И.Лобачевский

4. Параболический фонтан и лучи прожектора

ПАРАБОЛИЧЕСКИЙ ФОНТАН И ЛУЧИ
ПРОЖЕКТОРА

5. Библиотека с крышей в форме параболы в Норвегии и падение баскетбольного мяча

БИБЛИОТЕКА С КРЫШЕЙ В ФОРМЕ ПАРАБОЛЫ В
НОРВЕГИИ И ПАДЕНИЕ БАСКЕТБОЛЬНОГО МЯЧА

7. АЛГОРИТМ ПОСТРОЕНИЯ ГРАФИКА КВАДРАТИЧНОЙ ФУНКЦИИ

y = ax2+bx+c
Определить направление ветвей
параболы(a>0- ветви направлены вверх, a<0ветви направлены вниз)
Определить координаты вершины параболы
(n; m) и отметить ее в координатной
плоскости: n = -b/2a; m = y(n)
Заполнить таблицу
Построить график (можно воспользоваться
шаблоном y = ax2)
y=
y
3
2
1
0
-1
1 2
– 4x – 2
График функции парабола, ветви которой
направлены вверх (a=1).
4
-3 -2 -1
2
x
3 4 5 6
-2
-3
-4
Координаты вершины:
x х = -b/2a = -(-4)/2 = 2;
y = y(2) = 22- 4∙2 – 2 = -6
Почему в таблице значения
записаны разным цветом?
-5
-6
х
0
1
2
3
4
у
-2
-5
-6
-5
-2
Сформулируйте правила построения
графиков функций у=а(х- n)2 + m.
Два параллельных переноса:
вдоль оси у на m единиц вверх,
если m>0; или на m единиц вниз,
если m<0;
вдоль оси х на n единиц вправо,
если n>0; или на m единиц влево,
если n<0
(можно воспользоваться шаблоном y =
ax2)
Построить графики функции
1)у=(х- 3)2 + 1; 2)у=(х+ 2)2 – 2; 3)у=-(х- 1)2 — 3

10. С помощью каких преобразований получили данные графики функций?

С ПОМОЩЬЮ КАКИХ
ПРЕОБРАЗОВАНИЙ ПОЛУЧИЛИ
ДАННЫЕ ГРАФИКИ ФУНКЦИЙ?

Написать формулу для
графиков квадратичной
функции
Установите соответствие
y ( x 5) 2 2
y 2( x 4) 2
y ( x 1) 2 1
y ( x 1) 2

13. ПОРЕШАЕМ. Но сначала всё выясним о коэффициентах и свободном члене.

ПОРЕШАЕМ.
НО СНАЧАЛА ВСЁ ВЫЯСНИМ О
КОЭФФИЦИЕНТАХ И СВОБОДНОМ
ЧЛЕНЕ.

14. Решение заданий из сборника «ОГЭ 3000 задач»

РЕШЕНИЕ ЗАДАНИЙ ИЗ СБОРНИКА
«ОГЭ 3000 ЗАДАЧ»

15. Решение заданий из сборника «ОГЭ 3000 задач»

РЕШЕНИЕ ЗАДАНИЙ ИЗ СБОРНИКА
«ОГЭ 3000 ЗАДАЧ»

16.

Решение заданий из сборника «ОГЭ 3000 задач»РЕШЕНИЕ ЗАДАНИЙ ИЗ СБОРНИКА
«ОГЭ 3000 ЗАДАЧ»

17. Решение заданий из сборника «ОГЭ 3000 задач»

РЕШЕНИЕ ЗАДАНИЙ ИЗ СБОРНИКА
«ОГЭ 3000 ЗАДАЧ»

18. Решение заданий из сборника «ОГЭ 3000 задач»

РЕШЕНИЕ ЗАДАНИЙ ИЗ СБОРНИКА
«ОГЭ 3000 ЗАДАЧ»

19. Самостоятельная работа !

САМОСТОЯТЕЛЬНАЯ РАБОТА !
Задания из сборника «ОГЭ 3000 задач»
1 вариант- № 1488, 1491, 1494, 1504
2 вариант-№ 1489, 1492, 1495, 1505

20. ДОМАШНЕЕ ЗАДАНИЕ : №1512-1516 (из сборника заданий «ГИА 3000 задач»)

ДОМАШНЕЕ ЗАДАНИЕ :
№1512-1516 (ИЗ СБОРНИКА ЗАДАНИЙ
«ГИА 3000 ЗАДАЧ»)

21. Итоги урока

ИТОГИ УРОКА
Сформулируйте алгоритм построения графика
квадратичной функции.
Что узнали на уроке?
Чему научились на уроке?
В чем испытывали трудности?

22. Древняя китайская мудрость Скажи мне — и я забуду, Покажи мне — и я запомню, Вовлеки меня – и я пойму.

ДРЕВНЯЯ КИТАЙСКАЯ МУДРОСТЬ
СКАЖИ МНЕ — И Я ЗАБУДУ,
ПОКАЖИ МНЕ — И Я ЗАПОМНЮ,
ВОВЛЕКИ МЕНЯ – И Я ПОЙМУ.

English     Русский Правила

Преобразование графиков

Репетиторы ❯ Математика ❯ Преобразование графиков

Автор: Валентин В., онлайн репетитор по математике

●

10.10.2011

●

Раздел: Математика

Мы знаем уже несколько «стандартных» функций, например, y = х², у = f(х) и др. Теперь же рассмотрим варианты их преобразований.

Графики функций y = ах², y = ах³.

Мы знаем, что графиком функции y = ах² является парабола. Чтобы построить график функции y = ах², нужно «растянуть» или «сжать» параболу y = х² от оси х с коэффициентом |а|.

Если а < 0, то график функции нужно еще симметрично отобразить относительно оси х.

Все полученные графики – так же, как и первоначальный график – называются параболами. При а > 0 ветви параболы направлены вверх, при а < 0 – вниз.

Аналогично строится и график функции y = ах³ – кубическая парабола.

График функции у = f(х – m) + n

Точкой отсчета для построения графика этой функции является построение графика функции у = f(х). Итак, для создания графика функции у = f(х – m) + n нужно:

1. Выполнить параллельный перенос плоскости, выбрав началом новой системы координат х´у´ точку
О (m; n).

2. В новой плоскости построить график функции у = f(х).

Полученный график и будет графиком заданной функции, а именно – у = f(х – m) + n.

График квадратичной функции.

Квадратичной мы называем функцию вида у = ах²

+ bх + c, где а, b и c – любые действительные числа и
а ≠ 0.

Чтобы построить график функции у = ах² + bх + c, нам необходимо:

1. Произвести выделение полного квадрата квадратного трехчлена у = ах² + bх + c, в результате которого мы получаем

ах² + bх + c = а(х + b/2а)² + 4ас – b²/4а.

2. Построим график полученной функции, т.е. у = а(х + b/2а)² + 4ас – b²/4а.

Для этого нам нужно выполнить параллельный перенос плоскости, поместив в начало новой системы координат х´у´ точку О (-b/2а; 4ас – b²/4а), а также в плоскости х´у´ построить параболу – график функции
у´ = а (х´)².

Прямая х = -b/2а получила название ось симметрии параболы, а точка О´ (-b/2а; 4ас – b²/4а) – вершина параболы.

Если а > 0, то ветви параболы будут направлены вверх, если а < 0 – вниз.

Построить график квадратичной функции можно несколькими способами.

Способ 1.

Отыскание координат вершины параболы по формулам:

х₀ = -b/2а

у₀ = 4ас – b²/4а.

Используя приведенные формулы, мы сможем получить координаты вершины нашей параболы и еще нескольких точек.

Способ 2.

Построение параболы по точкам с ординатой, равной свободному члену квадратного трехчлена
ах² + bх + c. При построении графика этим способом нам нужно будет решить уравнение, чтобы найти координаты наших двух «опорных» точек. После мы сможем найти координаты вершины параболы и собственно через 3 точки построить параболу.

Способ 3.

Построение параболы по корням квадратного трехчлена. Для этого нам предстоит найти корни квадратного трехчлена х

₁ и х₂. Далее мы определим координаты наших опорных точек и вершины. А после построим сам график.

График функции у = f(kх).

Рассмотрим случай, когда k > 0, k ≠ 1.

Сопоставляя нашу функцию с функцией у = f(х), приходим к выводу, что график функции у = f(kх) получается из графика функции у = f(х) сжатием с коэффициентом k к оси у.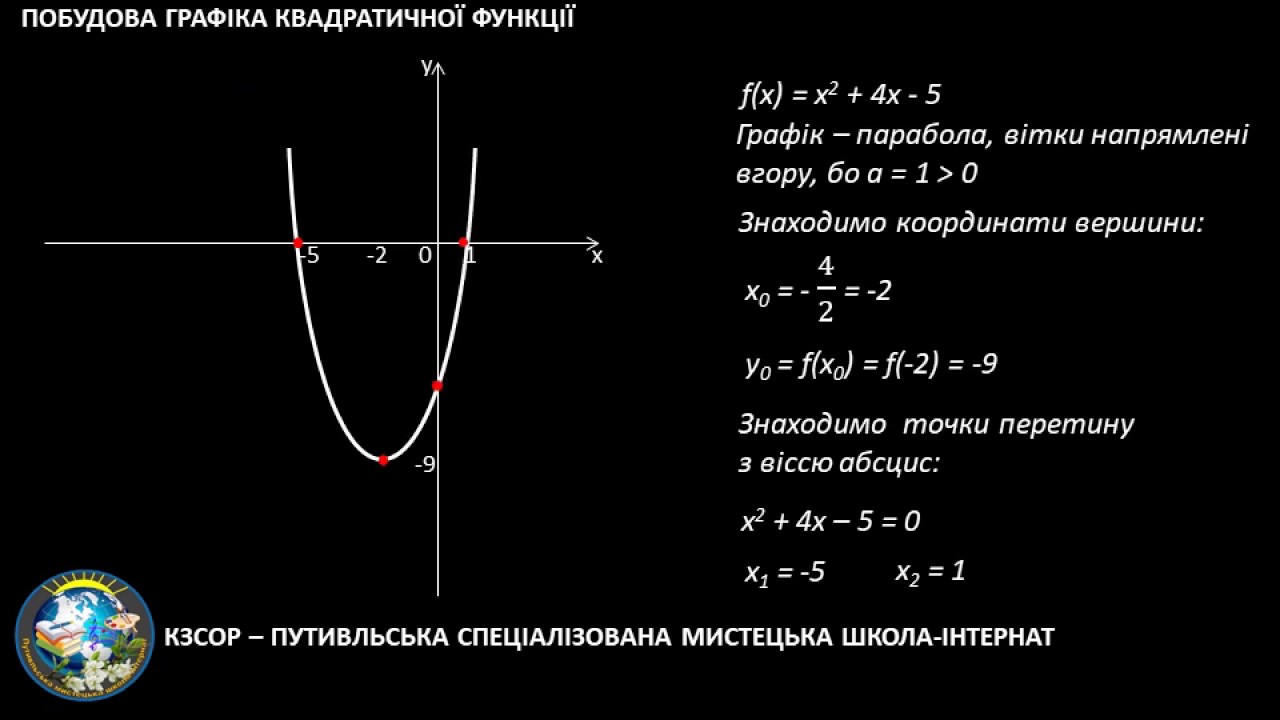

Сжиматься и растягиваться могут и графики тригонометрических функций (например, у = m sin kx, у = m cos kx и др.).

Построение подобных графиков проходят в три стадии:

1. Строим график «простой», знакомой нам функции у = sin x.

2. Строим график функции у = sin kx.

3. Строим график функции у = m sin kx.

На практике же легче всего построить график для функции у = m sin kx сжатием или растяжением одной полуволны графика у = sin x, а затем построить весь график.

© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.

Остались вопросы?

Задайте свой вопрос и получите ответ от профессионального преподавателя.

Задать вопрос

Математика

Курсы по математике 10 класс

Математика

Курсы по математике 9 класс

Математика

Математика 11 класс

Математика

Курсы по геометрии 7 класс

Математика

Курсы по алгебре 7 класс

Математика

Алгебра 8 класс

Математика

Курсы по геометрии 8 класс

Французский язык

Курсы французского языка для начинающих

Parabola Calculator

Онлайн-калькулятор параболы находит стандартные и вершинные параболические уравнения и вычисляет фокус, направление, вершину и важные точки параболы. 2 + 10y + 16 \)? 92 + 4x + 10$$

$$Без точки пересечения с осью.$$

Однако онлайн-калькулятор гиперболы поможет вам определить центр, эксцентриситет, фокусный параметр, главную и асимптоту для заданных значений в уравнение гиперболы.

Как найти директрису параболы?

Возьмем стандартную форму уравнения параболы: \( (x – h)2 = 4p (y – k) \)

• В этом уравнении основное внимание уделяется: \( (h, k + p)\)
• Принимая во внимание, что направляющая равна \( y = k – p \).

Если мы повернем параболу, то ее вершина будет: \( (h,k) \). Однако ось симметрии параллельна оси x, и ее уравнение будет таким: \( (y – k)2 = 4p (x – h)\) ,

• Теперь фокус: \( (h + р, к)\)
• Направляющая параболы равна \( x = h – p \).

Кроме того, директриса параболы также может быть рассчитана с помощью простого уравнения: \(y = c – \frac{(b² + 1)}{(4a)}\) .

Как работает калькулятор параболы?

Калькулятор уравнения параболы делает расчет быстрее и без ошибок, поскольку он использует математическое уравнение параболы. Для удобства вам необходимо выполнить следующие шаги:

Ввод:

• Сначала выберите уравнение параболы из раскрывающегося списка. Вы можете выбрать стандартную форму, форму вершины, три точки или вершину и точки для ввода.
• Теперь будет отображаться выбранное уравнение для параболы. Поэтому просто введите значения в данные поля соответственно.
• Нажмите кнопку расчета.

Вывод:

Калькулятор уравнения параболы вычисляет:

• Уравнение параболы в стандартной форме.
• Уравнение параболы в вершинной форме.
• Все параметры, такие как вершина, фокус, эксцентриситет, директриса, широкая прямая кишка, ось симметрии, пересечение по оси x, пересечение по оси y.
• Приведите пошаговые расчеты, когда парабола проходит через разные точки.
• Наряду со всеми этими математическими значениями, этот графограф параболы отображает график параболы в конце.

Часто задаваемые вопросы:

Как расстояние между фокусом и директрисой влияет на форму параболы?

Всякий раз, когда расстояние между фокусом и директрисой параболы увеличивается, |a| уменьшится. Это означает, что парабола расширяется с увеличением расстояния между двумя ее параметрами.

Как построить параболу?

Для быстрых и простых расчетов вы можете использовать онлайн-график парабол, который строит графическое представление данного уравнения параболы. Однако для ручного построения графика параболы необходимо выполнить несколько шагов:

• Прежде всего, найдите следующие параметры:
• y-перехват.
• x-перехватов.
• Ищите дополнительные точки, чтобы иметь не менее пяти точек для построения графика.
• Теперь просто нанесите точки и нарисуйте график параболы.

Какие существуют два типа трансформации?

Первый тип преобразования известен как преобразование. Он перемещает узел из одного положения в другое вместе с одной из осей, связанных с его начальным положением.

Второй тип — вращение. Он перемещает узел по кругу вокруг точки вращения.

Как вы описываете преобразование параболы?

Вертикальное перемещение параболы дает возможность построить новую параболу. Это будет то же самое, что и основная парабола. Таким же образом можно перевести параболу по горизонтали.

Заключение:

Калькулятор параболы используется для получения быстрых результатов и построения графика для любого заданного параболического уравнения. Этот поиск уравнения параболы делает ваш расчет быстрее и проще, решая все связанные свойства параболического уравнения. Это также позволяет вам понять, как поместить значения в формулу параболы. Итак, этот инструмент всегда готов предоставить свои услуги всем в мгновение ока и без каких-либо затрат.

Каталожные номера:

Из источника Википедии: Декартова система координат, Сходство с единичной параболой, Положение фокуса.

Из источника онлайн-заметок Пола: Параболы, Зарисовка парабол, Направление оси.

Из источника ООР Услуги: Графики парабол с вершинами в начале координат, Стандартные формы парабол с вершинами, Ось x как ось симметрии.

Другие языки: Parabol Hesaplama, Kalkulator Parabola, Kalkulator Paraboli, Parabel Rechner, 放物線 計算.

Ось симметрии — уравнение, формула, определение, примеры, парабола

Ось симметрии — это воображаемая прямая линия, которая делит фигуру на две одинаковые части, тем самым создавая одну часть как зеркальное отражение другой части. При складывании по оси симметрии две части накладываются друг на друга. Прямая линия называется линией симметрии/зеркальной линией. Эта линия может быть вертикальной, горизонтальной или наклонной.

Мы можем видеть эту ось симметрии даже в природе, такой как цветы, берега рек, здания, листья и так далее. Мы можем наблюдать это в Тадж-Махале, культовом мраморном сооружении в Индии.

1.	Что такое ось симметрии?
2.	Ось симметрии параболы
3.	Уравнение оси симметрии
4.	Ось симметрии Формула
5.	Найти ось симметрии
6.	Вывод оси симметрии
7.	Идентификация оси симметрии
8.	Часто задаваемые вопросы об оси симметрии

Что такое ось симметрии?

Ось симметрии представляет собой прямую линию, делающую форму объекта симметричной. Ось симметрии создает точные отражения на каждой из своих сторон. Он может быть горизонтальным, вертикальным или боковым. Если мы складываем и разворачиваем объект вдоль оси симметрии, две стороны идентичны. Разные фигуры имеют разные линии симметрии. У квадрата четыре оси симметрии, у прямоугольника две оси симметрии, у круга бесконечные оси симметрии, а у параллелограмма нет осей симметрии.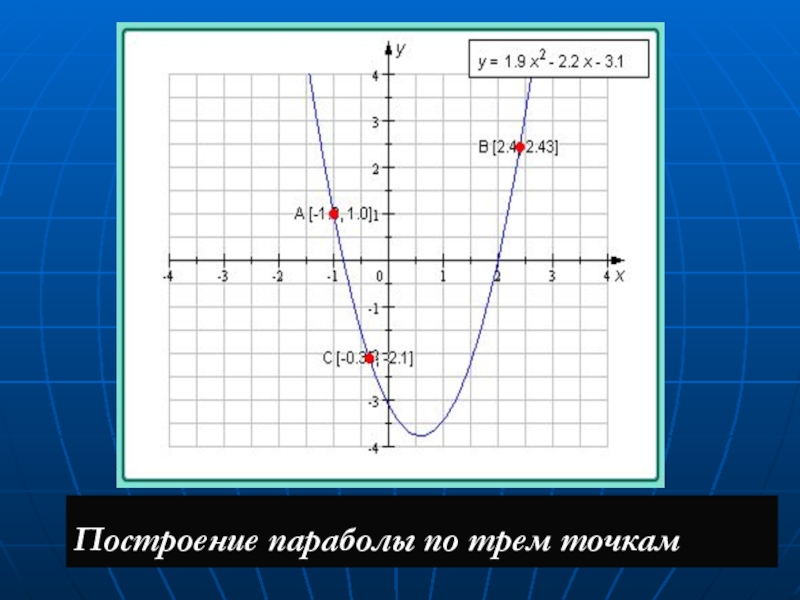 Правильный многоугольник из n сторон имеет n осей симметрии.

Ось симметрии Определение

Ось симметрии — это воображаемая линия, которая делит фигуру на две одинаковые части, каждая из которых является зеркальным отражением друг друга. При складывании фигуры по оси симметрии две одинаковые части накладываются друг на друга.

Ось симметрии параболы

Парабола имеет одну линию симметрии. Ось симметрии — это прямая линия, которая делит параболу на две симметричные части. Парабола может быть четырех видов. Он может быть как горизонтальным, так и вертикальным, обращенным влево или вправо. Ось симметрии определяет форму параболы.

• Если ось симметрии вертикальна, то и парабола вертикальна (раскрывается вверх/вниз).
• Если она горизонтальна, то и парабола горизонтальна (открывается влево/вправо).

Горизонтальная ось симметрии имеет нулевой наклон, а вертикальная ось симметрии имеет неопределенный наклон.

Уравнение оси симметрии

Вершина — это точка пересечения оси симметрии с параболой. Это ключевой момент для определения его уравнения. Если парабола раскрывается вверх или вниз, ось симметрии вертикальна и в этом случае ее уравнением является вертикальная линия, проходящая через ее вершину. Если парабола открывается вправо или влево, ось симметрии горизонтальна, а ее уравнением является горизонтальная линия, проходящая через ее вершину. то есть

• Ось уравнения симметрии параболы, вершина которой равна (h, k) и направлена ​​вверх/вниз, равна x = h.
• Ось уравнения симметрии параболы, вершина которой равна (h, k) и открывается влево/вправо, равна y = k.

Ось симметрии Формула

Формула оси симметрии применяется к квадратным уравнениям, где используется стандартная форма уравнения и линия симметрии. Линия, которая делит или раздваивает любой объект на две равные половины, обе половины которых являются зеркальным отображением друг друга, называется осью симметрии. Эта линия оси, разделяющая объекты, может быть любого из трех типов: горизонтальная (ось X), вертикальная (ось Y) или наклонная линия.

Уравнение оси симметрии может быть представлено, когда парабола имеет две формы:

• Стандартная форма
• Вершинная форма

Стандартная форма

Квадратное уравнение в стандартной форме : y = ax ² + b x+c

, где a, b и c — действительные числа.

Здесь формула оси симметрии: x = — b/2a.

Вершинная форма

Квадратное уравнение в вершинной форме: y = a (x-h) ² + k

где (h, k) — вершина параболы.

Здесь формула оси симметрии равна x = h.

Вывод оси симметрии параболы

Ось симметрии всегда проходит через вершину параболы. Таким образом, идентификация вершины помогает нам вычислить положение оси симметрии. Формула оси симметрии параболы: x = -b/2a. Выведем уравнение оси симметрии.

Квадратное уравнение параболы: y = ax ² + bx + c (парабола вверх/вниз).

Постоянный член ‘c’ не влияет на параболу. Поэтому рассмотрим, что y = ax ² + bx.

Ось симметрии является средней точкой двух пересечений с х. Чтобы найти точку пересечения, подставьте y = 0.

x(ax+b)=0

x = 0 и (ax+b)=0

x = 0 и x = -b/a

формула средней точки x = (x ₁ + x ₂ ) / 2

x= [0 + (-b/a)] / 2

Следовательно, x = -b/2a

Примечание: Если парабола открыта влево/вправо, то найдите середину y -перехватывает.

Найти ось симметрии

Пример 1: Найти ось симметрии квадратного уравнения y = x ² — 4x + 3.

Решение:

Дано: y = x ² — 4x + 3

Использование формула оси симметрии,

x = -b/2a

x = -(-4)/2(1)

x = 4/2

= 2

Следовательно, ось симметрии уравнения y = x ² — 4x + 3 равно x = 2.

Пример 2: Найдите ось симметрии параболы y = 4x ² .

Решение:

Используя формулу оси симметрии а у = 4x ​​ ² равно x = 0,

Идентификация оси симметрии

Определим ось симметрии данной параболы, используя формулу, изученную в предыдущем разделе.

1) Рассмотрим уравнение y = x ² — 3x + 4. Сравнивая это с уравнением стандартной формы параболы (y = ax ² + bx + c), имеем

a = 1, b = -3 и c = 4

Это вертикальная парабола. Таким образом, он имеет вертикальную ось симметрии.

Мы знаем, что x = -b/2a есть уравнение оси симметрии.

x = -(-3)/2(1) = 1,5

x = 1,5 — ось симметрии параболы y = x ² — 3x + 4.

2) Рассмотрим другой пример. х = 4у ² +5у+3.

Сравнивая со стандартной формой квадратного уравнения, получаем a = 4, b = 5 и c = 3. Эта парабола горизонтальна, и ось симметрии тоже горизонтальна.

Мы знаем, что y = -b/2a есть уравнение оси симметрии.

y = -b/2a

y = -5/2(4)

y = -0,625

3) Если даны две точки, находящиеся на одинаковом расстоянии от вершины параболы, то определяем уравнение оси симметрии путем нахождения середины этих точек. Предположим, что две точки (3, 4) и (9, 4) являются точками на параболе, тогда вершина проходит через точку пересечения, которая образует середину этих заданных точек. Таким образом, x = (3+9)/2 = 12/2 = 6. Следовательно, уравнение оси симметрии имеет вид x = 6,9.0003

Пример: Если ось симметрии уравнения y = qx ² – 32x – 10 равна 8, то найдите значение q.

Решение: Дано,

y = qx ² – 32x – 10

Ось симметрии x = 8

По формуле:

x = — б/2а

, где а = q, b = -32 и x = 8

8 = -(-32) / (2 × q)

8 = 32/2q

16q = 32

q = 2

Следовательно, значение q = 2

Важные замечания по оси симметрии

• Ось симметрии — это воображаемая линия, которая делит фигуру на две одинаковые части, являющиеся зеркальным отображением друг друга.
• Для параболы y = ax ² + b x+c ось симметрии определяется как x = -b/2a
• Правильный многоугольник с ‘n’ сторонами имеет ‘n’ осей симметрии.

☛ Статьи по теме:

• Линии симметрии в прямоугольнике
• Линии симметрии параллелограмма

Часто задаваемые вопросы об оси симметрии

Что такое ось симметрии в алгебре?

Ось симметрии — это воображаемая линия, которая делит фигуру на две одинаковые части, каждая из которых является зеркальным отражением друг друга. Правильный многоугольник из n сторон имеет n осей симметрии.

Что такое определение оси симметрии?

Ось симметрии — воображаемая прямая, которая делит фигуру на две одинаковые части или делает фигуру симметричной. Например, у квадрата 4, а у прямоугольника 2 оси симметрии.

Что такое формула оси симметрии?

Формула оси симметрии использует стандартную форму квадратного уравнения, а также форму вершины. Симметрия делит любую геометрическую фигуру на две равные половины. Формула оси симметрии задается как для квадратного уравнения стандартной формы y = ax ² + bx + c: x = -b/2a. Если парабола имеет форму вершины y = a(x-h) ² + k, то формула будет следующей: x = h.

Какая формула используется для расчета оси симметрии стандартной формы?

Формула, используемая для нахождения оси симметрии квадратного уравнения стандартной формы y = ax ² + bx + c, выглядит следующим образом: x = -b/2a.

Что такое формула оси симметрии для формы вершины?

Квадратное уравнение представляется в вершинной форме как: y = a(x−h) ² + k , где (h, k) — вершина параболы. Поскольку ось симметрии и форма вершины лежат на одной линии, формула x = h.

Найдите ось симметрии квадратного уравнения y = 5x

² — 10х + 3.

Дано: у = 5х ² — 10х + 3
Используя формулу оси симметрии,
х = -b/2а
х = -(-10)/2(5)
х = 10/10
х = 1
Следовательно, ось симметрии уравнения y = 5x ² — 10x + 3 равна x = 1.

Что такое ось симметрии параболы?

Ось симметрии — это прямая линия, которая делит параболу на две симметричные части. Он проходит через вершину параболы. Ось симметрии параболы может быть горизонтальной или вертикальной.

Как найти ось симметрии, используя вершинную форму уравнения?

Квадратное уравнение в вершинной форме имеет вид y = a(x-h) ² +k. Ось симметрии находится там, где вершина пересекает параболу в точке, обозначенной вершиной (h, k). h — координата x. а в вершинной форме x = h и h = -b/2a, где b и a — коэффициенты в стандартной форме уравнения, y = ax ² + bx + c.

Что такое ось симметрии на графике?

Горизонтальная или вертикальная линия на графике, проходящая через вершину параболы, образует ось симметрии параболы. В случае любого другого графика осью симметрии является уравнение линии, которая делит фигуру на две равные части, одна из которых является зеркальным отражением другой.

Является ли ось симметрии такой же, как и линия симметрии?

Да, линия симметрии и ось симметрии совпадают.