Что такое параллелограмм? Ответ на webmath.ru
Поможем решить контрольную, написать реферат, курсовую и диплом от 800р
Содержание:
- Определение параллелограмма
- Свойства параллелограмма
- Признаки параллелограмма
- Примеры решения задач
Определение параллелограмма
Определение
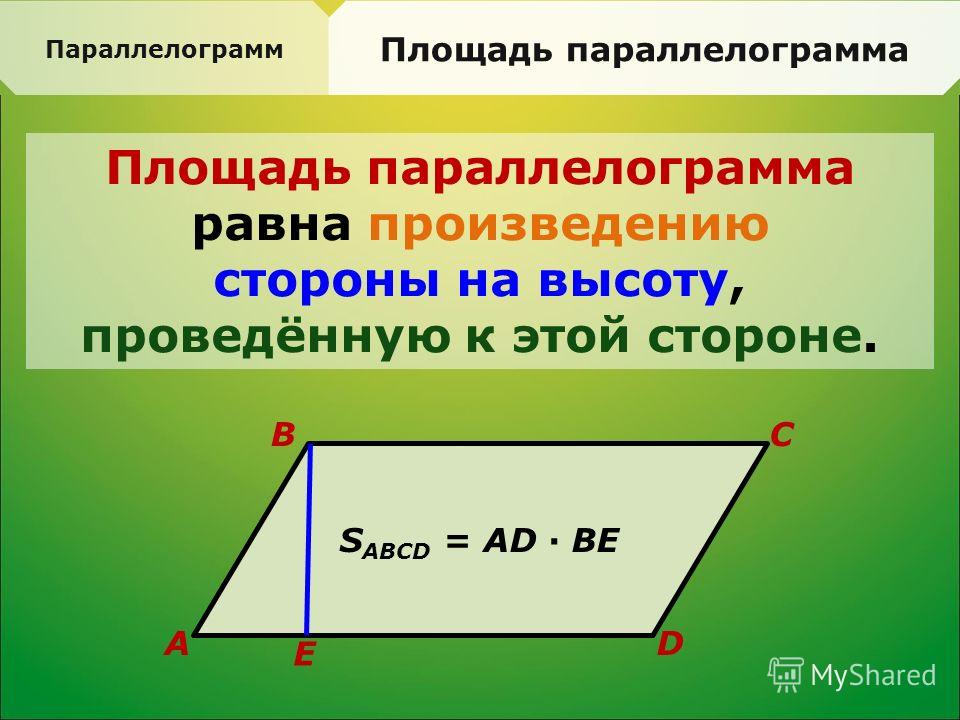
Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны.
На рисунке 1 изображен параллелограмм $A B C D, A B\|C D, B C\| A D$.
Свойства параллелограмма
- В параллелограмме противоположные стороны равны: $A B=C D, B C=A D$ (рис 1).
- В параллелограмме противоположные углы равны $\angle A=\angle C, \angle B=\angle D$ (рис 1).
- Диагонали параллелограмма в точке пересечения делятся пополам $A O=O C, B O=O D$ (рис 1).
- Диагональ параллелограмма делит его на два равных треугольника.
Сумма углов параллелограмма, прилежащих к одной стороне равна $180^{\circ}$:
$$\angle A+\angle B=180^{\circ}, \angle B+\angle C=180^{\circ}$$
$$\angle C+\angle D=180^{\circ}, \angle D+\angle A=180^{\circ}$$
Диагонали и стороны параллелограмма связаны следующим соотношением:
$$d_{1}^{2}+d_{2}^{2}=2 a^{2}+2 b^{2}$$
- В параллелограмме угол между высотами равен его острому углу: $\angle K B H=\angle A$.
 {\circ}$
{\circ}$236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Стороны параллелограмма равны 18 см и 15 см, а высота, проведенная к меньшей стороне, равна 6 см. Найти другую высоту параллелограмма.
Решение. Сделаем рисунок (рис. 2)
По условию, $a=15$ см, $b=18$ см, $h_{a}=6$ см. Для параллелограмма справедливы следующие формулы для нахождения площади:
$$S=a \cdot h_{a}, \quad S=b \cdot h_{b}$$
Приравняем правые части этих равенств, и выразим, из полученного равенства, $h_{b} $:
$$a \cdot h_{a}=b \cdot h_{b} \Rightarrow h_{b}=\frac{a \cdot h_{a}}{b}$$
Подставляя исходные данные задачи, окончательно получим:
$h_{b}=\frac{15 \cdot 6}{18} \Rightarrow h_{b}=5$ (см)
Ответ. $h_{b}=5$
Читать дальше: что такое трапеция.

Теоремы параллелограмма
☰
Параллелограмм представляет собой четырехугольник, у которого противоположные стороны попарно параллельны. Это определение уже достаточно, так как остальные свойства параллелограмма следуют из него и доказываются в виде теорем.
Основными свойствами параллелограмма являются:
- параллелограмм — это выпуклый четырехугольник;
- у параллелограмма противоположные стороны попарно равны;
- у параллелограмма противоположные углы попарно равны;
- диагонали параллелограмма точкой пересечения делятся пополам.
Параллелограмм — выпуклый четырехугольник
Докажем сначала теорему о том, что параллелограмм является выпуклым четырехугольником
. Многоугольник является выпуклым тогда, когда какая бы его сторона не была продлена до прямой, все остальные стороны многоугольника окажутся по одну сторону от этой прямой.Пусть дан параллелограмм ABCD, у которого AB противоположная сторона для CD, а BC — противоположная для AD.
 Тогда из определения параллелограмма следует, что AB || CD, BC || AD.
Тогда из определения параллелограмма следует, что AB || CD, BC || AD.У параллельных отрезков нет общих точек, они не пересекаются. Это значит, что CD лежит по одну сторону от AB. Поскольку отрезок BC соединяет точку B отрезка AB с точкой C отрезка CD, а отрезок AD соединяет другие точки AB и CD, то отрезки BC и AD также лежат по ту же сторону от прямой AB, где лежит CD. Таким образом, все три стороны — CD, BC, AD — лежат по одну сторону от AB.
Аналогично доказывается, что по отношению к другим сторонам параллелограмма три остальные стороны лежат с одной стороны.
Противоположные стороны и углы равны
Параллелограмм является четырехугольником. Значит, у него две диагонали.
 Так как параллелограмм — это выпуклый четырехугольник, то любая из них делит его на два треугольника. Рассмотрим в параллелограмме ABCD треугольники ABC и ADC, полученные в результате проведения диагонали AC.
Так как параллелограмм — это выпуклый четырехугольник, то любая из них делит его на два треугольника. Рассмотрим в параллелограмме ABCD треугольники ABC и ADC, полученные в результате проведения диагонали AC.У этих треугольников одна сторона общая — AC. Угол BCA равен углу CAD, как вертикальные при параллельных BC и AD. Углы BAC и ACD также равны как вертикальные при параллельных AB и CD. Следовательно, ∆ABC = ∆ADC по двум углам и стороне между ними.
В этих треугольниках стороне AB соответствует сторона CD, а стороне BC соответствует AD. Следовательно, AB = CD и BC = AD.
Углу B соответствует угол D, т. е. ∠B = ∠D. Угол A параллелограмма представляет собой сумму двух углов — ∠BAC и ∠CAD. Угол же C равен состоит из ∠BCA и ∠ACD. Так как пары углов равны друг другу, то ∠A = ∠C.
Таким образом, доказано, что в параллелограмме противоположные стороны и углы равны.
Диагонали делятся пополам
Так как параллелограмм — это выпуклый четырехугольник, то у него две две диагонали, и они пересекаются.
 Пусть дан параллелограмм ABCD, его диагонали AC и BD пересекаются в точке E. Рассмотрим образованные ими треугольники ABE и CDE.
Пусть дан параллелограмм ABCD, его диагонали AC и BD пересекаются в точке E. Рассмотрим образованные ими треугольники ABE и CDE.У этих треугольников стороны AB и CD равны как противоположные стороны параллелограмма. Угол ABE равен углу CDE как накрест лежащие при параллельных прямых AB и CD. По этой же причине ∠BAE = ∠DCE. Значит, ∆ABE = ∆CDE по двум углам и стороне между ними.
Также можно заметить, что углы AEB и CED вертикальные, а следовательно, тоже равны друг другу.
Так как треугольники ABE и CDE равны друг другу, то равны и все их соответствующие элементы. Стороне AE первого треугольника соответствует сторона CE второго, значит, AE = CE. Аналогично BE = DE. Каждая пара равных отрезков составляет диагональ параллелограмма. Таким образом доказано, что диагонали параллелограмма делятся точкой пересечения пополам.
Параллелограмм Факты для детей
Детская энциклопедия Факты
Параллелограмм представляет собой многоугольник с четырьмя сторонами (четырехугольник).
 Он имеет две пары параллельных сторон (стороны, которые никогда не пересекаются) и четыре ребра. Противоположные стороны параллелограмма имеют одинаковую длину (равнодлинны). Слово «параллелограмм» происходит от греческого слова «parallelogrammon» ( , ограниченное параллельными линиями ). Прямоугольники, ромбы и квадраты являются параллелограммами.
Он имеет две пары параллельных сторон (стороны, которые никогда не пересекаются) и четыре ребра. Противоположные стороны параллелограмма имеют одинаковую длину (равнодлинны). Слово «параллелограмм» происходит от греческого слова «parallelogrammon» ( , ограниченное параллельными линиями ). Прямоугольники, ромбы и квадраты являются параллелограммами.Как показано на рисунке справа, поскольку треугольники ABE и CDE конгруэнтны (имеют одинаковую форму и размер),
Во всех параллелограммах противоположные углы равны друг другу. Углы, не противоположные в параллелограмме, в сумме дают 180 градусов.
Характеристики
Простой (несамопересекающийся) четырехугольник является параллелограммом тогда и только тогда, когда верно любое из следующих утверждений:
- Две пары противоположных сторон равны по длине
- Две пары противоположных углов равны по мере
- Диагонали делят друг друга пополам
- Одна пара противоположных сторон параллельна и равна по длине
- Смежные углы являются дополнительными
- Каждая диагональ делит четырехугольник на два равных треугольника
- Сумма квадратов сторон равна сумме квадратов диагоналей.
 (Это закон параллелограмма)
(Это закон параллелограмма) - Обладает вращательной симметрией 2-го порядка
- Имеет две оси симметрии
Свойства
- Противоположные стороны параллелограмма параллельны.
- Любая линия, проходящая через середину параллелограмма, делит площадь пополам.
- Параллелограммы — это четырехугольники.
это параллелограмм
хороший факт параллелограмм в нем параллелограмм Параллелограмм это многоугольник с четырьмя сторонами (четырехугольник). Он имеет две пары параллельных сторон (стороны, которые никогда не пересекаются) и четыре ребра. Противоположные стороны параллелограмма имеют одинаковую длину (равнодлинны). Слово «параллелограмм» происходит от греческого слова «parallelogrammon» (ограниченный параллельными линиями).[1] Прямоугольники, ромбы и квадраты являются параллелограммами.
Как показано на рисунке справа, поскольку треугольники ABE и CDE конгруэнтны (имеют одинаковую форму и размер),
{\displaystyle AE=CE} {\displaystyle AE=CE} {\displaystyle BE=DE.
 } {\ displaystyle BE = DE.} Во всех параллелограммах противоположные углы равны друг другу. Углы, не противоположные в параллелограмме, в сумме дают 180 градусов.
} {\ displaystyle BE = DE.} Во всех параллелограммах противоположные углы равны друг другу. Углы, не противоположные в параллелограмме, в сумме дают 180 градусов.Содержание 1 Характеристики 2 Свойства 3 Ссылки 4 Другие веб-сайты Характеристики Простой (несамопересекающийся) четырехугольник является параллелограммом тогда и только тогда, когда верно любое из следующих утверждений:[2][3]
Две пары противоположных сторон равны по длине Две пары противоположных углов равны по размеру Диагонали делят друг друга пополам Одна пара противоположных сторон параллельна и равна по длине Смежные углы смежные Каждая диагональ делит четырехугольник на два равных треугольника сумма квадратов сторон равна сумме квадратов диагоналей. (Это закон параллелограмма) Он имеет вращательную симметрию порядка 2 Он имеет две линии симметрии Свойства Противоположные стороны параллелограмма параллельны. Любая прямая, проходящая через середину параллелограмма, делит площадь пополам. Параллелограммы — это четырехугольники.

Эту короткую статью о математике можно сделать длиннее. Вы можете помочь Википедии, дополнив ее.
это параллелограмм хороший факт параллелограмм параллелограмм в нем
Категория: Многоугольники Меню навигации Не авторизован Обсуждение Вклады Зарегистрироваться Войти PageTalk ЧитатьИзменитьИзменить источникПросмотр историиПоиск Поиск Википедия На главную Простой старт Простой разговор Новые изменения Показать любую страницу Помощь Связаться с нами Дать в Википедию О Википедии Инструменты Какие здесь ссылки Связанные изменения Загрузить файл Специальные страницы Постоянная ссылка Информация о странице Цитировать эту страницу Элемент Викиданных Песочница Печать/экспорт Сделать книгу Скачать в формате PDF Страница для печати В других проектах Wikimedia Commons
На других языках Deutsch English Español Français 한국어 Italiano Tagalog Tiếng Việt 中文 Еще 79 Изменить ссылки Последний раз эта страница была изменена 12 января 2021 г.

Изображения для детей
Все содержимое статей энциклопедии Kiddle (включая изображения статей и факты) можно свободно использовать по лицензии Attribution-ShareAlike, если не указано иное. Цитируйте эту статью:
Факты о параллелограмме для детей. Энциклопедия Киддла.
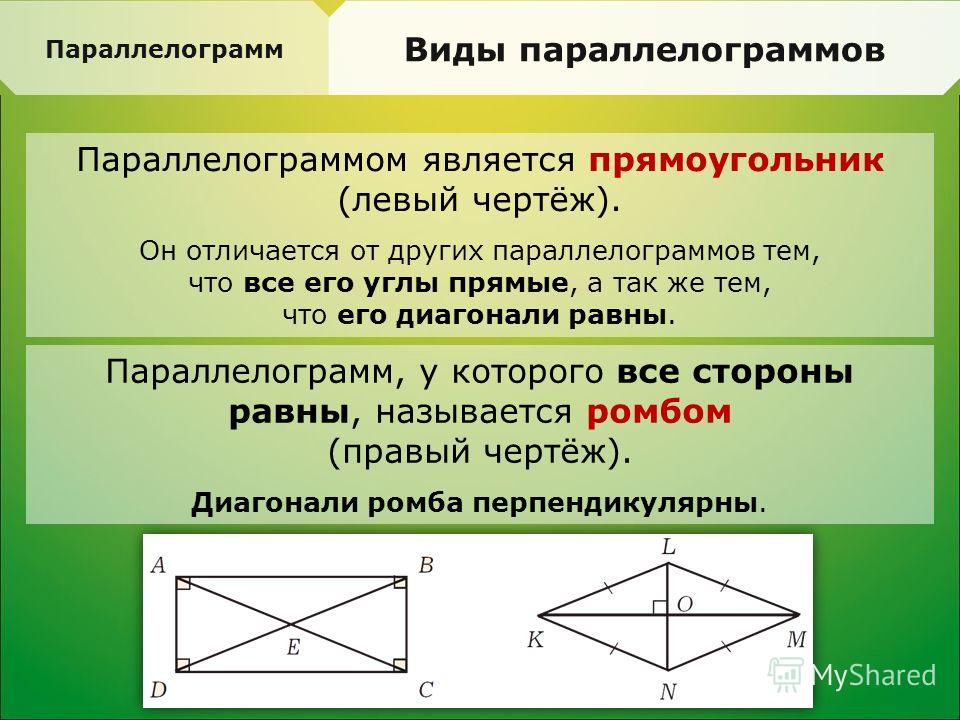
Является ли прямоугольник параллелограммом? Или параллелограмм — это прямоугольник?
Является ли прямоугольник параллелограммом? Или параллелограмм — это прямоугольник?
Эндрю Ли
24 июня 2021 г.
онлайн -репетиторство
,
Алгебра
,
Математика
Оба прямоугольника и параллеал. Но является ли прямоугольник параллелограммом? Или параллелограмм это прямоугольник? Вот обзор различных свойств как параллелограммов, так и прямоугольников.

Параллелограмм – это четырехугольник, который имеет:
- Две пары параллельных сторон
- Две пары противоположных сторон, которые конгруэнтны
Прямоугольник – это четырехугольник, имеющий:
- Четыре прямых угла
- Две пары противоположных сторон, которые конгруэнтны
Ромб – это четырехугольник, который имеет:
- Четыре стороны одинаковой длины
- Две пары равных противоположных углов
Свойства прямоугольника и параллелограмма
Изображение предоставлено Desmos
Когда прямоугольник имеет четыре прямых угла, все внутренние углы равны. Вершины соединяются с соседними сторонами под углом 90°, что означает, что противоположные стороны прямоугольника являются параллельными линиями. Поскольку он имеет два набора параллельных сторон и две пары противоположных сторон, которые конгруэнтны, прямоугольник обладает всеми свойствами параллелограмма. Вот почему прямоугольник всегда является параллелограммом.

Однако параллелограмм не всегда является прямоугольником. Ниже приведен пример параллелограмма, у которого нет четырех прямых углов. Далее мы объясним свойства этой формы.
Свойства прямоугольника по сравнению с ромбом
Фигура выше — это ромб, который мы определили выше. Поскольку ромб похож на прямоугольник, давайте поговорим о сходстве между ними.
Прямоугольник не всегда ромб. У прямоугольника два набора конгруэнтных сторон, тогда как все четыре стороны ромба конгруэнтны.
Но всегда ли ромб параллелограмм? Ответ — да! Две пары противоположных углов ромба всегда равны, как всегда равны две пары противоположных углов параллелограмма. Это означает, что ромб — это всего лишь частный случай параллелограмма, у которого все четыре стороны равны.
Является ли прямоугольник параллелограммом?
Прямоугольники, параллелограммы и ромбы — это особые четырехугольники с определенными свойствами.
Параллелограмм – это четырехугольник, имеющий:
- Две пары параллельных сторон
- Две пары противоположных сторон, которые конгруэнтны
Прямоугольник – это четырехугольник, имеющий:
- Четыре прямых угла
- Две пары противоположных сторон, которые конгруэнтны
Ромб – это четырехугольник, у которого:
- Четыре стороны одинаковой длины
- Две пары равных противоположных углов
Существует гораздо больше типов четырехугольников, чем мы рассмотрели здесь.


 {\circ}$
{\circ}$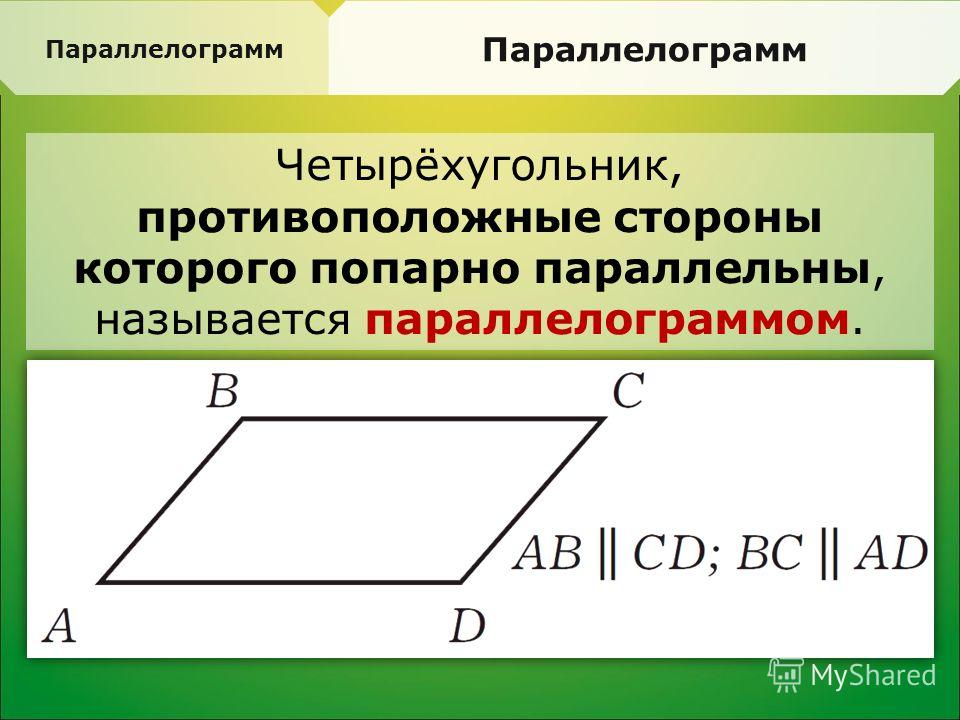
 Тогда из определения параллелограмма следует, что AB || CD, BC || AD.
Тогда из определения параллелограмма следует, что AB || CD, BC || AD.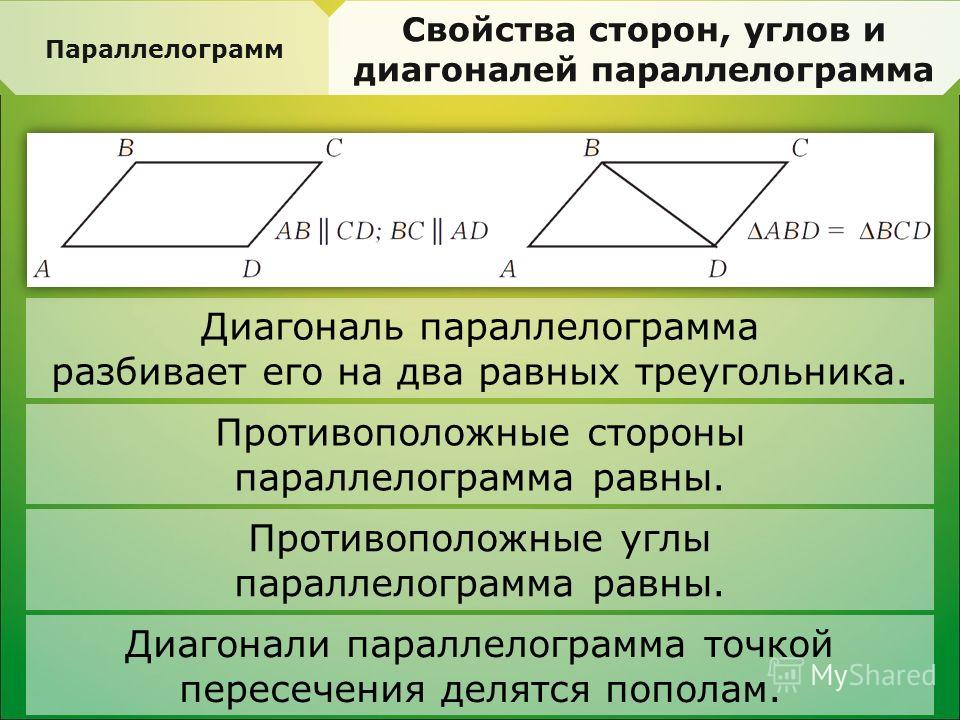 Так как параллелограмм — это выпуклый четырехугольник, то любая из них делит его на два треугольника. Рассмотрим в параллелограмме ABCD треугольники ABC и ADC, полученные в результате проведения диагонали AC.
Так как параллелограмм — это выпуклый четырехугольник, то любая из них делит его на два треугольника. Рассмотрим в параллелограмме ABCD треугольники ABC и ADC, полученные в результате проведения диагонали AC. Пусть дан параллелограмм ABCD, его диагонали AC и BD пересекаются в точке E. Рассмотрим образованные ими треугольники ABE и CDE.
Пусть дан параллелограмм ABCD, его диагонали AC и BD пересекаются в точке E. Рассмотрим образованные ими треугольники ABE и CDE. Он имеет две пары параллельных сторон (стороны, которые никогда не пересекаются) и четыре ребра. Противоположные стороны параллелограмма имеют одинаковую длину (равнодлинны). Слово «параллелограмм» происходит от греческого слова «parallelogrammon» ( , ограниченное параллельными линиями ). Прямоугольники, ромбы и квадраты являются параллелограммами.
Он имеет две пары параллельных сторон (стороны, которые никогда не пересекаются) и четыре ребра. Противоположные стороны параллелограмма имеют одинаковую длину (равнодлинны). Слово «параллелограмм» происходит от греческого слова «parallelogrammon» ( , ограниченное параллельными линиями ). Прямоугольники, ромбы и квадраты являются параллелограммами. (Это закон параллелограмма)
(Это закон параллелограмма) } {\ displaystyle BE = DE.} Во всех параллелограммах противоположные углы равны друг другу. Углы, не противоположные в параллелограмме, в сумме дают 180 градусов.
} {\ displaystyle BE = DE.} Во всех параллелограммах противоположные углы равны друг другу. Углы, не противоположные в параллелограмме, в сумме дают 180 градусов.