Упростить выражение 5 класс правило: Упрощение выражений — урок. Математика, 5 класс.

Упрощение выражений

Одно из самых распространенных заданий в алгебре звучит так: «Упростите выражение». Сделать это можно используя один из ниже перечисленных приемов, но чаще всего тебе потребуется их комбинация.

Приведение подобных слагаемых.

Это самый простой из приемов. Подобными называются те слагаемые, у которых одинаковая буквенная часть. Например, подобными будут выражения 5а и -6а; -3ху и 3ух; 2 и 10. Так вот. Складывать можно только подобные слагаемые; если буквенная часть у слагаемых различна, то такие слагаемые складывать уже нельзя. Согласись, если в жизни мы будем складывать яблоки с гвоздями, то у нас какая-то дичь получится) В математике точно так же.

Для примера упростим такое выражение:

Подобные слагаемые я выделю разными цветами и посчитаю. Кстати, знак перед слагаемым относится к этому слагаемому.

Как видишь, больше одинаковых буквенных частей нет. Выражение упрощено.

Умножение одночленов и многочленов.

Не буду спорить — числа ты умножать умеешь. А если к ним добавятся буквы, степени, скобки?

Одночлен — это выражение, состоящее из произведения чисел, букв, степеней, причем необязательно должно быть всё сразу. Удивительно, но просто число 5 тоже является одночленом, так же как и одинокая переменная х.

При умножении одночленов используют правила умножения степеней.

Перемножим три одночлена:

Разными цветами выделю то, что буду последовательно перемножать.

Многочлен — это сумма одночленов.

Чтобы умножить одночлен на многочлен выражение за скобками умножить на каждое слагаемое в скобках. Подробности в следующем примере.

Осталось вспомнить умножение многочлена на многочлен. При таком вот умножении надо каждое слагаемое в первых скобках умножить на каждое слагаемое во вторых скобках, результаты сложить или вычесть в зависимости от знаков слагаемых.

Вынесение общего множителя за скобки.

Разбираться будем на примере.

Дано такое выражение:

Что общего у этих двух слагаемых? Правильно, в них обоих присутствует множитель x. Он и будет являться общим множителем, который надо вынести за скобку.

Возьмем другой пример.

Оба числа в слагаемых делятся на 2, значит число 2 — общий множитель. Но еще в этих одночленах есть одинаковая буква а — одна в первой степени, другая — во второй. Берем ее в меньшей степени, т.е. в первой, — это и будет второй общий множитель. В общем, получится вот такая запись:

Ну и давайте третий пример, только уже без комментариев.

Проверить правильность вынесения общего множителя за скобки можно путем раскрытия скобок (умножением).

Разложение многочлена на множители способом группировки.

Если надо разложить многочлен на множители, то способ группировки тебе пригодится.

Сгруппировать выражения можно лишь путем вынесения общих множителей за скобку. Но сделать это нужно так, чтобы скобки в итоге получились одинаковые. Зачем? Да затем, чтобы потом эти скобки вынести за другие скобки. 

На примере будет яснее)

Беру пример самый простой, чисто для понимания того, что надо делать.

В первых двух слагаемых общим множителем является переменная а: выносим ее за скобку. Во вторых двух слагаемых общим множителем является число 6. Его тоже выносим за скобки.

Видишь получились две одинаковые скобки? Теперь они являются общим множителем. Выносим их за скобку и получаем милое произведение двух скобок:

Разложение квадратного трехчлена на множители.

Пусть дан квадратный трехчлен:

Чтобы разложить его на множители надо решить квадратное уравнение

Далее корни уравнения х₁ и х₂ подставить в следующую формулу:

Пробуем.

Возьмем вот такой трехчлен:

Найдем корни квадратного уравнения.

Подставим их в формулу для разложения квадратного трехчлена на множители:

Что-то слишком много минусов во второй скобке. Чуть-чуть преобразуем ее:

Теперь замечательно)

 

Еще могут тебе пригодится:

— умения работать с обыкновенными дробями;

— умение сокращать дроби;

— знание формул сокращенного умножения.

 

А вот такие задания могут тебе встретится на экзамене.

1) Упростить:

Решение тут.

2) Найти значение выражения при заданных значениях переменных:

Решение тут.

3) Найти значение выражения при заданных значениях переменных:

Решение тут.

Подобных заданий много — их все не уместишь)

 

Остались вопросы? Напиши мне!

Твой персональный преподаватель.

Упрощение выражений в 4 и 5 классе

Представьте, что у вас нет калькулятора, и нужно найти значение вот такого выражения:
500 + 399∙242 – (788 — 402∙260)

Для вычисления такого рода выражений существуют специальные приёмы, которые мы рассмотрим вначале на простых примерах, а потом на сложных.

1. Раскрытие скобок

Если перед скобкой стоит знак плюс, то скобки можно просто убрать

2 + 8 + (5 — 4) = 2 + 8 + 5 — 4

Если перед скобкой стоит знак минус, то при раскрытии скобок знаки в скобках заменяются на противоположные — минус меняется на плюс, а плюс (или отсутствие знака, если число стоит первым в скобках) — на минус.

2 + 8 — (10 — 4 + 3) = 2 + 8 — 10 + 4 — 3

Проверим, что левая и правая части равны. Выражение в скобках (10 — 4 + 3) в левой части равно 9.

2 + 8 — 9 = 1

Выражение в правой части тоже равно 1

Таким образом, правило, что в случае минуса перед скобкой знаки внутри скобок меняются на противоположные, работает верно.

Хотите, чтобы ваш ребёнок обучался самостоятельно?
Вам поможет наш ВИДЕОКУРС

2. Раскрытие скобок с множителем перед ними.

Если перед скобкой есть множитель, то перед раскрытием скобок надо или вычислить выражение в скобках и умножить его на множитель, или множитель умножить на каждый элемент в скобках.

Пример:

12 + 3∙(15 — 2 + 6) = 12 + 3∙19 = 12 + 57 = 69

Или же выражение мы можем записать так:

12 + 3∙15 — 3∙2 + 3∙6 = 12 + 45 — 6 + 18 = 69

Мы получили тот же результат — 69, что и в первом случае.

Если перед скобками стоит минус и у скобок есть множитель, то правило, что при раскрытии скобок знаки внутри скобок меняются на противоположные, сохраняется.

Пример:

160 — 4∙(20 — 5 — 3) = 160 — 4∙20 + 4∙5 + 4∙3 = 160 — 80 + 20 + 12 = 112

Если мы вначале посчитаем выражение в скобках, а потом умножим его на множитель перед скобками, то получим
тот же результат:

160 — 4∙(20 — 5 — 3) = 160 — 4∙12 = 160 — 48 = 112

3. Раскрытие скобок с делимым перед ними.

Если делить стоит перед скобками, то вначале надо вычислить выражение
в скобках, и только после этого поделить делимое на выражение в скобках.

Пример:

2 + 20:(3+2) = 2 + 20:5 = 2 + 4 = 6

4. Раскрытие скобок с делителем после них

Если делитель стоит после скобок, то можно или вначале вычислить выражение в скобках, а потом поделить его на делитель, или каждый элемент в скобках поделить на делитель

Пример:

15 + (30 + 18):6 = 15 + 48:6 = 15 + 8 = 23

или

15 + (30 + 18):6 = 15 + 30:6 + 18:6 = 15 + 5 + 3 = 23

5. Вынесение общего множителя за скобки
5∙6 + 5∙4 = 30 + 20 = 50

или

5∙6 + 5∙4 = 5∙(6 + 4) = 5∙10 = 50

6. Вынесение общего делителя за скобки

25:5 + 35:5 = 5 + 7 = 12
или
(25 + 35):5 = 60:5 = 12

7. Представление одного числа в виде суммы или разности других чисел

13∙11 + 12∙2

Можно решить напрямую, вычислив два произведения:

13∙11 + 12∙2 = 143 + 24 = 167

или представим 12 как 13-1

13∙11 + (13 – 1)∙2 = 13∙11 + 13∙2 – 2 = 13 (11 + 2) – 2 = 13∙13 – 2 = 169 — 2 = 167

другой пример:

16∙20 + 22∙17

Представим 22 как 20 + 2

16∙20 + 17∙(20 + 2) = 16∙20 + 17∙20 + 17∙2

Вынесем 20 за скобки:

16∙20 + 17∙20 + 17∙2 = 20∙(16 + 17) + 34 = 20∙33 + 34 = 660 + 34 = 694

8. Разложение числа на множители

12∙14 + 18∙6 = 168 + 108 = 276

или представим 18 как 9∙2

12∙14 + 9∙2∙6 = 12∙14 + 9∙12 = 12(14 + 9) = 12∙23 = 276

ВИДЕОКУРС 2plus2.online по решению олимпиадных задач по математике для 4 класса и задач из вступительных экзаменов в 5-й класс физматшколы.

1. 4875∙7 + 4875∙3 = 4875∙(7 + 3) = 4875∙10 = 48750

2. 952:17 — 442:17 = (952 — 442):17 = 510:17 = 30

3. 589∙23 + 589∙27 — 589∙40 = 589(23 + 27 — 40) = 589∙10 = 5890

4. 153∙241 — 199∙41 + 200 + 241∙46 = 241(153 + 46) + 200 — 199∙41 = 241∙199 + 200 — 199∙41 =
199(241 — 41) + 200 = 199∙200 + 200 = 200∙(199 + 1) = 200∙200 = 40000

5. 265∙222 — 360∙180 — 85∙260 + 138∙265

= 265(222 + 138) — 360∙180 — 85∙260 =
265∙360 — 360∙180 — 85∙260 =
360(265 — 180) — 85∙260 = 360∙85 — 85∙260 = 85(360 — 260) = 85∙100=8500

6. 384∙17 + 385∙19 + 386∙14 = 384∙17 + (384 + 1)∙19 + (384 + 2)∙14 =
384∙17 + 384∙19 + 19 + 384∙14 + 2∙14 =
384(17 + 19 + 14) + 19+ 28 = 384∙50 + 47 = 19200 + 47 = 19247

7.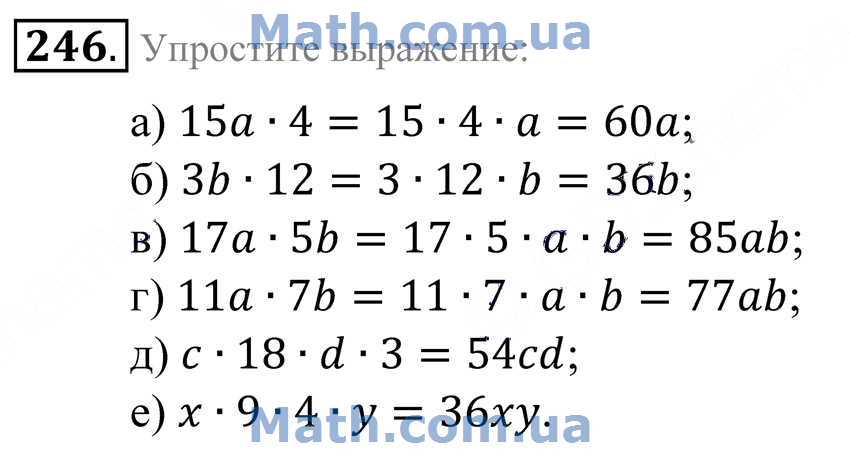 576∙242 + 121∙108 — 210∙711 = 576∙242 + 121∙2∙54 — 210∙711 =
576∙242 + 242∙54 — 210∙711 = 242(576 + 54) — 210∙711 =
242∙630-210∙711 = 242∙630 — 210∙3∙237 = 242∙630 — 630∙237=
630(242 — 237) = 630∙5 = 3150

8. То самое выражение из начала нашего урока

500 + 399∙242 – (788 — 402∙260) = 500 + 399∙242 – 788 + 402∙260 =
500 + 399∙242 — 2∙394 + (399 + 3)∙260 =
500 + 399∙242 — 2∙(399 – 5) + 399∙260 + 260∙3 =

500 + 399∙242 — 2∙399 + 10 + 399∙260 + 260∙3 =
500 + 399∙(242 – 2 + 260) + 10 + 780 =
500 + 399∙500 + 790 = 500(1 + 399) + 790 = 500∙400 + 790 = 20790

Упрощение выражений (примеры, методы + определение)

Упрощение выражений и набор навыков, необходимых для точного упрощения выражений, являются важными строительными блоками в алгебре. На занятиях по алгебре и более продвинутой математике вы будете использовать эти правила и приемы, поэтому овладение ключевыми этапами упрощения выражений даст вам преимущество в дальнейшем.

В этой статье мы рассмотрим основы PEMDAS и обновим различные алгебраические свойства, которые пригодятся при упрощении выражений. У вас будет возможность попробовать разные задачи, чтобы проверить свое понимание. К концу нашего обсуждения вы почувствуете себя уверенно, чтобы работать над более сложными выражениями!

Каковы этапы упрощения выражений?

При упрощении выражений группируйте соответствующие термины вместе и применяйте правила работы в правильном порядке. Написание окончательного и упрощенного выражения в его стандартной форме — это последний важный шаг. Это означает, что существуют разные подходы к упрощению выражений, но вот несколько шагов, которые помогут вам:

Шаг 1 :   Удалите скобки и квадратные скобки, оценивая, распределяя и комбинируя термины внутри них.

Шаг 2 :   Перепишите термины так, чтобы они имели одинаковую форму, поэтому оценивайте термины с показателями степени и переписывайте смешанные числа в дроби.

Шаг 3 :   Умножение и деление терминов при необходимости и при наличии этих операций.

Шаг 4 :   Сложите и вычтите термины слева направо, чтобы объединить похожие термины.

Шаг 5 :   Когда вы больше не можете комбинировать термины, остановитесь и перепишите окончательное выражение в стандартной форме.

Эти шаги кажутся вам знакомыми? Потому что вы уже встречались с некоторыми из этих правил в форме правила PEMDAS. Напомним, что PEMDAS — это арифметическое правило, которое означает: P арентез, E экспонент, M умножение, D видение, A сложение и S 90 вычитание. Это общее правило, которому следует следовать при выполнении ряда арифметических операций.

Применение правил PEMDAS в арифметических операциях 92\,\,\color{DarkGreen}\text{скобки}\\&= 5\times 4 + 3\times 3 — {\color{DarkGreen}9}\,\,\color{DarkGreen}\text {Показатель степени}\\&={\color{DarkGreen}20} + {\color{DarkGreen}9} — 9\,\,\color{DarkGreen}\text{Multiplication}\\&= {\color{DarkGreen} }29} — 9\,\,\color{DarkGreen}\text{Сложение и вычитание}\\&=20\end{aligned}

Посмотрите, как выражение, показанное выше, вычисляется и упрощается. чтобы еще лучше оценить правило PEMDAS. Помимо внимательного следования PEMDAS при упрощении выражений, важно научиться определять похожие термины. Напомним, что 92

Подобные термины должны иметь как переменную, так и мощность. Важно, чтобы оба эти условия были соблюдены при объединении подобных терминов. Это очень важно при упрощении алгебраических выражений, поэтому давайте покажем вам пример того, как эти правила применяются к алгебраическим терминам.

Применение правил PEMDAS с алгебраическими терминами ,\color{DarkOrange}\text{скобки}\\&= {\color{DarkOrange}(3mn — 8mn)} + {\color{DarkOrange}(-2n + 6n)}\,\,\color{ DarkOrange}\text{Групповые термины}\\&={\color{DarkOrange}-5mn} + {\color{DarkOrange}4n}\,\,\color{DarkOrange}\text{Сложение и вычитание}\\& = 4n — 5mn\end{выровнено} 92, что нужно сделать в первую очередь? A. Перепишите 4 2 в целое число, 16. B. Сгруппируйте все похожие термины, проверив переменную и общую мощность. 2 сгруппированные члены заключены в круглые скобки с постоянным коэффициентом 3.  Это означает, что при упрощении данного алгебраического выражения необходимо сначала удалить скобки. Следовательно, первый шаг состоит в том, чтобы распределить по 3 на каждый член в скобках, чтобы D был правильным ответом . Задача 2 Определите, являются ли каждая пара терминов похожими терминами или разными терминами. а. 12mn, 10mn При определении того, являются ли два термина похожими или нет, проверьте переменные и мощность этих переменных для каждого из этих терминов. Term Variable Power 12mn m n 1 1 10mn m n 1 1 Отсюда видно, что оба термина имеют одни и те же переменные, и каждая переменная имеет одинаковую мощность. Следовательно, два термина подобны терминам 92	x	y
1	2

Взглянув на таблицу, легко увидеть, что обе они имеют одни и те же переменные. Однако каждая переменная не имеет одной и той же мощности. Помните, что для того, чтобы два термина были одинаковыми, каждая из переменных должна иметь одинаковую мощность. Следовательно, два терма отличаются от термов .

После упрощения выражения и получения непохожих терминов это признак того, что вы подошли к концу процесса. Дополнительным шагом может быть переписывание результирующего выражения в стандартной форме, если таковая имеется, чтобы упростить проверку или просмотр в дальнейшем.

К этому моменту вы, вероятно, встречали термины распределение, дроби и даже показатели степени в ходе обсуждения. Это потому, что процесс упрощения выражений использует широкий спектр правил и свойств, которые вы узнали в прошлом. В зависимости от сложности выражения, которое необходимо упростить, вам необходимо убедиться, что вам удобно использовать эти правила.

Что такое дополнительные правила упрощения выражений?

Существуют дополнительные правила, которые помогут вам упростить выражения, и некоторые из них:

• Правильный способ сложения и вычитания одинаковых членов с использованием их коэффициентов.
• Точное применение распределительного свойства.

\begin{align}k(a + b) &= k\cdot a + k\cdot b\\k(a — b) &= k\cdot a — k\cdot b\end{align}

• При умножении отрицательного коэффициента следите за тем, чтобы знаки слагаемых также менялись.
• Обеспечьте правильное применение правил экспоненты.

Помните об этих указателях при упрощении выражений. В этом разделе будут показаны различные примеры применения этих правил. А пока быстро освежите в памяти, как объединять одинаковые термины, добавляя или вычитая их коэффициенты. 92г.

б. 12ab + 3mn – 6ab + 2mn

 Когда вас просят упростить термины с тремя или более терминами, всегда сначала группируйте похожие термины.

\begin{выровнено}{\color{DarkBlue}12ab} + {\color{DarkBlue}3mn} {\color{DarkBlue}-6ab} + {\color{DarkRed}2mn}&= {\color{DarkBlue}(12ab — 6ab)} + {\color{DarkRed}(3mn + 2mn)} \end{выровнено}

Теперь, когда похожие термины сгруппированы вместе, упростите каждую группу терминов, применяя тот же процесс. Сосредоточьтесь на коэффициентах для каждой пары подобных терминов при их упрощении.

\begin{align}{\color{DarkBlue}(12ab — 6ab)} + {\color{DarkRed}(3mn + 2mn)} &= {\color{DarkBlue}(12 — 6)ab} + {\color{ DarkRed}(3 +2)mn}\\&= 6ab + 5mn\end{выровнено}

Поскольку результирующие члены больше не используют одни и те же переменные и степени, нет необходимости дополнительно упрощать выражение. Следовательно, упрощенная форма 12ab + 3mn – 6ab + 2mn равна 6ab + 5mn.

Упрощение выражений с помощью распределительного свойства

Упрощение выражений с помощью распределительного свойства обычно является первым шагом, который вы делаете, когда выражение содержит коэффициенты перед квадратными или круглыми скобками. При распределении коэффициента или множителя в скобках умножьте каждое слагаемое внутри скобок на коэффициент.

\begin{align}k(a + b) &= k\cdot a + k\cdot b\\k(a — b) &= k\cdot a — k\cdot b\end{align}

Если коэффициент отрицательный, учтите его отрицательный знак и обязательно измените знаки членов в скобках. После распределения любых существующих факторов удалите скобки, заключающие каждый термин.

\begin{align}4(3x + 2y) &={\color{Orchid}4}(3x) +{\color{Orchid}4}(2y)\\&=12x +8y\\\\-2( 5a — b) &={\color{Орхидея}-2}(5a) +{\color{Орхидея}-2}(-b)\\&=-10a + 2b\end{выровнено}

Теперь, когда вы быстро вспомнили, как применять свойство распределения, почему бы вам не попробовать упростить выражение, показанное ниже?

Задача 4

Упростите следующее выражение 2(x – m) + 4(x + m), используя другие изученные вами правила.

При работе с выражениями с одной или двумя скобками сначала удалите их. Когда вы видите перед скобками коэффициенты, такие как 2 и 4, примените распределительное свойство.

\begin{align}2(x – m) + 4(x + m)&={\color{Orchid}2}(x) -{\color{Orchid}2}(m) +{\color{бирюзовый} 4}(x) +{\color{бирюзовый}4}(m)\\&= 2x — 2m + 4x + 4m\end{выровнено}

При осмотре мы все же можем сказать, что есть похожие термины, которые все еще можно комбинировать. Сгруппируйте похожие термины и оцените их, чтобы еще больше упростить выражение.

\begin{align}2x — 2 м + 4x + 4 м &= {\color{Орхидея}(4 м — 2 м)} + {\color{Бирюзовый} (2x +4x)}\\&={\color{Орхидея}( 4-2)} m + {\ color {бирюзовый} (2 + 4)} x \\ & = 2m + 6x \ end {выровнено}

Применяя правильные свойства и правила, 2(x – m) + 4(x + m) было упрощено до 2m + 6x.

Упрощение выражений с помощью показателей  92.

Эти примеры показали, что, применяя правильные свойства и алгебраическое правило в правильном порядке, упрощение выражений не будет таким пугающим. Применяя системный подход, вы избегаете серьезных арифметических ошибок. Просматривайте эту статью всякий раз, когда вам нужно, и снова тренируйтесь с задачами, если хотите!

примеров упрощения выражений | Физика Валлах

Показатели используются во многих задачах по алгебре, поэтому важно понимать правила работы с показателями. Давайте подробно рассмотрим каждое правило и рассмотрим несколько примеров.

ПРАВИЛА 1:

Есть два простых «правила 1», которые нужно запомнить.

Во-первых, любое число, возведенное в степень «единицы», равно самому себе. Это имеет смысл, потому что степень показывает, во сколько раз основание умножается само на себя. Если он умножается только один раз, то логично, что он равен самому себе.

Во-вторых, возведённый в любую степень — это единица. Это тоже логично, потому что один раз один раз один, столько раз, сколько вы его умножаете, всегда равно единице.

х1 = х

31 = 3

1м = 1

14 = 1 ⋅ 1 ⋅ 1 ⋅ 1

= 1

ПРАВИЛО ПРОДУКТА:

Экспоненциальное «правило произведения» говорит нам, что при умножении двух степеней, имеющих одно и то же основание, вы можете складывать показатели степени. В этом примере вы можете увидеть, как это работает. Добавление показателей — это всего лишь короткий путь!

хм⋅ хп = хм + п

42⋅ 43 = 4 ⋅ 4 ⋅ 4 ⋅ 4 ⋅ 4

42 + 3 = 45

ПРАВИЛО СИЛЫ:

«Правило степени» говорит нам, что для возведения степени в степень нужно просто умножить показатели степени. Здесь вы видите, что 52, возведенное в третью степень, равно 56.

хмн = хмн

(52)3 = 52 × 3 = 56

ЧАСТНОЕ ПРАВИЛО:

Правило частного говорит нам, что мы можем разделить две степени с одним и тем же основанием, вычитая показатели степени. Вы можете понять, почему это работает, если изучите показанный пример.

xm÷ xn = xm – n

х ≠ 0

45÷ 42 =

45 – 2 = 43

НУЛЕВОЕ ПРАВИЛО:

Согласно «правилу нуля» любое ненулевое число, возведенное в нулевую степень, равно 1.

хо = 1

х ≠ 0

ОТРИЦАТЕЛЬНЫЕ ПОКАЗАТЕЛИ:

Последнее правило в этом уроке говорит нам, что любое ненулевое число, возведенное в отрицательную степень, равно его обратному числу, возведенному в противоположную положительную степень.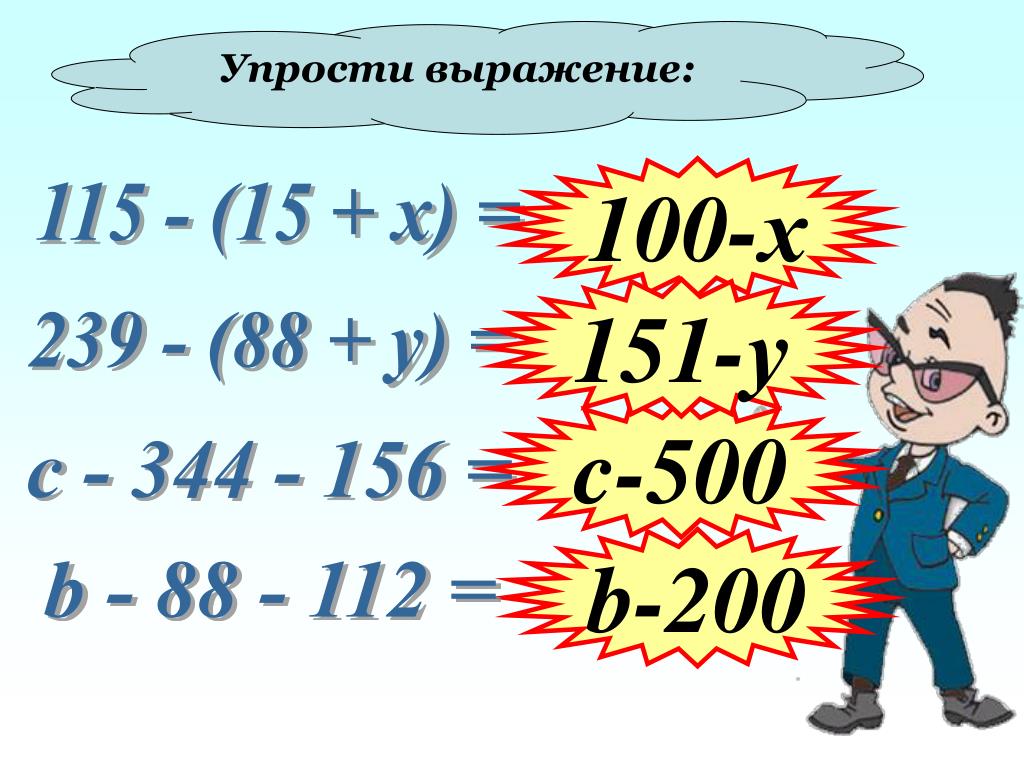

например Упростить (x3)(x4)

Чтобы упростить это, я могу думать с точки зрения того, что означают эти показатели. «К третьему» означает «умножение трех копий», а «к четвертому» означает «умножение четырех копий». Используя этот факт, я могу «расширить» два фактора, а затем вернуться к упрощенной форме:

(х3)(х4)= (ххх)(хххх)

= хххххх 
= x7

Обратите внимание, что x7 также равно x(3+4). Это демонстрирует первое основное правило экспоненты: всякий раз, когда вы умножаете два термина с одним и тем же основанием, вы можете складывать экспоненты:

( х м ) ( х н ) = х ( м + п )

Однако мы НЕ МОЖЕМ упростить (x4)(y3), потому что основания разные: (x4)(y3) = xxxxyyy = (x4)(y3). Ничего не совмещает.

вопрос 1. Упростить (x2)4

Решение: Как и в предыдущем упражнении, я могу думать о том, что означают показатели степени. «В четвертый» означает, что я умножаю четыре копии x2:

(x2)4 =(x2)(x2)(x2)(x2) 
=(хх)(хх)(хх)(хх)
= ххххххх 
= x8

Обратите внимание, что x8 также равно x( 2×4 ). Это демонстрирует второе правило экспоненты: Всякий раз, когда у вас есть выражение экспоненты, возведенное в степень, вы можете умножить экспоненту и степень:

( xm ) n = x m n

Если у вас есть продукт внутри круглых скобок и мощность в скобках, то мощность распространяется на каждый элемент внутри. Например, (xy2)3 = (xy2)(xy2)(xy2) = (xxx)(y2y2y2) = (xxx)(yyyyyy) = x3y6 = (x)3(y2)3. Другой пример:

вопрос 2. Упростить [(3x4y7z12)5 (–5x9y3z4)2]0

Все, что находится в нулевой степени, равно 1.

Решение: Нулевая мощность снаружи означает, что стоимость всего этого всего 1.

вопрос 3. Оценить 2×3 – x2 + y для x = –3, y = 2.

Решение: 2×3 – x2 + y = 2 (–3)3 – (–3)2 + 2 Замените каждый x на –3, каждый y на 2.

= 2 (–27) – (9) + 2 Выполните указанные операции.

= –54 – 9 + 2

= –61

вопрос 4. Оценить x2 – x3y + 6 для x = 2, y = 9

Сол. x2 – x3y + 6 = (2)2 – (2)3⋅ (9) + 6 Поместите значения в скобки

= 4 – 8 ⋅ 9 + 6 Выполнить операции с показателями степени

= 4 – 72 + 6 Умножить

= –62

вопрос5 . Чтобы проиллюстрировать важность заключения подставляемых значений в круглые скобки, давайте оценим 2×3 – x2 + y для x = –3, y = 2 без использования круглых скобок:

2×3 – x2 + у = 2 – 33 – 32 + 2

Решение: В полученном выражении справа сложно уследить за отрицательными знаками и указанными операциями. Легко увидеть, как могут возникать ошибки без круглых скобок.

НРАВИТСЯ УСЛОВИЯ:

Подобные термины — это термины, которые содержат одни и те же переменные, возведенные в одну и ту же степень. Отличаются только числовые коэффициенты. В выражении могут сочетаться только одинаковые термины. Мы объединяем одинаковые термины, чтобы сократить и упростить алгебраические выражения, чтобы нам было легче с ними работать. Чтобы объединить одинаковые термины, мы добавляем коэффициенты и оставляем переменные одинаковыми. Мы не можем объединять разные термины, потому что это все равно, что пытаться сложить яблоки и апельсины!

Посмотрите на эти 10 терминов. Найдем все подобные термины, которые можно комбинировать.

3 x2y 2x2y2 –2xy2

4xy2 –7x2yz

–8x2y –5xy2z

–8x2y 3x2y	все эти термины имеют x2y
	все эти термины имеют xy2
–7x2yz	это единственный термин x2yz
	это единственный термин xy
2x2y2 7x2y2	все эти термины имеют x2y2
–5x2z	это единственный термин xy2z

Будьте осторожны при комбинировании!

Такие термины, как x2yz и xy2z , очень похожи, но они не являются и не могут быть объединены. Внимательно пишите термины при решении задач.

Не упускайте из виду похожие термины!

Термины подчиняются ассоциативному свойству умножения, то есть xy и yx похожи на термины, как и xy2 и y2x.

ОБЪЕДИНИТЕ ПОДОБНЫЕ УСЛОВИЯ:

вопрос 1. 5x – 2г + 3x – 7г

= 8x – 2y – 7y Объедините члены с переменной x.

= 8x – 9y Объедините члены с переменной y

вопрос 2. 8x3y2 + 3×3 – 7x2y3 + 9x3y2

= (8 + 9)x3y2 + 3×3 – 7x2y3 Объедините члены с переменными x3y2.

= 17x3y2 + 3×3 – 7x2y3 Все одинаковые члены объединены

УПРОЩЕНИЕ

Прежде чем вычислять алгебраическое выражение, его необходимо упростить. Это значительно упростит все ваши расчеты. Вот основные шаги для упрощения алгебраического выражения:

• удалить круглые скобки, умножив коэффициенты
• использовать правила экспоненты для удаления круглых скобок в терминах с экспонентами
• объединять одинаковые термины, добавляя коэффициенты
• объединить константы

Давайте поработаем на примере.

5(2 + х) + 3(5х + 4) – (х2)2

При упрощении выражения первое, на что следует обратить внимание, — это возможность очистки скобок. Часто вы можете использовать распределительное свойство для очистки скобок, умножая множители на члены в скобках. В этом выражении мы можем использовать распределительное свойство, чтобы избавиться от первых двух наборов скобок.

= 10 + 5х + 15х + 12 – (х2)2

Теперь мы можем избавиться от круглых скобок в члене с показателями степени, используя ранее изученные правила построения степени. Когда член с показателем степени возводится в степень, мы умножаем показатели степени, поэтому (x2)2 становится x4.

= 10 + 5х + 15х + 12 – х4

Следующим шагом в упрощении является поиск похожих терминов и их объединение. Термины 5x и 15x подобны терминам, потому что они имеют одну и ту же переменную, возведенную в одну и ту же степень, а именно, в первую степень, поскольку показатель степени равен 1. Мы можем объединить эти два термина, чтобы получить 20x.

No related posts.