Тригонометрические функции, их свойства и графики. — Студопедия
Поделись
Все тригонометрические функции (синус, косинус, тангенс и котангенс) относятся к основным элементарным функциям. Сейчас мы рассмотрим их графики и перечислим свойства.
Тригонометрическим функциям присуще понятие периодичности (повторяемости значений функции при различных значениях аргумента, отличных друг от друга на величину периода , где Т — период), поэтому, в список свойств тригонометрических функций добавлен пункт «наименьший положительный период». Также для каждой тригонометрической функции мы укажем значения аргумента, при которых соответствующая функция обращается в ноль.
Теперь разберемся со всеми тригонометрическими функциями по-порядку.
Функция синус y = sin(x).Изобразим график функции синус, его называют «синусоида«.
Свойства функции синус y = sinx.
— Областью определения функции синус является все множество действительных чисел, то есть, функция y = sinx определена при .
— Наименьший положительный период функции синуса равен двум пи: .
— Функция обращается в ноль при , где , Z – множество целых чисел.
— Функция синус принимает значения из интервала от минус единицы до единицы включительно, то есть, ее область значений есть .
— Функция синус — нечетная, так как .
— Функция убывает при ,
возрастает при .
— Функция синус имеет локальные максимумы в точках ,
локальные минимумы в точках .
— Функция y = sinx вогнутая при ,
выпуклая при .
— Координаты точек перегиба .
— Асимптот нет.
Функция косинус y = cos(x).График функции косинус (его называют «косинусоида») имеет вид:
Свойства функции косинус y = cosx.
— Область определения функции косинус: .
— Наименьший положительный период функции y = cosx равен двум пи: .
— Функция обращается в ноль при , где рimg src=»https://www.
ok-t.ru/studopediaru/baza13/488088887583.files/image085.gif» /> , Z – множество целых чисел.
— Область значений функции косинус представляет интервал от минус единицы до единицы включительно: .
— Функция косинус — четная, так как .
— Функция убывает при ,
возрастает при .
— Функция y = cosx имеет локальные максимумы в точках ,
локальные минимумы в точках .
— Функция вогнутая при ,
выпуклая при .
— Координаты точек перегиба .
— Асимптот нет.
Функция тангенс y = tg(x).График функции тангенс (его называют «тангенсоида») имеет вид:
Свойства функции тангенс y = tgx.
— Область определения функции тангенс:
, где , Z – множество целых чисел.
Поведение функции y = tgx на границе области определения
Следовательно, прямые , где , являются вертикальными асимптотами.
— Наименьший положительный период функции тангенс .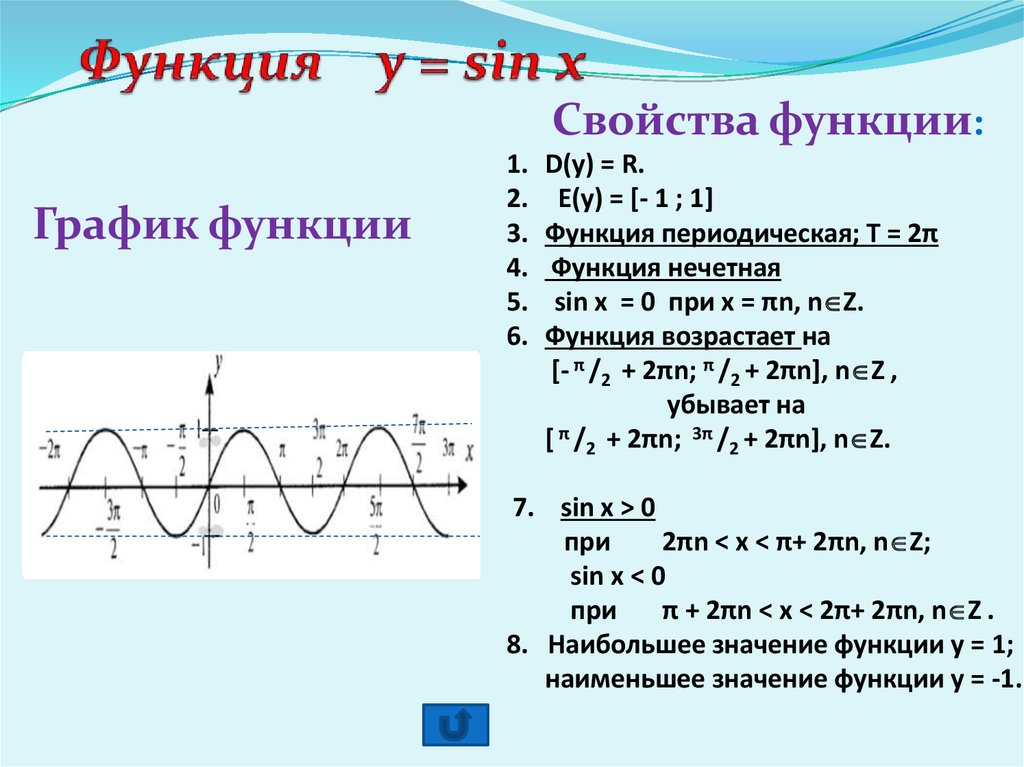
— Функция обращается в ноль при , где , Z – множество целых чисел.
— Область значений функции y = tgx: .
— Функция тангенс — нечетная, так как .
— Функция возрастает при .
— Функция вогнутая при ,
выпуклая при .
— Координаты точек перегиба .
— Наклонных и горизонтальных асимптот нет.
Функция котангенс y = ctg(x).Изобразим график функции котангенс (его называют «котангенсоида»):
Свойства функции котангенс y = ctgx.
— Область определения функции котангенс: , где , Z – множество целых чисел.
Поведение на границе области определения
Следовательно, прямые , где являются вертикальными асимптотами.
— Наименьший положительный период функции y = ctgx равен пи: .
— Функция обращается в ноль при , где , Z – множество целых чисел.
— Область значений функции котангенс: .
— Функция нечетная, так как .
— Функция y = ctgx убывает при .
— Функция котангенс вогнутая при ,
выпуклая при .
— Координаты точек перегиба .
— Наклонных и горизонтальных асимптот нет.
| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | sin(45 град. ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | csc(45 град. ) | ||
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | sin(120) | ||
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) | |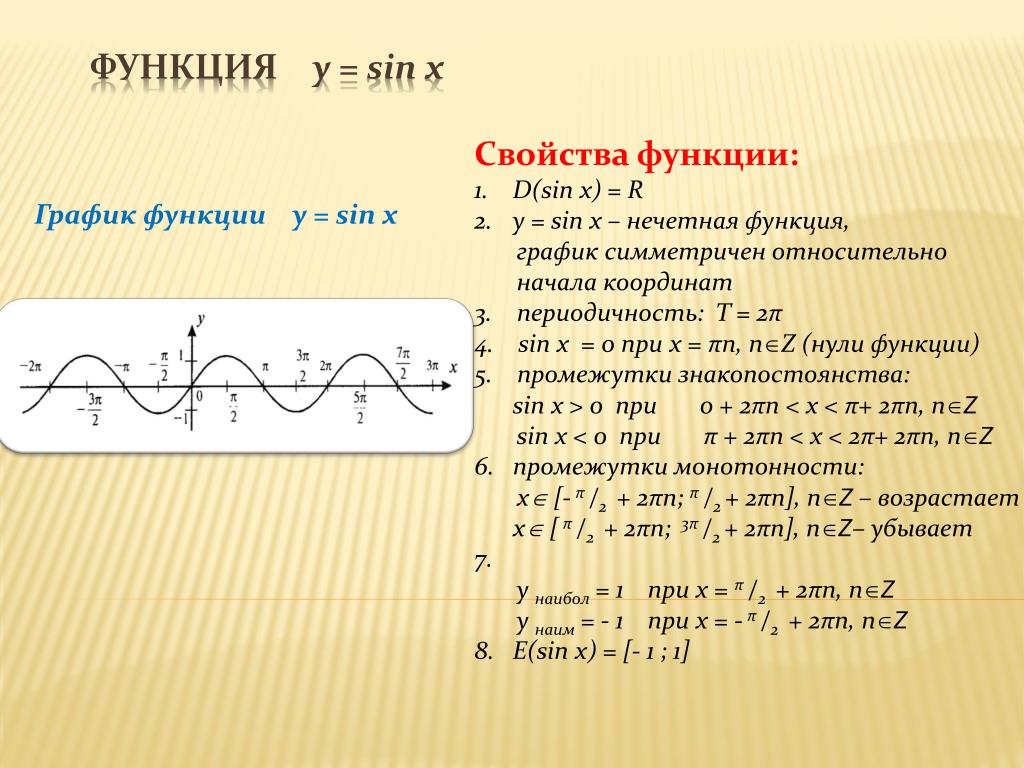
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) | |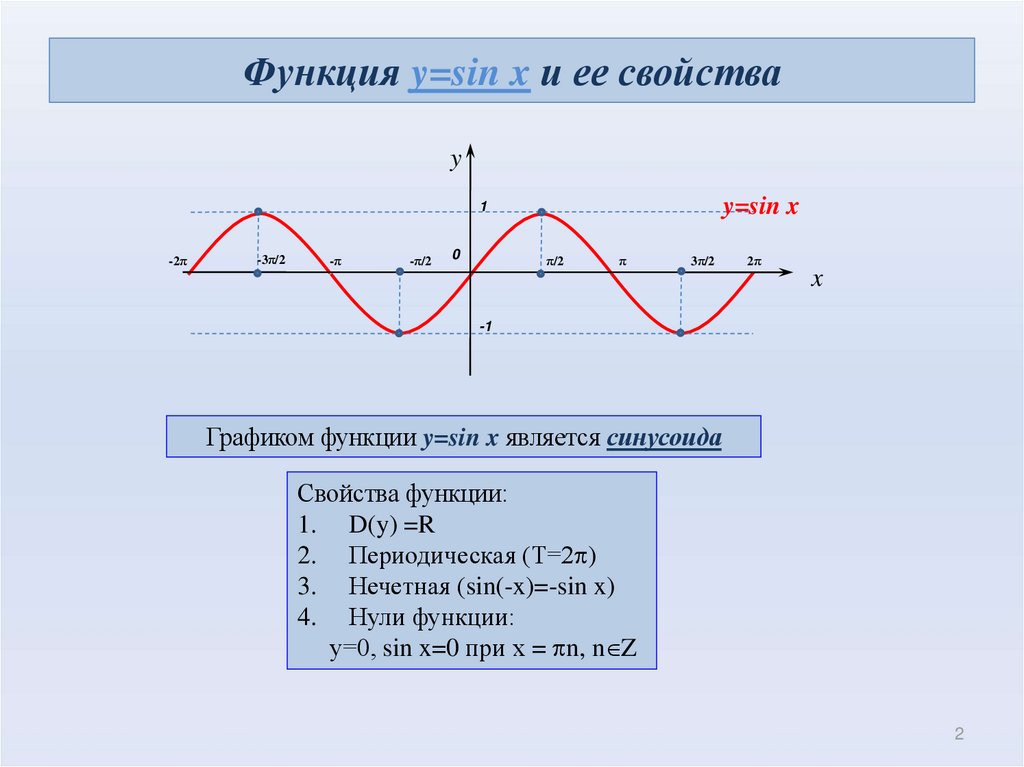
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
исчисление — Доказательство свойств синуса и косинуса из их определений ряда Тейлора
спросил
Изменено 5 лет, 2 месяца назад
Просмотрено 282 раза
$\begingroup$
Мне очень хотелось бы знать, есть ли у кого-нибудь строгий способ доказать, что функция $t \mapsto (\cos t, \sin t )$ дает параметризацию единичного круга на плоскости, взяв за отправную точку определение функций окружности с помощью их рядов Тейлора.
{2}t=1\tag{1}$$, а также то, что эти функции непрерывны/дифференцируемы со значениями $\cos 0=1,\sin 0=0$. Чтобы доказать периодичность этих функций с периодом $2\pi$, необходимо некоторое представление о $\pi$. 9{2}t$, то получаем $g'(t)=0$, так что $g(t)=g(0)=1$ и равенство $(1)$ доказано.
Чтобы ввести $\pi$, нам нужно немного поработать. Можно показать, что $\cos t$ меняет знак в $[0,2]$ и, следовательно, обращается в нуль где-то в этом интервале. Кроме того, производная $—\sin t$ сохраняет знак в $(0,2)$, откуда следует, что существует единственное число $\xi\in(0,2)$ такое, что $\cos \xi=0$ и мы определяем $\pi=2\xi$. Тогда легко доказывается, что $\sin(\pi/2)=1$.
Доказать периодичность немного сложно, и один из способов сделать это — установить формулы сложения. Это можно сделать, заметив, что оба $\cos t, \sin t$ являются решениями $f»(t) +f(t)=0$, а общее решение этого уравнения есть $f(t) = f( 0)\cos t+f'(0)\sin t$. Для доказательства общего решения рассмотрим функцию $$h(t) =f(t) — f(0)\cos t-f'(0)\sin t$$, тогда $h»(t) +h(t ) =0, h(0)=h'(0)=0$.
{2}$. Ясно, что $\phi'(t)=0$ и, следовательно, $\phi(t) =\phi(0)=0$ и, следовательно, $h(t) =h'(t)=0$. Это дает нам $f(t) =f(0)\cos t+f'(0)\sin t$.
Так как $\cos (a+t)$ также удовлетворяет уравнению $f»+f=0$, то из предыдущего следует, что $\cos (a+t) =\cos a \cos t-\sin a \sin t $ и аналогично можно установить формулу сложения для $\sin t $. Используя эти формулы сложения, мы можем показать, что $\cos(t+2\pi)=\cos t, \sin(t+2\pi)=\sin t$.
$\endgroup$
$\begingroup$
Начните с определения $\sin$ и $\cos$ как уникальных решений дифференциального уравнения $y» = -y$ с граничными условиями $y(0) = 0, y'(0) = 1$ и $y(0) = 1, y'(0) = 0$ соответственно. (Нетрудно показать, что такие функции существуют и единственны, и можно проверить, что обычные ряды Тейлора удовлетворяют уравнению.) Затем стандартные рассуждения о равномерной сходимости показывают, что $\sin$ и $\cos$ гладки на $\mathbb {Р} $.
1$; то есть $f$ онтотен и инъективен, за исключением того, что $f(0) = f(N)$.
Осталось только показать, что $N = 2\pi$. Это немного сложнее; это зависит от того, какое определение вы хотите использовать для $\pi$. Продолжая тему исчисления, давайте определим $\pi$ как половину окружности единичного круга. Тогда обычная формула для длины дуги дает $N = 2\pi$, так как $f'(t) = (-\sin t, \cos t)$ имеет $|f'(t)| = 1$ везде.
(Мы также не обсуждали формулы суммы углов. Их можно получить, переформулировав их в терминах экспоненциальной функции, определяемой как единственное решение дифференциального уравнения $y’ = y$ с граничным условием $y( 0) = 1$ Так как $y(t + t_0)/y(t_0)$ также является решением для любого $t_0$, мы должны $y(t + t’) = y(t)y(t’) $ для всех $t, t’$. Мы могли бы также работать с $\exp t$ в начале, но, похоже, это не то, к чему вы стремились.) 92 t = 1$ для всех $t$, тогда довольно легко показать, что для каждой точки на окружности существует $t$ с $(\cos t, \sin t)$ в качестве этой точки через промежуточное значение теорема.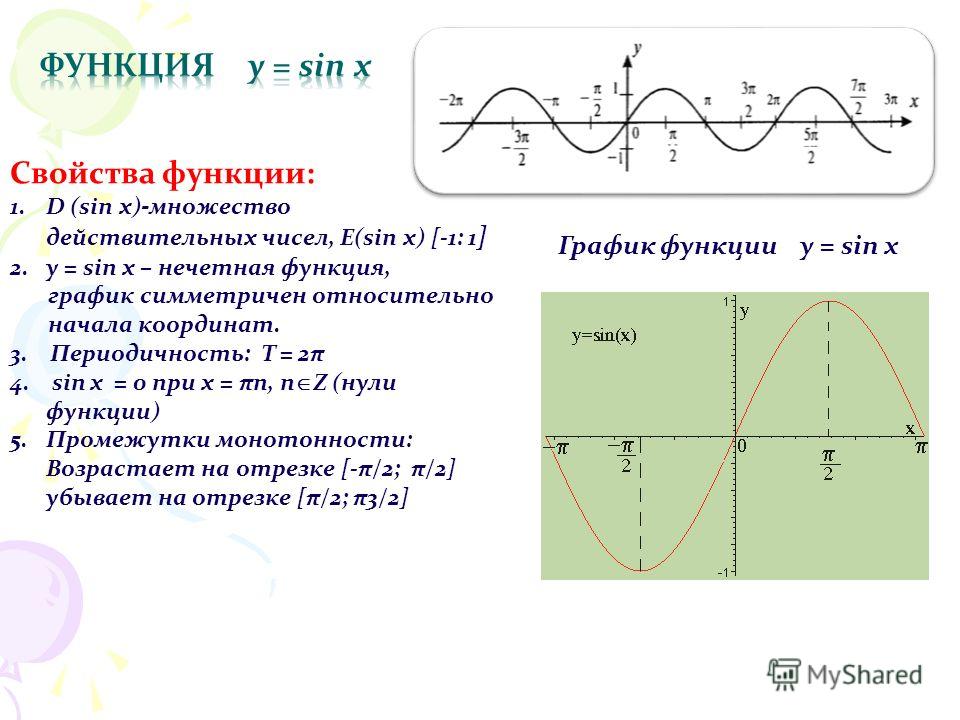
Это не тот подход, который вы искали, я знаю, но это хороший строгий способ получить синусы и косинусы, что может быть тем, что вы хотели, и он не требует сходимости степенных рядов и других подобных вещей.
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Обсуждать дискретное преобразование Фурье с точки зрения физических метафор, таких как «детекторы» и «бины», или даже статистических понятий, таких как корреляция, немного неискренне. В каком-то смысле этот стиль дискурса берет множество захватывающих математических соотношений и сводит их к набору конструкций, поддающихся мышлению по аналогии, но гораздо менее математически глубоких. 1 Вероятно, лучше признать, что синусоиды обладают рядом (иногда ошеломляющих) свойств, которые делают их особенно подходящими для использования в качестве баз системы координат . Я не хочу подробно исследовать системы координат и базы в этом учебнике, но я хотел бы предоставить вам некоторые связанные с ними визуализации, которые вы обычно не найдете в соответствующей литературе. Ортогональность является важным свойством базисных векторов системы координат. [1, 0, 0] Легко показать, что эти векторы ортогональны друг другу. Мы можем доказать это, выписав все скалярные произведения или просто заметив, что скалярное произведение между любым из двух векторов должно быть равно нулю, так как каждая 1 будет умножаться на 0. Немного более неожиданно можно показать, что любые две синусоидальные волны , частоты которых кратны друг другу, также ортогональны, независимо от их фаз . Это утверждение немного сложнее мысленно проверить. Вы можете принять это на веру или посмотреть несколько примеров, прежде чем копаться в доказательствах.
| 1. Это немного нелогично, поскольку я почти ничего не знаю о Дугласе Хофштадтере, но мне очень понравился его доклад под названием «Аналогия как ядро познания». | ||
Если мы возьмем две синусоидальные волны с одинаковой частотой и суммируем их вместе, результатом всегда будет синусоида с точной той же частотой. Это несколько любопытный результат, и он остается верным, даже если две синусоиды имеют совершенно разные фазы и амплитуды. Ни один другой периодический сигнал не обладает этим свойством . На рис. 2 показано суммирование двух синусоид с одинаковой частотой. Вы можете использовать ползунки для настройки фазы и амплитуды второй синусоиды. Обратите внимание, что частота суммирования всегда равна частоте двух входных синусоид.
Синусоидальные волны совершенно завораживают. Их особая природа делает их особенно подходящими для использования в качестве «атомарных» компонентов сложных сигналов. Я бы посоветовал вам поиграть с синусоидами и тригонометрическими тождествами. Успешная практика обработки сигналов требует некоторой интеллектуальной близости с синусоидальными волнами. |
Два вектора (сигнала) ортогональны друг другу, если их скалярное произведение равно нулю. Геометрически, когда два вектора ортогональны, они указывают друг на друга под прямым углом. натуральные основания — основания по умолчанию для декартовой системы — ортогональны друг другу. Если у нас есть трехмерная декартова система, три естественных базисных вектора: