|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов… Проблема типологии научных революций: Глобальные научные революции и типы научной рациональности… Комплексной системы оценки состояния охраны труда на производственном объекте (КСОТ-П): Цели и задачи Комплексной системы оценки состояния охраны труда и определению факторов рисков по охране труда… Интересное: Средства для ингаляционного наркоза: Наркоз наступает в результате вдыхания (ингаляции) средств, которое осуществляют или с помощью маски… Уполаживание и террасирование склонов: Если глубина оврага более 5 м необходимо устройство берм. Варианты использования оврагов для градостроительных целей. Наиболее распространенные виды рака: Раковая опухоль — это самостоятельное новообразование, которое может возникнуть и от повышенного давления… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
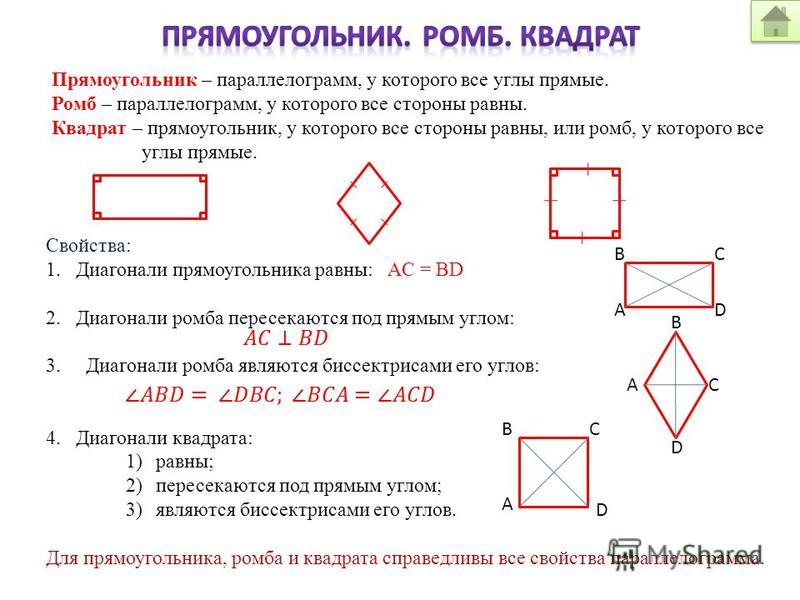
⇐ ПредыдущаяСтр 7 из 9Следующая ⇒ Напомним, что параллелограмм – это четырёхугольник, у которого противоположные стороны попарно параллельны. Рис. 1 Параллелограмм обладает целым рядом свойств: противоположные углы равны ( ), противоположные стороны равны ( ). Кроме того, диагонали параллелограмма в точке пересечения делятся пополам, сумма углов, прилежащих к любой стороне параллелограмма, равна и т.д. Но для того, чтобы пользоваться всеми этими свойствами, необходимо быть абсолютно уверенными в том, что рассматриваемый четырёхугольник – параллелограмм. Для этого и существуют признаки параллелограмма: то есть те факты, из которых можно сделать однозначный вывод, что четырёхугольник является параллелограммом. На предыдущем уроке мы уже рассмотрели два признака. Сейчас рассмотрим третий. Третий признак параллелограмма и его доказательство Если в четырёхугольнике диагонали в точке пересечения делятся пополам, то данный четырёхугольник является параллелограммом. Дано: – четырёхугольник; ; . Доказать: – параллелограмм. Доказательство: Для того чтобы доказать данный факт, необходимо доказать параллельность сторон параллелограмма. А параллельность прямых чаще всего доказывается через равенство внутренних накрест лежащих углов при этих прямых. Таким образом, напрашивается следующий способ доказательства третьего признака параллелограмма: через равенство треугольников . Докажем равенство этих треугольников. Действительно, из условия следует: . Кроме того, поскольку углы – вертикальные, то они равны. То есть: (первый признак равенства треугольников – по двум сторонам и углу между ними). Из равенства треугольников: (так как равны внутренние накрест лежащие углы при этих прямых и секущей ). Кроме того, из равенства треугольников следует, что . Значит, мы получили, что в четырёхугольнике две стороны равны и параллельны. По первому признаку параллелограмма: – параллелограмм. Доказано. Пример задачи на третий признак параллелограмма и обобщение Рассмотрим пример на применение третьего признака параллелограмма. Пример 1 Дано: –параллелограмм; . – середина , – середина , – середина , – середина (см. Рис. 2). Рис. 2 Доказать: – параллелограмм. Доказательство: Значит, в четырёхугольнике диагонали в точке пересечения делятся пополам. По третьему признаку параллелограмма из этого следует, что – параллелограмм. Доказано. Если провести анализ третьего признака параллелограмма, то можно заметить, что этот признак соответствует свойству параллелограмма. То есть, то, что диагонали делятся пополам, является не просто свойством параллелограмма, а его отличительным, характеристическим свойством, по которому его можно выделить из множества четырёхугольников. На следующем уроке мы рассмотрим решение различных задач про параллелограмм. Домашнее задание 1. Диагонали четырёхугольника пересекаются в точке . 2. Диагонали четырёхугольника пересекаются в точке . Известно, что . Докажите, что данный четырёхугольник – параллелограмм. Урок 9: Задачи на параллелограмм. На уроке мы, прежде всего, повторим уже изученные ранее свойства и признаки параллелограмма и все основные понятия, которые связаны с этой геометрической фигурой. Главной целью занятия будет рассмотрение нескольких примеров на применение знаний о параллелограмме. В процессе решения примеров познакомимся с важнейшей теоремой, связанной с параллельностью прямых, – теоремой Фалеса. 1. Повторение определения, свойств и признака параллелограмма Сегодня мы основное внимание уделим задачам на параллелограмм. Для этого нам необходимо владеть определением параллелограмма, его свойствами и признаками. Повторим эти факты, обобщим и структурируем их. Определение. Параллелограмм– четырехугольник, у которого каждые две противоположные стороны параллельны (см. Рис. 1. Параллелограмм Основные свойства параллелограмма: Теорема.Первый признак параллелограмма.Если в четырехугольнике две противоположные стороны равны и параллельны (см. Рис. 2), то этот четырехугольник – параллелограмм. параллелограмм. Рис. 2. Первый признак параллелограмма Рис. 3. Второй признак параллелограмма Теорема. Второй признак параллелограмма.Если в четырехугольнике каждые две противоположные стороны равны (см. Рис. 3), то этот четырехугольник –параллелограмм. параллелограмм. Теорема. Третий признак параллелограмма.Если в четырехугольнике диагонали точкой пересечения делятся пополам (см. Рис. 4), то этот четырехугольник – параллелограмм. параллелограмм. Рис. 4. Третий признак параллелограмма Задачи на параллелограммы Теперь рассмотрим решение задач с использованием определения, свойств и признаков параллелограмма. Пример 1. В параллелограмме проведены биссектрисы и , которые пересекаются в точке . Найти . Решение. Изобразим Рис. 5. Рис. 5 Обозначим для удобства: . Следовательно, поскольку и биссектрисы. По теореме о сумме внутренних углов треугольника . Вспомним свойство параллелограмма о сумме углов, прилежащих к одной стороне: . Тогда: . Ответ. . Пример 2. Прямая , проведенная через середину стороны параллельно стороне треугольника пересекает третью его сторону в середине. Доказать, что – это середина . Доказательство. Изобразим Рис. 6 с дополнительными построениями: проведем . Рис. 6 Рассмотрим четырехугольник : параллелограмм по определению. Тогда по свойству равенства противоположных сторон , но по условию еще известно, что , следовательно, . Рассмотрим треугольники и : по второму признаку равенства треугольников (по стороне и прилежащим углам). Из равенства указанных треугольников следует равенство их соответствующих сторон, т. Доказано. Методы, которые мы рассмотрели сегодня на примерах, демонстрирующих свойства и признаки параллелограмма, помогут нам в дальнейшем при работе с параллелограммами в более сложных случаях. Домашнее задание 1. В параллелограмме см, см, биссектрисы углов и пересекают сторону в точках и . Найдите длину отрезка . 2. Угол между высотами параллелограмма, проведенными из вершины тупого угла, равен . Найдите периметр параллелограмма, если его высоты равны 4 см и 6 см. 3. * Через середину диагонали параллелограмма проведена прямая, которая пересекает стороны и в точках и соответственно. Докажите, что четырехугольник параллелограмм.
Урок 10: Прямоугольник На данном уроке мы будем рассматривать частный случай параллелограмма – прямоугольник. Мы введем его основные свойства, докажем теорему о равенстве диагоналей прямоугольника и сформулируем признак прямоугольника.
⇐ Предыдущая123456789Следующая ⇒ Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства… Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций… Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим… Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого… |
Все правила про параллелограмм. Параллелограмм и его свойства
1. Определение параллелограмма.
Если пару параллельных прямых пересечём другой парой параллельных прямых, то получим четырёхугольник, у которого противоположные стороны попарно параллельны.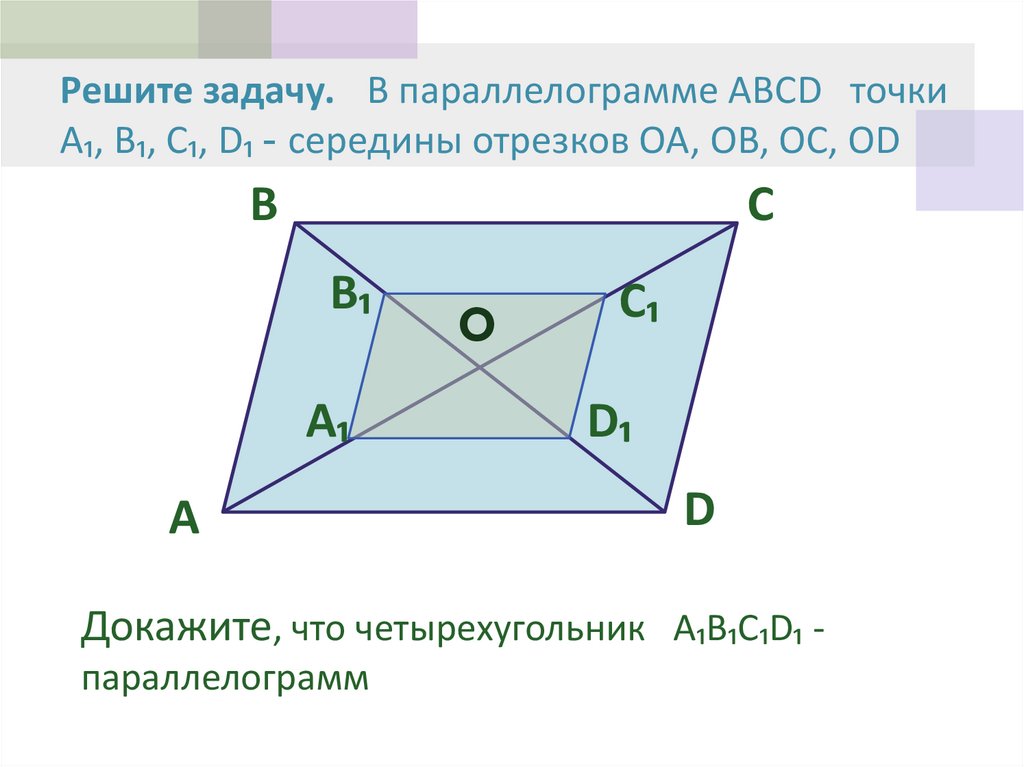
В четырёхугольниках ABDС и ЕFNМ (рис. 224) ВD || АС и AB || СD;
ЕF || МN и ЕМ || FN.
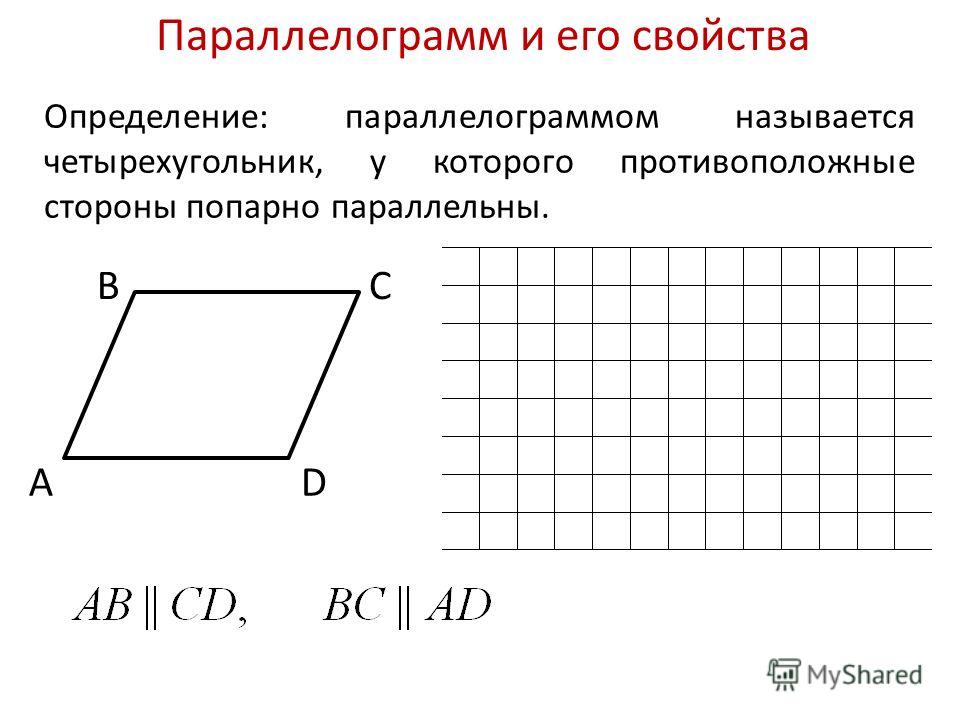
Четырёхугольник, у которого противоположные стороны попарно параллельны, называется параллелограммом.
2. Свойства параллелограмма.
Теорема . Диагональ параллелограмма делит его на два равных треугольника.
Пусть имеется параллелограмм ABDС (рис. 225), в котором AB || СD и АС || ВD.
Требуется доказать, что диагональ делит его на два равных треугольника.
Проведём в параллелограмме ABDС диагональ СВ. Докажем, что \(\Delta\)CAB = \(\Delta\)СDВ.
Сторона СВ общая для этих треугольников; ∠ABC = ∠BCD, как внутренние накрест лежащие углы при параллельных AB и СD и секущей СВ; ∠ACB = ∠СВD, тоже как внутренние накрест лежащие углы при параллельных АС и ВD и секущей CB.
Отсюда \(\Delta\)CAB = \(\Delta\)СDВ.
Таким же путём можно доказать, что диагональ AD разделит параллелограмм на два равных треугольника АСD и ABD.
Следствия:
1 . Противоположные углы параллелограмма равны между собой.
∠А = ∠D, это следует из равенства треугольников CAB и СDВ.
Аналогично и ∠С = ∠В.
2. Противоположные стороны параллелограмма равны между собой.
AB = СD и АС = ВD, так как это стороны равных треугольников и лежат против равных углов.
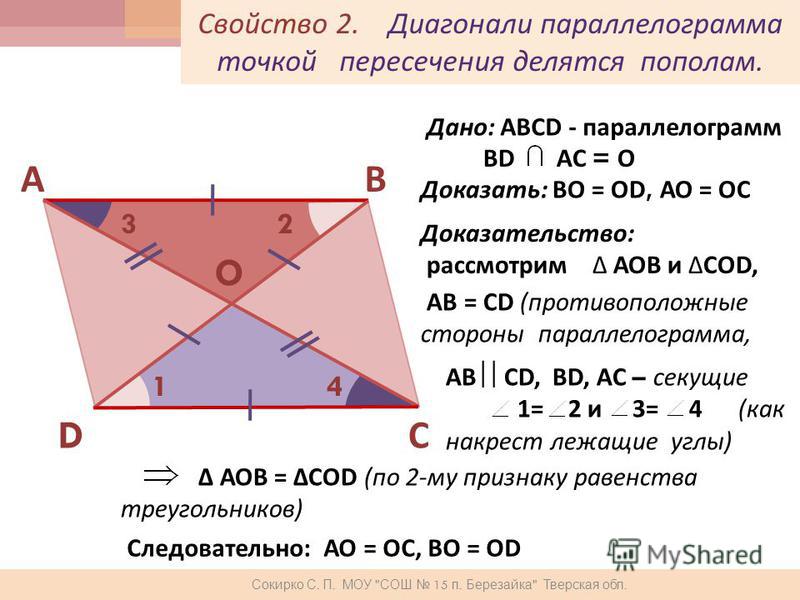
Теорема 2. Диагонали параллелограмма в точке их пересечения делятся пополам.
Пусть BC и AD — диагонали параллелограмма AВDС (рис. 226). Докажем, что АО = OD и СО = OB.
Для этого сравним какую-нибудь пару противоположно расположенных треугольников, например \(\Delta\)AOB и \(\Delta\)СОD.
В этих треугольниках AB = СD, как противоположные стороны параллелограмма;
∠1 = ∠2, как углы внутренние накрест лежащие при параллельных AB и СD и секущей AD;
∠3 = ∠4 по той же причине, так как AB || СD и СВ — их секущая.
Отсюда следует, что \(\Delta\)AOB = \(\Delta\)СОD. А в равных треугольниках против равных углов лежат равные стороны. Следовательно, АО = OD и СО = OB.
А в равных треугольниках против равных углов лежат равные стороны. Следовательно, АО = OD и СО = OB.
Теорема 3. Сумма углов, прилежащих к одной стороне параллелограмма, равна 180° .
В параллелограмме ABCD проведем диагональ АС и получим два треугольника ABC и ADC.
Треугольники равны, так как ∠1 = ∠4, ∠2 = ∠3 (накрест лежащие углы при параллельных прямых), а сторона АС общая.
Из равенства \(\Delta\)ABC = \(\Delta\)ADC следует, что AB = CD, BC = AD, ∠B = ∠D.
Сумма углов, прилежащих к одной стороне, например углов А и D, равна 180° как односторонних при параллельных прямых.
Это четырёхугольник, противоположные стороны которого попарно параллельны.
Свойство 1 . Любая диагональ параллелограмма делит его на два равных треугольника.
Доказательство . По II признаку (накрест лежащие углы и общая сторона).
Теорема доказана .
Свойство 2
. В параллелограмме противолежащие стороны равны, противолежащие углы равны.
Доказательство
.
Аналогично,
Теорема доказана .
Свойство 3. В параллелограмме диагонали точкой пересечения делятся пополам.
Доказательство .
Теорема доказана .
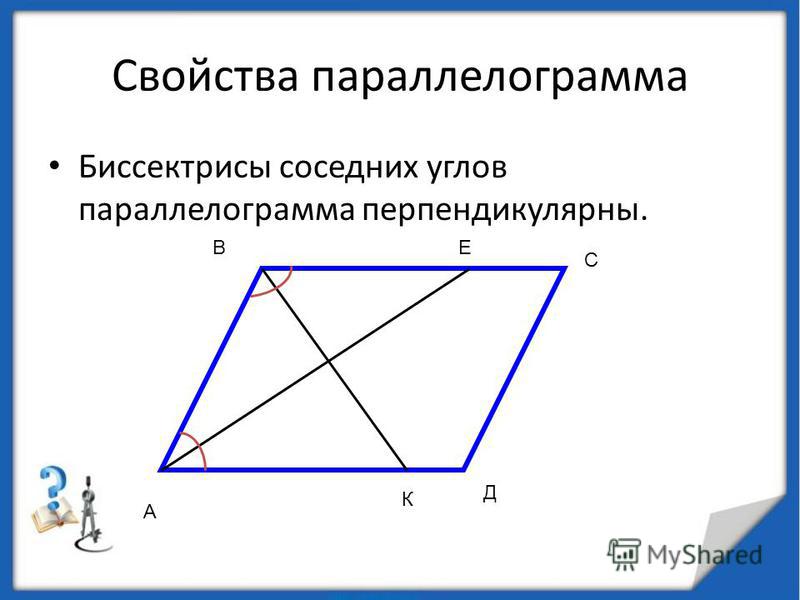
Свойство 4 . Биссектриса угла параллелограмма, пересекая противоположную сторону, делит его на равнобедренный треугольник и трапецию. (Ч. сл. — вершину — два равнобедренных?-ка).
Доказательство
.
Теорема доказана .
Свойство 5 . В параллелограмме отрезок с концами на противоположных сторонах, проходящий через точку пересечения диагоналей, делится этой точкой пополам.
Доказательство .
Теорема доказана .
Свойство 6 . Угол между высотами, опущенными из вершины тупого угла параллелограмма, равен острому углу параллелограмма.
Доказательство .
Теорема доказана .
Свойство 7 . Сумма углов параллелограмма, прилежащих к одной стороне, равна 180°.
Доказательство .
Теорема доказана .
Построение биссектрисы угла.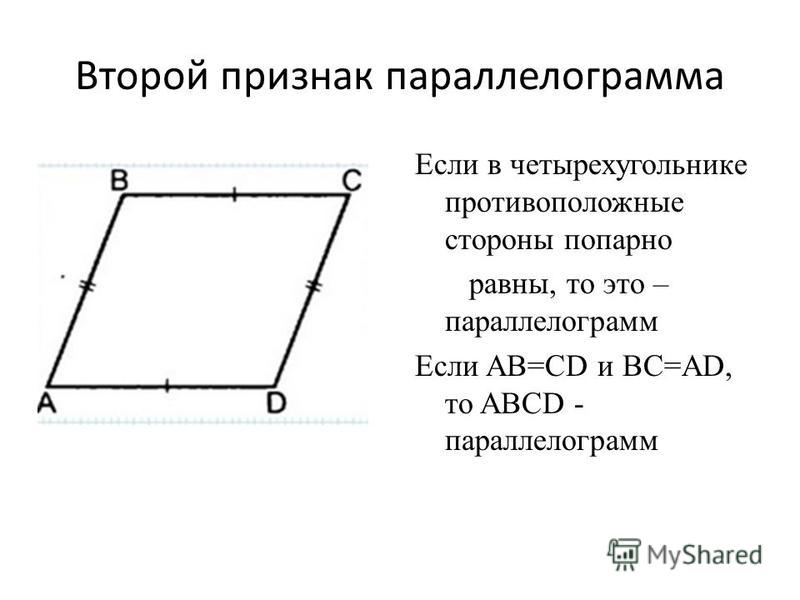 Свойства биссектрисы угла треугольника.
Свойства биссектрисы угла треугольника.
1) Построить произвольный луч DE.
2) На данном луче построить произвольную окружность с центром в вершине и такую же
с центром в начале построенного луча.
3) F и G — точки пересечения окружности со сторонами данного угла, H — точка пересечения окружности с построенным лучом
Построить окружность с центром в точке H и радиусом, равным FG.
5) I — точка пересечения окружностей построенного луча.
6) Провести прямую через вершину и I.
IDH — требуемый угол.
)
Свойство 1 . Биссектриса угла треугольника разбивает противоположную сторону пропорционально прилежащим сторонам.
Доказательство . Пусть x, y-отрезки стороны c. Продолжим луч BC. На луче BC отложим от C отрезок CK, равный AC.
Конспект урока.
Алгебра 8 класс
Учитель Сысой А.К.
Школа 1828
Тема урока: «Параллелограмм и его свойства»
Тип урока: комбинированный
Цели урока:
1) Обеспечить усвоение нового понятия – параллелограмм и его свойств
2) Продолжить развитие навыков и умений решения геометрических задач;
3) Развитие культуры математической речи
План урока:
1. Организационный момент
Организационный момент
(Слайд 1)
На слайде демонстрируется высказывание Льюиса Кэрролла. Ученикам сообщается о цели урока. Проверяется готовность учеников к уроку.
2. Актуализация знаний
(Слайд 2)
На доске задачи для устной работы. Учитель предлагает ученикам подумать над этими задачами и поднять руку тем, кто понял, как задачу решать. После решения двух задач, на доказательство теоремы о сумме углов вызывается к доске ученик, который самостоятельно делает дополнительные построения на чертеже и доказывает устно теорему.
Учениками используется формула суммы углов многоугольника:
3. Основная часть
(Слайд 3)
На доске определение параллелограмма. Учитель говорит о новой фигуре и формулирует определение, делая с помощью чертежа необходимые пояснения. Затем на клетчатой части презентации, с помощью маркера и линейки, показывает, как можно рисовать параллелограмм (возможно несколько случаев)
(Слайд 4)
Учитель формулирует первое свойство параллелограмма.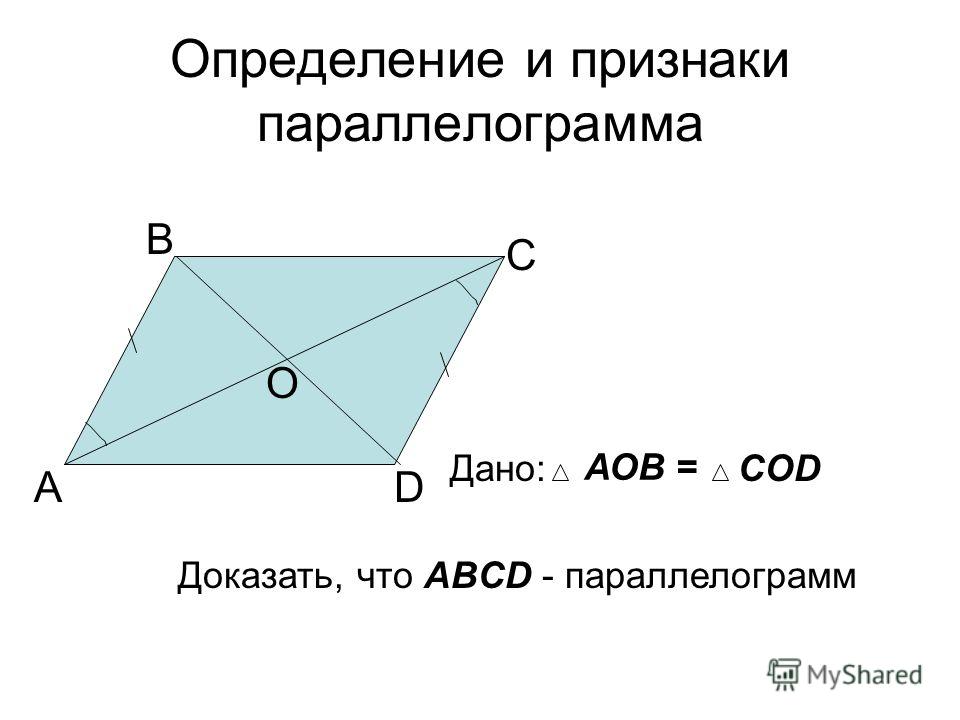 Предлагает ученикам сказать, по рисунку, что дано и что необходимо доказать. После этого на доске появляется дано задачи. Ученики догадываются (может быть при помощи учителя) что искомые равенства надо доказать через равенства треугольников, которые можно получить проведя диагональ (на доске появляется диагональ). Далее ученики догадываются почему треугольники равны и называют признак равенства треугольников (появляется соответствующая форма). Устно сообщают факты, которые необходимы для равенства треугольников (по мере того как они их называют, появляется соответствующая визуализация). Далее ученики формулируют свойство равных треугольников, оно появляется в виде пункта 3 доказательства и затем самостоятельно завершают доказательство теоремы устно.
Предлагает ученикам сказать, по рисунку, что дано и что необходимо доказать. После этого на доске появляется дано задачи. Ученики догадываются (может быть при помощи учителя) что искомые равенства надо доказать через равенства треугольников, которые можно получить проведя диагональ (на доске появляется диагональ). Далее ученики догадываются почему треугольники равны и называют признак равенства треугольников (появляется соответствующая форма). Устно сообщают факты, которые необходимы для равенства треугольников (по мере того как они их называют, появляется соответствующая визуализация). Далее ученики формулируют свойство равных треугольников, оно появляется в виде пункта 3 доказательства и затем самостоятельно завершают доказательство теоремы устно.
(Слайд 5)
Учитель формулирует второе свойство параллелограмма. На доске появляется рисунок параллелограмма. Учитель предлагает по рисунку сказать что дано, что необходимо доказать. После того как ученики правильно сообщают о том, что дано и что необходимо доказать, появляется условие теоремы.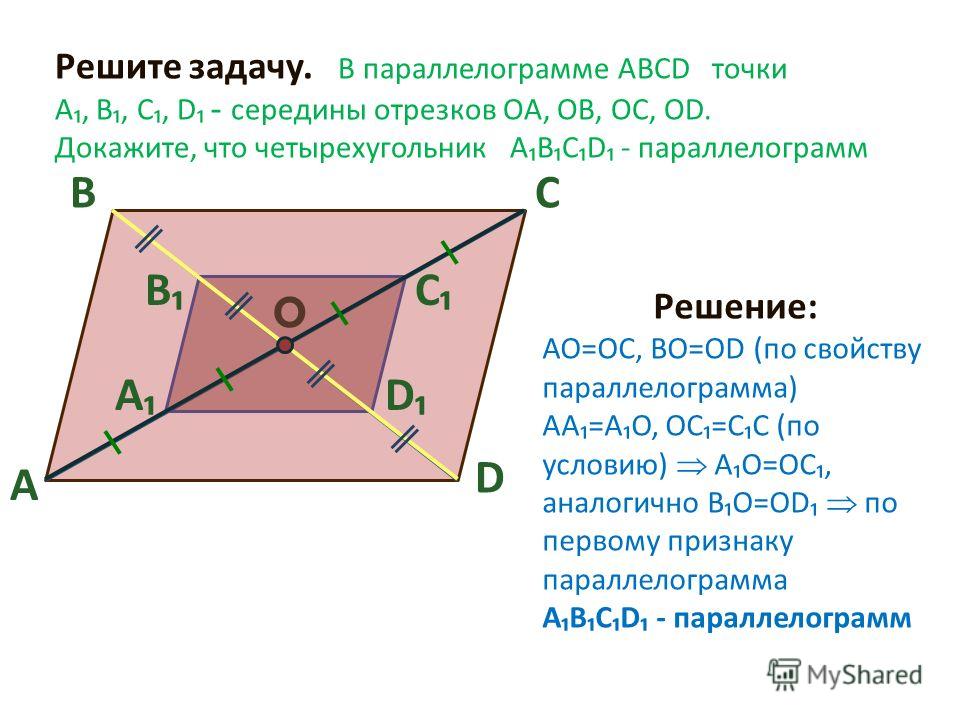 Ученики догадываются, что равенство частей диагоналей можно доказать через равенство треугольников
AOB
и
COD
. С помощью предыдущего свойства параллелограмма догадываются о равенстве сторон
AB
и
CD
. Затем понимают, что надо найти равные углы и с помощью свойств параллельных прямых доказывают равенство прилежащих к равным сторонам углов. Данные этапы визуализируются на слайде. Из равенства треугольников следует и истинность теоремы – проговаривают ученики на слайде появляется соответствующая визуализация.
Ученики догадываются, что равенство частей диагоналей можно доказать через равенство треугольников
AOB
и
COD
. С помощью предыдущего свойства параллелограмма догадываются о равенстве сторон
AB
и
CD
. Затем понимают, что надо найти равные углы и с помощью свойств параллельных прямых доказывают равенство прилежащих к равным сторонам углов. Данные этапы визуализируются на слайде. Из равенства треугольников следует и истинность теоремы – проговаривают ученики на слайде появляется соответствующая визуализация.
(Слайд 6)
Учитель формулирует третье свойство параллелограмма. В зависимости от времени, которое остаётся до конца урока, учитель может дать возможность ученикам самостоятельно доказать это свойство, или ограничится его формулировкой, а само доказательство оставить ученикам в качестве домашней работы. Доказательство может опираться на сумму углов вписанного многоугольника, которая повторялась в начале урока, или на сумму внутренних односторонних углов при двух параллельных прямых
AD
и
BC
, и секущей, например
AB
.
4. Закрепление материала
На этом этапе учащиеся, используя ранее изученные теоремы, решают задачи. Идеи к решению задачи подбирают ученики самостоятельно. Так как возможных вариантов оформления немало и все они зависят от того каким образом ученики будут искать решение задачи, визуализации решения задач нет, а ученики самостоятельно оформляют каждый этап решения на отдельной доске с записью решения в тетрадь.
(Слайд 7)
Появляется условие задачи. Учитель предлагает по условию сформулировать «Дано». После того, как ученики, верно составят краткую запись условия на доске появляется «Дано». Ход решения задачи может выглядеть следующим образом:
Проведём высоту BH (визуализировано)
Треугольник AHB – прямоугольный. Угол A равен углу C и равен 30 0 (по свойству о противоположных углах в параллелограмме). 2BH =AB (по свойству катета, лежащего напротив угла в 30 0 в прямоугольном треугольнике). Значит AB = 13 см.
AB
= CD
, BC
= AD
(по свойству противоположных сторон в параллелограмме) Значит AB
=CD
=13см.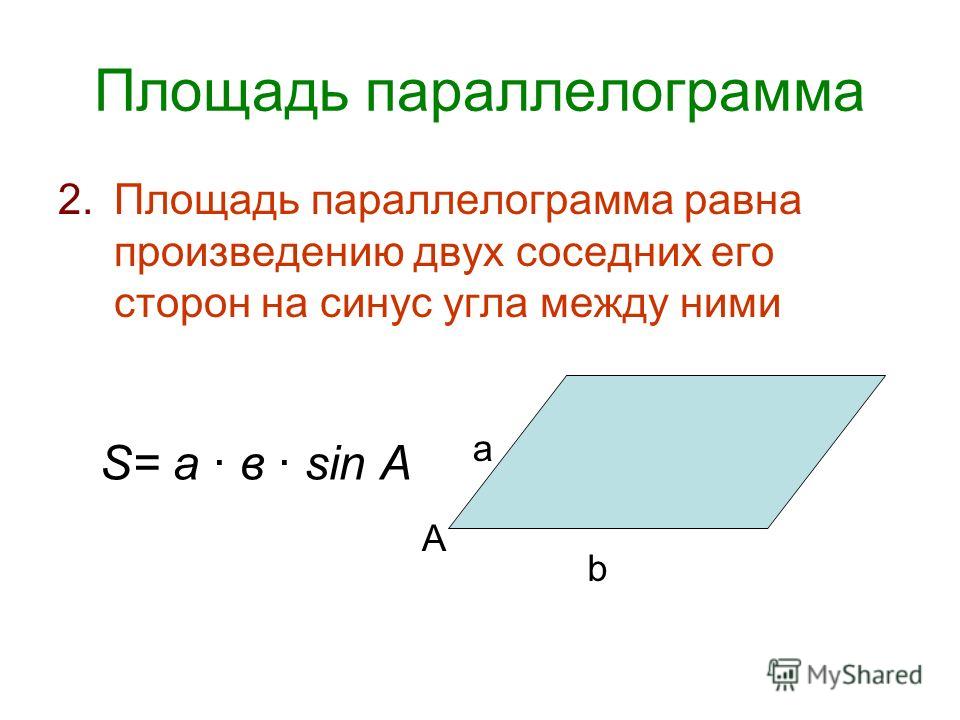 Так как периметр параллелограмма равен 50 см, то BC
=AD
=(50 – 26):2=12см.
Так как периметр параллелограмма равен 50 см, то BC
=AD
=(50 – 26):2=12см.
Ответ: AB = CD = 13 см, BC = AD = 12 см.
(Слайд 8)
Появляется условие задачи. Учитель предлагает по условию сформулировать «Дано». После появляется «Дано» на экране. С помощью красных линий выделяется четырёхугольник, про который нужно доказать, что он параллелограмм. Ход решения задачи может выглядеть следующим образом:
Т.к. BK и MD перпендикуляры к одной прямой, то прямы BK и MD параллельны.
Через смежные углы можно показать, что сумма внутренних односторонних углов при прямых BM и KD и секущей MD равна 180 0 . Поэтому данные прямые параллельны.
Так как у четырехугольника BMDK противоположные стороны попарно параллельны, то данный четырехугольник параллелограмм.
5. Окончание урока. Поведение итогов.
(Слайд 8)
На слайде появляются вопросы по новой теме, на которые ученики отвечают.
Для того, чтобы определить является ли данная фигура параллелограммом существует ряд признаков. Рассмотрим три основных признака параллелограмма.
Рассмотрим три основных признака параллелограмма.
1 признак параллелограмма
Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник будет являться параллелограммом.
Доказательство:
Рассмотрим четырехугольник ABCD. Пусть в нем стороны AB и СD параллельны. И пусть AB=CD. Проведем в нем диагональ BD. Она разделит данный четырехугольник на два равных треугольника: ABD и CBD.
Эти треугольники равны между собой по двум сторонам и углу между ними (BD — общая сторона, AB = CD по условию, угол1 = угол2 как накрест лежащие углы при секущей BD параллельных прямых AB и CD.), а следовательно угол3 = угол4.
А эти углы будут являться накрест лежащими при пересечении прямых BC и AD секущей BD. Из этого следует что BC и AD параллельны между собой. Имеем, что в четырехугольнике ABCD противоположные стороны попарно параллельны, и, значит, четырехугольник ABCD является параллелограммом.
2 признак параллелограмма
Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник будет параллелограммом.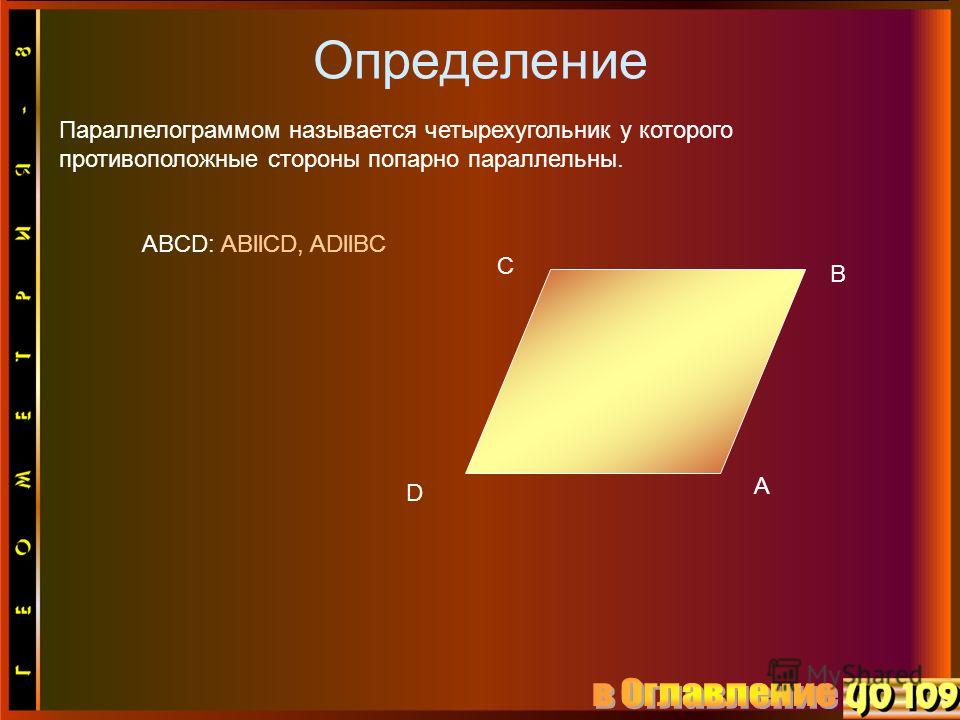
Доказательство:
Рассмотрим четырехугольник ABCD. Проведем в нем диагональ BD. Она разделит данный четырехугольник на два равных треугольника: ABD и CBD.
Эти два треугольника буду равны между собой по трем сторонам (BD — общая сторона, AB = CD и BC = AD по условию). Из этого можно сделать вывод, что угол1 = угол2. Отсюда следует, что AB параллельна CD. А так как AB = CD и AB параллельна CD, то по первому признаку параллелограмма, четырехугольник ABCD будет являться параллелограммом.
3 признак параллелограмма
Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник будет являться параллелограммом.
Рассмотрим четырехугольник ABCD. Проведем в нем две диагонали AC и BD, которые будут пересекаться в точке О и делятся этой точкой пополам.
Треугольники AOB и COD будут равны между собой, по первому признаку равенства треугольников. (AO = OC, BO = OD по условию, угол AOB = угол COD как вертикальные углы. ) Следовательно, AB = CD и угол1 = угол 2. Из равенства углов 1 и 2 имеем, что AB параллельна CD. Тогда имеем, что в четырехугольнике ABCD стороны AB равны CD и параллельны, и по первому признаку параллелограмма четырехугольник ABCD будет являться параллелограммом.
) Следовательно, AB = CD и угол1 = угол 2. Из равенства углов 1 и 2 имеем, что AB параллельна CD. Тогда имеем, что в четырехугольнике ABCD стороны AB равны CD и параллельны, и по первому признаку параллелограмма четырехугольник ABCD будет являться параллелограммом.
Определение параллелограма и его свойства. Параллелограмм и его свойства
Это четырёхугольник, противоположные стороны которого попарно параллельны.
Свойство 1 . Любая диагональ параллелограмма делит его на два равных треугольника.
Доказательство . По II признаку (накрест лежащие углы и общая сторона).
Теорема доказана .
Свойство 2 . В параллелограмме противолежащие стороны равны, противолежащие углы равны.
Доказательство
.
Аналогично,
Теорема доказана .
Свойство 3. В параллелограмме диагонали точкой пересечения делятся пополам.
Доказательство .
Теорема доказана .
Свойство 4
. Биссектриса угла параллелограмма, пересекая противоположную сторону, делит его на равнобедренный треугольник и трапецию. (Ч. сл. — вершину — два равнобедренных?-ка).
(Ч. сл. — вершину — два равнобедренных?-ка).
Доказательство
.
Теорема доказана .
Свойство 5 . В параллелограмме отрезок с концами на противоположных сторонах, проходящий через точку пересечения диагоналей, делится этой точкой пополам.
Доказательство .
Теорема доказана .
Свойство 6 . Угол между высотами, опущенными из вершины тупого угла параллелограмма, равен острому углу параллелограмма.
Доказательство .
Теорема доказана .
Свойство 7 . Сумма углов параллелограмма, прилежащих к одной стороне, равна 180°.
Доказательство .
Теорема доказана .
Построение биссектрисы угла. Свойства биссектрисы угла треугольника.
1) Построить произвольный луч DE.
2) На данном луче построить произвольную окружность с центром в вершине и такую же
с центром в начале построенного луча.
3) F и G — точки пересечения окружности со сторонами данного угла, H — точка пересечения окружности с построенным лучом
Построить окружность с центром в точке H и радиусом, равным FG.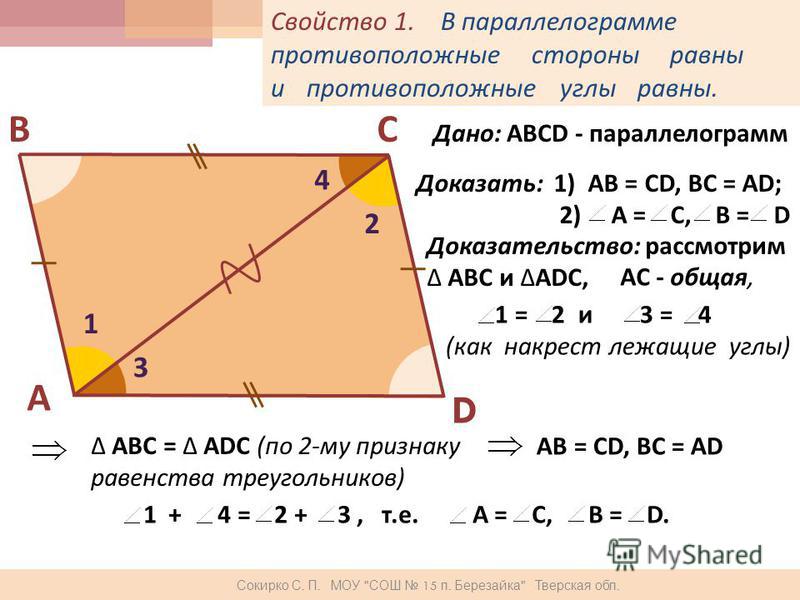
5) I — точка пересечения окружностей построенного луча.
6) Провести прямую через вершину и I.
IDH — требуемый угол.
)
Свойство 1 . Биссектриса угла треугольника разбивает противоположную сторону пропорционально прилежащим сторонам.
Доказательство . Пусть x, y-отрезки стороны c. Продолжим луч BC. На луче BC отложим от C отрезок CK, равный AC.
Параллелограмм представляет собой четырехугольник, у которого противоположные стороны попарно параллельны. Это определение уже достаточно, так как остальные свойства параллелограмма следуют из него и доказываются в виде теорем.
Основными свойствами параллелограмма являются:
- параллелограмм — это выпуклый четырехугольник;
- у параллелограмма противоположные стороны попарно равны;
- у параллелограмма противоположные углы попарно равны;
- диагонали параллелограмма точкой пересечения делятся пополам.
Параллелограмм — выпуклый четырехугольник
Докажем сначала теорему о том, что параллелограмм является выпуклым четырехугольником . Многоугольник является выпуклым тогда, когда какая бы его сторона не была продлена до прямой, все остальные стороны многоугольника окажутся по одну сторону от этой прямой.
Многоугольник является выпуклым тогда, когда какая бы его сторона не была продлена до прямой, все остальные стороны многоугольника окажутся по одну сторону от этой прямой.
Пусть дан параллелограмм ABCD, у которого AB противоположная сторона для CD, а BC — противоположная для AD. Тогда из определения параллелограмма следует, что AB || CD, BC || AD.
У параллельных отрезков нет общих точек, они не пересекаются. Это значит, что CD лежит по одну сторону от AB. Поскольку отрезок BC соединяет точку B отрезка AB с точкой C отрезка CD, а отрезок AD соединяет другие точки AB и CD, то отрезки BC и AD также лежат по ту же сторону от прямой AB, где лежит CD. Таким образом, все три стороны — CD, BC, AD — лежат по одну сторону от AB.
Аналогично доказывается, что по отношению к другим сторонам параллелограмма три остальные стороны лежат с одной стороны.
Противоположные стороны и углы равны
Одним из свойств параллелограмма является то, что в параллелограмме противоположные стороны и противоположные углы попарно равны .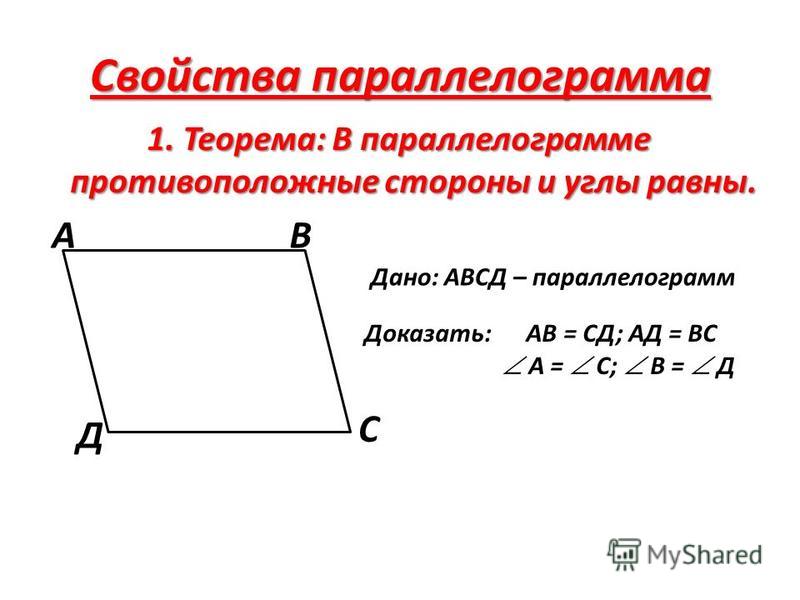 Например, если дан параллелограмм ABCD, то у него AB = CD, AD = BC, ∠A = ∠C, ∠B = ∠D. Доказывается эта теорема следующим образом.
Например, если дан параллелограмм ABCD, то у него AB = CD, AD = BC, ∠A = ∠C, ∠B = ∠D. Доказывается эта теорема следующим образом.
Параллелограмм является четырехугольником. Значит, у него две диагонали. Так как параллелограмм — это выпуклый четырехугольник, то любая из них делит его на два треугольника. Рассмотрим в параллелограмме ABCD треугольники ABC и ADC, полученные в результате проведения диагонали AC.
У этих треугольников одна сторона общая — AC. Угол BCA равен углу CAD, как вертикальные при параллельных BC и AD. Углы BAC и ACD также равны как вертикальные при параллельных AB и CD. Следовательно, ∆ABC = ∆ADC по двум углам и стороне между ними.
В этих треугольниках стороне AB соответствует сторона CD, а стороне BC соответствует AD. Следовательно, AB = CD и BC = AD.
Углу B соответствует угол D, т. е. ∠B = ∠D. Угол A параллелограмма представляет собой сумму двух углов — ∠BAC и ∠CAD. Угол же C равен состоит из ∠BCA и ∠ACD. Так как пары углов равны друг другу, то ∠A = ∠C.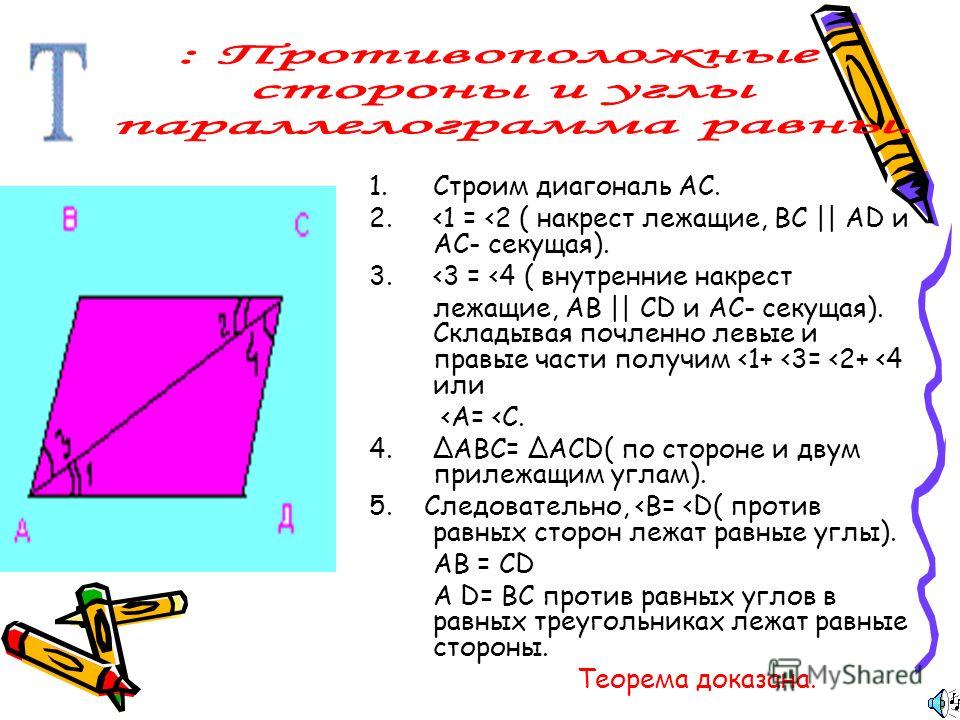
Таким образом, доказано, что в параллелограмме противоположные стороны и углы равны.
Диагонали делятся пополам
Так как параллелограмм — это выпуклый четырехугольник, то у него две две диагонали, и они пересекаются. Пусть дан параллелограмм ABCD, его диагонали AC и BD пересекаются в точке E. Рассмотрим образованные ими треугольники ABE и CDE.
У этих треугольников стороны AB и CD равны как противоположные стороны параллелограмма. Угол ABE равен углу CDE как накрест лежащие при параллельных прямых AB и CD. По этой же причине ∠BAE = ∠DCE. Значит, ∆ABE = ∆CDE по двум углам и стороне между ними.
Также можно заметить, что углы AEB и CED вертикальные, а следовательно, тоже равны друг другу.
Так как треугольники ABE и CDE равны друг другу, то равны и все их соответствующие элементы. Стороне AE первого треугольника соответствует сторона CE второго, значит, AE = CE. Аналогично BE = DE. Каждая пара равных отрезков составляет диагональ параллелограмма. Таким образом доказано, что диагонали параллелограмма делятся точкой пересечения пополам .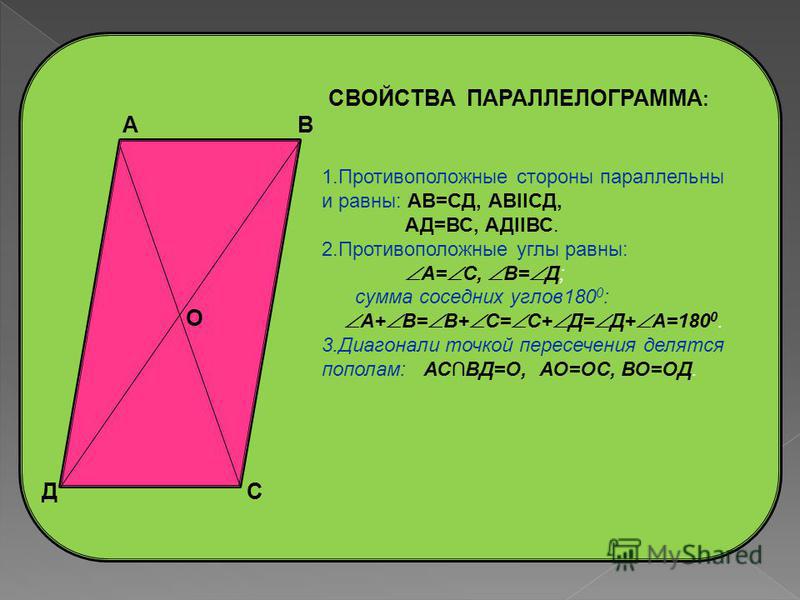
Понятие параллелограмма
Определение 1
Параллелограмм — это четырехугольник, в котором противоположные стороны параллельны между собой (рис. 1).
Рисунок 1.
Параллелограмм имеет два основных свойства. Рассмотрим их без доказательства.
Свойство 1: Противоположные стороны и углы параллелограмма равны, соответственно, между собой.
Свойство 2: Диагонали, проведенные в параллелограмме, делятся пополам их точкой пересечения.
Признаки параллелограмма
Рассмотрим три признака параллелограмма и представим их в виде теорем.
Теорема 1
Если две стороны четырехугольника равны между собой, а также параллельны, то этот четырехугольник будет параллелограммом.
Доказательство.
Пусть нам дан четырехугольник $ABCD$. В котором $AB||CD$ и $AB=CD$ Проведем в нем диагональ $AC$ (рис. 2).
Рисунок 2.
Рассмотрим параллельные прямые $AB$ и $CD$ и их секущую $AC$. Тогда
\[\angle CAB=\angle DCA\]
как накрест лежащие углы.
По $I$ признаку равенства треугольников,
так как $AC$ — их общая сторона, а $AB=CD$ по условию. Значит
\[\angle DAC=\angle ACB\]
Рассмотрим прямые $AD$ и $CB$ и их секущую $AC$, по последнему равенству накрест лежащих углов получим, что $AD||CB$.}Следовательно, по определению $1$, данный четырехугольник является параллелограммом.
Теорема доказана.
Теорема 2
Если противоположные стороны четырехугольника равны между собой, то он является параллелограммом.
Доказательство.
Пусть нам дан четырехугольник $ABCD$. В котором $AD=BC$ и $AB=CD$. Проведем в нем диагональ $AC$ (рис. 3).
Рисунок 3.
Так как $AD=BC$, $AB=CD$, а $AC$ — общая сторона, то по $III$ признаку равенства треугольников,
\[\triangle DAC=\triangle ACB\]
\[\angle DAC=\angle ACB\]
Рассмотрим прямые $AD$ и $CB$ и их секущую $AC$, по последнему равенству накрест лежащих углов получим, что $AD||CB$.
Следовательно, по определению $1$, данный четырехугольник является параллелограммом.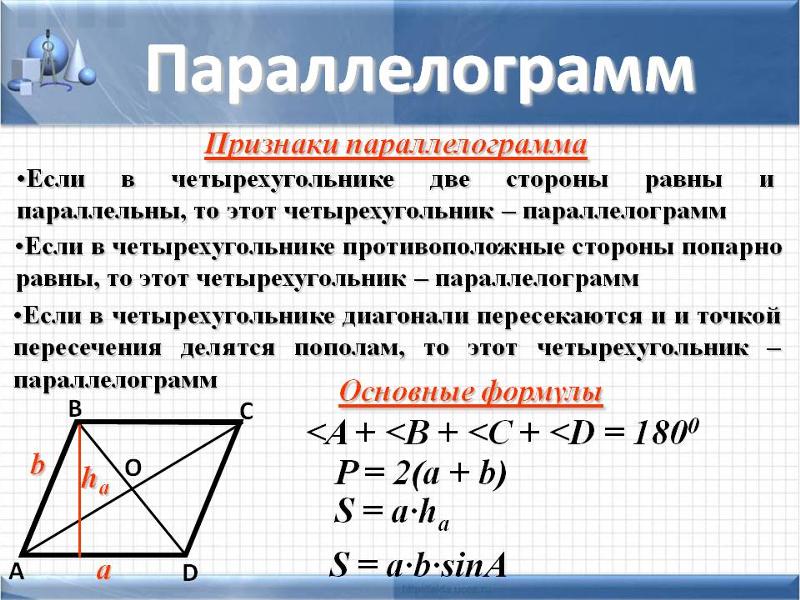
\[\angle DCA=\angle CAB\]
Рассмотрим прямые $AB$ и $CD$ и их секущую $AC$, по последнему равенству накрест лежащих углов получим, что $AB||CD$. Следовательно, по определению 1, данный четырехугольник является параллелограммом.
Теорема доказана.
Теорема 3
Если диагонали, проведенные в четырехугольнике, своей точкой пересечения делятся на две равные части, то этот четырехугольник является параллелограммом.
Доказательство.
Пусть нам дан четырехугольник $ABCD$. Проведем в нем диагонали $AC$ и $BD$. Пусть они пересекаются в точке $O$ (рис. 4).
Рисунок 4.
Так как, по условию $BO=OD,\ AO=OC$, а углы $\angle COB=\angle DOA$ как вертикальные, то, по $I$ признаку равенства треугольников,
\[\triangle BOC=\triangle AOD\]
\[\angle DBC=\angle BDA\]
Рассмотрим прямые $BC$ и $AD$ и их секущую $BD$, по последнему равенству накрест лежащих углов получим, что $BC||AD$. Также $BC=AD$. Следовательно, по теореме $1$, данный четырехугольник является параллелограммом.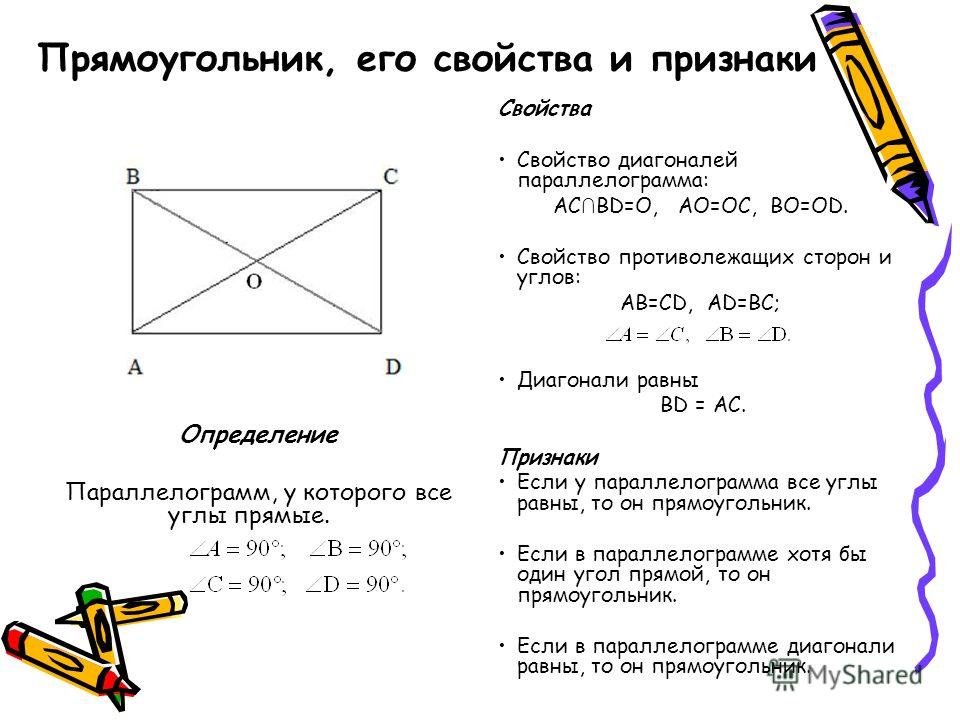
Параллелограммом называется четырехугольник, у которго противоположные стороны параллельны, т.е. лежат на параллельных прямых
Свойства параллелограмма:
Теорема 22. Противоположные стороны параллелограма равны.
Доказательство. В параллелограмме АВСD проведем диагональ АС. Треугольники АСD и АСВ равны, как имеющие общую сторону АС и две пары равных углов. прилежащих к ней: ∠
САВ=∠
АСD, ∠
АСВ=∠
DAC (как накрест лежащие углы при параллельных прямых AD и ВС). Значит, АВ=CD и ВС=AD, как соответственные стороны равных треугольников, ч.т.д. Из равенства этих треугольников также следует равенство соответственных углов треугольников:
Теорема 23. Противоположные углы параллелограмма равны: ∠
А=∠
С и ∠
В=∠
D.
Равенство первой пары идет из равенства треугольников АВD и CBD, а второй — АВС и ACD.
Теорема 24. Соседние углы параллелограмма, т.е. углы, прилежащие к одной стороне, составляют в сумме 180 градусов.
Это так, потому что они являются внутренними односторонними углами.
Теорема 25. Диагонали параллелограмма делят друг друга в точке их пересечения пополам.
Доказательство. Рассмотрим треугольники ВОС и АОD. По первому свойству AD=ВС ∠
ОАD=∠
ОСВ и ∠
ОDА=∠
ОВС как накрест лежащие при параллельных прямых AD и ВС. Поэтому треугольники ВОС и АОD равны по стороне и прилежащим к ней углам. Значит, ВО=ОD и АО=ОС, как соответственные стороны равных треугольников, ч.т.д.
Признаки параллелограмма
Теорема 26. Если противоположные стороны четырехугольника попарно равны, то он является параллелограммом.
Доказательство. Пусть у четырехугольника АВСD стороны AD и ВС, АВ и CD соответственно равны (рис2). Проведем диагональ АС. Треугольникик АВС и ACD равны по трем сторонам. Тогда углы ВАС и DСА равны и, следовательно, АВ параллельна CD. Параллельность сторон ВС и AD следует из равенства углов CAD и АСВ.
Теорема 27. Если противоположные углы четырехугольника попарно равны, то он является параллелограммом.
Пусть ∠
А=∠
С и ∠
В=∠
D. Т.к. ∠
А+∠
В+∠
С+∠
D=360 о, то ∠
А+∠
В=180 о и стороны AD и ВС параллельны (по признаку параллельности прямых). Также докажем и параллельность сторон АВ и CD и заключим, что АВСD является параллелограммом по определению.
Т.к. ∠
А+∠
В+∠
С+∠
D=360 о, то ∠
А+∠
В=180 о и стороны AD и ВС параллельны (по признаку параллельности прямых). Также докажем и параллельность сторон АВ и CD и заключим, что АВСD является параллелограммом по определению.
Теорема 28. Если соседние углы четырехугольника, т.е. углы, прилежащие к одной стороне, составляют в сумме 180 градусов, то он является параллелограммом.
Если внутренние односторонные углы в сумме составляют 180 градусов, то прямые праллельны. Значит АВ парал CD и ВС парал AD. Четырехугольник оказывается параллелограммом по определению.
Теорема 29. Если диагонали четырехугольника взаимно делятся в точке пересечения пополам, то четырехугольник — параллелограмм.
Доказательство. Если АО=ОС, ВО=ОD, то треугольники АOD и ВОС равны, как имеющие равны углы (вертикальные) при вершине О, заключенные между парами равных сторон. Из равенства треугольников заключаем, что AD и ВС равны. Также равны стороны АВ и CD, и четырехугольник оказывается параллелограммом по признаку 1.
Теорема 30. Если четырехугольник имеет пару равных, параллельных между собой сторон, то он является параллелограммом.
Пусть в четырехугольнике АВСD стороны АВ и CD параллельны и равны. Проведем диагонали АС и ВD. Из параллельности этих прямых следует равенство накрест лежащих углов АВО=СDО и ВАО=ОСD. Треугольники АВО и CDО равны по стороне и прилежащим к ней углам. Поэтому АО=ОС, ВО=ОD, т.е. диагонали точкой пересечения делятся пополам и четырехугольник оказывается параллелограммом по признаку 4.
В геометрии рассматривают частные случаи параллелограмма.
Свойства параллелограмма, Определение, Формула
- Автор Принц
- Последнее изменение 19-07-2022
Свойства параллелограмма : Параллелограмм — это тип четырехугольника, в котором противоположные стороны параллельны и равны. Параллелограмм – это четырехугольник, у которого при вершинах четыре угла. Крайне важно, чтобы вы понимали свойства параллелограмма, которые будут полезны для вычислений в задачах, связанных со сторонами и углами параллелограмма в двумерной геометрии.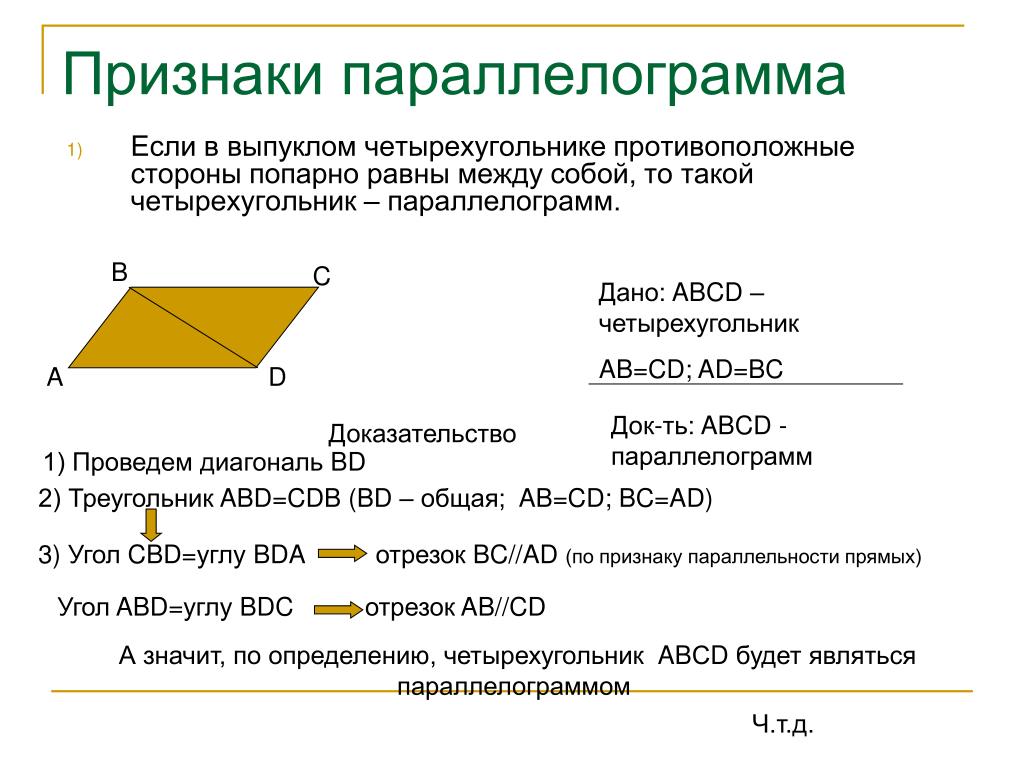 Кроме того, есть много других атрибутов параллелограмма, которые мы подробно раскроем и объясним в этой статье.
Кроме того, есть много других атрибутов параллелограмма, которые мы подробно раскроем и объясним в этой статье.
В евклидовой геометрии параллелограмм представляет собой особый тип четырехугольника, который имеет равные и параллельные противоположные стороны. Противоположные стороны параллелограмма имеют одинаковую длину и противоположные углы параллелограмма равны.
На рисунке выше ABCD — параллелограмм. Здесь АБ || CD и AD || ДО Н.Э.
Кроме того, AB = CD и AD = BC
∠A = ∠C и ∠B = ∠D
Кроме того, ∠A и ∠D являются дополнительными углами, поскольку эти внутренние углы лежат на одной стороне поперечной. Точно так же ∠B и ∠C являются дополнительными углами.
Следовательно,
∠A + ∠D = 180°
∠B + ∠C = 180°
Теперь, когда вы разобрались с определением параллелограмма, давайте посмотрим, каковы все свойства параллелограмма.
Проверьте также свойства других геометрических фигур. Подробно рассмотрим каждое свойство:
- Противоположные стороны параллельны и конгруэнтны.

- Противоположные углы равны.
- Последовательные углы параллелограмма являются дополнительными.
- Если один угол параллелограмма прямой, то все углы прямые.
- Диагонали параллелограмма делят друг друга пополам, и каждая из них делит параллелограмм на два равных треугольника.
- Закон параллелограмма.
Изучите концепции 10-го экзамена CBSE
Давайте разберемся со всеми свойствами параллелограмма на примере:
Свойство 1: Противоположные стороны равны и конгруэнтны.
В параллелограмме ABCD первое свойство гласит, что
AD ≅ BC и CD ≅ AB.
Длина AD равна BC, а длина CD равна AB. Более того, они конгруэнтны, что означает, что противоположные стороны идентичны, и они точно совпадают, когда их накладывают друг на друга или помещают друг на друга.
Свойство 2: Противоположные углы равны и конгруэнтны.
Второе свойство утверждает, что
∠A ≅ ∠C и ∠B ≅ ∠D.
Противоположные углы равны и равны друг другу.
Свойство 3: Смежные углы в параллелограмме являются дополнительными.
Это свойство параллелограмма гласит, что смежные углы параллелограмма являются дополнительными. Это означает, что сумма двух смежных углов равна 180°
Здесь
∠A + ∠D = 180°
∠B + ∠C = 180°
∠A + ∠B = 180°
∠C + ∠D = 180°
Обратите внимание, что сумма всех внутренних углов параллелограмма равна 360°.
Свойство 4: Если один угол параллелограмма прямой, то все углы прямые.
Если известно, что параллелограмм имеет один прямой угол, то с помощью свойства смежных внутренних углов можно доказать, что все его углы прямые.
Следовательно, такой параллелограмм становится ‘ Прямоугольник ’.
Доказательство:
Предположим, что ABCD — параллелограмм, а угол C равен 90°.
Теперь, поскольку ABCD — параллелограмм, то мера угла будет равна мере угла A, то есть
м∠C = m∠A
=90° (Противоположные углы параллелограмма равны)
и m∠A + m∠B = 180 (соответствующие углы)
⇒ 90 + m∠B = 180
⇒ m∠B = 90
Кроме того, m∠B = m∠D
= 90° (противоположные углы параллелограмма равный).
Таким образом, m∠A = m∠B = m∠C = m∠D = 90°.
Так как все углы параллелограмма равны 90°, то ABCD — прямоугольник, по свойствам прямоугольника.
Значит доказано.
Свойство 5: Свойства диагоналей параллелограмма.
Диагонали параллелограмма имеют два атрибута:
(i) Две диагонали делят друг друга пополам.
(ii) Каждая диагональ делит параллелограмм пополам на два равных треугольника.
Первый атрибут утверждает, что две диагонали AC и BD параллелограмма ABCD делят друг друга пополам. Другими словами,
AE = EC и DE = EB.
Второй атрибут утверждает, что диагональ AC делит параллелограмм ABCD на два конгруэнтных треугольника, △ADC и △ABC. Точно так же диагональ BD делит параллелограмм ABCD на два равных треугольника, △ABD и △BCD.
Следовательно, △ADC ≅ △ABC
△ABD ≅ △BCD
Практика 10-го экзамена CBSE Вопросы
Свойство 6: Закон параллелограмма
Этот закон гласит, что сумма квадратов всех сторон параллелограмма равна сумме квадратов его диагоналей.
In other words, in a parallelogram ABCD, we have:
AB 2 + BC 2 + CD 2 + AD 2 = AC 2 + BD 2
Proof:
Пусть AD = BC = x, AB = CD = y и ∠ BAD = α
Используя закон косинусов в △BAD, получаем
x 2 + y 2 – 2xy cos(α) = BD 2 ——-(1)
Мы знаем, что в параллелограмме смежные углы дополнительные. Итак,
∠ADC = 180 – α
Теперь снова используем закон косинусов в △ADC
x 2 + y 2 – 2xy cos(180 – α) = AC 2 —(2)
Применить тригонометрическое тождество cos(180 – x) = – cos x в (2)
x 2 + y 2 + 2xy cos(α) = AC 2
Теперь сумма квадратов диагоналей (BD 2 + AC 2 ) представлены в виде0151 2 + 2xy cos(α)
Упростим приведенное выше выражение, получим;
BD 2 + AC 2 =2x 2 + 2 y 2 ——-(3)
Вышеприведенное уравнение представляется в виде: 2 + 2(BC) 2
Таким образом, закон параллелограмма доказан.
Решенные примеры на параллелограмме
Здесь мы предоставили несколько примеров параллелограмма с решениями:
Вопрос 1: Найдите меры ∠C и ∠B в параллелограмме ABCD.
Решение: По второму свойству параллелограмма противоположные углы параллелограмма равны. Итак, имеем
м∠С = м∠А
Из диаграммы м∠А = 70°.
м∠C = 70°
По третьему свойству параллелограмма последовательные углы параллелограмма являются дополнительными. Итак, имеем
м∠А + м∠В = 180°
Из диаграммы м∠А = 70°.
70° + m∠B = 180°
Вычтите 70° с обеих сторон.
м∠B = 110°
Вопрос 2: Ниже показан параллелограмм с размерами в см:
Чему равен периметр параллелограмма в см?
Решение: Треугольник в левой части рисунка имеет углы 30° и 90°. Поскольку сумма всех углов треугольника должна составлять 180°, мы можем найти угловую меру третьего угла:
30 + 90 = 120
180 − 120 = 60°
Наш третий угол равен 60°, и мы имеем треугольник 30−60−90.
Стороны треугольника 30−60−90 находятся в соответствующем отношении x−x√3−2x. В этом случае сторона, противоположная нашему углу 30°, равна 6, поэтому
x=6
Теперь мы также знаем, что
x√3 = 6√3
∴ 2x = 12
Теперь мы знаем длины всех недостающих сторон. Правая и левая стороны параллелограмма будут равны по 12. Нижняя и верхняя стороны будут равны по 20+6√3. Объединим их, чтобы найти периметр:
Периметр = (2w+2l)
2⋅(12) + 2⋅(20 + 6√3)
24 + 40 + 12√3
64+12√3
Вопрос 3: Найдите периметр следующего параллелограмма:
Решение: Формула для периметра параллелограмма:
Р = 2(сторона) + 2(основание).
Подставляя наши значения, получаем:
P = 2(4√2m) + 2(19m)
P = 38 + 8√2m
Попытка 10-го экзамена CBSE Пробные тесты
В вопросе 4: параллелограмм ABCD, чему равен х?
Решение: Противоположные углы равны, а сумма смежных углов должна составлять 180°.
Следовательно, мы можем составить уравнение для решения для z:
(z – 15) + 2z = 180
3z – 15 = 180
3z = 195
z = 65
Теперь найдите x:
2z = x
= 130°
Получите математические формулы для классов с 6 по 12 ниже:
Свойства параллелограммов: практические вопросы
Здесь мы предоставили некоторые практические вопросы свойства параллелограмма Класс 9 для практики:
| Вопрос 1: Напишите любые два свойства параллелограмма. Вопрос 2: ABCD — параллелограмм, в котором ∠A = 110°. Найдите величину каждого из углов ∠B, ∠C и ∠D. Вопрос 3: Два смежных угла параллелограмма равны. Чему равен каждый из этих углов? Вопрос 4: Два смежных угла параллелограмма относятся как 4:5. Найдите величину каждого из его углов. Вопрос 5: Сумма двух противоположных углов параллелограмма равна 130°. Вопрос 6: Периметр параллелограмма равен 140 см. Если одна из сторон длиннее другой на 10 см, найдите длину каждой из его сторон. Вопрос 7: Назовите каждый из следующих параллелограммов. Вопрос 8: В параллелограмме ABCD O — это любая точка на диагонали BD. Докажите, что площадь △OAB = площади △COB. |
Часто задаваемые вопросы о свойствах параллелограмма
Здесь мы предоставили некоторые из часто задаваемых вопросов, связанных с параллелограммом и их свойствами:
Q1: Как вы доказываете, что фигура является параллелограммом?
A: Двухмерная геометрическая фигура будет параллелограммом, если ее противоположные стороны равны и параллельны друг другу. Если они не равны, фигуру нельзя назвать параллелограммом.
Если они не равны, фигуру нельзя назвать параллелограммом.
Q2: Что такое параллелограмм?
A: Параллелограмм — это особый тип четырехугольника, у которого параллельные и равные противоположные стороны.
Q3: Является ли Square параллелограммом?
О: Да, квадрат удовлетворяет всем условиям параллелограмма. Так что да, это тип параллелограмма. По сути, прямоугольник и ромб также являются разновидностями параллелограмма.
Q4: Каковы 6 свойств параллелограмма?
A: Шесть свойств параллелограмма:
(i) Противоположные стороны параллельны и конгруэнтны.
(ii) Противоположные углы равны.
(iii) Последовательные углы параллелограмма являются дополнительными.
(iv) Если один угол параллелограмма прямой, то все углы прямые.
(v) Диагонали параллелограмма делят друг друга пополам, и каждая из них делит параллелограмм на два конгруэнтных треугольника.
(vi) Сумма квадратов всех сторон параллелограмма равна сумме квадратов его диагоналей.
Q5: Каковы примеры параллелограмма?
A: Параллелограмм – это четырехугольник, у которого две пары противоположных сторон параллельны и конгруэнтны. Кроме того, противоположные углы равны. Некоторые примеры геометрических фигур, являющихся параллелограммами:
(i) Квадрат
(ii) Прямоугольник
(iii) Ромб
Пройдите бесплатные пробные тесты на параллелограмме сейчас
Теперь у вас есть вся необходимая информация о свойствах параллелограммов. Практикуйте больше вопросов и осваивайте эту концепцию. Учащиеся могут использовать Решения NCERT для математики, предоставленные Embibe для подготовки к экзаменам.
Мы надеемся, что эта подробная статья поможет вам. Если у вас есть какие-либо вопросы относительно этой статьи, свяжитесь с нами через раздел комментариев ниже, и мы свяжемся с вами как можно скорее.
Определение параллелограмма, теорема (свойство) и задачи доказательства | Hatsudy
Одной из задач, которые даются в математике, является доказательство. Вам нужно доказать, что фигуры треугольников равны. В этом случае в доказательствах часто используются параллелограммы.
Вас почти никогда не попросят доказать, что фигура является параллелограммом. С другой стороны, часто встречаются задачи, требующие доказательства конгруэнтности каждого треугольника с использованием свойств параллелограмма.
Чтобы решать доказательства, нужно понимать свойства параллелограммов. Итак, каково определение параллелограмма? А какие теоремы вытекают из определения параллелограмма?
Изучив свойства параллелограммов, мы объясним, как решать задачи на доказательство. 9
- 1.1. Две пары противоположных сторон равны по длине Углы равны
- 1.
 4.1 Доказательство того, что диагонали пересекаются в середине
4.1 Доказательство того, что диагонали пересекаются в середине
- 2.1 Если все четыре стороны равны, это ромб
Определение и четыре свойства параллелограммов
Прежде всего, какой формы является параллелограмм? Определение параллелограмма выглядит следующим образом.
- Четырехугольник с двумя парами противоположных сторон, параллельных друг другу.
В параллелограмме стороны четырехугольника, обращенные друг к другу, называются противоположными сторонами. В параллелограмме углы, обращенные друг к другу в четырехугольнике, называются противоположными углами. Противоположные стороны и противоположные углы следующие.
В параллелограмме все противоположные стороны параллельны. В этом случае мы имеем следующие свойства.
- Противоположные стороны двух пар имеют одинаковую длину.

- Противоположные углы двух пар равны.
- Сумма последовательных углов составляет 180°.
- Две диагонали пересекаются посередине.
Давайте рассмотрим свойства каждого из них.
Две пары противоположных сторон равны по длине
Если две пары противоположных сторон параллельны друг другу, длины противоположных сторон всегда будут одинаковыми. Учтите, что длина каждой стороны будет такой же, как показано ниже.
Когда в задаче представлен параллелограмм, попробуйте решить задачу, используя свойство равенства длин противоположных сторон. Например, если длина одной стороны параллелограмма 10 см, то длина противоположной стороны 10 см.
Две пары противоположных углов равны друг другу
В параллелограмме противоположные углы равны. Это свойство часто используется для вычисления углов и доказательства конгруэнтности (или подобия) треугольников.
Помните, что углы, обращенные друг к другу, всегда равны. Например, если один угол равен 60°, противоположный угол также равен 60°.
Например, если один угол равен 60°, противоположный угол также равен 60°.
Доказательство того, что противоположные стороны и углы равны
Итак, правда ли, что в параллелограмме противоположные стороны и противоположные углы равны? Попробуем это доказать. Чтобы доказать это, проведите диагональ, как показано ниже.
Из определения параллелограмма AB||DC и AD||BC. В этом случае рассмотрим △ABC и △CDA. Результат следующий.
- В △ABC и △CDA
- AC = CA: общая линия – (1)
- ∠BAC = ∠DCA: Параллельные прямые имеют равные альтернативные углы – (2)
- ∠ACB = ∠CAD: Параллельные прямые имеют равные противоположные углы – (3)
- Из (1), (2) и (3), так как Угол – Сторона – Угол (ASA), △ABC≅△CDA
Поскольку △ABC≅△CDA, AB= DC и AD=BC. Другими словами, противоположные стороны равны.
Кроме того, ∠B = ∠D, значит, противоположные углы равны. Для других противоположных углов мы можем доказать, что углы равны, проведя другую диагональ и доказав, что треугольники конгруэнтны.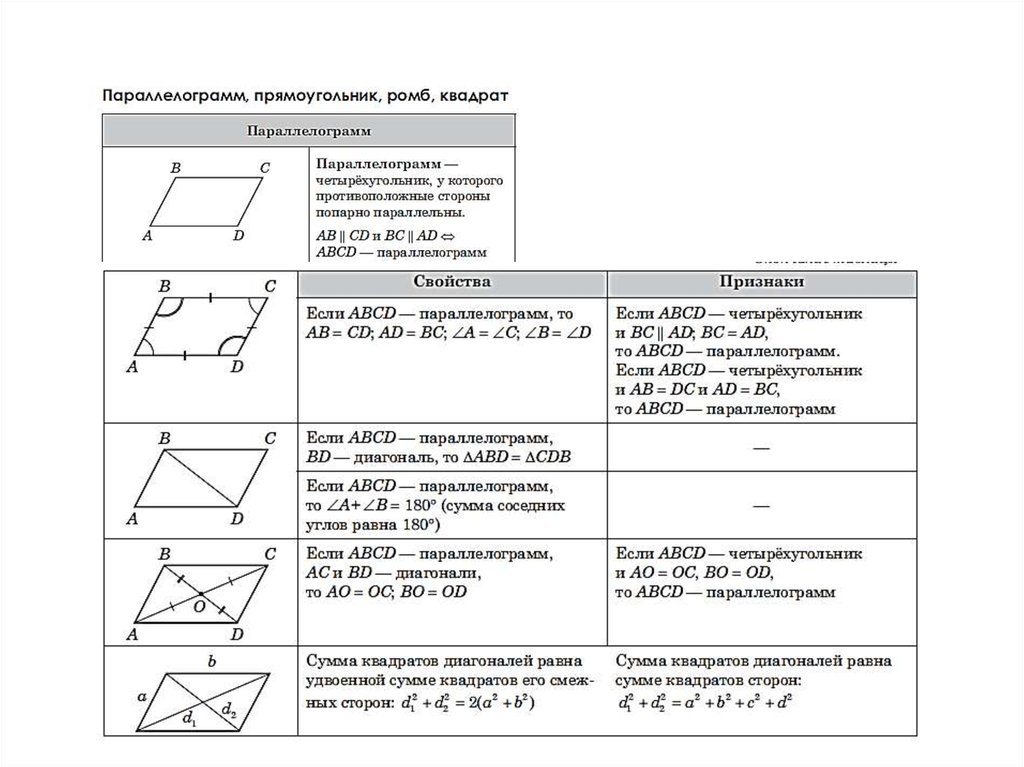 В любом случае в параллелограмме противоположные углы всегда равны.
В любом случае в параллелограмме противоположные углы всегда равны.
Последовательные углы в сумме составляют 180°
Поскольку противоположные углы равны, а прямые параллельны друг другу, параллелограммы обладают другими свойствами. Теорема параллелограмма состоит в том, что сумма последовательных углов равна 180°.
В задачах на параллелограмм мы часто используем эту теорему для решения задач.
Почему сумма последовательных углов составляет 180°? В параллелограмме противоположные стороны параллельны. А в параллельных прямых соответствующие углы имеют одинаковый угол. Поэтому имеем следующее.
В параллелограмме, если известен один угол, можно вычислить все остальные углы. Мы уже объяснили, что противоположные углы равны. Другой угол можно вычислить, вычитая известный угол из 180°.
Две диагонали пересекаются в своих серединах
Существует еще одна теорема о параллелограммах. В параллелограмме можно провести две диагонали, и точка пересечения диагоналей будет серединой. Это происходит следующим образом.
Это происходит следующим образом.
Поскольку это средняя точка, она создает две линии одинаковой длины. Нам часто приходится использовать это свойство для решения геометрических задач.
Доказательство пересечения диагоналей в середине
Почему диагонали параллелограмма пересекаются в середине? Объясним причину с доказательством. Рассмотрим следующий параллелограмм.
Для △AOB и △COD докажите, что они конгруэнтны. Тогда мы можем объяснить, что пересечение диагоналей является серединой.
- В △AOB и △COD
- AB = DC: противоположные стороны параллелограмма равны – (1)
- ∠BAO = ∠DCO: противоположные углы в параллельных прямых равны – (2)
- ∠ ABO = ∠CDO: Альтернативные углы в параллельных прямых равны – (3)
- Из (1), (2) и (3), поскольку Угол – Сторона – Угол (ASA), △AOB≅△COD
Поскольку △AOB≅△COD, AO=CO и BO=DO. Следовательно, мы знаем, что в параллелограмме точка пересечения диагоналей является серединой.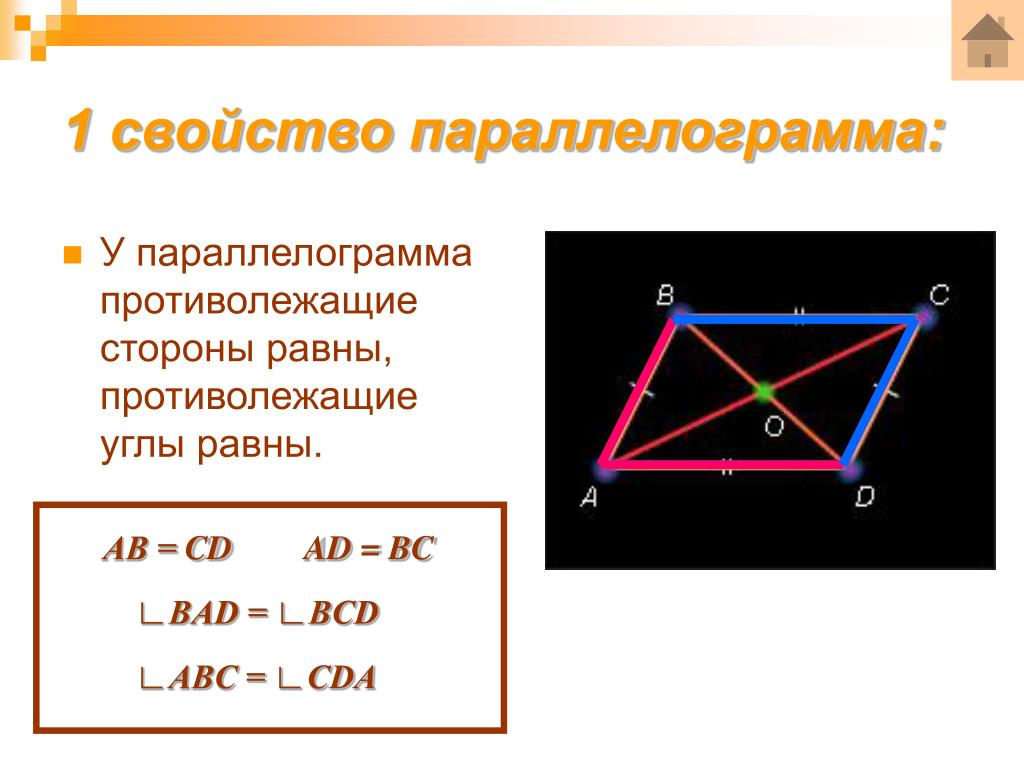
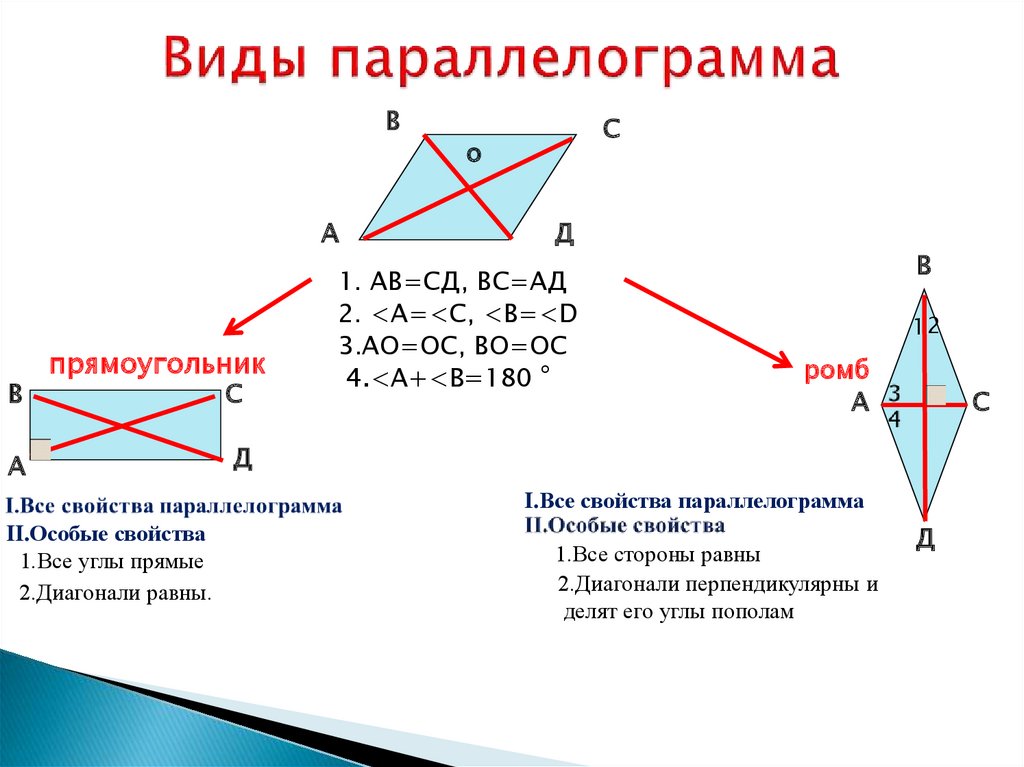
Когда все четыре угла равны, получается прямоугольник
Среди параллелограммов есть некоторые особые формы. Один из них прямоугольник. При соблюдении определенных условий параллелограмм становится прямоугольником. Как упоминалось выше, параллелограммы имеют равные противоположные углы. Если все углы равны, то это прямоугольник.
Чтобы все углы были равны, углы должны быть 90°. Хотя длины сторон могут быть разными, но если все углы равны, то верно следующее.
Прямоугольник имеет параллельные противоположные стороны и является разновидностью параллелограмма. Однако параллелограмм, у которого все углы равны, называется прямоугольником.
Если все четыре стороны равны, то это ромб
Существует еще один особый вид параллелограмма. Это ромб. У ромба все стороны равны по длине.
В прямоугольнике все углы равны. С другой стороны, в ромбе все стороны равны по длине, но не обязательно, чтобы все углы были равны.
По определению ромба все четыре стороны равны по длине. Теорема, полученная из этого определения, состоит в том, что диагонали пересекаются перпендикулярно. Это происходит следующим образом.
Теорема, полученная из этого определения, состоит в том, что диагонали пересекаются перпендикулярно. Это происходит следующим образом.
Проводя диагонали ромба, мы можем построить прямоугольные треугольники.
-Квадрат имеет свойства прямоугольника и ромба
А как насчет квадрата, у которого все углы и длины сторон одинаковы? В этом случае он будет обладать свойствами и прямоугольника, и ромба. Конечно, диагонали пересекаются перпендикулярно.
Упражнение: доказательство соответствия
Q1: Докажите следующий рисунок.
Имеется параллелограмм ABCD. Пусть O будет точкой пересечения диагоналей, и докажите, что △AOE≅△COF, когда OE=OF.
A1: Ответ.
Почему важно понимать свойства параллелограмма? Это потому, что без понимания определения и теоремы параллелограмма вы не сможете решать математические задачи. Изучите свойства параллелограммов, чтобы решать задачи.
Используя определения и теоремы параллелограмма, мы можем доказать следующее.
- В △AOE и △COF
- OE = OF: Дано – (1)
- ∠AOE = ∠COF: Вертикальные углы равны – (2)
- AO=CO: Диагонали в параллелограмме пересекаются в середине – (3)
- Из (1), (2) и (3), поскольку Сторона – Угол – Сторона (SAS), △AOE≅△COF
В задачах по геометрии, в которых используются параллелограммы, существует высокая вероятность что вы будете использовать теорему о параллелограмме для решения проблемы. Обязательно запомните свойства параллелограммов, потому что вы не сможете решить их, если не запомните их.
Использование свойств параллелограммов для решения задач на доказательства
В математике много раз приходится решать задачи с фигурами. Итак, вам нужно понять свойства параллелограмма.
Как и во всех задачах по геометрии, вам нужно помнить, какими свойствами обладает фигура, чтобы решить задачу. Поэтому важно помнить не только о свойствах треугольников, таких как равнобедренные треугольники и прямоугольные треугольники, но и о параллелограммах.
Параллелограмм — это фигура, у которой две пары противоположных сторон параллельны. Из этого определения можно вывести четыре основных свойства. Используя эти теоремы, мы можем решать задачи, связанные с формами.
В частности, свойства параллелограммов часто используются при доказательстве фигур. Докажем равенство (или подобие) треугольников, используя свойства параллелограмма.
Рейтинг
Потребности, желания и требования: три основных понятия в маркетинге (с примерами)
ЯМР-связывание бензольных колец: орто-мета-пик и химические сдвиги
Ориентация и реакционная способность ароматических соединений: орто, мета, пара Проявляющий растворитель
Теорема о вписанном угле: центральный угол и длина дуги
Параллелограммы: значение, примеры и свойства
Подумайте о разметке на пешеходном переходе. Это замкнутые 4-сторонние фигуры с противоположными сторонами, которые равны и параллельны. Такие фигуры называются параллелограммами.
Такие фигуры называются параллелограммами.
Четырехсторонняя плоская фигура известна как четырехугольник . В этой статье мы рассмотрим особый тип четырехугольника, известный как параллелограмм .
Определение параллелограмма
Четырехугольник с двумя парами противоположных параллельных сторон называется параллелограммом .
Мы знаем, что у четырехугольника 4 стороны. В параллелограмме эти 4 стороны состоят из 2 пар противоположных параллельных сторон.
На следующей диаграмме показан параллелограмм.
Иллюстрация параллелограмма — StudySmarter Originals
На приведенном выше рисунке:
- AB // CD
- AC // BD
Свойства параллелограммов
В дополнение к вышесказанному мы можем определить различные свойства параллелограммов.
Мы будем использовать следующий параллелограмм ABDC с диагоналями d 1 =BC и d 2 =AD для иллюстрации свойств.
Параллелограмм с диагоналями d1 и d2 — StudySmarter Originals
В параллелограмме противоположные стороны равны.
Это означает, что в приведенном выше параллелограмме AB=CD и AC=BD.
В параллелограмме противоположные углы равны.
Это означает, что в приведенном выше параллелограмме , ∠CAB=∠CDB и ∠ACD=∠ABD
В параллелограмме последовательные углы являются дополнительными.
В любом параллелограмме можно выделить 4 пары последовательных углов. Они всегда являются дополнительными (что означает, что сумма углов составляет 180 градусов). В приведенном выше параллелограмме:
∠CAB + ∠ABD = 180,
∠ABD + ∠BDC = 180,
∠BDC + ∠DCA = 180,
∠DCA + ∠CAB = 180 .

Если любой угол в параллелограмме прямой, это означает, что все 4 внутренних угла прямые.
Это прямое следствие вышеуказанного свойства. Если какой-либо угол в параллелограмме прямой, то прилежащий к нему угол равен 180-90=90 (согласно указанному выше свойству). В свою очередь, следующий смежный угол будет прямым и так далее. Следовательно, в любом параллелограмме, если вы идентифицируете любой угол как прямой, вы можете прямо заключить, что все 4 угла прямые.
Диагонали параллелограмма делят друг друга пополам.
В приведенном выше параллелограмме точка O является серединой обеих диагоналей d 1 и д 2 .
Каждая диагональ параллелограмма делит параллелограмм на два равных треугольника .
В приведенном выше параллелограмме диагональ d 1 разделила бы параллелограмм на два конгруэнтных треугольника, ΔABC и ΔBCD.
 Точно так же диагональ d 2 разделила бы параллелограмм на два конгруэнтных треугольника, ΔABD и ΔACD.
Точно так же диагональ d 2 разделила бы параллелограмм на два конгруэнтных треугольника, ΔABD и ΔACD.
Площадь параллелограмма
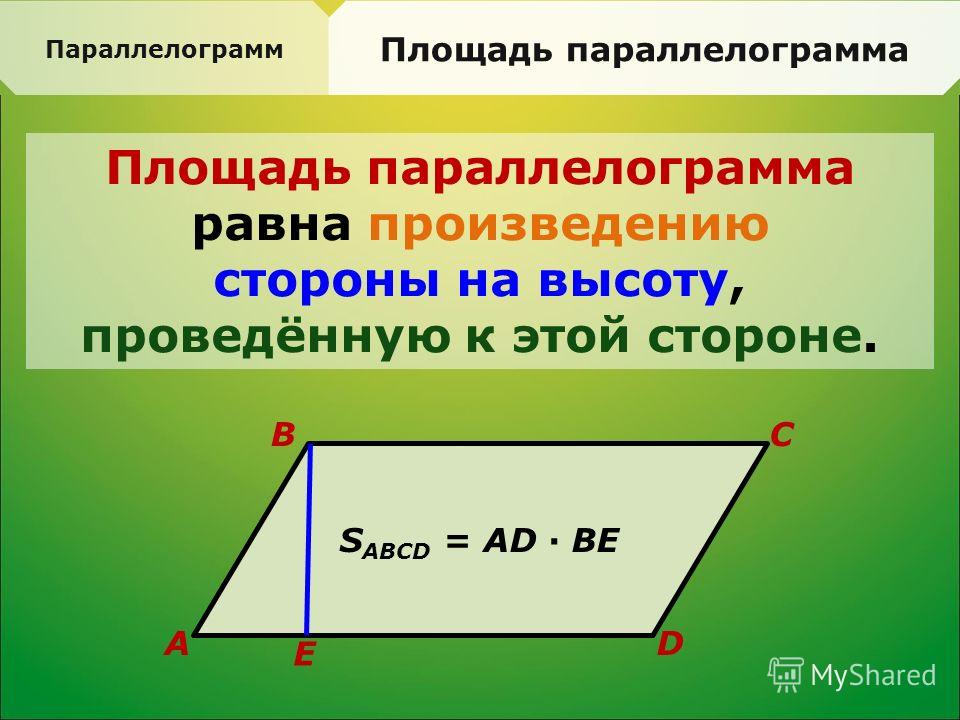
Рассмотрим следующий параллелограмм:Параллелограмм с основанием b и высотой h — StudySmarter Originals
Площадь параллелограмма определяется по формуле:
Площадь = b × h
где b = основание, h = высота
Теперь значение b равно длине стороны AB, которая здесь считается основанием. Условно за основание принимают одну из длинных сторон параллелограмма. Значение h является высотой параллелограмма. Его также иногда называют высотой. Высота – это длина линии, проведенной от основания к противоположной стороне. Высота перпендикулярна основанию.
Параллелограмм: Примеры задач
В этом разделе мы рассмотрим примеры математических задач, которые могут возникнуть при работе с параллелограммами и их свойствами.
Параллелограмм с основанием 8 футов имеет площадь 20 футов 2 . Какова высота параллелограмма?
Какова высота параллелограмма?
В следующем параллелограмме ∠ABD = 47°, ∠CBD = 72°. Найдите ∠CDA.
Иллюстрация параллелограмма — StudySmarter Originals
∠ABC = ∠ABD + ∠CBD
= 47 + 72 = 119.
Противолежащие углы параллелограмма равны. Следовательно,
∠CDA = ∠ABC = 119°
Различные типы параллелограммов
В этом разделе мы определим 3 специальных типа параллелограммов, каждый со своими характеристиками и свойствами:
Ромб
0Прямоугольник
Квадрат
Ромб
0009 равносторонний ). Оказывается, противоположные пары сторон ромба всегда параллельны. Это делает каждый ромб параллелограммом. И наоборот, мы можем сказать, что равносторонний параллелограмм является ромбом. Диагонали ромба всегда пересекаются под прямым углом.
Поскольку ромб является особым типом параллелограмма, ромб также обладает всеми свойствами параллелограмма.
Прямоугольник
Прямоугольник — это параллелограмм, все внутренние углы которого прямые. Так как в прямоугольнике все углы равны, то равноугольный .
Поскольку прямоугольник представляет собой особый тип параллелограмма, он также обладает всеми свойствами параллелограмма.
Квадрат
Квадрат – это четырехугольник, у которого все 4 стороны равны, а все углы прямые. Это делает квадрат типом параллелограмма, типом ромба и типом прямоугольника! Таким образом, квадрат демонстрирует все свойства параллелограмма, ромба и прямоугольника.
Параллелограммы — ключевые выводы
- Четырехугольник с двумя парами противоположных параллельных сторон называется параллелограммом.
- В параллелограмме противоположные стороны равны.
- В параллелограмме противоположные углы равны.
- В параллелограмме смежные углы являются дополнительными.
- Если любой угол в параллелограмме прямой, это означает, что все 4 внутренних угла прямые.


 То есть, если – параллелограмм, то (см. Рис. 1).
То есть, если – параллелограмм, то (см. Рис. 1).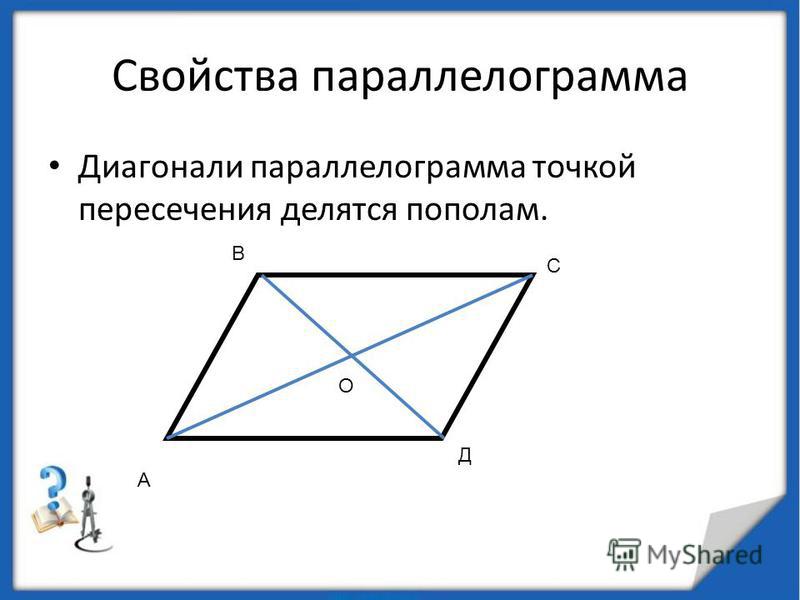
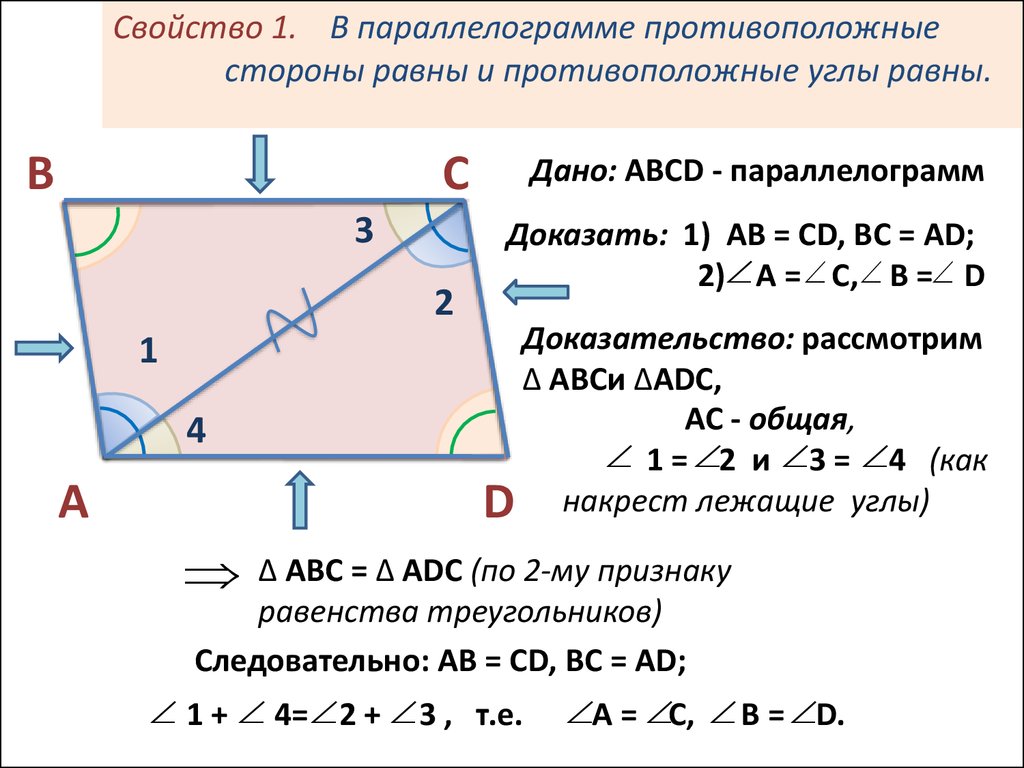 Является ли данный четырёхугольник параллелограммом, если , , , . Ответ обоснуйте.
Является ли данный четырёхугольник параллелограммом, если , , , . Ответ обоснуйте.

 е., например, что . Это означает, что точка является серединой стороны . Что и требовалось доказать.
е., например, что . Это означает, что точка является серединой стороны . Что и требовалось доказать. Затем решим достаточно много задач, которые связаны с этой фигурой.
Затем решим достаточно много задач, которые связаны с этой фигурой.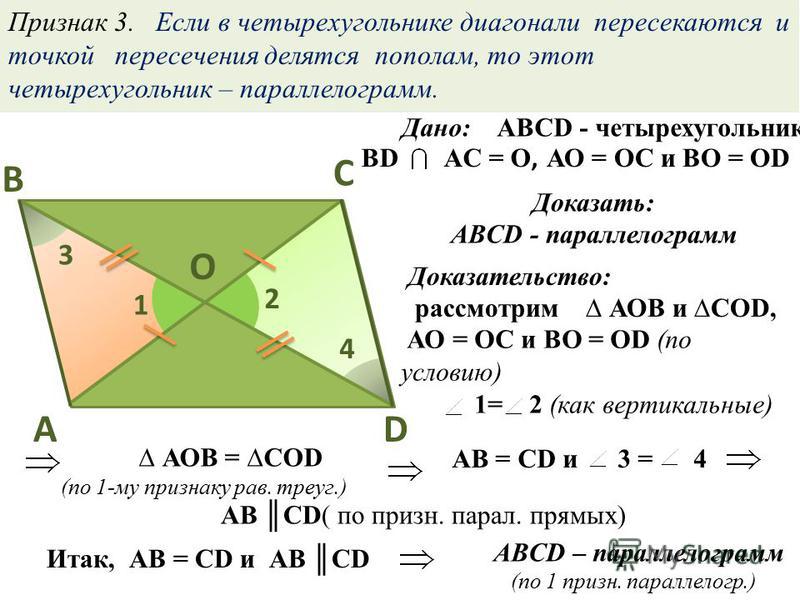
 Найдите величину каждого из его углов.
Найдите величину каждого из его углов.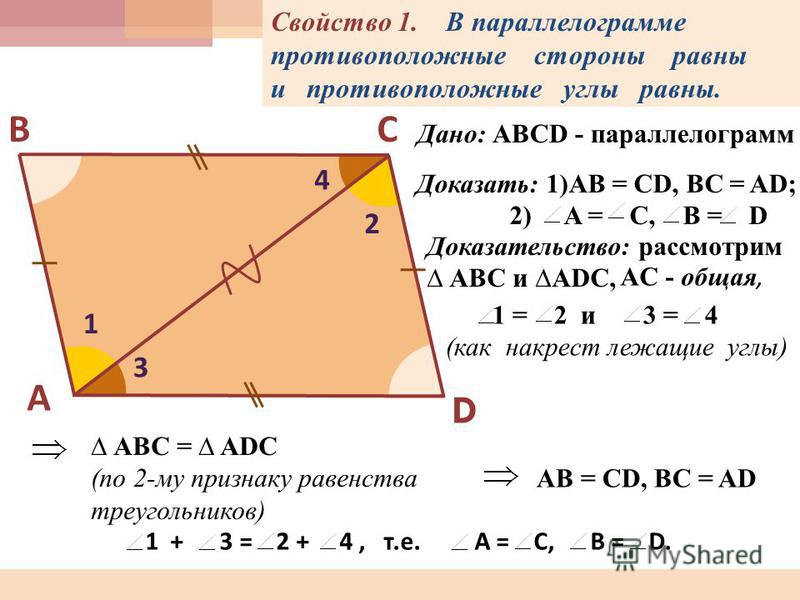 4.1 Доказательство того, что диагонали пересекаются в середине
4.1 Доказательство того, что диагонали пересекаются в середине

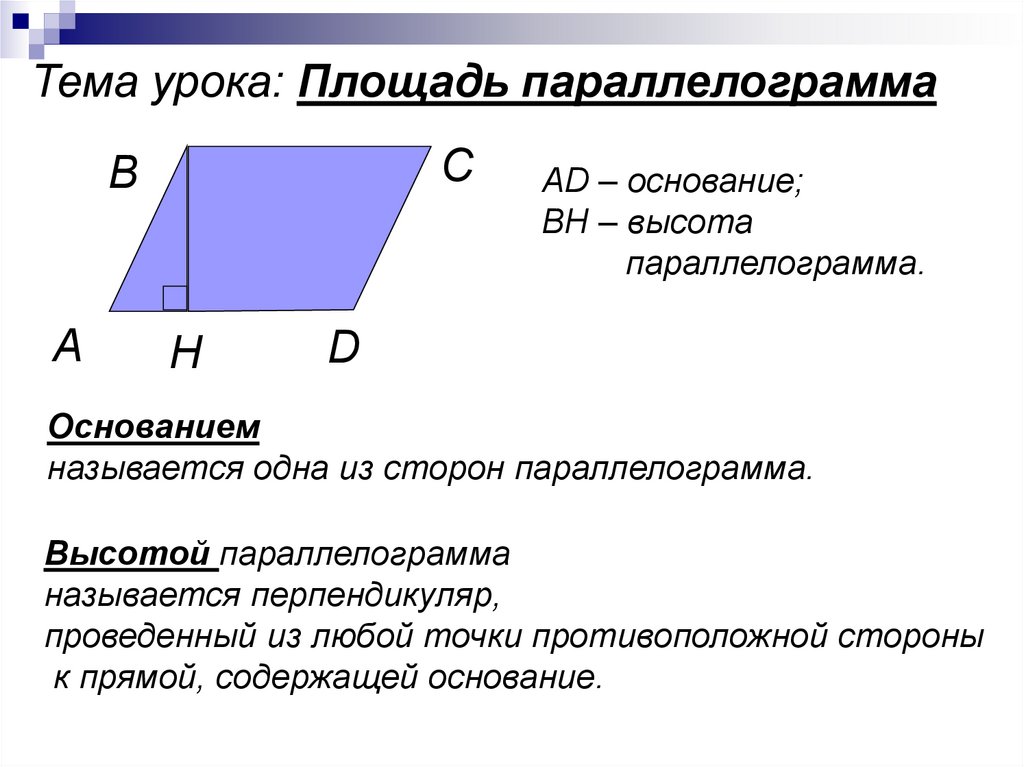 Точно так же диагональ d 2 разделила бы параллелограмм на два конгруэнтных треугольника, ΔABD и ΔACD.
Точно так же диагональ d 2 разделила бы параллелограмм на два конгруэнтных треугольника, ΔABD и ΔACD.