Параллелограмм с равными сторонами: Ничего не найдено

Параллелограмм С Равными Сторонами 4 Буквы

Решение этого кроссворда состоит из 4 букв длиной и начинается с буквы Р

---

Ниже вы найдете правильный ответ на Параллелограмм с равными сторонами 4 буквы, если вам нужна дополнительная помощь в завершении кроссворда, продолжайте навигацию и воспользуйтесь нашей функцией поиска.

ответ на кроссворд и сканворд

Четверг, 6 Июня 2019 Г.

---

---

РОМБ

предыдущий следующий

---

---

ты знаешь ответ ?

ответ:

связанные кроссворды

1. Ромб
1. Частный случай дельтоида
2. Геометрическая фигура
2. Ромб
1. Высшего офицерского знака различия такой формы на петлицах в красной армии (с 1919 по 1943 г. ) 4 буквы
2. В математике: параллелограмм, все стороны которого равны 4 буквы
3. Как называется площадка в бейсболе 4 буквы
4. Название офицерского знака различия в петлицах в красной армии с 1919 по 1943 год 4 буквы

похожие кроссворды

1. Четырёхугольник с равными сторонами
2. Параллелограмм, у которого один из углов прямой
3. В математике: призма, основанием которой служит параллелограмм 14 букв
4. В математике: параллелограмм, все стороны которого равны 4 буквы
5. Параллелограмм, все стороны которого равны 4 буквы
6. Это параллелограмм 4 буквы
7. Призма, основанием которой является параллелограмм 14 букв
8. Равносторонний параллелограмм 4 буквы
9. Ровный параллелограмм 4 буквы
10. Параллелограмм 4 буквы
11. Параллелограмм
12. То же, что параллелограмм
13. Линия, проходящая через точки с равными значениями барической тенденции
14. (октагон) восьмиугольный объем с равными гранями
15. Его с равными правами можно назвать александровичем 7 букв
16. Равными частями 7 букв
17. Промежуток между приблизительно равными частями чего-нибудь 8 букв

Параллелограмм с равными сторонами.

Параллелограмм

Параллелограммом называется четырехугольник, противоположные стороны которого попарно параллельны (рис. 233).

Для произвольного параллелограмма имеют место следующие свойства:

1. Противоположные стороны параллелограмма равны.

Доказательство. В параллелограмме ABCD проведем диагональ АС. Треугольники ACD и АС В равны, как имеющие общую сторону АС и две пары равных углов, прилежащих к ней:

(как накрест лежащие углы при параллельных прямых AD и ВС). Значит, и как стороны равных треугольников, лежащие против равных углов, что и требовалось доказать.

2. Противоположные углы параллелограмма равны:

3. Соседние углы параллелограмма, т. е. углы, прилежащие к одной стороне, составляют в сумме и т. д.

Доказательство свойств 2 и 3 сразу получается из свойств углов при параллельных прямых.

4. Диагонали параллелограмма делят друг друга в точке их пересечения пополам. Иначе говоря,

Доказательство. Треугольники AOD и ВОС равны, так как равны их стороны AD и ВС (свойство 1) и углы, к ним прилежащие (как накрест лежащие углы при параллельных прямых).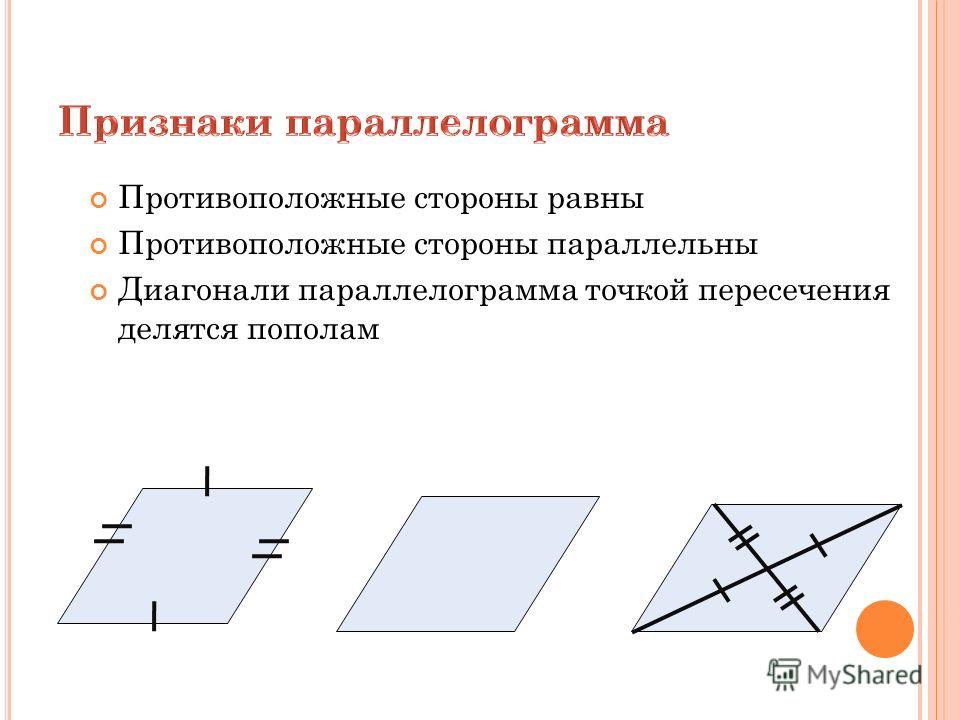

Отсюда следует и равенство соответствующих сторон этих треугольников: АО что и требовалось доказать.

Каждое из названных четырех свойств характеризует параллелограмм, или, как говорят, является его характеристическим свойством, т. е. всякий четырехугольник, обладающий хотя бы одним из этих свойств, является параллелограммом (и, значит, обладает и всеми остальными тремя свойствами).

Проведем доказательство для каждого свойства отдельно.

1″. Если противоположные стороны четырехугольника попарно равны, то он является параллелограммом.

Доказательство. Пусть у четырехугольника ABCD стороны AD и ВС, АВ и CD соответственно равны (рис. 233). Проведем диагональ АС. Треугольники ABC и CDА будут равны, как имеющие три пары равных сторон.

Но тогда углы ВАС и DCА равны и . Параллельность сторон ВС и AD следует из равенства углов CAD и АСВ.

2. Если у четырехугольника две пары противоположных углов равны, то он является параллелограммом.

Доказательство. Пусть .

Так как то и стороны AD и ВС параллельны (по признаку параллельности прямых).

3. Предоставляем формулировку и доказательство читателю.

4. Если диагонали четырехугольника взаимно делятся в точке пересечения пополам, то четырехугольник — параллелограмм.

Доказательство. Если АО = ОС, BO = OD (рис. 233), то треугольники AOD и ВОС равны, как имеющие равные углы (вертикальные!) при вершине О, заключенные между парами равных сторон АО и СО, ВО и DO. Из равенства треугольников заключаем, что стороны AD и ВС равны. Также равны стороны АВ и CD, и четырехугольник оказывается параллелограммом по характеристическому свойству Г.

Таким образом, для того чтобы доказать, что данный четырехугольник является параллелограммом, достаточно убедиться в справедливости любого из четырех свойств. Читателю предлагается самостоятельно доказать еще одно характеристическое свойство параллелограмма.

5. Если четырехугольник имеет пару равных, параллельных между собой сторон, то он является параллелограммом.

Иногда какая-нибудь пара параллельных сторон параллелограмма называется его основаниями, тогда две другие называются боковыми сторонами. Отрезок прямой, перпендикулярной к двум сторонам параллелограмма, заключенный между ними, называется высотой параллелограмма. Параллелограмм на рис. 234 имеет высоту h, проведенную к сторонам AD и ВС, вторая его высота представлена отрезком .

Это четырёхугольник, противоположные стороны которого попарно параллельны.

Свойство 1 . Любая диагональ параллелограмма делит его на два равных треугольника.

Доказательство . По II признаку (накрест лежащие углы и общая сторона).

Теорема доказана .

Свойство 2 . В параллелограмме противолежащие стороны равны, противолежащие углы равны.

Доказательство .
Аналогично,

Теорема доказана .

Свойство 3. В параллелограмме диагонали точкой пересечения делятся пополам.

Доказательство .

Теорема доказана .

Свойство 4 . Биссектриса угла параллелограмма, пересекая противоположную сторону, делит его на равнобедренный треугольник и трапецию. (Ч. сл. — вершину — два равнобедренных?-ка).

Доказательство .

Теорема доказана .

Свойство 5 . В параллелограмме отрезок с концами на противоположных сторонах, проходящий через точку пересечения диагоналей, делится этой точкой пополам.

Доказательство .

Теорема доказана .

Свойство 6 . Угол между высотами, опущенными из вершины тупого угла параллелограмма, равен острому углу параллелограмма.

Доказательство .

Теорема доказана .

Свойство 7 . Сумма углов параллелограмма, прилежащих к одной стороне, равна 180°.

Доказательство .

Теорема доказана .

Построение биссектрисы угла. Свойства биссектрисы угла треугольника.

1) Построить произвольный луч DE.

2) На данном луче построить произвольную окружность с центром в вершине и такую же
с центром в начале построенного луча.

3) F и G — точки пересечения окружности со сторонами данного угла, H — точка пересечения окружности с построенным лучом

Построить окружность с центром в точке H и радиусом, равным FG.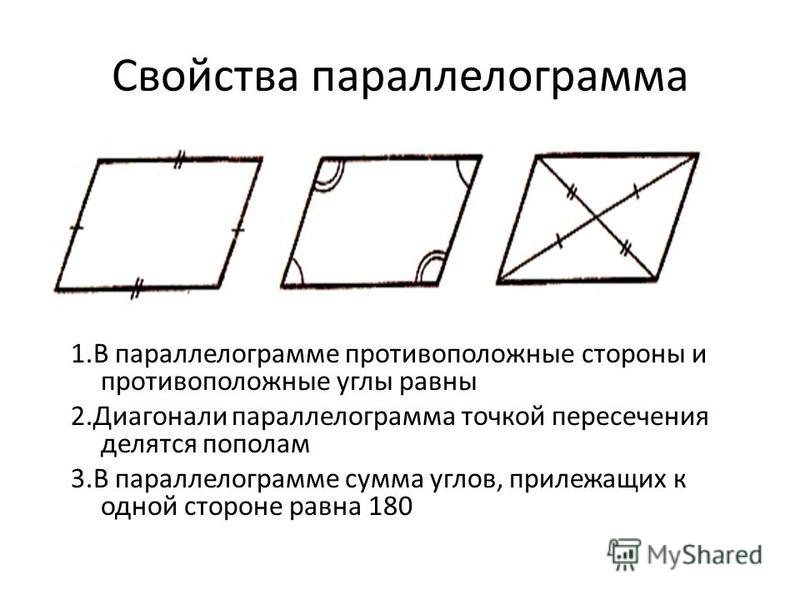

5) I — точка пересечения окружностей построенного луча.

6) Провести прямую через вершину и I.

IDH — требуемый угол.
)

Свойство 1 . Биссектриса угла треугольника разбивает противоположную сторону пропорционально прилежащим сторонам.

Доказательство . Пусть x, y-отрезки стороны c. Продолжим луч BC. На луче BC отложим от C отрезок CK, равный AC.

Параллелограмм — четырехугольник, у которого противоположные стороны попарно параллельны. Площадь параллелограмма равна произведению его основания (a) на высоту (h). Также можно найте его площадь через две стороны и угол и через диагонали.

Свойства параллелограмма

1. Противоположные стороны тождественны.

Первым делом проведем диагональ \(AC \) . Получаются два треугольника: \(ABC \) и \(ADC \) .

Так как \(ABCD \) — параллелограмм, то справедливо следующее:

\(AD || BC \Rightarrow \angle 1 = \angle 2 \) как лежащие накрест.

\(AB || CD \Rightarrow \angle3 = \angle 4 \) как лежащие накрест.

Следовательно, (по второму признаку: и \(AC \) — общая).

И, значит, \(\triangle ABC = \triangle ADC \) , то \(AB = CD \) и \(AD = BC \) .

2. Противоположные углы тождественны.

Согласно доказательству свойства 1 мы знаем, что \(\angle 1 = \angle 2, \angle 3 = \angle 4 \) . Таким образом сумма противоположных углов равна: \(\angle 1 + \angle 3 = \angle 2 + \angle 4 \) . Учитывая, что \(\triangle ABC = \triangle ADC \) получаем \(\angle A = \angle C \) , \(\angle B = \angle D \) .

3. Диагонали разделены пополам точкой пересечения.

По свойству 1 мы знаем, что противоположные стороны тождественны: \(AB = CD \) . Еще раз отметим накрест лежащие равные углы.

Таким образом видно, что \(\triangle AOB = \triangle COD \) по второму признаку равенства треугольников (два угла и сторона между ними). То есть, \(BO = OD \) (напротив углов \(\angle 2 \) и \(\angle 1 \) ) и \(AO = OC \) (напротив углов \(\angle 3 \) и \(\angle 4 \) соответственно).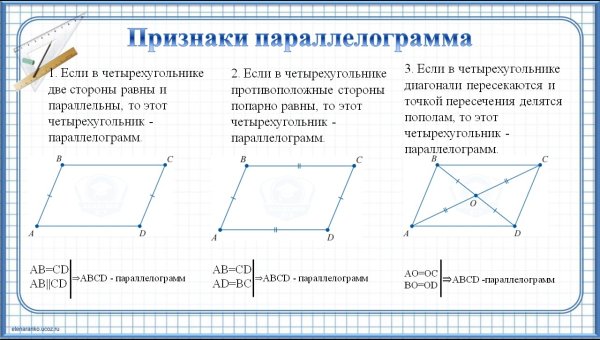

Признаки параллелограмма

Если лишь один признак в вашей задаче присутствует, то фигура является параллелограммом и можно использовать, все свойства данной фигуры.

Для лучшего запоминания, заметим, что признак параллелограмма будет отвечать на следующий вопрос — «как узнать?» . То есть, как узнать, что заданная фигура это параллелограмм.

1. Параллелограммом является такой четырехугольник, у которого две стороны равны и параллельны.

\(AB = CD \) ; \(AB || CD \Rightarrow ABCD \) — параллелограмм.

Рассмотрим подробнее. Почему \(AD || BC \) ?

\(\triangle ABC = \triangle ADC \) по свойству 1 : \(AB = CD \) , \(\angle 1 = \angle 2 \) как накрест лежащие при параллельных \(AB \) и \(CD \) и секущей \(AC \) .

Но если \(\triangle ABC = \triangle ADC \) , то \(\angle 3 = \angle 4 \) (лежат напротив \(AD || BC \) (\(\angle 3 \) и \(\angle 4 \) — накрест лежащие тоже равны).

Первый признак верен.

2. Параллелограммом является такой четырехугольник, у которого противоположные стороны равны.

{\circ} \) . Но \(\alpha \) и \(\beta \) являются внутренними односторонними при секущей \(AB \) .

Видеокурс «Получи пятерку» включает все темы, необходимые для успешной сдачи ЕГЭ по математике на 60-65 баллов. Полностью все задачи 1-13 Профильного ЕГЭ по математике. Подходит также для сдачи Базового ЕГЭ по математике. Если вы хотите сдать ЕГЭ на 90-100 баллов, вам надо решать часть 1 за 30 минут и без ошибок!

Курс подготовки к ЕГЭ для 10-11 класса, а также для преподавателей. Все необходимое, чтобы решить часть 1 ЕГЭ по математике (первые 12 задач) и задачу 13 (тригонометрия). А это более 70 баллов на ЕГЭ, и без них не обойтись ни стобалльнику, ни гуманитарию.

Вся необходимая теория. Быстрые способы решения, ловушки и секреты ЕГЭ. Разобраны все актуальные задания части 1 из Банка заданий ФИПИ. Курс полностью соответствует требованиям ЕГЭ-2018.

Курс содержит 5 больших тем, по 2,5 часа каждая. Каждая тема дается с нуля, просто и понятно.

Сотни заданий ЕГЭ. Текстовые задачи и теория вероятностей. Простые и легко запоминаемые алгоритмы решения задач. Геометрия. Теория, справочный материал, разбор всех типов заданий ЕГЭ. Стереометрия. Хитрые приемы решения, полезные шпаргалки, развитие пространственного воображения. Тригонометрия с нуля — до задачи 13. Понимание вместо зубрежки. Наглядное объяснение сложных понятий. Алгебра. Корни, степени и логарифмы, функция и производная. База для решения сложных задач 2 части ЕГЭ.

При-зна-ки па-рал-ле-ло-грам-ма

1. Определение и основные свойства параллелограмма

Нач-нем с того, что вспом-ним опре-де-ле-ние па-рал-ле-ло-грам-ма.

Опре-де-ле-ние. Па-рал-ле-ло-грамм — че-ты-рех-уголь-ник, у ко-то-ро-го каж-дые две про-ти-во-по-лож-ные сто-ро-ны па-рал-лель-ны (см. Рис. 1).

Рис. 1. Па-рал-ле-ло-грамм

Вспом-ним ос-нов-ные свой-ства па-рал-ле-ло-грам-ма :

Для того, чтобы иметь воз-мож-ность поль-зо-вать-ся всеми этими свой-ства-ми, необ-хо-ди-мо быть уве-рен-ным, что фи-гу-ра, о ко-то-рой идет речь, — па-рал-ле-ло-грамм.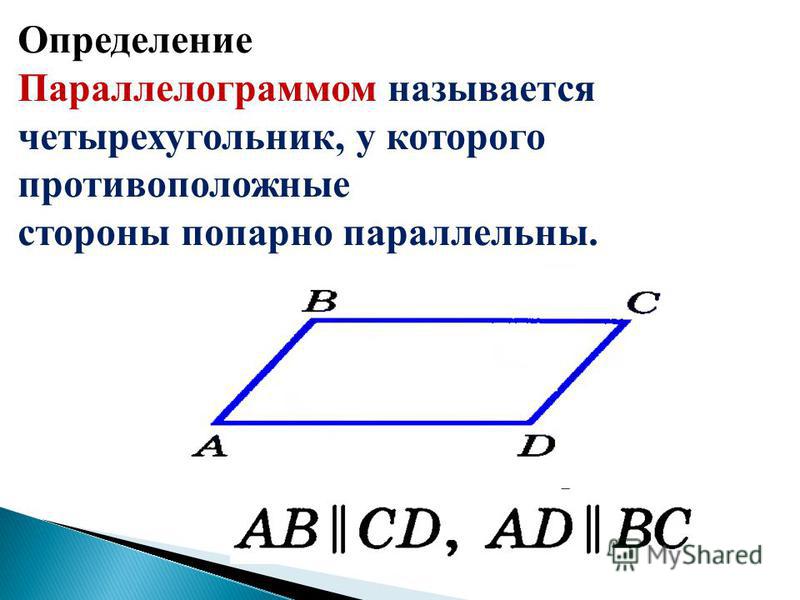 Для этого необ-хо-ди-мо знать такие факты, как при-зна-ки па-рал-ле-ло-грам-ма. Пер-вые два из них мы се-год-ня и рас-смот-рим.

2. Первый признак параллелограмма

Тео-ре-ма. Пер-вый при-знак па-рал-ле-ло-грам-ма. Если в че-ты-рех-уголь-ни-ке две про-ти-во-по-лож-ные сто-ро-ны равны и па-рал-лель-ны, то этот че-ты-рех-уголь-ник — па-рал-ле-ло-грамм . .

Рис. 2. Пер-вый при-знак па-рал-ле-ло-грам-ма

До-ка-за-тель-ство. Про-ве-дем в че-ты-рех-уголь-ни-ке диа-го-наль (см. Рис. 2), она раз-би-ла его на два тре-уголь-ни-ка. За-пи-шем, что мы знаем об этих тре-уголь-ни-ках:

по пер-во-му при-зна-ку ра-вен-ства тре-уголь-ни-ков.

Из ра-вен-ства ука-зан-ных тре-уголь-ни-ков сле-ду-ет, что по при-зна-ку па-рал-лель-но-сти пря-мых при пе-ре-се-че-нии их се-ку-щей. Имеем, что:

До-ка-за-но.

3. Второй признак параллелограмма

Тео-ре-ма. Вто-рой при-знак па-рал-ле-ло-грам-ма. Если в че-ты-рех-уголь-ни-ке каж-дые две про-ти-во-по-лож-ные сто-ро-ны равны, то этот че-ты-рех-уголь-ник — па-рал-ле-ло-грамм . .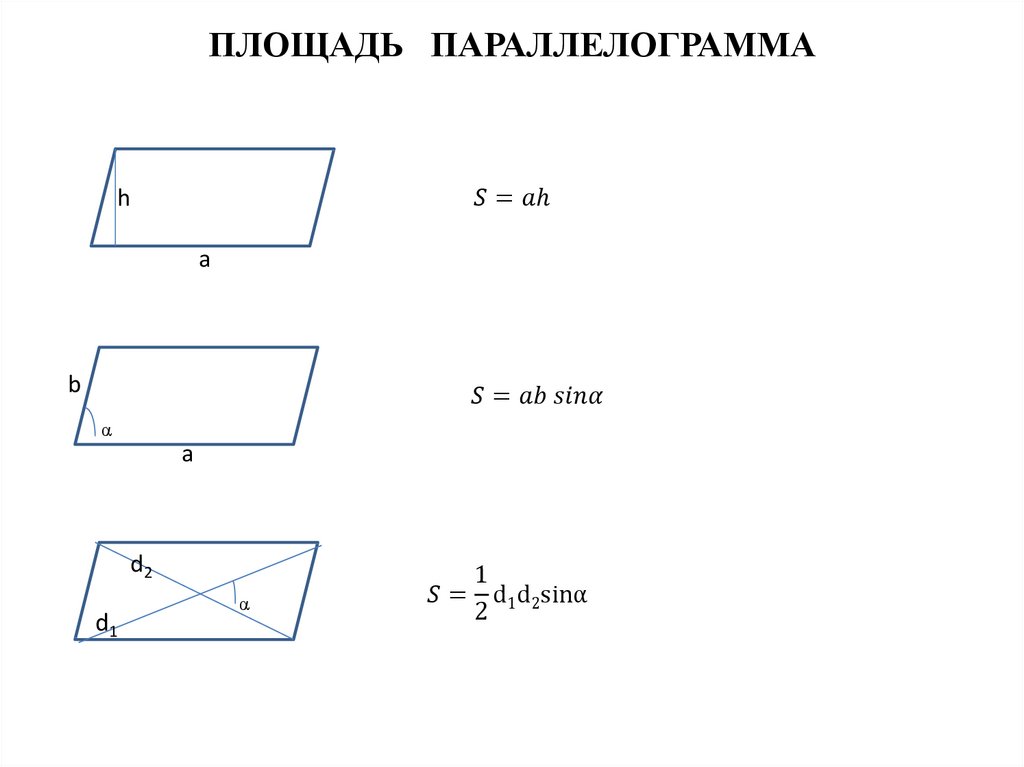

Рис. 3. Вто-рой при-знак па-рал-ле-ло-грам-ма

До-ка-за-тель-ство. Про-ве-дем в че-ты-рех-уголь-ни-ке диа-го-наль (см. Рис. 3), она раз-би-ва-ет его на два тре-уголь-ни-ка. За-пи-шем, что мы знаем об этих тре-уголь-ни-ках, ис-хо-дя из фор-му-ли-ров-ки тео-ре-мы:

по тре-тье-му при-зна-ку ра-вен-ства тре-уголь-ни-ков.

Из ра-вен-ства тре-уголь-ни-ков сле-ду-ет, что и по при-зна-ку па-рал-лель-но-сти пря-мых при пе-ре-се-че-нии их се-ку-щей. По-лу-ча-ем:

па-рал-ле-ло-грамм по опре-де-ле-нию. Что и тре-бо-ва-лось до-ка-зать.

До-ка-за-но.

4. Пример на применение первого признака параллелограмма

Рас-смот-рим при-мер на при-ме-не-ние при-зна-ков па-рал-ле-ло-грам-ма.

При-мер 1. В вы-пук-лом че-ты-рех-уголь-ни-ке Найти: а) углы че-ты-рех-уголь-ни-ка; б) сто-ро-ну .

Ре-ше-ние. Изоб-ра-зим Рис. 4.

па-рал-ле-ло-грамм по пер-во-му при-зна-ку па-рал-ле-ло-грам-ма.

А. по свой-ству па-рал-ле-ло-грам-ма о про-ти-во-по-лож-ных углах, по свой-ству па-рал-ле-ло-грам-ма о сумме углов, при-ле-жа-щих к одной сто-роне.

Б. по свой-ству ра-вен-ства про-ти-во-по-лож-ных сто-рон.

ре-тий при-знак па-рал-ле-ло-грам-ма

5. Повторение: определение и свойства параллелограмма

На-пом-ним, что па-рал-ле-ло-грамм — это че-ты-рёх-уголь-ник, у ко-то-ро-го про-ти-во-по-лож-ные сто-ро-ны по-пар-но па-рал-лель-ны. То есть, если — па-рал-ле-ло-грамм, то (см. Рис. 1).

Па-рал-ле-ло-грамм об-ла-да-ет целым рядом свойств: про-ти-во-по-лож-ные углы равны (), про-ти-во-по-лож-ные сто-ро-ны равны (). Кроме того, диа-го-на-ли па-рал-ле-ло-грам-ма в точке пе-ре-се-че-ния де-лят-ся по-по-лам, сумма углов, при-ле-жа-щих к любой сто-роне па-рал-ле-ло-грам-ма, равна и т.д.

Но для того, чтобы поль-зо-вать-ся всеми этими свой-ства-ми, необ-хо-ди-мо быть аб-со-лют-но уве-рен-ны-ми в том, что рас-смат-ри-ва-е-мый че-ты-рёх-уголь-ник — па-рал-ле-ло-грамм. Для этого и су-ще-ству-ют при-зна-ки па-рал-ле-ло-грам-ма: то есть те факты, из ко-то-рых можно сде-лать од-но-знач-ный вывод, что че-ты-рёх-уголь-ник яв-ля-ет-ся па-рал-ле-ло-грам-мом.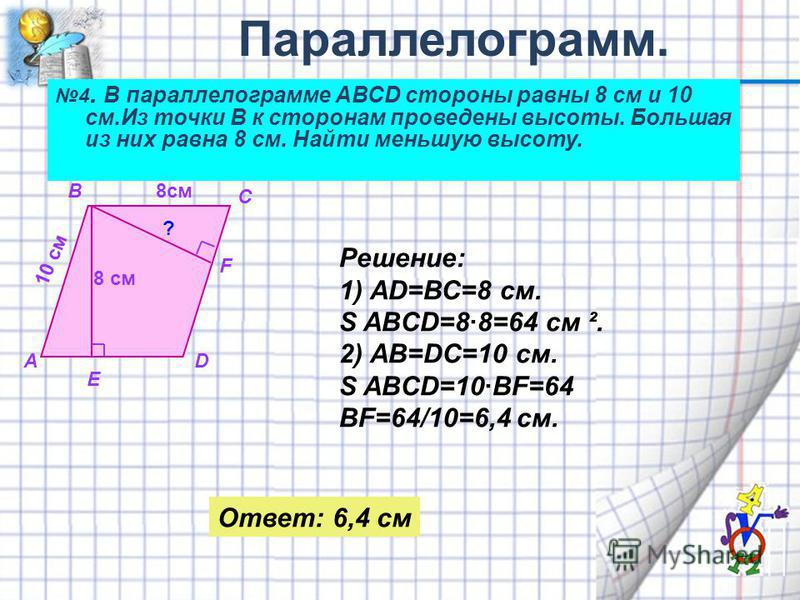 На преды-ду-щем уроке мы уже рас-смот-ре-ли два при-зна-ка. Сей-час рас-смот-рим тре-тий.

6. Третий признак параллелограмма и его доказательство

Если в че-ты-рёх-уголь-ни-ке диа-го-на-ли в точке пе-ре-се-че-ния де-лят-ся по-по-лам, то дан-ный че-ты-рёх-уголь-ник яв-ля-ет-ся па-рал-ле-ло-грам-мом.

Дано:

Че-ты-рёх-уголь-ник; ; .

До-ка-зать:

Па-рал-ле-ло-грамм.

До-ка-за-тель-ство:

Для того чтобы до-ка-зать дан-ный факт, необ-хо-ди-мо до-ка-зать па-рал-лель-ность сто-рон па-рал-ле-ло-грам-ма. А па-рал-лель-ность пря-мых чаще всего до-ка-зы-ва-ет-ся через ра-вен-ство внут-рен-них на-крест ле-жа-щих углов при этих пря-мых. Таким об-ра-зом, на-пра-ши-ва-ет-ся сле-ду-ю-щий спо-соб до-ка-за-тель-ства тре-тье-го при-зна-ка па-рал-ле-ло-грам-ма: через ра-вен-ство тре-уголь-ни-ков .

До-ка-жем ра-вен-ство этих тре-уголь-ни-ков. Дей-стви-тель-но, из усло-вия сле-ду-ет: . Кроме того, по-сколь-ку углы — вер-ти-каль-ные, то они равны.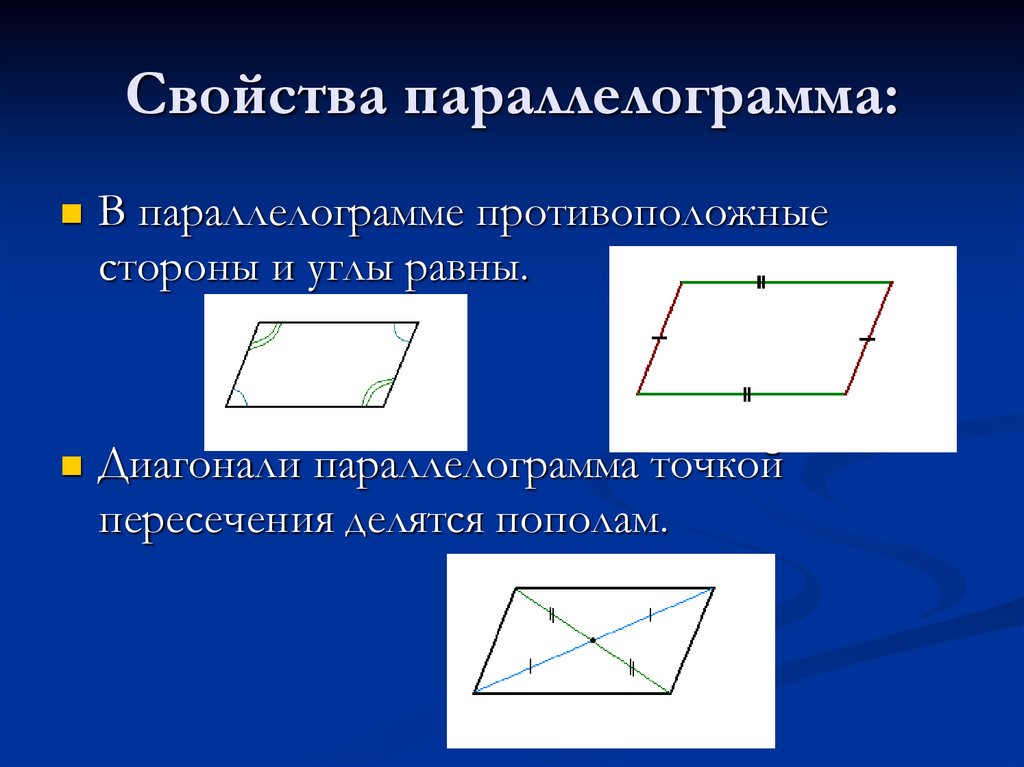 То есть:

(пер-вый при-знак ра-вен-ства тре-уголь-ни-ков — по двум сто-ро-нам и углу между ними).

Из ра-вен-ства тре-уголь-ни-ков: (так как равны внут-рен-ние на-крест ле-жа-щие углы при этих пря-мых и се-ку-щей ). Кроме того, из ра-вен-ства тре-уголь-ни-ков сле-ду-ет, что . Зна-чит, мы по-лу-чи-ли, что в че-ты-рёх-уголь-ни-ке две сто-ро-ны равны и па-рал-лель-ны. По пер-во-му при-зна-ку па-рал-ле-ло-грам-ма: — па-рал-ле-ло-грамм.

До-ка-за-но.

7. Пример задачи на третий признак параллелограмма и обобщение

Рас-смот-рим при-мер на при-ме-не-ние тре-тье-го при-зна-ка па-рал-ле-ло-грам-ма.

При-мер 1

Дано:

— па-рал-ле-ло-грамм; . — се-ре-ди-на , — се-ре-ди-на , — се-ре-ди-на , — се-ре-ди-на (см. Рис. 2).

До-ка-зать: — па-рал-ле-ло-грамм.

До-ка-за-тель-ство:

Зна-чит, в че-ты-рёх-уголь-ни-ке диа-го-на-ли в точке пе-ре-се-че-ния де-лят-ся по-по-лам. По тре-тье-му при-зна-ку па-рал-ле-ло-грам-ма из этого сле-ду-ет, что — па-рал-ле-ло-грамм.

До-ка-за-но.

Если про-ве-сти ана-лиз тре-тье-го при-зна-ка па-рал-ле-ло-грам-ма, то можно за-ме-тить, что этот при-знак со-от-вет-ству-ет свой-ству па-рал-ле-ло-грам-ма. То есть, то, что диа-го-на-ли де-лят-ся по-по-лам, яв-ля-ет-ся не про-сто свой-ством па-рал-ле-ло-грам-ма, а его от-ли-чи-тель-ным, ха-рак-те-ри-сти-че-ским свой-ством, по ко-то-ро-му его можно вы-де-лить из мно-же-ства че-ты-рёх-уголь-ни-ков.

ИСТОЧНИК

http://interneturok.ru/ru/school/geometry/8-klass/chyotyrehugolniki/priznaki-parallelogramma

http://interneturok.ru/ru/school/geometry/8-klass/chyotyrehugolniki/tretiy-priznak-parallelogramma

http://www.uchportfolio.ru/users_content/675f9820626f5bc0afb47b57890b466e/images/46TThxQ8j4Y.jpg

http://cs10002.vk.me/u31195134/116260458/x_56d40dd3.jpg

http://wwww.tepka.ru/geometriya/16.1.gif

Многоугольники — Четырехугольники — В глубину

Их много Различные виды четырехугольников, но все они имеют несколько общих черт: все они имеют четыре стороны, компланарны, имеют две диагонали и сумма их четырех внутренних углов равен 360 градусов.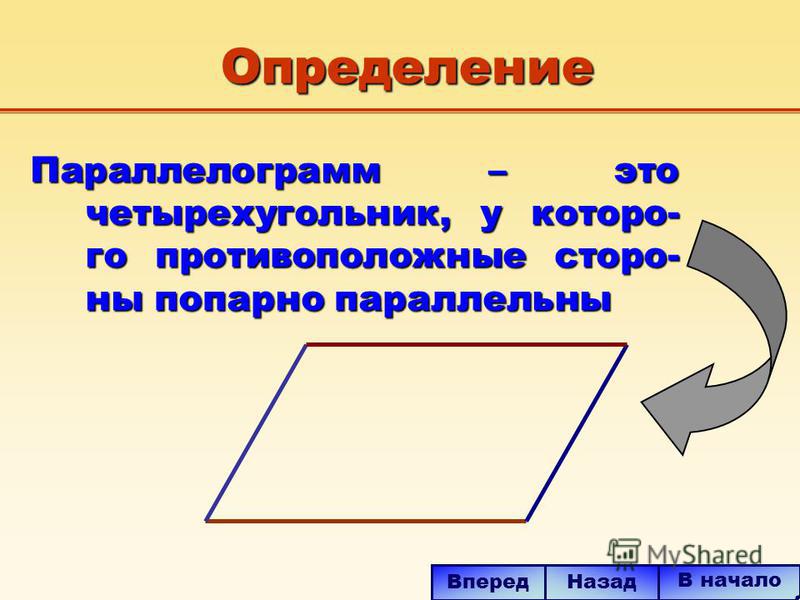 Вот чем они похожи, но чем они отличаются?

Мы знаем многих четырехугольники по их особым формам и свойствам, как и квадраты. Помните, если вы видите слово четырехугольник, это не обязательно означает фигуру с специальные свойства, такие как квадрат или прямоугольник! В словесных задачах будьте осторожны не предполагать, что четырехугольник имеет параллельные стороны или равные стороны, если только что заявлено.

Специальные четырехугольники

	А параллелограмм имеет две параллельные пары противоположных сторон.
	A прямоугольник имеет две пары параллельных противоположных сторон и четыре прямых угла. это также параллелограмм, так как у него две пары параллельных сторон.
	А квадратный имеет две пары параллельных сторон, четыре прямых угла и все четыре стороны равны. Это также прямоугольник и параллелограмм.
	А ромб определяется как параллелограмм с четырьмя равными сторонами. Всегда ли ромб Прямоугольник? Нет, потому что у ромба не обязательно должно быть 4 прямых угла.
	Трапеции имеют только одну пару параллельных сторон. Это тип четырехугольника, который не является параллелограммом. (Британское название: Трапеция )
	Воздушные змеи имеют две пары равных смежных сторон.

Мы можно использовать диаграмму Венна, чтобы помочь нам сгруппировать типы четырехугольников.

Диаграмма Венна использует перекрывающиеся круги, чтобы показать отношения между группами объектов. Все «четырехугольники» можно разделить на три подгруппы: общие четырехугольники, параллелограммы и трапеции.

Прямоугольник всегда ромб? Нет, потому что все четыре стороны прямоугольника не обязательно быть равным. Однако множества прямоугольников и ромбов пересекаются, и их пересечение представляет собой набор квадратов: все квадраты являются прямоугольниками. и ромб.

Мы можем поставить квадраты на пересечении двух кругов.

Из этой диаграммы видно, что квадрат — это четырехугольник, параллелограмм, прямоугольник, и ромб!

Является трапецией параллелограмм? Нет, потому что у трапеции только одна пара параллельных сторон. Вот почему мы должны показать набор трапеций в отдельном круге на Диаграмма Венна.

Как насчет воздушных змеев? Воздушные змеи — это четырехугольники, которые может быть параллелограммом. Если их две пары стороны равны, он становится ромбом, а если их углы равны, то он становится квадратом.

Ссылки по теме:
Формулы площади
Формулы периметра

назад наверх

Основы работы с параллелограммами | Красная и белая материя Классы

Что такое параллелограмм?

Параллелограмм – это четырехугольник с двумя парами параллельных сторон.

• Противоположные стороны параллелограмма параллельны и имеют одинаковую длину.
• Противоположные углы параллелограмма также равны. То есть ∠ А = ∠ С; ∠ B = ∠ D

Теперь давайте посмотрим на некоторые из наиболее известных параллелограммов.

Ромб

Это параллелограмм, все четыре стороны которого имеют одинаковую длину.

Его также называют равносторонним четырехугольником , потому что он имеет четыре равные стороны (точно так же, как мы называем треугольник с тремя равными сторонами равносторонним треугольником).

Итак, периметр ромба = 4 × сторона

Параллелограмм, описанный вокруг окружности, является ромбом.

Прямоугольник

Это параллелограмм, у которого две диагонали одинаковой длины, и все его четыре угла тоже прямые (как у квадрата). Однако равны только его противоположные стороны.

Значит, его смежные стороны составляют угол 90° друг с другом.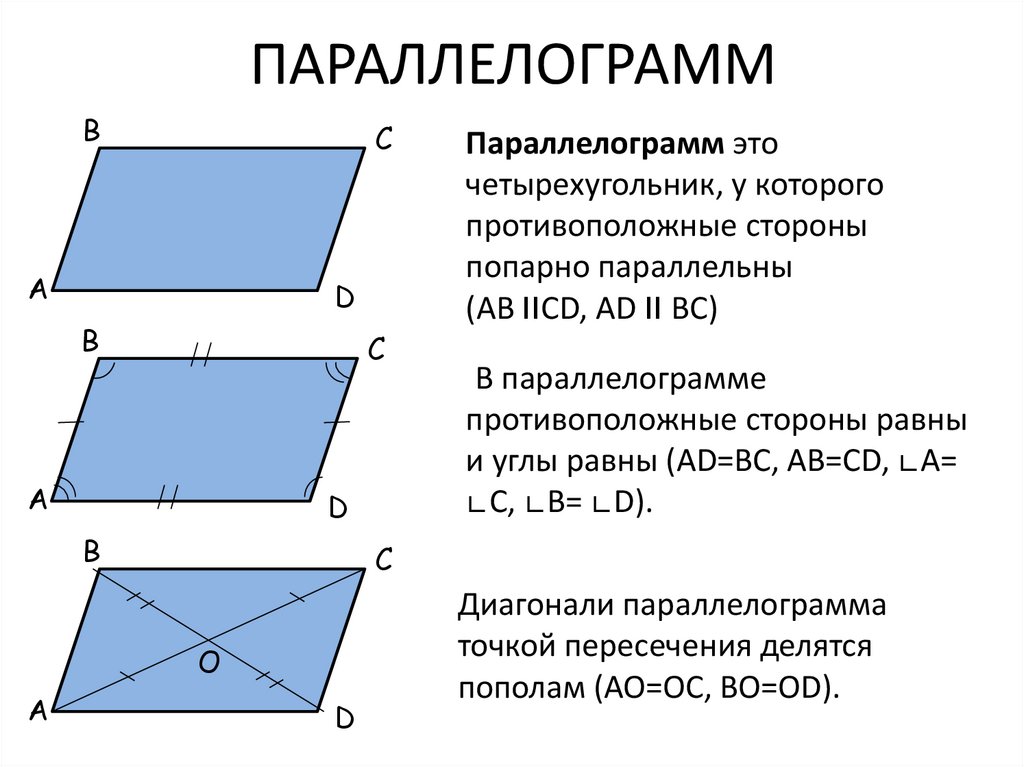

АВ = постоянный ток; BC = AD
AC = BD
∠ A = ∠ B = ∠ C = ∠ D = 90°

Периметр прямоугольника = 2 (длина + ширина) = 2 (l + b)

Если все четыре стороны прямоугольника равны, то он называется Квадратом . Итак, квадрат — это частный случай прямоугольника.

Вписанный в окружность параллелограмм представляет собой прямоугольник.

Квадрат

Это параллелограмм, у которого не только все четыре стороны одинаковой длины (как у ромба), но и все его углы прямые (как у прямоугольника).

Итак, периметр квадрата = 4 × сторона

Квадрат — Прямоугольник, у которого четыре стороны одинаковой длины.

То есть все его четыре угла равны по 90°, и все его четыре стороны равны.

Итак, в некотором смысле квадрат — это частный случай прямоугольника.

По сути, Квадрат — это и Прямоугольник, и Ромб. Однако обратное не обязательно, то есть прямоугольник или ромб не обязательно должны быть квадратом.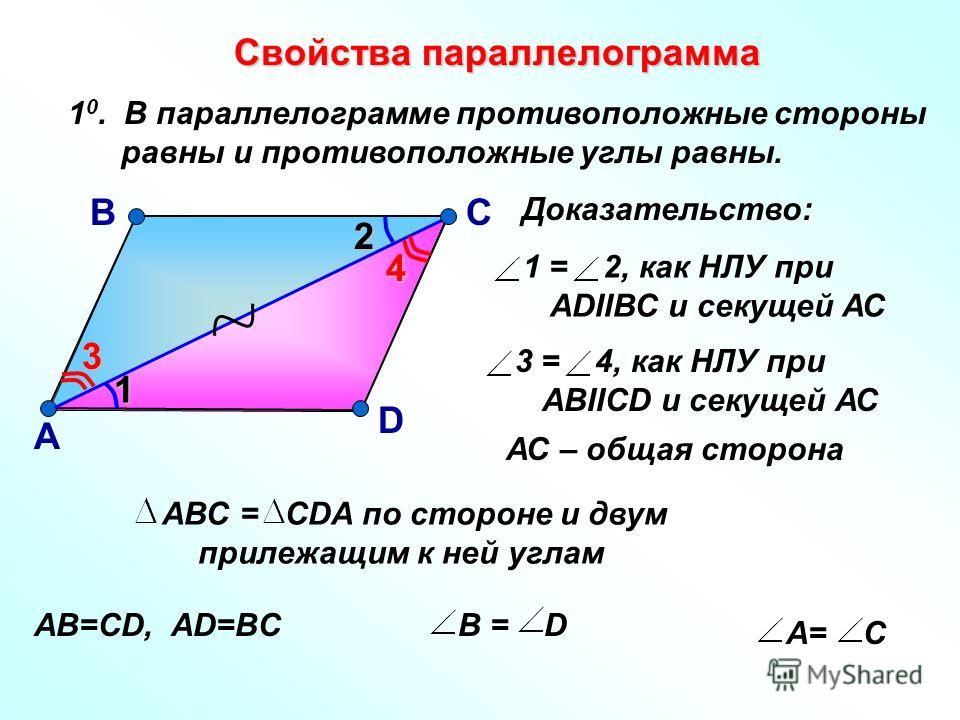

---

Свойства параллелограмма

Эти свойства справедливы для параллелограмма любого типа.

Свойство 1: Углы

В параллелограмме сумма любых двух последовательных углов всегда является дополнительной.

На приведенном выше рисунке ∠A + ∠B = ∠B + ∠C = ∠C + ∠D = ∠D + ∠A = 180° .

В случае Прямоугольник и квадрат : Все углы равны, так как все углы равны 90°.

Свойство 2: Диагонали

Свойство 2a

В параллелограмме диагонали всегда делят друг друга пополам. 92$

В случае Квадрат :

• Диагонали равны по длине (в отличие от ромба).
• Диагонали пересекают друг друга перпендикулярно.
• Диагонали являются биссектрисами углов.

Диагональ квадрата = $\sqrt{2}$ Сторона, т.е. d = $\sqrt{2}$ a

В случае Прямоугольник :

• Диагонали равны по длине (как Квадрат , в отличие от ромба).
• Диагонали делят друг друга пополам (как Квадрат и Ромб), но не перпендикулярно. (в отличие от Квадрата и Ромба) 92}$

  Свойство 3: Биссектрисы параллелограмма

  Свойство 3a

  В параллелограмме биссектрисы любых двух последовательных углов составляют угол 90°.

  На приведенном выше рисунке ∠AOB = 90°

  Свойство 3b

  Биссектрисы четырех углов параллелограмма образуют прямоугольник.

  На приведенном выше рисунке PQRS представляет собой прямоугольник.

  Однако есть несколько свойств, которые верны только для определенных типов параллелограммов. Давайте посмотрим и на это.

  Свойство 4: Середины сторон

  В случае ромба

  Отрезки, соединяющие середины сторон ромба, образуют прямоугольник.

  На приведенном выше рисунке PQRS представляет собой прямоугольник.

  В случае квадрата

  Отрезки, соединяющие середины сторон квадрата, образуют квадрат.

  На приведенном выше рисунке PQRS представляет собой квадрат.

  No related posts.