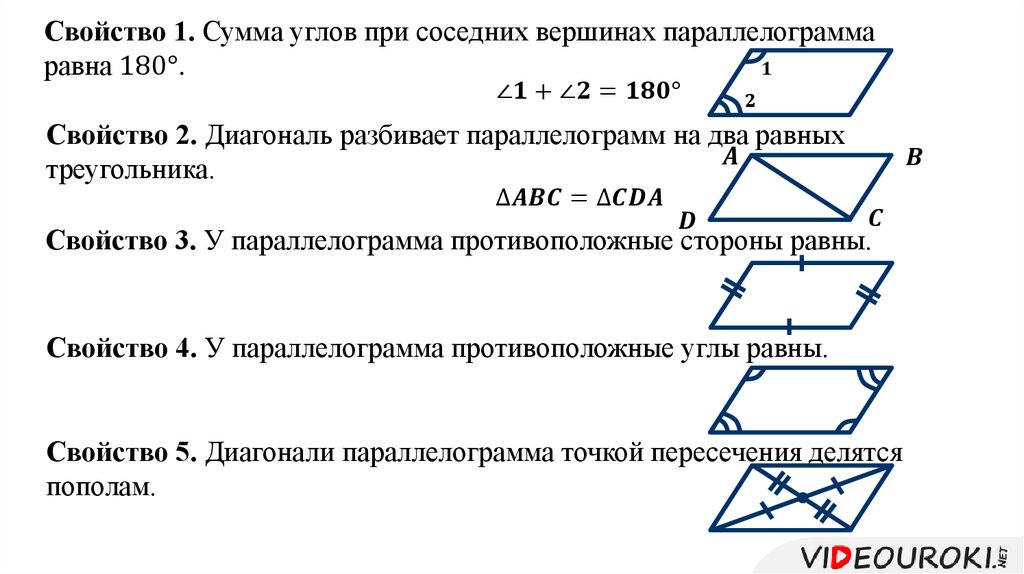
Параллелограмм. Свойства параллелограмма презентация, доклад
Методическая разработка Савченко Е.М.
МОУ гимназия №1, г. Полярные Зори, Мурманской обл.
Геометрия 8 класс
Параллелограмм
Свойства параллелограмма
В
А
С
D
Параллелограммом называется четырехугольник,
у которого противоположные стороны попарно параллельны.
АВIIDС, ADIIBC
Из равных параллелограммов можно построить красивый паркет
a
b
c
d
e
f
Сколько параллелограммов можно увидеть на чертеже?
a II c, d II e II f II b II g
g
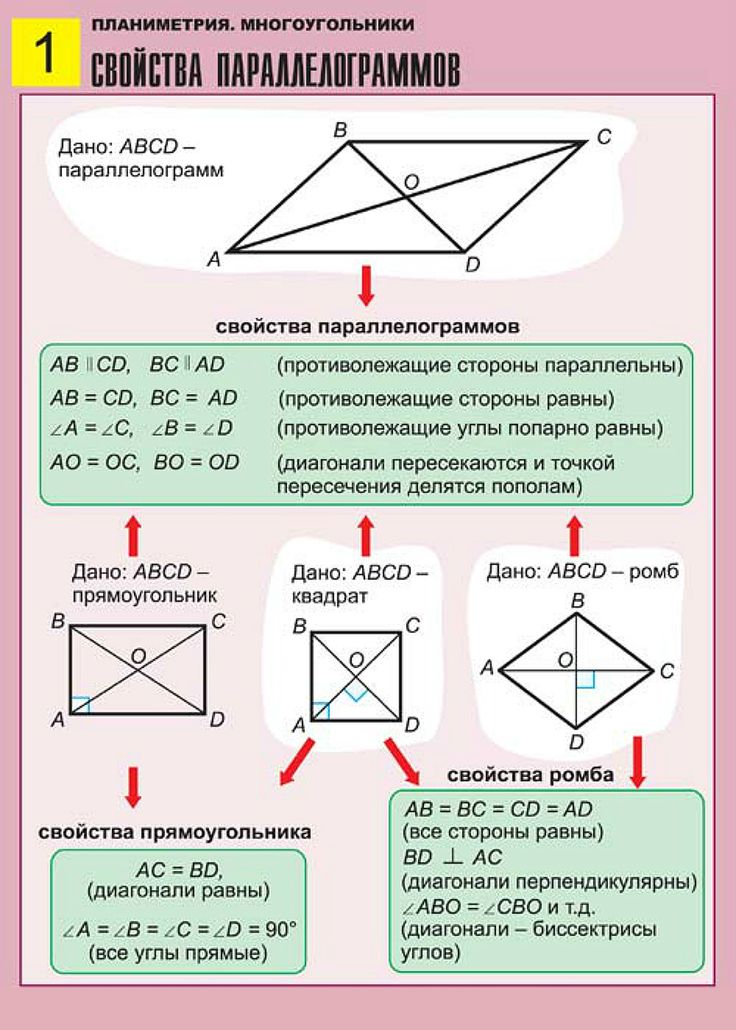
Свойства параллелограмма
10. В параллелограмме противоположные стороны
В параллелограмме противоположные стороны
равны и противоположные углы равны.
В
А
С
D
Доказательство:
АС – общая сторона
АВ=СD, AD=BC
Свойства параллелограмма
20. Диагонали параллелограмма точкой пересечения
делятся пополам.
В
А
С
D
Доказательство:
AB=СD, как противоположные стороны параллелограмма
АО=ОС, ВО=ОD
О
А
Эти рисунки иллюстрируют все рассмотренные
свойства
В
А
С
D
В
С
D
В
С
D
А
О
В
А
С
D
АВIIDС, ADIIBC
Дополнительные
свойства.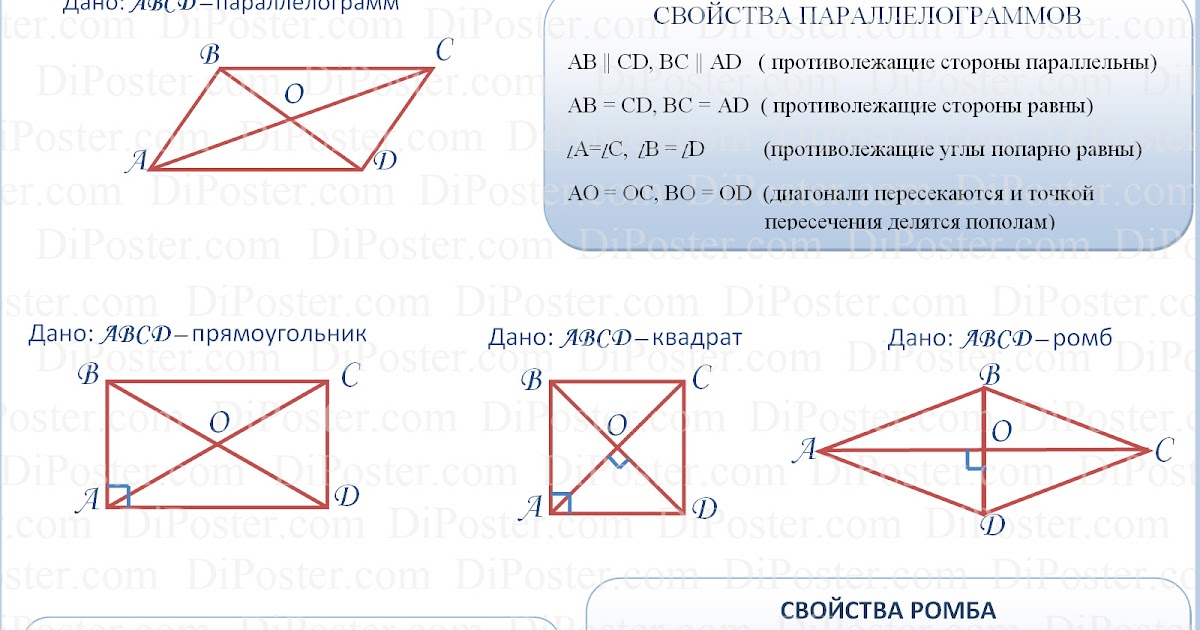
Сумма соседних углов параллелограмма равна 1800.
Обоснуй…
Периметр параллелограмма равен 20 см.
Может ли быть одна из диагоналей 11 см?
Какое наибольшее целое значение может принимать длина одной из диагоналей этого параллелограмма?
В
А
С
D
11 см
не существует
Найдите стороны параллелограмма АВСD, зная, что его периметр равен 24 см.
Тренировочные задания на готовых чертежах.
В
А
С
D
АD – АВ = 3 см
Сторона AD на 3 см
больше стороны АВ
х
х+3
Р=24см
2(х+х+3) = 24
р=12см
х+х+3 = 12
Найдите стороны параллелограмма АВСD, зная, что его периметр равен 24 см.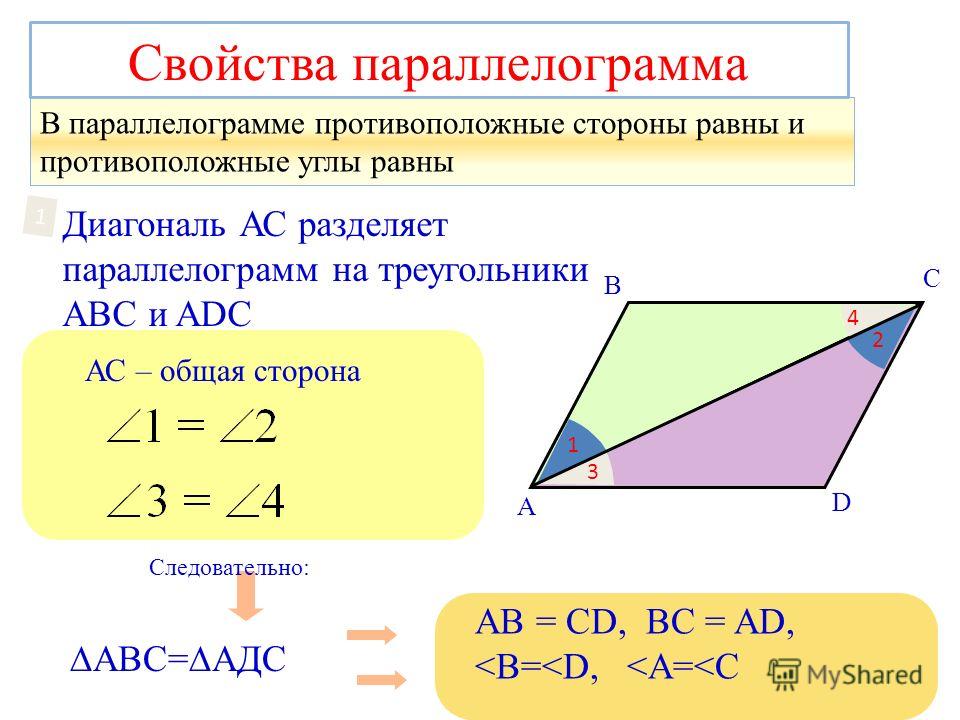
В
А
С
D
АВ : ВС = 1 : 2
х
2х
Р=24см
2(х+2х) = 24
р=12см
х+2х = 12
450
Найдите стороны параллелограмма АВСD, зная, что его периметр равен 24 см.
В
А
С
D
МС – МВ = 3 см
х
х+3
Р=24см
2(х+х+х+3) = 24
р=12см
х+х+х+3 = 12
М
Отрезок МС на 3 см
больше отрезка МВ
450
450
х
Найдите стороны параллелограмма АВСD, зная, что его периметр равен 24 см.
В
А
С
D
Найдите стороны параллелограмма АВСD, зная, что его периметр равен 24 см.
В
А
С
D
Найдите стороны параллелограмма АВСD, зная, что его периметр равен 24 см.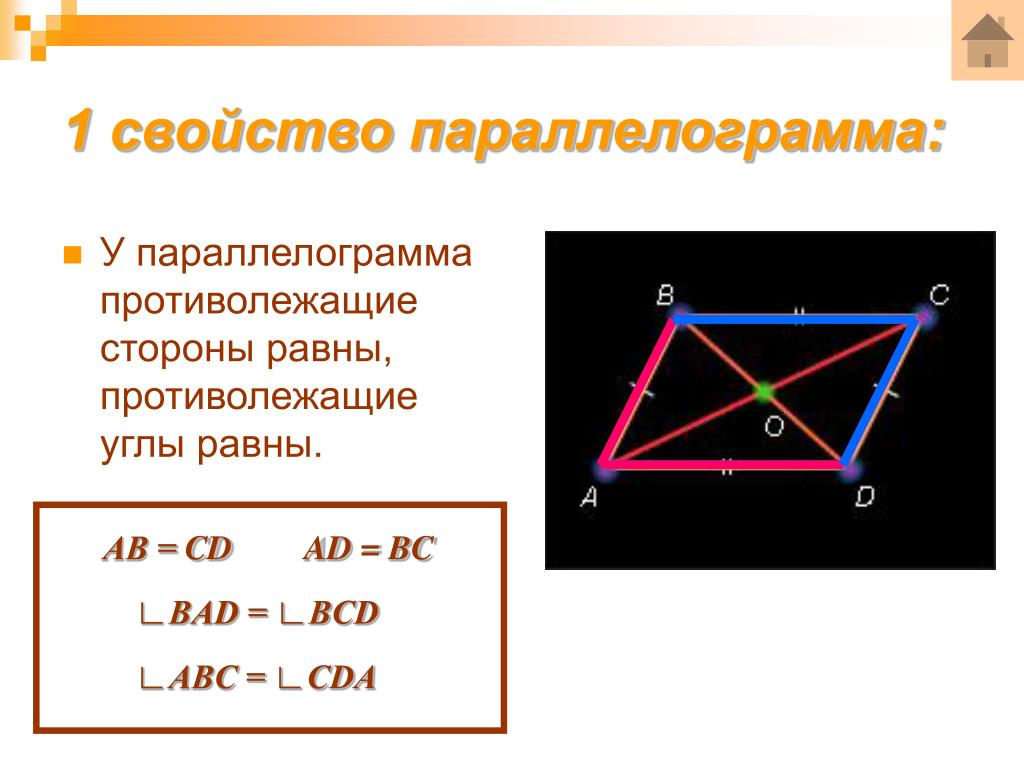
В
А
С
D
О
Длина одной из сторон параллелограмма составляет 80% от длины другой стороны. Найдите длину меньшей стороны этого параллелограмма, если его полупериметр равен 18 см.
В
А
С
D
х
0,8х
р=18см
х + 0,8х = 18
Длина одной из сторон параллелограмма на 15% больше длины другой стороны. Найдите длину большей стороны этого параллелограмма, если его полупериметр равен 8,6 см
В
А
С
D
х
1,15х
р = 8,6см
х + 1,15х = 8,6
Найдите углы параллелограмма АВСD.
В
А
С
D
Угол В больше угла А на 300
х
х+30
Найдите углы параллелограмма АВСD.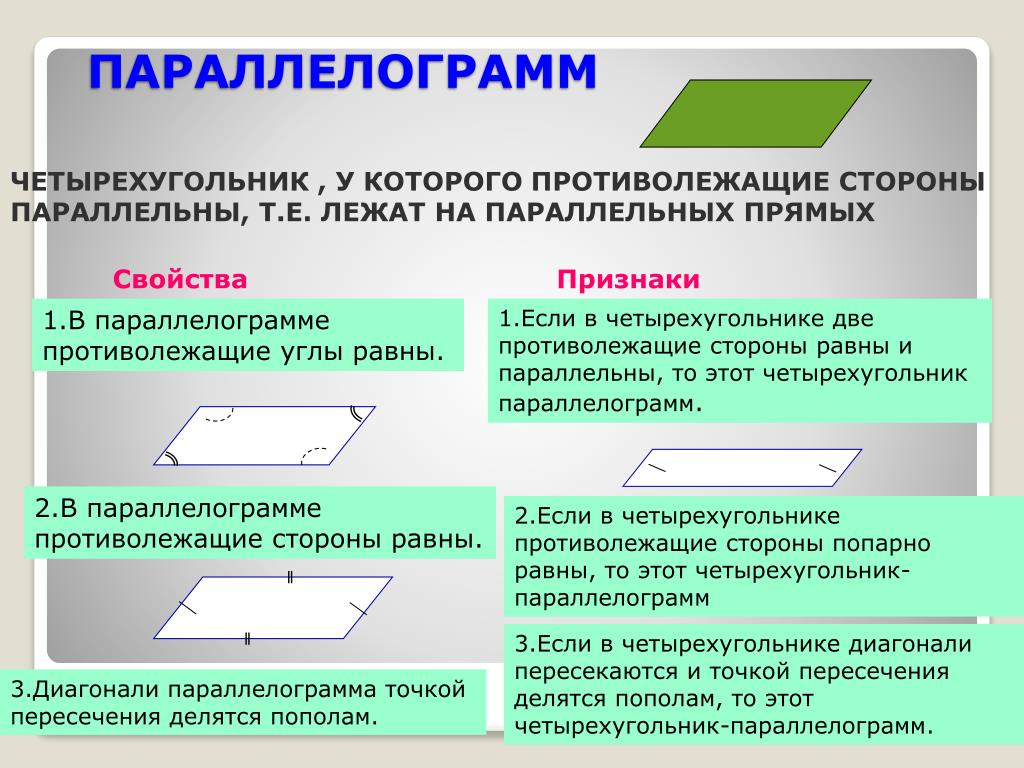
В
А
С
D
х
3х
Сумма градусных мер трех углов параллелограмма равна 3000. Найдите величину тупого угла этого параллелограмма.
В
А
С
D
х
180-х
х
Найдите углы параллелограмма АВСD
В
А
С
D
400
400
1800-400
1400
1400
( )
: 2
№ 376 (в) Найдите углы параллелограмма
АВСD, если
В
А
С
D
710
710
1090
1090
В
А
С
D
Угол А в 2 раза больше угла В
2х
х
№ 376 (в) Найдите углы параллелограмма
АВСD, если
4 см
4 см
Найдите периметр параллелограмма
В
А
С
D
5 см
3 см
6 см
2 см
К
6 см
5 см
3 см
200
Найдите все неизвестные углы параллелограмма
В
А
С
D
400
400
200
200
1800 – (200+400)
200
200
1800 – (200+200)
400
1400
Найдите все неизвестные углы параллелограмма
В
А
С
D
F
700
700
300
700
300
Биссектриса СК угла ВСD параллелограмма АВСD делит сторону АD на отрезки АК = 3 и КD = 5.
В
А
С
D
К
5
3
5
1
2
3
О – точка пересечения диагоналей параллелограмма АВСD. Периметр треугольника ВОС на 5 больше периметра треугольника СОD. Найдите разность длин сторон АD и АВ.
В
А
С
D
*
О
х
х
у
у
m
n
n
(n+m+y)
(n+m+x)
– = 5
Через вершины треугольника АВС провели прямые, параллельные противоположным сторонам этого треугольника. Эти прямые попарно пересекаются в точках М, К и Н. Найдите периметр треугольника АВС, если сумма периметров всех получившихся при этом параллелограммов равна 32 см.
А
В
С
*
а
а
b
b
а
b
c
c
а
c
2a+2b
+2b+2c
+2a+2c
= 32
Скачать презентацию
Параллелограмм (свойства, признаки, кроссворд) (9 слайдов)
Слайд 1
ПАРАЛЛЕЛОГРАММ
Слайд 2
Параллелограмм
А
В
С
D
ABCD –четырех-
угольник
AB ║CD
BC ║AD
определение
Четырехугольник у которого противолежащие стороны попарно параллельны называется параллелограммом
=> ABCD -параллелограмм
Слайд 3
А
В
С
D
O
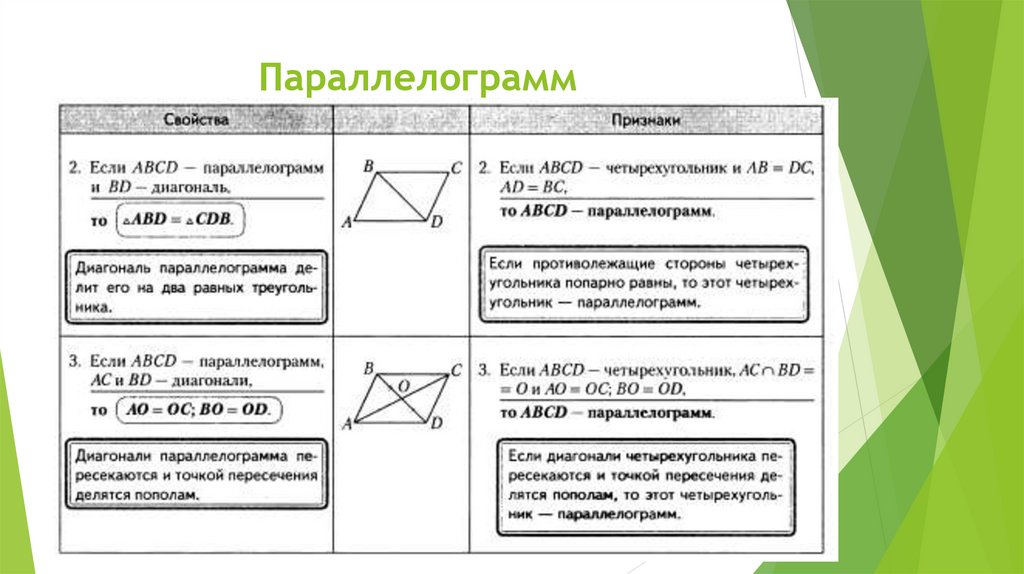
3. Диагонали точкой пересечения делятся пополам
AO=OC BO=OD
Диагонали точкой пересечения делятся пополам
AO=OC BO=OD
Свойства параллелограмма
1.Противоположные стороны попарно равны
AD=BC AB=CD
2.Противоположные углы попарно равны
А = С В = D
Слайд 4
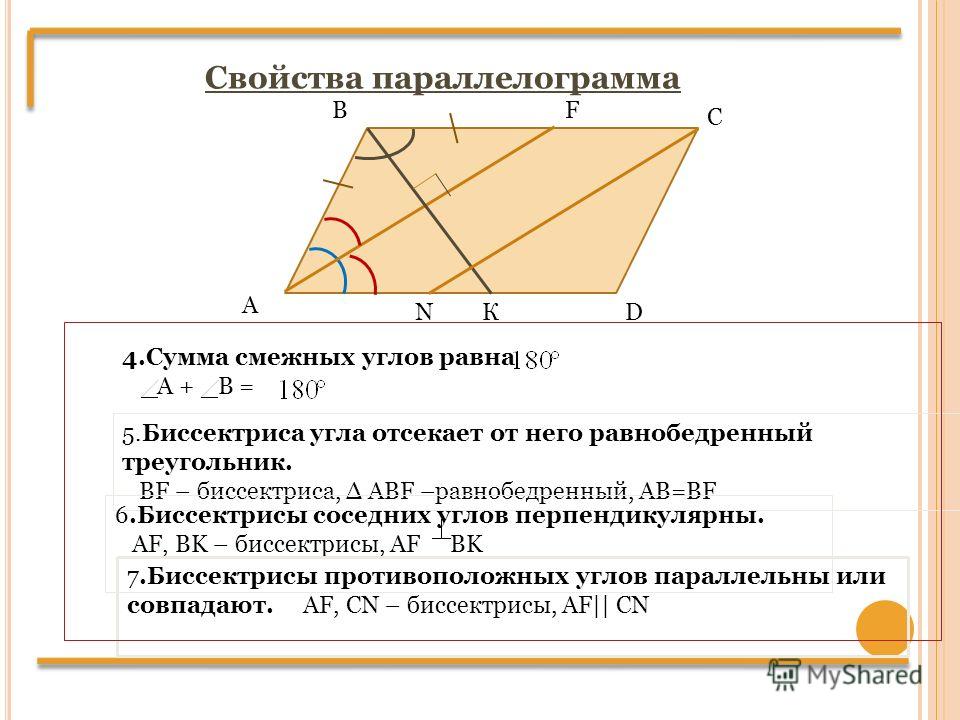
Свойства параллелограмма
4.Сумма смежных углов равна
А + В =
А
В
С
D
5.Биссектриса угла отсекает от него равнобедренный треугольник.
BF – биссектриса, ∆ ABF –равнобедренный, AB=BF
F
6.Биссектрисы соседних углов перпендикулярны.
AF, BK – биссектрисы, AF BK
К
7.Биссектрисы противоположных углов параллельны или совпадают. AF, CN – биссектрисы, AF|| CN
N
Слайд 5
Признаки параллелограмма
Если в четырехугольнике противоположные стороны параллельны и равны, то этот четырехугольник параллелограмм.
D
А
В
С
ABCD – четырех-ник
AB || CD
AB = CD
=> ABCD- параллелограмм
Слайд 6
Признаки параллелограмма
Если в четырехугольнике противоположные стороны попарно параллельны, то этот четырехугольник — параллелограмм
D
А
В
С
ABCD – четырех-ник
ВС = АD
AB = CD
=> ABCD- параллелограмм
Слайд 7
Признаки параллелограмма
Если в четырехугольнике диагонали точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм
D
А
В
С
ABCD – четырех-ник
AО = CО
ВО = ОD
О
=> ABCD- параллелограмм
Слайд 8
кроссворд
1. Четырехугольник, у которого противоположные стороны попарно равны
2.Единица измерения угла
3.Отрезок, соединяющий две несмежные вершины
4.Луч, делящий угол пополам
5.Множество точек прямой, заключенных между двумя точками.
6.Фигура,состоящая из двух лучей, исходящих из одной точки.
7.Сколько сантиметров в метре?
8.(горизонталь) Отрезок, перпендикулярный к стороне.
Четырехугольник, у которого противоположные стороны попарно равны
2.Единица измерения угла
3.Отрезок, соединяющий две несмежные вершины
4.Луч, делящий угол пополам
5.Множество точек прямой, заключенных между двумя точками.
6.Фигура,состоящая из двух лучей, исходящих из одной точки.
7.Сколько сантиметров в метре?
8.(горизонталь) Отрезок, перпендикулярный к стороне.
8.(вертикаль) Точка из которой исходят стороны многоугольника
9. «+», — это …
10.Стороны прямоугольного треугольника, образующие прямой угол.
11Отрезок исходящий из вершины треугольника к середине противоположной стороны (множественное число).
Посмотреть ответ
Слайд 9
кроссворд
1.Четырехугольник, у которого противоположные стороны попарно равны
2.Единица измерения угла
3.Отрезок, соединяющий две несмежные вершины
4.Луч, делящий угол пополам
5.Множество точек прямой, заключенных между двумя точками.
6.Фигура,состоящая из двух лучей, исходящих из одной точки.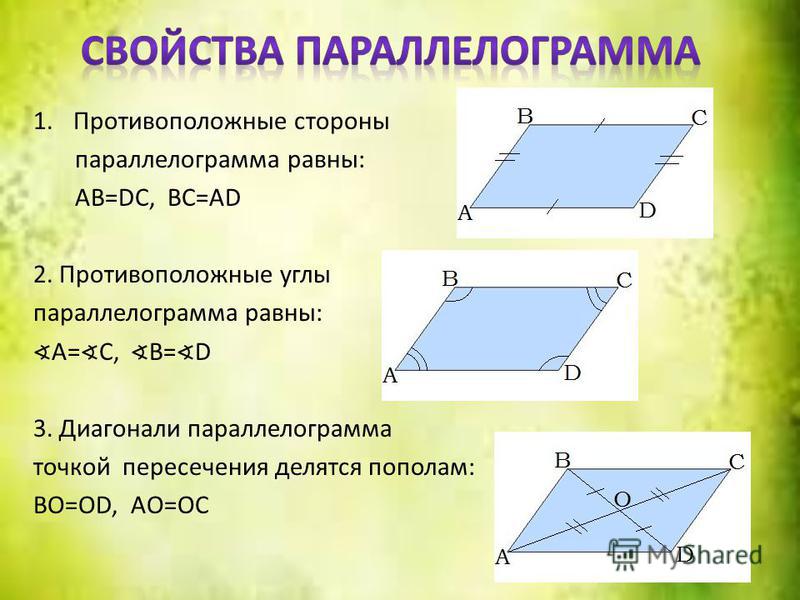 7.Сколько сантиметров в метре?
8.(горизонталь) Отрезок, перпендикулярный к стороне.
7.Сколько сантиметров в метре?
8.(горизонталь) Отрезок, перпендикулярный к стороне.
8.(вертикаль) Точка из которой исходят стороны многоугольника
9. «+», — это …
10.Стороны прямоугольного треугольника, образующие прямой угол.
11Отрезок исходящий из вершины треугольника к середине противоположной стороны (множественное число).
5
11
6
7
9
8
10
назад
Свойства параллелограммов. Теоремы, доказательства и примеры решений
Параллелограмм — это четырехугольник, у которого противоположные стороны параллельны и равны, а противоположные углы равны. Параллелограмм образован пересечением двух пар параллельных прямых.
Важные свойства параллелограмма
Параллелограмм — это четырехугольник, у которого противоположные стороны параллельны и равны по длине. Кроме того, противоположные углы также равны. Вот несколько важных свойств параллелограмма:
- Противоположные стороны параллелограмма равны по длине и параллельны друг другу.

- Противоположные углы параллелограмма равны.
- Сумма всех внутренних углов параллелограмма равна 360°.
- Смежные углы параллелограмма смежные (180°).
Свойства диагоналей параллелограмма
Различные свойства диагоналей параллелограмма:
- Обе диагонали параллелограмма делят друг друга пополам.
- Параллелограмм делится пополам на два равных треугольника по каждой диагонали.
- По закону параллелограмма сумма квадратов диагоналей параллелограмма равна сумме квадратов всех сторон параллелограмма.
Теоремы о свойствах параллелограмма
Ниже в этой статье обсуждаются несколько важных теорем о свойствах параллелограмма:
Теорема 1: Противоположные стороны параллелограмма равны.
Дано: ABCD — параллелограмм
Доказать: AB = CD & DA = BC
Доказательство:
Обращение к теореме 1: если противоположные стороны равны четырехугольник, то это параллелограммДан ABCD — параллелограмм.
Следовательно,
AB || округ Колумбия и реклама || BC
Сейчас, AD || BC и AC пересекают A и C соответственно.
∠DAC = ∠BCA…(i) [Альтернативные внутренние углы]
Сейчас, AB || DC и AC пересекают A и C соответственно.
∠BAC = ∠D …(ii) [Альтернативные внутренние углы]
Теперь, в ΔADC и ΔCBA
∠DAC = ∠BCA [из (i)]
AC = AC [общая сторона]
∠DCA = ∠BAC [из (ii)]Итак, по ASA(Angle- Сторона-угол) критерий конгруэнтности
ΔADC ≅ ΔCBA
AB = CD & DA = BC [Соответствующие части конгруэнтных треугольников равны]
Отсюда доказано
Дано: Противоположные стороны четырехугольника ABCD равны, AB = CD и BC = AD.
Доказать: Четырехугольник ABCD — параллелограмм.
В четырехугольнике ABCD AB = CD и AD = BC.
В треугольниках ABC и CDA имеем
AC = AC (общие стороны)
AD = BC (данные)
AB = CD (поскольку внутренние углы равны)Таким образом, по критерию конгруэнтности SSS треугольники ABC и CDA конгруэнтны, поэтому согласно CPCT соответствующие углы треугольников равны. Таким образом, ∠BAC = ∠DCA и ∠BCA = ∠DAC.
Сейчас AB || CD, Британская Колумбия || AD и, следовательно, ABCD — параллелограмм.
Теорема 2: Противолежащие углы параллелограмма равны.
Приведено: ABCD — это параллелограмм
, чтобы доказать: ♂ = ♂ и ♂ = ABCD
Доказательство:
Дано дано. Следовательно,
AB || округ Колумбия и реклама || BC
Сейчас, AB || DC и AD пересекают их в точках A и D соответственно.
∠A + ∠D = 180º …(i) [Сумма последовательных внутренних углов равна 180º]
Теперь, AD || BC и DC пересекают их в точках D и C соответственно.
секрет +♂ = 180º… (ii) [Сумма последовательных углов внутренних дел составляет 180º]
от (i) и (ii), мы получаем
reta +тнаген Таким образом, ∠A = ∠C
Аналогично, ∠B = ∠D
∠A = ∠C и ∠B = ∠D
Отсюда доказано
Обращение к теореме 2: если противоположные углы в четырехугольнике равны. , то это параллелограмм
Дано: В четырехугольнике ABCD ∠A = ∠C и ∠B = ∠D
Доказать: ABCD — параллелограмм.
Доказательство:
Даны ∠A = ∠C и ∠B = ∠D в четырехугольнике ABCD. Мы должны доказать, что ABCD является параллелограммом
∠A + ∠B + ∠C + ∠D = 360º (данные ∠A = ∠C и ∠B = ∠D )
2(∠A + ∠B) =360º
∠А + ∠В = 180º.
Таким образом, AD || ДО Н.Э. Аналогично можно показать, что AB || CD.
Следовательно, AD || до н.э. и АВ || CD. Следовательно, ABCD — параллелограмм.
Теорема 3.
 Диагонали параллелограмма делят друг друга пополам.
Диагонали параллелограмма делят друг друга пополам.
Дано: ABCD — параллелограмм
Доказать: OA = OC & OB = OD
Доказательство:
0 AB | округ Колумбия и реклама || BC
Сейчас, AB || DC и AC пересекают A и C соответственно.
∠BAC = ∠DCA [ Альтернативные внутренние углы равны ]
Итак, ∠BAO = ∠DCO
Теперь, AB || DC и BD пересекают B и D соответственно.
↑ABD = ↑CDB [Альтернативные внутренние углы равны]
SO, ▲ = тнагдо
Теперь в ΔAOB & ΔCOD мы имеем,
♂ = ♂да [противоположная сторона параллеи.
ab = CD
↑BO = секрет
SO, по ASA (угловым углу) Критерий конгруэнтности
ΔAOB ≅ ΔCOD
OA = OB = OD
Следовательно, доказано
Convers Теорема 3: Если диагонали четырехугольника делят друг друга пополам, то это параллелограмм.
Дано: Диагонали AC и BD делят друг друга пополам.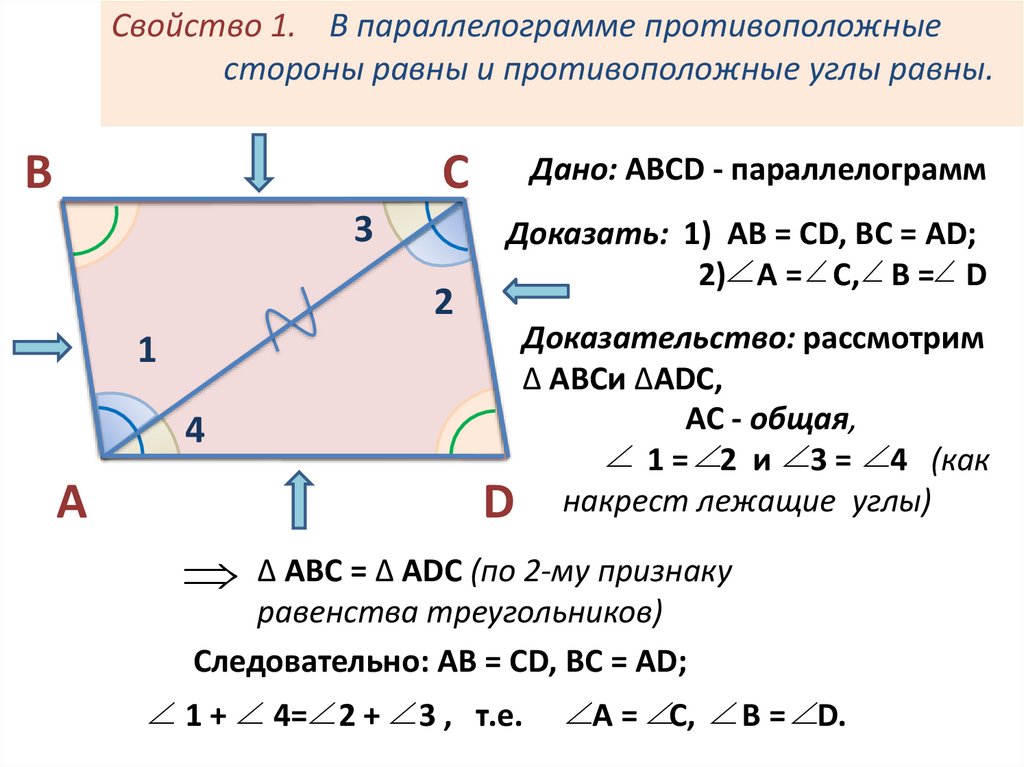
Доказать: ABCD — параллелограмм.
Доказательство:
Если диагонали AB и CD делят друг друга пополам. Тогда в Δ AOB и Δ COD
AO = CO (диагонали делят друг друга пополам)
BO = DO (диагонали делят друг друга пополам)
∠AOB =∠COD (вертикально противоположные углы)Таким образом, по критерию конгруэнтности SAS треугольники конгруэнтны. Таким образом, ∠CAB = ∠DCA и ∠DBA = ∠CDB. Следовательно, АВ || КД и БК || ОБЪЯВЛЕНИЕ. Таким образом, ABCD — параллелограмм.
Решенный пример свойств параллелограмма
Пример 1: ABCD — четырехугольник с AB = 10 см. Диагонали ABCD пересекаются под прямым углом пополам. Затем найдите периметр треугольника ABCD.
Решение:
Мы знаем, что если диагонали четырехугольника делятся пополам под прямым углом, то это ромб.
Таким образом, ABCD — ромб и AB = BC = CD = DA.
Таким образом, периметр ABCD = 4(AB) = 4(10) = 40 см
Пример 2: Найдите площадь параллелограмма, основание которого равно 6 см, а высота 12 см.
Решение:
Дано, Основание = 6 см и Высота = 12 см.
Мы знаем,
Площадь = Основание x Высота
Площадь = 6 × 12
Площадь = 72 см
Ответ:
Параллелограмм – это четырехугольник, у которого противоположные стороны параллельны и равны. А противоположные углы в параллелограмме равны. Его также считают вписанным четырехугольником.
Вопрос 2: Можно ли назвать ромб параллелограммом?
Ответ:
Противоположные стороны ромба равны и параллельны, и его противоположные углы также равны. Поэтому он считается параллелограммом.
Вопрос 3: Каковы четыре важных свойства параллелограмма?
Ответ:
Четыре важных свойства параллелограмма:
- Противоположные стороны параллелограмма параллельны и конгруэнтны равны
- Диагонали параллелограмма делят друг друга пополам.
Вопрос 4: Каков порядок вращательной симметрии в параллелограмме?
Ответ:
Порядок вращательной симметрии параллелограмма равен 2.
Вопрос 5: Имеет ли параллелограмм отражательную симметрию?
Ответ:
Нет, отражательная симметрия невозможна в параллелограмме.
Вопрос 6. Равны ли диагонали параллелограмма?
Ответ:
Диагонали параллелограмма вообще НЕ равны. В некоторых особых случаях параллелограммы, такие как квадраты и прямоугольники, имеют равные диагонали.
Связанные ресурсы
- Площадь параллелограмма
- Конгруэнтность треугольника
Свойства параллелограмма — Концепция — Геометрия Видео от Brightstorm
Свойства параллелограммов часто обнаруживаются в геометрических задачах и доказательствах.
Свойства параллелограмма применимы к прямоугольникам, ромбам и квадратам. В параллелограмме противоположные стороны равны, противоположные углы равны, смежные углы смежны, а диагонали делят друг друга пополам. Другими важными свойствами многоугольника, которые нужно знать, являются свойства трапеции и свойства воздушного змея.
противоположные стороны параллельно противоположные углы односторонние внутренние углы диагонали делить пополам последовательные углы ромб прямоугольник квадрат
Свойства четырехугольников проявляются
во всей геометрии, в доказательствах, в
верных и ложных вопросах, в множественном
выборе и заполнении пробела.Итак,
действительно полезно знать свойстваразличных четырехугольников. Параллелограммы обладают свойствами, применимыми к прямоугольникам,
ромбам и квадратам. Итак,
, что бы мы ни решили, что параллелограммы
имеют свойства
, применимо и к этим трем параллелограммам
.Во-первых, противоположные стороны конгруэнтны.
Ну, если я посмотрю на противоположные стороны,
я отмечу, что эти две стороны
конгруэнтны друг другу.
Но откуда мы знаем, что это параллелограмм?
Определение параллелограмма
состоит в том, что у нас есть две пары параллельных
сторон. Итак, обратите внимание на параллелограмм
, что все четыре стороны не обязательно должны быть конгруэнтными. Если бы они были, то
были бы ромбами.Второй ключевой момент заключается в том, что противоположные углы
совпадают. Итак, если я посмотрю на этот угол
прямо здесь, он будет противоположным.
В принципе, если бы я начертил диагональ,
где был бы этот угол? Таким образом,
противоположных углов равны.Я обозначу
эти два угла как
конгруэнтные друг другу, но не конгруэнтные
другим последовательным углам.Следующее, что последовательные углы
являются дополнительными. Если я назову
этот угол X, то это будет угол
Y. Значит, это будет X, а это
будет Y. Как бы я ни смотрел на
этих последовательных углов, X плюс Y,
они будут равны 180 градусам.
Почему? Если у меня есть
две параллельные линии, то эту сторону здесь
можно рассматривать как поперечную,
у нас есть внутренние углы одной стороны, которые
всегда являются дополнительными. То же самое
можно сказать об этих двух параллельных линиях
, где у нас есть поперечная.
Таким образом, независимо от того, как я смотрю на это, я
будет иметь те же боковые внутренние углы
.И последняя ключевая вещь
, что диагонали делят друг друга на
пополам. Итак, я нарисую
маркером другого цвета.
Итак, если я нарисую диагональ прямо здесь
, а если я нарисую другую диагональ,
, то в параллелограмме будет только две диагонали,
обратите внимание, что эти
не будут конгруэнтны друг другу.


 Следовательно,
Следовательно,  В треугольниках ABC и CDA имеем
В треугольниках ABC и CDA имеем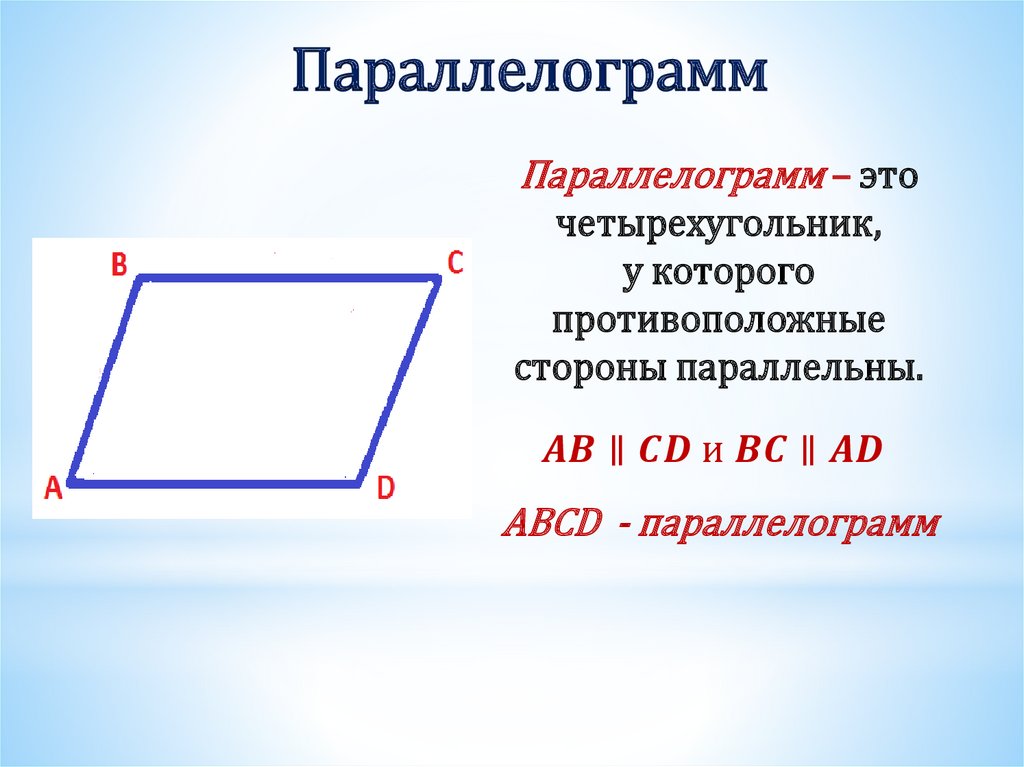

 Свойства параллелограмма применимы к прямоугольникам, ромбам и квадратам. В параллелограмме противоположные стороны равны, противоположные углы равны, смежные углы смежны, а диагонали делят друг друга пополам. Другими важными свойствами многоугольника, которые нужно знать, являются свойства трапеции и свойства воздушного змея.
Свойства параллелограмма применимы к прямоугольникам, ромбам и квадратам. В параллелограмме противоположные стороны равны, противоположные углы равны, смежные углы смежны, а диагонали делят друг друга пополам. Другими важными свойствами многоугольника, которые нужно знать, являются свойства трапеции и свойства воздушного змея. Итак,
Итак,  Я обозначу
Я обозначу