Что такое параллелограмм? Ответ на webmath.ru
Поможем решить контрольную, написать реферат, курсовую и диплом от 800р
Содержание:
- Определение параллелограмма
- Свойства параллелограмма
- Признаки параллелограмма
- Примеры решения задач
Определение параллелограмма
Определение
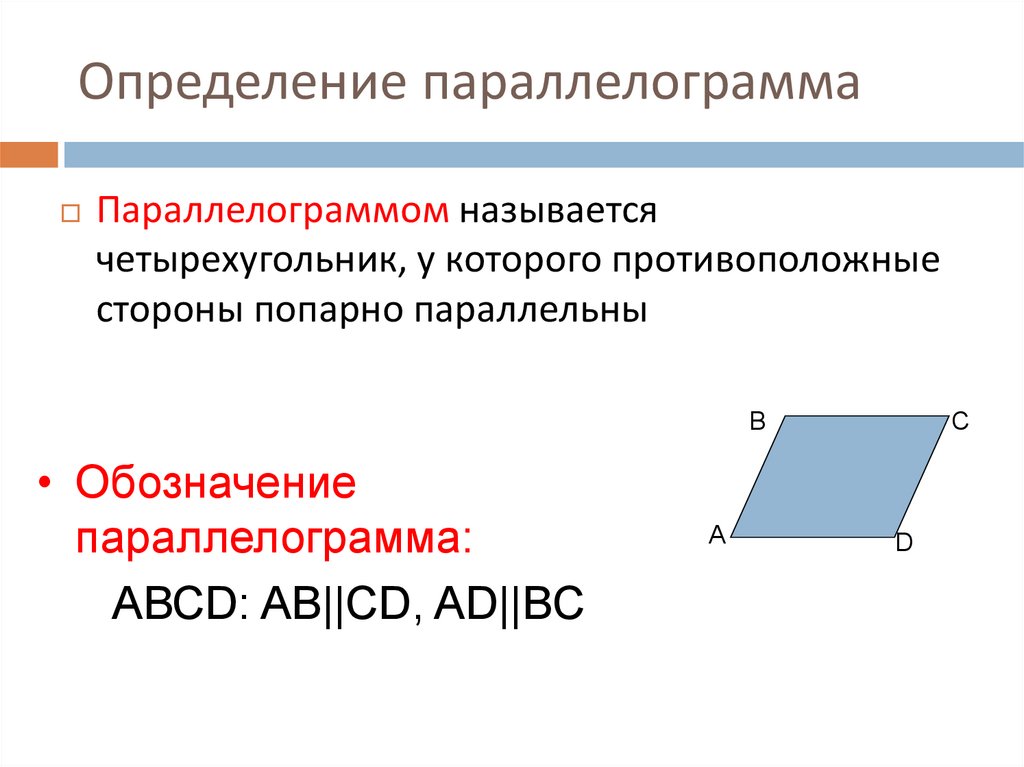
Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны.
На рисунке 1 изображен параллелограмм $A B C D, A B\|C D, B C\| A D$.
Свойства параллелограмма
- В параллелограмме противоположные стороны равны: $A B=C D, B C=A D$ (рис 1).
- В параллелограмме противоположные углы равны $\angle A=\angle C, \angle B=\angle D$ (рис 1).
- Диагонали параллелограмма в точке пересечения делятся пополам $A O=O C, B O=O D$ (рис 1).
- Диагональ параллелограмма делит его на два равных треугольника.
Сумма углов параллелограмма, прилежащих к одной стороне равна $180^{\circ}$:
$$\angle A+\angle B=180^{\circ}, \angle B+\angle C=180^{\circ}$$
$$\angle C+\angle D=180^{\circ}, \angle D+\angle A=180^{\circ}$$
Диагонали и стороны параллелограмма связаны следующим соотношением:
$$d_{1}^{2}+d_{2}^{2}=2 a^{2}+2 b^{2}$$
- В параллелограмме угол между высотами равен его острому углу: $\angle K B H=\angle A$.
{\circ}$236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Стороны параллелограмма равны 18 см и 15 см, а высота, проведенная к меньшей стороне, равна 6 см. Найти другую высоту параллелограмма.
Решение. Сделаем рисунок (рис. 2)
По условию, $a=15$ см, $b=18$ см, $h_{a}=6$ см. Для параллелограмма справедливы следующие формулы для нахождения площади:
$$S=a \cdot h_{a}, \quad S=b \cdot h_{b}$$
Приравняем правые части этих равенств, и выразим, из полученного равенства, $h_{b} $:
$$a \cdot h_{a}=b \cdot h_{b} \Rightarrow h_{b}=\frac{a \cdot h_{a}}{b}$$
Подставляя исходные данные задачи, окончательно получим:
$h_{b}=\frac{15 \cdot 6}{18} \Rightarrow h_{b}=5$ (см)
Ответ. $h_{b}=5$
Читать дальше: что такое трапеция.
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия
Поиск по сайту:
Справочник по математике Геометрия (Планиметрия) Четырехугольники Свойства и признаки параллелограмма Свойства и признаки прямоугольника Свойства и признаки ромба Свойства и признаки квадрата Замечание. Мы рассматриваем только выпуклые четырёхугольникивыпуклые четырёхугольники.
Свойства и признаки параллелограмма
Тип утверждения Фигура Рисунок Формулировка Определение Параллелограмм Параллелограммом называют четырёхугольник, у которого противолежащие стороны параллельны Определение Диагонали параллелограмма Диагональю параллелограмма называют отрезок, соединяющий противоположные вершины Определение Высота параллелограмма Высотой параллелограмма называют перпендикуляр, опущенный из любой точки на стороне параллелограмма на противоположную сторону параллелограмма или ее продолжение Свойство Равенство противолежащих сторон Если четырёхугольник является параллелограммом, то его противолежащие стороны равны Признак Если у четырёхугольника противолежащие стороны равны, то он является параллелограммом Признак Равенство и параллельность двух противолежащих сторон Если у четырёхугольника две противолежащие стороны равны и параллельны, то он является параллелограммом Свойство Диагонали точкой пересечения делятся пополам Если четырёхугольник является параллелограммом, то его диагонали точкой пересечения делятся пополам Признак Если у четырёхугольника диагонали точкой пересечения делятся пополам, то он является параллелограммом Свойство Суммы углов, прилежащих к сторонам Если четырёхугольник является параллелограммом, то сумма углов, прилежащих к любой его стороне равна 180° Признак Если у четырёхугольника сумма углов, прилежащих к любой его стороне равна 180°, то четырёхугольник является параллелограммом Свойство Равенство противолежащих углов Если четырёхугольник является параллелограммом, то его противолежащие углы равны Признак Если у четырёхугольника противолежащие углы равны, то четырёхугольник является параллелограммом Свойство Два треугольника, на которые каждая диагональ делит четырёхугольник Если четырёхугольник является параллелограммом, то каждая диагональ делит его на два равных треугольника Признак Если каждая диагональ четырёхугольника делит его на два равных треугольника, то четырёхугольник является параллелограммом Свойство Четыре треугольника, на которые диагонали делят четырёхугольник Если четырёхугольник является параллелограммом, то диагонали делит его на четыре треугольника равной площади (равновеликих треугольника) Признак Если диагонали четырёхугольника делят его на четыре треугольника равной площади (равновеликих треугольника), то четырёхугольник является параллелограммом Определение: параллелограмм Параллелограммом называют четырёхугольник, у которого противолежащие стороны параллельны Определение: диагонали параллелограмма Диагональю параллелограмма называют отрезок, соединяющий противоположные вершины Определение: высота параллелограмма Высотой параллелограмма называютперпендикуляр, опущенный из любой точки на стороне параллелограмма на противоположную сторону параллелограмма или ее продолжение Свойство: равенство противолежащих сторон Если четырёхугольник является параллелограммом, то его противолежащие стороны равны Признак: равенство противолежащих сторон Если у четырёхугольника противолежащие стороны равны, то он является параллелограммом Признак: равенство и параллельность двух противолежащих сторон Если у четырёхугольника две противолежащие стороны равны и параллельны, то он является параллелограммом Свойство: диагонали точкой пересечения делятся пополам Если четырёхугольник является параллелограммом, то его диагонали точкой пересечения делятся пополам Признак: диагонали точкой пересечения делятся пополам Если у четырёхугольника диагонали точкой пересечения делятся пополам, то он является параллелограммом Свойство: суммы углов, прилежащих к сторонам Если четырёхугольник является параллелограммом, то сумма углов, прилежащих к любой его стороне равна 180° Признак: суммы углов, прилежащих к сторонам Если у четырёхугольника сумма углов, прилежащих к любой его стороне равна 180°, то четырёхугольник является параллелограммом Свойство: равенство противолежащих углов Если четырёхугольник является параллелограммом, то его противолежащие углы равны Признак: равенство противолежащих углов Если у четырёхугольника противолежащие углы равны, то четырёхугольник является параллелограммом Свойство: два треугольника, на которые каждая диагональ делит четырёхугольник Если четырёхугольник является параллелограммом, то каждая диагональ делит его на два равных треугольника Признак: два треугольника, на которые каждая диагональ делит четырёхугольник Если каждая диагональ четырёхугольника делит его на два равных треугольника, то четырёхугольник является параллелограммом Свойство: четыре треугольника, на которые диагонали делят четырёхугольник Если четырёхугольник является параллелограммом, то диагонали делит его на четыре треугольника равной площади (равновеликих треугольника) Признак: четыре треугольника, на которые диагонали делят четырёхугольник Если диагонали четырёхугольника делят его на четыре треугольника равной площади (равновеликих треугольника), то четырёхугольник является параллелограммом Параллелограмм Определение: Параллелограммом называют четырёхугольник, у которого противолежащие стороны параллельны
Диагонали параллелограмма Определение: Диагональю параллелограмма называют отрезок, соединяющий противоположные вершины
Высота параллелограмма Определение: Высотой параллелограмма называют перпендикуляр, опущенный из любой точки на стороне параллелограмма на противоположную сторону параллелограмма или ее продолжение
Равенство противолежащих сторон Свойство: Если четырёхугольник является параллелограммом, то его противолежащие стороны равны.
Признак: Если у четырёхугольника противолежащие стороны равны, то он является параллелограммом.
Равенство и параллельность двух противолежащих сторон Признак: Если у четырёхугольника две противолежащие стороны равны и параллельны, то он является параллелограммом.
Диагонали точкой пересечения делятся пополам Свойство: Если четырёхугольник является параллелограммом, то его диагонали точкой пересечения делятся пополам.
Признак: Если у четырёхугольника диагонали точкой пересечения делятся пополам, то он является параллелограммом.
Суммы углов, прилежащих к сторонам Свойство: Если четырёхугольник является параллелограммом, то сумма углов, прилежащих к любой его стороне равна 180°.
Признак: Если у четырёхугольника сумма углов, прилежащих к любой его стороне равна 180°, то четырёхугольник является параллелограммом.
Равенство противолежащих углов Свойство: Если четырёхугольник является параллелограммом, то его противолежащие углы равны.
Признак: Если у четырёхугольника противолежащие углы равны, то четырёхугольник является параллелограммом.
Два треугольника, на которые каждая диагональ делит четырёхугольник Свойство: Если четырёхугольник является параллелограммом, то каждая диагональ делит его на два равных треугольника.
Признак: Если каждая диагональ четырёхугольника делит его на два равных треугольника, то четырёхугольник является параллелограммом.
Четыре треугольника, на которые диагонали делят четырёхугольник Свойство: Если четырёхугольник является параллелограммом, то диагонали делит его на четыре треугольника равной площади (равновеликих треугольника)
Признак: Если диагонали четырёхугольника делят его на четыре треугольника равной площади (равновеликих треугольника), то четырёхугольник является параллелограммом.
Свойства и признаки прямоугольника
Тип утверждения Фигура Рисунок Формулировка Определение Прямоугольник Прямоугольником называют параллелограмм, у которого все углы прямые Свойство Равенство диагоналей Если параллелограмм является прямоугольником, то его диагонали равны Признак Если у параллелограмма диагонали равны, то он является прямоугольником Определение: прямоугольник Прямоугольником называют параллелограмм, у которого все углы прямые Свойство: равенство диагоналей Если параллелограмм является прямоугольником, то его диагонали равны Признак: равенство диагоналей Если у параллелограмма диагонали равны, то он является прямоугольником Прямоугольник Определение: Прямоугольником называют параллелограмм, у которого все углы прямые.
Равенство диагоналей Свойство: Если параллелограмм является прямоугольником, то его диагонали равны.
Признак: Если у параллелограмма диагонали равны, то он является прямоугольником.
Свойства и признаки ромба
Тип утверждения Фигура Рисунок Формулировка Определение Ромб Ромбом называют параллелограмм, у которого все стороны равны Свойство Биссектрисы углов
диагоналиЕсли параллелограмм является ромбом, то его диагонали является биссектрисами углов Признак Если у параллелограмма диагонали являются биссектрисами углов, то параллелограмм является ромбом Свойство Перпендикулярность диагоналей Если параллелограмм является ромбом, то его диагонали перпендикулярны Признак Если у параллелограмма диагонали перпендикулярны, то он является ромбом Определение: ромб Ромбом называют параллелограмм, у которого все стороны равны Свойство: биссектрисы углов и диагонали Если параллелограмм является ромбом, то его диагонали являются биссектрисами углов Признак: биссектрисы углов и диагонали Если у параллелограмма диагонали являются биссектрисами углов, то параллелограмм является ромбом Свойство: перпендикулярность диагоналей Если параллелограмм является ромбом, то его диагонали перпендикулярны Признак: перпендикулярность диагоналей Если у параллелограмма диагонали перпендикулярны, то он является ромбом Ромб Определение: Ромбом называют параллелограмм, у которого все стороны равны
Биссектрисы углов и диагонали Свойство: Если параллелограмм является ромбом, то его диагонали являются биссектрисами углов
Признак: Если у параллелограмма диагонали являются биссектрисами углов, то параллелограмм является ромбом
Перпендикулярность диагоналей Свойство: Если параллелограмм является ромбом, то его диагонали перпендикулярны
Признак: Если у параллелограмма диагонали перпендикулярны, то он является ромбом
Свойства и признаки квадрата
Тип утверждения Фигура Рисунок Формулировка Определение Квадрат Квадратом называют параллелограмм, у которого все стороны равны и все углы равны Свойство Перпендикулярность
и равенство диагоналейЕсли параллелограмм является квадратом, то его диагонали перпендикулярны и равны Признак Если у параллелограмма диагонали перпендикулярны и равны, то он является квадратом Свойство Перпендикулярность диагоналей Если прямоугольник является квадратом, то его диагонали перпендикулярны Признак Если у прямоугольника диагонали перпендикулярны, то он является квадратом Свойство Равенство диагоналей Если ромб является квадратом, то его диагонали равны Признак Если у ромба диагонали равны, то он является квадратом Определение: квадрат Квадратом называют параллелограмм, у которого все стороны равны и все углы равны Свойство: перпендикулярность и равенство диагоналей Если параллелограмм является квадратом, то его диагонали перпендикулярны и равны Признак: перпендикулярность и равенство диагоналей Если у параллелограмма диагонали перпендикулярны и равны, то он является квадратом Свойство: перпендикулярность диагоналей Если прямоугольник является квадратом, то его диагонали перпендикулярны Признак: перпендикулярность диагоналей Если у прямоугольника диагонали перпендикулярны, то он является квадратом Свойство: равенство диагоналей Если ромб является квадратом, то его диагонали равны Признак: равенство диагоналей Если у ромба диагонали равны, то он является квадратом Квадрат Определение: Квадратом называют параллелограмм, у которого все стороны равны и все углы равны
Перпендикулярность и равенство диагоналей Свойство: Если параллелограмм является квадратом, то его диагонали перпендикулярны и равны
Признак: Если у параллелограмма диагонали перпендикулярны и равны, то он является квадратом
Перпендикулярность диагоналей Свойство: Если прямоугольник является квадратом, то его диагонали перпендикулярны
Признак: Если у прямоугольника диагонали перпендикулярны, то он является квадратом
Равенство диагоналей Свойство: Если ромб является квадратом, то его диагонали равны
Признак: Если у ромба диагонали равны, то он является квадратом
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Параллелограмм | Encyclopedia.com
gale
просмотров обновлен 27 июня 2018
Обратная сторона. Эта четырехсторонняя фигура называется многоугольником (двумерная [2D] фигура, состоящая из трех или более прямых сторон) или, точнее, четырехугольником (двумерная фигура, состоящая из четырех прямых сторон).
Во всех типах параллелограммов диагонали делят друг друга пополам (или делят пополам) в месте пересечения. (Диагональ — это линия, соединяющая два противоположных угла геометрической фигуры, например параллелограмма.)
Три особых типа параллелограммов называются ромбами, прямоугольниками и квадратами.
Ромб представляет собой параллелограмм, все четыре стороны которого имеют одинаковую длину, но стороны не обязательно пересекаются под прямым углом друг к другу.Прямоугольник представляет собой параллелограмм, смежные стороны которого перпендикулярны (встречаются под прямым углом) друг к другу, а противоположные стороны равны по длине.
Квадрат представляет собой параллелограмм, смежные стороны которого перпендикулярны (под углом 90°) и равны по длине. То есть все четыре стороны равны по длине, а стороны, содержащие общую точку, находятся под прямым углом друг к другу.
Площадь (А) параллелограмма равна расстоянию (длине) одной стороны, называемой его основание b, умноженное на кратчайшее расстояние (длину) до противоположной стороны, называемое его высотой или высотой h. Это можно записать как A = bh. Поскольку все четыре стороны (s) квадрата равны, то b= h= s, и его уравнение можно записать как A= 2s. Окружность (С) параллелограмма (или расстояние вокруг него) обозначается: С= 2b+ 2H. В случае квадрата (где все четыре стороны равны по длине) уравнение принимает вид: C = 4s.
Научная энциклопедия Гейла
Гейл
просмотров обновлено 11 мая 2018
Параллелограмм — это плоскость четырехсторонней фигуры, противоположные стороны которой параллельны .
Ромб представляет собой параллелограмм, все четыре стороны которого имеют одинаковую длину; прямоугольник является параллелограммом, смежные стороны которого перпендикулярны ; а квадрат — это параллелограмм, смежные стороны которого перпендикулярны и равны по длине.Площадь параллелограмма равна длине его основание в раз больше длины его высоты .
Научная энциклопедия Гейла
Оксфорд
просмотра обновлено 11 июня 2018 г. н. четырехсторонняя плоская прямолинейная фигура, противоположные стороны которой параллельны.
параллелограммы
Оксфордский карманный словарь современного английского языка
oxford
просмотров обновлено 18 мая 2018 г.
параллелограмм Четырехугольник (четырехсторонняя плоская фигура), у которого каждая пара противоположных сторон параллельна и равна.
Оба противоположных угла параллелограмма также равны. Его площадь равна произведению одной стороны на перпендикулярное расстояние от противоположной стороны. Параллелограмм, у которого все четыре стороны равны, является ромбом. Всемирная энциклопедия
Разница между ромбом и параллелограммом (со сравнительной таблицей)
Последнее обновление by Surbhi S
В геометрии существует много типов четырехугольников, т. е. параллелограмм, ромб, квадрат, прямоугольник, трапеция и воздушный змей, которые имеют общие характеристики, из-за которых люди сталкиваются с трудностями при понимании этих фигур. Ромб можно назвать наклонным квадратом, у которого смежные стороны равны. Напротив, параллелограмм представляет собой наклонный прямоугольник с двумя наборами параллельных противоположных сторон.
Основное различие между ромбом и параллелограммом заключается в их свойствах, т.е. все стороны ромба имеют одинаковую длину, а параллелограмм – это прямолинейная фигура, противоположные стороны которой параллельны.
Содержание: Ромб против параллелограмма
- Сравнительная таблица
- Определение
- Ключевые отличия
- Заключение
Сравнительная таблица
Основание для сравнения Ромб Параллелограмм Значение Ромбом называется четырехсторонняя фигура плоской формы, все стороны которой конгруэнтны. Параллелограмм представляет собой четырехстороннюю плоскую фигуру, противоположные стороны которой параллельны друг другу. Равные стороны Все четыре стороны имеют одинаковую длину. Противоположные стороны имеют одинаковую длину. Диагонали Диагонали делятся пополам под прямым углом, образуя разносторонний треугольник. Диагонали делят друг друга пополам, образуя два конгруэнтных треугольника. Площадь (pq)/2, где p и q — диагонали bh, где b = основание и h = высота Периметр 4 a, где a = сторона 2 (a+b), где a = сторона, b = основание Определение ромба
Четырехугольник, длины сторон которого равны, называется ромбом.
Он имеет плоскую форму и четыре стороны; при этом обращенные стороны параллельны друг другу (см. рисунок ниже).Противоположные углы ромба равны, т.е. имеют один и тот же градус. Его диагонали пересекаются друг с другом под углом 90 градусов (прямой угол), следовательно, перпендикулярны друг другу и образуют два равносторонних треугольника. Его смежные стороны дополнительные, а значит, сумма их мер равна 180 градусам. Он также известен как равносторонний параллелограмм.
Определение параллелограмма
Параллелограмм, как следует из его названия, представляет собой плоскую фигуру, имеющую четыре стороны, множество противоположных сторон которых параллельны и конгруэнтны (см. рисунок ниже).
Мера его противолежащих углов равна, а последовательные углы являются дополнительными, т.е. сумма их мер равна 180 градусам. Его диагонали делят друг друга пополам, образуя два конгруэнтных треугольника.
Ключевые различия между ромбом и параллелограммом
Различие между ромбом и параллелограммом может быть ясно показано на следующих основаниях:
- Мы определяем ромб как четырехугольник плоской формы, у которого длины всех сторон равны.
{\circ}$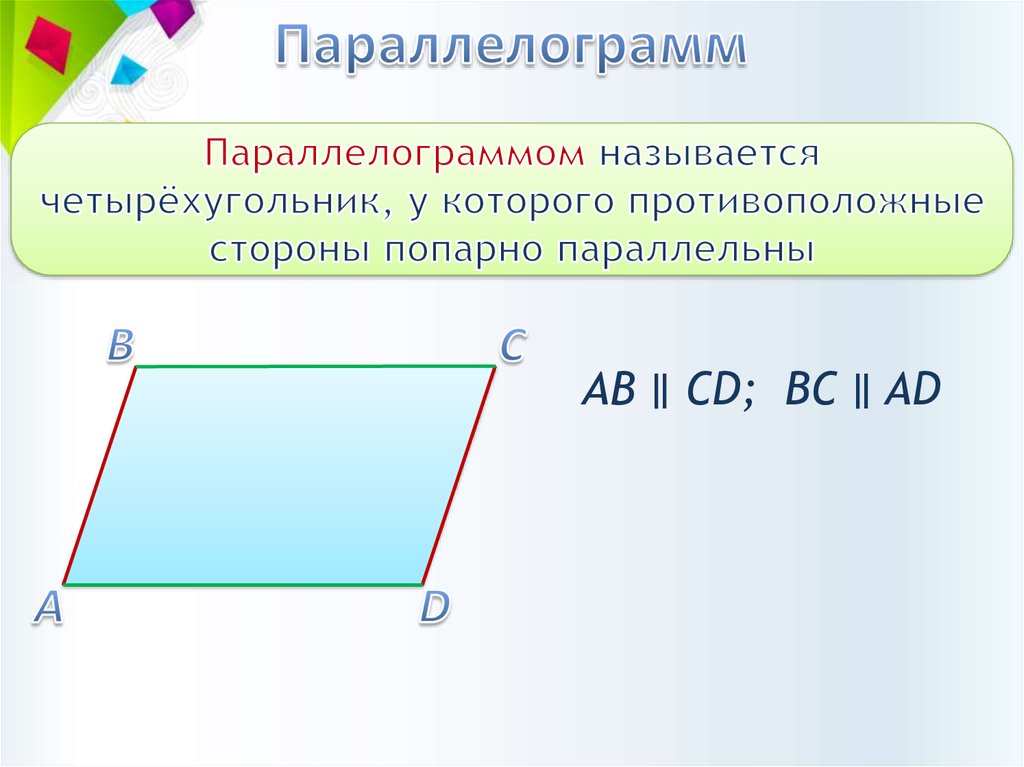
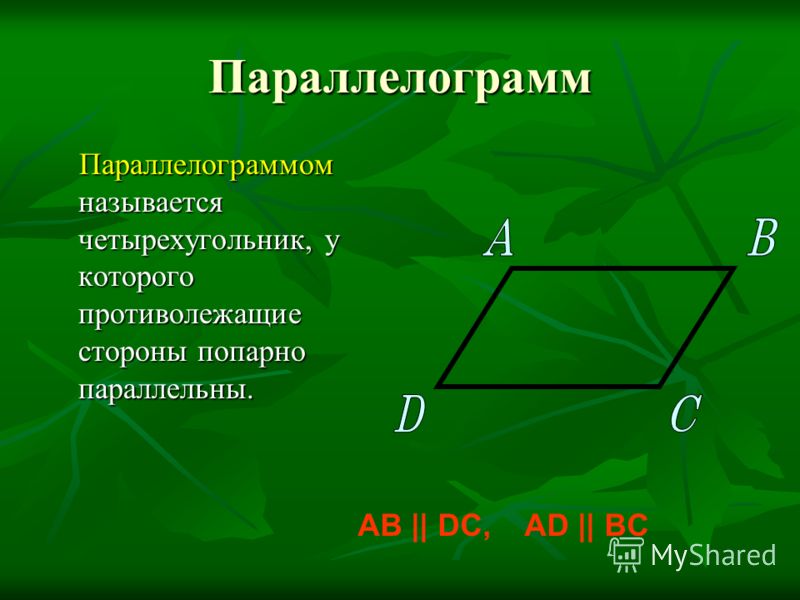
Ромб представляет собой параллелограмм, все четыре стороны которого имеют одинаковую длину; прямоугольник является параллелограммом, смежные стороны которого перпендикулярны ; а квадрат — это параллелограмм, смежные стороны которого перпендикулярны и равны по длине.
Оба противоположных угла параллелограмма также равны. Его площадь равна произведению одной стороны на перпендикулярное расстояние от противоположной стороны. Параллелограмм, у которого все четыре стороны равны, является ромбом. 
Он имеет плоскую форму и четыре стороны; при этом обращенные стороны параллельны друг другу (см. рисунок ниже).