Процентиль: что это простыми словами
- 17.06.20
- 0 комментариев
- 112019
Что такое процентиль?
Термин ″процентиль″ (percentile) часто встречается в зарубежной литературе про инвестиции и вообще в статистических исследованиях – одно из таких исследований я упоминал в этой статье. Другими вариантами русских названий являются ″персентиль″ и ″перцентиль″. Думаю, что небольшая известность термина в России не вполне заслужена, поскольку нередко именно в процентилях удобно выразить полученные результаты.
Процентиль это определенная часть выборки данных
Возьмем простой пример. Группа студентов из 200 человек пишет тест, состоящий из 100 вопросов. Проходной порог, когда тест считается сданным, составляет 2/3 правильных ответов, т.е. не менее 66. Что получается с точки зрения отдельного студента?
Допустим, Иван правильно ответил на 70 вопросов. Задачу он выполнил — тест засчитан. Результат каждого участника теста также сравнивается с числом 66: если правильных ответов больше, тест сдан. В результате формируется список сдавших и не сдавших: каждый студент проходил через это. Пока ничего нового.
В результате формируется список сдавших и не сдавших: каждый студент проходил через это. Пока ничего нового.
Но задачу можно поставить и по-другому: нужно сравнить результаты студентов не с проходным баллом в 66 пунктов, а между собой. Зачем это нужно? В данном случае, например, для объективной оценки сложность теста, что достигается группировкой результатов.
Вернемся к Ивану, который получил 70 правильных ответов. Много это или мало по сравнению с остальными? Это и покажет процентиль.
Процентили делят всю выборку на определенные части. Например, пятый процентиль охватывает 5% объема выборки. Предположим, показатель Ивана равен пятому процентилю. Это означает, что Иван написал тест лучше, чем 5% студентов (10 человек из 200 получили от нуля до 70 баллов). Не густо, поскольку в этом случае остальные 190 человек набрали больше, чем 70. Значит, тест был очень легкий и порог в 66 баллов можно и повысить.
Но в том же самом тесте может быть и обратная ситуация: результат Ивана равен 90-ому процентилю.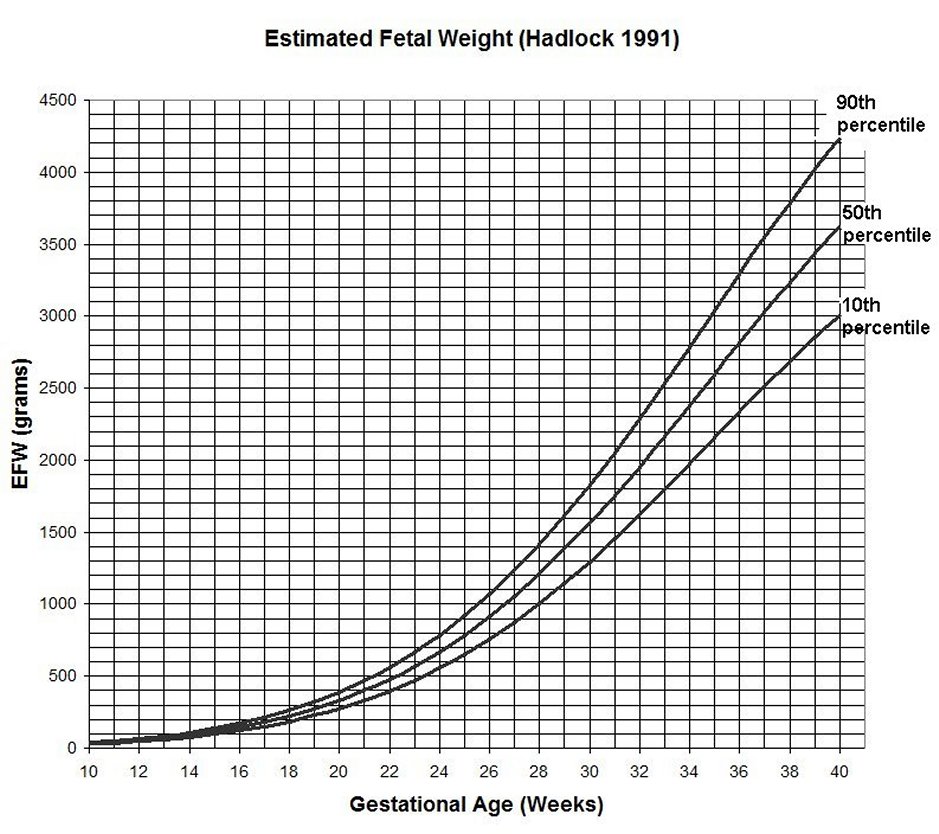 Это значит, что Иван написал тест лучше, чем 90% студентов. Или по другому: только 10% (20 человек) набрали более 70 правильных ответов. Следовательно, тест был весьма трудным. Преимущество метода еще и в том, что разбивкой на процентили можно сравнивать тесты с разным числом участников.
Это значит, что Иван написал тест лучше, чем 90% студентов. Или по другому: только 10% (20 человек) набрали более 70 правильных ответов. Следовательно, тест был весьма трудным. Преимущество метода еще и в том, что разбивкой на процентили можно сравнивать тесты с разным числом участников.
Функция Гаусса
Процентиль можно пояснить и на примере симметричного распределения Гаусса, которое часто встречается в статистике для оценки веса, роста и т.п. На рисунке выше показаны 25, 50, 75 и 100 процентили. Случаи 25 и 75-ого процентиля, включающие четверть и три четверти выборки соответственно, называются квартилями.
Чем более высок процентиль, тем больше данных он включает
Расчет процентиля в Excel
Процентиль несложно вычислить по формуле:
но проще обрабатывать массив данных одноименной функцией Excel. Для примера возьмем произвольную выборку полученных баллов и рассчитаем в ней процентили:
Функция PERCENTILE (ПЕРСЕНТИЛЬ) включает в себя ввод диапазона ячеек данных (А1:А10) и значения процентиля К, деленного на 100%. Т.е. в данном случае ввод 0.3 означает нахождение тридцатого процентиля. Смысл расчета: к 30-му процентилю будут относиться все результаты, меньше или равные 7.9.
Т.е. в данном случае ввод 0.3 означает нахождение тридцатого процентиля. Смысл расчета: к 30-му процентилю будут относиться все результаты, меньше или равные 7.9.
Если мы хотим узнать процентиль участника, получившего 10 баллов, то это несложно сделать, варьируя значение К до тех пор, пока значение в ячейке С12 не станет близким 10. Получится примерно 34-ый процентиль. При увеличении процентиля в выборку попадает больше табличных значений:
Итого, в 80-ый процентиль попадает уже 8 табличных значений из 10, которые меньше или равны 47.2. При этом подчеркнуть результат можно диапазоном процентилей — например, между восьмидесятым и сотым. В этом случае значения будут лежать между 47.2 и 67 (максимальным числом выборки).
Поделись с друзьями!
- Теги:
- кэф
Please enable JavaScript to view the comments powered by Disqus.
Почему расчет перцентилей работает не так как вы ожидаете? / Хабр
Часто клиенты спрашивают нас о p99-метрике (99-й перцентиль).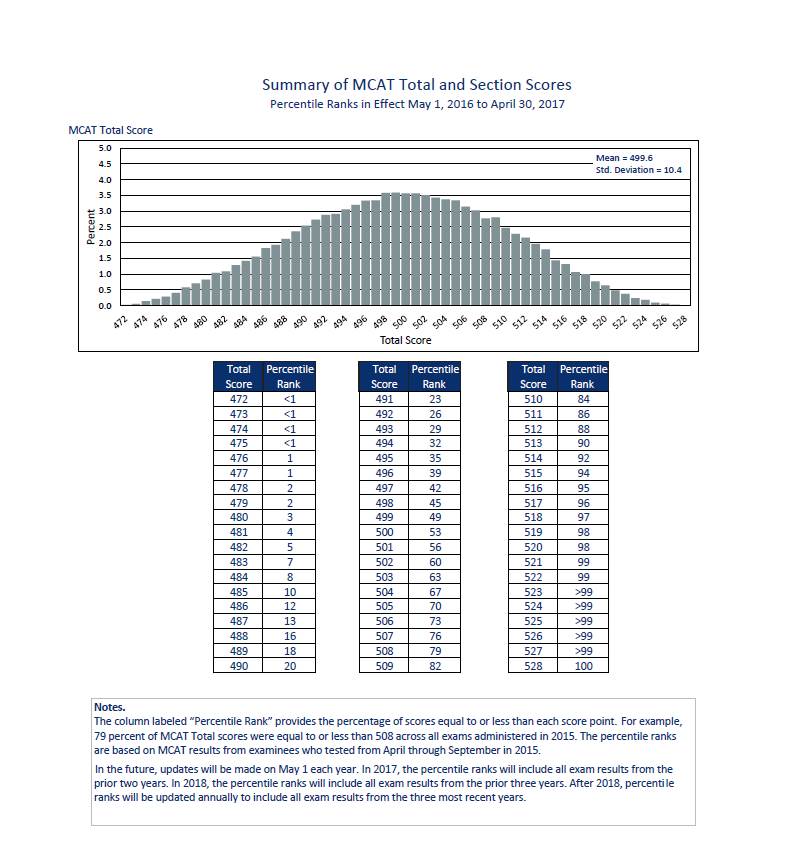
Это определенно разумная просьба и мы планируем добавить подобную функциональность в VividCortex (об этом расскажу позже). Но в то же время, когда клиенты спрашивают об этом, они подразумевают нечто совершенно определенное — нечто, что может быть проблемой. Они просят не 99-й перцентиль по какой-то метрике, они просят метрику по 99-му перцентилю. Это обычное дело для таких систем как Graphite, но все это дает не тот результат, который от таких систем ожидается. Это пост расскажет вам о том, что, возможно, у вас неверные представления про перцентили, о точной степени ваших заблуждений и о том, что вы все таки можете сделать правильно в этом случае.
(Это перевод статьи которую написал Baron Schwartz.)

Средние значения являются проблемой и практически не помогают когда речь идет о мониторинге. Если вы просто наблюдаете за средними, вы скорее всего пропустите те данные, которые производят наибольшее влияние на вашу систему: при поиске каких-либо проблем, особенно важные для вас события по определению будут являться выбросами. Есть две проблемы со средними значениями в случае наличия выбросов:
- Средние скрывают выбросы и вы их не видите.
- Выбросы смещают средние значения, так что в системе в которой существуют выбросы, средние значения уже не отражают нормальное состояние системы.
Так что когда вы усредняете какую-либо метрику в системе с ошибками, вы объединяете все худшее: вы наблюдаете уже не совсем обычное состояние системы, но в то же время не видите ничего необычного.
Кстати работа большинства программных систем просто кишит экстремальными выбросами.
Просмотр выбросов находящихся в длинном хвосте по частоте появления очень важен потому что показывает вам как именно плохо вы обратываете запросы в некоторых редких случаях. Вы не увидите этого, если будете работать только со средними.
Вы не увидите этого, если будете работать только со средними.
Как сказал Werner Vogels из Amazon на открытии re:Invent: единственное, о чем вам могут сказать средние значения — это то что половину ваших клиентов вы обслуживаете еще хуже. (Хотя это заявление абсолютно корректно по духу, оно не совсем отражает действительность: тут более правильно было бы сказать о медиане (она же 50-й перцентиль) — именно эта метрика обеспечивает указанное свойство)
Компания Optimizely опубликовала запись в этом посте пару лет назад. Она отлично поясняет почему средние могут приводить к неожиданным последствиям:
“Хотя средние значения очень легко понять они также могут привести к сильнейшим заблуждениям. Почему? Потому что наблюдение за средним временем отклика подобно измерению средней температуры больницы. В то время как то, что действительно вас заботит — это температура каждого из пациентов и в особенно кто из пациентов нуждается в вашей помощи в первую очередь.”
Brendan Gregg также хорошо объяснил это:
“Как статистическая характеристика, средние значения (включая среднее арифметическое) в практическом применении имеют множество достоинств.Однако возможность описания распределения значений не является одним их них.”
Перцентили (квантили — в более широком представлении) часто превозносятся как средство для преодоления этого фундаментального недостатка средних значений. Смысл 99-го перцентиля в том чтобы собрать всю совокупность данных (другими словами всю коллекцию измерений системы) и отсортировать их, затем откинуть 1% наибольших и взять наибольшее значение из оставшихся. Полученное значение обладает двумя важными свойствами:
- Это наибольшее значение из значений, которые получаются в 99% случаев. Если это значение, например, является измерением времени загрузки веб-страницы, то оно отражает самый худший случай обслуживания, которое получается как минимум при 99% посещений вашего сервиса.
- Это значение устойчиво к действительно сильным выбросам, которые происходят по множеству причин, включая ошибки измерения.
Само собой, вы не обязаны выбирать именно 99%.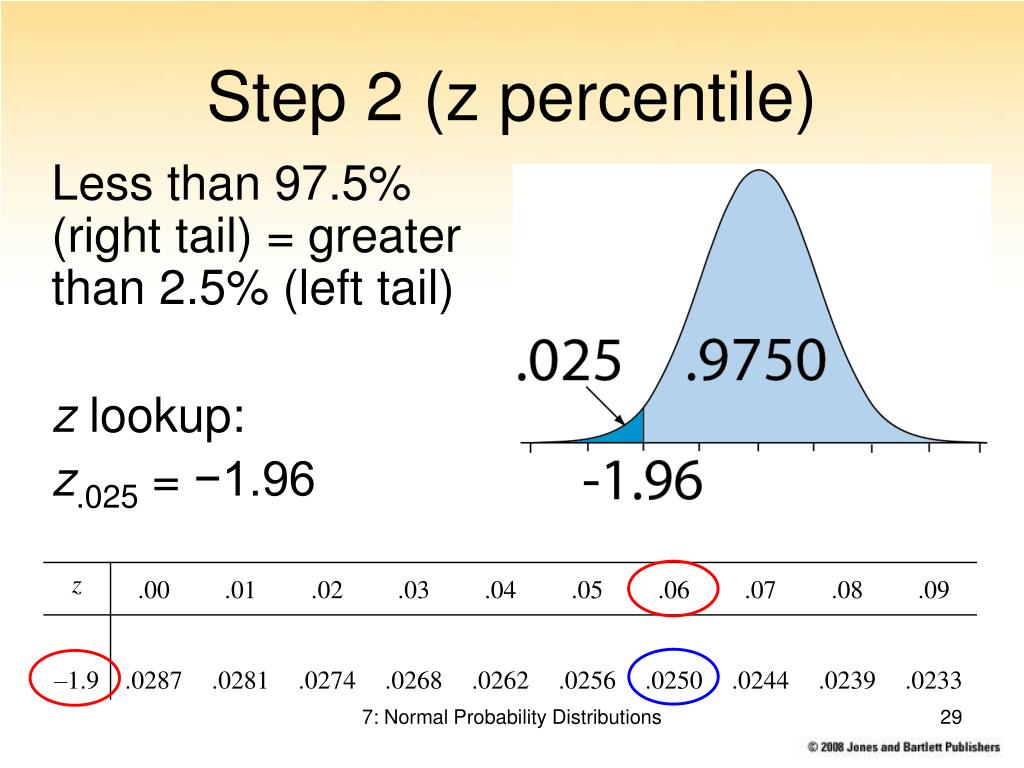
И теперь вы предположите: средние это плохо, а перцентили это отлично — давайте вычислим перцентили по метрикам и сохраним их в наше хранилище для хранения временных рядов (TSDB)? Но все не так просто.
Существует большая проблема с перцентилями во временных рядах данных. Проблема заключается в том, что большинство TSDB почти всегда хранят аггрегированные метрики на временных промежутках, а не всю выборку измеренных событий. Впоследствии TSDB усредняют эти метрики по времени в целом ряде случаев. Наиболее важные:
- Они усредняют метрики в том случае, если дискретность времени в вашем запросе отличается от дискретности времени которое было использовано при аггрегирование данных при сохранении. Если вы хотите вывести график метрики за день, например, шириной 600px, то каждый пиксел будет отражать 144 секунд данных.
 Это усреднение неявно и пользователи о нем никак не подозревают. А на самом деле эти сервисы должны бы были вывести предупреждение!
Это усреднение неявно и пользователи о нем никак не подозревают. А на самом деле эти сервисы должны бы были вывести предупреждение! - TSDB усредняют данные в случае когда сохраняют их для долговременного хранения в более низком разрешении, что и происходит в большинстве TSDB на самом деле.
И вот тут появляется проблема. Вы снова имеете дело с усреднением в какой-то форме. Усреднение перцентилей не работает, поскольку для вычисляения перцентиля в новом масштабе вы должны иметь полную выборку событий. Все вычисления на самом деле некорректны. Усреднение перцентилей не имеет никакого смысла. (Последствия этого могут быть произвольными. Я вернусь к этому позже.)
К сожалению, некоторые распространенные open-source продукты для мониторинга подстрекают к использованию перцентильных метрик, которые на самом деле будут затем передискретизированы при сохранении. Например StatsD, позволяет рассчитывать желаемый перцентиль после чего генерирует метрику с именем вроде foo.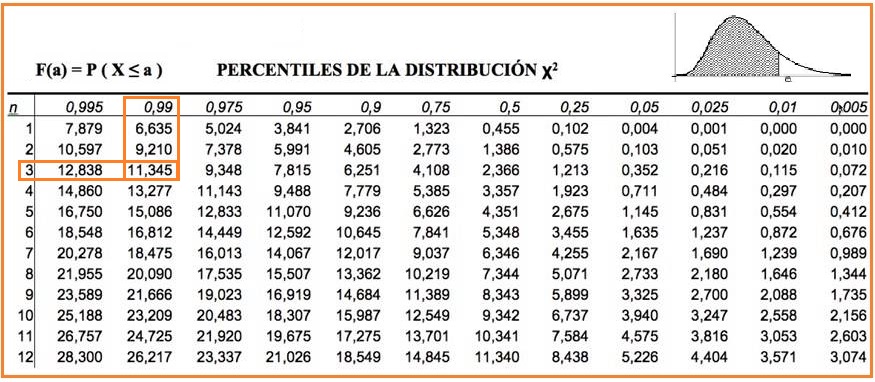
Непонимание того, как все эти вычисления происходят, крайне распространено. Чтение ветки комментариев к вот этому StatsD GitHub тикету отлично это иллюстрирует. Некоторые товарищи там говорят про вещи, которые не имеют ничего общего с реальностью.
— Сьюзи, сколько будет 12+7?
— Миллиард!
— Спасибо!
— … ээ, но это же вроде не может быть правдой?
— тоже самое она говорила про 3+4
Возможно самым кратким способом обозначить проблему будет сказать так: Перцентили вычисляются из коллекции измерений и должны пересчитываться полностью каждый раз когда эта коллекция меняется. TSDB периодически усредняют данные по различным промежуткам времени, но в то же время не хранят исходную выборку измерений.
Но, если расчет перцентилей действительно требует полной выборки оригинальных событий (например каждой время каждой загрузки веб-страницы), то в таком случае у нас появляется большая проблема. Проблема «Больших Данных» — будет точнее сказать так. Именно поэтому правдивый расчет перцентилей чрезвычайно затратен.
Проблема «Больших Данных» — будет точнее сказать так. Именно поэтому правдивый расчет перцентилей чрезвычайно затратен.
Существует несколько способов расчета *приблизительных» перцентилей которые почти также хороши как хранение полной выборки измерений с последующей ее сортировкой и вычислением. Вы сможете найти множество научных исследований по различным направлениям включая:
- гистограммы, которые разделяют всю коллекцию событий по диапазонам (или корзинам) и после этого рассчитывают сколько именно событий попадает в каждый из диапазонов (корзин)
- приблизительные потоковые структуры данных и алгоритмы (подсчет набросков, «sketchs»)
- хранилища которые делают выборку из коллекции событий для обеспечения приблизительных ответов
- решения с ограничениями по времени, количеству или обо обоим сразу
Суть большинства из этих решений заключается в приближении распределения коллекции тем или иным способом. Из информации о распределении вы сможете рассчитать приблизительные перцентили, а также некоторые другие интересные метрики. Опять же из блога компании Optimizely, можно привести интересный пример распределения времен отклика, а также среднего и 99-го перцентиля:
Опять же из блога компании Optimizely, можно привести интересный пример распределения времен отклика, а также среднего и 99-го перцентиля:
Есть множество способов рассчета и хранения приблизительных распределений, однако гистограммы особенно популярны из-за их относительной простоты. Некоторые решения по мониторингу поддерживают гистограммы. Circonus например, один из таких. Theo Schlossnagle, CEO компании Circonus, часто пишет о преимуществах гистограмм.
В конечном счете, располагать распределением исходной коллекции событий полезно не только для расчета перцентилей, но также позволяет выявить некоторые вещи о которых перцентили сказать не могут. В конце концов, перцентиль — это всего лишь число, которое всего лишь пытается отразить большое количество информации о данных. Я не буду заходить так далеко, как это сделал Theo когда он твитнул о том, что “99-й ничуть не лучше среднего”, потому как тут я согласен с фанатами перцентилей в том, что перцентили гораздо более информативнее, чем средние значения в представлении некоторых важных характеристик исходной выборки.
Лучшим способом вычисления перцентилей в TSDB будет сбор метрик по диапазонам. Я высказал подобное предположение, поскольку множество TSDB на деле являются всего лишь упорядоченными по временным меткам коллекциями «ключ-значение» без возможности хранения гистограмм.
Диапазонные метрики обеспечивают те же самые возможности, что и последовательность гистограмм во времени. Все что вам нужно сделать — это выбрать лимиты, которые будут разделять значения по диапазонам, а затем рассчитать все метрики отдельно по каждому из диапазонов. Метрика будет такой же как и для гистограммы: а именно число событий значения которых попали в этот диапазон.
Но в общем, выбор диапазонов для разделения является непростой задачей. Обычно хорошим выбором будут являться диапазоны с логарифмически прогрессирующими размерами или диапазоны которые обеспечивают хранение огрубленных значений для ускорения расчетов (ценой отказа от плавного роста счетчиков). Но диапазоны с одинаковыми размерами вряд ли будут хорошим выбором. Больше информации по этой теме есть в заметке от Brendan Gregg.
Обычно хорошим выбором будут являться диапазоны с логарифмически прогрессирующими размерами или диапазоны которые обеспечивают хранение огрубленных значений для ускорения расчетов (ценой отказа от плавного роста счетчиков). Но диапазоны с одинаковыми размерами вряд ли будут хорошим выбором. Больше информации по этой теме есть в заметке от Brendan Gregg.
Есть фундаментальное противоречие между количеством сохраняемых данных и их степенью их точности. Однако даже грубое распреределение диапазонов обеспечивает лучшее представление данных чем среднее. Например, Phusion Passenger Union Station показывает диапазонные метрики времени ожидания по 11-ти диапазонам. (Мне вовсе не кажется, что приведенная иллюстрация наглядна; значение по оси y несколько смущает, на самом деле это 3D график, спроецированный в 2D нелинейным способом. Нем не менее он все равно дает больше информации чем это могло бы дать среднее значение.)
Как это можно реализовать при помощи популярных open-source продуктов? Вы должны определить диапазоны и создать столбики в виде штабелей как на рисунке выше.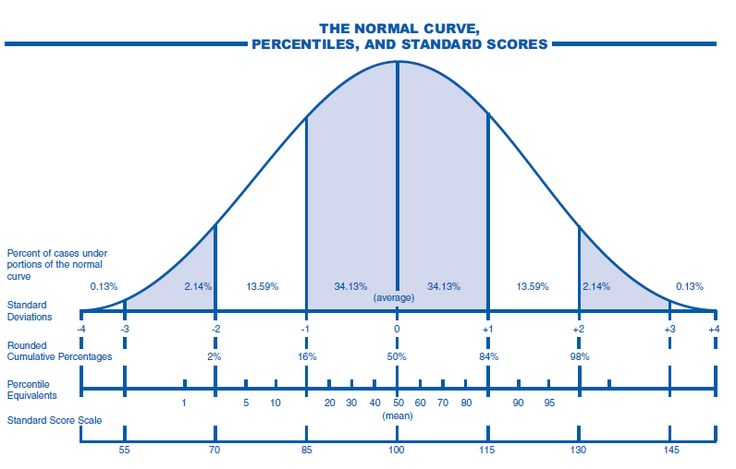
Но рассчитать перцентиль по этим данным теперь будет гораздо труднее. Вы будете должны пройтись по всем диапазонам в обратном порядке, от больших к меньшим, суммируя счетчики количества событий по пути. Как только вы получите сумму числа событий большую чем 1% от общего количества, то именно этот диапазон будет хранить значение 99% перцентиля. Тут есть много нюансов — нестрогие равенства; как именно обрабатывать пограничные случаи, какое значение выбрать для перцентиля (диапазона сверху или снизу? а может посередине? или может взвешенное от всех?).
И вообще подобные вычисления могут сильно запутывать. Например, вы можете предположить что вам нужно 100 диапазонов для вычисления 99-го перцентиля, но на самом деле все может быть иначе. Если у вас всего два диапазона и в верхний попадает 1% от всех значений, то вы сможете получить 99% перцентиль и так. (Если для вас это кажется странным, то поразмышляйте о квантилях вообще; я считаю, что понимание сути квантилей очень ценно.)
Так что тут не все просто. Это возможно в теории, но на практике сильно зависит от того поддерживает ли хранилище нужные типы запросов для получения приблизительных значений перцентилей по диапазонным метрикам. Если вы знаете хранилища в которых это возможно — напишите в комментариях (на сайте автора — прим. пер.)
Это возможно в теории, но на практике сильно зависит от того поддерживает ли хранилище нужные типы запросов для получения приблизительных значений перцентилей по диапазонным метрикам. Если вы знаете хранилища в которых это возможно — напишите в комментариях (на сайте автора — прим. пер.)
Хорошо то, что в системах подобных Graphite (то есть в тех, которые рассчитывают на то, что все метрики можно свободно усреднять и передискретизировать) все диапазонные метрики абсолютно устойчивы к этим типам преобразований. Вы получите корректные значения потому как все вычисления коммутативны по отношению к времени.
Перцентиль — это всего лишь число, так же как и среднее. Среднее отображает центр масс выборки, перцентиль показывает отметку верхнего уровня указанной доли выборки. Подумайте о перцентилях как о следах волн на пляже. Но, хотя перцентиль отображает верхние уровни, а не только центральный тренд как среднее, он все равно не так информативен и подробен по сравнению с распределением, которое в свою очередь описывает все выборку целиком.
Знакомьтесь, существуют тепловые карты — которые на самом деле являются 3D графиками в которых гистограммы повернуты и совмещены вместе по течению времени, а значения отображаются цветом. И снова, компания Circonus предоставляет отличный пример визуализации тепловых карт.
С другой стороны, как мне известно, Graphite пока не обеспечивает возможность создавать тепловые карты по диапазонным метрикам. Если я не прав и это можно сделать с помощью какого-то трюка — дайте мне знать (автору статьи — прим.пер.).
Тепловые карты также отлично подходят для отображения формы и плотности задержек в частности. Другой пример тепловой карты по задержкам — это сводка по потоковой доставке от компании Fastly.
Даже некоторые древние инструменты которые вам уже кажутся примитивными могут создавать тепловые карты. Например Smokeping, использует затемнение для отображения диапазонов значений. Ярко-зеленый обозначает среднее:
Хорошо, после всех упомянутых сложностей и нюансов которые нужно бы учесть, возможно старая добрая StatsD-метрика upper_99 для показа перцентилей не кажется вам такой плохой. В конце концов, это очень просто, удобно и уже готово к использованию. Действительно ли эта метрика так плоха?
В конце концов, это очень просто, удобно и уже готово к использованию. Действительно ли эта метрика так плоха?
Все зависит от обстоятельств. Для множества сценариев использования они отлично подходят. Я имею в виду, что в любом случае вы все равно ограничиваете себя тем, что перцентили не всегда хорошо описывают данные. Но если вам и это не важно, тогда наибольшая проблема для вас это передискретизация этих метрик, что будет означать что вы будете затем наблюдать за неверными данными.
Но измерения вообще неверная штука — в любом случае, и кроме того, множество неправильных по сути вещей тем не менее все равно как-то полезны. Например, я мог бы рассказать, что добрая половина метрик, на которые смотрят люди, на самом деле уже сознательно искажена. Наприме показателен load average для систем. Этот параметр бесспорно полезен, но как только вы узнаете как именно делается эта «колбаса», вы возможно поначалу испытаете шок. (На хабре есть отличная статья про вычисление LA — прим. пер.) Подобным же образом множество систем подобным же образом сжато отображают различные метрики своей производительности. Множество метрик из Cassandra являются результатом работы библиотеки Metrics library (Coda Hale) и на самом деле являются плавающим усреднением (экспоненциально взвешенное плавающее среднее), к которому у множества людей есть стойкое отвращение.
пер.) Подобным же образом множество систем подобным же образом сжато отображают различные метрики своей производительности. Множество метрик из Cassandra являются результатом работы библиотеки Metrics library (Coda Hale) и на самом деле являются плавающим усреднением (экспоненциально взвешенное плавающее среднее), к которому у множества людей есть стойкое отвращение.
Но вернемся к метрикам по перцентилям. Если вы сохраните метрику p99, а затем уменьшите и просмотрите усредненную версию за большой промежуток времени — хотя может это и не будет “правильно” и даже может быть что график будет весьма отличным от реального значения 99-го перцентиля, но то, что это будет неправильно, необязательно означает то, что этот график нельзя использовать в желаемых целях, а именно для понимания худших случаев во взамодействии пользователей с вашим приложением.
Так что все зависит от случая к случаю. Если вы понимаете то, как перценили работают и то, что проводить усреднение перцентилей неправильно, и вас это устраивает, то хранение перцентилей может оказаться допустимым и даже полезным. Но тут вы вносите моральную дилемму: с таким подходом вы можете сильно смутить ничего не подозревающих людей (возможно даже ваших коллег). Посмотрите на комментарии к тикету на StatsD еще раз: непонимание сути процесса прямо ощущается.
Но тут вы вносите моральную дилемму: с таким подходом вы можете сильно смутить ничего не подозревающих людей (возможно даже ваших коллег). Посмотрите на комментарии к тикету на StatsD еще раз: непонимание сути процесса прямо ощущается.
Позвольте мне провести не самую лучшую аналогию: я иногда употребляю из моего холодильника такие явства, которые никогда бы не предложил другим. Просто спросите мою жену об этом. (Жену автора — прим.пер.). Если вы дадите людям бутылку с надписью “алкоголь”, а в ней будет содержаться метанол, то эти люди ослепнут. Но некоторые спросят: «а какой именно алкоголь содержится в этой бутылке?» Вам лучше придерживаться такой же меры ответственности по отношению к подобным вопросам.
На текущий момент наша TSDB не поддерживает гистограммы и мы не поддерживаем расчет и сохранение перцентилей (хотя вы можете просто присылать нам любые свои метрики, если это необходимо).
На будущее мы планируем поддержку хранения диапазонных метрик высокого разрешения, то есть метрик с большим количеством диапазонов. Мы сможем реализовать нечто подобное, поскольку большинство диапазонов по всей видимости будут пустыми и наша TSDB сможет эффективно обрабатывать разреженные данные (также вероятно, что после усреднения по времени они уже не будут столько разреженными — прим.пер.). Это даст нам возможность выдавать гистограммы раз в секунду (все наши данные хранятся с разрешением в 1 секунду). Диапазонные метрики будут передескритизированы в 1-минутное разрешение после заданного в настройках периода, который установлен по умолчанию в 3 дня. При этом диапазонные метрики будут передискретизированы в 1-минутное разрешение без всяких математических проблем.
Мы сможем реализовать нечто подобное, поскольку большинство диапазонов по всей видимости будут пустыми и наша TSDB сможет эффективно обрабатывать разреженные данные (также вероятно, что после усреднения по времени они уже не будут столько разреженными — прим.пер.). Это даст нам возможность выдавать гистограммы раз в секунду (все наши данные хранятся с разрешением в 1 секунду). Диапазонные метрики будут передескритизированы в 1-минутное разрешение после заданного в настройках периода, который установлен по умолчанию в 3 дня. При этом диапазонные метрики будут передискретизированы в 1-минутное разрешение без всяких математических проблем.
И в итоге, из этих диапазонных метрик мы получим позможность получить любой желаемый перцентиль, показать оценку ошибки, показать тепловую карту и показать кривую распределения.
Это будет не быстрым в реализации и потребует больших усилий от инженеров, но работа начата и система уже разработана с учетом всего этого. Не могу обещать когда именно это будет реализовано, но считаю нужным рассказать о наших долгосрочных планах.
Пост получился несколько длиннее, чем я задумывал сначала, но я затронул много тем.
- Если вы планируете вычислять перцентили за какой-то интервал и впоследствии сохранять результат в виде временных рядов — как это делают некоторые существующие хранилища — вы можете получить не совсем то на что рассчитываете.
- Точное вычисление перцентилей требует больших вычислительных затрат.
- Приблизительные значения перцентилей могут быть высчитаны по данным гистограмм, диапазонных метрик, а также другими полезными вычислительными техниками.
- Такие данные также позволят выдавать распределения и тепловые карты, что будет еще более информативным чем простые перцентили.
- Если все это недоступно прямо сейчас или вы не можете себе этого позволить, валяйте, используйте метрики по по перцентилям, но помните о последствиях.
Надеюсь все это было полезным для вас.
- Кто то упомянул в твиттере про эффект: «упс, пнтнко, я оказывается делаю все как-то неправильно.
 Но я переключился на подсчет процента запросов которые выполняются за время меньшее/большее чем указанное значение и сохраняю эту метрику вместо прежней.» Но это также не работает. Подход с вычислением средних по долям (а процент — это доля) все равно не работает. Вместо этого, сохраняйте метрику числа запросов которые не выполняются за желаемое время. Вот это будет работать.
Но я переключился на подсчет процента запросов которые выполняются за время меньшее/большее чем указанное значение и сохраняю эту метрику вместо прежней.» Но это также не работает. Подход с вычислением средних по долям (а процент — это доля) все равно не работает. Вместо этого, сохраняйте метрику числа запросов которые не выполняются за желаемое время. Вот это будет работать. - Не сразу смог найти отличный пост от Theo на эту тему. Вот он: http://www.circonus.com/problem-math/
Процентили, ранг процентилей и диапазон процентилей: определение и примеры
Определения статистики > Процентили, ранг процентилей и диапазон процентилей
Содержание :
- Процентили
- Процентильный ранг
- Как найти процентиль
- Процентильный диапазон
1. Что такое процентили?
Посмотрите видео с обзором и несколькими примерами:
Процентили Определение и примеры
Посмотрите это видео на YouTube.
Видео не видно? Кликните сюда.
Изображение: UPRM.edu «Процентиль» используется в повседневной жизни, но для него нет универсального определения. Наиболее распространенным определением процентиля является число, при котором определенный процент баллов падает ниже этого числа. Возможно, вы знаете, что на тесте вы набрали 67 баллов из 90. Но эта цифра не имеет реального значения, если вы не знаете, в какой процентиль вы попадаете. Если вы знаете, что ваша оценка находится в 90-й процентиль означает, что вы набрали больше баллов, чем 90% людей, прошедших тест.
Процентили обычно используются для представления результатов тестов, таких как SAT, GRE и LSAT. например, 70-й процентиль на GRE 2013 года составлял 156. Это означает, что если вы набрали 156 баллов на экзамене, ваш результат был лучше, чем у 70 процентов тестируемых.
25-й процентиль также называется первым квартилем.
50-й процентиль обычно является медианой (если вы используете третье определение — см. ниже).
ниже).
75-й процентиль также называется третьим квартилем.
Разница между третьим и первым квартилями представляет собой межквартильный диапазон.
2. Процентильный ранг
Слово «процентиль» используется неформально в приведенном выше определении. В обычном использовании процентиль обычно указывает, что определенный процент падает ниже этого процентиля. Например, если вы набрали 25-й процентиль, то 25% тестируемых имеют результат ниже вашего. Число «25» называется -м процентилем 9-го ранга.0007 . В статистике все может быть немного сложнее, так как на самом деле существует три определения «процентиля». Вот первые два (см. ниже определение 3), основанные на произвольном «25-м процентиле»: ) баллов. В этом примере наше n равно 25, поэтому мы ищем наименьшее значение, превышающее 25%.
Определение 2: n -й процентиль — это наименьший балл, который больше или равен определенному проценту баллов. Перефразируя это, это процент данных, которые соответствуют определенному наблюдению или ниже него. Это определение используется в статистике точек доступа. В этом примере 25-й процентиль — это оценка, которая больше или равна 25% оценок.
Перефразируя это, это процент данных, которые соответствуют определенному наблюдению или ниже него. Это определение используется в статистике точек доступа. В этом примере 25-й процентиль — это оценка, которая больше или равна 25% оценок.
Они могут показаться очень похожими, но могут привести к большим различиям в результатах, хотя оба они относятся к 25-му процентилю. Возьмите следующий список результатов тестов, отсортированных по рангу:
| Оценка | Ранг |
|---|---|
| 30 | 1 |
| 33 | 2 |
| 43 | 3 |
| 53 | 4 |
| 56 | 5 |
| 67 | 6 |
| 68 | 7 |
| 72 | 8 |
3. Как найти процентиль
Нужна помощь? Посетите нашу обучающую страницу!
Пример вопроса: Узнайте, где находится 25-й процентиль в приведенном выше списке.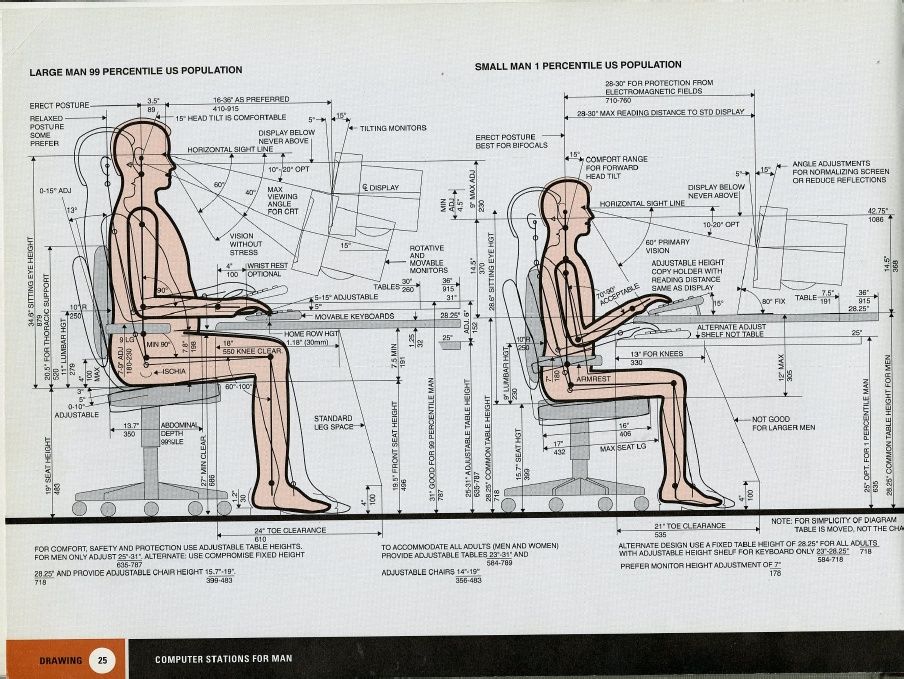
Шаг 1: Рассчитайте, какое место занимает 25-й процентиль. Используйте следующую формулу:
Ранг = Процентиль / 100 * (количество элементов + 1)
Ранг = 25 / 100 * (8 + 1) = 0,25 * 9 = 2,25.
Ранг 2,25 соответствует 25-му процентилю. Однако не существует ранга 2,25 (вы когда-нибудь слышали о ранге 2,25 в старшей школе? Я не слышал!), поэтому вы должны либо округлить в большую, либо в меньшую сторону. Поскольку 2,25 ближе к 2, чем к 3, я буду округлять до 2,9.0004
Шаг 2: Выберите определение 1 или 2:
Определение 1 : Наименьшая оценка, которая на больше 25% оценок. Это соответствует 43 баллам в этом списке (ранг 3).
Определение 2: Наименьшая оценка, превышающая или равная 25% баллов. Это соответствует 33 баллам в этом списке (ранг 2).
В зависимости от того, какое определение вы используете, 25-й процентиль может быть равен 33 или 43! Третье определение пытается исправить эту возможную неверную интерпретацию:
Определение 3: Средневзвешенное значение процентилей из первых двух определений.
В приведенном выше примере процентиль будет рассчитан с использованием средневзвешенного значения следующим образом:
- Умножьте разницу между оценками на 0,25 (доля ранга, которую мы вычислили выше). Баллы были 43 и 33, что дало нам разницу в 10:
(0,25)(43 – 33) = 2,5. - Добавьте результат к меньшему счету. 2,5 + 33 = 35,5
В этом случае оценка 25-го процентиля равна 35,5, что имеет больше смысла, поскольку находится между 43 и 33.
В большинстве случаев процентилем обычно является определение №1. Однако было бы целесообразно перепроверить, что любая статистика о процентилях создается с использованием этого первого определения.
4. Диапазон процентилей
Диапазон процентилей — это разница между двумя указанными процентилями. теоретически это могут быть любые два процентиля, но наиболее распространенным является диапазон 10-90 процентилей. Чтобы найти диапазон 10-90 процентилей:
- Вычислите 10-й процентиль, используя описанные выше шаги.

- Вычислите 90-й процентиль, используя описанные выше шаги.
- Вычтите шаг 1 (10-й процентиль) из шага 2 (90-й процентиль).
Ссылки
Кенни, Дж. Ф. и Кипинг, Э. С. «Процентильные ранги». §3.6 в математике статистики, Pt. 1, 3-е изд. Принстон, Нью-Джерси: Ван Ностранд, стр. 38–39, 1962.
УКАЗЫВАЙТЕ ЭТО КАК:
Стефани Глен . «Процентили, процентильный ранг и процентильный диапазон: определение и примеры» из StatisticsHowTo.com : Элементарная статистика для всех нас! https://www.statisticshowto.com/probability-and-statistics/percentiles-rank-range/
————————————————— ————————-
Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в данной области. Ваши первые 30 минут с репетитором Chegg бесплатны!
Комментарии? Нужно опубликовать исправление? Пожалуйста, Свяжитесь с нами .
Процентили
Процентили: значение, ниже которого падает процент данных.
Пример: Вы четвертый самый высокий человек в группе из 20
80% людей ниже вас:
Это означает, что вы находитесь в 80-м процентиле .
Если ваш рост 1,85 м, то «1,85 м» — это 80-й процентиль роста в этой группе.
Заказ
Имейте данные в порядке , чтобы вы знали, какие значения выше и ниже.
- Чтобы рассчитать процентили роста: расположите данные в порядке роста (отсортированные по росту).
- Чтобы рассчитать процентили возраста: расположите данные в порядке возраста.
- И так далее.
Сгруппированные данные
Когда данные сгруппированы:
Сложите все проценты ниже балл,
плюс половина процент на балла.
Пример: Вы получили четверку!
В тесте 12% получили D, 50% получили C, 30% получили B и 8% получили A
для общего процентиля 12% + 50% + 15% = 77%
Другими словами, вы справились «так же хорошо или лучше, чем 77% класса»
(Зачем брать половину B? Потому что вы не следует думать, что вы получили «лучшую четверку» или «худшую четверку», просто среднюю четверку. )
)
Децили
Децили похожи на процентили (звучит как десятичная дробь и процентиль вместе), так как они разбивают данные на 10% группы :
- который делит данные, так что 10% ниже него)
- 2-й дециль — это 20-й процентиль (значение, которое делит данные, поэтому 20% находится ниже него)
- и т.д.!
Пример: (продолжение)
Вы находитесь в 8-м дециле (80-й процентиль).
Квартили
Другая родственная идея — Квартили, которые разбивают данные на четверти:
Пример: 1, 3, 3, 4, 5, 6, 6, 7, 8, 8
Числа идут по порядку. Разделите список на четверти:
В этом случае квартиль 2 находится посередине между 5 и 6:
Q2 = (5+6)/2 = 5,5
И результат:
- Квартиль 1 (Q1) = 3
- Квартиль 2 (Q2) = 5,5
- Квартиль 3 (Q3) = 7
Квартили также делят данные на разделы 25%, так что:
- Квартиль 1 (Q1) можно назвать 25-м процентилем
- Квартиль 2 (Q2) можно назвать 50-м процентилем
- Квартиль 3 (Q3) можно назвать 75-м процентилем
Пример: (продолжение)
Для 1, 3, 3, 4, 5, 6, 6, 7, 8, 8 :
- 25-й процентиль = 3
- 50-й процентиль = 5,5
- 75-й процентиль = 7
Оценка процентилей
Мы можем оценить процентили по линейному графику.
Пример: Покупки
Всего за 12 часов торговый центр посетило 10 000 человек:
| Время (часы) | Люди |
|---|---|
| 0 | 0 |
| 2 | 350 |
| 4 | 1100 |
| 6 | 2400 |
| 8 | 6500 |
| 10 | 8850 |
| 12 | 10 000 |
а) Оценка 30-й процентиль (когда прибыло 30% посетителей).
б) Оценка какой процентиль посетителей был прибыл после 11 часов.
Первый розыгрыш линейный график данных: нанесите точки и соедините их плавной кривой:
а) 30-е число
процентиль возникает, когда количество посещений достигает 3000.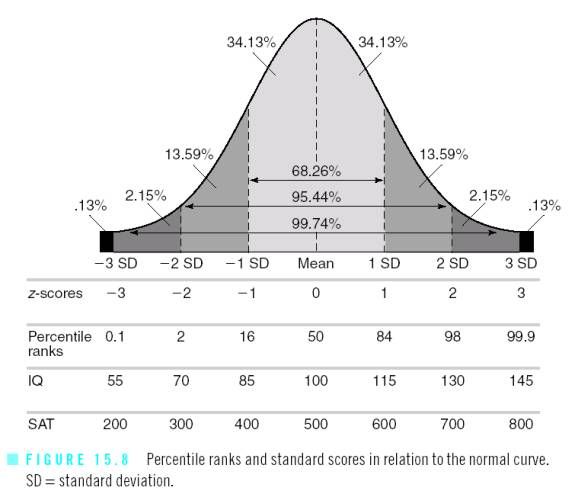

 Однако возможность описания распределения значений не является одним их них.”
Однако возможность описания распределения значений не является одним их них.”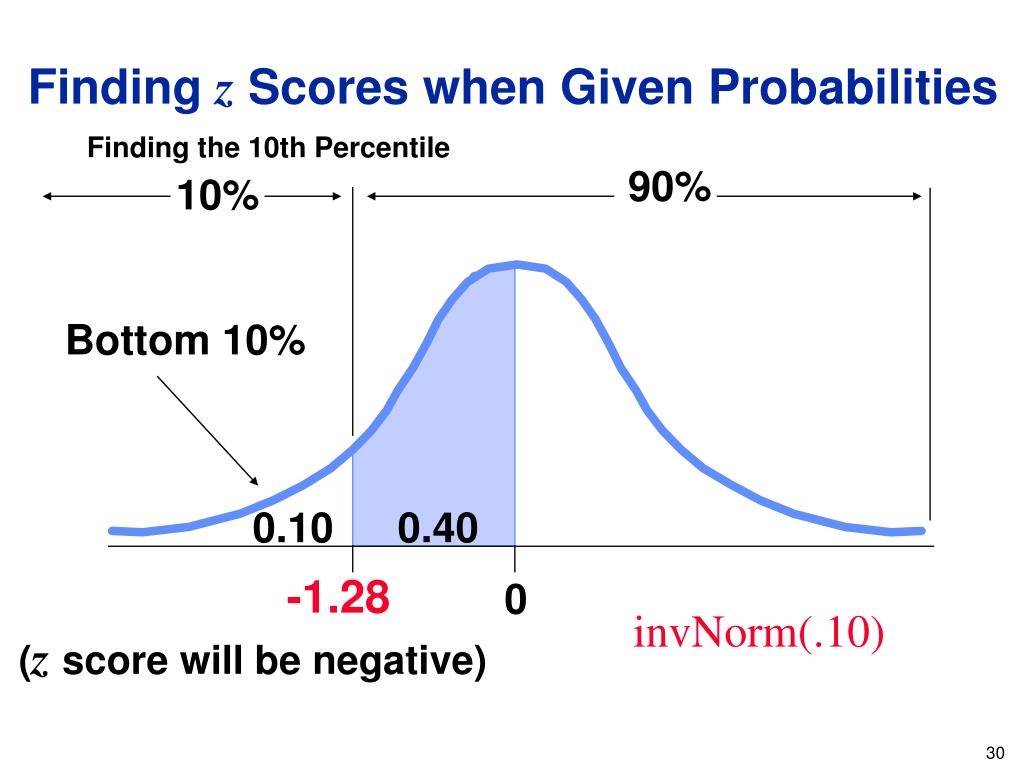 Это усреднение неявно и пользователи о нем никак не подозревают. А на самом деле эти сервисы должны бы были вывести предупреждение!
Это усреднение неявно и пользователи о нем никак не подозревают. А на самом деле эти сервисы должны бы были вывести предупреждение! Но я переключился на подсчет процента запросов которые выполняются за время меньшее/большее чем указанное значение и сохраняю эту метрику вместо прежней.» Но это также не работает. Подход с вычислением средних по долям (а процент — это доля) все равно не работает. Вместо этого, сохраняйте метрику числа запросов которые не выполняются за желаемое время. Вот это будет работать.
Но я переключился на подсчет процента запросов которые выполняются за время меньшее/большее чем указанное значение и сохраняю эту метрику вместо прежней.» Но это также не работает. Подход с вычислением средних по долям (а процент — это доля) все равно не работает. Вместо этого, сохраняйте метрику числа запросов которые не выполняются за желаемое время. Вот это будет работать.