Свойства умножения: переместительное, сочетательное и распределительное
- Переместительное свойство умножения
- Сочетательное свойство умножения
- Распределительное свойство умножения
Переместительное свойство умножения
От перестановки сомножителей местами произведение не меняется.
Следовательно, для любых чисел a и b верно равенство:
a · b = b · a,
выражающее переместительное свойство умножения.
Примеры:
6 · 7 = 7 · 6 = 42;
4 · 2 · 3 = 3 · 2 · 4 = 24.
Обратите внимание, что данное свойство можно применять и к произведениям, в которых более двух множителей.
Сочетательное свойство умножения
Результат умножения трёх и более множителей не изменится, если какую-либо группу множителей заменить их произведением.
Следовательно, для любых чисел a, b и c верно равенство:
a · b · c = (a · b) · c = a · (b · c),
выражающее сочетательное свойство умножения.
Пример:
3 · 2 · 5 = 3 · (2 · 5) = 3 · 10 = 30
или
3 · 2 · 5 = (3 · 2) · 5 = 6 · 5 = 30.
Сочетательное свойство используется для удобства и упрощения вычислений при умножении. Например:
25 · 15 · 4 = (25 · 4) · 15 = 100 · 15 = 1500.
В данном случае можно было вычислить всё последовательно:
25 · 15 · 4 = (25 · 15) · 4 = 375 · 4 = 1500,
но проще и легче сначала умножить 25 на 4 и получить 100, а уже потом умножить 100 на 15.
Распределительное свойство умножения
Сначала рассмотрим распределительное свойство умножения относительно сложения:
Чтобы число умножить на сумму чисел, можно это число умножить отдельно на каждое слагаемое и полученные произведения сложить.
Следовательно, для любых чисел a, b и m верно равенство:
m · (a + b) = m · a + m · b,
выражающее распределительное свойство умножения.
Так как в данном случае число и сумма являются множителями, то, поменяв их местами, используя переместительное свойство, можно сформулировать распределительное свойство так:
Чтобы сумму чисел умножить на число, можно каждое слагаемое отдельно умножить на это число и полученные произведения сложить.
Следовательно, для любых чисел a, b и m верно равенство:
(a + b) · m = a · m + b · m.
Теперь рассмотрим распределительное свойство умножения относительно вычитания:
Чтобы число умножить на разность чисел, можно это число умножить отдельно на уменьшаемое и вычитаемое и из первого полученного произведения вычесть второе.
Следовательно, для любых чисел a, b и m верно равенство:
m · (a — b) = m · a — m · b.
Так как в данном случае число и разность являются множителями, то поменяв их местами, используя переместительное свойство, можно сформулировать распределительное свойство так:
Чтобы разность чисел умножить на число, можно уменьшаемое и вычитаемое отдельно умножить на это число и из первого полученного произведения вычесть второе.
Следовательно, для любых чисел a, b и m верно равенство:
(a — b) · m = a · m — b · m.
Переход от умножения:
m · (a + b) и m · (a — b)
соответственно к сложению и вычитанию:
m · a + m · b и m · a — m · b
называется раскрытием скобок.
Переход от сложения и вычитания:
m · a + m · b и m · a — m · b
к умножению:
m · (a + b) и m · (a — b)
называется вынесением общего множителя за скобки.
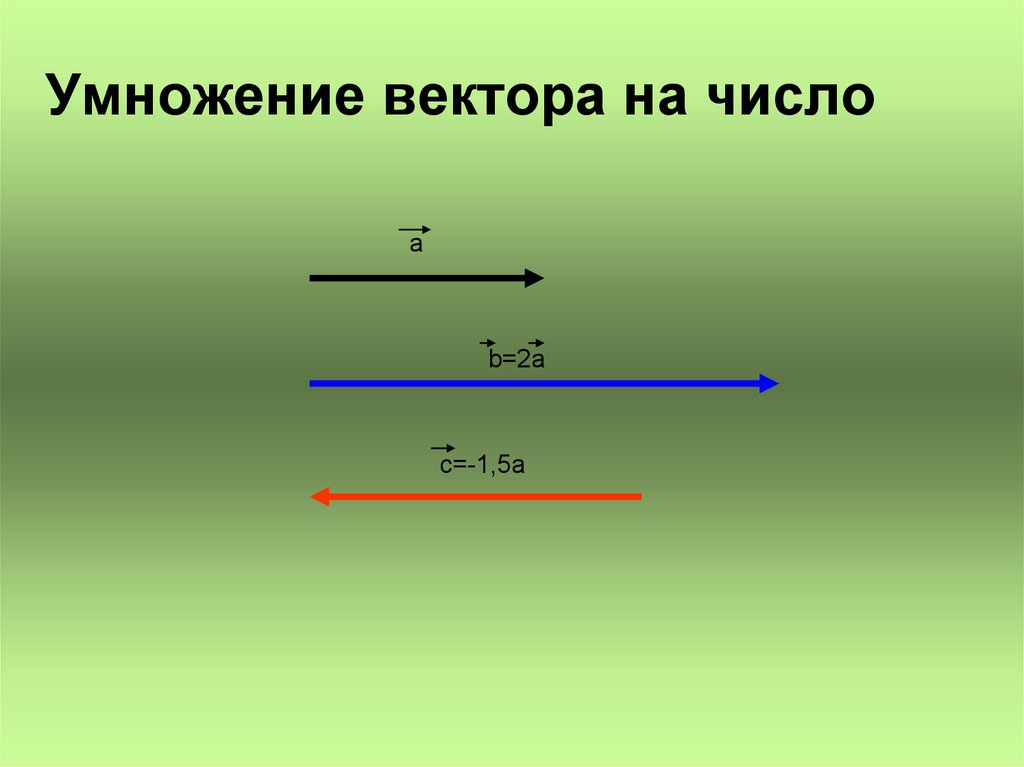
Геометрия Умножение вектора на число
Материалы к уроку
Конспект урока
5. Умножение вектора на число
|
Произведением ненулевого вектора а на число k называется такой вектор b, длина которого равна модуль |k| умноженный на модуль|а|, причем векторы а и b сонаправлены, если k положительно и противоположно направлены, если k отрицательно. Произведение вектора а на число k обозначается так: ka.
|
Текст Умножение вектора на число
|
|
Для любого числа k и любого вектора а векторы а и ka коллинеарны. Произведением нулевого вектора на любое число считается нулевой вектор. Произведение любого вектора на число нуль есть нулевой вектор.
|
Текст Умножение вектора на число
|
|
Рассмотрим основные свойства умножения вектора на число. Первое. Произведение k и l, умноженное на вектор а, равно произведению k на вектор lа. Это свойство известно как сочетательный закон. На рисунке, на примере показано это свойство.
|
Текст Свойства умножения вектора на число
Рисунок векторов
Текст
|
|
Второе свойство, первый распределительный закон. Произведение числа k на сумму векторов а и b равно сумме произведений этого числа на векторы а и b. На рисунке, на примере показано это свойство.
|
Текст Свойства умножения вектора на число
|
 Произведение суммы чисел k и l на вектор равно сумме произведений чисел k и l на вектор а.
На рисунке, на примере показано это свойство.
|
Текст Свойства умножения вектора на число
|
|
Стоит отметить, что произведение числа -1 на любой вектор дает вектор противоположный данному. Согласно определению произведения вектора на число, их длины равны, а направления противоположны. При условии, что вектор а ненулевой.
|
Текст
|
|
Для векторов в пространстве, как и в планиметрии, выполняется следующее условие: Если векторы a и b коллинеарны (то есть лежат на одной прямой или на параллельных прямых) и вектор а ненулевой, то существует число k такое что вектор b равен произведению числа k на вектор а. |
|
|
Решим задачу №347 (а) Необходимо упростить выражение. |
|
|
Решение. Первый распределительный закон позволяет нам раскрыть скобки. А переместительное свойство сложения векторов – привести подобные.
|
.
|
Для любых векторов а,b и любых чисел k и l справедливы равенства:
Остались вопросы по теме? Наши репетиторы готовы помочь!
Подготовим к ЕГЭ, ОГЭ и другим экзаменам
Найдём слабые места по предмету и разберём ошибки
Повысим успеваемость по школьным предметам
Поможем подготовиться к поступлению в любой ВУЗ
Выбрать репетитора
Скалярное умножение векторов
Горячая математика
Если ты → знак равно 〈 ты 1 , ты 2 〉 имеет величину | ты → | и направление д , тогда н ты → знак равно н 〈 ты 1 , ты 2 〉 знак равно 〈 н ты 1 , н ты 2 〉 куда н положительное действительное число, величина равна | н ты → | , а его направление д .
Обратите внимание, что если н отрицательно, то направление н ты является противоположностью г .
Пример :
Позволять
ты
знак равно
〈
−
1
,
3
〉
, Находить
7
ты
.
7 ты знак равно 7 〈 − 1 , 3 〉 знак равно 〈 7 ( − 1 ) , 7 ( 3 ) 〉 знак равно 〈 − 7 , 21 〉
Позволять
ты
а также
в
быть векторами, пусть
с
а также
д
быть скалярами.
Тогда верны следующие свойства.
Свойства скалярного умножения | |
| Величина масштабированного вектора равна абсолютному значению скаляра, умноженному на величину вектора. | ‖ с в ‖ знак равно | с | в |
| Ассоциативное свойство | с ( д ты ) знак равно ( с д ) ты |
| Коммутативное свойство | с ты знак равно ты с |
| Распределительное свойство | ( с + д ) ты знак равно с ты + д ты с ( ты + в ) знак равно с ты + с в |
| Идентификационное свойство | 1 ⋅ ты знак равно ты |
| Мультипликативное свойство − 1 | ( − 1 ) с знак равно − с |
| Мультипликативное свойство 0 | 0 ( ты ) знак равно 0 |
Линейные комбинации векторов.
ОсновыВ линейной алгебре мы определяем понятие линейных комбинаций в терминах векторов. Но на самом деле можно говорить о линейных комбинациях чего угодно, если вы понимаете основную идею линейной комбинации:
(скаляр)(что-то 1) + (скаляр)(что-то 2) + (скаляр)(что-то 3)
Эти «что-то» могут быть «повседневными» переменными, такими как \(x\) и \(y\) (\(3x\) + \(2y\) является линейной комбинацией \(x\) и \(y\) например) или что-то более сложное, например полиномы. В общем, линейная комбинация — это особый способ объединения вещей (переменных, векторов и т. д.) с использованием скалярного умножения и сложения.
реклама
Работа с векторами
Вернемся к векторам. Допустим, у нас есть следующие векторы:
\(\vec{v}_1 = \left[ \begin{array}{c}1\\ 2\\ 3\end{array} \right]\), \(\vec{v}_2 = \left[ \begin{array}{c}3\\ 5\\ 1\end{array} \right]\), \(\vec{v}_3 = \left[ \begin{array}{c}0\\ 0 \\ 8\конец{массив} \право]\)
Как будут выглядеть линейные комбинации этих векторов? Что ж, линейной комбинацией этих векторов будет любая их комбинация, использующая сложение и скалярное умножение.
Вектор \(\vec{b} = \left[ \begin{array}{c}3\\ 6\\ 9\end{array} \right]\) представляет собой линейную комбинацию \(\vec{v} _1\), \(\vec{v}_2\), \(\vec{v}_3\).
Почему это так? Этот вектор можно записать как комбинацию трех заданных векторов с помощью скалярного умножения и сложения. В частности,
\(\left[ \begin{array}{c}3\\ 6\\ 9\end{массив} \right] = 3\left[ \begin{array}{c}1\\ 2\\ 3\end {массив} \right] + 0\left[ \begin{array}{c}3\\ 5\\ 1\end{массив} \right] + 0\left[ \begin{array}{c}0\\ 0\\ 8\конец{массив} \право]\)
Или, используя имена, данные каждому вектору:
\(\vec{b} = 3\vec{v}_1 + 0\vec{v}_2 + 0\vec{v}_3\)
Вектор \(\vec{x} = \left[ \begin{array}{c}2\\ 3\\ -6\end{array} \right]\) является линейной комбинацией \(\vec{v }_1\), \(\vec{v}_2\), \(\vec{v}_3\).
Еще раз, мы можем показать, что это правда, показав, что вы можете комбинировать векторы \(\vec{v}_1\), \(\vec{v}_2\) и \(\vec{v}_3 \) с использованием сложения и скалярного умножения таким образом, чтобы результатом был вектор \(\vec{x}\).
\(\left[ \begin{array}{c}2\\ 3\\ -6\end{массив} \right] = -1\left[ \begin{array}{c}1\\ 2\\ 3 \end{массив} \right] + 1\left[ \begin{array}{c}3\\ 5\\ 1\end{массив} \right] + \left(-\dfrac{1}{2}\ вправо)\влево[ \begin{массив}{c}0\\ 0\\ 8\конец{массив} \вправо]\)
или эквивалентно
\(\vec{x} = -1\vec{v}_1 +1\vec{v}_2 + \left(-\dfrac{1}{2}\right)\vec{v}_3\)
Конечно, можно долго продолжать, так как существует множество различных вариантов скаляров и способов объединения трех векторов. В общем, набор ВСЕХ линейных комбинаций этих трех векторов будет называться их размахом. Это будет записано как \(\textrm{Span}\left(\vec{v}_1, \vec{v}_2, \vec{v}_3\right)\). Два приведенных выше вектора являются элементами или членами этого множества. 9{n}\) и \(c_1, c_2, \cdots , c_n\) — скаляры. Тогда вектор \(\vec{b}\), где \(\vec{b} = c_1\vec{v}_1 + c_2\vec{v}_2 + \dots + c_n\vec{v}_n\) называется линейной комбинацией из \(\vec{v}_1, \vec{v}_2, \vec{v}_3, … \vec{v}_n\).