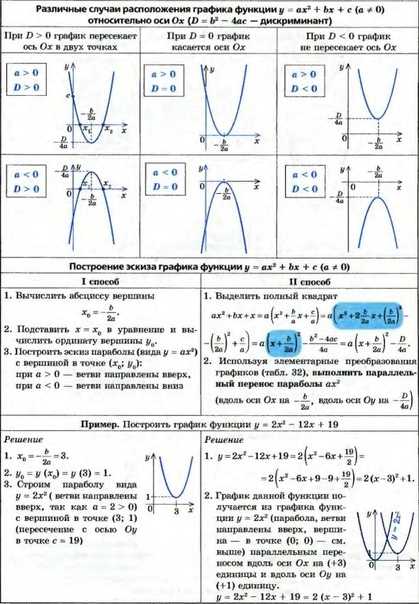
Движение гиперболы по осям. Преобразования графиков. Ii случай, «a» отлично от единицы
Параллельный перенос.
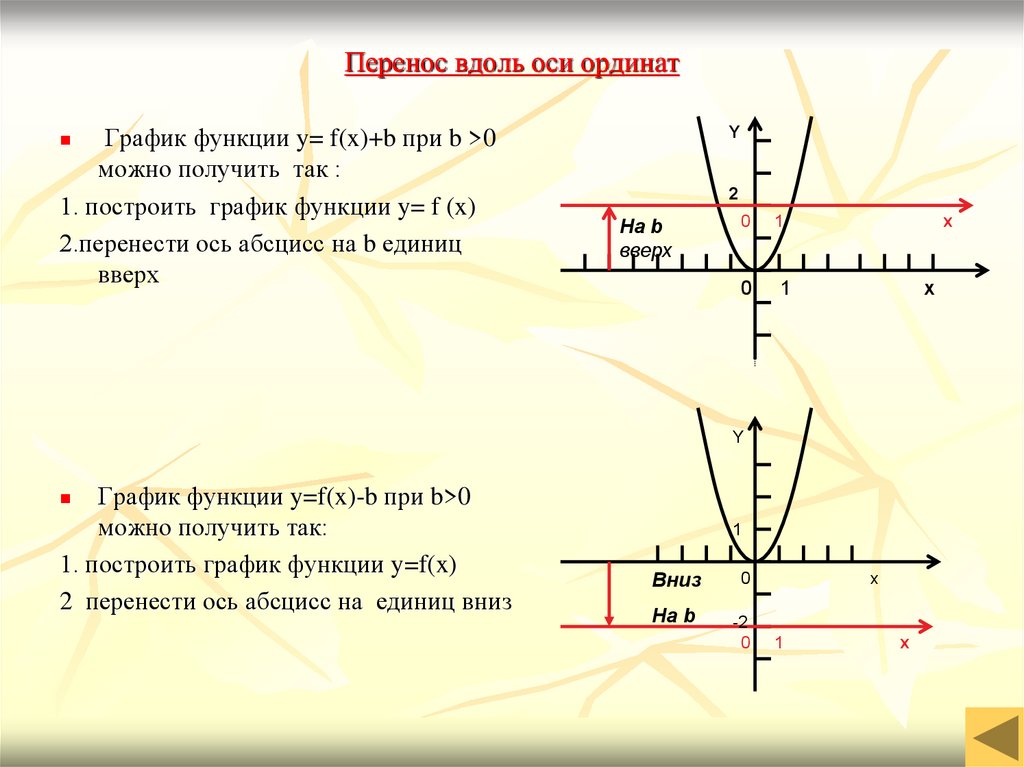
ПЕРЕНОС ВДОЛЬ ОСИ ОРДИНАТ
f(x) => f(x) — b
Пусть требуется построить график функции у = f(х) — b. Нетрудно заметить, что ординаты этого графика для всех значений x на |b| единиц меньше соответствующих ординат графика функций у = f(х) при b>0 и на |b| единиц больше — при b 0 или вверх при b Для построения графика функции y + b = f(x) следует построить график функции y = f(x) и перенести ось абсцисс на |b| единиц вверх при b>0 или на |b| единиц вниз при b
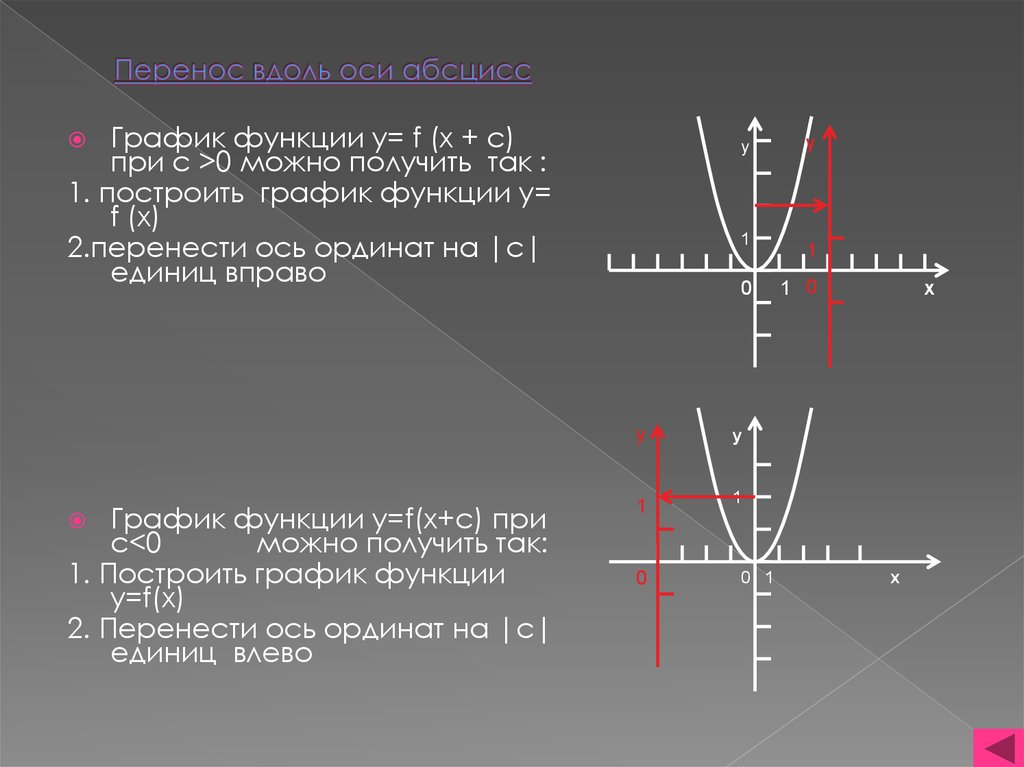
ПЕРЕНОС ВДОЛЬ ОСИ АБСЦИСС
f(x) => f(x + a)
Пусть требуется построить график функции у = f(x + a). Рассмотрим функцию y = f(x), которая в некоторой точке x = x1 принимает значение у1 = f(x1). Очевидно, функция у = f(x + a) примет такое же значение в точке x2, координата которой определяется из равенства x2 + a = x1, т.
Примеры:
1.y=f(x+a)
2.y=f(x)+b
Отражение.
ПОСТРОЕНИЕ ГРАФИКА ФУНКЦИИ ВИДА Y = F(-X)
f(x) => f(-x)
Очевидно, что функции y = f(-x) и y = f(x) принимают равные значения в точках, абсциссы которых равны по абсолютной величине, но противоположны по знаку. Иначе говоря, ординаты графика функции y = f(-x) в области положительных (отрицательных) значений х будут равны ординатам графика функции y = f(x) при соответствующих по абсолютной величине отрицательных (положительных) значениях х.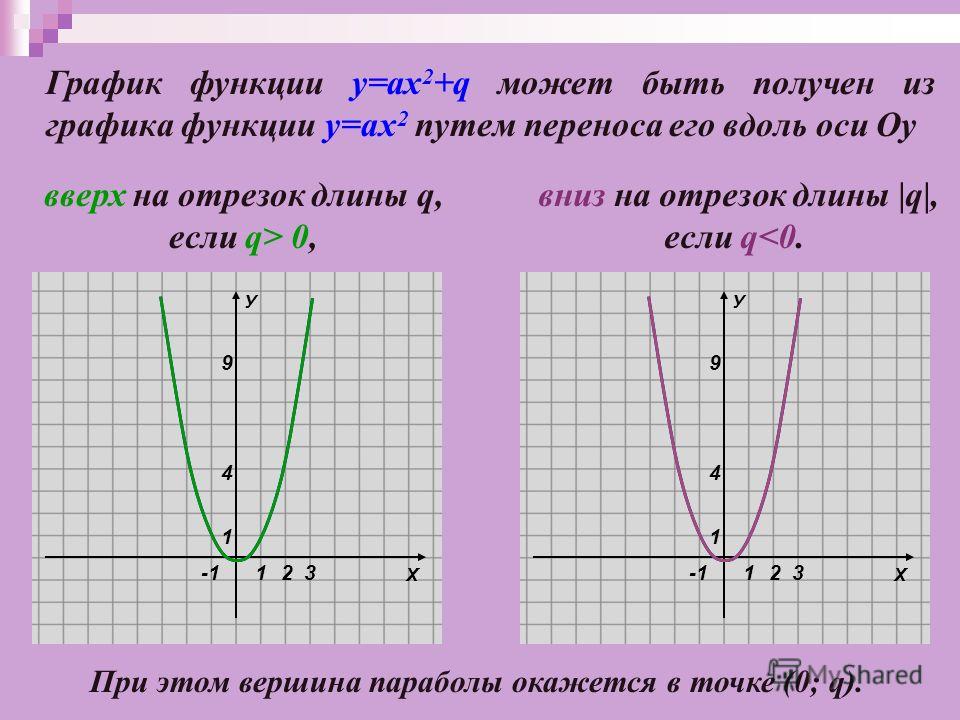
Для построения графика функции y = f(-x) следует построить график функции y = f(x) и отразить его относительно оси ординат. Полученный график является графиком функции y = f(-x)
ПОСТРОЕНИЕ ГРАФИКА ФУНКЦИИ ВИДА Y = — F(X)
f(x) => — f(x)
Ординаты графика функции y = — f(x) при всех значениях аргумента равны по абсолютной величине, но противоположны по знаку ординатам графика функции y = f(x) при тех же значениях аргумента. Таким образом, получаем следующее правило.
Для построения графика функции y = — f(x) следует построить график функции y = f(x) и отразить его относительно оси абсцисс.
Примеры:
1.y=-f(x)
2.y=f(-x)
3.y=-f(-x)
Деформация.
ДЕФОРМАЦИЯ ГРАФИКА ВДОЛЬ ОСИ ОРДИНАТ
f(x) => k f(x)
Рассмотрим функцию вида y = k f(x), где k > 0. Нетрудно заметить, что при равных значениях аргумента ординаты графика этой функции будут в k раз больше ординат графика функции у = f(x) при k > 1 или 1/k раз меньше ординат графика функции y = f(x) при k Для построения графика функции y = k f(x) следует построить график функции y = f(x) и увеличить его ординаты в k раз при k > 1(произвести растяжение графика вдоль оси ординат) или уменьшить его ординаты в 1/k раз при k
k > 1 — растяжение от оси Ох
0 — сжатие к оси OX
ДЕФОРМАЦИЯ ГРАФИКА ВДОЛЬ ОСИ АБСЦИСС
f(x) => f(k x)
Пусть требуется построить график функции y = f(kx), где k>0.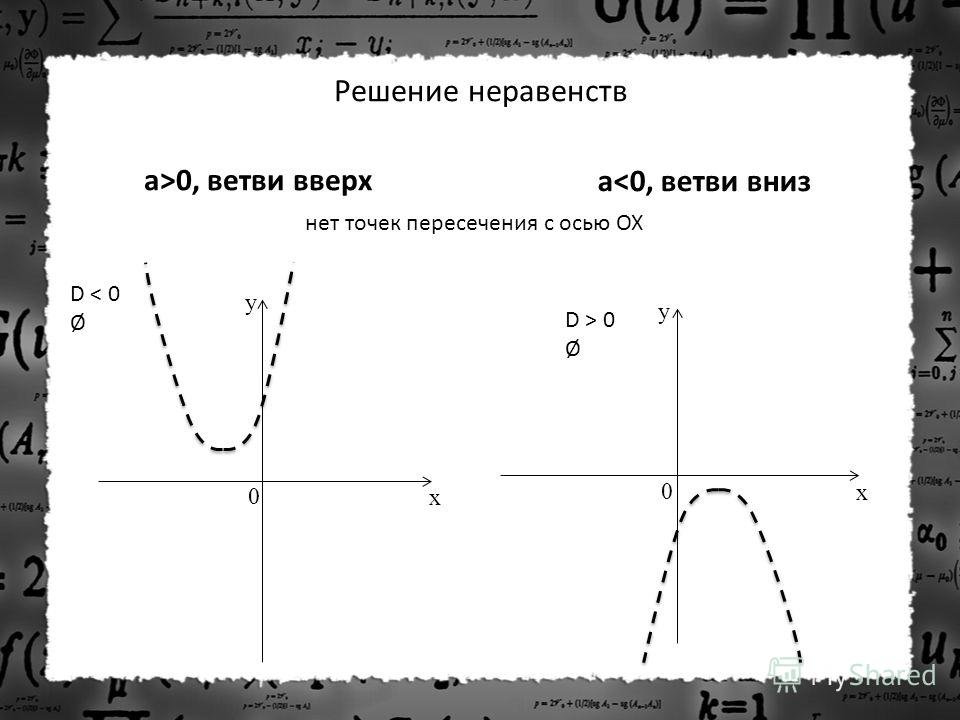
Рассмотрим функцию y = f(x), которая в произвольной точке x = x1 принимает значение y1 = f(x1). Очевидно, что функция y = f(kx) принимает такое же значение в точке x = x2, координата которой определяется равенством x1 = kx2, причем это равенство справедливо для совокупности всех значений х из области определения функции. Следовательно, график функции y = f(kx) оказывается сжатым (при k 1) вдоль оси абсцисс относительно графика функции y = f(x). Таким образом, получаем правило.
k > 1 — сжатие к оси Оу
0 — растяжение от оси OY
Работу выполнили Чичканов Александр, Леонов Дмитрий под руководством Ткач Т.В, Вязовова С.М, Островерховой И.В.
©2014
Основные элементарные функции в чистом виде без преобразования встречаются редко, поэтому чаще всего приходится работать с элементарными функциями, которые получили из основных с помощью добавления констант и коэффициентов.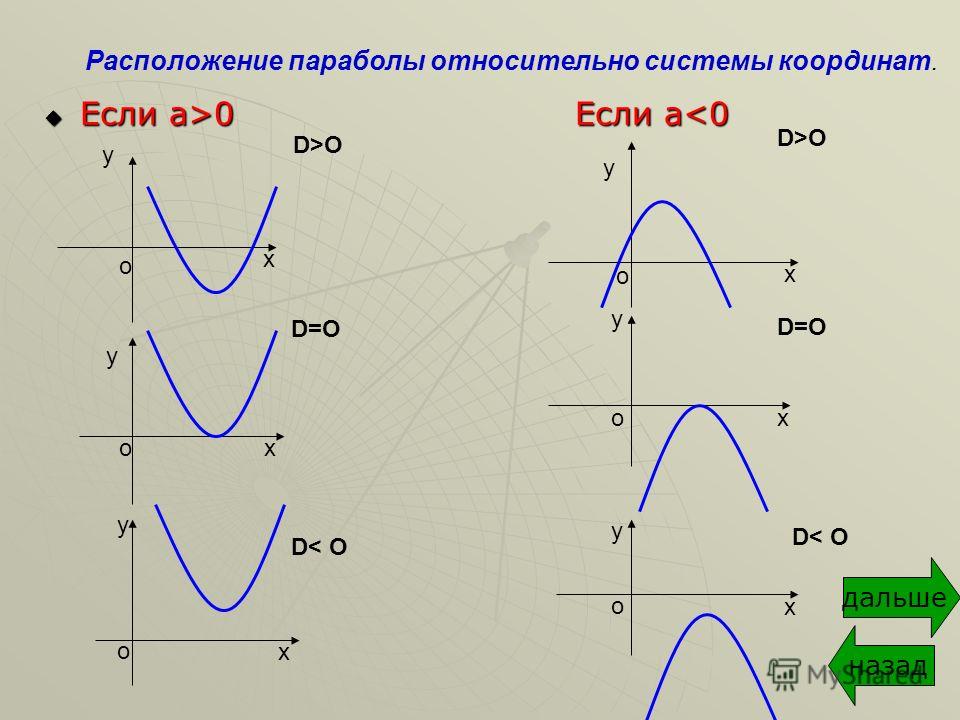
Рассмотрим на примере квадратичной функции вида y = — 1 3 x + 2 3 2 + 2 , графиком которой является парабола y = x 2 , которая сжата втрое относительно О у и симметрична относительно О х, причем сдвинутую на 2 3 по О х вправо, на 2 единицы по О у вверх. На координатной прямой это выглядит так:
Геометрические преобразования графика функции
Применяя геометрические преобразования заданного графика получаем, что график изображается функцией вида ± k 1 · f (± k 2 · (x + a)) + b , когда k 1 > 0 , k 2 > 0 являются коэффициентами сжатия при 0 1 , k 2 > 1 вдоль О у и О х. Знак перед коэффициентами k 1 и k 2 говорит о симметричном отображении графика относительно осей, a и b сдвигают ее по О х и по О у.
Определение 1
Существует 3 вида геометрических преобразований графика :
- Масштабирование вдоль О х и О у. На это влияют коэффициенты k 1 и k 2 при условии не равности 1 , когда 0 1 , k 2 > 1 , то график растягивается по О у и сжимается по О х.
- Симметричное отображение относительно координатных осей. При наличии знака « — » перед k 1 симметрия идет относительно О х, перед k 2 идет относительно О у. Если « — » отсутствует, тогда пункт при решении пропускается;
- Параллельный перенос (сдвиг) вдоль О х и О у. Преобразование производится при наличии коэффициентов a и b неравных 0 . Если значение a положительное, до график сдвигается влево на | а | единиц, если отрицательное a , тогда в право на такое же расстояние. Значение b определяет движение по оси О у, что значит при положительном b функция движется вверх, при отрицательном – вниз.
Рассмотрим решения на примерах, начиная со степенной функции.
Пример 1
Преобразовать y = x 2 3 и построить график функции y = — 1 2 · 8 x — 4 2 3 + 3 .
Решение
Представим функции таким образом:
y = — 1 2 · 8 x — 4 2 3 + 3 = — 1 2 · 8 x — 1 2 2 3 + 3 = — 2 x — 1 2 2 3 + 3
Где k 1 = 2 , стоит обратить внимание на наличие « — » , а = — 1 2 , b = 3 .
Отсюда получаем, что геометрические преобразования производятся с растяжения вдоль О у вдвое, отображается симметрично относительно О х, сдвигается вправо на 1 2 и вверх на 3 единицы.
Если изобразить исходную степенную функцию, получим, что
при растягивании вдвое вдоль О у имеем, что
Отображение, симметричное относительно О х, имеет вид
а движение вправо на 1 2
движение на 3 единицы вверх имеет вид
Преобразования показательной функции рассмотрим на примерах.
Пример 2
Произвести построение графика показательной функции y = — 1 2 1 2 (2 — x) + 8 .
Решение.
Преобразуем функцию, исходя из свойств степенной функции. Тогда получим, что
y = — 1 2 1 2 (2 — x) + 8 = — 1 2 — 1 2 x + 1 + 8 = — 1 2 · 1 2 — 1 2 x + 8
Отсюда видно, что получим цепочку преобразований y = 1 2 x:
y = 1 2 x → y = 1 2 · 1 2 x → y = 1 2 · 1 2 1 2 x → → y = — 1 2 · 1 2 1 2 x → y = — 1 2 · 1 2 — 1 2 x → → y = — 1 2 · 1 2 — 1 2 x + 8
Получаем, что исходная показательная функция имеет вид
Сжимание вдвое вдоль О у дает
Растягивание вдоль О х
Симметричное отображение относительно О х
Отображение симметрично относительно О у
Сдвигание на 8 единиц вверх
Рассмотрим решение на примере логарифмической функции y = ln (x) .
Пример 3
Построить функцию y = ln e 2 · — 1 2 x 3 при помощи преобразования y = ln (x) .
Решение
Для решения необходимо использовать свойства логарифма, тогда получаем:
y = ln e 2 · — 1 2 x 3 = ln (e 2) + ln — 1 2 x 1 3 = 1 3 ln — 1 2 x + 2
Преобразования логарифмической функции выглядят так:
y = ln (x) → y = 1 3 ln (x) → y = 1 3 ln 1 2 x → → y = 1 3 ln — 1 2 x → y = 1 3 ln — 1 2 x + 2
Изобразим график исходной логарифмической функции
Производим сжимание строе по О у
Производим растягивание вдоль О х
Производим отображение относительно О у
Производим сдвигание вверх на 2 единицы, получаем
Для преобразования графиков тригонометрической функциинеобходимо подгонять под схему решения вида ± k 1 · f (± k 2 · (x + a)) + b . Необходимо, чтобы k 2 приравнивался к T k 2 . Отсюда получаем, что 0
Рассмотрим примеры решения заданий с преобразованиями y = sin x .
Пример 4
Построить график y = — 3 sin 1 2 x — 3 2 — 2 с помощью преобразований функции y=sinx.
Решение
Необходимо привести функцию к виду ± k 1 · f ± k 2 · x + a + b . Для этого:
y = — 3 sin 1 2 x — 3 2 — 2 = — 3 sin 1 2 (x — 3) — 2
Видно, что k 1 = 3 , k 2 = 1 2 , a = — 3 , b = — 2 . Так как перед k 1 имеется « — » , а перед k 2 — нет, тогда получим цепочку преобразований вида:
y = sin (x) → y = 3 sin (x) → y = 3 sin 1 2 x → y = — 3 sin 1 2 x → → y = — 3 sin 1 2 x — 3 → y = — 3 sin 1 2 (x — 3) — 2
Подробное преобразование синусоиды. При построении графика исходной синусоиды y = sin (x) получаем, что наименьшим положительным периодом считается T = 2 π . Нахождение максимума в точках π 2 + 2 π · k ; 1 , а минимума — — π 2 + 2 π · k ; — 1 , k ∈ Z .
Производится растягивание по О у втрое, значит возрастание амплитуды колебаний возрастет в 3 раза. T = 2 π — это наименьший положительный период. Максимумы переходят в π 2 + 2 π · k ; 3 , k ∈ Z , минимумы — — π 2 + 2 π · k ; — 3 , k ∈ Z .
При растягивании по О х вдвое получаем, что наименьший положительный период увеличивается в 2 раза и равняется T = 2 π k 2 = 4 π . Максимумы переходят в π + 4 π · k ; 3 , k ∈ Z , минимумы – в — π + 4 π · k ; — 3 , k ∈ Z .
Изображение производится симметрично относительно О х. Наименьший положительный период в данном случае не меняется и равняется T = 2 π k 2 = 4 π . Переход максимума выглядит как — π + 4 π · k ; 3 , k ∈ Z , а минимума – π + 4 π · k ; — 3 , k ∈ Z .
Производится сдвижение графика вниз на 2 единицы. Изменение наименьшего общего периода не происходит. Нахождение максимумов с перехождением в точки — π + 3 + 4 π · k ; 1 , k ∈ Z , минимумов — π + 3 + 4 π · k ; — 5 , k ∈ Z .
На данном этапе график тригонометрической функции считается преобразованным.
Рассмотрим подробное преобразование функции y = cos x .
Пример 5
Построить график функции y = 3 2 cos 2 — 2 x + 1 при помощи преобразования функции вида y = cos x .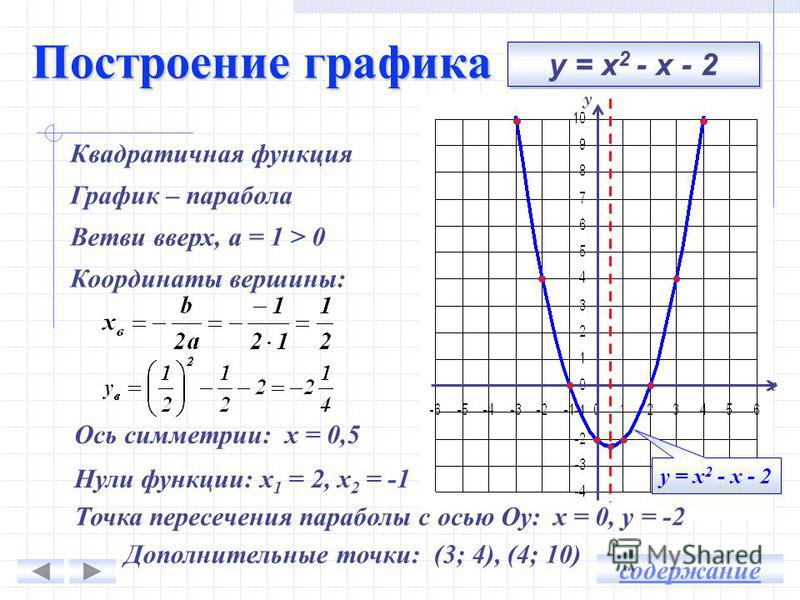
Решение
По алгоритму необходимо заданную функцию привести к виду ± k 1 · f ± k 2 · x + a + b . Тогда получаем, что
y = 3 2 cos 2 — 2 x + 1 = 3 2 cos (- 2 (x — 1)) + 1
Из условия видно, что k 1 = 3 2 , k 2 = 2 , a = — 1 , b = 1 , где k 2 имеет « — » , а перед k 1 он отсутствует.
Отсюда получаем, что получится график тригонометрической функции вида:
y = cos (x) → y = 3 2 cos (x) → y = 3 2 cos (2 x) → y = 3 2 cos (- 2 x) → → y = 3 2 cos (- 2 (x — 1)) → y = 3 2 cos — 2 (x — 1) + 1
Пошаговое преобразование косинусоиды с графической иллюстрацией.
При заданной графике y = cos (x) видно, что наименьший общий период равняется T = 2 π . Нахождение максимумов в 2 π · k ; 1 , k ∈ Z , а минимумов π + 2 π · k ; — 1 , k ∈ Z .
При растягивании вдоль О у в 3 2 раза происходит возрастание амплитуды колебаний в 3 2 раза. T = 2 π является наименьшим положительным периодом. Нахождение максимумов в 2 π · k ; 3 2 , k ∈ Z , минимумов в π + 2 π · k ; — 3 2 , k ∈ Z .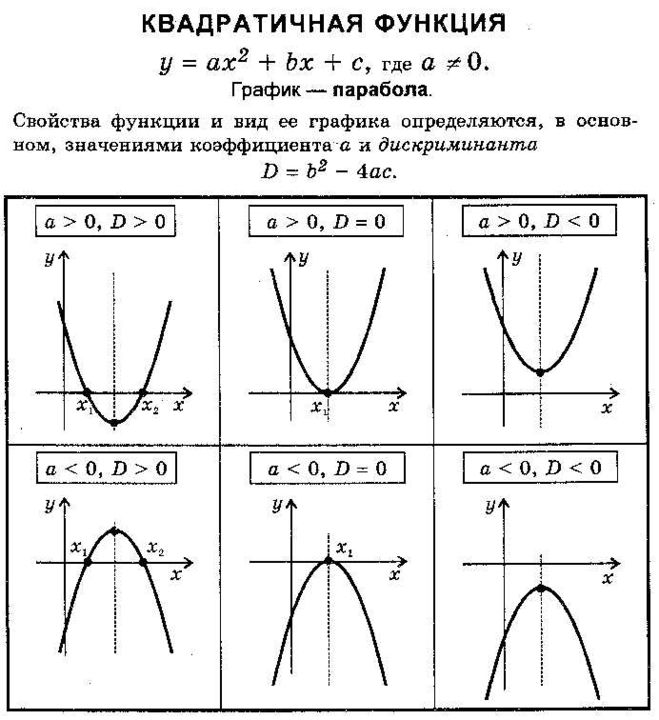
При сжатии вдоль О х вдвое получаем, что наименьшим положительным периодом является число T = 2 π k 2 = π . Производится переход максимумов в π · k ; 3 2 , k ∈ Z ,минимумов — π 2 + π · k ; — 3 2 , k ∈ Z .
Симметричное отображение относительно О у. Так как график нечетный, то он не будет изменяться.
При сдвигании графика на 1 . Отсутствуют изменения наименьшего положительного периода T = π . Нахождение максимумов в π · k + 1 ; 3 2 , k ∈ Z , минимумов — π 2 + 1 + π · k ; — 3 2 , k ∈ Z .
При сдвигании на 1 наименьший положительный период равняется T = π и не изменен. Нахождение максимумов в π · k + 1 ; 5 2 , k ∈ Z , минимумов в π 2 + 1 + π · k ; — 1 2 , k ∈ Z .
Преобразования функции косинуса завершено.
Рассмотрим преобразования на примере y = t g x .
Пример 6
Построить график функции y = — 1 2 t g π 3 — 2 3 x + π 3 при помощи преобразований функции y = t g (x) .
Решение
Для начала необходимо привести заданную функцию к виду ± k 1 · f ± k 2 · x + a + b , после чего получаем, что
y = — 1 2 t g π 3 — 2 3 x + π 3 = — 1 2 t g — 2 3 x — π 2 + π 3
Отчетливо видно, что k 1 = 1 2 , k 2 = 2 3 , a = — π 2 , b = π 3 , а перед коэффициентами k 1 и k 2 имеется « — » .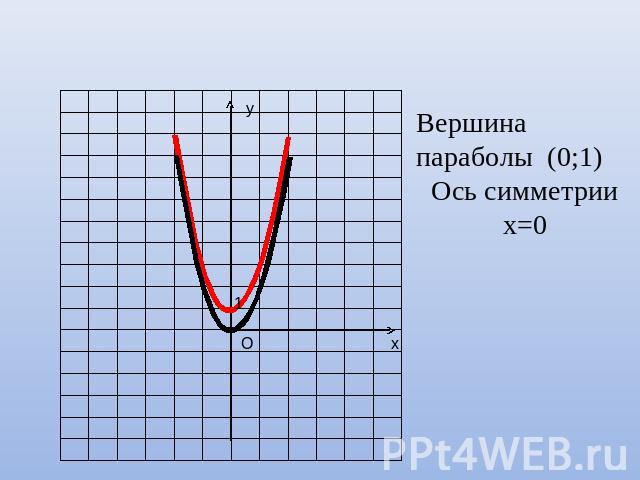
Значит, после преобразования тангенсоиды получаем
y = t g (x) → y = 1 2 t g (x) → y = 1 2 t g 2 3 x → y = — 1 2 t g 2 3 x → → y = — 1 2 t g — 2 3 x → y = — 1 2 t g — 2 3 x — π 2 → → y = — 1 2 t g — 2 3 x — π 2 + π 3
Поэтапное преобразование тангенсоиды с графическим изображением.
Имеем, что исходный график – это y = t g (x) . Изменение положительного периода равняется T = π . Областью определения считается — π 2 + π · k ; π 2 + π · k , k ∈ Z .
Сжимаем в 2 раза вдоль О у. T = π считается наименьшим положительным периодом, где область определения имеет вид — π 2 + π · k ; π 2 + π · k , k ∈ Z .
Растягиваем вдоль О х в 3 2 раза. Вычислим наименьший положительный период, причем равнялся T = π k 2 = 3 2 π . А область определения функции с координатами — 3 π 4 + 3 2 π · k ; 3 π 4 + 3 2 π · k , k ∈ Z , меняется только область определения.
Симметрия идет по сторону О х. Период не изменится в этот момент.
Необходимо симметрично отображать оси координат.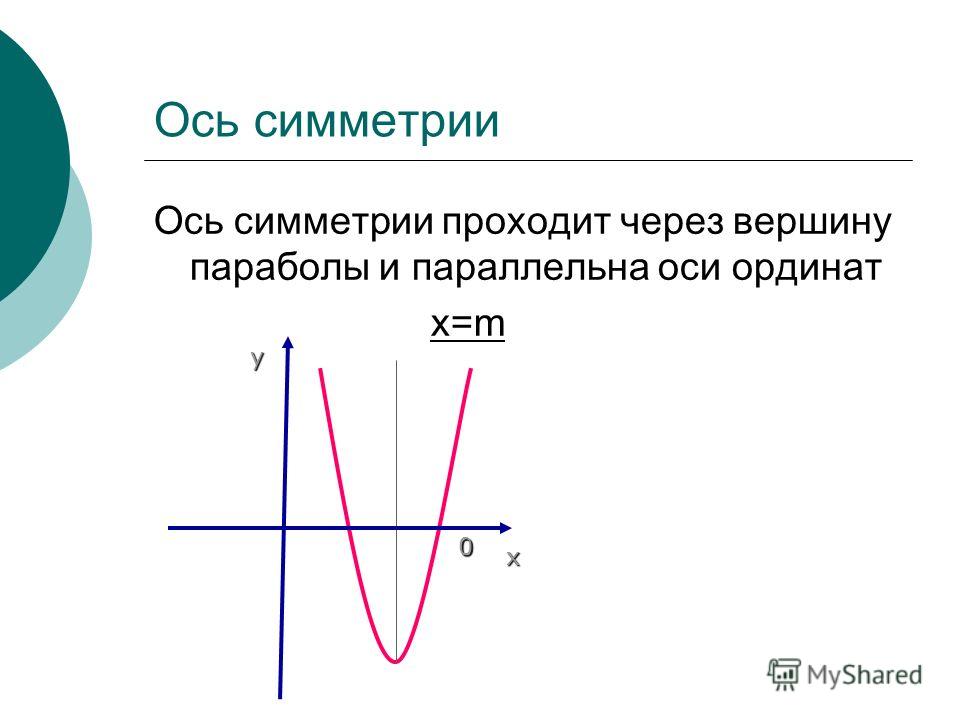
Область определения в данном случае неизменна. График совпадает с предыдущим. Это говорит о том, что функция тангенса нечетная. Если к нечетной функции задать симметричное отображение О х и О у, тогда преобразуем до исходной функции.
Решение
Для начала необходимо перейти от арккосинуса к арксинусу при помощи обратных тригонометрических функций a r c sin x + a r c o cos x = π 2 . Значит, получим, что a r c sin x = π 2 — a r c cos x .
Видно, что y = a r c cos x → y = — a r c cos x → y = — a r c cos x + π 2 .
Поэтапное преобразование арккосинуса и графическое изображение.
График, данный по условию
Производим отображение относительно О х
Производим движение вверх на π 2 .
Таким образом, осуществляется переход от арккосинуса к косинусу. Необходимо произвести геометрические преобразования арксинуса и его графика.
Видно, что k 1 = 2 , k 2 = 1 3 , a = — 1 , b = 0 , где отсутствует знак « — » у k 1 и k 2 .
Отсюда получаем, что преобразования y = a r c sin x примет вид:
y = a r c sin (x) → y = 2 a r c sin (x) → → y = 2 a r c sin 1 3 x → y = 2 a r c sin 1 3 (x — 1)
Поэтапное преобразование графика арксинуса и графическое изображение.
График y = a r c sin x имеет область определения вида x ∈ — 1 ; 1 , тогда интервал y ∈ — π 2 ; π 2 относится к области значений.
Необходимо растянуть вдвое по О у, причем область определения останется неизменной x ∈ — 1 ; 1 , а область значений y ∈ — π ; π .
Растягивание по О х строе. Происходит расширение области определения x ∈ — 3 ; 3 , но область значений остается неизменной y ∈ — π ; π .
, Конкурс «Презентация к уроку»
Презентация к уроку
Назад
Вперёд
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации.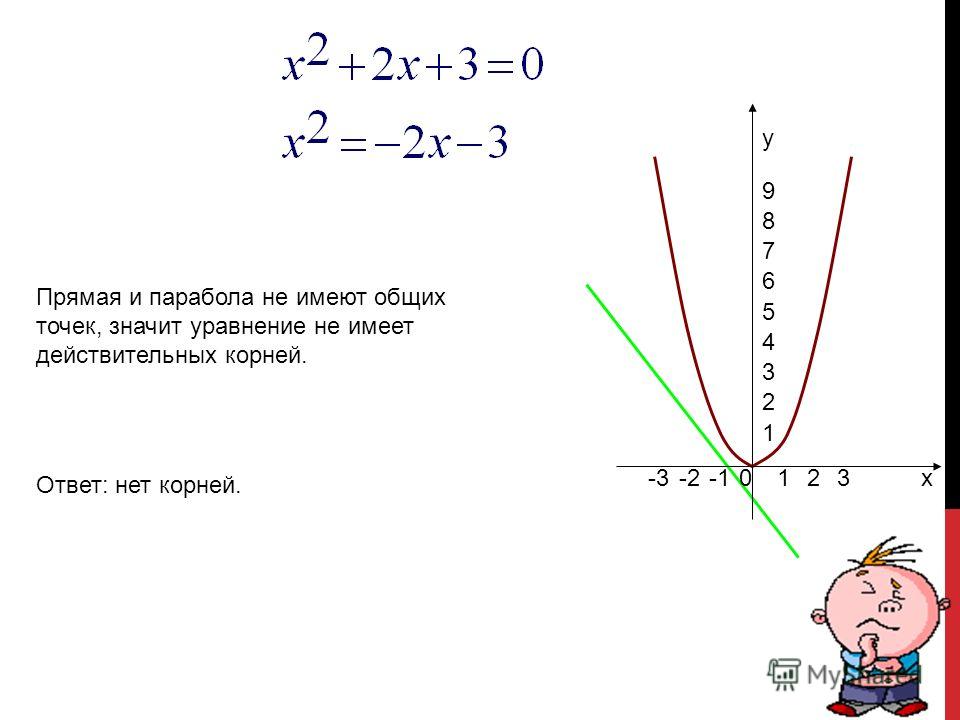
Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Цели урока:
Образовательная: исследовать смещение графика квадратичной функции, определить положение графика в зависимости от значений коэффициентов b, c .
Воспитательная: умение работать в группе, организованности.
Развивающая : навыки исследовательской работы, умение выдвигать гипотезы, анализировать полученные результаты, систематизировать полученные данные.
Структура урока
- Организационный момент – 3 минуты.
- Исследовательская работа – 20 минут.
- Закрепление изученного материала – 15 минут.
- Рефлексия – 2 минут.
- Итог урока – 3 минуты.
- Домашнее задание – 2 минуты.
Ход урока
1. Организационный момент.
Цель урока провести исследовательскую работу.
Объектом исследования будут квадратичные
функции разного вида. Вам предстоит определить,
как влияют коэффициенты b, c на график
функций вида y=x 2 +с, y=(x-b) 2 , y=(x-b) 2 +c.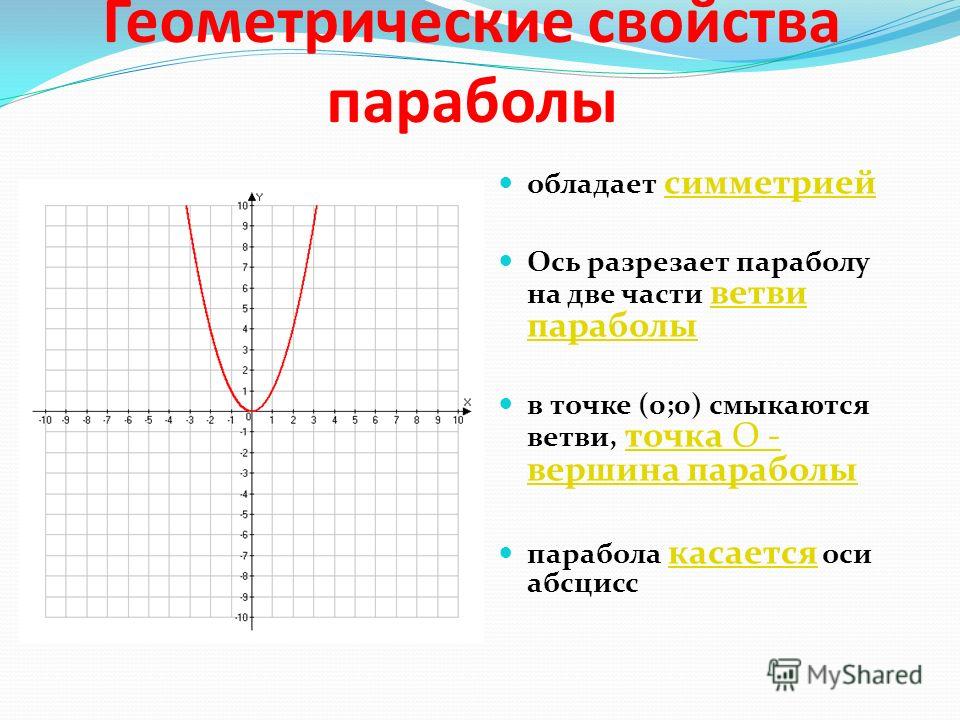
Для выполнения задания необходимо разделиться на группы (4 группы по 5 человек, одна группа “эксперты” наиболее подготовленные ученики).
Каждая группа получает план исследования , лист формата А3 для оформления результатов.
2. Исследовательская работа
.Две группы (уровень А) исследуют функции вида y= x 2 +с, одна группа (уровень В) исследует функцию вида y=(x-b) 2 , одна группа (уровень С) исследует функцию y=(x-b) 2 +c. Группа “Экспертов” исследует все функции.
| Функция | Результат | ||
| 1 группа | у=x 2 +3; | ||
| 2 группа | у=x 2 -5; | ||
| 3 группа | у=(х-4) 2 ; | ||
| 4 группа | у=(х-2) 2 +3. |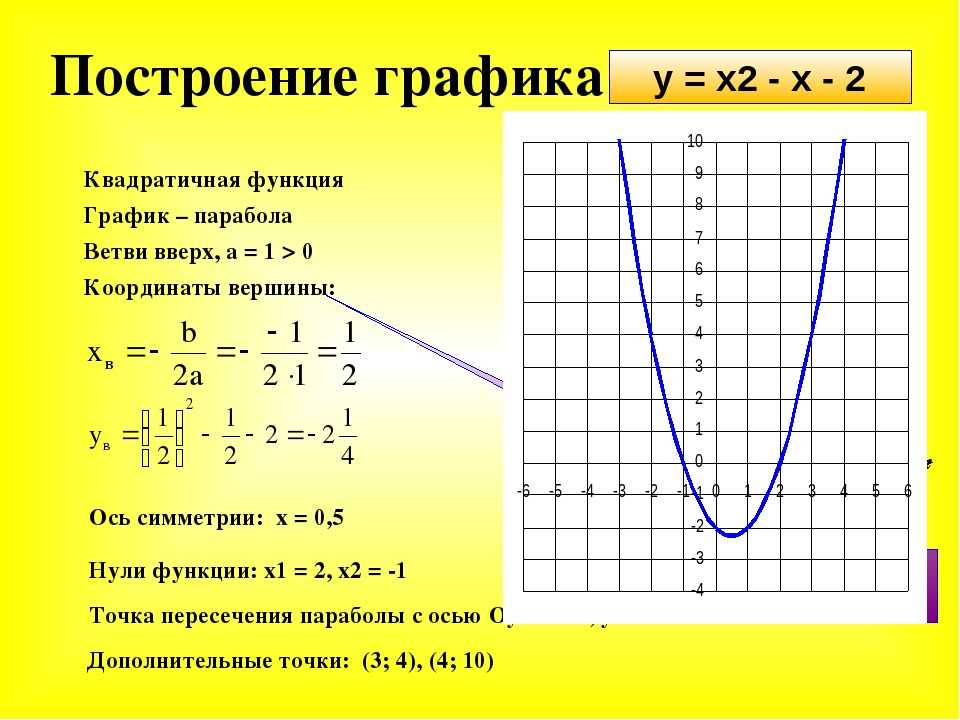
План работы
- Для того чтобы выдвинуть гипотезу сделайте предположение, как может выглядеть ваша функция.
- Постройте график исследуемых функций (определите вершину параболы (х 0 , y 0), задайте таблицей 4 точки).
- Сравните получившийся график с контрольным образцом y=x 2 .
- Сделайте вывод (как изменилось положение графика вашей функции относительно контрольного образца).
- Результаты оформите на листе формата А3 и представьте “экспертной” группе.
“Экспертная” группа сверяет результаты свои с результатами остальных групп, систематизирует и обобщает результаты, выступает с выводами. В случае неточностей или ошибок учитель вносит коррекционные замечания.
Сверка полученных результатов со слайдами №2-5.
Любую квадратичную функцию y=ax 2 +bx+c, можно
записать в виде y=a(x-x 0) 2 +y 0, где x 0
и y 0 выражаются через коэффициенты a, b, c.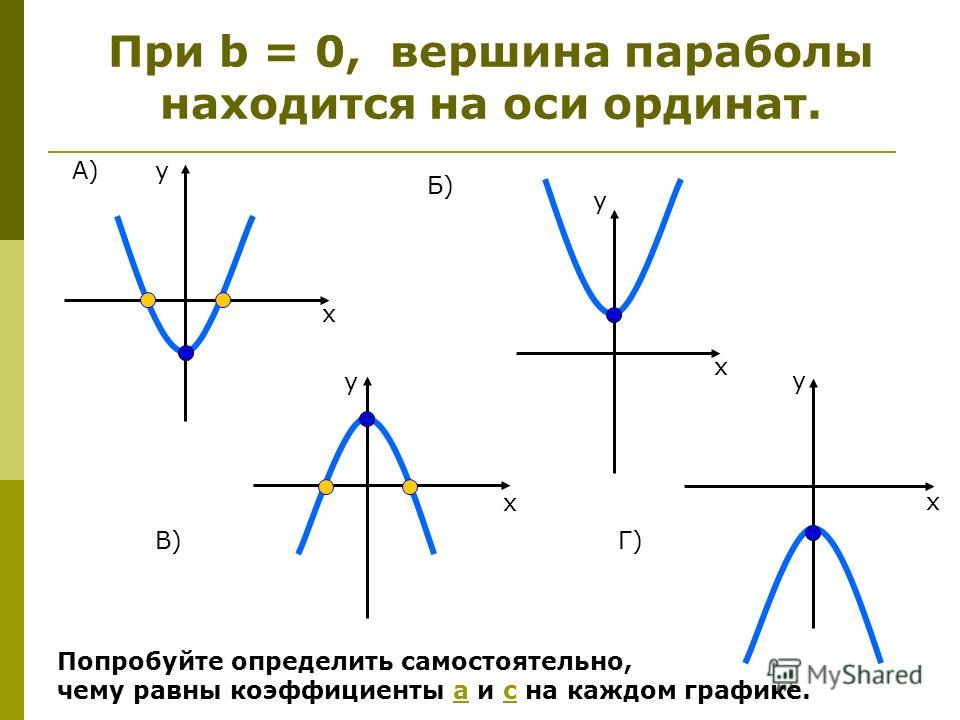
Таким образом, ваши коэффициенты b=x 0 , c=y 0
являются координатами вершины параболы.
3. Закрепление изученного материала.
Фронтальная работа с классом.
1. Найти ошибку в графиках функций (Слайды№6-9).
Коэффициент b | Нет ошибки |
Рисунок 1 | Рисунок 2 |
| у=(х+5) 2 -1 | у=(х-2) 2 +2 |
| Коэффициент b и с | Коэффициент b |
| Рисунок 3 | Рисунок 4 |
, Конкурс «Презентация к уроку»
Презентация к уроку
Назад
Вперёд
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации.
Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Цели урока:
Образовательная: исследовать смещение графика квадратичной функции, определить положение графика в зависимости от значений коэффициентов b, c .
Воспитательная: умение работать в группе, организованности.
Развивающая : навыки исследовательской работы, умение выдвигать гипотезы, анализировать полученные результаты, систематизировать полученные данные.
Структура урока
- Организационный момент – 3 минуты.
- Исследовательская работа – 20 минут.
- Закрепление изученного материала – 15 минут.
- Рефлексия – 2 минут.
- Итог урока – 3 минуты.
- Домашнее задание – 2 минуты.
Ход урока
1. Организационный момент.
Цель урока провести исследовательскую работу.
Объектом исследования будут квадратичные
функции разного вида. Вам предстоит определить,
как влияют коэффициенты b, c на график
функций вида y=x 2 +с, y=(x-b) 2 , y=(x-b) 2 +c.
Для выполнения задания необходимо разделиться на группы (4 группы по 5 человек, одна группа “эксперты” наиболее подготовленные ученики).
Каждая группа получает план исследования , лист формата А3 для оформления результатов.
2. Исследовательская работа
.Две группы (уровень А) исследуют функции вида y= x 2 +с, одна группа (уровень В) исследует функцию вида y=(x-b) 2 , одна группа (уровень С) исследует функцию y=(x-b) 2 +c. Группа “Экспертов” исследует все функции.
| Функция | Результат | ||
| 1 группа | у=x 2 +3; | ||
| 2 группа | у=x 2 -5; | ||
| 3 группа | у=(х-4) 2 ; | ||
| 4 группа | у=(х-2) 2 +3. |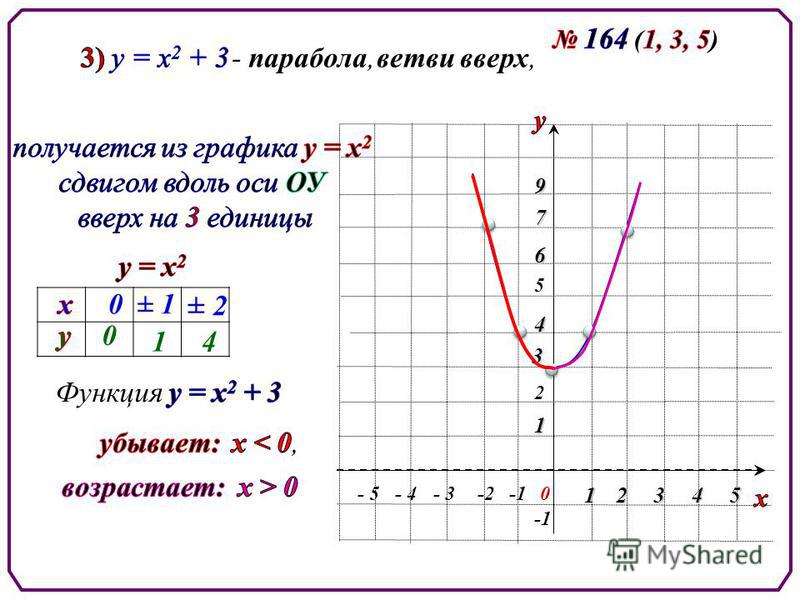
План работы
- Для того чтобы выдвинуть гипотезу сделайте предположение, как может выглядеть ваша функция.
- Постройте график исследуемых функций (определите вершину параболы (х 0 , y 0), задайте таблицей 4 точки).
- Сравните получившийся график с контрольным образцом y=x 2 .
- Сделайте вывод (как изменилось положение графика вашей функции относительно контрольного образца).
- Результаты оформите на листе формата А3 и представьте “экспертной” группе.
“Экспертная” группа сверяет результаты свои с результатами остальных групп, систематизирует и обобщает результаты, выступает с выводами. В случае неточностей или ошибок учитель вносит коррекционные замечания.
Сверка полученных результатов со слайдами №2-5.
Любую квадратичную функцию y=ax 2 +bx+c, можно
записать в виде y=a(x-x 0) 2 +y 0, где x 0
и y 0 выражаются через коэффициенты a, b, c.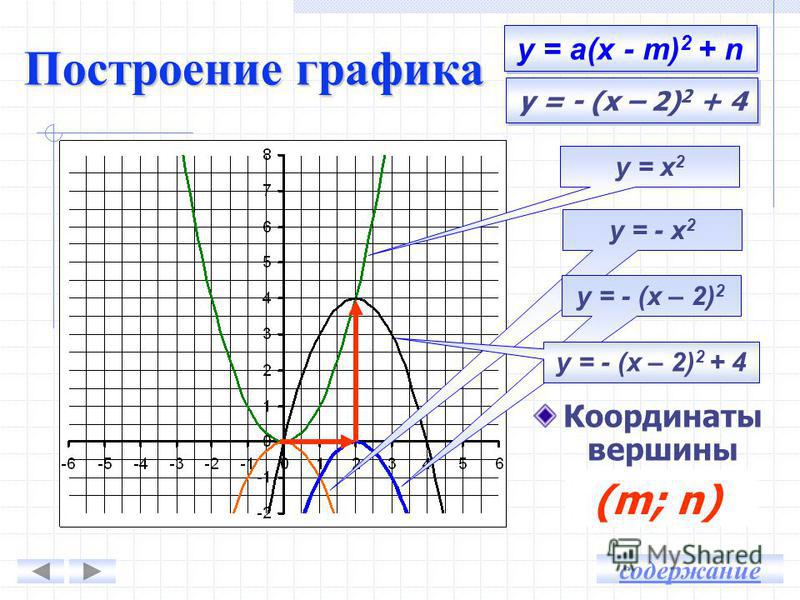
Таким образом, ваши коэффициенты b=x 0 , c=y 0
являются координатами вершины параболы.
3. Закрепление изученного материала.
Фронтальная работа с классом.
1. Найти ошибку в графиках функций (Слайды№6-9).
Коэффициент b | Нет ошибки |
Рисунок 1 | Рисунок 2 |
| у=(х+5) 2 -1 | у=(х-2) 2 +2 |
| Коэффициент b и с | Коэффициент b |
| Рисунок 3 | Рисунок 4 |
Результаты
Какой коэффициент вам помог найти ошибку?
2.
Соотнесите графики функций согласно цветам (слайд
№10) .
Рисунок 5
4. Рефлексия.
Группа “Экспертов” отвечают на вопросы:
– Какие ошибки допустили группы?
– Достигнута ли цель занятия?
– Соответствуют ли полученные результаты исследования поставленной гипотезе?
5. Итог урока (слайд №11)
:На положение графика функции y=(x-b) 2 +c влияют коэффициенты b и c,
“+b” парабола сдвинута вправо по оси абсцисс на b единичных отрезков,
“–b” парабола сдвинута влево по оси абсцисс на b единичных отрезков,
“+с” парабола сдвинута вверх по оси ординат на с единичных отрезков,
“-с” парабола сдвинута вниз по оси ординат на с единичных отрезков.
6. Домашнее задание
- Построить график квадратичной функции, имеющую вершину в точке А(1;-2), коэффициент a=1.
- Подумайте, в какой области можно использовать
знания по данной теме (практическое применение).
Математика падения: параболическое движение
Дон Линкольн, доктор философии, Университет Нотр-Дам
Параболическое движение в физике можно наблюдать во многих повседневных ситуациях, например, при подбрасывании мяча. На движение влияет множество факторов, а именно сила тяжести, скорость, ускорение и время. Математика складывает все эти факторы в формулы, объясняющие, как формируется движение и как оно продолжается. В общем, когда объект движется вперед и вверх или вниз одновременно, он имеет параболическое движение.
Параболическое движение брошенного объекта можно рассчитать по математическим формулам. (Изображение: Сергей Нивенс/Shutterstock)Когда бейсболист бросает мяч, он начинает движение в системе координат: x и y, которые перпендикулярны друг другу. Направление x параллельно земле, и y является вертикальным. Другим фактором, участвующим в движении, является гравитация, обозначаемая по г. Скорость и ускорение также имеют значение. Как появляются эти элементы вместе в формулах параболического движения и падения?
Гравитация и падение
Элементы, участвующие в
падение было кратко указано.
Гравитация, или g, — это направленная вниз сила,
притягивает движущийся объект к земле параллельно оси Y. Оно имеет
значение 9,8 метра в секунду в квадрате. Вес также является результатом гравитации,
но в формуле падения это относится к ускорению под действием силы тяжести.
Движущийся объект начинает движение с начальной скоростью в начальном месте до
он получает ускорение свободного падения.
Узнайте больше о том, как работает полет.
‘d
0 ’, ‘v 0 ’ и ‘a’ ‘d 0 ’ относятся к начальному положению объекта до того, как он начнет двигаться. Начальная скорость объекта обозначается как «v 0 ». Когда есть скорость, есть и ускорение, будь то постоянный или изменяющийся элемент. Ускорение обозначается буквой «а». Имея под рукой всю эту информацию, можно определить местоположение мяча на все времена — или «t». Соединяя все эти элементы вместе, мы получаем простое квадратное уравнение для расстояния: t = d 0 + vt + 1/2at 2 .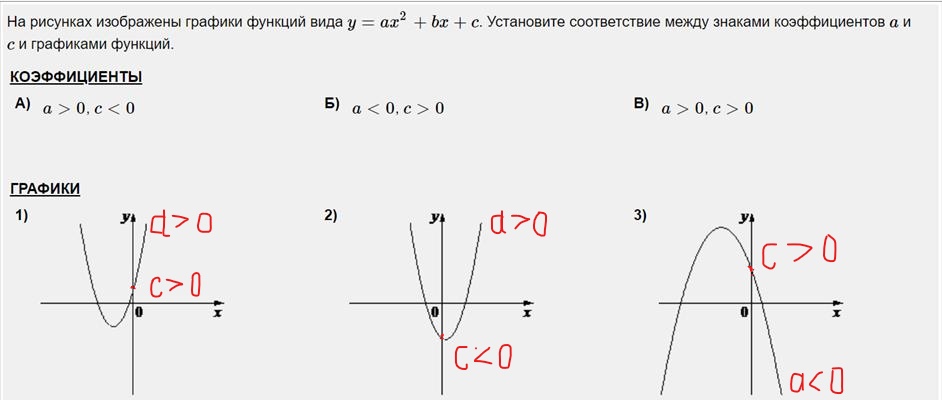
Узнайте больше о E=mc2 и других мифах относительности.
Упрощение уравнения падения
Направления x и y в физику можно рассматривать совершенно независимо. Таким образом, квадратное уравнение можно записать в двух вариантах, один для x и один для y, предполагая, что ускорение постоянна и что t равно нулю в момент выпуска мяча.
Чтобы получить простое уравнение для метания мяча, многие элементы следует считать постоянными. (Изображение: Элейн Уиллкок/Shutterstock) Из-за нисходящей g 9,8 м/с,
a y при t=0 равно -9,8, а x равно нулю, поскольку существует
отсутствие ускорения под действием силы тяжести в горизонтальном направлении. Уравнение может быть
далее упрощается, если предположить, что оба x 0 и y 0 равны
ноль в момент броска. Тогда уравнения превратятся в x = v x t
– 1/2gt 2 и y = v y t – 1/2gt 2 . Скорости и
ускорения постоянны. Таким образом, их можно заменить символами констант,
например, A и B.
Для какой формы можно использовать эти уравнения? А
парабола.
Это стенограмма из серии видео Понимание заблуждений науки . Смотрите прямо сейчас, на Вондриуме.
Параболическое движение
В самом параболическом движение брошенного мяча, упрощающие предположения больше не применяются. математические расчеты будут намного сложнее, и другие факторы будут также влияют на движение. Тем не менее, в случае с мячом объект пойдет вверх и вперед, пока не достигнет пика движения. Затем вертикальное движение становится равным нулю, и мяч начинает двигаться вперед и вниз. Движение вперед происходит за счет начальной энергии метания, а движение вниз движение за счет силы тяжести.
Узнайте больше о том, как работает квантовая механика.
Падение с пика
Когда объект начинает
падение, оно начинается с нулевого вертикального движения, но гравитация заставляет объект
ускоряться все быстрее и быстрее.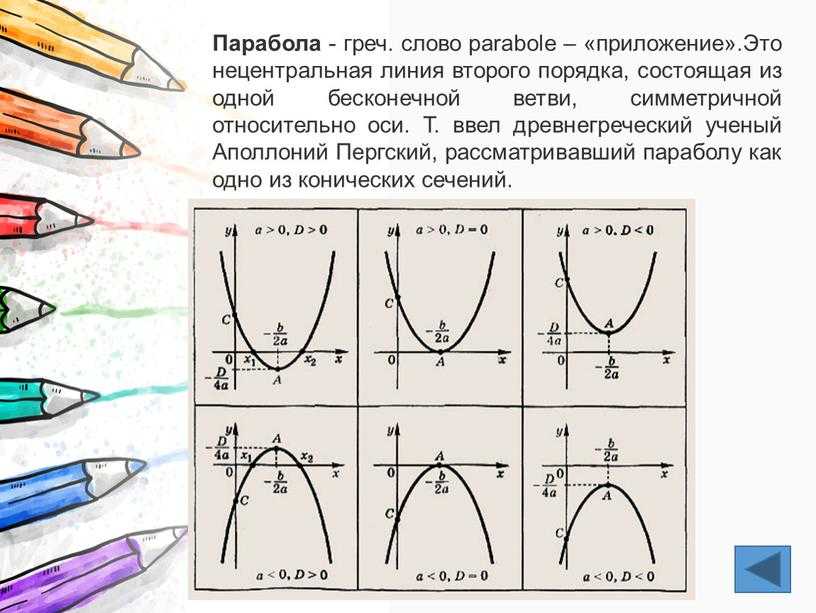
Однако присутствует и сопротивление воздуха.
Если предполагаемый мяч — бейсбольный, парабола выглядит почти симметричной. На
С другой стороны, если это пляжный мяч, движение будет другим, даже
если вес шаров одинаков. Пляжный мяч намного больше и сталкивается
более высокое сопротивление воздуха; следовательно, меньшее расстояние делается во второй половине
способ.
Все эти предположения были сделано для бейсбольного мяча, который представляет собой небольшой предмет, предназначенный для метания. Тем не менее, те же самые формулы применимы и к другим объектам, будь то перо или ракета. Следовательно, формула падения та же, но параболическое движение иногда может быть сильно нарушено другими факторами, такими как сопротивление воздуха.
Общие вопросы о параболическом движении
В: Почему объекты движутся по параболе?
По опыту почти каждый знает, что когда объект брошен, он поднимается (или прямо, в зависимости от угла) на некоторое расстояние, а затем снова опускается.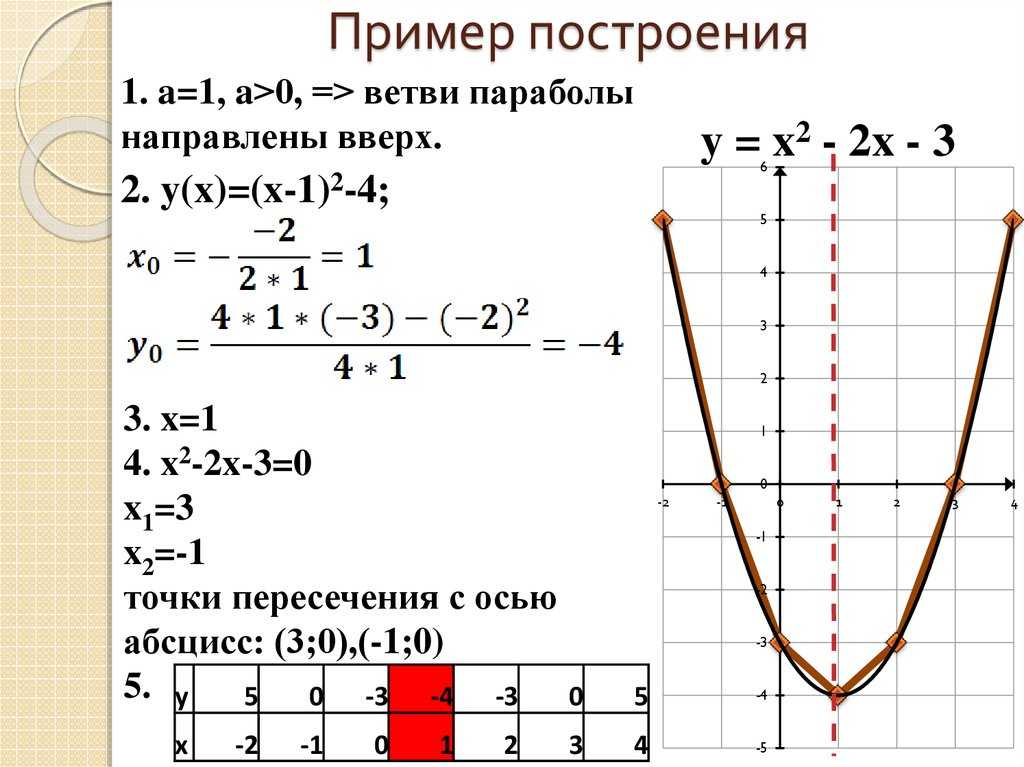
По правилам физики на вертикальное положение объекта влияет только постоянное ускорение, и горизонтальная скорость также обычно постоянна. Таким образом, объект будет иметь параболическое движение.
В: Что означает параболический в физике?
Когда объект брошен, он движется вперед, но при этом постоянно подвергается гравитации. Следовательно, он будет двигаться вниз под действием гравитации, создавая параболическое движение объекта. Дуга и ширина параболы зависят от множества факторов.
В: Что такое двумерное движение?
Когда объект движется одновременно по осям x и y, он имеет двумерное движение. Положение объекта в двумерном пространстве можно изобразить по его координате (x, y). Параболическое движение является своего рода двухмерным движением, поскольку объект движется одновременно вверх (или вниз) и вперед.
В: Что является примером двумерного движения?
Очень распространенным примером двумерного движения является случай, когда объект брошен вперед: выстрел из пушки, подбрасывание бейсбольного или волейбольного мяча.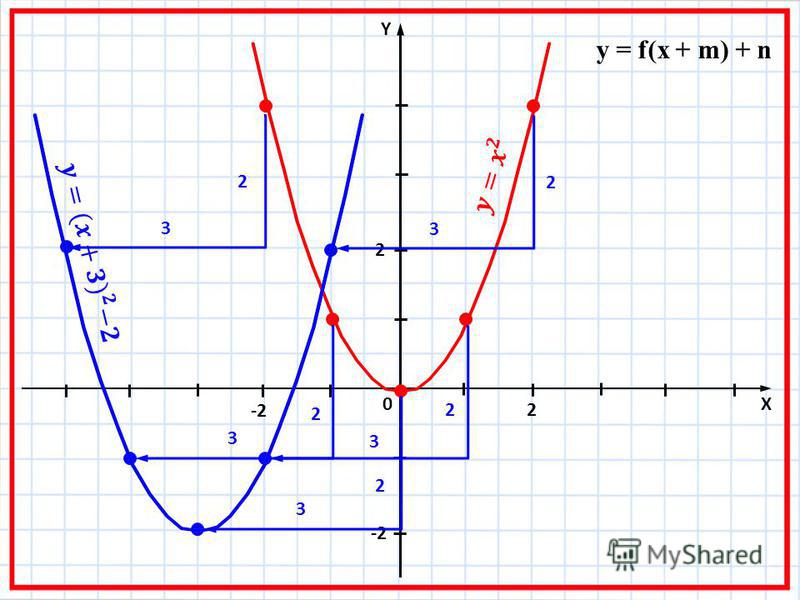
Есть и другие примеры, но метание и его параболическое движение — одни из самых известных.
Продолжайте читать
Принцип эквивалентности Эйнштейна: расширение нашего взгляда на гравитацию
Развитие и подтверждение квантовой теории поля
Развитие квантовой механики
Как найти ось симметрии параболы
Как найти ось симметрии параболы
Эндрю Ли
28 января 2021
70Онлайн-репетиторство
7 Советы
,
Геометрия
,
Математика
Ось симметрии — это вертикальная линия, проходящая через вершину параболы, поэтому левая и правая стороны параболы симметричны. Для упрощения эта линия разбивает график квадратного уравнения на два зеркальных отображения.
В этом уроке мы покажем вам, как найти ось симметрии, взглянув на само квадратное уравнение.
Уравнение оси симметрии параболы
Уравнение оси симметрии параболы можно записать так:
Помните, что любую квадратичную функцию можно записать в стандартной форме .
График квадратичной функции называется параболой, где каждая точка этой параболы представляет собой x и y , который решает квадратичную функцию.
Вершина квадратичной функции — это самая высокая или самая низкая точка на графике. Таким образом, координата вершины параболы является решением x и y для самой низкой или самой высокой точки параболы.
Вершина красной параболы (-2, -1), а вершина синей параболы (0, -2).
Вычисление оси симметрии параболы
Опять же, осью симметрии параболы является линия на графике, которая проходит через вершину параболы и делит график на две симметричные стороны.
Это выражается как:
И когда вы представляете квадратичную функцию в стандартной форме, это .
Например, мы можем ввести квадратное уравнение для красной параболы в ее стандартной форме, где a = 1, b = 4 и c = 3. Зеленая линия является осью симметрии .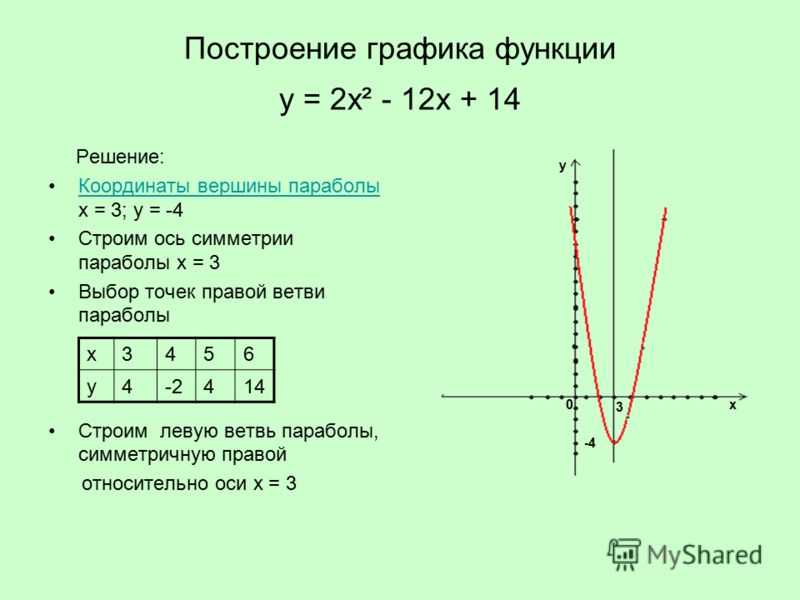
Или x = -2 после подстановки значений на и на b .
Вот как эта формула выглядит на графике. Обратите внимание, где находится зеленая линия и как она делит параболу.
Нахождение вершины параболы
Чтобы найти фактические координаты вершины параболы, просто подставьте значение x в полиномиальное выражение, чтобы найти соответствующее значение y . Помните, что каждая точка на квадратичном графике является решением уравнения.
Продолжая предыдущий пример, мы знаем, что x = -2.
Мы заменяем это значение на x в исходной квадратичной функции.
Решение дает y = -1. Теперь мы знаем, что вершина параболы — это координата (-2, -1). Найти вершину параболы не может быть проще.
Как найти ось симметрии
Вот что вам нужно запомнить: Если вам нужна ось симметрии или полные координаты вершины параболы, используйте эту формулу, чтобы начать построение квадратного уравнения.