В кругах Эйлера | SKVOT
Хаос — off, логика — on.
15 февраля, 2021 Статья
Работа креатора — это не только генерить идеи. Но и вовремя включить критическое мышление — чтобы найти в концепциях противоречия и отбросить то, что не выживет.
Инструменты есть не только для креативного, но и для логического мышления. И круги Эйлера — как раз из этого списка. Рассказываем, что это, и на примере креативных проектах показываем принцип работы кругов.
Рисовать, чтобы думать
Круги Эйлера — это шесть простых геометрических схем, которые помогают разобраться в соотношении понятий. Математик Леонард Эйлер придумал их еще в XVIII веке и предположил, что этот инструмент упростит размышления любому, кто мыслит.
Эйлер предложил шесть типов отношений: равнозначность, подчинение
Вот как они объясняются с помощью окружностей: По сути, круги Эйлера — способ визуализировать отношения между любыми объектами, группами объектов и даже абстрактными понятиями. Например, чтобы искать точки пересечения между любителями «Звездных войн», жителями швейцарских горных сел и посетителями музыкального фестиваля Sziget.
Чем больше понятий, тем сложнее представить их связи мысленно, цифрами, списками — и тем эффективнее делать схему. Например, в сериале «Теория большого взрыва» Говард при помощи кругов Эйлера объясняет Леонарду, почему ему стоит забить на поиски идеальной женщины.
Круги Эйлера используют для решения логических задач уже в средней школе. Но схемы универсальны — и действительно пригодятся любому, кто размышляет.
Нарисуй, распечатай, запомни круги Эйлера — и используй, если нужно:
- — Разработать стратегию и проверять, как идея/проект с ней соотносятся.
- — Анализировать контент конкурентов, кампании каннских победителей, рекламу Superbowl — и понять ключевые схемы.
- — Выбрать tone of voice, героя истории, стиль вижуала, маскот для бренда, месседж для слогана.
- — Найти противоречия и логические ямы в брифе, сценарии, посте для соцсетей.
- — Освоить новый скил, но с направлением определиться трудно.
Эйлер на кейсах
Самый надежный способ разобраться в механизме системы, которую придумал Эйлер, — найти примеры в готовых кейсах. Увидишь, как работает равнозначность в стратегии бренда или пересечение в поисках героя для рекламного ролика, — поймешь, как использовать этот подход в своих целях.
#1. Равнозначность
У Эйлера этот тип взаимодействия понятий выглядит как два круга, которые полностью совпадают. Одно равно другому, как ни назови. Стивен Хокинг = автор книги «Краткая история времени». Или «Пираты Карибского моря: на странных берегах» = самый дорогой фильм в истории (пока).
Один рекламный ролик не сможет за минуту убедить пользователей, что пиво = Guinness, мыло = Dove, а детское масло = Johnson’s Baby.
Нужна эффективная (часто многолетняя) маркетинговая стратегия, которая приведет к этому убеждению.
В идеале название бренда будет однозначно ассоциироваться с целой индустрией или продуктом. Слышишь «мебель для самостоятельной сборки» — сразу понимаешь, что это IKEA. Видишь пошаговый гайд по сборке — точно IKEA. А с помощью этих прочных связей бренд может говорить на самые разные темы: экологичность, ресайклинг, домашний уют и социальная ответственность.
Посмотреть эту публикацию в Instagram
Публикация от Ogilvy (@ogilvy)
#2. Подчинение
Допустим, общее понятие — это большой круг. Внутри него находится другой, маленький, и это — частность большого. Зимних олимпийских видов спорта много, и бобслей, например, один из них.
Такой тип отношений — мощный инструмент для рекламного месседжа.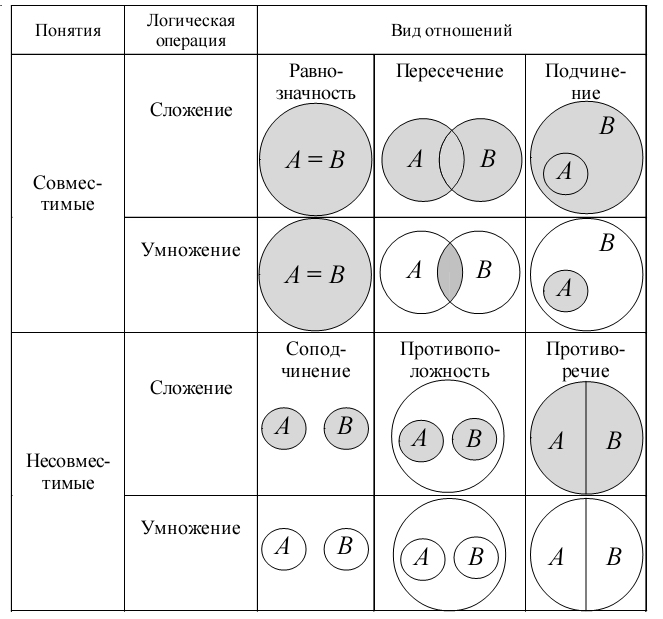
Особенно если его целью оказывается инклюзия: включение незаметной, неожиданной, уязвимой группы в сообщество. Nike на протяжении нескольких лет топит за спорт как удовольствие, независимо от телосложения, опыта, целей и происхождения. И на уровне продукта, и на уровне рекламных кампаний.
Коллекцию Victory Swim разработали для спортсменок-мусульманок — и Nike промит ее идеальным роликом, где женщины в хиджабах участвуют в соревнованиях, серфят, занимаются дайвингом и учат дочек плавать. И становятся частью сообщества Nike:
#3. Соподчинение
Графический ключ к этому соотношению — большой круг, внутри которого помещаются несколько маленьких. Маленькие понятия на равных и полностью включены в какое-то общее. Например, актеры, получившие Оскар, — Хоакин Феникс, Гэри Олдман, Леонардо Ди Каприо.
Если поместишь ключевое понятие в не самую очевидную область и будешь искать соподчинение в ней, выйдет крутой экспириенс.
Например, очевидно было с началом пандемии находить параллели в прошлом — в частности, с эпидемией «испанки».
Креаторы латвийского агентства Nord DDB во время весеннего локдауна разработали серию принтов о бедах, которые мы уже пережили (а значит, есть все шансы пережить и жесткий карантин). Среди самых страшных событий прошлого: шлепанцы на носки и кроксы с платформой. Реально страшно:
Посмотреть эту публикацию в Instagram
Публикация от NORD DDB RIGA (@nordddbriga)
#4. Пересечение
Эта диаграмма Эйлера — самая культовая и попсовая: ее растащили в коуч-пособия и мемы. Суть в том, что объем одного понятия частично совпадает с объемом другого — у них есть что-то общее.
Это крутой визуальный инструмент для поиска инсайта. Если представить бренд как исходный круг и строить вокруг него пересечения с ценностями и потребностями ЦА, попадешь в область, где совпадение будет максимальным.
Например, у Starbucks есть фишка: писать имя посетителя на кофейном стаканчике. Этот факт даже не про кофе, он — маленькая деталь в общем объеме информации о бренде. Но среди посетителей кофеен точно есть те, кто хочет сказать свое имя — и услышать его от бариста. Значит, нужно найти героя, который только в Starbucks может назвать себя как угодно, а не так, как написано в паспорте.
#5. Противоречие
В отличие от противоположности, противоречие держится на конфликте. Круг разделен пополам. Одна его часть утверждает, что не является второй частью. И наоборот.
На этом принципе строятся самые остроумные рекламные войны между брендами: Audi vs BMW, Pepsi vs Coca Cola, Old Spice vs Axe. Чаще это противостояние скрытое — борьба стратегий, разделение целевых аудиторий, — но иногда начинается прямой троллинг конкурента.
Рекламная борьба между McDonald’s и Burger King — самая долгая и зрелищная.
Клоун, маскот Мака, шифруется и приходит в Burger King за воппером. Потом Burger King показывает, что весь год снимал рекламу вопперов, заслоняя ими бигмаки. Конкуренты меряются вкусом и размером бургеров, близостью ресторанов уже больше 20 лет.
А зарывают топор войны только ради социально важных поступков, но и тогда это соревнование в благородстве. В начале осеннего локдауна французский Burger King опубликовал в медиа призыв покупать в McDonald’s и других сетях фастфуда — чтобы индустрия выжила. Конечно, воппер будет лучшим решением, но и бигмак сойдет.
Посмотреть эту публикацию в Instagram
Публикация от Burger King UK (@burgerkinguk)
#6. Противоположность
Понятия с противоположными характеристиками Эйлер представляет как две части круга, между которыми остается свободное пространство — это все остальное.
Проза и поэзия — две противоположности, а между ними: верлибр и ритмическая проза, например.
Противоположности — это мирные антонимы, которые не вступают в конфликт и не строят свою идентичность на отрицании друг друга. Это холодное, а это горячее. Это промышленное, а это DIY.
Wunderman Thompson построили на противоположности крутую кампанию для West Australian Ballet. В качестве промо новой постановки «Дракула» на стенах общественных туалетов разместили необычные принты. Изображение вампира в зеркале не отражается — постер пустой. Тут Дракула есть — там нет:
Логический вывод
В системе Эйлера — шесть простых геометрических схем, которые нарисует от руки даже ребенок. По отдельности каждая из них определяет только одно взаимодействие. Но если берешься за большую тему, в твоей схеме могут сочетаться сразу несколько типов соотношений.
Например, целевая аудитория бренда — подростки от 13 до 18. Среди них есть те, кто использует инстаграм, и те, кто использует тикток. Тиктокеры и инста-teens входят в целевую по принципу соподчинения. Но есть небольшая группа, которая зависает в обеих соцсетях — и между собой они взаимодействуют по принципу
Тестить мир на противоречия и связи — суперполезно и суперувлекательно. Хорошие новости: ты не сможешь остановиться. Плохие новости: ты не сможешь остановиться.
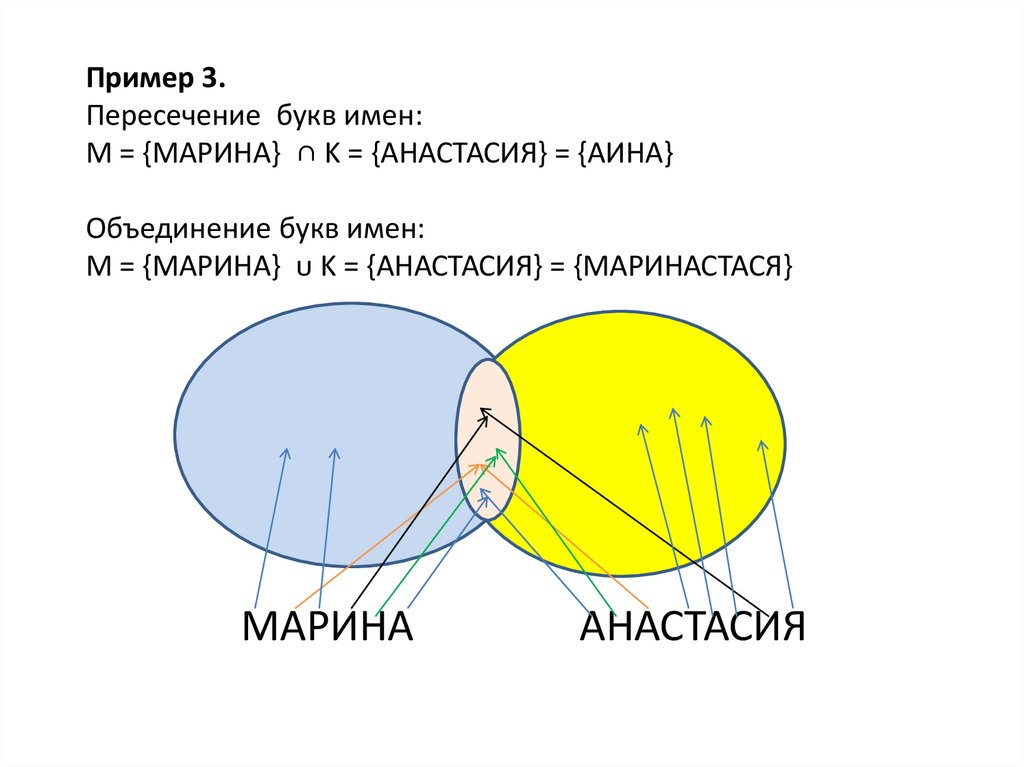
Презентация по теме «Круги Эйлера»
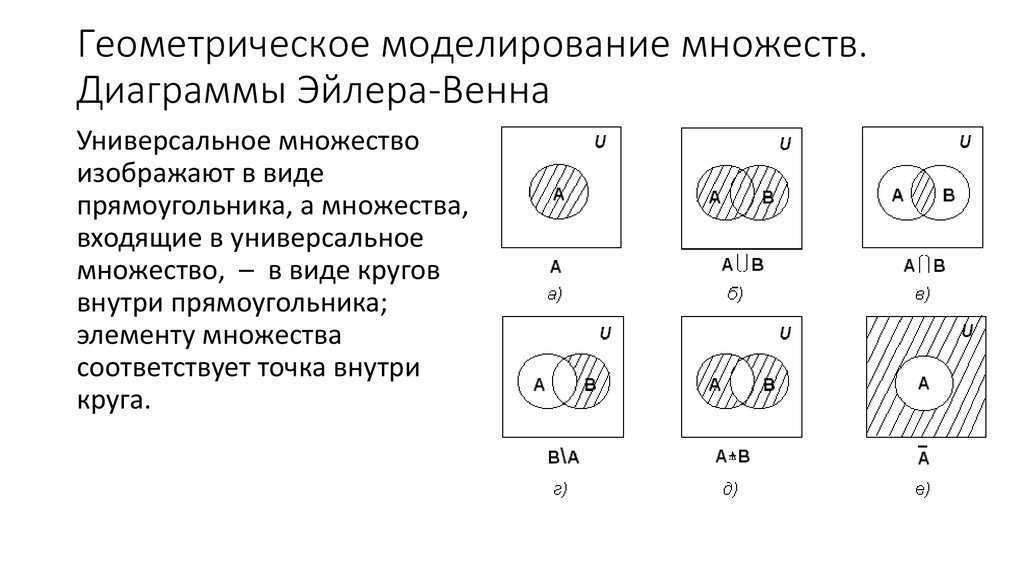
Соотношения между множествами принято
иллюстрировать с помощью кругов.
Эти круги называют кругами Эйлера
по имени ученого, который придумал
метод решения задач с их помощью.
Леонардо Эйлер (1707 – 1783)
Знаменитый математик, механик, физик и астроном, Л.Эйлер родился в 1707 году, он вырос в Швейцарии, а работал в основном в России и Германии.
За свою жизнь Л.Эйлер написал более 850 научных работ. В одной из них и появились круги, которые, по его словам, «очень подходят для того, чтобы облегчить наши размышления».
Рассмотрим, действительно ли это так ?
Запишем на символическом языке соотношения между множествами.
А и В
А и С
С и В
А, В и С
А B
С
A C
А
B C
В
A B C
A является подмножеством множества В, а В является подмножеством множества С
Пересечение множеств.
Пересечение множеств А и В — это множество, состоящее из элементов, входящих одновременно в А и В.
Пересечение А и В –
записывают с помощью символа
А В
В
А
А В
Пересечение множеств.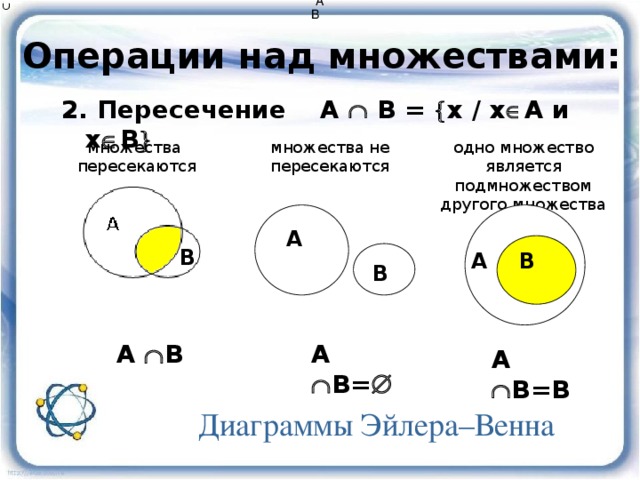
Пусть А = { 2, 4, 6} , a B = { 2, 4, 6, 8, 10}
Пересечение множеств А и В
А В = А
В
А
Объединение множеств.
Объединением множеств А и B называют множество, состоящее из элементов, входящих хотя бы в одно из множеств А или В.
Объединение множеств А и В обозначают символом
В
А
Объединение множеств.
Пусть А = { 2, 4, 6} , a B = { 2, 4, 6, 8, 10}
Объединение множеств А и В
А В = В
В
А
Рассмотрим, как можно решить задачу с помощью кругов Эйлера
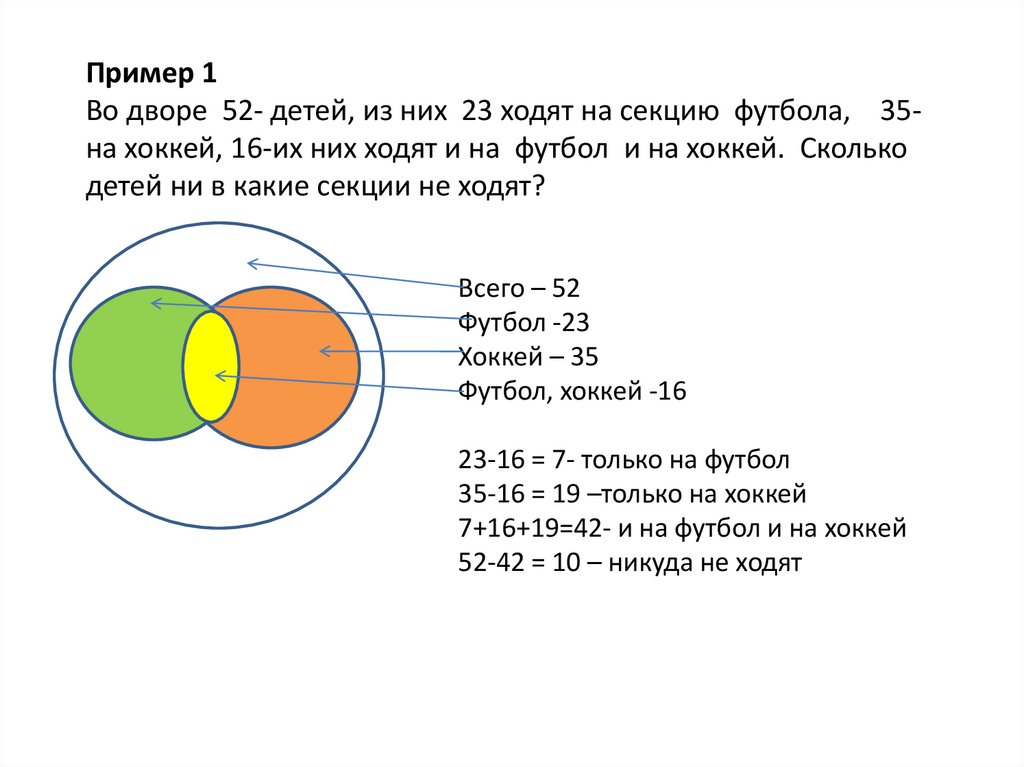
Задача: По результатам опроса 52 шестиклассников было установлено, что 23 из них собирают значки, 35 собирают марки, а 16 – и значки, и марки. Остальные не увлекаются коллекционированием. Сколько человек не увлекаются коллекционированием?
Решение:
З
?
Собирают значки
М
Собирают марки
Собирают и значки и марки
Не увлекаются
коллекционированием
Решение задачи ( продолжение)
1) Значки и марки собирают 16 человек.
Впишем число 16 в пересечение кругов З и М.
2) Значки собирают 23 человека. Тогда только значки собирают: 23-16 = 7 человек. Впишем число 7 в свободную часть круга З
3) Только марки собирают: 35-16 = 19 человек. Занесем число 19 в схему.
4) Теперь мы можем узнать, сколько человек занимаются коллекционированием: 16+7+19 = _______ человека
5) Не занимаются коллекционированием:
52 — __ = __________ человек.
Ответ: _____ человек.
З
7
М
16
19
№ 227,стр.87 ПРТ
Результаты опроса жильцов дома о том, смотрели ли они в новогоднюю ночь основные телеканалы — Первый канал и Россию — 1.
Используя данные на схеме, ответьте на вопросы:
25
Р-1
П
46
43
31
№ 227,стр.87 ПРТ
1.Сколько человек не смотрело ни тот, ни другой канал?
2.
Сколько человек включало то один, то другой канал?
3. Сколько человек смотрело только Первый канал?
4. Сколько человек смотрело канал Россия-1?
5. Сколько человек смотрело хотя бы один из этих каналов?
25
(25)
Р-1
П
(46)
46
(43)
43
31
(31+46)
(120)
Задание . На полке стояло 25 волшебных книг по заклинаниям, все они были прочитаны Гермионой, Гарри Поттером или Роном.
При этом не было не одной книги, которую бы прочитали все.
4 книги прочитали и Гарри Поттер, и Рон.
Гермиона прочитала 7 книг, которых не читали ни Гарри Поттер, ни Рон, и две книги, которые читал Гарри Поттер.
Всего Гарри Поттер прочитал 11 книг. Сколько книг прочитали только Гарри Поттер и только Рон?
1. Обозначим: P- множество книг, прочитанных Гарри Поттером;
R-множество книг, прочитанных Роном;
G- множество книг, прочитанных Гермионой
2.
Расставим известные данные в круги Эйлера.
3. Найдем количество книг, которые прочитал только Гарри Поттер: 11 — 4 — 2 = 5 книг. 6. А теперь, чтобы узнать количество прочитанных книг только Роном, нужно из всего количества книг вычесть известное количество прочитанных книг: 25 ― (11+7)= 7 книг прочел только Рон.
R
P
G
4
7
2
7
5
Мы работаем отлично, Отдохнуть не прочь сейчас. И зарядка к нам привычно На урок приходит в класс. Выше руки, выше пятки Улыбнитесь веселей! Мы попрыгаем как зайки Сразу станем всех бодрей! Потянулись и вздохнули. Отдохнули? Отдохнули!
Встали и потянулись
Стряхнули руки
Подняли руки вверх
Работа по карточкам
Вариант 1
Из 40 учащихся шестых классов 32 любят молоко, 21 — лимонад, а 15 и молоко и лимонад.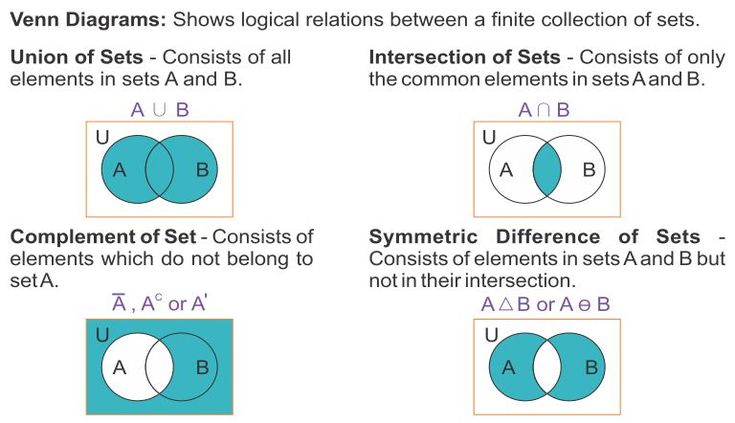
Сколько ребят не любят ни лимонад, ни молоко?
Вариант 2
12 шестиклассников любят читать детективы, 18-фантастику, трое с удовольствием читают и то и другое, а один вообще ничего не читает. Сколько учеников в шестом классе?
Ответ: 2 ученика
Ответ: 28 учеников.
№ 231,стр.90 ПРТ
В математической олимпиаде для 6-кл. участвовали 50 человек. Из них арифметическую задачу решили 40 человек, а геометрическую — 20.
Покажите на схеме решение задачи.
Г
А
10
30
10
Давайте обсудим
- Что называют объединением множеств?
Приведите пример.
2. Что называют пересечением множеств?
Приведите пример.
3. Пусть С-множество чисел, кратных 9, и D-множество чисел, кратных 3. Какое соотношение связывает эти множества?
4.
Понравилось вам использовать метод кругов Эйлера для решения задач?
12.2: Использование диаграмм Венна-Эйлера для проверки недействительности
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 22035
- Брэдли Х. Дауден
- Калифорнийский государственный университет Сакраменто
В логике классов мы можем создавать диаграммы, чтобы помочь нам проверить аргументы на достоверность. Однако прежде чем мы это сделаем, давайте улучшим наше умение рассуждать о дополнении классов, то есть о множестве всех вещей, не входящих в класс. Если вы американец, то как мы называем неамериканцев? Это «иностранец». Чем больше американцы путешествуют, тем больше они встречают неамериканцев.
Предполагая, что никто не может быть и евреем, и христианином, было бы верно сказать, что все евреи нехристиане, и верно сказать, что некоторые неевреи являются нехристианами, но было бы ложным сказать, что все неевреи — Христиане — евреи, и неверно говорить, что все нехристиане — неевреи. Вау! Поздравления и комплименты, если вы смогли тщательно понять сложности этих дополнений о классах. Если бы вы могли, вы могли бы правильно завершить эту проверку концепции.
Упражнение \(\PageIndex{1}\)
Мартин (на фото выше) не белый мужчина, если Мартин
a. белый не мужчина.
б. небелый мужчина,
c. небелый не мужчина.
д. любой из вышеперечисленных.
- Ответить
Ответ (г). Отвечать на подобные вопросы было бы намного проще, если бы у нас был какой-то метод с картинками или диаграммами, который показывал бы нам, что происходит. Может быть, вы можете изобрести один. Эйлер пытался сделать это еще в XVIII веке в Швейцарии.
Для построения диаграмм Венна-Эйлера необходим навык отрицания членов. Этот метод построения диаграмм помогает быстро оценить дедуктивную достоверность аргументов в логике классов. Это может привести вас к правильной оценке, когда аргумент слишком сложен для анализа в вашей голове. Представляя этот метод, мы сначала введем диаграммы для классов, затем обобщим метод, чтобы его можно было использовать для отображения того, истинны или ложны предложения о классах, а затем снова обобщим метод, чтобы его можно было использовать для демонстрации того, являются ли предложения о классах истинными или ложными. аргументы, использующие эти предложения, являются дедуктивно действительными.
Окружность ниже представляет собой диаграмму Эйлера класса яблок.
р
На этой двумерной диаграмме любая точка внутри круга представляет собой яблоко, а любая точка вне круга представляет собой не-яблоко, например мусульманина или карандаш. Обычай маркировки состоит в том, чтобы использовать заглавную букву для начала названия региона (класса) и строчную букву для имени конкретного члена региона (класса).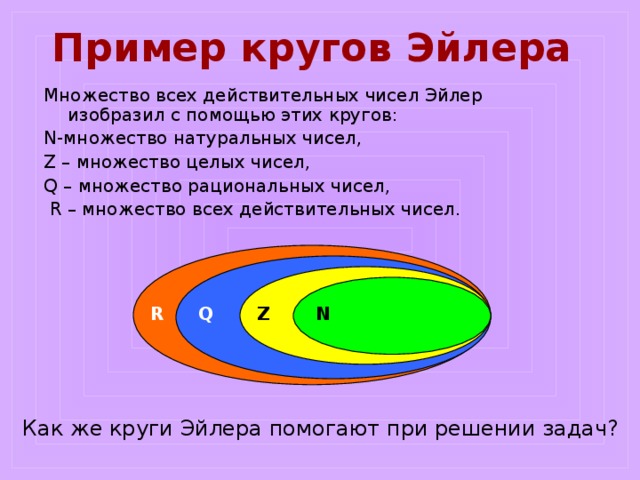
Маленькая буква «r» обозначает точку справа от круга, которая представляет конкретное не-яблоко, скажем, Томаса Эдисона, американского изобретателя и основателя General Electric Corporation. В форме региона нет ничего важного. Эллипс или прямоугольник подойдут, лишь бы было понятно, что в области, а что снаружи, то есть что в классе, а что нет. Размер круга также не важен. Мы также не обращаем внимания на перемещение диаграммы влево или вправо, вверх или вниз. Все эти изменения будут давать одну и ту же диаграмму в том, что касается логики классов.
Ниже приведена более сложная диаграмма, представляющая как класс яблок, так и класс фруктов. В реальном мире класс яблок полностью включен в более крупный класс фруктов. На диаграмме представлена картина этих отношений в реальном мире:
Приведенная выше диаграмма отражает истинность предложения «Все яблоки — фрукты», но вы можете рисовать диаграммы, которые не отображают то, как устроен мир.
Любая метка для области может находиться внутри или вне ее, при условии, что нет двусмысленности в отношении того, какая метка относится к какому региону.
Иногда мы будем называть овальные области «кругами», поскольку не обращаем внимания на разницу между кругом и эллипсом.
Вот диаграмма Эйлера, в которой утверждения вида «Нет А есть В» верны:
В этой диаграмме важно то, что две окружности не пересекаются (перекрываются). Окружности также не должны касаться друг друга, поскольку в этом случае будет сложно сказать, имеют ли два класса общий элемент.
Вот диаграмма Венна, показывающая ту же информацию, но менее интуитивно:
На диаграмме Венна все окружности должны взаимно перекрываться. Это не требуется для диаграмм Эйлера. Рассмотрим точки x, y и z на следующей диаграмме. Классы А и В пересекаются, то есть имеют общие элементы. Один из этих участников — y.
Точка x не принадлежит ни к классу A, ни к классу B. Она находится в дополнении каждого из них. Точка y находится и в A, и в B. Точка z находится в B, но не в A. Просмотрев диаграмму, вы можете увидеть, что некоторые элементы B находятся в A, а некоторые нет.
Однако вы не можете сказать, имеет ли A больше членов, чем B. Если область A больше, чем B на диаграмме, вы не можете сказать, имеет ли A больше членов, чем B. В этом отношении вы даже не можете сказать, является ли класс вообще не имеет членов. Однако теперь во всех диаграммах мы будем предполагать, что начинаем с непустых классов.
Вот диаграмма, представляющая реальные отношения между яблоками, фруктами, апельсинами, яблоками в Париже, яблоками в ресторанах в Париже и фруктами, принадлежащими нашему другу Хуану:
Для ясности, мы всегда будем использовать заглавные буквы или заглавные слова для обозначения классов вещей. Если мы хотим добавить информацию о том, что какой-то конкретный объект является членом одного из классов, мы будем использовать строчную букву для представления члена. На предыдущей диаграмме строчная буква а обозначает одно яблоко в моем холодильнике. Вы можете видеть, что буква а находится вне круга P; это показывает, что яблоко в моем холодильнике не из Парижа.
Обратите внимание, что сам Хуан не принадлежит ни к одному из классов на приведенной выше диаграмме; информация о Хуане содержится в определении J. Изучив диаграмму, вы можете сказать, что у Хуана нет парижских яблок (поскольку J и P не пересекаются), но яблоки у него есть (поскольку J пересекает A), владеет апельсинами (поскольку J пересекается с O) и владеет некоторыми другими неопределенными фруктами (поскольку J находится в F, но не все J находится в A или O).
Пусть A = граждане США, проживающие в Нью-Йорке, B = горожане, C = американцы. Вот диаграмма Эйлера, показывающая их отношения в реальном мире.
Вот как отобразить те же отношения на диаграмме Венна:
На диаграммах Венна заштрихованные области — это пустое множество; они ничего не содержат. При применении метода Венна к трем множествам три окружности должны пересекаться друг с другом, в отличие от диаграмм Эйлера.
Как бы вы нарисовали диаграмму, на которой верно утверждение, что некоторые яблоки из Канады, а некоторые нет? Это поможет:
C = класс вещей из Канады
А = сорт яблок
Шаблон предложения «Все A не являются B» верен на следующей диаграмме:
Обратите внимание, что это то же самое, что и диаграмма, которую вы нарисовали бы для «Нет А, а не В».
Логически эквивалентные предложения имеют одинаковые виды диаграмм — это ключевая идея классовой логики
Приведенная выше диаграмма представляла бы ложное предложение «Техасцы не являются американцами», если бы использовался следующий словарь:
A = техасцы
B = американцы
Хотя это предложение ложно в реальном мире, диаграмма показывает, каким был бы мир, если бы это предложение было истинным. То же самое делается, когда говорят, что диаграмма — это картина того, что верно в определенном «возможном мире», который не является реальным миром.
Упражнение \(\PageIndex{1}\)
Сделайте утверждение «Все техасцы неамериканцами» истинным на диаграмме, используя приведенный выше словарь для A и B.
- Ответить
Обратите внимание, что на этой диаграмме каждый техасец A находится за пределами Америки B и, следовательно, не является американцем. Так что этот возможный мир не является реальным миром.
Пусть A будет классом яблок. На двух приведенных ниже диаграммах предложение «Все яблоки — бананы» верно (хотя в реальном мире это предложение ложно):
.Но обратите внимание на разницу в двух диаграммах. В изображении слева некоторые бананы не являются яблоками. На схеме справа это не так. На второй диаграмме класс яблок и класс бананов — это один и тот же класс. Вместо этого диаграмма реальных отношений между яблоками и бананами выглядела бы так:
Упражнение \(\PageIndex{1}\)
Нарисуйте диаграмму яблок и фруктов, на которой неверно следующее предложение: «Все яблоки — фрукты». Предложение верно в реальном мире, но не в возможном мире, представленном на вашей диаграмме.
- Ответить
Существует несколько типов диаграмм, которые будут работать.
С таким предложением, как «Все яблоки — фрукты», у аналитика есть возможность трактовать его в логике классов или логике предложений. В логике классов это логически эквивалентно «Все вещи из класса яблок также являются вещами из класса фруктов». Это устанавливает отношения между двумя классами. В сентенциальной логике это предложение логически эквивалентно фразе «Если это яблоко, то это фрукт». Это устанавливает условную связь между двумя подпредложениями.
Теперь мы можем обобщить метод диаграмм на метод оценки дедуктивной достоверности аргументов при условии, что предложения, составляющие аргумент, описывают, как классы объектов связаны друг с другом. Метод диаграммы Венна-Эйлера для оценки аргументов работает только для дедуктивных аргументов в логике классов. Он показывает, что аргумент действителен, если нет диаграммы контрпримера к аргументу. По определению контрпример к аргументу — это возможная ситуация или интерпретация аргумента, показывающая, как он может иметь истинные посылки и ложный вывод.
Более конкретно вот как применить метод проверки на валидность в логике класса:
Переведите посылки и заключение аргумента в соответствующие предложения классовой логики. Ищите контрпример. То есть, попытайтесь изобразить эти предложения в логике классов так, чтобы посылки на диаграмме оказались истинными, а заключение — ложным. Если есть подобная диаграмма, то эта диаграмма контрпримера показывает, что аргумент дедуктивно недействителен. Однако, если все возможные диаграммы не приводят к контрпримеру, то аргумент объявляется дедуктивно верным.
Этот метод никогда не даст неправильного ответа, если вы на самом деле правильно изучили все возможные схемы. Аргумент действителен, если не существует контрпримера, а не только если вы не можете его найти. Может быть, вы не можете найти его, потому что не искали внимательно. Таким образом, применение метода диаграмм Венна-Эйлера рискованно, поскольку его ответ зависит от того, правы ли вы, когда говорите, что смотрели и уверены, что контрпримера не существует.
Чтобы увидеть технику в действии, давайте попробуем ее на следующем шаблоне аргумента:
Никакие A не являются B.
Никакие C не являются B.
Итак, никакие A не являются C.
Вот диаграмма, которая делает все предпосылки верными:
Ни один из кругов не пересекается и не содержится внутри другого. На этой диаграмме вывод верен. Можем ли мы заключить, что шаблон аргумента действителен? Нет, не из этой информации. Вместо этого мы должны были искать, чтобы убедиться, что нет диаграммы, которая делает посылки истинными, но заключение ложным. На самом деле есть такая схема:
Здесь заключение ложно, когда посылки верны, явный признак недействительности. Поэтому метод диаграммы объявляет шаблон аргумента недопустимым.
Упражнение \(\PageIndex{1}\)
Используйте метод диаграммы, чтобы показать правильность этого шаблона аргумента:
Все A являются B.
Все B являются C.
Итак, все A являются C.
- Ответить
Вот как можно нарисовать диаграмму истинности обеих предпосылок
Могут быть и другие схемы посылок: допустить, чтобы окружность А равнялась окружности В, или чтобы В равнялась С.
Однако во всех возможных схемах посылок вывод на схеме оказывается верным. Так что контрпример привести нельзя. Следовательно, метод Венна-Эйлера объявляет этот шаблон аргумента действительным.
Однако во всех возможных схемах посылок вывод на схеме оказывается верным. Так что контрпример привести нельзя. Следовательно, метод Венна-Эйлера объявляет этот шаблон аргумента действительным.Упражнение \(\PageIndex{1}\)
Используйте метод диаграммы для оценки правильности или недействительности этого аргумента. Интерпретируйте some как «по крайней мере один и, возможно, все».
Некоторые кошки относятся к кошачьим.
Некоторые животные относятся к кошачьим.
Итак, некоторые животные — кошки.
- Ответить
Аргумент недействителен; следующая диаграмма служит контрпримером:
Некоторые C являются F.
Некоторые A являются F.
Некоторые A являются C
При попытке найти логическую форму аргумента не всегда можно сказать, следует ли искать его форму в логике классов или в логике предложений. Поэкспериментируйте, чтобы увидеть, что будет работать.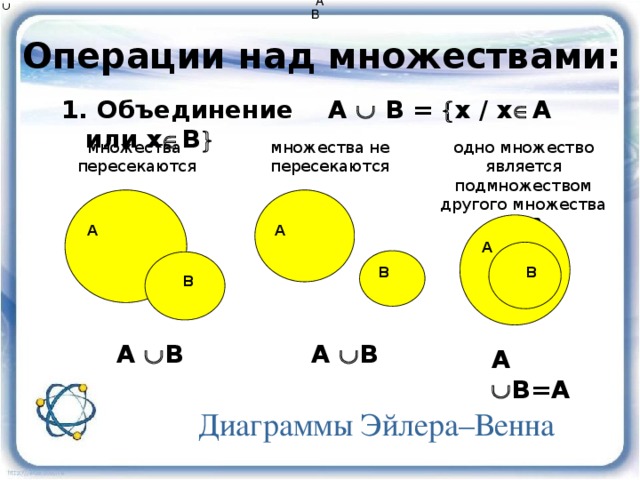
Некоторые аргументы имеют логические формы, которые не могут быть адекватно выражены в любом случае, и тогда к аргументу необходимо применить более мощную логику, такую как логика предикатов.
Кроме того, некоторые аргументы дедуктивно верны, хотя их валидность не зависит от логической формы, использующей какую-либо формальную логику. Вот пример:
Джон — холостяк.
Значит, он не женат.
Справедливость обусловлена не только формой, но и содержанием — в частности, тем фактом, что определение холостяка предполагает, что все холостяки не состоят в браке. Мы могли бы заставить этот аргумент быть действительным благодаря его логической форме в логике классов, если бы мы могли закодировать идею о том, что все холостяки не женаты в логике классов, и мы можем. Просто добавьте предпосылку: все холостяки не женаты. Действительные аргументы, не требующие вставки определений, называются формально действительными. Все формально верные аргументы верны дедуктивно, но обратное утверждение неверно.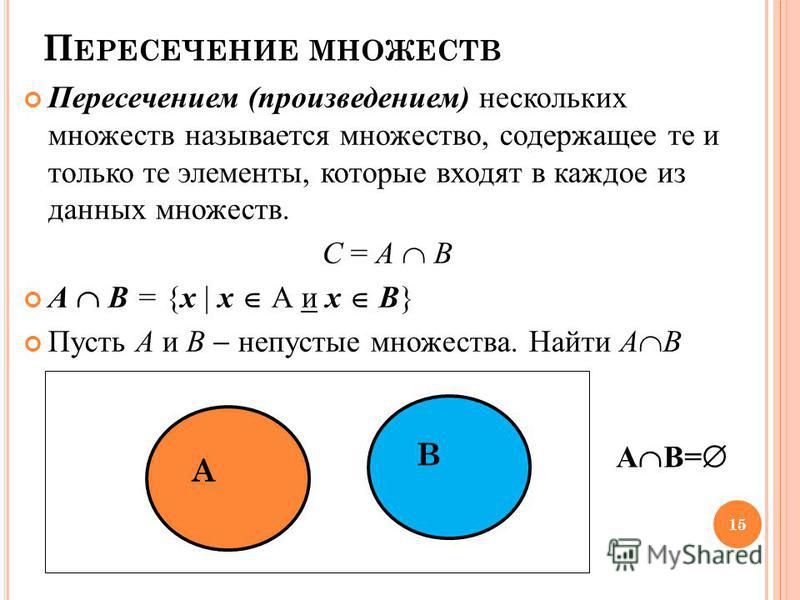
Однако в нашем курсе мы не будем обращать внимание на это тонкое различие. Если вы видите, что определение необходимо для того, чтобы сделать аргумент действительным, продолжайте вставлять его и не беспокойтесь о том, что это показывает, что ваш аргумент дедуктивно действителен, но не формально действителен.
Диаграммы Венна-Эйлера могут использоваться не только для проверки достоверности. Если два предложения могут иметь одну и ту же диаграмму, то они логически эквивалентны в логике классов. Диаграммы также можно использовать для проверки согласованности. Если есть диаграмма, на которой каждое предложение в наборе предложений оказывается истинным, то набор логически непротиворечив .
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Брэдли Х. Дауден
- Лицензия
- CC BY-NC-SA
- Показать оглавление
- нет
- Теги
- Диаграмма Эйлера
Дауденпутей и схем Эйлера
\(\def\d{\displaystyle}
\def\курс{Математика 228}
\ новая команда {\ f} [1] {\ mathfrak # 1}
\ новая команда {\ s} [1] {\ mathscr # 1}
\def\N{\mathbb N}
\def\B{\mathbf{B}}
\def\circleA{(-.5,0) круг (1)}
\ деф \ Z {\ mathbb Z}
\def\circleAlabel{(-1.5,.6) узел[выше]{$A$}}
\def\Q{\mathbb Q}
\def\circleB{(.5,0) круг (1)}
\def\R{\mathbb R}
\def\circleBlabel{(1.5,.6) узел[выше]{$B$}}
\def\C{\mathbb C}
\def\circleC{(0,-1) круг (1)}
\def\F{\mathbb F}
\def\circleClabel{(.5,-2) узел[справа]{$C$}}
\def\А{\mathbb А}
\def\twosetbox{(-2,-1.
{-1}}
\def\nrml{\triangleleft}
\ деф \ ст {:}
\ деф \ ~ {\ широкая тильда}
\def\rem{\mathcal R}
\def\sigalg{$\sigma$-алгебра }
\def\Гал{\mbox{Гал}}
\def\iff{\leftrightarrow}
\def\If{\Leftrightarrow}
\ деф \ земля {\ клин}
\def\И{\bigwedge}
\защита\вход{\вход}
\def\AAnd{\d\bigwedge\mkern-18mu\bigwedge}
\def\Ви{\bigvee}
\def\VVee{\d\Vee\mkern-18mu\Vee}
\ деф \ имп {\ стрелка вправо}
\def\Imp{\Rightarrow}
\def\Fi{\Leftarrow}
\def\var{\mbox{var}}
\def\Th{\mbox{Th}}
\защита\вход{\вход}
\def\sat{\mbox{Sat}}
\def\con{\mbox{Con}}
\def\iffmodels{\bmodels\models}
\def\dbland{\bigwedge \!\!\bigwedge}
\def\дом{\mbox{дом}}
\def\rng{\mbox{диапазон}}
\def\isom{\cong}
\DeclareMathOperator{\wgt}{wgt}
\newcommand{\vtx}[2]{узел[заливка,круг,внутренний интервал=0pt, минимальный размер=4pt,метка=#1:#2]{}}
\ новая команда {\ va} [1] {\ vtx {выше} {# 1}}
\ новая команда {\ vb} [1] {\ vtx {ниже} {# 1}}
\ новая команда {\ vr} [1] {\ vtx {право} {# 1}}
\ новая команда {\ vl} [1] {\ vtx {слева} {# 1}}
\renewcommand{\v}{\vtx{выше}{}}
\def\circleA{(-.
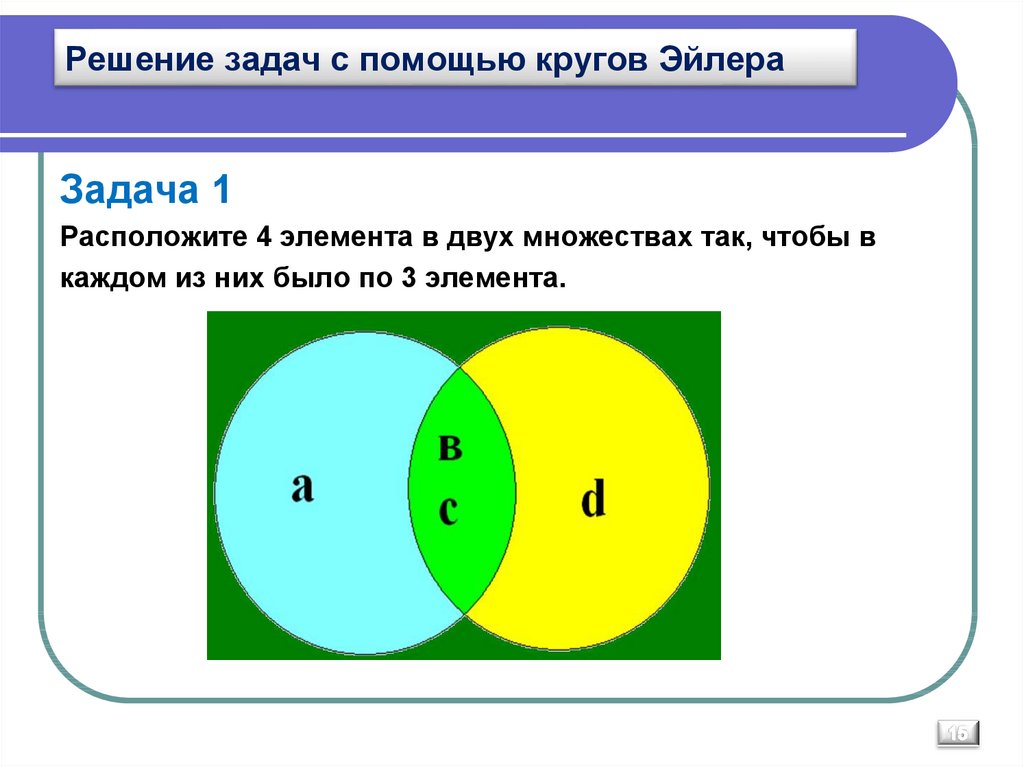5,0) круг (1)}
\def\circleAlabel{(-1.5,.6) узел[выше]{$A$}}
\def\circleB{(.5,0) круг (1)}
\def\circleBlabel{(1.5,.6) узел[выше]{$B$}}
\def\circleC{(0,-1) круг (1)}
\def\circleClabel{(.5,-2) узел[справа]{$C$}}
\def\twosetbox{(-2,-1.4) прямоугольник (2,1.4)}
\def\threesetbox{(-2.5,-2.4) прямоугольник (2.5,1.4)}
\def\ansfilename{практика-ответы}
\def\shadowprops{{fill=black!50,shadow xshift=0.5ex,shadow yshift=0.5ex,path fading={круг с размытым краем 10 процентов}}}
\ новая команда {\ hexbox} [3] {
\def\x{-cos{30}*\r*#1+cos{30}*#2*\r*2}
\def\y{-\r*#1-sin{30}*\r*#1}
\рисовать (\х,\у) +(90:\r) — +(30:\r) — +(-30:\r) — +(-90:\r) — +(-150:\r) — +(150: \r) — цикл;
\draw (\x,\y) узел{#3};
}
\renewcommand{\bar}{\overline}
\newcommand{\card}[1]{\left| #1 \справа|}
\newcommand{\twoline}[2]{\begin{pmatrix}#1 \\ #2 \end{pmatrix}}
\новая команда{\lt}{<}
\новая команда{\gt}{>}
\newcommand{\amp}{&}
\)
Расследуй!35
Путь Эйлера в графе или мультиграфе — это обход графа, в котором каждое ребро используется ровно один раз.
Схема Эйлера — это путь Эйлера, который начинается и заканчивается в одной и той же вершине. Наша цель — найти быстрый способ проверить, имеет ли граф (или мультиграф) эйлеров путь или цепь.
Какие из приведенных ниже графов имеют пути Эйлера? Какие имеют схемы Эйлера?
Перечислите степени каждой вершины приведенных выше графов. Есть ли связь между степенями и существованием эйлеровых путей и контуров?
Может ли граф с вершиной степени 1 иметь эйлеров цикл? Если да, нарисуйте один. Если нет, объясните почему. Как насчет пути Эйлера?
Что если каждая вершина графа имеет степень 2. Существует ли путь Эйлера? Цепь Эйлера? Нарисуйте несколько графиков.
Ниже представлена часть графика. Даже если вы можете видеть только некоторые вершины, можете ли вы сделать вывод, будет ли граф иметь эйлеров путь или цепь?
Если мы начнем с вершины и проследим вдоль ребер, чтобы добраться до других вершин, мы создадим обход по графу.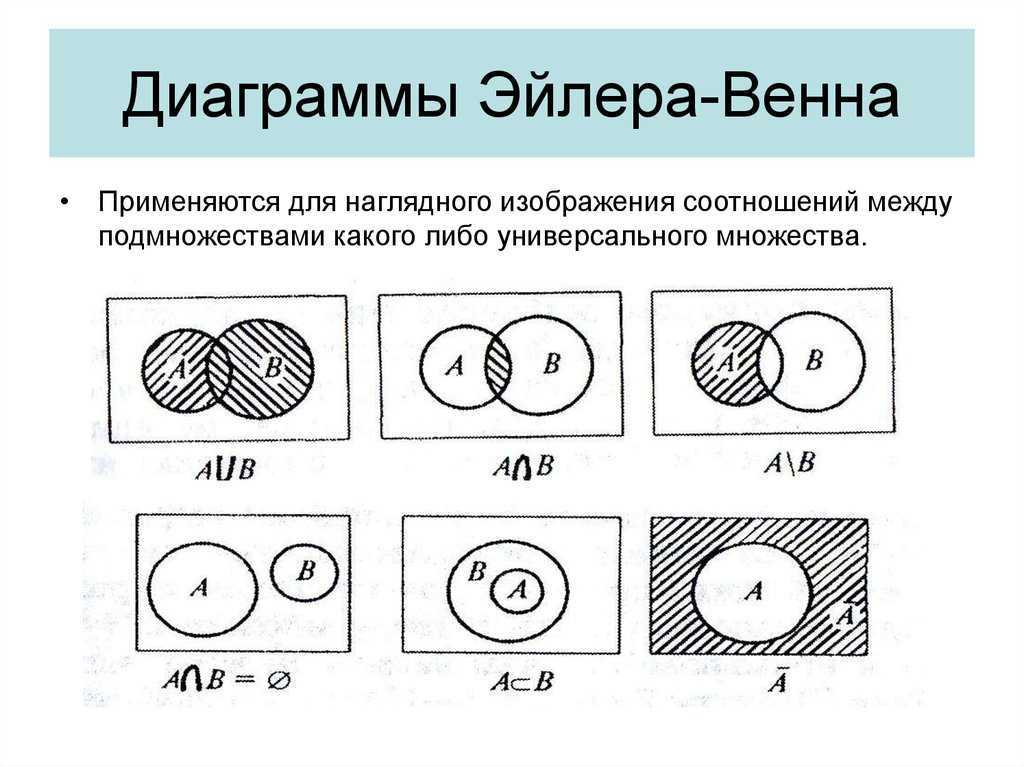
Точнее ходить в графе — это последовательность вершин, такая, что каждая вершина в последовательности смежна с вершинами до и после нее в последовательности. Если блуждание проходит по каждому ребру ровно один раз, то блуждание называется эйлеровым путем (или эйлеровым обходом ). Если, кроме того, начальная и конечная вершины совпадают (таким образом, вы проходите по каждому ребру ровно один раз и заканчиваете там, где начали), то обход называется эйлеровым циклом (или эйлеровым туром ). Конечно, если граф несвязен, нет никакой надежды найти такой путь или цепь. В оставшейся части этого раздела предположим, что все обсуждаемые графы связаны.
Задача о мостах Кёнигсберга на самом деле является вопросом о существовании эйлеровых путей. Будет маршрут, который пересекает каждый мост ровно один раз, если и только если граф ниже имеет путь Эйлера:
Этот граф достаточно мал, чтобы мы могли проверить все возможные обходы, не использующие повторно ребра, и при этом убедиться, что эйлерова пути не существует (не говоря уже об эйлеровом цикле).
На небольших графах, у которых есть путь Эйлера, найти его обычно нетрудно. Наша цель — найти быстрый способ проверить, есть ли в графе эйлерова путь или цепь, даже если граф довольно большой.
Один из способов гарантировать, что граф , а не имеет эйлерову схему, состоит в том, чтобы включить «шип», вершину степени 1.
Вершина \(a\) имеет степень 1, и если вы попытаетесь построить эйлеров обход, вы увидите, что застрянете в вершине. Это тупик. То есть, если вы не начнете там. Но тогда уже нет возможности вернуться, поэтому нет надежды найти эйлерову схему. Однако существует путь Эйлера. Он начинается в вершине \(a\text{,}\) и зацикливается вокруг треугольника. Вы закончите в вершине степени 3.
Вы сталкиваетесь с похожей проблемой всякий раз, когда у вас есть вершина любой нечетной степени. Если вы начнете с такой вершины, вы не сможете там закончить (после прохождения каждого ребра ровно один раз). После использования одного ребра для выхода из начальной вершины у вас останется четное количество ребер, исходящих из вершины.
Половину из них можно использовать для возврата в вершину, а другую половину — для выхода. Итак, вы возвращаетесь, а затем уходите. Вернитесь, затем уходите. Единственный способ израсходовать все ребра — использовать последнее, оставив вершину. С другой стороны, если у вас есть вершина с нечетной степенью, в которой вы не начинаете путь, то в конечном итоге вы застрянете в этой вершине. Путь будет использовать пары ребер, инцидентных вершине, чтобы войти и выйти снова. В конце концов, все эти ребра, кроме одного, будут израсходованы, останется только ребро, по которому можно добраться, и больше не останется ни одного ребра, по которому можно было бы уйти.
Все это говорит о том, что если в графе есть путь Эйлера и две вершины с нечетной степенью, то путь Эйлера должен начинаться в одной из вершин нечетной степени и заканчиваться в другой. В такой ситуации каждая другая вершина должна иметь четную степень , поскольку нам нужно равное количество ребер, чтобы попасть в эти вершины и выйти из них.
Как у нас может быть схема Эйлера? В графе не может быть вершины с нечетной степенью, поскольку путь Эйлера должен был бы начинаться там или заканчиваться там, но не и то, и другое. Таким образом, чтобы граф имел эйлеров цикл, все вершины должны иметь четную степень.
Верно и обратное: если все вершины графа имеют четную степень, то граф имеет эйлеров цикл, а если ровно две вершины с нечетной степенью, то граф имеет эйлеров путь. Доказать это немного сложно, но основная идея состоит в том, что вы никогда не застрянете, потому что для каждого «входящего» ребра в каждой вершине есть «исходящее» ребро. Если вы попытаетесь создать путь Эйлера и пропустите несколько ребер, вы всегда сможете «склеить» схему, используя ребра, которые вы ранее пропустили.
Эйлеровы пути и схемы
Поскольку мосты Кенигсбергского графа имеют все четыре вершины с нечетной степенью, эйлерова пути через граф не существует. Таким образом, горожане не могут пересечь каждый мост ровно по одному разу.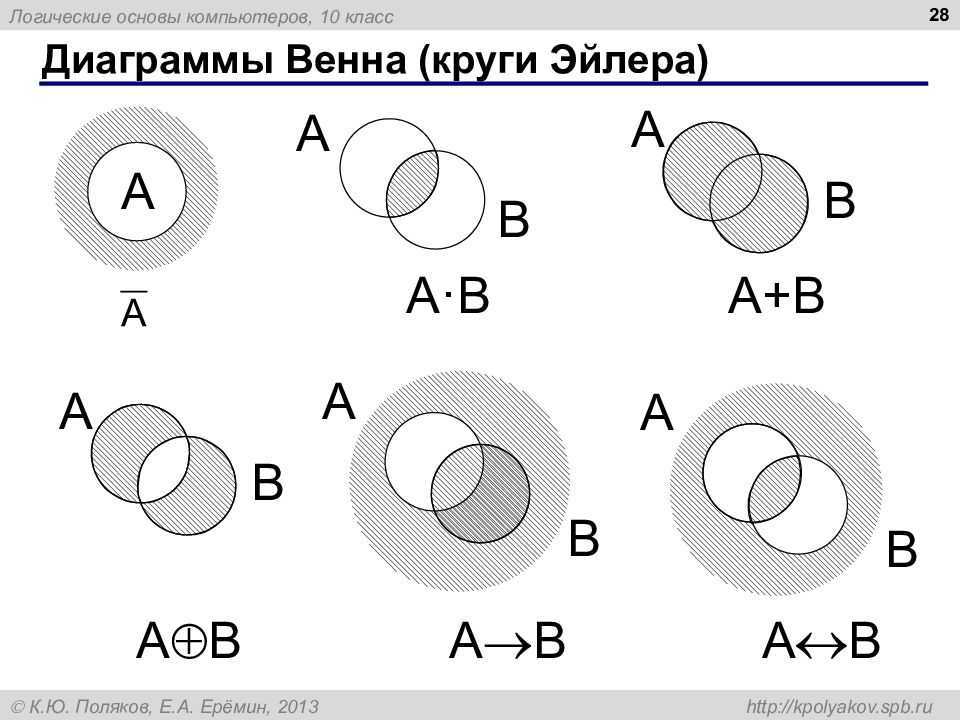
ПодразделГамильтон Пути
¶Предположим, вы хотите совершить поездку по Кёнигсбергу таким образом, чтобы вы посетили каждую часть суши (два острова и оба берега) ровно один раз. Это можно сделать. В терминах теории графов мы спрашиваем, существует ли путь, который посещает каждую вершину ровно один раз. Такой путь называется Гамильтонов путь (или Гамильтонов путь ). Мы могли бы также рассмотреть циклов Гамильтона , которые являются путями Хэмлитона, которые начинаются и заканчиваются в одной и той же вершине.
Пример 4.4.1
Определите, есть ли на приведенных ниже графах путь Гамильтона.
Решение
Граф слева имеет путь Гамильтона (на самом деле много разных), как показано здесь:
Граф справа не имеет пути Гамильтона. Вам нужно будет посетить каждую из «внешних» вершин, но как только вы посетите одну из них, вы застрянете.
Обратите внимание, что этот граф не имеет пути Эйлера, хотя есть графы с путями Эйлера, но нет путей Гамильтона.
Похоже, что нахождение путей Гамильтона будет проще, потому что графы часто имеют больше ребер, чем вершин, поэтому требуется выполнить меньше требований. Однако никто не знает, правда ли это. Не существует известного простого теста на наличие в графе пути Гамильтона. Для небольших графов это не проблема, но по мере роста размера графа становится все труднее и труднее проверять, существует ли путь Гамильтона. На самом деле, это пример вопроса, который, насколько нам известно, слишком сложен для решения компьютеров; это пример NP-полной задачи.
ПодразделУпражнения
¶1
Вы и ваши друзья хотите совершить путешествие по юго-западу на машине. Вы посетите девять штатов ниже, со следующим довольно странным правилом: вы должны пересечь каждую границу между соседними штатами ровно один раз (так, например, вы должны пересечь границу Колорадо-Юта ровно один раз).
Ты можешь сделать это? Если да, имеет ли значение, где вы начнете свое путешествие? Какой факт из теории графов решает эту проблему?
Решение
Это вопрос о нахождении путей Эйлера. Нарисуйте граф с вершиной в каждом состоянии и соедините вершины, если их состояния имеют общую границу. Ровно две вершины будут иметь нечетную степень: вершины для Невады и Юты. Таким образом, вы должны начать свое путешествие в одном из этих штатов, а закончить его в другом.
2
Какие из следующих графов содержат путь Эйлера? Какие из них содержат схему Эйлера?
- \(К_4\)
- \(К_5\текст{.}\)
- \(К_{5,7}\)
- \(К_{2,7}\)
- \(С_7\)
- \(P_7\)
Решение
- \(K_4\) не имеет эйлерова пути или цепи.
- \(K_5\) имеет эйлерову схему (а значит, и эйлеров путь).
- \(K_{5,7}\) не имеет эйлерова пути или схемы.
- \(K_{2,7}\) имеет эйлеров путь, но не эйлерову схему.
- \(C_7\) имеет схему Эйлера (это граф цепи!)
- \(P_7\) имеет путь Эйлера, но не имеет схемы Эйлера.
3
Эдвард А. Маус только что закончил свой новый дом. План этажа показан ниже:
Эдвард хочет провести экскурсию по своей новой квартире подружке-мышке. Могут ли они пройти через каждый дверной проем ровно один раз? Если да, то в каких комнатах они должны начинать и заканчивать экскурсию? Объяснять.
Можно ли обойти дом, посетив каждую комнату ровно один раз (не обязательно через каждый дверной проем)? Объяснять.
Через несколько мышиных лет Эдвард решает перестроиться. Он хотел бы добавить несколько новых дверей между комнатами, которые у него есть. Конечно, он не может добавить двери снаружи дома. Может ли в каждой комнате быть нечетное количество дверей? Объяснять.
4
Для каких \(n\) граф \(K_n\) содержит эйлерову схему? Объяснять.
Решение
Когда \(n\) нечетно, \(K_n\) содержит схему Эйлера.
Это связано с тем, что каждая вершина имеет степень \(n-1\text{,}\), поэтому нечетное \(n\) приводит к тому, что все степени четные.
5
Для каких \(m\) и \(n\) граф \(K_{m,n}\) содержит путь Эйлера? Цепь Эйлера? Объяснять.
Решение
Если и \(m\), и \(n\) четны, то \(K_{m,n}\) имеет эйлерову схему. Когда оба нечетны, пути или цепи Эйлера не существует. Если одно равно 2, а другое нечетно, то существует эйлерова путь, но не эйлерова схема.
6
Для каких \(n\) \(K_n\) содержит путь Гамильтона? Цикл Гамильтона? Объяснять.
Решение
Все значения \(n\text{.}\) В частности, \(K_n\) содержит \(C_n\) в качестве подгруппы, которая представляет собой цикл, включающий каждую вершину.
7
Для каких \(m\) и \(n\) граф \(K_{m,n}\) содержит путь Гамильтона? Цикл Гамильтона? Объяснять.
Решение
Пока \(|m-n| \le 1\text{,}\) граф \(K_{m,n}\) будет иметь путь Гамильтона.
Чтобы иметь цикл Гамильтона, мы должны иметь \(m=n\text{.}\)
8
В Кенигсберг приехал строитель мостов и хочет добавить мосты так, чтобы можно было проехать по каждому мосту ровно один раз. Сколько мостов нужно построить?
Решение
Если мы построим один мост, у нас может быть путь Эйлера. Для схемы Эйлера необходимо построить два моста.
9
Ниже приведен график дружбы между группой студентов (каждая вершина — студент, а каждое ребро — дружба). Возможно ли, чтобы ученики сидели за круглым столом так, чтобы каждый ученик сидел между двумя друзьями? Какое отношение этот вопрос имеет к путям?
Решение
Мы ищем гамильтонов цикл, и на этом графе он есть:
10
Предположим, что граф имеет путь Гамильтона. Какое максимальное количество вершин степени один может иметь граф? Объясните, почему ваш ответ правильный.
Найдите граф, в котором нет пути Гамильтона, даже если ни одна вершина не имеет степени один.
