Равнобедренный треугольник
Что такое треугольник?
Треугольник — это замкнутая двумерная фигура, имеющая три стороны, три вершины и три угла. Это самая простая форма многоугольника. Треугольник можно составить, соединив любые три точки таким образом, чтобы отрезки прямой соединяли друг друга конец к концу. Три отрезка, соединяющие точки, являются сторонами треугольника, точка пересечения двух прямых называется вершиной, а пространство между ними называется углом. Также важно знать, что сумма всех внутренних углов треугольника всегда равна 180 градусам.
[Изображение будет загружено в ближайшее время]
Треугольники — простейшая форма многоугольника. Значение слова «Многоугольник» — это плоская фигура, состоящая из множества отрезков, соединенных встык. Одиночные или двойные отрезки вместе никогда не могут образовать многоугольник. Линия, соединяющая любые три точки, может образовывать треугольник, или любые три сегмента линии, соединенные друг с другом встык, также образуют треугольник. Треугольник — это трехсторонняя замкнутая двумерная фигура, имеющая три вершины и три угла.
Треугольник — это трехсторонняя замкнутая двумерная фигура, имеющая три вершины и три угла.
Типы треугольников:
Треугольники можно классифицировать на основе их размера, а также углов.
Классификация треугольников на основе их сторон выглядит следующим образом:
Равносторонний треугольник: Равносторонний треугольник — это треугольник, у которого все три стороны равны.
Равнобедренный треугольник: Равнобедренный треугольник — это треугольник, две стороны которого равны.
Разносторонний треугольник: Разносторонний треугольник — это треугольник, все три стороны которого не равны.
Классификация треугольников на основе их углов выглядит следующим образом:
Остроугольный треугольник: треугольник, все внутренние углы которого меньше 900.

Прямоугольный треугольник: A треугольник, у которого один внутренний угол равен 900.
Тупоугольный треугольник: Треугольник, один из внутренних углов которого больше 900.
Что такое равнобедренный треугольник?
Треугольник с двумя сторонами одинаковой длины называется равнобедренным. В равнобедренном треугольнике углы, прилежащие к равным сторонам, равны. В приведенном ниже треугольнике две стороны равны 5 дюймам, а одна сторона равна 3 дюймам. Таким образом, это равнобедренный треугольник.
[Изображение будет загружено в ближайшее время]
Свойства равнобедренного треугольника:
- 9001 8 Две стороны равнобедренного треугольника равны друг другу.
[Изображение будет загружено в ближайшее время]
На приведенном выше рисунке стороны AB и AC имеют равную длину «a».
Неравная сторона равнобедренного треугольника называется основанием.
Два угла, противоположные равным сторонам, равны друг другу. Значит, у него два равных угла при основании. ∠ B и ∠ C равномерны.
Угол при вершине — это угол, не равный двум углам при основании, которые равны.
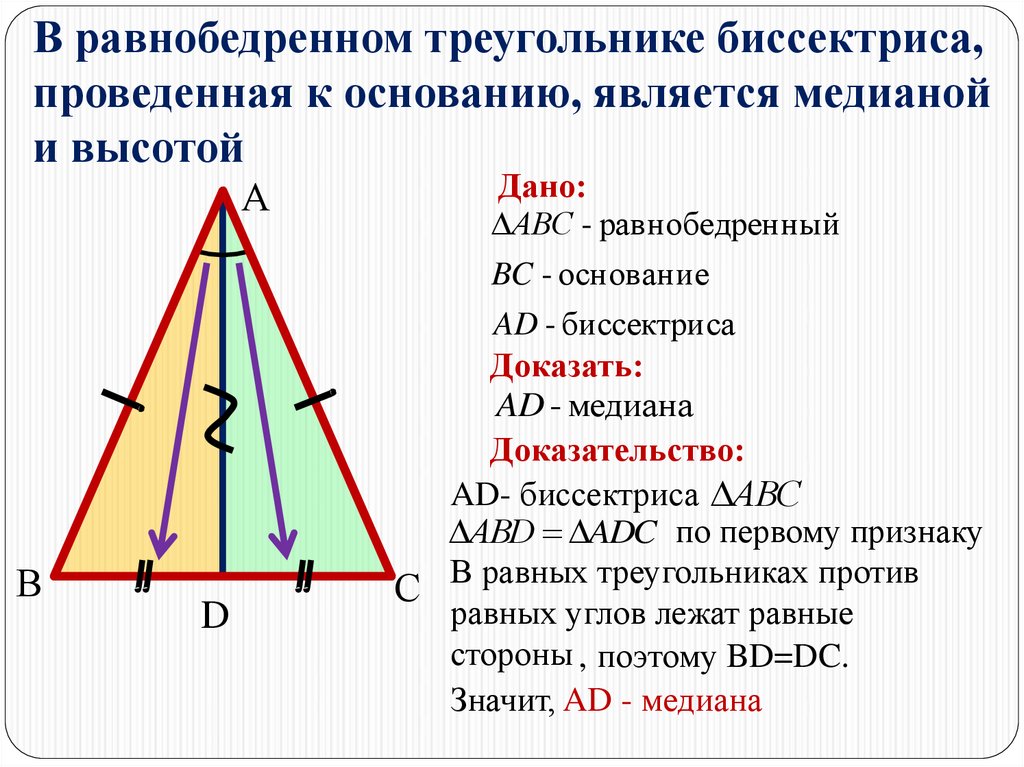
Высота, проведенная из вершины равнобедренного треугольника, делит основание на две равные части, а также делит угол при вершине на два равных угла.
Площадь равнобедренного треугольника = ½ × основание × высота
Периметр равнобедренного треугольника = сумма всех трех сторон
Третий неравный угол равнобедренного треугольника может быть острым или тупым.

Центр описанной окружности равнобедренного треугольника лежит внутри треугольника, если все три угла трех треугольников острые.
Стороны треугольника являются хордами описанной окружности.
Если один из углов равен 90 градусов, то центр описанной окружности лежит вне треугольника.
Центроид — это пересечение медиан равнобедренного треугольника.
Медиана, проведенная из вершины, делит треугольник под прямым углом.
Биссектрисы равнобедренного треугольника пересекаются в центре описанной окружности.
Биссектрисы равнобедренного треугольника пересекаются в центре вписанной стороны.
Окружность, нарисованная с центром в центре, касается трех сторон треугольника внутри.

Каждая медиана делит равнобедренный треугольник на два равных треугольника, имеющих одинаковую площадь.
Площадь треугольника можно оценить:
Если известны меры одного угла и одной стороны
Если даны три стороны треугольника.
Если даны две стороны равнобедренного треугольника и углы между ними.
Соединение середины трех сторон делит треугольник на 4 меньших треугольника той же площади.
Когда нарисована окружность с диаметром, равным основанию:
Для тупоугольного равнобедренного треугольника вершина лежит внутри окружности.

В прямоугольном равнобедренном треугольнике вершина лежит на окружности.
В остроугольном равнобедренном треугольнике вершина лежит вне треугольника.
Когда вершина средней точки принимается за радиус и рисуется круг с серединой основания в качестве центра.
Для остроугольного равнобедренного треугольника вершины основания лежат внутри окружности.
Для прямоугольного равнобедренного треугольника вершины основания лежат на окружности
Для тупоугольного равнобедренного треугольника вершины основания лежат вне окружности.
В прямоугольном равнобедренном треугольнике высота гипотенузы всегда равна половине длины гипотенузы.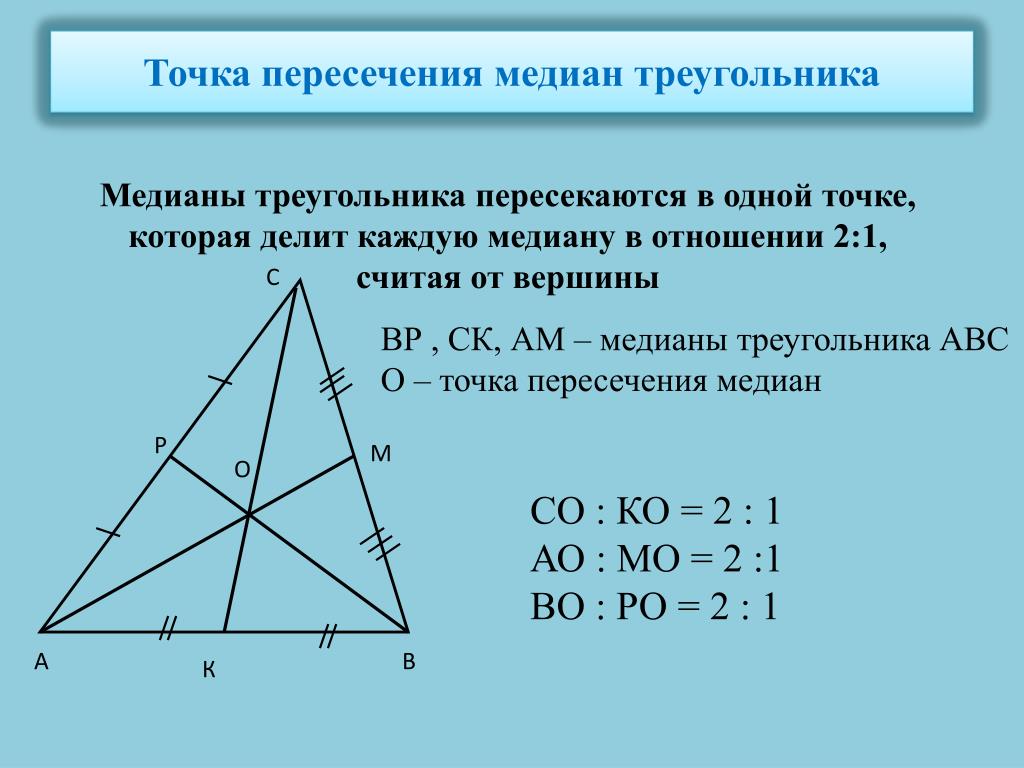
В прямоугольном равнобедренном треугольнике центр описанной окружности лежит на гипотенузе, а радиус описанной окружности равен половине длины гипотенузы. 92}}}{4}} \]
Периметр треугольника?
Периметр треугольника равен сумме длин его трех сторон.
[Изображение будет загружено в ближайшее время]
Периметр треугольника (P) = Сторона1 + Сторона2 +Сторона3
Здесь a, b и c — три стороны треугольника.
Таким образом, периметр треугольника (P) = a+b+c
Периметр равнобедренного треугольника
Две стороны равнобедренного треугольника равны.
Итак, периметр равнобедренного треугольника = 2a + c
[Изображение будет загружено в ближайшее время]
Пример: В треугольнике ABC две стороны треугольника (a) = 20 см
Основание (c) = 8 см
Периметр = 2(20) + 8
= 48 см.
Как найти высоту треугольника (прямоугольного, равностороннего, равнобедренного)
Автор:
Malcolm McKinsey