Mathway | Популярные задачи
| 1 | Найти объем | сфера (5) | |
| 2 | Найти площадь | окружность (5) | |
| 3 | Найти площадь поверхности | сфера (5) | |
| 4 | Найти площадь | окружность (7) | |
| 5 | Найти площадь | окружность (2) | |
| 6 | Найти площадь | окружность (4) | |
| 7 | Найти площадь | окружность (6) | |
| 8 | сфера (4) | | |
| 9 | Найти площадь | окружность (3) | |
| 10 | Вычислить | (5/4(424333-10220^2))^(1/2) | |
| 11 | Разложить на простые множители | 741 | |
| 12 | Найти объем | сфера (3) | |
| 13 | Вычислить | 3 квадратный корень из 8*3 квадратный корень из 10 | |
| 14 | Найти площадь | окружность (10) | |
| 15 | Найти площадь | окружность (8) | |
| 16 | Найти площадь поверхности | сфера (6) | |
| 17 | Разложить на простые множители | 1162 | |
| 18 | Найти площадь | окружность (1) | |
| 19 | Найти длину окружности | окружность (5) | |
| 20 | Найти объем | сфера (2) | |
| 21 | Найти объем | сфера (6) | |
| 22 | Найти площадь поверхности | сфера (4) | |
| 23 | Найти объем | сфера (7) | |
| 24 | Вычислить | квадратный корень из -121 | |
| 25 | Разложить на простые множители | 513 | |
| 26 | Вычислить | квадратный корень из 3/16* квадратный корень из 3/9 | |
| 27 | Найти объем | прямоугольный параллелепипед (2)(2)(2) | |
| 28 | Найти длину окружности | окружность (6) | |
| 29 | Найти длину окружности | окружность (3) | |
| 30 | Найти площадь поверхности | сфера (2) | |
| 31 | Вычислить | ||
| 32 | Найти объем | прямоугольный параллелепипед (5)(5)(5) | |
| 33 | Найти объем | прямоугольный параллелепипед (10)(10)(10) | |
| 34 | Найти длину окружности | окружность (4) | |
| 35 | Перевести в процентное соотношение | 1. 2-4*-1+2 2-4*-1+2 | |
| 45 | Разложить на простые множители | 228 | |
| 46 | Вычислить | 0+0 | |
| 47 | Найти площадь | окружность (9) | |
| 48 | Найти длину окружности | окружность (8) | |
| 49 | Найти длину окружности | окружность (7) | |
| 50 | Найти объем | сфера (10) | |
| 51 | Найти площадь поверхности | сфера (10) | |
| 52 | Найти площадь поверхности | сфера (7) | |
| 53 | Определить, простое число или составное | 5 | |
| 54 | 3/9 | ||
| 55 | Найти возможные множители | 8 | |
| 56 | Вычислить | (-2)^3*(-2)^9 | |
| 57 | Вычислить | 35÷0. 2 2 | |
| 60 | Преобразовать в упрощенную дробь | 2 1/4 | |
| 61 | Найти площадь поверхности | сфера (12) | |
| 62 | Найти объем | сфера (1) | |
| 63 | Найти длину окружности | окружность (2) | |
| 64 | Найти объем | прямоугольный параллелепипед (12)(12)(12) | |
| 65 | Сложение | 2+2= | |
| 66 | Найти площадь поверхности | прямоугольный параллелепипед (3)(3)(3) | |
| 67 | Вычислить | корень пятой степени из 6* корень шестой степени из 7 | |
| 68 | Вычислить | 7/40+17/50 | |
| 69 | Разложить на простые множители | 1617 | |
| 70 | Вычислить | 27-( квадратный корень из 89)/32 | |
| 71 | Вычислить | 9÷4 | |
| 72 | Вычислить | 2+ квадратный корень из 21 | |
| 73 | Вычислить | -2^2-9^2 | |
| 74 | Вычислить | 1-(1-15/16) | |
| 75 | Преобразовать в упрощенную дробь | 8 | |
| 76 | Оценка | 656-521 | |
| 77 | Вычислить | 3 1/2 | |
| 78 | Вычислить | -5^-2 | |
| 79 | Вычислить | 4-(6)/-5 | |
| 80 | Вычислить | 3-3*6+2 | |
| 81 | Найти площадь поверхности | прямоугольный параллелепипед (5)(5)(5) | |
| 82 | Найти площадь поверхности | сфера (8) | |
| 83 | Найти площадь | окружность (14) | |
| 84 | Преобразовать в десятичную форму | 11/5 | |
| 85 | Вычислить | 3 квадратный корень из 12*3 квадратный корень из 6 | |
| 86 | Вычислить | (11/-7)^4 | |
| 87 | Вычислить | (4/3)^-2 | |
| 88 | Вычислить | 1/2*3*9 | |
| 89 | Вычислить | 12/4-17/-4 | |
| 90 | Вычислить | 2/11+17/19 | |
| 91 | Вычислить | 3/5+3/10 | |
| 92 | Вычислить | 4/5*3/8 | |
| 93 | Вычислить | 6/(2(2+1)) | |
| 94 | Упростить | квадратный корень из 144 | |
| 95 | Преобразовать в упрощенную дробь | 725% | |
| 96 | Преобразовать в упрощенную дробь | 6 1/4 | |
| 97 | Вычислить | 7/10-2/5 | |
| 98 | Вычислить | 6÷3 | |
| 99 | Вычислить | 5+4 | |
| 100 | Вычислить | квадратный корень из 12- квадратный корень из 192 |
Как перевести десятичную дробь в обыкновенную
- org/BreadcrumbList»>
- Альфашкола
- Статьи
- Как перевести десятичную дробь в обыкновенную: 2 способа
Способ 1
Действуем по алгоритму:
- Придадим десятичной дроби вид обычной: поместим десятичную дробь в числитель, а в знаменатель поставим 1 (при делении на 1 число не меняется):
- 0,35 = 0,35/1
- 2,34 = 2,34/1
- Числитель и знаменатель умножим на число с таким количеством нулей, которое поможет убрать запятую в десятичной дроби (если после запятой десятые – умножим на 10, если сотые – на 100, если тысячные – на 1000 и т.д.). Не забываем параллельно добавлять нули и в знаменателе:
- 0,35 = 0,35/1 = 3,5/10 = 35/100
- 2,34 = 2,34/1 = 23,4/10 = 234/100
- Сокращаем числитель и знаменатель – делим их на общее кратное:
- 0,35 = 35/100 разделим на 5, получим 6/20 – можно разделить еще на 2 и получим 3/10 – это и будет наша итоговая обычная дробь равнозначная десятичной 0,35.

- 2,34 = 234/100 разделим на общее кратное 2 и получим 117/50 – то есть 2 целых 17/50 и есть наша итоговая обычная дробь равнозначная десятичной 2,34.
Важно!
Если у вас пример с отрицательным числом, не забывайте про минус – это частая ошибка при решении подобных примеров.
Способ 2
Действуем так:
- Считаем цифры после запятой в десятичной дроби. Например, в числе 0,25 две цифры после запятой, в числе 1,0211 – четыре. Далее будем называть число цифр после запятой буквой n.
- Перепишем нашу дробь в виде: а/10 n, где а – это наше изначальное число десятичной дроби (например, 0,25), а n – количество цифр после запятой (то есть 2). Выходит, нам нужно поделить первоначальную десятичную дробь на число с n нулями: 0,25/(10*2)= 0,0125
- Теперь предельно сокращаем – находим общие кратные и получаем:
125/10000 делим на 25 = 5/40 поделим еще на 5 = 1/8
Наша простая дробь – 1/8.
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Людмила Владимировна Коченова
Репетитор по математике
Стаж (лет)
Образование:
Южно-Российский государственный политехнический университет им. М.И. Платова
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Екатерина Владимировна Широкова
Репетитор по математике
Стаж (лет)
Образование:
Национальный исследовательский Томский государственный университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Елена Анатольевна Вьюгина
Репетитор по математике
Стаж (лет)
Образование:
БГПУ им. М.Танка
М.Танка
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Предметы
- Математика
- Репетитор по физике
- Репетитор по химии
- Репетитор по русскому языку
- Репетитор по английскому языку
- Репетитор по обществознанию
- Репетитор по истории России
- Репетитор по биологии
- Репетитор по географии
- Репетитор по информатике
- Высшая математика
- Ментальная арифметика
Специализации
- Подготовка к ОГЭ по математике
- Репетитор по геометрии
- Репетитор по алгебре
- Репетитор по русскому языку для подготовки к ОГЭ
- Английский язык для начинающих
- Репетитор по английскому для взрослых
- Репетитор для подготовки к ВПР по русскому языку
- Подготовка к ОГЭ по информатике
- Scratch
Похожие статьи
- Производная
- Сфера
- ЕГЭ по математике, базовый уровень.
 Простейшие уравнения (вариант 2)
Простейшие уравнения (вариант 2) - Степенные ряды
- Пищевые отравления: как защитить ребенка в лагере, деревне и городе
- 15 советов по воспитанию ребенка от Медведя из мультика Маша и Медведь
- Как животные помогали людям во время ВОВ
- Как перевести обыкновенную дробь в десятичную: 2 способа
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Текст с ошибкой:
Расскажите, что не так
3-8 9 Оценить квадратный корень из 12 10 Оценить квадратный корень из 20 11 Оценить квадратный корень из 50 94Преобразование дробей в десятичные числа и проценты (видео и практика)
СтенограммаЧасто задаваемые вопросыИнформационный бюллетеньПрактика
Привет и добро пожаловать в это видео о преобразовании дробей в десятичные числа и проценты! В этом видео мы рассмотрим:
- Как визуально преобразовать дроби в десятичные дроби и процентов и
- Как численно преобразовать дроби в десятичные дроби и проценты
Прежде чем мы начнем, давайте рассмотрим пару ключевых понятий, которые мы будем использовать, чтобы сделать математику более понятной.
Рассмотрим дробь \(\frac{10}{10}\). Один из способов думать о дробях — думать о них как о делении.
\(\frac{10}{10}=1\)
Другими словами, десять десятых составляют одно целое.
\(\frac{10}{10}\) эквивалентно записи \(\frac{100}{100}\). Дробная полоса может быть выражена как «на», поэтому это выражение можно сказать как «100 на 100». Слово «процент» буквально означает «на 100», поэтому «100 на 100» означает 100 процентов.
Дробная полоса может быть выражена как «на», поэтому это выражение можно сказать как «100 на 100». Слово «процент» буквально означает «на 100», поэтому «100 на 100» означает 100 процентов.
Следовательно, когда одно и то же число делится само на себя, в десятичном виде получается 1, а в процентах — 100%.
Но что произойдет, если наша дробь меньше 1? Давайте взглянем.
Рассмотрим дробь \(\frac{1}{4}\). Визуально это происходит так:
На диаграмме видно, что \(\frac{1}{4}\) целого равно \(\frac{25}{100}\). \(\frac{25}{100}\) означает «25 на 100», т. е. равно 25%.
Теперь давайте разберемся, как преобразовать это в десятичное число.
Мы возьмем дробь \(\frac{1}{4}\), что равносильно делению 1 на 4. Но, используя наше знание разрядного значения , мы можем заставить его работать:
Во-первых, перепишем 1 как 1.0. Вместо 1 делимое теперь составляет десять десятых.
Во-вторых, 4 единицы перейдут в разряд десяти десятых две десятых.
В-третьих, \(4\умножить на 0,2=0,8\).
Четвертый, \(1,0 -0,8 = 0,2\).
В-пятых, мы собираемся переписать исходное делимое как стосотые и уменьшить новый 0.
В-шестых, 4 единицы составляют 20-сотых 5-сотых раз.
В-седьмых, умножаем \(4\умножить на 0,05=0,20\). Затем мы вычтем, чтобы получить 0.
Это означает \(\frac{1}{4}=0,25\).
Как преобразовать дробь в проценты
Давайте посмотрим на эту работу с дробью, отличной от единицы, например \(\frac{3}{16}\).
Вот как выглядит отделение. Последовательность добавления десятичной дроби и деления повторяется столько раз, сколько необходимо, пока либо остаток не станет равным 0, либо десятичная дробь не начнет повторяться.
Итак, \(\frac{3}{16}=0,1875\) и \(0,1875=\frac{1,875}{10,000}=\frac{18,75}{100}\). Следовательно, 0,1875 совпадает с 18,75%, потому что это 18,75 на 100.
Как насчет повторяющегося десятичного числа ? Все то же самое и процесс можно остановить, когда станет ясно, что десятичная дробь повторяется. Вот простой пример: \(\frac{1}{3}\).
Вот простой пример: \(\frac{1}{3}\).
Процесс вычитания 9 единиц из 10 повторяется, вызывая повторение десятичной дроби.
Наконец, рассмотрим дробь больше 1, например \(\frac{5}{2}\).
Визуально вот что мы имеем:
Мы видим, что заштрихованная величина равна \(\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+ \frac{1}{2}+\frac{1}{2}=\frac{5}{2}\). Каждый \(\frac{1}{2}=50\), поэтому мы можем эквивалентно сказать \(\frac{250}{100}\), что в десятичном виде равно 2,5 (что означает \(2\frac{ 1}{2}\) целых, что и показано на схеме). Мы также можем эквивалентно сказать 250 на 100 или 250%.
То же самое работает и для отдела:
Спасибо за просмотр и приятного изучения!
Часто задаваемые вопросы
Q
Как преобразовать дробь в проценты?
A
Преобразование дроби в процент можно выполнить за \(2\) быстрых шагов.
Шаг 1: Разделите числитель на знаменатель.
Шаг 2: умножьте это десятичное число на \(100\).
Например, \(\frac{2}{5}\) показывает числитель \(2\) и знаменатель \(5\).
Step 1:
| \(5\phantom{.}\) | \(\phantom{.}2\) |
is the same as
| \(5\фантом{.}\) | \(\фантом{.}2\) | . | \(0\) | \(0\) |
, что равно \(0,4\) при использовании процесса деления в большую сторону.
Шаг 2: \(0,4\times100=40\). Это означает, что дробь \(\frac{2}{5}\) представляет собой \(40\%\).
Q
Как преобразовать дроби в десятичные?
A
Дроби можно преобразовать в десятичные с помощью длинного деления. Например, дробь \(\frac{4}{25}\) выражает «\(4\) разделить на \(25\)». Это может быть установлено как 25⟌4. Поместите десятичную дробь и нули после \(4\), чтобы получилось \(4.00\). Сейчас у нас 25⟌4.00. \(25\) не переходит в \(4\), но входит в \(40\) один раз. Отсюда применяются стандартные правила деления в большую сторону. Результат будет \(0,16\). Важно помнить, что дробная черта представляет собой деление, поэтому дроби можно вычислять как десятичные, разделив числитель на знаменатель.
Отсюда применяются стандартные правила деления в большую сторону. Результат будет \(0,16\). Важно помнить, что дробная черта представляет собой деление, поэтому дроби можно вычислять как десятичные, разделив числитель на знаменатель.
Q
Что означает дробь?
A
Дробь представляет «часть» «целого». Дробная черта, разделяющая «часть» и «целое», представляет деление. Например, дробь \(\frac{5}{9}\) представляет собой \(5\) частей из \(9\) частей или «\(5\text{ разделить на }9\)». Другой способ думать об этом состоит в том, что дробная полоса представляет собой «за». Например, \(\frac{40}{100}\) означает «\(40\text{ на }100\)».
Q
Что означает процент?
A
Процент означает «\(\text{на }100\)». Например, \(96\%\) представляет собой \(96\) на \(100\). Это также представляет дробь \(\frac{96}{100}\). Все проценты могут быть выражены в виде дроби, потому что проценты всегда выходят за пределы \(100\). Проценты иногда будут меньше \(1\) и больше \(100\). Например, процент \(125\%\) представляет собой \(\frac{125}{100}\), а процент \(0,5\%\) представляет \(\frac{0,5}{100}\).
Проценты иногда будут меньше \(1\) и больше \(100\). Например, процент \(125\%\) представляет собой \(\frac{125}{100}\), а процент \(0,5\%\) представляет \(\frac{0,5}{100}\).
Q
Зачем нужно делить дробь, чтобы превратить ее в десятичную?
A
Дроби представляют собой «часть» из «целого». Дробная черта, разделяющая «часть» и «целое», представляет деление . Это означает, что все дроби можно преобразовать в десятичные, разделив числитель на знаменатель.
Например, дробь \(\frac{4}{5}\) представляет собой \(4\) из \(5\) или \(4\), деленное на \(5\). Эту дробь можно преобразовать в десятичную, разделив \(4\) на \(5\). 5⟌4 можно решить, если справа от \(4\) добавить десятичную точку и нули. 5⟌4 становится 5⟌4,00. \(5\) превращается в \(40\) \(8\) раз, а остальная часть процесса следует стандартным правилам деления в большую сторону. Результат равен \(0,8\).
Информационный бюллетень
Практические вопросы
Вопрос №1:
Что такое \(\frac{42}{100}\) в процентах?
42%
4,2%
0,42%
420%
Показать ответ
Ответ:
Правильный ответ: 42%. Процент означает «на 100», поэтому, чтобы превратить дробь в проценты, преобразуйте знаменатель в 100, а числитель — ваш процент.
Процент означает «на 100», поэтому, чтобы превратить дробь в проценты, преобразуйте знаменатель в 100, а числитель — ваш процент.
Скрыть ответ
Вопрос № 2:
Что такое \(\frac{16}{100}\) в виде десятичной дроби?
16.00
0.016
0.16
1.6
Показать ответ
Ответ:
Правильный ответ 0.16. Так как 16 больше 100, запишите десятичную дробь так, чтобы 6 стояло в сотых, а значит, 1 будет в десятых.
Скрыть ответ
Вопрос № 3:
Что из следующего не является правильным способом перезаписи \(\frac{96}{1000}\)?
0,096
96%
9,6%
0,09600
Показать ответ
Ответ:
%. \(\frac{96}{1,000}\) в виде десятичного числа равно 0,096, а добавление нулей в конце десятичного числа не меняет его значения, поэтому 0,09600 эквивалентно 0,096. \(\frac{96}{1000}\) в процентах составляет 9,6%. 96% в виде дроби равно \(\frac{96}{100}\).
\(\frac{96}{1,000}\) в виде десятичного числа равно 0,096, а добавление нулей в конце десятичного числа не меняет его значения, поэтому 0,09600 эквивалентно 0,096. \(\frac{96}{1000}\) в процентах составляет 9,6%. 96% в виде дроби равно \(\frac{96}{100}\).Скрыть ответ
Вопрос №4:
Что такое \(\frac{7}{20}\) в процентах?
7%
20%
28%
35%
Показать ответ
Ответ:
Правильный ответ: 35%. Процент означает «на 100», поэтому, чтобы превратить дробь в проценты, преобразуйте знаменатель в 100, а числитель — ваш процент. Чтобы преобразовать \(\frac{7}{20}\) в знаменатель, равный 100, умножьте и числитель, и знаменатель на 5, что даст вам \(\frac{35}{100}\). 35 — числитель, поэтому \(\frac{7}{20}=35%\).
Скрыть ответ
Вопрос № 5:
Что такое \(\frac{23}{125}\) в виде десятичной дроби?
0,23
1,25
1,86
0,184
Показать ответ
Ответ:
Правильный ответ 0. 184. Чтобы преобразовать дробь в десятичную, сначала преобразуйте дробь так, чтобы ее знаменатель был кратен 10. Это можно сделать, умножив \(\frac{23}{125}\) на \(\frac{8}{) 8}\). \(\frac{23}{125}\times\frac{8}{8}=\frac{184}{1000}\), и, поскольку 184 больше 1000, поместите 4 в тысячные доли десятичного знака, что ставит 8 на сотые места, а 1 на десятые, 0,184.
184. Чтобы преобразовать дробь в десятичную, сначала преобразуйте дробь так, чтобы ее знаменатель был кратен 10. Это можно сделать, умножив \(\frac{23}{125}\) на \(\frac{8}{) 8}\). \(\frac{23}{125}\times\frac{8}{8}=\frac{184}{1000}\), и, поскольку 184 больше 1000, поместите 4 в тысячные доли десятичного знака, что ставит 8 на сотые места, а 1 на десятые, 0,184.
Скрыть ответ
Вопрос № 6:
Запишите дробь \(\frac{4}{5}\) в виде десятичной дроби.
0,8
0,6
0,5
0,4
Показать ответ
Ответ:
Правильный ответ: 0,8. Чтобы преобразовать дробь в десятичную, разделите числитель на знаменатель. В этом случае разделите 4 на 5. Для этого можно использовать длинное деление:
Скрыть ответ
Вопрос №7:
Запишите дробь \(\frac{5}{8}\) в виде десятичной дроби.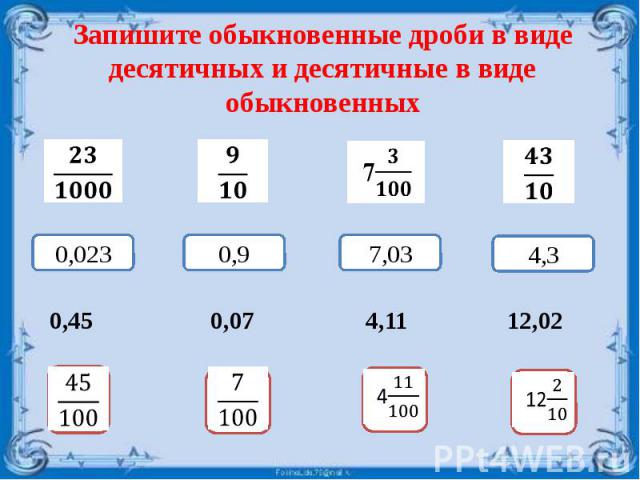
5,8
0,58
0,625
0,562
Показать ответ
Ответ:
Правильный ответ: 0,625. Чтобы преобразовать дробь в десятичную, разделите числитель на знаменатель. В этом случае разделите 5 на 8. Для этого можно использовать длинное деление:
Скрыть ответ
Вопрос №8:
Запишите дробь \(\frac{1}{5}\) в виде десятичный.
0,5
0,2
0,1
2,0
Показать ответ
Ответ:
Правильный ответ 0,2. Чтобы преобразовать дробь в десятичную, разделите числитель на знаменатель. В этом случае разделите 1 на 5. Для этого можно использовать длинное деление:
Скрыть ответ
Вопрос №9:
Запишите дробь \(\frac{5}{6}\) в виде десятичный.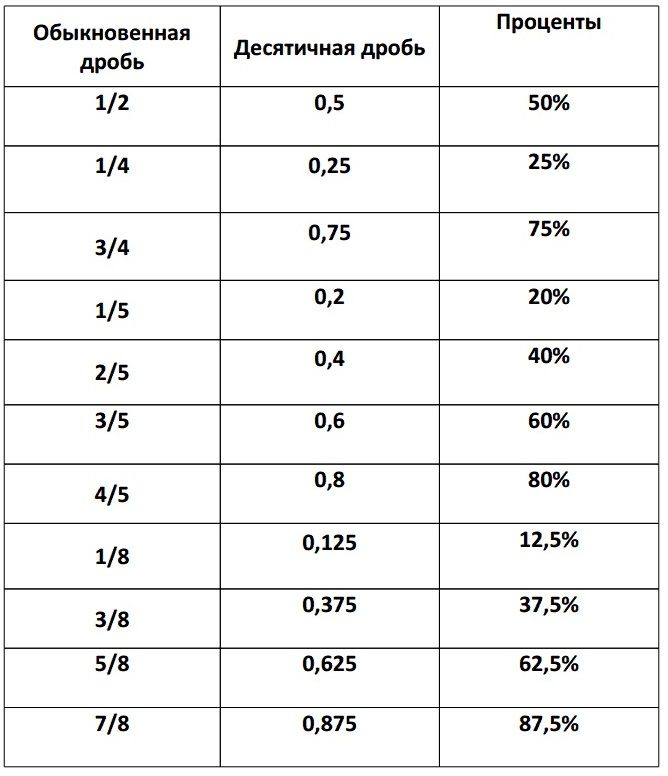


 Простейшие уравнения (вариант 2)
Простейшие уравнения (вариант 2)