Что такое 1/3 в целом числе? – Обзоры Вики
Так как цифра после запятой меньше 5, она будет округлена до 0. Следовательно, 1/3 как целое число будет равно 0.
Аналогично, что такое 10 и 1 треть как неправильная дробь? Неправильная дробь 31/3. эквивалентно смешанному числу 10 1/3.
Как записать 1/3 в виде дроби? Ответ и объяснение: Смешанное число 1 1/3 равно неправильной дроби. 4/3.
Что такое 1/3 в виде дроби? Таблица преобразования десятичных и дробных чисел
| Доля | Эквивалентные дроби | Десятичная дробь |
|---|---|---|
| 1/3 | 2/6 | .333 |
| 2/3 | 4/6 | .666 |
| 1/4 | 2/8 | .25 |
| 3/4 | 6/8 | .75 |
Во-вторых, что такое 1/3 в десятичной дроби? Ответ: 1/3 выражается как 0. 3333 в десятичной форме.
3333 в десятичной форме.
Как решать неправильные дроби?
Чтобы преобразовать смешанную дробь в неправильную, выполните следующие действия:
- Умножьте целую числовую часть на знаменатель дроби.
- Добавьте это в числитель.
- Затем напишите результат над знаменателем.
тогда Как умножать дроби? Есть 3 простых шага для умножения дробей
- Умножьте верхние числа (числители).
- Умножьте нижние числа (знаменатели).
- При необходимости упростите дробь.
Как упростить неправильную дробь? Чтобы упростить неправильную дробь, начните с превратить его в смешанное число, разделив числитель на знаменатель. Затем превратите остаток в дробь, поместив его над знаменателем исходной дроби. При необходимости упростите последнюю дробь, чтобы получить ответ.
Что такое и 3/10 как десятичная дробь?
Таблица преобразования дробей в десятичные
| Доля | Десятичная дробь |
|---|---|
| 8/9 | 0. 88888889 88888889 |
| 1/10 | 0.1 |
| 2/10 | 0.2 |
| 3/10 | 0.3 |
Что означает 3 больше 10 в виде десятичной дроби? Ответ: 3/10 в виде десятичной дроби выражается как 0.3.
Как превратить 1.33 в дробь?
Примеры алгебры
Преобразуйте десятичное число в дробь, поместив десятичное число больше десятичной степени. Так как справа от десятичной точки есть 2 числа, поместите десятичное число над 102 (100) . Затем прибавьте целое число слева от десятичной дроби. Конвертировать 133100 1 33 100 в неправильную дробь.
Как сделать 1/3 на калькуляторе? Хотя вы не можете отображать недесятичные дроби на калькуляторе без функции дробей, вы все равно можете их вводить. Сначала введите числитель дроби, затем нажмите клавишу деления и введите знаменатель. Нажмите клавишу «равно», и дробь отобразится в виде десятичной дроби.
Что такое 1/3?
Ответ: Дроби, эквивалентные 1/3, равны 2/6, 3/9, 4/12 и т. д. Эквивалентные дроби имеют одинаковое значение в сокращенном виде.
д. Эквивалентные дроби имеют одинаковое значение в сокращенном виде.
Как перевести 1/3 в процент?
Преобразовать 1/3 в проценты, изменив знаменатель
Поскольку «процент» означает части на сотню, если мы можем преобразовать дробь, чтобы иметь 100 в качестве знаменателя, мы тогда знаем, что верхнее число, числитель, является процентом. Наша процентная доля равна 33.333333333333/100, что означает, что 13 в процентах равно 33.33%.
Что такое половина 1 3-го? Скачать диаграмму
| Первоначальная сумма | Половина суммы | Одна треть суммы |
|---|---|---|
| 1 / 3 чашки | 2 ст. Л. + 2 ч. Л. | 1 столовая ложка + 1-1 / 4 чайной ложки |
| 1 / 4 чашки | 2 ст.л. | 1 ст. Л. + 1 ч. Л. |
| 1 ст.л. | 1-1 / 2 ч. Л. | 1 ч.л. |
| 1 ч.л. | 1 / ч. л 2 | 1 / ч. л 4 |
• 27 декабря 2021 г.
Как написать смешанные дроби? Шаг 1: Умножьте знаменатель на целое число. Шаг 2: Добавьте числитель к произведению, полученному на шаге 1. Шаг 3: Запишите смешанную дробь с помощью сумма, полученная от шаг 2 как числитель и знаменатель исходной дробной части смешанной дроби.
Как решить дробь с целым числом?
Как превратить смешанную дробь в целое число? Как преобразовать смешанное число в десятичное
- Превратите дробь в десятичную: разделите числитель на знаменатель.
- Прибавьте это десятичное число к целой части смешанного числа.
Как решить двойные дроби?
com/embed/6KgViCl7Xto» frameborder=»0″ allowfullscreen=»allowfullscreen» data-original-w=»720″ data-original-h=»520″>Что такое деление дробей?
Разделить две дроби — это то же самое, что умножить первую дробь на обратную вторую дробь. Первый шаг к делению дробей — найти обратную величину (поменять местами числитель и знаменатель) второй дроби. Затем умножьте два числителя. Затем умножьте два знаменателя.
Как дробь превратить в смешанное число? Ответ: Чтобы преобразовать неправильную дробь в смешанную, разделите числитель на знаменатель, запишите частное как целое число, а остаток как числитель поверх того же знаменателя. Давайте посмотрим на пример этого преобразования. Пояснение: Преобразуйте 23/4 в смешанную дробь.
Как превратить дроби в десятичные?
Чтобы преобразовать дробь в десятичную, мы просто разделить числитель...по знаменателю. В нашем примере мы разделим 1 на 4. 1 разделить на 4 равно 0. Чтобы продолжить деление, мы добавим десятичную точку и ноль после 1.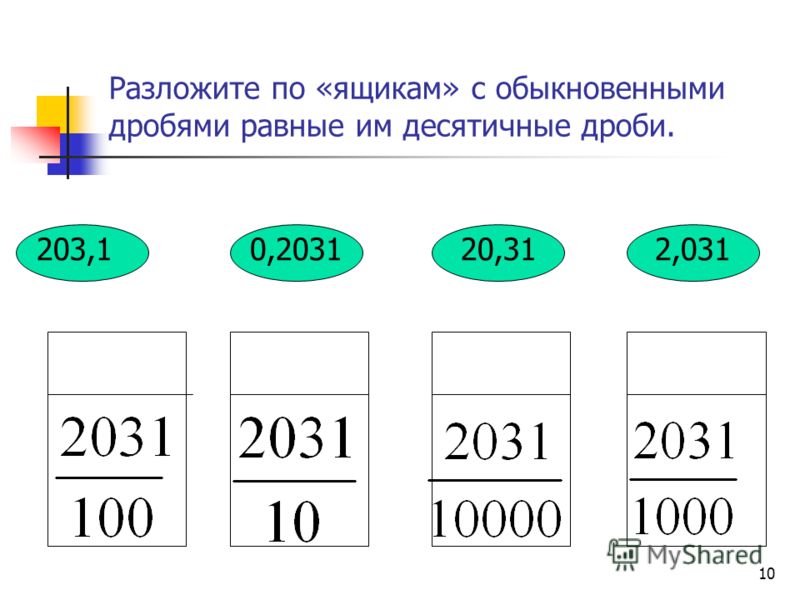
Как преобразовать дробь в целое число? Разделите числитель на знаменатель. Запишите результат в виде целого числа. Запишите любой остаток как числитель дроби. Знаменатель остается прежним.
Возведение дроби в десятичную дробь. Перевод десятичных чисел в дробь и наоборот — онлайн калькулятор
Десятичная дробь состоит из двух частей, которые разделены запятыми. Первая часть — это целая единица, вторая часть — это десятки (если число после запятой одно), сотни (два числа после запятой, как два нуля в ста), тысячные итд. Посмотрим на примеры десятичной дроби: 0, 2; 7, 54; 235,448; 5,1; 6,32; 0,5. Всё это — десятичные дроби. Как же перевести десятичную дробь в обыкновенную?
Пример первый
У нас есть дробь, к примеру, 0,5. Как уже выше писалось, она состоит из двух частей. Первое число 0, показывает, сколько целых единиц у дроби. В нашем случае их нет. Второе число показывает десятки. Дробь даже читается ноль целых пять десятых. Десятичное число перевести в дробь теперь не составит труда, пишем 5/10. Если видите, что у цифр есть общий делитель, можете сократить дробь. У нас это число 5, поделив обе части дроби на 5, получаем — 1/2.
Если видите, что у цифр есть общий делитель, можете сократить дробь. У нас это число 5, поделив обе части дроби на 5, получаем — 1/2.
Пример второй
Возьмем более сложную дробь — 2,25. Читается она так — две целых и двадцать пять сотых. Обратите внимание — сотых, так как чисел после запятой две. Теперь можно перевести в обыкновенную дробь. Записываем — 2 25/100. Целая часть — 2, дробная 25/100. Как и в первом примере, эту часть можно сократить. Общим делителем для цифр 25 и 100 является число 25. Заметьте, что мы всегда подбираем наибольший общий делитель. Разделив обе части дроби на НОД, получили 1/4. Итак, 2, 25 это 2 1/4.
Пример третий
И для закрепления материала возьмем десятичную дробь 4,112 — четыре целых и сто двенадцать тысячных. Почему тысячных, думаю, ясно. Записываем теперь 4 112/1000. По алгоритму находим НОД чисел 112 и 1000. В нашем случае — это число 6. Получаем 4 14/125.
Вывод
- Разбиваем дробь на целую и дробную части.
- Смотрим, сколько цифр после запятой.
 Если одна — это десятки, две — сотни, три -тысячные итд.
Если одна — это десятки, две — сотни, три -тысячные итд. - Записываем дробь в обыкновенном виде.
- Сокращаем числитель и знаменатель дроби.
- Записываем полученную дробь.
- Выполняем проверку, делим верхнюю часть дроби на нижнюю. Если есть целая часть, прибавляем к полученной десятичной дроби. Получился исходный вариант — замечательно, значит, вы все сделали правильно.
На примерах я показала, как можно перевести десятичную дробь в обыкновенную. Как видите, сделать это очень легко и просто.
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)
Дроби в старших классах не сильно досаждают. До поры до времени. Пока не столкнётесь со степенями с рациональными показателями да логарифмами. А вот там…. Давишь, давишь калькулятор, а он все полное табло каких-то циферок кажет. Приходится головой думать, как в третьем классе.
Давайте уже разберёмся с дробями, наконец! Ну сколько можно в них путаться!? Тем более, это всё просто и логично.
Виды дробей. Преобразования.
Дроби бывают трёх видов.
1. Обыкновенные дроби , например:
Иногда вместо горизонтальной чёрточки ставят наклонную черту: 1/2, 3/4, 19/5, ну, и так далее. Здесь мы часто будем таким написанием пользоваться. Верхнее число называется числителем , нижнее — знаменателем. Если вы постоянно путаете эти названия (бывает…), скажите себе с выражением фразу: «Ззззз апомни! Ззззз наменатель — вниззззз у!» Глядишь, всё и ззззапомнится.)
Чёрточка, что горизонтальная, что наклонная, означает деление верхнего числа (числителя) на нижнее (знаменатель). И всё! Вместо чёрточки вполне можно поставить знак деления — две точки.
Когда деление возможно нацело, это надо делать. Так, вместо дроби «32/8» гораздо приятнее написать число «4». Т.е. 32 просто поделить на 8.
32/8 = 32: 8 = 4
Я уж и не говорю про дробь «4/1». Которая тоже просто «4».
2. Десятичные дроби , например:
Именно в таком виде нужно будет записывать ответы на задания «В».
3. Смешанные числа , например:
Смешанные числа практически не используются в старших классах. Для того, чтобы с ними работать, их всяко надо переводить в обыкновенные дроби. Но это точно надо уметь делать! А то попадётся такое число в задачке и зависните… На пустом месте. Но мы-то вспомним эту процедуру! Чуть ниже.
Наиболее универсальны обыкновенные дроби . С них и начнём. Кстати, если в дроби стоят всякие логарифмы, синусы и прочие буковки, это ничего не меняет. В том смысле что все действия с дробными выражениями ничем не отличаются от действий с обыкновенными дробями
!Основное свойство дроби.
Итак, поехали! Для начала я вас удивлю. Всё многообразие преобразований дробей обеспечивается одним-единственным свойством! Оно так и называется, основное свойство дроби . Запоминайте: если числитель и знаменатель дроби умножить (разделить) на одно и то же число, дробь не изменится. Т.е:
Запоминайте: если числитель и знаменатель дроби умножить (разделить) на одно и то же число, дробь не изменится. Т.е:
Понятно, что писать можно дальше, до посинения. Синусы и логарифмы пусть вас не смущают, с ними дальше разберёмся. Главное понять, что все эти разнообразные выражения есть одна и та же дробь . 2/3.
А оно нам надо, все эти превращения? Ещё как! Сейчас сами увидите. Для начала употребим основное свойство дроби для сокращения дробей . Казалось бы, вещь элементарная. Делим числитель и знаменатель на одно и то же число и все дела! Ошибиться невозможно! Но… человек — существо творческое. Ошибиться везде может! Особенно, если приходится сокращать не дробь типа 5/10, а дробное выражение со всякими буковками.
Как правильно и быстро сокращать дроби, не делая лишней работы, можно прочитать в особом Разделе 555 .
Нормальный ученик не заморачивается делением числителя и знаменателя на одно и то же число (или выражение)! Он просто зачеркивает всё одинаковое сверху и снизу! Здесь-то и таится типичная ошибка, ляп, если хотите.
Например, надо упростить выражение:
Тут и думать нечего, зачеркиваем букву «а» сверху и двойку снизу! Получаем:
Все правильно. Но реально вы поделили весь числитель и весь знаменатель на «а». Если вы привыкли просто зачеркивать, то, впопыхах, можете зачеркнуть «а» в выражении
и получить снова
Что будет категорически неверно. Потому что здесь весь числитель на «а» уже не делится
! Эту дробь сократить нельзя. Кстати, такое сокращение – это, гм… серьезный вызов преподавателю. Такого не прощают! Запомнили? При сокращении делить надо весь числитель и весь знаменатель!Сокращение дробей сильно облегчает жизнь. Получится где-нибудь у вас дробь, к примеру 375/1000. И как теперь с ней дальше работать? Без калькулятора? Умножать, скажем, складывать, в квадрат возводить!? А если не полениться, да аккуратненько сократить на пять, да ещё на пять, да ещё… пока сокращается, короче. Получим 3/8! Куда приятнее, правда?
Основное свойство дроби позволяет переводить обыкновенные дроби в десятичные и наоборот без калькулятора ! Это важно на ЕГЭ, верно?
Как переводить дроби из одного вида в другой.

С десятичными дробями всё просто. Как слышится, так и пишется! Скажем, 0,25. Это ноль целых, двадцать пять сотых. Так и пишем: 25/100. Сокращаем (делим числитель и знаменатель на 25), получаем обычную дробь: 1/4. Всё. Бывает, и не сокращается ничего. Типа 0,3. Это три десятых, т.е. 3/10.
А если целых — не ноль? Ничего страшного. Записываем всю дробь без всяких запятых в числитель, а в знаменатель — то, что слышится. Например: 3,17. Это три целых, семнадцать сотых. Пишем в числитель 317, а в знаменатель 100. Получаем 317/100. Ничего не сокращается, значит всё. Это ответ. Элементарно, Ватсон! Из всего сказанного полезный вывод: любую десятичную дробь можно превратить в обыкновенную .
А вот обратное преобразование, обыкновенной в десятичную, некоторые без калькулятора не могут сделать. А надо! Как вы ответ записывать будете на ЕГЭ!? Внимательно читаем и осваиваем этот процесс.
Десятичная дробь чем характерна? У неё в знаменателе всегда стоит 10, или 100, или 1000, или 10000 и так далее. Если ваша обычная дробь имеет такой знаменатель, проблем нет. Например, 4/10 = 0,4. Или 7/100 = 0,07. Или 12/10 = 1,2. А если в ответе на задание раздела «В» получилось 1/2? Что в ответ писать будем? Там десятичные требуются…
Если ваша обычная дробь имеет такой знаменатель, проблем нет. Например, 4/10 = 0,4. Или 7/100 = 0,07. Или 12/10 = 1,2. А если в ответе на задание раздела «В» получилось 1/2? Что в ответ писать будем? Там десятичные требуются…
Вспоминаем основное свойство дроби ! Математика благосклонно позволяет умножать числитель и знаменатель на одно и то же число. На любое, между прочим! Кроме нуля, разумеется. Вот и применим это свойство себе на пользу! На что можно умножить знаменатель, т.е. 2 чтобы он стал 10, или 100, или 1000 (поменьше лучше, конечно…)? На 5, очевидно. Смело умножаем знаменатель (это нам надо) на 5. Но, тогда и числитель надо умножить тоже на 5. Это уже математика требует! Получим 1/2 = 1х5/2х5 = 5/10 = 0,5. Вот и всё.
Однако, знаменатели всякие попадаются. Попадётся, например дробь 3/16. Попробуй, сообрази тут, на что 16 умножить, чтоб 100 получилось, или 1000… Не получается? Тогда можно просто разделить 3 на 16. За отсутствием калькулятора делить придётся уголком, на бумажке, как в младших классах учили.
А бывают и совсем скверные знаменатели. Например, дробь 1/3 ну никак не превратишь в хорошую десятичную. И на калькуляторе, и на бумажке, мы получим 0,3333333… Это значит, что 1/3 в точную десятичную дробь не переводится . Так же, как и 1/7, 5/6 и так далее. Много их, непереводимых. Отсюда ещё один полезный вывод. Не каждая обыкновенная дробь переводится в десятичную !
Кстати, это полезная информация для самопроверки. В разделе «В» в ответ надо десятичную дробь записывать. А у вас получилось, например, 4/3. Эта дробь не переводится в десятичную. Это означает, что где-то вы ошиблись по дороге! Вернитесь, проверьте решение.
Итак, с обыкновенными и десятичными дробями разобрались. Осталось разобраться со смешанными числами. Для работы с ними их всяко нужно перевести в обыкновенные дроби. Как это сделать? Можно поймать шестиклассника и спросить у него. Но не всегда шестиклассник окажется под руками… Придётся самим. Это несложно. Надо знаменатель дробной части умножить на целую часть и прибавить числитель дробной части.
Пусть в задачке вы с ужасом увидели число:
Спокойно, без паники соображаем. Целая часть — это 1. Единица. Дробная часть — 3/7. Стало быть, знаменатель дробной части — 7. Этот знаменатель и будет знаменателем обыкновенной дроби. Считаем числитель. 7 умножаем на 1 (целая часть) и прибавляем 3 (числитель дробной части). Получим 10. Это будет числитель обыкновенной дроби. Вот и всё. Еще проще это выглядит в математической записи:
Ясненько? Тогда закрепите успех! Переведите в обыкновенные дроби. У вас должно получится 10/7, 7/2, 23/10 и 21/4.
Обратная операция — перевод неправильной дроби в смешанное число — в старших классах редко требуется. Ну если уж… И если Вы — не в старших классах — можете заглянуть в особый Раздел 555 . Там же, кстати, и про неправильные дроби узнаете.
Ну вот, практически и всё. Вы вспомнили виды дробей и поняли, как переводить их из одного вида в другой. Остаётся вопрос: зачем это делать? Где и когда применять эти глубокие познания?
Остаётся вопрос: зачем это делать? Где и когда применять эти глубокие познания?
Отвечаю. Любой пример сам подсказывает необходимые действия. Если в примере смешались в кучу обыкновенные дроби, десятичные, да ещё и смешанные числа, переводим всё в обыкновенные дроби. Это всегда можно сделать . Ну а если написано, что-нибудь типа 0,8 + 0,3, то так и считаем, безо всякого перевода. Зачем нам лишняя работа? Мы выбираем тот путь решения, который удобен нам !
Если в задании сплошь десятичные дроби, но гм… злые какие-то, перейдите к обыкновенным, попробуйте! Глядишь, всё и наладится. Например, придется в квадрат возводить число 0,125. Не так-то просто, если от калькулятора не отвыкли! Мало того, что числа перемножать столбиком надо, так ещё думай, куда запятую вставить! В уме точно не получится! А если перейти к обыкновенной дроби?
0,125 = 125/1000. Сокращаем на 5 (это для начала). Получаем 25/200. Ещё раз на 5. Получаем 5/40. О, ещё сокращается! Снова на 5! Получаем 1/8.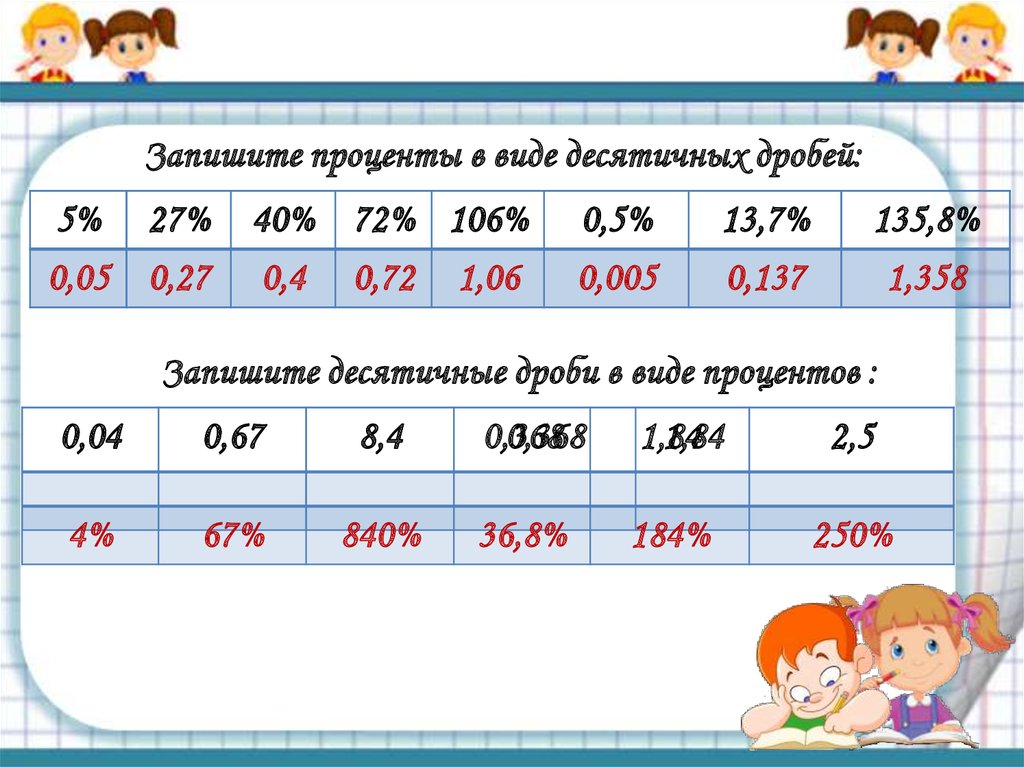 Легко возводим в квадрат (в уме!) и получаем 1/64. Всё!
Легко возводим в квадрат (в уме!) и получаем 1/64. Всё!
Подведём итоги этого урока.
1. Дроби бывают трёх видов. Обыкновенные, десятичные и смешанные числа.
2. Десятичные дроби и смешанные числа всегда можно перевести в обыкновенные дроби. Обратный перевод не всегда возможен.
3. Выбор вида дробей для работы с заданием зависит от этого самого задания. При наличии разных видов дробей в одном задании, самое надёжное — перейти к обыкновенным дробям.
Теперь можно потренироваться. Для начала переведите эти десятичные дроби в обыкновенные:
3,8; 0,75; 0,15; 1,4; 0,725; 0,012
Должны получиться вот такие ответы (в беспорядке!):
На этом и завершим. В этом уроке мы освежили в памяти ключевые моменты по дробям. Бывает, правда, что освежать особо нечего…) Если уж кто совсем крепко забыл, или ещё не освоил… Тем можно пройти в особый Раздел 555 . Там все основы подробненько расписаны. Многие вдруг всё понимать начинают. И решают дроби с лёту).
Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Если нам нужно разделить 497 на 4, то при делении мы увидим, что 497 не делится на 4 нацело, т.е. остаётся остаток от деления.
В таких случаях говорят, что выполнено деление с остатком , и решение записывают в таком виде:
497: 4 = 124 (1 остаток).
Компоненты деления в левой части равенства называют так же, как при делении без остатка: 497 — делимое , 4 — делитель .
Результат деления при делении с остатком называют неполным частным . В нашем случае это число 124. И, наконец, последний
компонент, которого нет в обычном делении, — остаток .
В тех случаях, когда остатка нет, говорят, что одно число разделилось на другое без остатка, или нацело . Считают, что при
таком делении остаток равен нулю. В нашем случае остаток равен 1.
Считают, что при
таком делении остаток равен нулю. В нашем случае остаток равен 1.
Остаток всегда меньше делителя.
Проверку при делении можно сделать умножением. Если, например, имеется равенство 64: 32 = 2, то проверку можно сделать так: 64 = 32 * 2.
Часто в случаях, когда выполняется деление с остатком, удобно использовать равенство
а = b * n + r ,
где а — делимое, b — делитель, n — неполное частное, r — остаток.
Частное от деления натуральных чисел можно записать в виде дроби.
Числитель дроби — это делимое, а знаменатель — делитель.
Поскольку числитель дроби — это делимое, а знаменатель — делитель, считают, что черта дроби означает действие деление . Иногда бывает удобно записывать деление в виде дроби, не используя знак «:».
Частное от деления натуральных чисел m и n можно записать в виде дроби \(\frac{m}{n} \), где числитель m — делимое, а
знаменатель п — делитель:
\(m:n = \frac{m}{n} \)
Верны следующие правила:
Чтобы получить дробь \(\frac{m}{n} \), надо единицу разделить на n равных частей (долей) и взять m таких частей.
Чтобы получить дробь \(\frac{m}{n} \), надо число m разделить на число n.
Чтобы найти часть от целого, надо число, соответствующее целому, разделить на знаменатель и результат умножить на числитель дроби, которая выражает эту часть.
Чтобы найти целое по его части, надо число, соответствующее этой части, разделить на числитель и результат умножить на знаменатель дроби, которая выражает эту часть.
Если и числитель, и знаменатель дроби умножить на одно и то же число (кроме нуля), величина дроби не изменится:
\(\large \frac{a}{b} = \frac{a \cdot n}{b \cdot n} \)
Если и числитель, и знаменатель дроби разделить на одно и то же число (кроме нуля), величина дроби не изменится:
\(\large \frac{a}{b} = \frac{a: m}{b: m} \)
Это свойство называют основным свойством дроби .
Два последних преобразования называют сокращением дроби .
Если дроби нужно представить в виде дробей с одним и тем же знаменателем, то такое действие называют приведением дробей к
общему знаменателю .
Правильные и неправильные дроби. Смешанные числа
Вы уже знаете, что дробь можно получить, если разделить целое на равные части и взять несколько таких частей. Например, дробь \(\frac{3}{4} \) означает три четвёртых доли единицы. Во многих задачах предыдущего параграфа обыкновенные дроби использовались для обозначения части целого. Здравый смысл подсказывает, что часть всегда должна быть меньше целого, но как тогда быть с такими дробями, как, например, \(\frac{5}{5} \) или \(\frac{8}{5} \)? Ясно, что это уже не часть единицы. Наверное, поэтому такие дроби, у которых числитель больше знаменателя или равен ему, называют неправильными дробями . Остальные дроби, т. е. дроби, у которых числитель меньше знаменателя, называют правильными дробями .
Как вы знаете, любую обыкновенную дробь, и правильную, и неправильную, можно рассматривать как результат деления числителя на
знаменатель. Поэтому в математике, в отличие от обычного языка, термин «неправильная дробь» означает не то, что мы что-то сделали
неправильно, а только то, что у этой дроби числитель больше знаменателя или равен ему.
Если число состоит из целой части и дроби, то такие дроби называются смешанными .
Например:
\(5:3 = 1\frac{2}{3} \) : 1 — целая часть, а \(\frac{2}{3} \) — дробная часть.
Если числитель дроби \(\frac{a}{b} \) делится на натуральное число n, то, чтобы разделить эту дробь на n, надо её числитель
разделить на это число:
\(\large \frac{a}{b} : n = \frac{a:n}{b} \)
Если числитель дроби \(\frac{a}{b} \) не делится на натуральное число n, то, чтобы разделить эту дробь на n, надо её
знаменатель умножить на это число:
\(\large \frac{a}{b} : n = \frac{a}{bn} \)
Заметим, что второе правило справедливо и в том случае, когда числитель делится на n. Поэтому мы можем его применять тогда, когда трудно с первого взгляда определить, делится числитель дроби на n или нет.
Действия с дробями. Сложение дробей.
С дробными числами, как и с натуральными числами, можно выполнять арифметические действия. Рассмотрим сначала сложение дробей.
Легко сложить дроби с одинаковыми знаменателями. Найдем, например, сумму \(\frac{2}{7} \) и \(\frac{3}{7} \).
Легко понять, что \(\frac{2}{7} + \frac{2}{7} = \frac{5}{7} \)
Найдем, например, сумму \(\frac{2}{7} \) и \(\frac{3}{7} \).
Легко понять, что \(\frac{2}{7} + \frac{2}{7} = \frac{5}{7} \)
Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить прежним.
Используя буквы, правило сложения дробей с одинаковыми знаменателями можно записать так:
\(\large \frac{a}{c} + \frac{b}{c} = \frac{a+b}{c} \)
Если требуется сложить дроби с разными знаменателями, то их предварительно следует привести к общему знаменателю. Например:
\(\large \frac{2}{3}+\frac{4}{5} = \frac{2\cdot 5}{3\cdot 5}+\frac{4\cdot 3}{5\cdot 3} = \frac{10}{15}+\frac{12}{15} = \frac{10+12}{15} = \frac{22}{15} \)
Для дробей, как и для натуральных чисел, справедливы переместительное и сочетательное свойства сложения.
Сложение смешанных дробей
Такие записи, как \(2\frac{2}{3} \), называют смешанными дробями . При этом число 2 называют целой частью смешанной
дроби, а число \(\frac{2}{3} \) — ее дробной частью . Запись \(2\frac{2}{3} \) читают так: «две и две трети».
Запись \(2\frac{2}{3} \) читают так: «две и две трети».
При делении числа 8 на число 3 можно получить два ответа: \(\frac{8}{3} \) и \(2\frac{2}{3} \). Они выражают одно и то же дробное число, т.е \(\frac{8}{3} = 2 \frac{2}{3} \)
Таким образом, неправильная дробь \(\frac{8}{3} \) представлена в виде смешанной дроби \(2\frac{2}{3} \). В таких случаях говорят, что из неправильной дроби выделили целую часть .
Вычитание дробей (дробных чисел)
Вычитание дробных чисел, как и натуральных, определяется на основе действия сложения: вычесть из одного числа другое — это значит
найти такое число, которое при сложении со вторым дает первое. Например:
\(\frac{8}{9}-\frac{1}{9} = \frac{7}{9} \) так как \(\frac{7}{9}+\frac{1}{9} = \frac{8}{9} \)
Правило вычитания дробей с одинаковыми знаменателями похоже на правило сложения таких дробей:
чтобы найти разность дробей с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй, а знаменатель
оставить прежним.
С помощью букв это правило записывается так:
\(\large \frac{a}{c}-\frac{b}{c} = \frac{a-b}{c} \)
Умножение дробей
Чтобы умножить дробь на дробь, нужно перемножить их числители и знаменатели и первое произведение записать числителем, а второе — знаменателем.
С помощью букв правило умножения дробей можно записать так:
\(\large \frac{a}{b} \cdot \frac{c}{d} = \frac{a \cdot c}{b \cdot d} \)
Пользуясь сформулированным правилом, молено умножать дробь на натуральное число, на смешанную дробь, а также перемножать смешанные дроби. Для этого нужно натуральное число записать в виде дроби со знаменателем 1, смешанную дробь — в виде неправильной дроби.
Результат умножения надо упрощать (если это возможно), сокращая дробь и выделяя целую часть неправильной дроби.
Для дробей, как и для натуральных чисел, справедливы переместительное и сочетательное свойства умножения, а также распределительное свойство умножения относительно сложения.
Деление дробей
Возьмем дробь \(\frac{2}{3} \) и «перевернем» ее, поменяв местами числитель и знаменатель. Получим дробь \(\frac{3}{2} \).
Эту дробь называют обратной дроби \(\frac{2}{3} \).
Получим дробь \(\frac{3}{2} \).
Эту дробь называют обратной дроби \(\frac{2}{3} \).
Если мы теперь «перевернем» дробь \(\frac{3}{2} \), то получим исходную дробь \(\frac{2}{3} \). Поэтому такие дроби, как \(\frac{2}{3} \) и \(\frac{3}{2} \) называют взаимно обратными .
Взаимно обратными являются, например, дроби \(\frac{6}{5} \) и \(\frac{5}{6} \), \(\frac{7}{18} \) и \(\frac{18}{7} \).
С помощью букв взаимно обратные дроби можно записать так: \(\frac{a}{b} \) и \(\frac{b}{a} \)
Понятно, что произведение взаимно обратных дробей равно 1 . Например: \(\frac{2}{3} \cdot \frac{3}{2} =1 \)
Используя взаимно обратные дроби, можно деление дробей свести к умножению.
Правило деления дроби на дробь:
чтобы разделить одну дробь на другую, нужно делимое умножить на дробь, обратную делителю.
Используя буквы, правило деления дробей можно записать так:
\(\large \frac{a}{b} : \frac{c}{d} = \frac{a}{b} \cdot \frac{d}{c} \)
Если делимое или делитель является натуральным числом или смешанной дробью, то, для того чтобы воспользоваться правилом деления
дробей, его надо предварительно представить в виде неправильной дроби.
Для того, чтобы ответить на этот вопрос нужно изучить некоторое количество теоретического материала. Отвечать на вопрос я буду в форме алгоритма, а для улучшения понимания — дам пример.
Что такое десятичная и смешанная дробь
Десятичная дробь — это число с остатком, остаток у которого записывается в той же строке, что и целая часть, после запятой. Пример десятичной дроби: 3,5. Смешанная дробь — это число с остатком, но в отличии от десятичной дроби, остаток у неё записывается в виде простой дроби. Как правило число оставляют в смешанной дроби по причине невозможности перевода числа в десятичную дробь, или потому что так легче решить задачу. Пример смешанной дроби: 2 1/3.
Как осуществить перевод смешанной дроби в десятичную дробь?
Как говорил в самом начале, для более понятного объяснения я буду использовать алгоритм и осуществить это можно 2 способами.
Способ первый:
- Сначала перевести смешанную дробь в неправильную, то есть умножить целую часть на знаменатель и прибавить к этому числу числитель.

- Затем поделить числитель на знаменатель.
- Записать ответ.
Второй способ:
- Поделить числитель на знаменатель, при этом не трогая целую часть.
- После целой части добавить запятую и записать число, полученное в результате деления в первом пункте. Но если во время деления, вы получили число с целой частью, то его нужно будет прибавить к целой части, данной в примере.
- Записать ответ.
Пример перевода смешанной дроби в десятичную
Для примера я буду использовать первый способ:
- 4 1/4= 17/3;
- 17/4= 4,25.
- Ответ: 4,25.
Все дроби делятся на два вида: обыкновенные и десятичные. Обыкновенными называются дроби такого вида: 9/8,3/4,1/2,1 3/4 . В них выделяют верхнее число (числитель) и нижнее число (знаменатель). Когда числитель меньше, чем знаменатель, то дробь называется правильной, в противоположном случае дробь – неправильная. Такие дроби, как 1 7/8 состоят из целой части (1) и дробной части (7/8) и называются смешанными.
Итак, дроби бывают:
- Обыкновенными
- Правильными
- Неправильными
- Смешанными
- Десятичными
Как из обыкновенной дроби сделать десятичную
Как перевести обыкновенную дробь в десятичную, учит курс математики основной школы. Все предельно просто: нужно числитель поделить на знаменатель «вручную» или, если совсем лень, то на микрокалькуляторе. Вот пример: 2/5=0,4;3/4=0,75; 1/2=0,5. Не намного сложнее перевести в десятичную неправильную дробь. Пример: 1 3/4= 7/4= 1,75. Последний результат можно получить и без деления, если учесть, что 3/4=0,75 и прибавить единицу:1+0,75=1,75.
Однако далеко не со всеми обыкновенными дробями все так просто. Например, попробуем перевести 1/3 из обыкновенных дробей в десятичные. Даже тот, кто имел по математике тройку (по пяти бальной системе) заметит, что, сколько бы ни продолжалось деление, после нуля и запятой будет бесконечное количество троек 1/3=0,3333…. . Принято читать так: ноль целых, три в периоде. Записывается соответственно так: 1/3=0,(3). Аналогичная ситуация будет, если попытаться перевести в десятичную дробь 5/6: 5/6=0,8(3). Такие дроби называются бесконечными периодическими. Вот пример для дроби 3/7: 3/7= 0,42857142857142857142857142857143… , то есть 3/7=0,(428571).
Записывается соответственно так: 1/3=0,(3). Аналогичная ситуация будет, если попытаться перевести в десятичную дробь 5/6: 5/6=0,8(3). Такие дроби называются бесконечными периодическими. Вот пример для дроби 3/7: 3/7= 0,42857142857142857142857142857143… , то есть 3/7=0,(428571).
Итак, в результате превращения обыкновенной дроби в десятичную может получаться:
- непериодическая десятичная дробь;
- периодическая десятичная дробь.
Следует отметить, что существуют и бесконечные непериодические дроби, которые получаются при выполнении таких действий: взятие корня n-ой степени, логарифмирование, потенцирование. Например, √3= 1,732050807568877… . Знаменитое число π≈ 3,1415926535897932384626433832795…. .
Давайте теперь умножим 3 на 0,(3): 3×0,(3)=0,(9)=1. Получается, что 0,(9) – это иная форма записи единицы. Точно так же 9=9/9,16=16,0, и т.д.
Правомерен и вопрос, противоположный к приведенному в заголовке этой статьи: «как десятичную дробь перевести в обычную». Ответ на данный вопрос дает пример: 0,5= 5/10=1/2. В последнем примере мы сократили числитель и знаменатель дроби 5/10 на 5. То есть для превращения десятичной дроби в обыкновенную нужно представить ее в виде дроби со знаменателем 10.
Ответ на данный вопрос дает пример: 0,5= 5/10=1/2. В последнем примере мы сократили числитель и знаменатель дроби 5/10 на 5. То есть для превращения десятичной дроби в обыкновенную нужно представить ее в виде дроби со знаменателем 10.
О том, что такое дроби вообще интересно будет посмотреть видео:
О том как перевести десятичную дробь в обыкновенную смотрите тут:
Как перевести дробное число. Перевод десятичной дроби в обыкновенную и наоборот: правило, примеры
Дробь представляет собой число, которое состоит из одной или нескольких долей единицы. В математике существует три вида дробей: обыкновенные, смешанные и десятичные.
Обыкновенные дроби
Обыкновенная дробь записывается как соотношение, в котором в числителе отражается, сколько взято частей от числа, а знаменатель показывает, на сколько частей разделена единица. Если числитель меньше знаменателя, то перед нами правильная дробь.Например: ½, 3/5, 8/9.
Если числитель равен знаменателю или больше его, то мы имеем дело с неправильной дробью. Например: 5/5, 9/4, 5/2 При делении числителя может получиться конечное число. Например, 40/8 = 5. Следовательно, любое целое число может быть записано в виде обыкновенной неправильной дроби или ряда таких дробей. Рассмотрим записи одного и того же числа в виде ряда различных .
Например: 5/5, 9/4, 5/2 При делении числителя может получиться конечное число. Например, 40/8 = 5. Следовательно, любое целое число может быть записано в виде обыкновенной неправильной дроби или ряда таких дробей. Рассмотрим записи одного и того же числа в виде ряда различных .
- Смешанные дроби
В общем виде смешанная дробь может быть представлена формулой:
Таким образом, смешанная дробь записывается как целое число и обыкновенная правильная дробь, а под такой записью понимают сумму целого и его дробной части.
- Десятичные дроби
Десятичная дробь – это особая разновидность дроби, у которой знаменатель может быть представлен как степень числа 10. Существуют бесконечные и конечные десятичные дроби. При записи этой разновидности дроби сначала указывается целая часть, затем через разделитель (точку или запятую) фиксируется дробная часть.
Запись дробной части всегда определяется ее размерностью. Десятичная запись выглядит следующим образом:
Правила перевода между различными видами дробей
- Перевод смешанной дроби в обыкновенную
Смешанную дробь можно перевести только в неправильную. Для перевода необходимо целую часть привести и тому же знаменателю, что и дробную. В общем виде это будет выглядеть следующим образом:
Для перевода необходимо целую часть привести и тому же знаменателю, что и дробную. В общем виде это будет выглядеть следующим образом:
Рассмотрим использование этого правила на конкретных примерах:
- Перевод обыкновенной дроби в смешанную
Неправильную обыкновенную дробь можно превратить в смешанную путем простого деления, в результате которого находится целая часть и остаток (дробная часть).
Для примера переведем дробь 439/31 в смешанную:
- Перевод обыкновенной дроби
В некоторых случаях перевести дробь в десятичную достаточно просто. В этом случае применяется основное свойство дроби, числитель и знаменатель умножаются на одно и то же числу, для того, чтобы привести делитель к степени числа 10.
Например:
В некоторых случаях может понадобиться найти частное путем деления уголком или с помощью калькулятора. А некоторые дроби невозможно привести к конечной десятичной дроби. Например, дробь 1/3 при делении никогда не даст конечный результат.
Большое количество учащихся, и не только, задаются вопросом, как перевести дробь в число. Чтобы это сделать, имеется несколько достаточно простых и понятных способов. Выбор конкретного способа зависит от предпочтений решающего.
В первую очередь нужно знать, как дроби записываются. А записываются они следующим образом:
- Обыкновенная. Пишется с числителем и знаменателем через наклонную или столбиком (1/2).
- Десятичная. Пишется через запятую (1,0, 2,5 и так далее).
Перед тем как приступить к решению, нужно знать, что такое неправильная дробь, ведь она встречается достаточно часто. Она имеет числитель больше знаменателя, например, 15/6. Неправильную дробь также можно решать такими способами, без каких-либо усилий и затрат времени.
Смешанное число — это когда в результате выходит целое число и дробная часть, к примеру 52/3.
Любое натуральное число можно записать дробью с совершенно разными натуральными знаменателями, например:1= 2/2=3/3 = и т.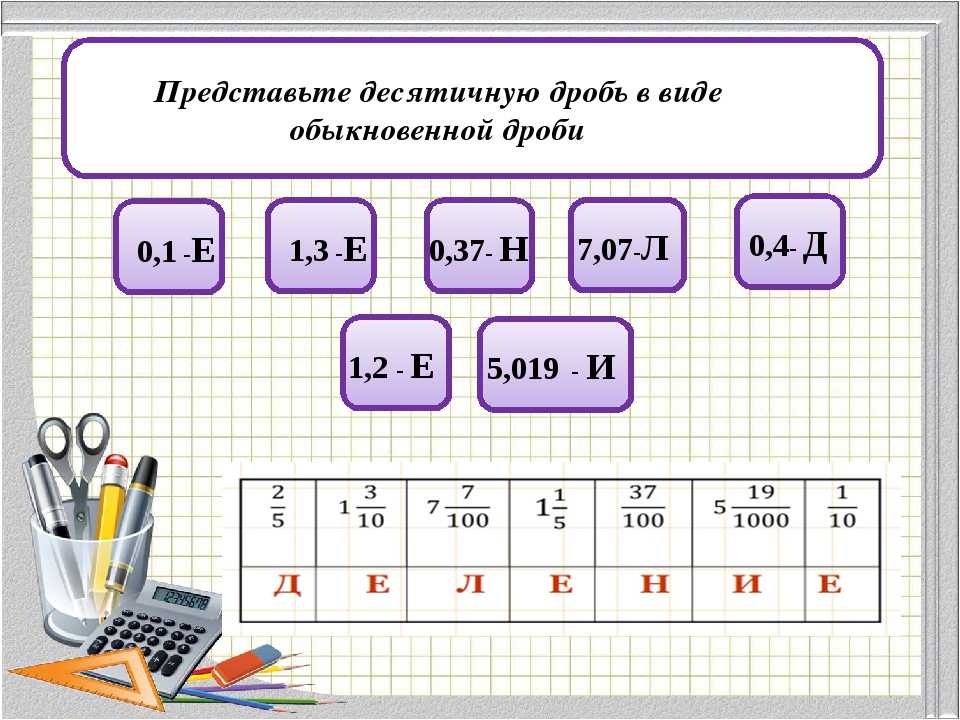 д.
д.
Перевести можно еще и с помощью калькулятора, но не все они имеют такую функцию. Существует специальный инженерный калькулятор, где есть такая функция, но не всегда есть возможность его использовать, особенно в школе. Поэтому лучше разобраться в данной теме.
Первым делом стоит обратить внимание на то, какая дробь. Если ее можно с легкостью множить до 10 на одинаковые с числителем значения, то можно воспользоваться первым способом. Например: обыкновенная ½ умножаете в числителе и знаменателе на 5 и получаете 5/10, которое можно записать как 0,5.
Данное правило основано на том, что десятичная всегда имеет в знаменателе круглое значение, такое как 10,100,1000 и так далее.
Из этого выходит, что если множить числитель и знаменатель, то нужно добиваться получения в знаменателе именно такого значения в результате умножения, независимо от того, что выходит в числителе.
Стоит помнить, что некоторые дроби нельзя перевести, для этого необходимо перед началом решения проверить ее.
Например: 1,3333, где цифра 3 повторяется до бесконечности, причем калькулятор тоже не избавит от нее. Решением такой проблемы может быть только округление таким образом, чтобы получилось целое число, если это возможно. Если такой возможности не имеется, то следует вернуться в начало примера и проверить правильность решения задачи, возможно, была допущена ошибка.
Рисунок 1-3. Перевод дробей путем умножения.
Рассмотрим для закрепления описанной информации следующий пример перевода:
- Например, необходимо перевести 6/20 в десятичную. Первым делом ее следует проверить, как показано на рисунке 1.
- Только после того как убедились, что можно разложить, как в данном случае на 2 и 5, нужно приступать к самому переводу.
- Наиболее простым вариантом будет умножить знаменатель, получив результат 100, является 5, так как 20х5=100.
- Следуя примеру на рисунке 2, в итоге получится 0,3.
Можно закрепить результат и еще раз все просмотреть по рисунку 3. Для того чтобы полностью разобраться в теме и больше не прибегать к изучению этого материала. Эти знания помогут не только ребенку, но и взрослому человеку.
Для того чтобы полностью разобраться в теме и больше не прибегать к изучению этого материала. Эти знания помогут не только ребенку, но и взрослому человеку.
Перевод путем деления
Второй вариант перевода дробей является немного сложней, но более популярным. Таким методом в основном пользуются в школах учителя для объяснения. В целом, он намного проще объясняется и быстрее понимается.
Стоит помнить, что для правильного преобразования простой дроби необходимо ее числитель поделить на знаменатель. Ведь если задуматься, то решение это и есть процесс деления.
Для того чтобы понять это простое правило, нужно рассмотреть следующий пример решения:
- Возьмем 78/200, которую нужно перевести в десятичную. Для этого следует 78 разделить на 200, то есть числитель на знаменатель.
- Но перед тем как начать, стоит провести проверку, как показано на рисунке 4.
- После того как убедились, что ее можно решить, следует приступать к процессу. Для этого стоит разделить числитель на знаменатель в столбик или уголком, как показано на рисунке 5.
 В начальных классах школ учат такому делению, и трудностей с этим не должно возникнуть.
В начальных классах школ учат такому делению, и трудностей с этим не должно возникнуть.
На рисунке 6 показаны примеры наиболее распространенных примеров, их просто можно запомнить, чтобы при необходимости не тратить время для решения. Ведь в школе на каждую контрольную или самостоятельную работы дается мало времени для решения, поэтому не стоит тратить его на то, что можно выучить и просто помнить.
Перевод процентов
Переводить проценты в десятичное число тоже достаточно легко. Этому начинают учить в 5 классе, а в некоторых школах еще раньше. Но если ваш ребенок на уроке математики не понял эту тему, можно наглядно ему еще раз объяснить. Для начала следует выучить определения понятия, что такое процент.
Процент — это одна сотая часть от какого-либо числа, другими словами, абсолютная произвольная. Например, от 100 это будет 1 и так далее.
На рисунке 7 показан наглядный пример перевода процентов.
Чтобы перевести процент, надо всего лишь убрать значок %, а затем разделить его на 100.
Еще 1 пример показан на рисунке 8.
Если надо провести обратную «конвертацию», необходимо все сделать с точностью до наоборот. Другими словами, число необходимо умножить на сто и после приписать значок процентов.
А для того чтобы обычную перевести в проценты, также можно использовать этот пример. Только изначально следует перевести дробь в число и только потом в проценты.
Исходя из описанного выше, можно легко понять принцип перевода. С помощью этих способов можно ребенку объяснять тему, если он ее не понял или не присутствовал на уроке в момент ее прохождения.
И никогда не будет необходимости нанимать репетитора, чтобы он объяснил ребенку, как перевести дробь в число или процент.
Вот, казалось бы, перевод десятичной дроби в обычную — элементарная тема, но многие ученики её не понимают! Поэтому сегодня мы подробно рассмотрим сразу несколько алгоритмов, с помощью которых вы разберётесь с любыми дробями буквально за секунду.
Напомню, что существует как минимум две формы записи одной и той же дроби: обыкновенная и десятичная. Десятичные дроби — это всевозможные конструкции вида 0,75; 1,33; и даже −7,41. А вот примеры обыкновенных дробей, которые выражают те же самые числа:
Десятичные дроби — это всевозможные конструкции вида 0,75; 1,33; и даже −7,41. А вот примеры обыкновенных дробей, которые выражают те же самые числа:
Сейчас разберёмся: как от десятичной записи перейти к обычной? И самое главное: как сделать это максимально быстро?
Основной алгоритм
На самом деле существует как минимум два алгоритма. И мы сейчас рассмотрим оба. Начнём с первого — самого простого и понятного.
Чтобы перевести десятичную дробь в обыкновенную, необходимо выполнить три шага:
Важное замечание по поводу отрицательных чисел. Если в исходном примере перед десятичной дробью стоит знак «минус», то и на выходе перед обыкновенной дробью тоже должен стоять «минус». Вот ещё несколько примеров:
Примеры перехода от десятичной записи дробей к обычной
Особое внимание хотелось бы обратить на последний пример. Как видим, в дроби 0,0025 присутствует много нулей после запятой. Из-за этого приходится аж целых четыре раза умножать числитель и знаменатель на 10. {3}}=1000$. Во-вторых, если убрать из десятичной записи запятую, то мы получим вот это: 0,004 → 0004. Вспомним, что нули слева надо убрать, поэтому по факту у нас число 4. Дальше всё просто: делим, сокращаем и получаем ответ.
{3}}=1000$. Во-вторых, если убрать из десятичной записи запятую, то мы получим вот это: 0,004 → 0004. Вспомним, что нули слева надо убрать, поэтому по факту у нас число 4. Дальше всё просто: делим, сокращаем и получаем ответ.
Наконец, последний пример:
Особенность этой дроби — наличие целой части. Поэтому на выходе у нас получается неправильная дробь 47/25. Можно, конечно, попытаться разделить 47 на 25 с остатком и таким образом вновь выделить целую часть. Но зачем усложнять себе жизнь, если это можно сделать ещё на этапе преобразований? Что ж, разберёмся.
Что делать с целой частью
На самом деле всё очень просто: если мы хотим получить правильную дробь, то необходимо убрать из неё целую часть на время преобразований, а затем, когда получим результат, вновь дописать её справа перед дробной чертой.
Например, рассмотрим то же самое число: 1,88. Забьём на единицу (целую часть) и посмотрим на дробь 0,88. Она легко преобразуется:
Затем вспоминаем про «утерянную» единицу и дописываем её спереди:
\[\frac{22}{25}\to 1\frac{22}{25}\]
Вот и всё! Ответ получился тем же самым, что и после выделения целой части в прошлый раз. Ещё парочка примеров:
Ещё парочка примеров:
\[\begin{align}& 2,15\to 0,15=\frac{15}{100}=\frac{3}{20}\to 2\frac{3}{20}; \\& 13,8\to 0,8=\frac{8}{10}=\frac{4}{5}\to 13\frac{4}{5}. \\\end{align}\]
В этом и состоит прелесть математики: каким бы путём вы не пошли, если все вычисления выполнены правильно, ответ всегда будет одним и тем же.:)
В заключение хотел бы рассмотреть ещё один приём, который многим помогает.
Преобразования «на слух»
Давайте задумаемся о том, что вообще такое десятичная дробь. Точнее, как мы её читаем. Например, число 0,64 — мы читаем его как «ноль целых, 64 сотых», правильно? Ну, или просто «64 сотых». Ключевое слово здесь — «сотых», т.е. число 100.
А что насчёт 0,004? Это же «ноль целых, 4 тысячных» или просто «четыре тысячных». Так или иначе, ключевое слово — «тысячных», т.е. 1000.
Ну и что в этом такого? А то, что именно эти числа в итоге «всплывают» в знаменателях на втором этапе алгоритма. Т.е. 0,004 — это «четыре тысячных» или «4 разделить на 1000»:
Попробуйте потренироваться сами — это очень просто. Главное — правильно прочесть исходную дробь. Например, 2,5 — это «2 целых, 5 десятых», поэтому
Главное — правильно прочесть исходную дробь. Например, 2,5 — это «2 целых, 5 десятых», поэтому
А какое-нибудь 1,125 — это «1 целая, 125 тысячных», поэтому
В последнем примере, конечно, кто-то возразит, мол, не всякому ученику очевидно, что 1000 делится на 125. Но здесь нужно помнить, что 1000 = 10 3 , а 10 = 2 ∙ 5, поэтому
\[\begin{align}& 1000=10\cdot 10\cdot 10=2\cdot 5\cdot 2\cdot 5\cdot 2\cdot 5= \\& =2\cdot 2\cdot 2\cdot 5\cdot 5\cdot 5=8\cdot 125\end{align}\]
Таким образом, любая степень десятки раскладывается лишь на множители 2 и 5 — именно эти множители нужно искать и в числителе, чтобы в итоге всё сократилось.
На этом урок окончен. Переходим к более сложной обратной операции — см. «
Пытаясь решить математические задачи с дробями, школьник понимает, что ему недостаточно одного только желания решить эти задачи. Также необходимы и знания по вычислениям с дробными числами. В некоторых задачах все начальные данные подаются в условии в дробном виде. В других же часть их может быть дробями, а часть — целыми числами. Чтобы производить какие-то вычисления с этими заданными значениями, надо сначала привести их к единому виду, то есть целые числа перевести в дробные, а потом уже заниматься вычислениями. Вообще способ, как целое число перевести в дробь, очень прост. Для этого надо в числителе итоговой дроби написать само заданное число, а в ее знаменателе — единичку. То есть если надо перевести в дробь число 12, то полученная дробь будет 12/1.
В других же часть их может быть дробями, а часть — целыми числами. Чтобы производить какие-то вычисления с этими заданными значениями, надо сначала привести их к единому виду, то есть целые числа перевести в дробные, а потом уже заниматься вычислениями. Вообще способ, как целое число перевести в дробь, очень прост. Для этого надо в числителе итоговой дроби написать само заданное число, а в ее знаменателе — единичку. То есть если надо перевести в дробь число 12, то полученная дробь будет 12/1.
Такие модификации помогают приводить дроби к общему знаменателю. Это нужно для того, чтобы получить возможность проводить вычитание или сложение дробных чисел. При их умножении и делении общий знаменатель не требуется. Можно рассмотреть на примере, как перевести число в дробь и потом произвести сложение двух дробных чисел. Допустим надо сложить число 12 и дробное число 3/4. Первое слагаемое (число 12) приводится к виду 12/1. Однако его знаменатель равен 1 в то время, как у второго слагаемого он равен 4. Для последующего сложения этих двух дробей надо привести их к общему знаменателю. Благодаря тому, что у одного из чисел знаменатель равен 1, это сделать вообще просто. Надо взять знаменатель второго числа и умножить на него и числитель, и знаменатель первого.
Для последующего сложения этих двух дробей надо привести их к общему знаменателю. Благодаря тому, что у одного из чисел знаменатель равен 1, это сделать вообще просто. Надо взять знаменатель второго числа и умножить на него и числитель, и знаменатель первого.
В результате умножения получится: 12/1=48/4. Если 48 разделить на 4, то получается 12, значит дробь приведена к правильному знаменателю. Таким образом можно заодно и понять, как дробь перевести в целое число. Это касается только неправильных дробей, потому что у них числитель больше, чем знаменатель. В таком случае числитель делится на знаменатель и, если не получается остатка, будет целое число. С остатком же дробь так и остается дробью, но с выделенной целой частью. Теперь относительно приведения к общему знаменателю на рассмотренном примере. Если бы у первого слагаемого знаменатель был бы равен какому-нибудь другому числу, кроме 1, числитель и знаменатель первого числа надо бы было умножить на знаменатель второго, а числитель и знаменатель второго — на знаменатель первого.
Оба слагаемых приведены к их общему знаменателю и готовы к сложению. Получается, что в данной задаче нужно сложить два числа: 48/4 и 3/4. При сложении двух дробей с одинаковым знаменателем суммировать нужно только их верхние части, то есть числители. Знаменатель суммы останется без изменения. В этом примере должно получиться 48/4+3/4=(48+3) /4=51/4. Это и будет результат сложения. Но в математике принято неправильные дроби приводить к правильным. Выше рассматривалось, как превратить дробь в число, но в этом примере не получится целое число из дроби 51/4, так как число 51 не делится без остатка на число 4. Поэтому нужно выделить целую часть данной дроби и ее дробную часть. Целой частью будет то число, которое получается при делении нацело первого же меньшего, чем 51, числа.
То есть то, которое можно разделить на 4 без остатка. Первое число перед числом 51, которое нацело делится на 4, будет число 48. Разделив 48 на 4, получается число 12. Значит целой частью искомой дроби будет 12. Осталось только найти дробную часть числа. Знаменатель дробной части остается тем же, то есть 4 в данном случае. Чтобы найти числитель дробной части, надо от исходного числителя вычесть то число, которое делилось на знаменатель без остатка. В рассматриваемом примере требуется для этого вычесть из числа 51 число 48. То есть числитель дробной части равен 3. Результатом сложения будет 12 целых и 3/4. То же самое делается и при вычитании дробей. Допустим надо из целого числа 12 вычесть дробное число 3/4. Для этого целое число 12 переводится в дробное 12/1, а затем приводится к общему знаменателю со вторым числом — 48/4.
Осталось только найти дробную часть числа. Знаменатель дробной части остается тем же, то есть 4 в данном случае. Чтобы найти числитель дробной части, надо от исходного числителя вычесть то число, которое делилось на знаменатель без остатка. В рассматриваемом примере требуется для этого вычесть из числа 51 число 48. То есть числитель дробной части равен 3. Результатом сложения будет 12 целых и 3/4. То же самое делается и при вычитании дробей. Допустим надо из целого числа 12 вычесть дробное число 3/4. Для этого целое число 12 переводится в дробное 12/1, а затем приводится к общему знаменателю со вторым числом — 48/4.
При вычитании точно так же знаменатель обеих дробей остается без изменения, а с их числителями и проводят вычитание. То есть от числителя первой дроби вычитают числитель второй. В данном примере это будет 48/4-3/4=(48-3) /4=45/4. И опять получилась неправильная дробь, которую надо привести к правильной. Для выделения целой части определяют первое до 45 число, которое делится на 4 без остатка. Это будет 44. Если число 44 разделить на 4, получится 11. Значит целая часть итоговой дроби равна 11. В дробной части также знаменатель оставляют без изменения а из числителя исходной неправильной дроби вычитают то число, которое делилось на знаменатель без остатка. То есть надо из 45 вычесть 44. Значит числитель в дробной части равен 1 и 12-3/4=11 и 1/4.
Это будет 44. Если число 44 разделить на 4, получится 11. Значит целая часть итоговой дроби равна 11. В дробной части также знаменатель оставляют без изменения а из числителя исходной неправильной дроби вычитают то число, которое делилось на знаменатель без остатка. То есть надо из 45 вычесть 44. Значит числитель в дробной части равен 1 и 12-3/4=11 и 1/4.
Если дано одно число целое и одно дробное, но его знаменатель равен 10, то проще второе число перевести в десятичную дробь, а потом производить вычисления. Например надо сложить целое число 12 и дробное число 3/10. Если число 3/10 записать в виде десятичной дроби, получится 0,3. Теперь значительно легче к 12 прибавить 0,3 и получить 2,3, чем приводить дроби к общему знаменателю, производить вычисления, а затем выделять целую и дробную части из неправильной дроби. Даже самые простые задачки с дробными числами предполагают, что школьник (или студент) знает, как перевести целое число в дробь. Эти правила слишком просты и легко запоминаются. Зато с помощью них очень просто проводить вычисления дробных чисел.
Зато с помощью них очень просто проводить вычисления дробных чисел.
Материалов по дробям и изучать последовательно. Ниже для вас подробная информация с примерами и пояснениями.
1. Смешанное число в обыкновенную дробь. Запишем в общем виде число:
Запоминаем простое правило – целую часть умножаем на знаменатель и прибавляем числитель, то есть:
Примеры:
2. Наоборот, обыкновенную дробь в смешанное число. *Конечно, это возможно сделать только с неправильной дробью (когда числитель больше знаменателя).
При «небольших» числах никаких действий, в общем, и не нужно делать, результат «видно» сразу, например, дроби:
*Подробнее:
15:13 = 1 остаток 2
4:3 = 1 остаток 1
9:5 = 1 остаток 4
А вот если числа будут более, то без вычислений не обойтись. Здесь всё просто – делим уголком числитель на знаменатель до тех пор пока остаток не получится менее делителя. Схема деления:
Например:
*Числитель у нас – это делимое, знаменатель – это делитель.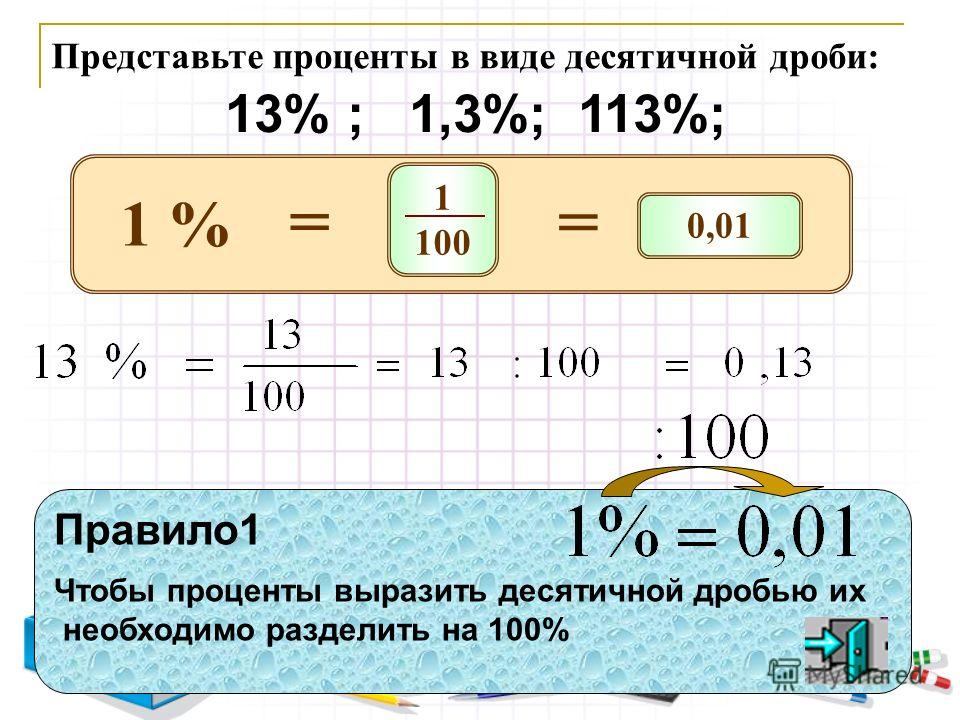
Получаем целую часть (неполное частное) и остаток. Записываем – целое, затем дробь (в числителе остаток, а знаменатель оставляем тот же):
3. Десятичную переводим в обыкновенную.
Частично в первом пункте, где рассказывали про десятичные дроби мы уже коснулись этого. Как слышим так и записываем. Например — 0,3; 0,45; 0,008; 4,38; 10,00015
Первые три дроби у нас без целой части. А четвёртая и пятая её имеют, переведём их в обыкновенные, это делать уже умеем:
*Мы видим, что дроби можно ещё и сократить, например 45/100 =9/20, 38/100=19/50 и другие, но мы здесь делать этого не будем. По сокращению вас ожидает отдельный пункт ниже, где подробно всё разберём.
4. Обыкновенную переводим в десятичную.
Тут не всё так просто. По каким-то дробям сразу видно и ясно, что с ней сделать, чтобы она стала десятичной, например:
Используем наше замечательное основное свойство дроби – умножаем числитель и знаменатель соответственно на 5, 25, 2, 5, 4, 2, получим:
Если имеется целая часть, то тоже ничего сложного:
Умножаем дробную часть соответственно на 2, 25, 2 и 5, получим:
А есть такие, по которым без опыта и не определить, что их можно перевести в десятичные, например:
На какие числа умножать числитель и знаменатель?
Тут опять на помощь приходит проверенный способ – деление уголком, способ универсальный, им для перевода обыкновенной дроби в десятичную можно пользоваться всегда:
Так вы сможете всегда определить переводится ли дробь в десятичную. Дело в том, что не каждую обыкновенную дробь можно перевести в десятичную, например такие как 1/9, 3/7, 7/26 не переводятся. А что же тогда получается за дробь при делении 1 на 9, 3 на 7, 5 на 11? Отвечаю – бесконечная десятичная (говорили о них в пункте 1). Разделим:
Дело в том, что не каждую обыкновенную дробь можно перевести в десятичную, например такие как 1/9, 3/7, 7/26 не переводятся. А что же тогда получается за дробь при делении 1 на 9, 3 на 7, 5 на 11? Отвечаю – бесконечная десятичная (говорили о них в пункте 1). Разделим:
На этом всё! Успеха вам!
С уважением, Александр Крутицких.
Перевести 33 целых 1/3 в десятичную дробь
Математика, 2021-09-01 02:47:54, RaidFrame
Ответ
Ответ разместил: ауе59
33 целых 1/3=33, 333333=33,(3)
Ответ
Ответ разместил: Akimneznaet123
100 делить на 30
Ответ
Ответ разместил: Reshebnikov
1 1/36
Превратим в неправильную дробь, целую часть умножив на знаменатель и прибавив к полученному значению числитель:
1*36+1=37
Получим дробь:
37/36 =(примерно) 1,03
Это не точное значение.
Ответ
Ответ разместил: Адамчик11
1 : 3=0,(3)
4+0,(3)=4,(3)
Ответ
Ответ разместил: supervitalik15
1 целая 1/3 =4/3
Ответ
Ответ разместил: ооо322
1/3 в десятичную дробь= 0,(3)()-значит в периоде
Ответ
Ответ разместил: pelmenev777
1/3 нельзя перевести в десятичную дробь так как чтобы перевести обычную дробь перевести в десятичную надо верхнее число разделить на нижнее. а делить 1 на 3 можно бесконечно
а делить 1 на 3 можно бесконечно
Ответ
Ответ разместил: radacherepkova
2 1/3=2,3333333333333
или 2,(3)
Читается две целых,3 в периоде
Ответ
Ответ разместил: ApollaKop
7/3
Умножаешь на знаменатель и прибавляешь числитель
Ответ
Ответ разместил: IDebil
8 целых так и останутся — 8 целых.
А вот дробь 1/3 — в десятичной записи — бесконечная.
1/3 = 0,3333333333 — период у этой дроби короткий — 3.
Для краткости записывают в виде
8 1/3 = 8,(3) = ОТВЕТ
Другие вопросы по: Математика
Первая бригада выполнила за 12 дней , другая за 21 день , третяя за 28 дней . за сколько дней 3 бригады выполнят при совместной работе?…
Опубликовано: 28.02.2019 03:10
Ответов: 3
Расстояние от дома до школы можно пройти пешком за 45мин. а на велосипеде за 20мин. на каком расстояние от дома находится школа, если скорость движения на велосипеде на 6 км/ч боль…
Опубликовано: 28.02.2019 06:10
Ответов: 2
Смежные стороны параллелограмма равны 32 см и 26 см, а один из углов равен 150 градусов. найдите площадь параллелограмма….
Опубликовано: 02.03.2019 06:30
Ответов: 2
Периметр квадрата 20 см. это на 6 см меньше, чем периметр прямоугольника. сторона квадрата равна ширине прямоугольника. найди длину прямоугольника….
Опубликовано: 03.03.2019 01:30
Ответов: 1
Какое проверочное слово к слово трактористы. скажите?…
Опубликовано: 03.03.2019 02:40
Ответов: 1
Рассчитайте количество всех веществ участвующих в реакции 4p+5o2=2p2o5 если прореагировало 310 грамм фосфора…
Опубликовано: 03.03.2019 10:00
Ответов: 1
Популярные вопросы
.(Втечении дня первые 2часа рабочий делал 12деталей в час. следующие 3ч-по10 деталей. а последние 3ч-по 7 деталей в час. сколько деталей в среднем сделал рабочий за 1час в этот ден…
следующие 3ч-по10 деталей. а последние 3ч-по 7 деталей в час. сколько деталей в среднем сделал рабочий за 1час в этот ден…
Опубликовано: 27.02.2019 23:50
Ответов: 2
Вычислите массу карбоната натрия образовавшегося припропускании 44,8 л углекислого гаа через избыток раствора гидроксида натрия…
Опубликовано: 28.02.2019 07:40
Ответов: 1
Решить дроби : 1) (а-5целых тринадцать четырнадцатых)+8целых тринадцать четырнадцатых= 15-3целых девять четырнадцатых 2) 12целых семь двадцать третьих-(6целых восемнадцать двадцать…
Опубликовано: 02.03.2019 13:00
Ответов: 1
Нужно вставить на месте пропусков слова. у рыб. из них плавники, а — непарные плавники….
Опубликовано: 03.03.2019 12:10
Ответов: 2
Цепочку решить) hno3—> nh5no3—> hno3—> o2…
Опубликовано: 04.03.2019 01:50
Ответов: 1
Вставьте необходимые предлоги: a tourist took a taxi the nightclub the hotel where he was staing. a) in/ up b) from/before c) in/to d) at/to e) from/to 2.дополните предложение: i t…
a) in/ up b) from/before c) in/to d) at/to e) from/to 2.дополните предложение: i t…
Опубликовано: 04.03.2019 03:30
Ответов: 1
Решить 5 класс: запишите десятичные дроби в виде суммы разрядных слагаемых 1)2,9; 4,61; 0,38; 0,036; 2)3,28; 9,641; 6,891; 5,085; 3)9,06; 7,901; 8,003; 5,0308….
Опубликовано: 04.03.2019 04:20
Ответов: 3
1) 6,3+19цел 1/2+3цел 2/3, 2) 2,64+5цел 2/3+2/15, 3)9, 25+3цел 5/6+ 1цел 2/3, 4) 2 цел 1/4+ 3,6+1/6, 5)0,05+10цел 7/12+1/5, 6)4цел 3/8+2,25+14цел 7/10, 7) 9,5+ 5 цел 9/10+ 6цел 1/3…
Опубликовано: 04.03.2019 06:50
Ответов: 2
Рыночная цена картофеля в связи с ненастной погодой повысилась на 20%. через некоторое время цена картофеля понизилась на 20%. когда картофель стоил дешевле : до повышения или посл…
Опубликовано: 06.03.2019 20:50
Ответов: 3
√из 51-13x =5 найти корень уравнения. ..
..
Опубликовано: 06.03.2019 21:50
Ответов: 1
Больше вопросов по предмету: Математика Случайные вопросы
Урок 62. деление положительных десятичных дробей. часть 1 — Математика — 6 класс
Математика
6 класс
Урок № 62
Деление положительных десятичных дробей. Часть 1
Перечень рассматриваемых вопросов:
- десятичная запись дробей;
- деление десятичной дроби на натуральное число;
- деление десятичной дроби на десятичную дробь;
- перевод обыкновенной дроби в десятичную.
Тезаурус
Десятичная дробь – это дробь, у которой знаменатель является степенью числа 10.
Десятичные дроби записывают без знаменателей, выделяя целую часть (целая часть правильной дроби считается равной 0) и отделяя её запятой от числителя дробной части.
Чтобы разделить десятичную дробь на натуральное число, нужно разделить дробь на это число, не обращая внимания на запятую, а в частном поставить запятую в тот момент, когда закончится деление целой части делимого.
Чтобы разделить десятичную дробь на десятичную, надо:
– перенести в делимом и в делителе запятые вправо на столько цифр, сколько их содержится после запятой в делителе;
– выполнить деление на натуральное число.
Чтобы записать обыкновенную дробь в виде десятичной, нужно числитель этой дроби разделить на знаменатель.
Обязательная литература:
- Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017, стр. 258.
Дополнительная литература:
- Чулков П. В. Математика: тематические тесты.5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина – М.: Просвещение, 2009, стр. 142.
- Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин – М.: Просвещение, 2014, стр. 95.
Теоретический материал для самостоятельного изучения
Частное двух десятичных дробей всегда можно записать в виде обыкновенной дроби. В то же время не любая обыкновенная дробь может быть записана как десятичная. На этом уроке мы рассмотрим только такие случаи, когда частное есть десятичная дробь или натуральное число.
В то же время не любая обыкновенная дробь может быть записана как десятичная. На этом уроке мы рассмотрим только такие случаи, когда частное есть десятичная дробь или натуральное число.
Рассмотрим несколько примеров, в которых десятичную дробь мы делим на натуральное число.
1,2 : 3 = 0,4, так как 0,4 · 3 = 1,2
2,4 : 8 = 0,3, так как 0,3 · 8 = 2,4
Но это случаи, когда деление можно выполнить устно. А что делать в случаях, когда устные вычисления невозможны?
Деление десятичных дробей будем производить так же, как и деление натуральных чисел – уголком.
Рассмотрим деление 42,12 на 18
Запишем деление уголком и будем делить, не обращая внимания на запятую. При этом запятую в частном поставим в тот момент, когда спишем первую цифру после запятой в делимом.
Проверим получившийся ответ.
2,34·18= 42,12
Деление выполнено верно.
Если целая часть делимого меньше делителя, то целая часть частного равна нулю.
Например,
4,42:13
4 целых разделить нацело на 13 нельзя, поэтому пишем 0. Производим вычитание и списываем из делимого первую цифру после запятой, и сразу ставим запятую в частном. Продолжаем выполнять деление. Получаем
Производим вычитание и списываем из делимого первую цифру после запятой, и сразу ставим запятую в частном. Продолжаем выполнять деление. Получаем
4,42:13=0,34
Рассмотрим ещё один пример.
Найдём частное
3,1:4
Мы остановили процесс деления, так как закончились цифры в делимом. При этом ноль в остатке мы ещё не получили. Вспомните, что справа после последней цифры в десятичной дроби можно приписать бесконечное количество нулей, от этого десятичная дробь не изменится. Получаем
3,1 = 3,10000…
Продолжаем деление.
Теперь мы можем находить частное от деления двух натуральных чисел даже в случае, если делимое не делится нацело на делитель.
Например,
21:5
Выполняем деление, помня о том, что 21 = 21,0000. Списывая первую цифру из дробной части, ставим запятую.
Итак, мы разобрались с делением десятичной дроби на целое число. Теперь рассмотрим деление на десятичную дробь.
Если делимое и делитель одновременно увеличить в 10,100,1000 и так далее раз, то частное не изменится. Это следует из основного свойства обыкновенной дроби.
Это следует из основного свойства обыкновенной дроби.
Пример
Значит, для того, чтобы разделить 12,88 на 4,6, нужно делимое и делитель одновременно умножить на 10, получим: 12,88:4,6 = 128,8 : 46. То есть в результате получим деление на натуральное число.
Таким образом, можно представлять обыкновенную дробь в виде десятичной. Помним, что дробная черта аналогична знаку деления.
Получаем
Решим уравнение.
9,2 · x = 3,68,
x = 3,68 : 9,2,
x = 0,4.
Ответ: 0,4.
Задача. Поезд проехал 138,6 км за 2,8 часов. Какое расстояние он проедет за 6,2 часа с той же скоростью?
Найдём скорость движения поезда. Для этого пройденное расстояние разделим на время пути.
138,6 км : 2,8 ч = 49,5 (км/ч) – скорость поезда.
Найдём расстояние, которое поезд проедет за 6,2 часа. Для этого скорость поезда умножим на время пути.
49,5 км/ч · 6,2 ч = 306,9 (км).
Ответ: 306,9 км – расстояние, которое проедет поезд за 6,2 часа.
Задача. Моторная лодка проплыла 20,08 км по течению реки и 41,23 км против течения. Сколько времени плыла лодка, если её собственная скорость равна 23,4 км/ч, а скорость течения равна 1,7 км/ч?
Сначала найдём скорость лодки по течению, для этого к скорости течения прибавим собственную скорость лодки.
23,4 км/ч + 1,7 км/ч = 25,1 (км/ч) – скорость по течению.
Найдём скорость против течения. Для этого из скорости лодки вычтем скорость течения.
23,4 км/ч – 1,7 км/ч = 21,7 (км/ч) – скорость против течения.
Найдём время, за которое лодка проплыла путь по течению. Для этого расстояние, пройденное по течению, разделим на скорость движения по течению.
20,08 км : 25,1 км/ч = 0,8 (ч) – время, которое плыла лодка по течению.
Найдём время, за которое лодка проплыла путь против течения. Для этого расстояние, пройденное против течения, разделим на скорость движения против течения.
41,23 км : 21,7 км/ч = 1,9 (ч) – время, которое плыла лодка против течения.
Найдём общее время нахождения лодки в пути.
1,9 ч + 0,8 ч = 2,7 (ч) – всего плыла лодка.
Ответ: лодка находилась в пути 2,7 ч.
Разбор заданий тренировочного модуля
Вычислите значение выражения и впишите правильный ответ.
168 : 0,7 – 9,28 : 11,6 – 30 : 96 + 0,1125 = …
Выполним деление.
168 : 0,7 = 1680 : 7= 240,
9,28 : 11,6 = 92,8 : 116 = 0,8,
30 : 96 = 0,3125.
Выполним вычитание.
240 – 0,8 = 239,2,
239,2 – 0,3125 = 238,8875.
Выполним сложение.
238,8875 + 0,1125 = 239.
Ответ: 239.
Что такое 1/3 в виде десятичной дроби? (Преобразовать 1/3 в десятичную)
Преобразование 1/3 в десятичную, возможно, является одним из самых простых вычислений, которые вы можете сделать. В этом (очень коротком) руководстве мы покажем вам, как превратить любую дробь в десятичную менее чем за 3 секунды! Вот так!
Хотите быстро узнать или показать учащимся, как преобразовать 1/3 в десятичную дробь? Включи это очень быстрое и веселое видео прямо сейчас!
Прежде всего, если вы не знаете, что такое числитель и знаменатель в дроби, нам нужно повторить это:
1 (числитель) / 3 (знаменатель)
Вот маленький секрет, с помощью которого можно мгновенно преобразовать любую дробь в десятичную: Просто разделите числитель на знаменатель:
= 1/3
= 1 ÷ 3
2 = 0,33333333333 0,33333333333 Вот буквально все! 1/3 в виде десятичной дроби равно 0,333333333333333.

Хотел бы я рассказать вам больше о преобразовании дроби в десятичную, но это действительно так просто, и мне больше нечего об этом сказать.
Если вы хотите потренироваться, возьмите ручку и блокнот и попробуйте самостоятельно вычислить некоторые дроби в десятичном формате. Если вы действительно чувствуете себя ленивым , вы можете вместо этого использовать наш калькулятор ниже!
Почему вы хотите преобразовать 1/3 в десятичную дробь?
Отличный вопрос. У нас есть много расчетов на этом сайте о преобразовании дроби в десятичную, но зачем вам вообще это нужно?
Ну, во-первых, это просто хороший способ представить дробь в лучшем виде, который позволяет вам выполнять с ними обычные арифметические действия (такие как сложение, вычитание, деление и умножение).
В реальной жизни мы в основном имеем дело с десятичными дробями (например, с валютой), и, поскольку наш мозг с юных лет приучают понимать и сравнивать десятичные дроби чаще, чем дроби, проще понимать и сравнивать дроби, если они сначала преобразовать в десятичную!
Вот небольшой пример из реальной жизни преобразования дроби в десятичную при использовании количества. Допустим, вы готовите, и обычно вы можете видеть, сколько ингредиента осталось в упаковке. Однако электронные весы измеряют вес в десятичных дробях, а не в долях оставшегося ингредиента. Это делает преобразование между дробями и десятичными дробями полезным навыком в кулинарии.
Допустим, вы готовите, и обычно вы можете видеть, сколько ингредиента осталось в упаковке. Однако электронные весы измеряют вес в десятичных дробях, а не в долях оставшегося ингредиента. Это делает преобразование между дробями и десятичными дробями полезным навыком в кулинарии.
Надеюсь, это руководство помогло вам понять, как преобразовать дробь в десятичное число. Теперь вы можете идти вперед и преобразовывать дроби в десятичные столько, сколько пожелает ваше маленькое сердце!
Процитируйте, дайте ссылку или ссылку на эту страницу
Если вы нашли этот контент полезным в своем исследовании, пожалуйста, сделайте нам большую услугу и используйте приведенный ниже инструмент, чтобы убедиться, что вы правильно ссылаетесь на нас, где бы вы его ни использовали. Мы очень ценим вашу поддержку!
«Что такое 1/3 в виде десятичной дроби?».
 VisualFractions.com . По состоянию на 27 сентября 2022 г. http://visualfractions.com/calculator/fraction-as-decimal/what-is-1-3-as-a-decimal/.
VisualFractions.com . По состоянию на 27 сентября 2022 г. http://visualfractions.com/calculator/fraction-as-decimal/what-is-1-3-as-a-decimal/.«Что такое 1/3 в виде десятичной дроби?». VisualFractions.com , http://visualfractions.com/calculator/fraction-as-decimal/what-is-1-3-as-a-decimal/. По состоянию на 27 сентября 2022 г.
Что такое 1/3 в виде десятичной дроби?. VisualFractions.com. Получено с http://visualfractions.com/calculator/fraction-as-decimal/what-is-1-3-as-a-decimal/.
Калькулятор преобразования дроби в десятичную дробь
Дробь в виде десятичной дроби
Введите числитель и знаменатель
Вычисление следующей дроби в десятичную дробь
- Что такое 1/4 в виде десятичной дроби?
Случайные дроби в десятичные числа
Если вы добрались до этого конца страницы, значит, вы ДЕЙСТВИТЕЛЬНО любите преобразовывать дроби в десятичные? Ниже приведена куча случайно сгенерированных вычислений для вашего удовольствия от десятичной любви:
Что такое 807/858 как десятичная
Что такое десятичное число 256/315?
Что такое десятичное число 95/965?
Что такое десятичное число 691/914?
Что такое десятичное число 950/966?
Десятичное число 892/949
Десятичное число 666/870
Десятичное число 548/973
Десятичное число 718/940
Десятичное число
890/92
Что такое 384/542 в виде десятичного числа
Что такое 89/914 в виде десятичного числа
Десятичное число 169/439
Десятичное число 105/978
Десятичное число 709/748
Десятичное число 904/911
Десятичное число 274/975
Десятичное число 455/576
Десятичное число 391/583
Десятичное число 613/811
Десятичное число 59
Что такое 108/340 в виде десятичного числа
Что такое 621/736 в виде десятичного числа
Десятичное число 224/597
Десятичное число 603/955
Десятичное число 184/938
Десятичное число 727/843
Десятичное число 6 a 226/28
Десятичное число 647/779
Десятичное число 539/801
Десятичное число 971/981
Десятичное число 865/961
Десятичное число 46
Что такое 73/494 в виде десятичного числа
Что такое 711/759 в виде десятичного числа
Десятичное число 566/796
Десятичное число 463/906
Десятичное число 348/550
Десятичное число 828/904
Десятичное число 128/90
Десятичное число 693/742
Десятичное число 921/940
Десятичное число 456/894
Десятичное число 990/995
Десятичное число 63 845/9002
Что такое 880/890 в виде десятичного числа
Что такое 547/976 в виде десятичного числа
Что такое десятичное число 107/145?
Что такое десятичное число 897/974?
Что такое десятичное число 824/846?
Что такое десятичное число 103/333?
Десятичное число 127/310
Десятичное число 312/728
Десятичное число 363/554
Десятичное число 453/944
Десятичное число 7 1
Что такое 490/947 в виде десятичного числа
Что такое 733/959 в виде десятичного числа
Что такое десятичное число 170/647?
Что такое десятичное число 955/995?
Что такое десятичное число 595/704?
Что такое десятичное число 573/933?
Десятичное число 845/917
Десятичное число 965/983
Десятичное число 914/1000
Десятичное число 192/528
Десятичное число 610/61
Что такое 318/922 в виде десятичного числа
Что такое 928/965 в виде десятичного числа
Десятичное число 37/689
Десятичное число 682/930
Десятичное число 679/708
Десятичное число 311/684
Десятичное число 676/73
Десятичное число 21/540
Десятичное число 312/901
Десятичное число 985/995
Десятичное число 340/540
Десятичное число 7 a 996/99
Что такое 706/909 в виде десятичного числа
Что такое 257/307 в виде десятичного числа
Десятичное число 197/347
Десятичное число 963/987
Десятичное число 238/341
Десятичное число 732/826
Десятичное число 9
Десятичное число 452/514
Десятичное число 426/936
Десятичное число 313/884
Десятичное число 579/830
Десятичное число 5 601/7
Что такое 803/941 в виде десятичного числа
Что такое 272/857 в виде десятичного числа
Десятичное число 817/878
Десятичное число 235/910
Десятичное число 47/736
Десятичное число 766/778
1/3 десятичное число Точка будущего
Сообщите нам о 1/3 в виде десятичной дроби.
Кроме того, что такое 3/4 в виде десятичной дроби?
Ответ: 3/4 выражается как 0,75 в десятичной форме.
Здесь что такое 1/3 в процентах?
пример значения
| Percent | decimal | Part |
|---|---|---|
| 33 1/3 % | 0.333 … | 1/3 |
| up to 50 | 0.5 | 1/2 |
| up to 75% | 0.75 | 3/4 |
| up to 80% | 0.8 | 4 /5 |
Также, чтобы знать, что 3 и 1/3 имеют в качестве десятичной дроби? Таким образом, ответ состоит в том, что 3 1/3 в виде десятичной дроби равно 3,33333333333333 .
Что такое 1/3 в виде десятичной дроби и процента?
Некоторые распространенные десятичные дроби и дроби
| Часть | десятичная | Проценты |
|---|---|---|
| 1/3 | 0,33309? | 33,333 ?% |
| 2 / 3 | 0,666? | 66,666?% |
| 1/4 | 0,25 | До 25% |
| 3/4 | 0,75 | до 75% | до 75% |
 9114.9114.99114.
9114.9114.99114.Метод 1: Запишите 1 3/4 в десятичном виде, используя метод деления. Чтобы преобразовать дробь в десятичную форму, нужно разделить ее числитель на знаменатель. Это дает ответ 1,75 . Итак, десятичная дробь до 1 3/4 равна 1,75.
Что такое 3/4 в процентах?Ответ: 3/4 выражается в процентах до 75%.
Как рассчитать 1/3 от суммы?Следовательно, это одна треть суммы. Подсчет третей 3. выполняется путем деления на . Например: Одна треть от 24 = 3/24 от 1 = 24/3 = 8.
Что такое 3/4 в процентах?Ответ: 3/4 выражается в процентах до 75%.
Что такое 3/100 как часть 1?Ответ: 1/3 от 100 составляет 100/3 или 33⅓.
Что такое 1/3 в калькуляторе? 1 / 3 = 13 0,3333333 .
Большинство людей напишет это как 0,33 , 0,333, 0,3333 и т. д. Используйте 13 как 0,333 или 0,33 в зависимости от уровня точности, требуемого в упражнении. 0,333,0,3333 является точным и, следовательно, точным.
Что такое 1 и 3/4 как дробь?Ответ и объяснение: Смешанное число 1 3/4 будет равно неправильной дроби 7 / 4 .
Что такое 1 и 3/4 в процентах?Результат: смешанное число 1 3/4 можно выразить как 175 процентов .
Что такое 3 и 3/4 в виде десятичной дроби?1 ответ эксперта
Таким образом, десятичная часть для этого 0,75 .
Что такое 3/4 в виде дроби?Таблица преобразования десятичных и дробных чисел
| Part | equivalent part | decimal |
|---|---|---|
| 3/4 | 6 / 8 | 75. |
| 1 / 5 | 2 / 10 | .2 |
| 2/5 | 4/10 | .4 |
| 3 /5 | 6 /10 | .6 |
Таблица преобразования десятичных и дробных чисел
| Part | equivalent part | |
|---|---|---|
| 2 / 3 | 4 / 6 | 8 / 12 |
| 1/4 | 2 / 8 | 4 / 16 |
| 3/ 4 | 6 / 8 | 12 /16 |
| 1 /5 | 2 /10 | 4 /20 |
для преобразования в проценты
Чтобы преобразовать дробь в десятичную, сначала преобразуйте ее в десятичную, а затем умножьте на 100. Таким образом, решение равно до 37,5% .
Как называется 1/3? называются дробями . 1/3 представляет собой 3 части из 1 равной части.
1/3 представляет собой 3 части из 1 равной части.
Половина больше трети. Поскольку две дроби, 1/3 и 1/2, имеют один и тот же числитель (помните, что числитель — это число вверху), их легко сравнивать. Если у двух дробей один и тот же числитель, то большей будет та дробь, у которой знаменатель меньше. Следовательно, 1/2 больше, чем 1/3.
Как упростить 4 3?
Вычесть 4/3 в наименьшем выражении
- Найдите НОД (или HCF) числителя и знаменателя. НОД чисел 4 и 3 равен 1.
- 4 13 1.
- Сокращенная дробь: 43. Следовательно, 4/3 равно 4/3 от упрощенного до наименьшего слагаемого.
1 из 5 совпадает с 20 процентов .
Что составляет треть от 3%?1/3 x 100 = 33,33
Если вы умножите 0,33 на 100, вы увидите, что вы получите тот же ответ, что и выше. Вам также может быть полезно знать, что если вы умножите 0,33 на 100, вы получите 33,33. Это означает, что наш ответ 33,33 на 100% равен 33,33.
Вам также может быть полезно знать, что если вы умножите 0,33 на 100, вы получите 33,33. Это означает, что наш ответ 33,33 на 100% равен 33,33.
3. Если лист разделен на три равные части, то говорят, что каждая часть составляет одну треть всего листа. Таким образом, одна из трех равных частей целого называется его одной третью и выражается как 1/3 , что записывается как одна треть или одна треть.
Просмотры сообщений: 56
Преобразование 1 3/16 в десятичную форму
1 3/16 равно 1,1875 в десятичной форме. Используйте наш калькулятор преобразования дробей в десятичные, чтобы преобразовать любую дробь в десятичную и узнать, является ли она завершающей или повторяющейся (повторяющейся) десятичной дробью.
Калькулятор / конвертер дробей в десятичные дроби
| Введите дробное значение: Пример: 1/2, 2 1/2, 5/3 и т. |
Ответ: |
Пошаговое решение: |
| Цитаты |
См. также:
- Калькулятор дробей
- Калькулятор десятичной дроби
- Калькулятор доли в процентах
- Фракции Simplifier/Reducer
- Калькулятор эквивалентных дробей
Таблица преобразования: дробь в десятичные дюймы и эквивалент в миллиметрах
Чтобы преобразовать дроби в десятичные дроби и миллиметры и наоборот, используйте эту формулу:
1 дюйм = 25,4 мм точно, поэтому …
Чтобы преобразовать из дюймов в миллиметры умножьте значение в дюймах на 25,4.
Чтобы преобразовать миллиметры в дюймы, разделите значение в миллиметрах на 25,4.
Проще всего это сделать с помощью приведенной ниже таблицы. Как?
Пример 1
Преобразование 1 1/32 дюйма в миллиметры:
Найдите 1 1/32 и прочитайте справа под столбцом мм! Вы найдете 26,1938. форма).
форма).
| fraction | decimal | mm | ||||||
|---|---|---|---|---|---|---|---|---|
| 1/64 | 0.0156 | 0.3969 | ||||||
| 1/32 | 0.0313 | 0.7938 | ||||||
| 3/64 | 0.0469 | 1.1906 | ||||||
| 1/16 | 0.0625 | 1.5875 | ||||||
| 5/64 | 0.0781 | 1.9844 | ||||||
| 3/32 | 0.0938 | 2.3813 | ||||||
| 7/64 | 0.1094 | 2.7781 | ||||||
| 1/8 | 0.1250 | 3.1750 | ||||||
| 9/64 | 0.1406 | 3.5719 | ||||||
| 5/32 | 0.1563 | 3.9688 | ||||||
| 11/64 | 0.1719 | 4.3656 | ||||||
| 3/16 | 0.1875 | 4.7625 | ||||||
| 13/64 | 0.2031 | 5.1594 | ||||||
| 7/32 | 0. 2188 2188 | 5.5563 | ||||||
| 15/64 | 0.2344 | 5.9531 | ||||||
| 1/4 | 0.2500 | 6.3500 | ||||||
| 17/64 | 0.2656 | 6.7469 | ||||||
| 9/32 | 0.2813 | 7.1438 | ||||||
| 19/64 | 0.2969 | 7.5406 | ||||||
| 5/16 | 0.3125 | 7.9375 | ||||||
| 21/64 | 0.3281 | 8.3344 | ||||||
| 11/32 | 0.3438 | 8.7313 | ||||||
| 23/64 | 0.3594 | 9.1281 | ||||||
| 3/8 | 0.3750 | 9.5250 | ||||||
| 25/64 | 0.3906 | 9.9219 | ||||||
| 13/32 | 0.4063 | 10.3188 | ||||||
| 27/64 | 0.4219 | 10.7156 | ||||||
| 7/16 | 0.4375 | 11.1125 | ||||||
| 29/64 | 0. 4531 4531 | 11.5094 | ||||||
| 15/32 | 0.4688 | 11.9063 | ||||||
| 31/64 | 0.4844 | 12.3031 | ||||||
| 1/2 | 0,5000 | 12,7000 | ||||||
| 33/64 | 0,5156 | 13.0969 | 13.0969 | 0013.0969 | 0013.0969 | 13.0969 | 13.0969 | .0317 |
| 35/64 | 0.5469 | 13.8906 | ||||||
| 9/16 | 0.5625 | 14.2875 | ||||||
| 37/64 | 0.5781 | 14.6844 | ||||||
| 19/32 | 0.5938 | 15.0813 | ||||||
| 39/64 | 0.6094 | 15.4781 | ||||||
| 5/8 | 0.6250 | 15.8750 | ||||||
| 41/64 | 0.6406 | 16.2719 | ||||||
| 21/32 | 0. 6563 6563 | 16.6688 | ||||||
| 43/64 | 0.6719 | 17.0656 | ||||||
| 11/16 | 0.6875 | 17.4625 | ||||||
| 45/64 | 0.7031 | 17.8594 | ||||||
| 23/32 | 0.7188 | 18.2563 | ||||||
| 47/64 | 0.7344 | 18.6531 | ||||||
| 3/4 | 0.7500 | 19.0500 | ||||||
| 49/64 | 0.7656 | 19.4469 | ||||||
| 25/32 | 0.7813 | 19.8438 | ||||||
| 51/64 | 0.7969 | 20.2406 | ||||||
| 13/16 | 0.8125 | 20.6375 | ||||||
| 53/64 | 0.8281 | 21.0344 | ||||||
| 27/32 | 0.8438 | 21.4313 | ||||||
| 55/64 | 0.8594 | 21.8281 | ||||||
| 7/8 | 0.8750 | 22.2250 | ||||||
| 57/64 | 0. 8906 8906 | 22.6219 | ||||||
| 29/32 | 0.9063 | 23.0188 | ||||||
| 59/ 64 | 0,9219 | 23.4156 | ||||||
| 15/16 | 0,9375 | 23,8125 | ||||||
| 6114 | ||||||||
| 6414 | ||||||||
| 64149125 | ||||||||
| 649125 | ||||||||
| 649125 | ||||||||
| 63,8125 | .31/320.9688 | 24.6063 | ||||||
| 63/64 | 0.9844 | 25.0031 | ||||||
| 1 | 1.0000 | 25.4000 |
| fraction | decimal | mm |
|---|---|---|
| 1 1/64 | 1.0156 | 25.7969 |
| 1 1/32 | 1.0313 | 26.1938 |
| 1 3/64 | 1.0469 | 26.5906 |
| 1 1/16 | 1.0625 | 26.9875 |
| 1 5/64 | 1. 0781 0781 | 27.3844 |
| 1 3/32 | 1.0938 | 27.7813 |
| 1 7 /64 | 1.1094 | 28.1781 |
| 1 1/8 | 1.1250 | 28.5750 |
| 1 9/64 | 1.1406 | 28.9719 |
| 1 5/32 | 1.1563 | 29.3688 |
| 1 11/64 | 1.1719 | 29.7656 |
| 1 3/16 | 1.1875 | 30.1625 |
| 1 13/64 | 1.2031 | 30.5594 |
| 1 7/32 | 1.2188 | 30.9563 |
| 1 15/64 | 1.2344 | 31.3531 |
| 1 1/4 | 1.2500 | 31.7500 |
| 1 17/64 | 1.2656 | 32.1469 |
| 1 9/32 | 1.2813 | 32.5438 |
| 1 19/64 | 1.2969 | 32. 9406 9406 |
| 1 5/16 | 1.3125 | 33.3375 |
| 1 21/64 | 1.3281 | 33.7344 |
| 1 11/32 | 1.3438 | 34.1313 |
| 1 23/64 | 1.3594 | 34.5281 |
| 1 3/8 | 1.3750 | 34.9250 |
| 1 25/64 | 1.3906 | 35.3219 |
| 1 13/32 | 1.4063 | 35.7188 |
| 1 27/64 | 1.4219 | 36.1156 |
| 1 7/16 | 1.4375 | 36.5125 |
| 1 29/64 | 1.4531 | 36.9094 |
| 1 15/32 | 1.4688 | 37.3063 |
| 1 31/64 | 1.4844 | 37.7031 |
| 1 1/2 | 1.5000 | 38.1000 |
| 1 33/64 | 1.5156 | 38. 4969 4969 |
| 1 17/32 | 1.5313 | 38.8938 |
| 1 35/64 | 1.5469 | 39.2906 |
| 1 9/16 | 1.5625 | 39.6875 |
| 1 37/64 | 1.5781 | 40.0844 |
| 1 19/32 | 1.5938 | 40.4813 |
| 1 39/64 | 1.6094 | 40.8781 |
| 1 5/8 | 1.6250 | 41.2750 |
| 1 41/64 | 1.6406 | 41.6719 |
| 1 21/32 | 1.6563 | 42.0688 |
| 1 43/64 | 1.6719 | 42.4656 |
| 1 11/16 | 1.6875 | 42.8625 |
| 1 45/64 | 1.7031 | 43.2594 |
| 1 23/32 | 1.7188 | 43.6563 |
| 1 47/64 | 1.7344 | 44. 0531 0531 |
| 1 3/4 | 1.7500 | 44.4500 |
| 1 49/64 | 1.7656 | 44.8469 |
| 1 25/32 | 1.7813 | 45.2438 |
| 1 51/64 | 1.7969 | 45.6406 |
| 1 13/16 | 1.8125 | 46.0375 |
| 1 53/64 | 1.8281 | 46.4344 |
| 1 27/32 | 1.8438 | 46.8313 |
| 1 55/64 | 1.8594 | 47.2281 |
| 1 7/8 | 1.8750 | 47.6250 |
| 1 57/64 | 1.8906 | 48.0219 |
| 1 29/32 | 1.9063 | 48.4188 |
| 1 59/64 | 1.9219 | 48.8156 |
| 1 15/16 | 1.9375 | 49.2125 |
| 1 61/64 | 1.9531 | 49. 6094 6094 |
| 1 31/32 | 1.9688 | 50.0063 |
| 1 63/64 | 1.9844 | 50.4031 |
| 2 | 2.0000 | 50.8000 |
| fraction | decimal | mm |
|---|---|---|
| 2 1/64 | 2.0156 | 51.1969 |
| 2 1/32 | 2.0313 | 51.5938 |
| 2 3/64 | 2.0469 | 51.9906 |
| 2 1/16 | 2.0625 | 52.3875 |
| 2 5/64 | 2.0781 | 52.7844 |
| 2 3/32 | 2.0938 | 53.1813 |
| 2 7/64 | 2.1094 | 53.5781 |
| 2 1/8 | 2.1250 | 53.9750 |
| 2 9/64 | 2.1406 | 54.3719 |
| 2 5/32 | 2.1563 | 54. 7688 7688 |
| 2 11/64 | 2.1719 | 55.1656 |
| 2 3/16 | 2.1875 | 55.5625 |
| 2 13/64 | 2.2031 | 55.9594 |
| 2 7/32 | 2.2188 | 56.3563 |
| 2 15/64 | 2.2344 | 56.7531 |
| 2 1/4 | 2.2500 | 57.1500 |
| 2 17/64 | 2.2656 | 57.5469 |
| 2 9/32 | 2.2813 | 57.9438 |
| 2 19/64 | 2.2969 | 58.3406 |
| 2 5/16 | 2.3125 | 58.7375 |
| 2 21/64 | 2.3281 | 59.1344 |
| 2 11/ 32 | 2.3438 | 59.5313 |
| 2 23/64 | 2.3594 | 59.9281 |
| 2 3/8 | 2.3750 | 60. 3250 3250 |
| 2 25/64 | 2.3906 | 60.7219 |
| 2 13/32 | 2.4063 | 61.1188 |
| 2 27/64 | 2.4219 | 61.5156 |
| 2 7/16 | 2.4375 | 61.9125 |
| 2 29/64 | 2,4531 | 62,3094 |
| 2 15/32 | 2,4688 | 62.7063 |
| 09 2 1/2 | 2.5000 | 63.5000 |
| 2 33/64 | 2.5156 | 63.8969 |
| 2 17/32 | 2.5313 | 64.2938 |
| 2 35/64 | 2.5469 | 64.6906 |
| 2 9/16 | 2.5625 | 65.0875 |
| 2 37/64 | 2. 5781 5781 | 65.4844 |
| 2 19/32 | 2.5938 | 65.8813 |
| 2 39/64 | 2.6094 | 66.2781 |
| 2 5/8 | 2.6250 | 66.6750 |
| 2 41/64 | 2.6406 | 67.0719 |
| 2 21/32 | 2.6563 | 67.4688 |
| 2 43/64 | 2.6719 | 67.8656 |
| 2 11/16 | 2.6875 | 68.2625 |
| 2 45/64 | 2.7031 | 68.6594 |
| 2 23/32 | 2.7188 | 69.0563 |
| 2 47/64 | 2.7344 | 69.4531 |
| 2 3/4 | 2.7500 | 69.8500 |
| 2 49/64 | 2.7656 | 70.2469 |
| 2 25/32 | 2.7813 | 70.6438 |
| 2 51/64 | 2. 7969 7969 | 71.0406 |
| 2 13/16 | 2.8125 | 71.4375 |
| 2 53/64 | 2.8281 | 71.8344 |
| 2 27/32 | 2.8438 | 72.2313 |
| 2 55/64 | 2.8594 | 72.6281 |
| 2 7/8 | 2.8750 | 73.0250 |
| 2 57/64 | 2.8906 | 73.4219 |
| 2 29/32 | 2.9063 | 73.8188 |
| 2 59/64 | 2.9219 | 74.2156 |
| 2 15/16 | 2.9375 | 74.6125 |
| 2 61/64 | 2.9531 | 75.0094 |
| 2 31/32 | 2.9688 | 75.4063 |
| 2 63/64 | 2.9844 | 75.8031 |
| 3 | 3.0000 | 76.2000 |
Fraction to Decimal Calculator
Ссылка на эту страницу! Просто щелкните правой кнопкой мыши на изображении выше, выберите «Скопировать адрес ссылки», а затем вставьте его в HTML-код.
Фракция выборки до десятичных расчетов
- 2 3/8 до десятичного десятичного от
- 1/80 до десятичного десятичного 2 51/21 до десятичной
- 3 35/92 до десятичной
- 1 69/47 до десятичной
- 1/883 до десятичной
- с 1 15/99 до десятичного десятичного детья
- 2 3/8 до десятичного десятичного от
- 1/53 до десятичного деть.
Несмотря на то, что прилагаются все усилия для обеспечения точности информации, представленной на этом веб-сайте, ни этот веб-сайт, ни его авторы не несут ответственности за какие-либо ошибки или упущения. Поэтому содержимое этого сайта не подходит для любого использования, связанного с риском для здоровья, финансов или имущества.
Преобразование процентов, десятичных знаков и дробей
Урок 4. Преобразование процентов, десятичных знаков и дробей
/en/decimals/multipliing-and-dividing-decimals/content/
Преобразование дробей, десятичных знаков и процентов
90 Когда мы говорим, мы часто используем разные слова, чтобы выразить одно и то же. Например, мы можем описать один и тот же автомобиль как крошечный или маленький или маленький . Все эти слова означают, что машина не большая. Дроби, десятичные числа и проценты подобны словам 9.0011 крошечный , маленький и маленький . Все они просто разные способы выражения частей целого .
Например, мы можем описать один и тот же автомобиль как крошечный или маленький или маленький . Все эти слова означают, что машина не большая. Дроби, десятичные числа и проценты подобны словам 9.0011 крошечный , маленький и маленький . Все они просто разные способы выражения частей целого .На этом изображении в каждой мерной чашке одинаковое количество сока. Но мы выразили эту сумму тремя способами: в виде дроби, в процентах и в виде десятичной дроби. Поскольку они выражают одно и то же количество, мы знаем, что 1/2, 50% и 0,5 равны друг другу. Каждый раз, когда мы видим 1/2, мы знаем, что это также может означать 50% или 0,5.
Иногда бывает полезно преобразовать один вид числа в другой. Например, гораздо проще сложить 1/4 и 0,5, если превратить 0,5 в дробь. Изучение того, как преобразовывать дроби, десятичные числа и проценты, также поможет вам в изучении более сложной математики.

Дроби и десятичные числа
Каждая дробь может быть записана как десятичная и наоборот. Возможно, вы не будете делать это очень часто, но преобразование десятичных и дробных чисел может помочь вам в математике. Например, проще вычесть 1/6 из 0,52, если сначала превратить 1/6 в десятичную дробь.
Преобразование дроби в десятичную
Преобразование дроби в десятичную. Мы будем использовать математический навык, который вы уже изучили: длинное деление. Чтобы освежить в памяти этот навык, вы можете просмотреть наш урок «Длинная дивизия».
Щелкните слайд-шоу, чтобы узнать, как преобразовать дробь в десятичную.
Давайте посмотрим, как мы можем преобразовать 1/4 в десятичную дробь.
Чтобы преобразовать дробь в десятичную, мы просто разделим числитель…
Чтобы преобразовать дробь в десятичную, мы просто разделим числитель… на знаменатель.
В нашем примере мы разделим 1 на 4.
1 разделить на 4 будет 0.
 1.
1.Мы также добавим десятичную точку после 0 сверху.
Теперь мы можем разделить 10 на 4.
10 разделить на 4 равно 2.
Теперь умножим 4 на 2.
4 умножить на 2 равно 8. Итак, мы вычтем 8 из 10.
Поскольку 2 больше 0, мы еще не закончили деление. Мы добавим еще один 0 после запятой и уменьшим его.
Теперь поделим 20 на 4.
20 разделить на 4 равно 5.
Теперь умножим. 4 умножить на 5 равно 20.
Когда мы вычитаем 20 из 20, мы получаем 0. 0 означает, что мы закончили деление.
1 разделить на 4 равно 0,25.
Итак, 1/4 равно 0,25.
Попробуйте!
Преобразуйте каждую из этих дробей в десятичное число .
Преобразование десятичного числа в дробь
Теперь сделаем это в обратном порядке. Преобразуем десятичную дробь в дробь.

Щелкните слайд-шоу, чтобы узнать, как преобразовать десятичную дробь в дробь.
Мы перепишем 0,85 в виде дроби. Чтобы преобразовать десятичную дробь в дробь, мы будем использовать разрядных значений .
В десятичных дробях число сразу справа от запятой находится в десятых разрядах.
Место справа от десятого разряда — это сотый разряд .
Чтобы преобразовать десятичное число, сначала мы проверим разрядное значение последнего числа справа.
В 0,85 5 стоит на сотых.
Это означает, что наша десятичная дробь равна 85 сотым. 85 сотых также можно записать как 85/100.
Теперь у нас есть дробь. Но всегда полезно сокращать дроби, когда это возможно, — это облегчает их чтение.
Чтобы уменьшить, нам нужно найти наибольшее число, которое будет равномерно входить как в 85, так и в 100. дробь на 5,
Сначала разделим числитель.
 85 разделить на 5 равно 17.
85 разделить на 5 равно 17.Теперь разделим знаменатель. 100 разделить на 5 равно 20. Это означает, что 85/100 можно уменьшить до 17/20.
Итак, 0,85 равно 17/20.
Уменьшение дроби может показаться ненужным при преобразовании десятичной дроби. Но это важно, если вы собираетесь использовать дробь в математической задаче. Если вы добавляете две дроби, вам может даже понадобиться уменьшить или изменить обе дроби так, чтобы у них был общий знаменатель .
Попробуй!
Преобразуйте эти десятичные дроби в дроби. Обязательно уменьшите каждую дробь до простейшей формы!
Проценты и десятичные дроби
Знание того, как преобразовывать проценты и десятичные дроби, поможет вам рассчитать такие вещи, как налог с продаж и скидки. Чтобы узнать, как это сделать, ознакомьтесь с нашим уроком «Проценты в реальной жизни».

Преобразование процентов в десятичные
Преобразование процентов в десятичные числа на удивление просто. Это займет всего несколько простых шагов.
Щелкните слайд-шоу, чтобы узнать, как преобразовать проценты в десятичные дроби.
Мы собираемся преобразовать 17% в десятичную дробь.
Сначала возьмем знак процента…
Сначала возьмем знак процента… и превратим его в десятичную точку.
Далее мы переместим десятичную точку два пробелов до осталось .
Теперь мы переместим десятичную точку на два пробела до слева .
Мы преобразовали наши проценты в десятичную дробь. 17% равно 0,17.
Давайте рассмотрим другой пример. На этот раз мы превратим 78% в десятичную дробь.
Во-первых, мы заменим знак процента на десятичную точку .

Затем мы переместим десятичную точку два пробела до слева .
Затем мы переместим десятичную точку на два пробела до слева .
78% равно 0,78.
Давайте рассмотрим другой пример. На этот раз мы превратим 8% в десятичную.
Во-первых, мы заменим знак процента на десятичную точку .
Затем мы переместим десятичную точку на два пробела в осталось .
Затем мы переместим десятичную точку на два пробела до слева .
Обратите внимание, что рядом с цифрой 8 есть дополнительный пробел. Мы не можем просто оставить пустое место, в котором ничего нет. Поскольку ноль ничему не равен, мы заменим пробел на ноль .
Обратите внимание, что рядом с цифрой 8 есть дополнительный пробел.
 Мы не можем просто оставить пустое место, в котором ничего нет. Так как ноль ничему не равен, мы заменим пробел на ноль .
Мы не можем просто оставить пустое место, в котором ничего нет. Так как ноль ничему не равен, мы заменим пробел на ноль .8% равно 0,08
Почему это работает?
Преобразование процентов в десятичные дроби настолько просто, что может показаться, что вы что-то упустили. Но не волнуйтесь — это действительно так просто! Вот почему метод, который мы вам показали, работает.
Когда мы превращаем процент в десятичную дробь, мы фактически делаем два шага. Сначала мы конвертируем наш процент в дробь. Поскольку все проценты выходят за пределы 100, мы просто помещаем проценты больше 100, например:
78% = 78/100
На втором этапе мы преобразуем 78/100 в десятичное число. Вы уже знаете, что это означает, что мы разделим числитель на знаменатель , вот так:
78 ÷ 100 = 0,78
Так почему же мы не показали эти шаги в слайд-шоу? Потому что вы можете получить ответ и без них.
 Вы знаете, что все проценты не равны 100, поэтому можете не превращать проценты в дроби. Вы должны разделить процент на 100, чтобы получить десятичную дробь, но есть быстрый способ сделать это. Просто переместите запятую на две позиции влево! Таким образом, вы можете получить тот же ответ всего за один простой шаг.
Вы знаете, что все проценты не равны 100, поэтому можете не превращать проценты в дроби. Вы должны разделить процент на 100, чтобы получить десятичную дробь, но есть быстрый способ сделать это. Просто переместите запятую на две позиции влево! Таким образом, вы можете получить тот же ответ всего за один простой шаг.Попробуй!
Преобразуйте эти проценты в десятичные дроби.
Преобразование десятичной дроби в проценты
Теперь обратим то, что вы только что узнали. Преобразуем десятичную дробь в проценты.
Щелкните слайд-шоу, чтобы узнать, как преобразовать десятичную дробь в проценты.
Мы собираемся преобразовать 0,45 в проценты.
Повторим то, что мы сделали в предыдущем разделе. На этот раз мы переместим десятичную точку на два разряда в 9.0011 справа .
Повторим то, что мы сделали в предыдущем разделе. На этот раз мы переместим запятую на два знака справа от .
Теперь заменим десятичную точку знаком процента.

Мы закончили преобразование нашей десятичной дроби в проценты. 0,45 равно 45%.
Давайте попробуем другой пример. На этот раз наша десятичная дробь имеет три числа справа от запятой.
Но мы все равно переместим десятичную точку на два деления вправо.
Но мы по-прежнему собираемся переместить десятичную точку на два пробела вправо.
У нас еще есть число справа от запятой. Число не равно 0, поэтому мы не можем его отбросить.
Вместо мы сохраним десятичную точку, а добавим знак процента в конце числа.
Итак, 0,635 равно 63,5%.
Попробуйте!
Вычислите эти десятичные дроби в процентах.
Проценты и дроби
Умение записывать проценты в виде дробей и наоборот может помочь вам в повседневной жизни.
 Например, предположим, что вы получили оценку 80% на тесте. Вы можете преобразовать 80% в дробь, чтобы узнать, сколько из ваших ответов были правильными. Когда ваш учитель оценивает тест, он может поступить наоборот. Если учащийся правильно ответил на 8 из 10 вопросов, учитель может преобразовать 8/10 в проценты, чтобы поставить учащемуся оценку.
Например, предположим, что вы получили оценку 80% на тесте. Вы можете преобразовать 80% в дробь, чтобы узнать, сколько из ваших ответов были правильными. Когда ваш учитель оценивает тест, он может поступить наоборот. Если учащийся правильно ответил на 8 из 10 вопросов, учитель может преобразовать 8/10 в проценты, чтобы поставить учащемуся оценку.Преобразование процентов в дроби
При преобразовании процентов в дроби полезно помнить, что проценты всегда выходят за пределы 100. Вы можете попрактиковаться с процентами в нашем уроке «Введение в проценты».
Щелкните слайд-шоу, чтобы узнать, как преобразовать проценты в дроби.
Преобразуем 30% в дробь.
В разделе «Введение в проценты» вы узнали, что все проценты выражаются из 100. На самом деле это то, что означает слово 9.0011 процентов означает.
Таким образом, любой процент равен самому себе больше 100. В нашем примере 30% равно 30/100.
Теперь мы преобразовали 30% в дробь, но нам еще нужно ее уменьшить.

10 — наибольшее число, которое равномерно делится на 30 и 100. Значит, мы можем разделить обе части дроби на 10.
Сначала разделим числитель дроби. 30 разделить на 10 равно 3.
Теперь разделим знаменатель. 100 разделить на 10 равно 10.
Итак, 30% равно 3/10.
Попробуйте!
Запишите эти проценты в виде дробей. Убедитесь, что уменьшите каждую дробь до простейшей формы.
Преобразование дроби в проценты
Преобразование дроби требует двух навыков, которые вы только что изучили: записи дроби в виде десятичной дроби и записи десятичной дроби в виде процентов . Давайте посмотрим, как мы можем использовать эти навыки для преобразования дроби в проценты.
Щелкните слайд-шоу, чтобы узнать, как преобразовать дробь в проценты.
Преобразуем 3/6 в проценты.
Точно так же, как при преобразовании дроби в десятичную, мы разделим числитель на знаменатель .

3 разделить на 6 равно 0,5.
Мы превратили нашу дробь в десятичную.
Теперь мы превратим десятичную дробь в проценты, переместив запятую на две позиции вправо.
Теперь мы превратим десятичную дробь в проценты, переместив запятую на две позиции вправо.
Мы также изменим десятичную точку на знак процента. 0,50 равно 50%.
Итак, 3/6 равно 50%.
Попробуйте!
Преобразуйте эти дроби в проценты.
Вернуться к учебнику
Предыдущий: Умножение и деление десятичных дробей
Далее:Вернуться к плейлисту: Десятичные дроби
Калькулятор дробей
Этот калькулятор выполняет основные и расширенные операции с дробями, выражения с дробями в сочетании с целыми, десятичными и смешанными числами. Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.
Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.Правила выражений с дробями:
Дроби — для деления числителя на знаменатель используйте косую черту, т.е. для пятисотых введите 5/100 . Если вы используете смешанные числа, оставьте пробел между целой и дробной частями.
Смешанные числа (смешанные числа или дроби) сохраняют один пробел между целым числом и дробью
и используют косую черту для ввода дробей, например, 1 2/3 . Пример отрицательной смешанной дроби: -5 1/2 .
Поскольку косая черта одновременно является знаком дробной строки и деления, используйте двоеточие (:) в качестве оператора деления дробей, т. е. 1/2 : 1/3 .
Decimals (десятичные числа) вводятся с десятичной точкой . и они автоматически преобразуются в дроби — т. е. 1,45 .
е. 1,45 .Математические символы
Символ Имя символа Символ Значение Пример + плюс знак Дополнение 1/2 + 1/3 — Минус. Умножение 2/3 * 3/4 × TIME SIGN Умножение 2/3 × 5/6. .1/2
• сложение дробей и смешанных чисел: 8/5 + 6 2/7
• деление целых чисел и дробей: 5 ÷ 1/2
• сложные дроби: 5/8 : 2 2/3
• десятичная дробь: 0,625
• Преобразование дроби в десятичную: 1/4
• Преобразование дроби в процент: 1/8 %
• сравнение дробей: 1/4 2/3
• умножение дроби на целое число: 6 * 3/4
• квадратный корень дроби: sqrt(1/16)
• сокращение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22
• выражение со скобками: 1/3 * (1/2 — 3 3/8)
• составная дробь: 3/4 от 5/7
• кратные дроби: 2/3 от 3/5
• разделить, чтобы найти частное: 3/5 ÷ 2/3Калькулятор следует известным правилам для порядка операций .
 Наиболее распространенные мнемоники для запоминания этого порядка операций:
Наиболее распространенные мнемоники для запоминания этого порядка операций:
PEMDAS — Скобки, Экспоненты, Умножение, Деление, Сложение, Вычитание.
BEDMAS — скобки, экспоненты, деление, умножение, сложение, вычитание
BODMAS — Скобки, Порядок, Деление, Умножение, Сложение, Вычитание.
GEMDAS — символы группировки — скобки (){}, показатели степени, умножение, деление, сложение, вычитание.
MDAS — Умножение и деление имеют тот же приоритет, что и сложение и вычитание. Правило MDAS является частью порядка операций правила PEMDAS.
Будь осторожен; всегда выполняйте умножение и деление перед сложением и вычитанием . Некоторые операторы (+ и -) и (* и /) имеют одинаковый приоритет и должны оцениваться слева направо.- Дробь и десятичная дробь
Пишите в виде дроби и десятичной дроби. Один и два плюс три и пять сотых - Вычислить выражение
Вычислить значение выражения z/3 — 2 z/9 + 1/6, для z = 2 - Ферма 6
На ферме 20 животных. Есть четыре курицы. Какую часть животных составляют куры? Выразите ответ дробью в простейшей форме.
Есть четыре курицы. Какую часть животных составляют куры? Выразите ответ дробью в простейшей форме. - Женитьба
У Жени было 1 1/2 дюжины яиц в холодильнике. Использовала 1/3 яйца. Какая часть яиц использовалась? - А класс IV.А
В классе 15 девочек и 30 мальчиков. Какая часть класса представляет мальчиков? - Корзина с фруктами
Если в корзине семь яблок и пять апельсинов, какая часть апельсинов в корзине с фруктами? - Зденек
Зденек набрал 15 литров воды из 100-литровой полной бочки. Напишите долю того, какую часть воды Зденека он собрал. - В столовой
В классной комнате Джейкоба 18 учеников. Шесть учеников приносят обед в школу. Остальные обедают в столовой. Проще говоря, какая часть студентов обедает в столовой? - Четверть
Четверть числа 72 это: - Кто-то
Кто-то съел 1/10 торта, осталось только 9/10. Если вы съедите 2/3 оставшегося торта, сколько всего торта вы съедите? - Одна суббота
Однажды субботним вечером в кинотеатре 40 девушек, 25 юношей, 18 женщин и 17 мужчин. Какую часть составляют девочки?
Какую часть составляют девочки?
more math problems »
- decimals
- fractions
- triangle ΔABC
- percentage %
- permille ‰
- prime factors
- complex numbers
- LCM
- GCD
- LCD
- combinatorics
- equations
- статистика
- … все математические калькуляторы
Смешанное число 1 3/100 в десятичной форме
Дробь 1 3/100 равна 0,13 при преобразовании в десятичную. Ниже подробно описано, как преобразовать дробь 1 3/100 в десятичное значение.
Как преобразовать дробь в десятичную?
Чтобы легко преобразовать дробь в десятичную, разделите числитель (верхнее число) на знаменатель (нижнее число).
Пример 1: Как преобразовать
4 / 8 в десятичное число?- Шаг 1: Разделите 4 на 8: 4 ÷ 8 = 1 ÷ 2 = 0,5
- Шаг 2: Умножьте результат на 100 и добавьте десятичный знак: 0,5 × 100%
- Ответ: 4 / 8 = 50%
Пример 2: Как преобразовать 1
1 / 3 в десятичное число?- Шаг 1: Разделите 1 на 3: 1 ÷ 3 = 0,3333
- Шаг 2:
Добавьте это значение к целой части: 1 + 0,3333 = 1,3333.

- Шаг 3: Умножьте результат на 100 и добавьте десятичный знак: 1,3333 × 100%
- Ответ: 1 1 / 3 = 133,33%
Примечание: результат округлен до 2 знаков после запятой.
Доли дюймов в десятичные дюймы и миллиметры (мм)
fraction inches mm 1/64 0.0156 0.3969 1/32 0.0313 0.7938 3/64 0.0469 1,1906 1/16 0,0625 1,5875 5/6444444917 0,0781 ,9844444917 0,0781 ,9444444 0,0781 ,9444444917 0,0781 ,9444444917 0,0781 .2.38137/64 0.1094 2.7781 1/8 0.1250 3.1750 9/64 0.  1406
14063.5719 5/32 0.1563 3.9688 11/64 0.1719 4.3656 3/16 0.1875 4.7625 13/64 0.2031 5.1594 7/32 0.2188 5.5563 15/64 0.2344 5.9531 1/4 0.2500 6.3500 fraction inches mm 17/64 0.2656 6.7469 9/32 0.2813 7.1438 19/64 0.2969 7.5406 5/16 0.3125 7.9375 21/64 0.3281 8.3344 11/32 0.3438 8.  7313
731323/64 0.3594 9.1281 3/8 0.3750 9.5250 25/64 0.3906 9.9219 13/32 0.4063 10.3188 27/64 0.4219 10.7156 7/16 0.4375 11.1125 29/64 0.4531 11.5094 15/32 0,4688 11,9063 31/64 9844 12.3031 12.3031 44.0307 fraction inches mm 33/64 0.5156 13.0969 17/32 0.5313 13.4938 35/64 0.5469 13.8906 9/16 0.  5625
562514.2875 37/64 0.5781 14.6844 19/32 0.5938 15.0813 39/64 0.6094 15.4781 5/8 0.6250 15.8750 41/64 0.6406 16.2719 21/ 32 0.6563 16.6688 43/64 0.6719 17.0656 11/16 0.6875 17.4625 45/64 0.7031 17.8594 23/32 0.7188 18.2563 47/64 0.7344 18.6531 3/4 0.7500 19.0500 fraction inches mm 49/64 0.  7656
765619.4469 25/32 0.7813 19.8438 51/64 0.7969 20.2406 13/16 0.8125 20.6375 53/64 0.8281 21.0344 27/32 0.8438 21.4313 55/64 0.8594 21.8281 7/8 0.8750 22.2250 57/64 0.8906 22.6219 29/32 0.9063 23.0188 59/64 0.9219 23.4156 15/16 0.9375 23.8125 61/64 0.9531 24.2094 31/32 0.9688 24.6063 63/64 0.9844 25.0031 1 1. 

 Если одна — это десятки, две — сотни, три -тысячные итд.
Если одна — это десятки, две — сотни, три -тысячные итд.
 В начальных классах школ учат такому делению, и трудностей с этим не должно возникнуть.
В начальных классах школ учат такому делению, и трудностей с этим не должно возникнуть. VisualFractions.com . По состоянию на 27 сентября 2022 г. http://visualfractions.com/calculator/fraction-as-decimal/what-is-1-3-as-a-decimal/.
VisualFractions.com . По состоянию на 27 сентября 2022 г. http://visualfractions.com/calculator/fraction-as-decimal/what-is-1-3-as-a-decimal/. д. Обратите внимание, что 2 1/2 означает два с половиной = 2 + 1/2 = 2,5
д. Обратите внимание, что 2 1/2 означает два с половиной = 2 + 1/2 = 2,5  Например, мы можем описать один и тот же автомобиль как крошечный или маленький или маленький . Все эти слова означают, что машина не большая. Дроби, десятичные числа и проценты подобны словам 9.0011 крошечный , маленький и маленький . Все они просто разные способы выражения частей целого .
Например, мы можем описать один и тот же автомобиль как крошечный или маленький или маленький . Все эти слова означают, что машина не большая. Дроби, десятичные числа и проценты подобны словам 9.0011 крошечный , маленький и маленький . Все они просто разные способы выражения частей целого .
 1.
1.
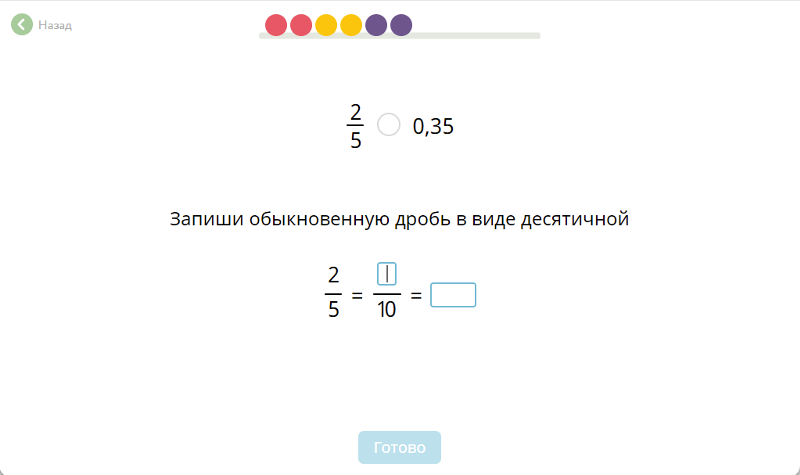 85 разделить на 5 равно 17.
85 разделить на 5 равно 17.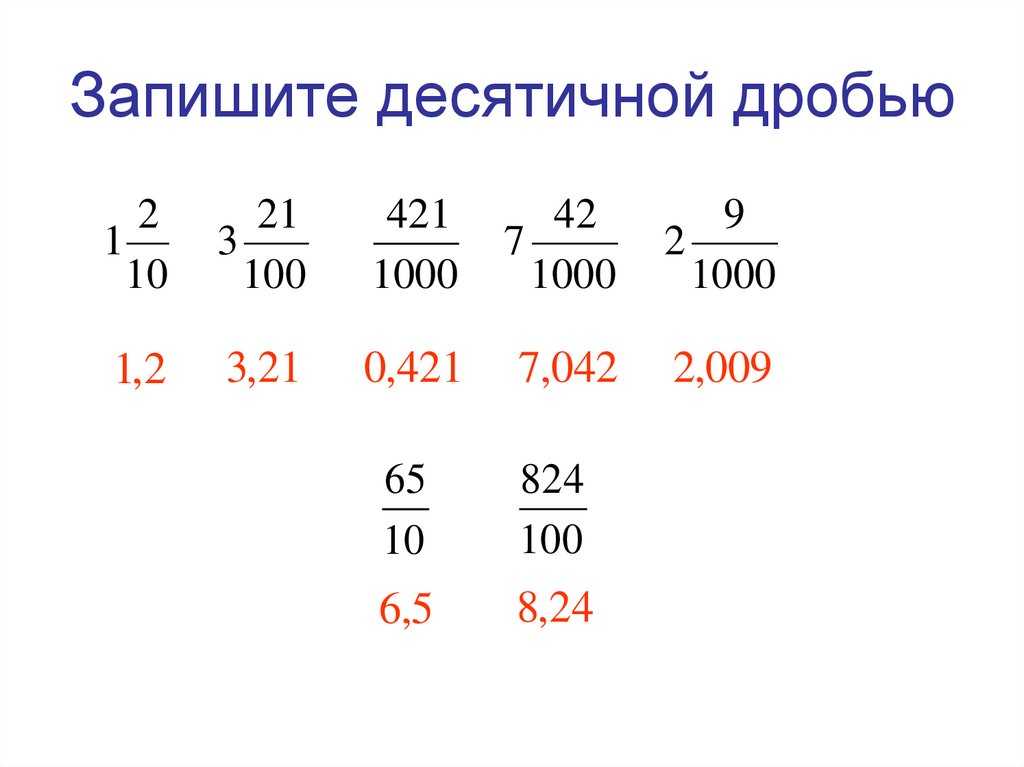

 Мы не можем просто оставить пустое место, в котором ничего нет. Так как ноль ничему не равен, мы заменим пробел на ноль .
Мы не можем просто оставить пустое место, в котором ничего нет. Так как ноль ничему не равен, мы заменим пробел на ноль . Вы знаете, что все проценты не равны 100, поэтому можете не превращать проценты в дроби. Вы должны разделить процент на 100, чтобы получить десятичную дробь, но есть быстрый способ сделать это. Просто переместите запятую на две позиции влево! Таким образом, вы можете получить тот же ответ всего за один простой шаг.
Вы знаете, что все проценты не равны 100, поэтому можете не превращать проценты в дроби. Вы должны разделить процент на 100, чтобы получить десятичную дробь, но есть быстрый способ сделать это. Просто переместите запятую на две позиции влево! Таким образом, вы можете получить тот же ответ всего за один простой шаг.
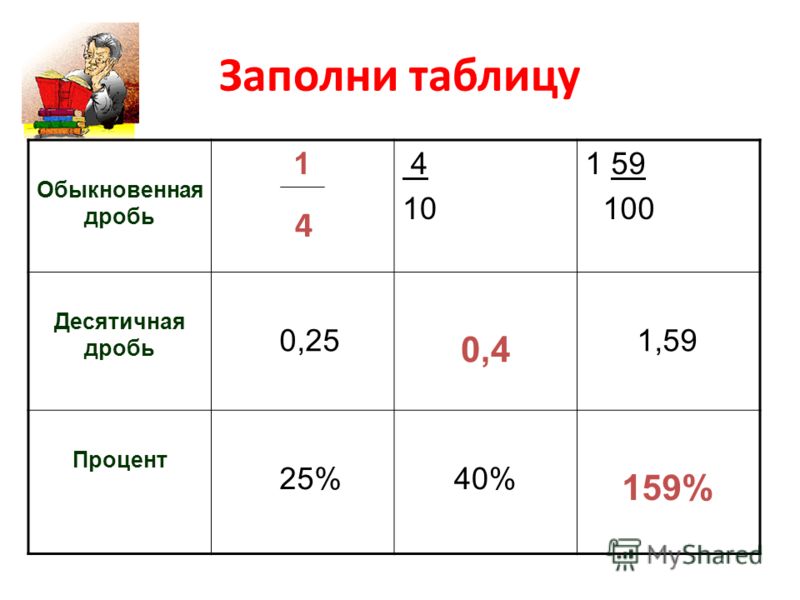 Например, предположим, что вы получили оценку 80% на тесте. Вы можете преобразовать 80% в дробь, чтобы узнать, сколько из ваших ответов были правильными. Когда ваш учитель оценивает тест, он может поступить наоборот. Если учащийся правильно ответил на 8 из 10 вопросов, учитель может преобразовать 8/10 в проценты, чтобы поставить учащемуся оценку.
Например, предположим, что вы получили оценку 80% на тесте. Вы можете преобразовать 80% в дробь, чтобы узнать, сколько из ваших ответов были правильными. Когда ваш учитель оценивает тест, он может поступить наоборот. Если учащийся правильно ответил на 8 из 10 вопросов, учитель может преобразовать 8/10 в проценты, чтобы поставить учащемуся оценку.

 Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.
Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении. е. 1,45 .
е. 1,45 . Наиболее распространенные мнемоники для запоминания этого порядка операций:
Наиболее распространенные мнемоники для запоминания этого порядка операций:  Есть четыре курицы. Какую часть животных составляют куры? Выразите ответ дробью в простейшей форме.
Есть четыре курицы. Какую часть животных составляют куры? Выразите ответ дробью в простейшей форме. Какую часть составляют девочки?
Какую часть составляют девочки?
 1406
1406 7313
7313 5625
5625 7656
7656