Как перевести sin в cos?
Как перевести sin в cos?
Перевод синуса в косинус и обратно выполняется посредством решения основного тригонометрического тождества sin2(x) + cos2(x) = 1. Смотрите также: — калькулятор вычисления синуса угла; — калькулятор вычисления косинуса угла.
Чему равен косинус и синус?
Синус, косинус острого угла треугольника Чтобы найти синус и косинус угла в прямоугольном треугольнике, нужно вспомнить определения. Синус угла равен отношению противоположного катета к гипотенузе. Косинус угла равен отношению прилежащего катета к гипотенузе.
Что такое cos в математике?
Изначально определения тригонометрических функций, аргументом которых является угол, выражались через соотношения сторон прямоугольного треугольника. Синус угла (sin α ) — отношение противолежащего этому углу катета к гипотенузе. Косинус угла (cosα ) — отношение прилежащего катета к гипотенузе.
Как найти косинус какого то числа?
Косинус острого угла можно определить с помощью прямоугольного треугольника — он равен отношению прилежащего катета к гипотенузе. Косинус числа можно определить с помощью числовой окружности – косинус числа равен абсциссе соответствующей точки на ней.
Как найти косинус по 3 сторонам?
Формулировка теоремы косинусов Теорема косинусов гласит: квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.
Как найти угол треугольника зная его 2 стороны?
Если известны стороны треугольника, можно рассчитать его углы, воспользовавшись теоремой косинусов. Здесь, квадрат одной стороны треугольника (а) равен сумме квадратов двух его других сторон (b,с), образующих искомый угол (α), плюс удвоенное произведение этих сторон (b,с) на косинус угла.
Как найти косинус через стороны?
Формула теоремы косинусов Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними. Теорема косинусов является обобщением теоремы Пифагора.
Как найти стороны треугольника если известна одна сторона и угол?
Теорема синусов: стороны треугольника пропорциональны синусам противолежащих углов. Если известны одна сторона и два прилежащих угла, то с помощью теоремы синусов можно вычислить остальные две стороны треугольника.
Как в прямоугольном треугольнике найти катет если известна гипотенуза и угол?
Если вам задан один из острых углов, например, A, и гипотенуза, то катеты можно найти из определений основных тригонометрических : a= c*sin(A), b= c*cos(A). Если задан один из острых углов, например, A, и один из катетов, например, a, то гипотенуза и другой катет вычисляются из соотношений: b=a*tg(A), c=a*sin(A).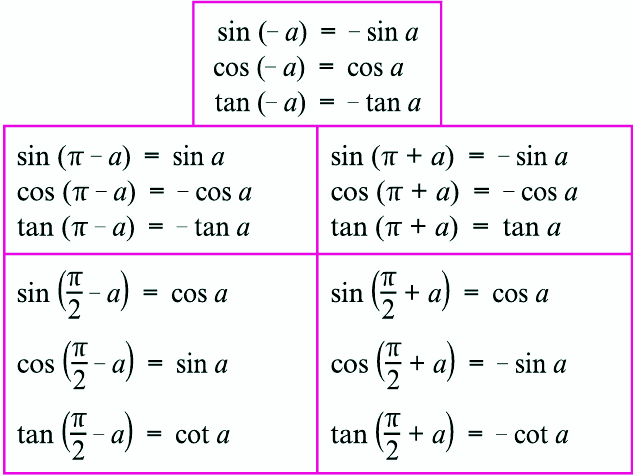
Как найти катет в прямоугольном треугольнике через угол?
Катет прямоугольного треугольника равен его гипотенузе, умноженной на синус противолежащего или на косинус прилежащего к этому катету угла. Катет равен другому катету, умноженному на тангенс противолежащего или котангенс прилежащего к первому катету угла.
Как найти одну сторону прямоугольного треугольника?
По теореме Пифагора, для того чтобы вычислить гипотенузу прямоугольного треугольника, нужно извлечь квадратный корень из суммы квадратов катетов. Катетами считаются стороны a и b, образующие друг с другом прямой угол, а гипотенузой – сторона, лежащая напротив него.
Как вычислить гипотенузу зная катеты?
Если известна длина обоих катетов, то ее размер вычисляется по теореме Пифагора: сумма квадратов двух катетов равняется квадрату гипотенузы. К примеру: катет a = 3 см, катет b = 4 см.
Как найти второй катет в прямоугольном треугольнике?
Теорема Пифагора, чтобы найти катет прямоугольного треугольника Если нам известны гипотенуза и катет, то мы можем найти длину неизвестного катета по теореме Пифагора.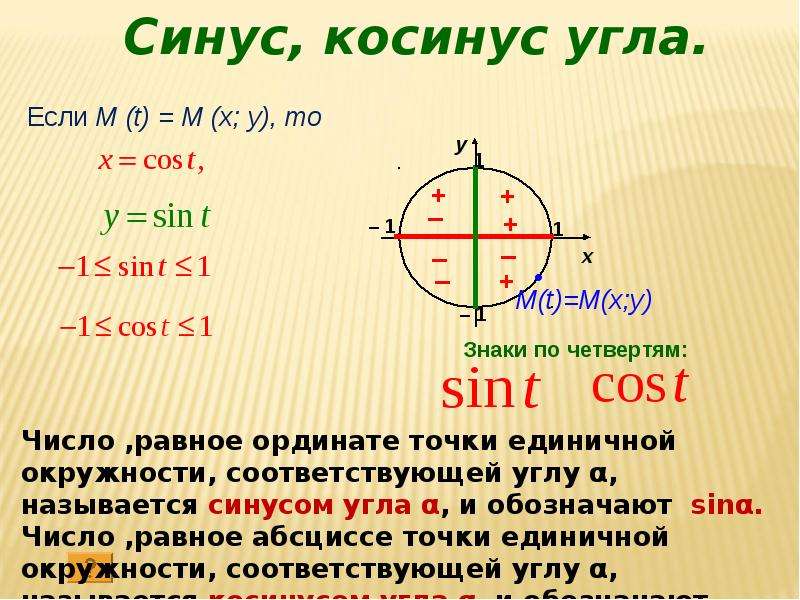 Звучит она так: “Квадрат гипотенузы равен сумме квадратов катетов”. Формула: c²=a²+b², где c – гипотенуза, a и b – катеты.
Звучит она так: “Квадрат гипотенузы равен сумме квадратов катетов”. Формула: c²=a²+b², где c – гипотенуза, a и b – катеты.
Как найти катет в прямоугольном треугольнике 8 класс?
Правило нахождения катета через гипотенузу: Катет прямоугольного треугольника равен произведению гипотенузы на синус противолежащего ему угла или на косинус прилежащего ему угла.
Как найти катет в прямоугольном треугольнике если известна площадь?
Ответ, проверенный экспертом Площадь прямоугольного треугольника равна половине произведения его катетов. Поэтому ab=2S(a и b — катеты(пусть b — катет с прилежащим к нему углом 30 градусов)).
Как найти площадь прямоугольного треугольника если известна гипотенуза?
Площадь прямоугольного треугольника через гипотенузу можно найти по формуле для площади треугольника через 2 стороны и синус угла между ними: S = 1 2 ⋅ a ⋅ c ⋅ sin (1).
Чему равна площадь треугольника?
S = (a * b * c) : (4 * R), где a, b, c — стороны, R — радиус описанной окружности.
Как определить площадь треугольника в 4 классе?
Площадь прямоугольного треугольника равна половине произведения его катетов. 4.
Можно ли найти площадь треугольника по трем сторонам?
Площадь треугольника по формуле Герона (по трем сторонам) Один из способов расчета площади треугольника — использование формулы Герона. Для того, что бы найти площадь треугольника, необходимо знать три его стороны.
Как найти площадь треугольника 7 класс?
площадь треугольника равна половине произведения длины высоты треугольника и длины стороны, к которой проведена высота S ABC = a ⋅ h 2 .
Нахождение значений синуса, косинуса, тангенса и котангенса, вычисление тригонометрических функций
Для того, чтобы определить значение угла α, необходимо воспользоваться подходящей функции из тригонометрии. Во время решения задач постоянно возникает необходимость в том, чтобы узнать значение углов. Для некоторых углов можно найти точные значения, для других сложно определить точную цифру и можно вывести только приблизительное значение.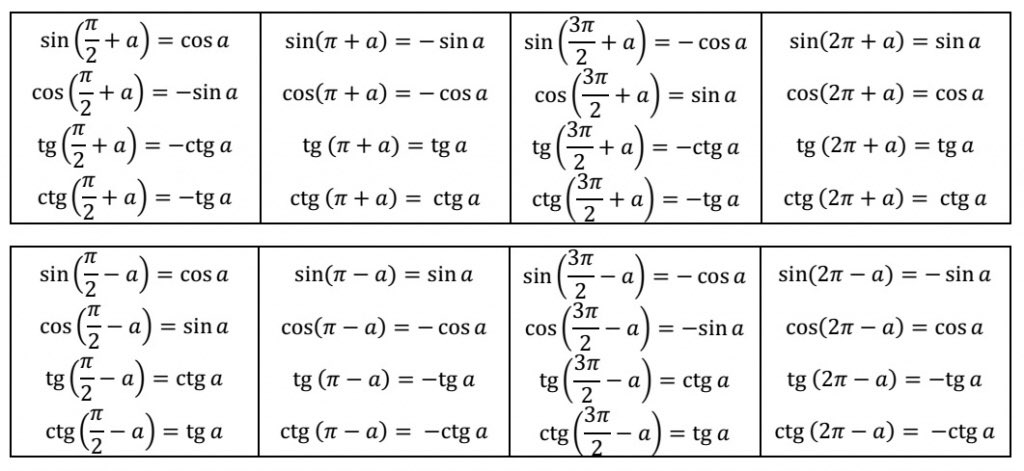
В этой статье мы подробно поговорим о функциях из тригонометрии. Мы не только расскажем о свойствах синуса, тангенса и других функций, но и узнаем, как правильно вычислять значения для каждого отдельного случая.
Рассмотрим подробно каждый случай.
Определение 1Приближенное число для каждой из известных функций можно найти по определению. Для одних можно указать точные значения, для других – только приблизительные.
Соотношения сторон и углов фигуры используются для того, чтобы определить значения для 30°, 45°, 60°. Если угол выходит за пределы 90°, то перед вычислением значения следует воспользоваться специальной формулой для того, чтобы привести угол к нужному виду.
Если известно значение синуса для α, можно быстро узнать значение косинуса для этого же угла. Это легко выполнить с помощью основных тождеств, которые представлены в геометрии.
В некоторых случаях для того, чтобы узнать sin или cos угла, можно использовать подходящую тригонометрическую формулу. Например, по известному значению синуса 45°, мы сможем определить значение синуса 30°, воспользовавшись правилом из тригонометрии.
Например, по известному значению синуса 45°, мы сможем определить значение синуса 30°, воспользовавшись правилом из тригонометрии.
Если для примера не подходит ни одно из приведенных выше решений, можно найти приближенное значение. В этом вам помогут таблицы основных тригонометрических функций, которые легко можно найти.
Если взять за основу определения, возможно определить значения для определенного угла α. Также можно вычислить значения тангенса и котангенса для определенного случая. Можно найти значений основных функций из тригонометрии для частных вариантов. Это углы 0°, 90°, 180°, 270°, 360°.
Разобьем эти углы на четыре группы: 360·z градусов (2π·z рад), 90+360·z градусов (π2+2π·z рад), 180+360·z градусов (π+2π·z рад) и 270+360·z градусов (3π2+2π·z рад), где z- любое целое число.
Изобразим данные формулы на рисунке:
Для каждой группы соответствуют свои значения.
Пример 1При повороте из точки A на 360·z°, она переходит в себя. А1(1, 0). Синус 0°, 360°, 720° равен 0, а косинус равен 1. Представим это в виде формулы: sin (360°·z)=0 и cos (360°·z)=1 .
Представим это в виде формулы: sin (360°·z)=0 и cos (360°·z)=1 .
Можно определить, что tg (360°·z)=01=0 , а котангенс не определен.
Пример 2Если А(1, 0) повернуть на 90+360·z°, то она перейдет в А1 (0, 1). По определению: sin (90°+360°·z) =1 и cos (90°+360°·z) =0 . Мы не сможем определить значение тангенса, но котангенс рассчитывается по данной формуле: ctg (90°+360°·z) =01=0 .
Рассмотрим особенности для третьей группы углов. После поворота точки А(1, 0) на любой из углов 180+360·z°, она перейдет в A1(−1, 0). Мы находим значения функций кроме тангенса.
Пример 4Рассмотрим правила для четвертой группы углов. При повороте точки на 270+360·z° мы попадем в A1(0, −1). Мы находим значения всех функций кроме тангенса.
Для углов, которые не относятся к перечню от 0 °, 90 °, 180 °, 270 °, 360 °…, точных значений нет. Мы можем найти лишь приближенные значения. Рассмотрим пример. Условия – найти основные значения для угла −52 °. Выполним построения.
Согласно рисунку, абсцисса А1 ≈ 0,62, а ордината ≈ −0,78. Соответственно, sin(-52°)≈-0,78 и cos(-52°)≈0,62 . Осталось определиться с тангенсом и котангенсом.
Выполняем вычисления: tg(-52°)≈-0, 780, 62≈-1,26 и ctg(-52°)≈0,62-0,78≈-0,79.
Чем точнее выполняется чертеж, тем более точными будут значения для каждого индивидуального случая. Выполнять вычисления удобно только в теории, так как на практике довольно сложно и долго выполнять рисунки.
Линии тригонометрических функций
Определение 2Линии тригонометрических функций – это линии, которые изображаются вместе с единичной окружностью. Они имеют точку отсчета и единичный отрезок, которая равна единице в координатной системе. Они используются для наглядного изображения значений.
Рассмотрим их на подробном рисунке
Как найти sin α, cos α, tg α, ctg α
Для тридцати-, сорокопяти-, шестидесятиградусных углов мы имеем определенные значения. Чтобы найти их, можно воспользоваться правилами о прямоугольном треугольнике с острыми углами. Для этого используется теорема Пифагора.
Для этого используется теорема Пифагора.
Для того, чтобы узнать значения для углов тридцати- и шестидесятиградусных углов изображаем прямоугольный треугольник с углами данной величины. Длина гипотенузы должна быть равна 1. Согласно теореме Пифагора, катет, лежащий напротив тридцатиградусного угла, равен половине гипотенузы. Воспользуемся теоремой: 12-122=32 . Так как синус угла – это катет, деленный на гипотенузу, вычисляем, что sin 30°=121=12 и sin 60°=321=32 .
Косинус можно найти по формуле, которая предполагает деление прилежащего катета на гипотенузу. Вычисляем: cos 30°=321=32 и cos 60°=121=12 .
Тангенс можно найти по формуле, которая предполагает деление противолежащего катета на прилежащий. Котангенс находим по такой же схеме – делим прилежащий катет на противолежащий.
Вычисляем: tg 30°=1232=13=33 и tg 60°=3212=3 . Находим котангенс по подобной схеме: сtg 30°=3212=3 и сtg 60°=1232=13=33 . После этого приступаем к вычислению значений основных тригонометрических функций для сорока пятиградусного угла.
Теперь мы сможем найти значения для основных тригонометрических функций. Используем формулу, которая предполагает деление длин соответствующих сторон рассматриваемого треугольника.
Выводим формулу: ctg 45°=2222=1 .
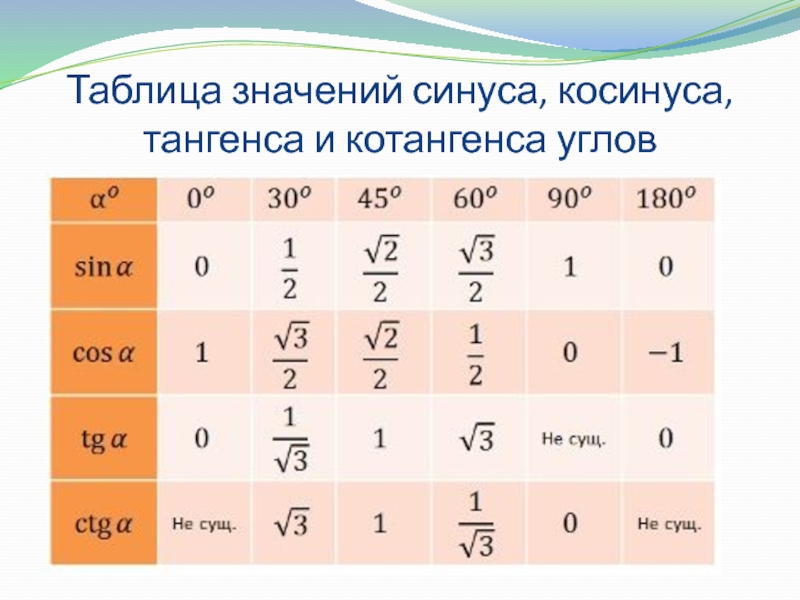
Полученные значения для тридцати-, сорокапяти-, шестидесятиградусных углов будут использоваться для решения различных задач. Запишите их – они часто будут использоваться. Для удобства можно использовать таблицу значений.
Проиллюстрируем значения для тридцати-, сорокапяти-, шестидесятиградусных углов с использованием окружности и линий.
Значения основных функций тригонометрии
Основные тождества из геометрии связывают с собой sin α, cos α, tg α, ctg α для определенного угла. С помощью одной функции вы легко сможете найти другую.
Для того, чтобы найти синус по известному косинусу, sin2α+cos2α=1 .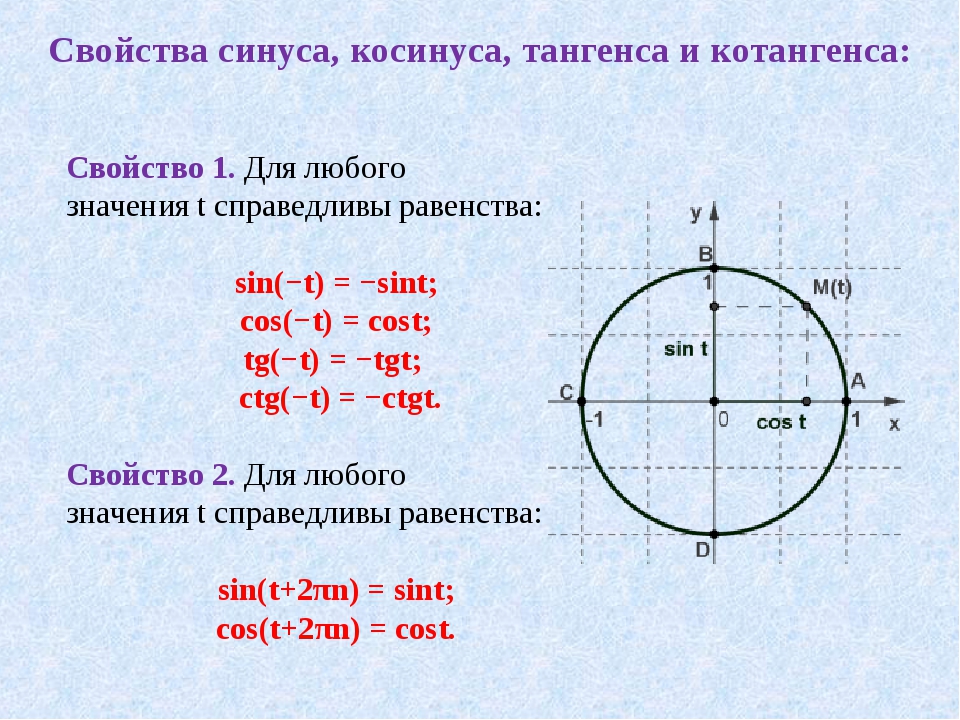
Тангенс по известному косинусу tg2α+1=1cos2α .
Определение 5Котангенс по известному синусу или наоборот 1+ctg2α= 1sin2α .
Определение 6Тангенс через котангенс или наоборот можно найти благодаря удобной формуле: tg α·ctg α=1 .
Для того, чтобы закрепить полученные знания, рассмотрим их на подробном примере
Пример 6Необходимо найти значение синуса угла π8, если tg π8=2-1 .
Сначала найдем котангенс угла: ctgπ8=1tgπ8=12-1=2+1(2-1)·(2+1)= 2+1(2)2-12=2+1 Воспользуемся формулой 1+ctg2α=1sin2α . Благодаря этому мы вычисляем значение синуса. Имеем
Для завершения необходимо определить значение синуса. Угол π8 является углом первой четверти, то синус является положительным. Чтобы точно определить знак, вы можете воспользоваться таблицей, в которой определены знаки по четвертям координатной плоскости. Таким образом, sin π8=sin2π8=2-24=2-22 . sin π8=2-22.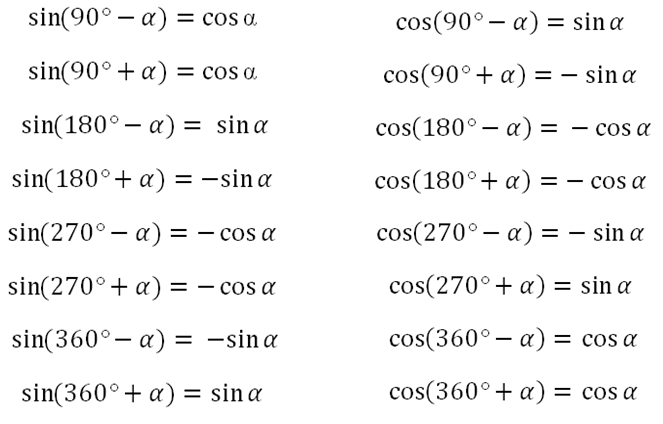
Сведение к углу
Удобнее всего находить значения для угла от 0 до 90 °. Сведение к углу из интервала от 0 до 90 °. Если угол не соответствует заданному интервалу, можно использовать законы и тождества, которые мы учили на уроках геометрии. Тогда мы сможем найти значение, которое будет равно для угла указанных пределах.
Пример 7Задача заключается в том, чтобы найти синус 210°. Представим 210 как разность или сумму, разложив число на несколько. Воспользуемся соответствующей формулой для приведения. Используем формулу для нахождения значения синуса 30°: sin 210°=sin(180°+30°)=-sin 30°=-12 , или косинуса 60 ° sin 210°=sin(270°-60°)=-cos 60°=-12.
Для того, чтобы решать задачи было намного проще, при нахождении значений переходите к углам из интервала от 0 до 90° с помощью формул приведения, если угол не находится в этих пределах.
Использование формул
Раннее мы рассмотрели подробности, касающиеся нахождению значений основных функций с использованием формул тригонометрии. Для того, чтобы определить значение для определенного угла, используйте формулы и значения основных функций для известных углов.
Для того, чтобы определить значение для определенного угла, используйте формулы и значения основных функций для известных углов.
Для примера вычислим значение тангенса π8, который был использован в предыдущем примере. Возьмем за основу основные формулы тригонометрии.
Пример 8Найдите значение tgπ8 .
Используя формулу тангенса, преобразуем уравнение до следующего равенства tg2π8=1-cosπ41+cosπ4 . Значения косинуса угла π4 известны из предыдущего примера. Благодаря этому мы быстро найдем значения тангенса.
Угол π8 является углом первой четверти. Согласно таблице основных тригонометрических функций по четвертям координатной плоскости, тангенс этого угла положителен. Продолжаем вычисления для дальнейшего решения: tgπ8=tg2π8=(2-2)22=2-22=2-1
tgπ8=2-1.
Частные случаи
Тригонометрия – довольно сложная наука. Далеко не всегда можно найти формулы, используемые для вычисления. Существует множество уравнений, которые не поддаются стандартным формулам. Некоторые значения очень сложно обозначить точной цифрой. Это не так просто, как может показаться.
Существует множество уравнений, которые не поддаются стандартным формулам. Некоторые значения очень сложно обозначить точной цифрой. Это не так просто, как может показаться.
Однако точные значения не всегда нужны. Хватает и тех, что не претендуют на высокую точность. Благодаря существующим таблицам, которые можно найти в математических учебниках, можно найти любое приближенное значение основных функций. Благодаря справочным материалам вычислять формулы будет намного проще. В таблицах содержатся значения с высокой точностью.
python — преобразование значения года в периодическое значение в Pandas DataFrame
спросил
Изменено 11 месяцев назад
Просмотрено 608 раз
У меня есть DataFrame следующим образом:
закрыть год День Sin День Cos Месяц Sin Месяц Cos Час Sin Час Cos 0 278,00 2015 -0,790776 -0,612106 -0,5 -0,866025 -0,707107 0,707107 1 278,14 2015 -0,790776 -0,612106 -0,5 -0,866025 -0,500000 0,866025 2 280,00 2015 -0,790776 -0,612106 -0,5 -0,866025 -0,258819 0,965926 3 280,89 2015 -0,897805 -0,440394 -0,5 -0,866025 0,000000 1,000000 4 280,36 2015 -0,897805 -0,440394 -0,5 -0,866025 0,258819 0,965926
Я преобразовал дни, месяцы и часы в соответствующие значения Sin и Cosine, поскольку они являются периодическими/циклическими значениями, которые повторяются через определенный интервал. Я сделал это следующим образом:
Я сделал это следующим образом:
импортировать numpy как np #Месяц df1['Месяц Sin'] = np.sin(2*np.pi*df1.month/12) df1['Месяц Cos'] = np.cos(2*np.pi*df1.month/12) #Час df1['Час Sin'] = np.sin(2*np.pi*df1.hour/24) df1['Hour Cos'] = np.cos(2*np.pi*df1.hour/24)
Но я застрял в том, как преобразовать значение года в значимое значение, поскольку год не является периодическим/циклическим значением. Он увеличивается с течением времени. Я хочу дать моей модели машинного обучения все функции, такие как год, дневной грех, дневной косинус, месячный грех, месячный косинус и т. д., чтобы предсказать запас закрыть значение . Можно ли в любом случае извлечь какую-то значимую информацию из значения года , чтобы можно было точно предсказать значение запаса , близкое к , даже в будущем, скажем, в 2023 году, в прошлом и настоящем.
- python
- python-3.x
- pandas
- dataframe
Преобразование дней и месяцев в значения синуса и косинуса может скорее помешать, чем помочь вам.
- Разница между последовательными значениями будет разной. Изменение синуса или косинуса месяцев непостоянно. Например, разница между синусоидальным значением января и февраля составляет ~ 0,36. Такая же разница для февраля и марта составляет ~0,13. В идеале вы бы хотели, чтобы они были одинаковыми, если вы использовали данные за месяц
- Для дней разные месяцы имеют разное количество дней, поэтому либо вы используете один и тот же интервал и в итоге получаете отсутствующий раздел, либо у вас разные промежутки между днями
Вместо этого вы можете использовать временную метку unix
из datetime import datetime dt = дата и время (год = 2015, месяц = 9, день = 2, час = 4, минута = 45) dt.timestamp ()
datetime docs ( datetime.timestamp docs)
Если акция имеет периодический характер, ИИ должен найти ее
1 Решение @nxe не совсем правильное. Да, разница между последовательными месяцами sin и cos различна, но cos и sin представляют собой основу для времени, следовательно, вместе они эквивалентны с точки зрения информации, и любой алгоритм способен это понять.
Для визуального представления см.:
https://www.ideadrops.info/post/how-to-encode-cyclo-time
Как видите, синусоидальные и косинусные представления предназначены для циклов. В конце концов, что мы действительно хотим зафиксировать с помощью sin/cos, так это то, что понедельники все одинаковы, хотя один понедельник приходится на 15-е, а другой на 22-е. Люди понимают это, но машины не могут, если мы не предоставим информацию в другом формате. Возможно, в ваших данных вы сможете найти несколько значимых циклов (в масштабе лет), чтобы преобразовать год в cos и sin. В противном случае вы не сможете преобразовать годы в cos и sin.
Альтернативой представлению cos/sin является простое масштабирование столбца года по минимуму-максимуму, что сохраняет линейность времени и, вероятно, достаточно для вашей задачи.
Наконец, последний комментарий, вот моя функция для добавления циклических функций в фрейм данных pandas:
def add_column_cyclecal_features(df, col_name_time, период, start_num=0):
значения = 2 * np. pi * (df [col_name_time] - start_num) / период
kwargs = {f'sin_{col_name_time}': лямбда x: np.sin(значения),
f'cos_{col_name_time}': лямбда x: np.cos(значения)}
вернуть df.assign(**kwargs).drop(столбцы=[col_name_time])
pi * (df [col_name_time] - start_num) / период
kwargs = {f'sin_{col_name_time}': лямбда x: np.sin(значения),
f'cos_{col_name_time}': лямбда x: np.cos(значения)}
вернуть df.assign(**kwargs).drop(столбцы=[col_name_time])
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google Зарегистрироваться через Facebook Зарегистрируйтесь, используя адрес электронной почты и парольОпубликовать как гость
Электронная почтаТребуется, но не отображается
Опубликовать как гость
Электронная почтаТребуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания и подтверждаете, что прочитали и поняли нашу политику конфиденциальности и кодекс поведения.
11.8 Законы синусов и косинусов — алгебра среднего уровня (преобразование в MathJax)
Тригонометрия прямого угла обычно ограничивается треугольниками, содержащими прямой угол. Можно использовать тригонометрию с непрямоугольными треугольниками, используя два закона: закон синуса и закон косинуса.
Закон синусов
Закон синусов – это отношение синусов и противоположных сторон. Закон имеет следующий вид:
\[\dfrac{a}{\text{sin}A}\hspace{0,25in} =\hspace{0,25in} \dfrac{b}{\text{sin}B}\hspace{0,25in} =\ hspace{0,25 дюйма} \dfrac{c}{\text{sin}C}\]
Иногда это пишется и используется как противоположность вышесказанному:
\[\dfrac{\text{sin}A}{a}\hspace{0,25in} =\hspace{0,25in} \dfrac{\text{sin}B}{b}\hspace{0,25in} =\ hspace{0,25 дюйма} \dfrac{\text{sin}C}{c}\]
Закон синуса применяют, когда известны либо две стороны и один противолежащий угол одной из сторон, либо когда известны два угла и одна сторона одного из углов. {\ circ}. [ /латекс]
{\ circ}. [ /латекс]
Закон синусов — очень полезный закон с одной оговоркой: иногда можно иметь два треугольника (один больший и один меньший), которые дают одинаковый результат. Это называется неоднозначным случаем и описано далее в этом разделе.
Есть также ошибки учебника, когда данные, приведенные для треугольника, невозможно создать. Например:
Может ли существовать следующий треугольник?
Если такой треугольник может существовать, то отношение синусов углов к противолежащим сторонам должно равняться. 9{\circ}}\]
Сокращение этого дает:
\[\dfrac{6}{0,5} \hspace{0,25 дюйма} = \hspace{0,25 дюйма}\dfrac{6}{0,5} \hspace{0,25 in} = \hspace{0,25in} \dfrac{10}{0,866}\]
Проверяя это, мы находим, что 12 = 12 ≠ 11,55.
Это означает, что этот треугольник не может существовать.
Найдите правильную длину стороны, противоположной 120°, в треугольнике, показанном ниже.
Для этого треугольника соотношение, которое нужно решить, равно: dfrac {6} {\ text {sin} 30 ^ {\ circ}} \ hspace {0,25 дюйма} = \ hspace {0,25 дюйма} \ dfrac {x} {\ text {sin} 120 ^ {\ circ}} \] 9{\circ}
\end{массив}\]
Неоднозначное дело
При наличии правильных данных можно создать два разных треугольника.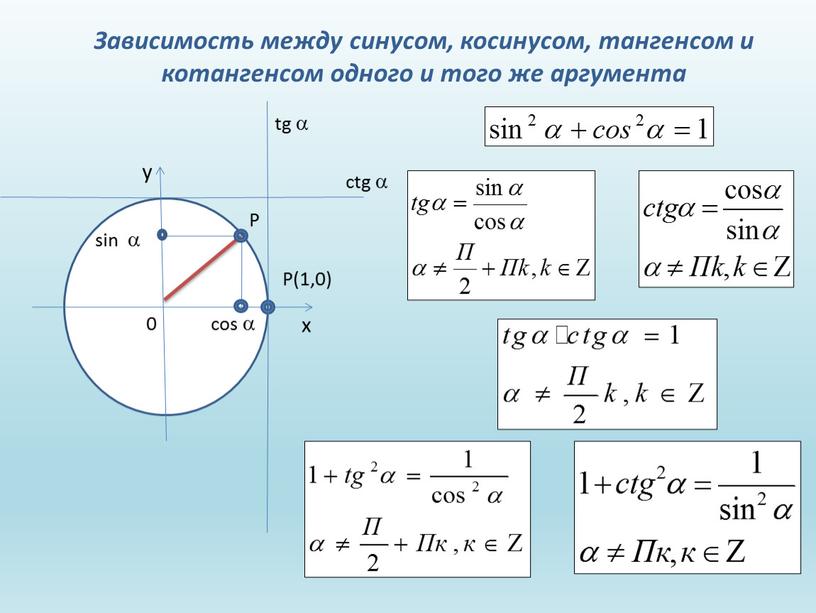

 pi * (df [col_name_time] - start_num) / период
kwargs = {f'sin_{col_name_time}': лямбда x: np.sin(значения),
f'cos_{col_name_time}': лямбда x: np.cos(значения)}
вернуть df.assign(**kwargs).drop(столбцы=[col_name_time])
pi * (df [col_name_time] - start_num) / период
kwargs = {f'sin_{col_name_time}': лямбда x: np.sin(значения),
f'cos_{col_name_time}': лямбда x: np.cos(значения)}
вернуть df.assign(**kwargs).drop(столбцы=[col_name_time])