Перевести math: Math.abs() — JavaScript | MDN

Math и Maths — в чём разница? Перевод Maths и Math? Происхождение – TERKA.RU

Math, Maths — перевод?

Я обеспокоен все более частым использованием слова «maths». Мне стало интересно, почему «math» теперь должен быть во множественном числе? К сожалению, этот вопрос никого не интересует, и мне пришлось самостоятельно провести небольшое расследование, чтобы понять почему так происходит. Как вы уже поняли, сегодня мы разберём в чём разница между словами Math и Maths, перевод и происхождение которых вы сможете выяснить ниже по тексту.

Math и Maths — дословно можно перевести, как «математика», «математический расчёт» или просто «математический».

Происхождение

Само слово «mathematics», источник всей этой «математической» деятельности, происходит от греческого «manthanein», что означает «учиться», что также связано с современными английскими словами «memory» (память) и «mind» (разум). Когда «mathematics» попала в английский язык из французского в 14 веке (в форме «mathematic»), она фактически обозначала любую область, которая включала числовые вычисления (астрономия, физика и т. д.). А широкий диапазон ее греческих корней продолжает жить в английском слове «polymath», означающем человека, обладающего опытом во многих областях.

«Math» как разговорная короткая форма «mathematics» впервые появилась в печати довольно давно, в 1847 году, хотя в этой «math» была точка в конце слова, например, «It rained so that we had a math. lesson indoors» (Шел дождь, так что у нас был урок математики в помещении) и таким образом, очевидно, что это простое неформальное сокращение. «Math» без прикрас появилась к 1870-м годам. Однако слово «maths» немного новее, впервые оно появилось в печати в 1911 году.

Однако нет никакой разницы между «math» и «maths», кроме буквы «s» в конце слова. Иногда вы слышите аргументы, что использование «maths» более уместно, потому что это сокращение от «mathematics» и, следовательно, должно быть множественное число. Но хотя область, которую называют «mathematics», включает в себя несколько дисциплин (например, геометрию, исчисление и т. д.), «mathematics» — это собирательное существительное (как и «physics»), поэтому оно считается единственным. Вы можете сказать это по тому, как «mathematics» трактуется с грамматической точки зрения, англичане говорят: «My favorite subject is mathematics» (Мой любимый предмет — математика), а не «…are mathematics». Форма «mathematics» на самом деле представляет собой то, что было обычной практикой, примерно во время первого появления этого слова, как в случае «acoustics», «physics», «linguistics» и многих других. Термины, которые пришли в английский язык раньше, такие как «arithmetic», не получили этой буквы «s» на конце.

Единственная действительно значимая разница между «math» и «maths» — это применение. «Maths» обычно используется в Великобритании, в то время как «math» является стандартом в США.

Ознакомившись с этой статьёй, вы смогли выяснить, в чём разница между Math и Maths, перевод на русский, и теперь не окажетесь в тупике, если однажды снова вы зададитесь данным вопросом.

Публикация математических текстов в Web с помощью MathML

Публикация математических текстов в Web с помощью MathML

(перевод статьи «Putting mathematics on the Web with MathML»)

В этой статье Вы узнаете, как включать MathML в веб-страницы для просмотра в большинстве современных браузеров.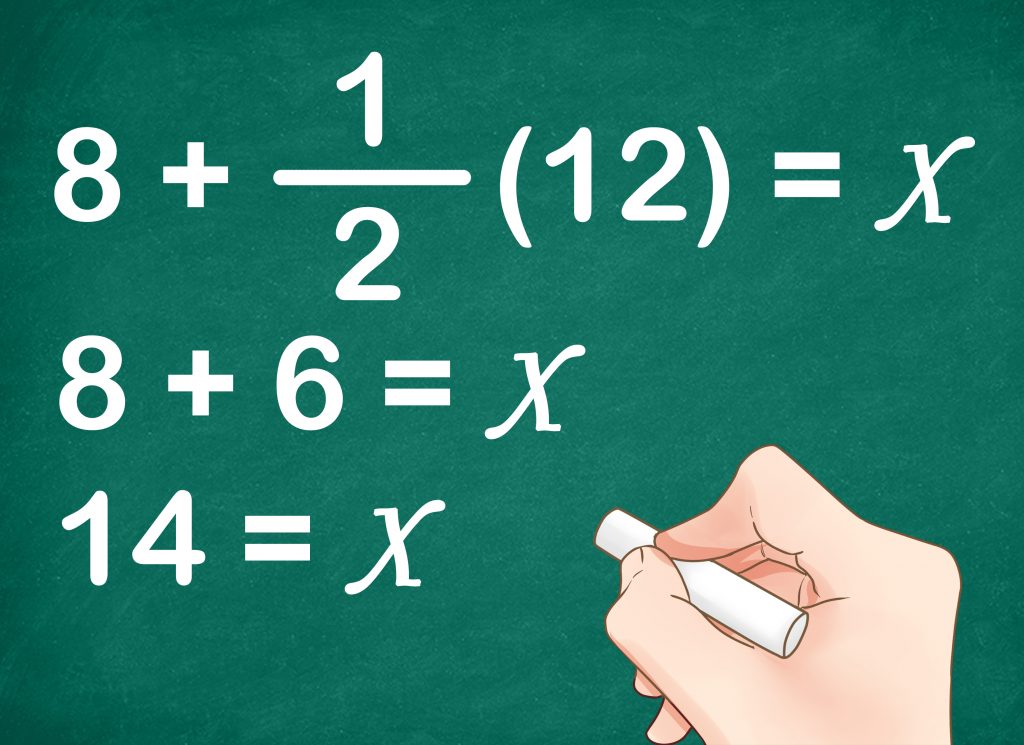

Вы также узнаете, как настроить браузеры для поддержки MathML. На настоящий момент веб-страницы, созданные с использованием описанной ниже техники, можно просматривать в следующих браузерах (знак ‘+’ означает, что более новые версии тоже работают):

• Windows:
  • IE 5.0 с плагином Techexplorer
  • IE 5.5 с плагинами MathPlayer или Techexplorer
  • IE 6.0+ (необязательно) с плагинами MathPlayer или Techexplorer
  • Netscape 6.1 с плагином Techexplorer
  • Netscape 7.0+
  • Amaya, все версии (только Presentation MathML)
  • Mozilla 0.9.9+
• Macintosh:
  • IE 5.0+ с плагином Techexplorer
  • Mozilla 0.9.9+
• Linux/Unix:
  • Netscape 6.1 с плагином Techexplorer
  • Netscape 7.0+
  • Mozilla 0.9.9+
  • Amaya, все версии (только Presentation MathML)

Для тестирование своего браузера загрузите простой пример, использующий Presentation MathML, или более сложный пример, демонстрирующий Content MathML (генерация страницы может занять некоторое время).

Руководство предназначено для авторов веб-страниц, желающих включить в них математические формулы, а также для тех, кто хочет читать такие страницы.

Подробное техническое описание происходящего можно посмотреть на странице, посвященной XSLT-таблицам для MathML. Смотрите также слайды с выступления David’а Carlisle на конференции, посвященной MathML.

Вставка MathML в страницу

Чтобы документ можно было просмотреть на максимальном числе платформ, он должен быть написан по описанным ниже правилам. Заметьте, что при использовании редактора, следующего стандартам W3C (например, Amaya), все описанное произойдет автоматически.

1. Создайте XHMTL-страницу со встроенным MathML

Веб-страница должна быть написана в формате XHTML со встроенной в нее разметкой MathML. Например:

<?xml version="1.0"?>
<html xmlns="http://www.w3.org/1999/xhtml">
  <head>...</head>
  <body>
    <h2>Пример</h2>
    ....
    <math xmlns="http://www. w3.org/1998/Math/MathML">
      <mi>x</mi><mo>+</mo><mn>3</mn>
    </math>
  </body>
</html>

Разметка MathML не должна находиться внутри тэга <object> и не должна быть в отдельном файле, подключаемом из тэга <embed>.

2. Добавьте обработку с помощью таблицы стилей

Выделенную жирным шрифтом строку нужно вставить в начало XHTML-страницы, перед открытием тэга <html>, но после XML-объявления <?xml...?> (если оно есть, конечно):

 <?xml version="1.0"?>
<?xml-stylesheet type="text/xsl" href="http://www.w3.org/Math/XSL/mathml.xsl"?>
<html xmlns="http://www.w3.org/1999/xhtml">
...

Это будет работать не во всех случаях (Например, Internet Explorer, в связи с обеспечением безопасности, не позволяет выполнять XSLT-таблицу, если она находится на сервере, отличном от сервера с XHTML-страницей. В этом случае следуйте инструкциям в пункте «Режим оффлайн» (ниже). Также в конце документа есть дополнительная информация о безопасности в Internet Explorer). Поэтому есть альтернативы:

• Режим оффлайн: Чтобы документ с формулами можно было просматривать локально, без интернет-соедининия, объявление должно выглядеть иначе:

  <?xml-stylesheet type="text/xsl" href="mathml.xsl"?>

  И копии следующих файлов нужно поместить на локальный компьютер, вместе с основным документом: mathml.xsl, pmathml.xsl, ctop.xsl and pmathmlcss.xsl.

• Presentation MathML: если в документе используется только Presentation MathML, то достаточно только двух файлов: pmathml.xsl и pmathml-css.xsl. В этом случае страница будет обрабатываться быстрее.

Вот и все. Дополнительную информацию смотрите ниже.

Указание предпочтений

Возможна ситуация, когда в браузере есть несколько способов обработать разметку MathML (например, Internet Explorer с плагином Techexplorer может еще отображать формулы с помощью CSS). Для таких случаев предоставляется возможность указать предпочтительный метод обработки, изменяя значение атрибута renderer. Например:

<?xml-stylesheet type="text/xsl" href="pmathml.xsl"?>
<html xmlns="http://www.w3.org/1999/xhtml"
      
 xmlns:pref="http://www.w3.org/2002/Math/preference"
      pref:renderer="css">
<head>...</head>
<body>...</body>
</html>

Здесь указывается, что предпочтителен метод с использованием CSS. Значения атрибута renderer:

• css: отображать формулы с помощью CSS (плагин не требуется).
• mathplayer-dl: в случае необходимости запросить установку плагина MathPlayer.
• mathplayer: использовать MathPlayer.
• techexplorer-plugin: использовать плагин Techexplorer.
• techexplorer: использовать Techexplorer.

Безопасность Microsoft Internet Explorer

По умолчанию, Internet Explorer не позволяет применять XSLT-таблицу к документу, если она находится на сервере, отличном от сервера с документом.

Поэтому так работать не будет:

<?xml-stylesheet type="text/xsl" href="http://www.w3.org/Math/XSL/mathml.xsl"?>

Вместо этого необходимо скопировать таблицы стилей на тот же сервер, где находится документ (как описано выше). В качестве альтернативы можно изменить настройки безопасности Internet Explorer, но такой способ нельзя порекомендовать, так как изменение настроек повлияет на всю работу браузера, а не только на загрузку таблицы стилей.

Презентация на MathML конференции

Эта таблица стилей была представлена на 2-ой Международной MathML конференции. Там были продемонстрированы примеры использования таблиц стилей для просмотра в полноэкранном режиме браузера. Для показа примеров одновременно использовались IE6, Mozilla 1.0, Amaya 6.1, и Netscape 7.0PR1.

В дополнение к MathML был также продемонстрирован небольшой пример расширения этой таблицы стилей для использования с SVG.

---

The W3C Math Working Group. Send comments, questions and fixes to www-math@w3. org

Translated by Alexey Shamrin

Трансляционная математика — геометрия, график, правила, функции

В 19 ^-м -м веке Феликс Кляйн предложил новый взгляд на геометрию, известный как трансформационная геометрия. Большинство доказательств в геометрии основано на преобразованиях объектов. Для графика функции возможны четыре типа преобразований (и перевод в математике — один из них). Это:

• Вращения
• Переводы
• Отражения
• Расширение

В этой главе мы узнаем о переводе в математике, используя определение математики перевода и примеры математики перевода. Попробуйте свои силы в нескольких математических задачах перевода по геометрии перевода в конце страницы.

1.	Что такое перевод в математике?
2.	Прообразы и образы перевода
3.	Переводы на координатной плоскости
4.	Как графически отображать переводы в математике?
5.	Перевод функций
6.	Преобразование, представленное вектором-столбцом или матрицей
7.	Часто задаваемые вопросы о переводах Math

Что такое перевод в математике?

Translation Math Definition

Перевод в математике перемещает фигуру влево или вправо и/или вверх или вниз. Переведенные фигуры выглядят точно такого же размера, как исходная фигура, и, следовательно, фигуры конгруэнтны друг другу. Они просто были смещены в одном или нескольких направлениях. Поскольку это просто перемещение формы из одного места в другое, форма не меняется.

Направление или путь этого изменения положения объекта может варьироваться, т. е. сначала объект может двигаться влево, затем поворачивать вправо и так далее. При перемещении все точки фигуры сместятся на одинаковое количество единиц. Например, если одна точка сдвинется на 2 единицы вправо, то все точки также сместятся на 2 единицы вправо.

Перевод — одно из преобразований в математике. Когда форма была преобразована, исходная форма называется прообразом, а вершины обычно обозначаются заглавными буквами (пример: ABCD). Переведенная фигура называется изображением, а вершины помечены заглавными буквами со словом «штрих» рядом с каждой (пример: A′B′C′D′ и произносится как «A-простой, B-простой, C-простой). , D-простое»).

Преобразование в геометрии Пример

На приведенном ниже рисунке прообразом является ABC, а его изображением является A’B’C’. Здесь ABC переводится следующими двумя способами (один за другим), чтобы сформировать A’B’C’.

• Перемещено вверх (по вертикали) на 3 единицы, а затем
• Сдвинут вправо (по горизонтали) на 2 единицы

Обратите внимание, что при перемещении треугольника влево/вправо/вверх/вниз мы сдвинули все точки треугольника на равное количество единиц в одном направлении.

Прообразы и образы перевода

Как мы только что видели, форма до применения переводов известна как «прообраз», а форма, полученная после применения переводов, известна как «изображение». Проще говоря:

• «Прообраз» — форма до перевода.
• «Изображение» — форма после перевода.

Посмотрите на следующий рисунок, где ABCD — прообраз, а A’B’C’D’ — образ ABC.

Переводы на координатной плоскости

Любой объект, представленный в координатной плоскости, можно перемещать по горизонтали (влево/вправо) или по вертикали (вверх/вниз). Давайте посмотрим на последний пример, чтобы понять переносы на координатной плоскости. График представлен в координатной плоскости, как показано на рисунке. При переводе четырехугольник смещается на 5 единиц по горизонтали вправо и на 1 единицу по вертикали вверх, что означает, что новая функция перевода для данной фигуры будет равна

(x, y) → (x + 5, y + 1)

К этому времени вы уже могли понимать процесс написания переводов. Влево/вправо влияют на координату x, а вверх/вниз влияют на координату y точки. Вот правила перевода.

Правила перевода

• Когда фигура сместится влево на k единиц, замените x на x — k.
• Когда фигура сдвинется вправо на k единиц, замените x на x + k.
• Когда фигура переместится вверх на k единиц, замените y на y + k.
• Когда фигура сдвинется вниз на k единиц, замените y на y — k.

Пример: Каковы новые координаты, когда перевод (x, y) → (x — 2, y + 3) применяется к точке (2, 5).

Решение:

Координаты старой точки (прообраза) равны (x, y) = (2, 5). Теперь, применяя данное преобразование к этой точке,

х — 2 = 2 — 2 = 0
y + 3 = 5 + 3 = 8

Таким образом, координаты перенесенной точки (изображения) равны (0, 8).

Как графически отображать переводы в математике?

Чтобы построить график перемещения фигуры, выполните следующие шаги:

• Определите вершины фигуры.
• Примените данное преобразование к каждой из вершин, чтобы найти новые вершины (как показано в приведенном выше примере).
• Затем просто нанесите новые точки на координатную плоскость и соедините их в соответствии с заданной формой.

Пример: Фигура сформирована с вершинами (1, 8), (-3, -5), (-4, 7) и (-6, -2). Постройте изображение этой формы относительно перевода (x, y) → (x + 6, y + 1).

Решение:

Вычислим новые координаты каждой из заданных вершин.

Старые координаты (до перевода)	Новые координаты (После перевода)
А (1, 8)	(1 + 6, 8 + 1) = (7, 9) = А’
Б (-3, -5)	(-3 + 6, -5 + 1) = (3, -4) = В’
С (-4, 7)	(-4 + 6, 7 + 1) = (2, 8) = С’
Д (-6, -2)	(-6 + 6, -2 + 1) = (0, -1) = Д’

Давайте просто построим прообраз и изображение.

Перевод функций

Горизонтальное перемещение кривых, представляющих функции, работает несколько иначе по сравнению с горизонтальным перемещением точек на координатной плоскости. Давайте рассмотрим пример ниже.

Здесь прообраз есть f(x), а образ есть f(x + 2). Удивительно, но f(x) сместилась на 2 единицы влево (вместо 2 единиц вправо), что дало f(x + 2). Да, это касается горизонтальных переводов функций. Но это не относится к вертикальным переводам. Вертикальные переносы работают точно так же, как они работают с переносами точек на координатной плоскости.

Правила перевода функций

В соответствии с приведенным выше наблюдением правила написания переведенных функций можно обобщить следующим образом:

Перевод функции	Когда k > 0	Когда k < 0
Горизонтальное перемещение f(x) становится f(x + k)	Перемещает f(x) «k» единиц влево.	Перемещает f(x) «k» единиц вправо.
Вертикальное перемещение f(x) становится f(x) + k	Перемещает f(x) «k» единиц вверх	Перемещает f(x) «k» единиц вниз

Вот несколько примеров:

1. f(x — 2) + 3 хода f(x) на 2 единицы вправо и на 3 единицы вверх.
2. g(x + 3) — 5 ходов g(x) на 3 единицы влево и на 5 единиц вниз.

Преобразование графиков функций

Чтобы отобразить переведенные графики, мы можем перемещать данный график влево/вправо/вверх/вниз, используя приведенные выше правила. Вместо этого мы можем перевести график, используя координаты некоторых точек на нем. Чтобы построить график перевода функции f(x + k) + C, когда задан график функции f(x), просто возьмите некоторые важные точки графика (где форма меняется или меняется) и найдите новые значения x и y координаты каждой точки следующим образом.

• Чтобы найти новую координату x, установите «x + k = старая координата x» и решите это для x.
• Чтобы найти новую координату Y, используйте «старая координата Y + C».

Найдя все новые точки, просто начертите их и соедините. Это даст переведенный график. Вы можете найти пример этого процесса в разделе «Примеры» ниже.

Преобразование, представленное вектором-столбцом или матрицей

Перевод любого объекта может быть представлен вектор-столбцом или матрицей-столбцом следующим образом: \(\left(\begin{array}{l}
а \\\
б
\end{array}\right)\),

, где a – количество единиц, на которое нужно сместиться вправо или влево по оси x, а b – количество единиц, на которые нужно сместиться вверх или вниз по оси y.

• Число вверху обозначает правое или левое движение. Положительное число означает движение вправо, а отрицательное число означает движение влево.
• Число внизу обозначает движение вверх и вниз. Положительное число означает движение вверх, а отрицательное число означает движение вниз.

На следующем рисунке треугольник ABC переводится в треугольник A’B’C’:

Перевод из ABC в A’B’C’ означает «2 единицы вправо и 3 единицы вниз» и вектор-столбец который представляет этот перевод: \(\left(\begin{array}{c}
2\\
-3
\конец{массив}\справа)\).

Важные замечания по математике перевода:

• При переводе все точки сместятся на одинаковое количество единиц.
• Форма или размер объекта остаются неизменными после перемещения.
• При горизонтальном переносе может быть затронут домен, тогда как при вертикальном переносе может быть затронут диапазон.

☛ Связанные темы:

• Типы функций
• Декартова плоскость
• Координатная геометрия

Часто задаваемые вопросы о переводах Math

Что такое переводческая математика?

Преобразование в математике (также называемое изометрией) — это преобразование формы на плоскости с сохранением длины, что означает, что объект трансформируется без изменения его размеров. то есть его можно просто сдвинуть влево/вправо/вверх/вниз.

Что такое процесс графического перевода?

Для графического переноса обратите внимание на следующее:

• В координатной плоскости (x, y) → (x + k, y + C) означает:
  перемещение по горизонтали вправо, если k > 0, и влево, если k < 0,
  перемещение вертикально вверх, если C > 0, и вниз, если C < 0.
• В случае функций f(x) → f(x + k) + C означает:
  перемещение по горизонтали влево, если k > 0, и вправо, если k < 0.
  перемещение вертикально вверх, если C > 0, и вниз, если C < 0.

Просто позаботьтесь о вышеперечисленных вещах и соответствующим образом переместите фигуру во время графического перевода.

Как вы решаете переводы?

Перевод любого объекта может быть решен в двух разделах, в зависимости от того, перемещается ли объект по горизонтали, вертикали или в обоих направлениях. Функция f(x) после переноса может быть представлена ​​в общем виде как f(x) = f(x + k) + C, где

• k — количество единиц, сдвинутых по горизонтали (вправо, если k < 0, и влево, если k > 0)
• C — количество единиц, сдвинутых по вертикали (вверх, если C > 0, и вниз, если C < 0)

Что такое правила перевода в математике?

Основные правила, которым необходимо следовать при перемещении объекта, следующие:

• Положительное перемещение по оси X или по горизонтали будет означать смещение влево, а отрицательное горизонтальное перемещение означает смещение вправо.
• Положительное смещение по оси Y или по вертикали будет означать смещение объекта вверх, а отрицательное вертикальное смещение означает смещение вниз.
• Форма или размер объекта остаются неизменными после перемещения.
• Все точки объекта сместятся на одинаковое количество единиц и в одном направлении.

Как графически отображать переводы функций?

Чтобы построить график преобразования f(x + k) + C функции f(x) в математике, выполните следующие действия.

• Запишите некоторые координаты старого графика (f(x)). Процесс нахождения координат x и y точки отличается и объясняется ниже.
• Установите для каждой старой координаты x значение x + k и найдите x, что даст новую координату x этой точки.
• Просто добавьте C к старой координате y, чтобы найти новую координату y.
• Просто нанесите все новые точки и соедините их в соответствии с формой заданной кривой.

Как перевести фигуру в математику?

Перемещение объекта в координатной плоскости включает изменение положения формы на заданное число единиц в заданном направлении. Размер и форма остаются неизменными после перевода. При переводе все точки сместятся на одинаковое количество единиц. Если одна точка на фигуре сдвинется на 4 единицы влево, то все точки также сместятся на 4 единицы влево.

Объяснение перевода геометрии — примеры и дополнительная практика! — Мэшап Математика

Следующее пошаговое руководство покажет вам, как выполнять геометрическое преобразование точек и фигур! (Включено бесплатное руководство в формате PDF!)

Добро пожаловать в это бесплатное руководство, которое сопровождает этот видеоурок по переводу геометрии, в котором вы узнаете ответы на следующие ключевые вопросы и информацию:

• Что такое определение математики перевода в математике преобразования?

• Как выполнить горизонтальное и вертикальное перемещение?

• Несколько примеров математических переводов.

  *Это руководство к уроку прилагается к нашему анимированному математическому видео «Геометрические переводы с объяснением».

  Хотите больше бесплатных уроков математики и видео? Подпишитесь на наш канал бесплатно!

  Прежде чем вы научитесь выполнять горизонтальные и вертикальные переводы, давайте быстро рассмотрим определение переводов в математических терминах.

  Математическое определение перевода:

  Перевод — это слайд из одного места в другое без изменения размера или ориентации.

  Обратите внимание, что перемещение отличается от других преобразований геометрии, включая повороты, отражения и расширения.

  Чтобы узнать больше о других типах трансформаций геометрии, щелкните по ссылкам ниже:

  • Геометрические вращения объяснены: Бесплатное руководство с примерами

  • Геометрия Размышления. Объяснение расширения геометрии: бесплатное руководство с примерами

  Горизонтальные перемещения и вертикальные перемещения

  Горизонтальное перемещение относится к перемещению слева направо или наоборот вдоль оси x (горизонтальный доступ).

  Вертикальное перемещение означает скольжение вверх или вниз по оси Y (вертикальный доступ).

  Во многих случаях перемещение будет как горизонтальным, так и вертикальным, что приводит к диагональному скольжению по координатной плоскости. Давайте посмотрим, как это работает, на следующих нескольких примерах:

  Обозначение преобразования геометрии

  Обратите внимание, что следующие обозначения используются, чтобы показать, какой вид преобразования выполняется.

  T a,b

  Где T обозначает перемещение, a представляет значение горизонтального перемещения, а b представляет значение вертикального перемещения.

  Рисунок 1

  Теперь вы готовы попробовать несколько примеров расширения геометрии!

  >>> Пример 01: Перемещение сегмента линии

  Выполните следующее преобразование на сегменте линии PQ: T-8,4

  В этом примере необходимо переместить отрезок PQ на -8 единиц по горизонтали и на +4 единицы по вертикали.

  Первым делом нужно записать координаты концов отрезка PQ. Из графика видно, что координаты равны P(3,0) и Q(6,-6).

  *Обратите внимание, что PQ называется прообразом, а новая фигура после завершения перевода P’Q’ (произносится как P Prime, Q Prime) будет изображением).

  В этом примере мы переводим отрезок на следующие значения:

  T -8,4

  Это означает, что цифра сдвигается на -8 единиц по горизонтали и +4 единицы по вертикали.

  Начнем с горизонтального перевода:

  Поскольку значение равно -8, вы должны добавить -8 (или просто вычесть 8) из x-координат точек P и Q следующим образом:

  С визуальной точки зрения это то же самое, что и перемещение отрезка PQ на 8 единиц влево от текущего положения.

  Теперь для вертикального перемещения:

  Поскольку значение равно 4, вам нужно добавить 4 к y-координатам точек P и Q следующим образом:

  С визуальной точки зрения это то же самое, что сдвинуть отрезок линии PQ на 4 единицы вверх от его текущего местоположения.

  Теперь, когда у нас есть путь, мы можем преобразовать PQ в P’Q’ следующим образом:

  Кроме того, мы можем подтвердить координаты P’ и Q’ следующим образом:

  Этот пример должен помочь вам визуально понять концепцию перевода геометрии. Далее вы узнаете, как перевести всю фигуру.

  <><><>

  >>> Пример 02: Перевести фигуру

  Построить образ △E’F’G’ после следующего преобразования: T 6,-1

  Как и в предыдущем примере, начнем с записи координат вершин прообраза △EFG: E(-8,-1), F(0,2), G(-3,-8 )

  Затем запланируйте добавить 6 к каждому значению x и вычесть 1 из каждого значения y:

  Это даст вам координаты переведенного изображения △E’F’G’: E(-2,-2), F(6,1), G(-3,-9)

  На графике это преобразование представляет собой горизонтальный сдвиг на 6 единиц вправо и вертикальный сдвиг на 1 единицу вниз:

  Последний шаг — выполнить перевод и построить △E’F’G’

  Кроме того, мы можем подтвердить координаты △E’F’G’ следующим образом:

  <><><>

  Бесплатное учебное пособие в формате PDF

  Ищете дополнительную помощь по математическим переводам?

  Нажмите на ссылку ниже, чтобы загрузить бесплатное руководство по уроку в формате PDF, соответствующее видеоуроку ниже!

  Щелкните здесь, чтобы загрузить бесплатное руководство к уроку в формате PDF.

  No related posts.