Ряды распределения.
Ряд распределения – это группировка, в которой для характеристики групп применяется только один показатель – численность групп.
Атрибутивный ряд — это ряд распределения, построенный по качественным признакам (не имеющим числового выражения).
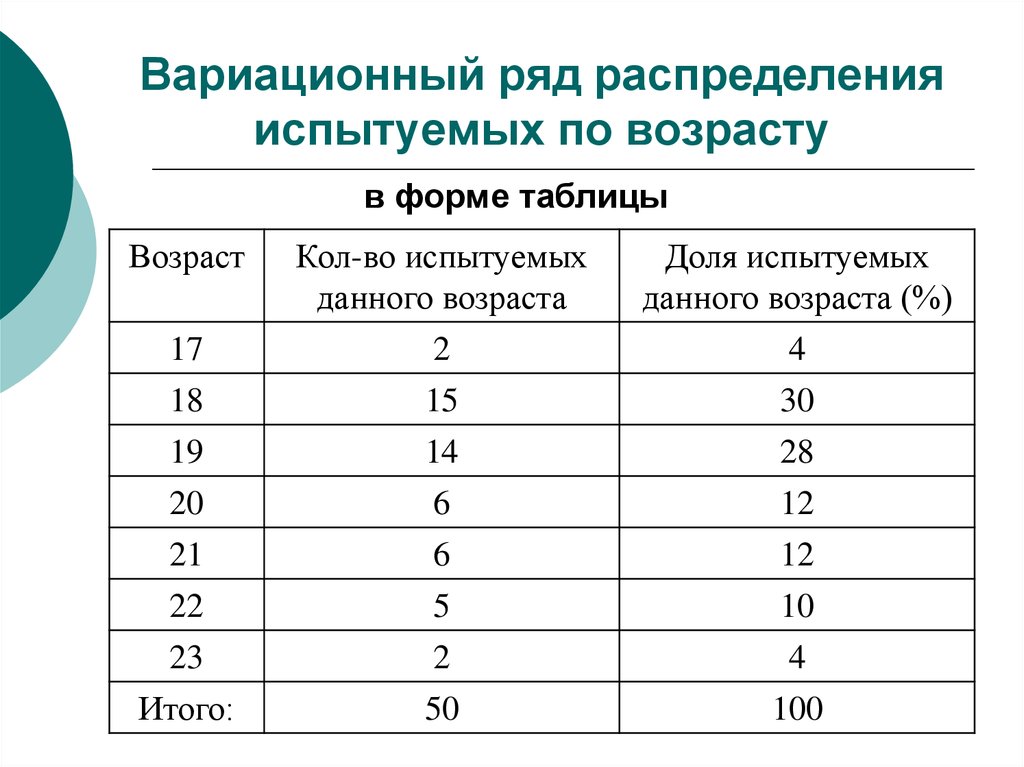
Вариационный ряд – это ряд распределения, построенный по количественному признаку.
Дискретный вариационный ряд – это ряд, который характеризует распределение единиц совокупности по дискретному признаку.
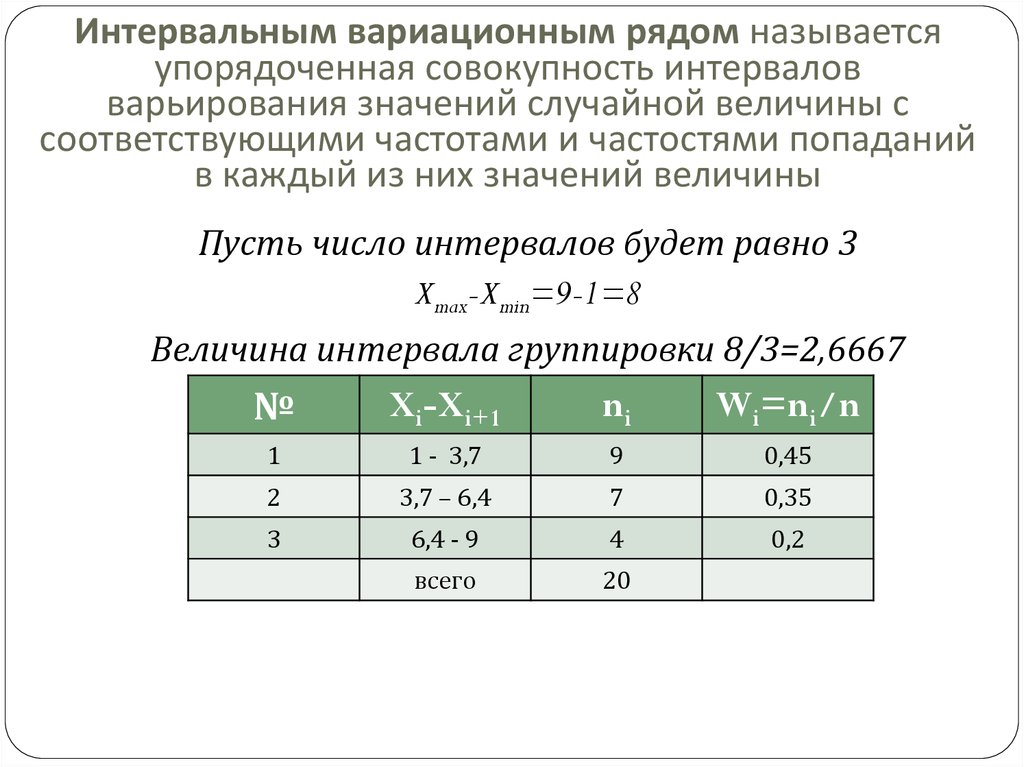
Интервальный вариационный ряд – это ряд, который характеризует распределение единиц совокупности по непрерывному признаку.
Варианта – это отдельное значение признака,
которое он принимает в вариационном
ряду.
Частота – это численность отдельной варианты или каждой группы вариационного ряда.
Графическое изображение ряда распределения осуществляется с помощью:
Полигон частот используется при изображении дискретных вариационных рядов. На оси Ох откладываются ранжированные значения признака, на оси Оу – значения частот. Полученные точки последовательно соединяются ломаной линией (полигон).
Гистограмма применяется для изображения интервального вариационного ряда. На оси Ох откладываются величины интервалов и на их основании строят прямоугольники, высота которых пропорциональна частотам
Кумулята (кривая сумм) используется для изображения вариационных рядов, изображает ряд накопленных частот.
Накопленная частота
показывает, сколько единиц совокупности
имеют значения признака не больше, чем
рассматриваемое значение.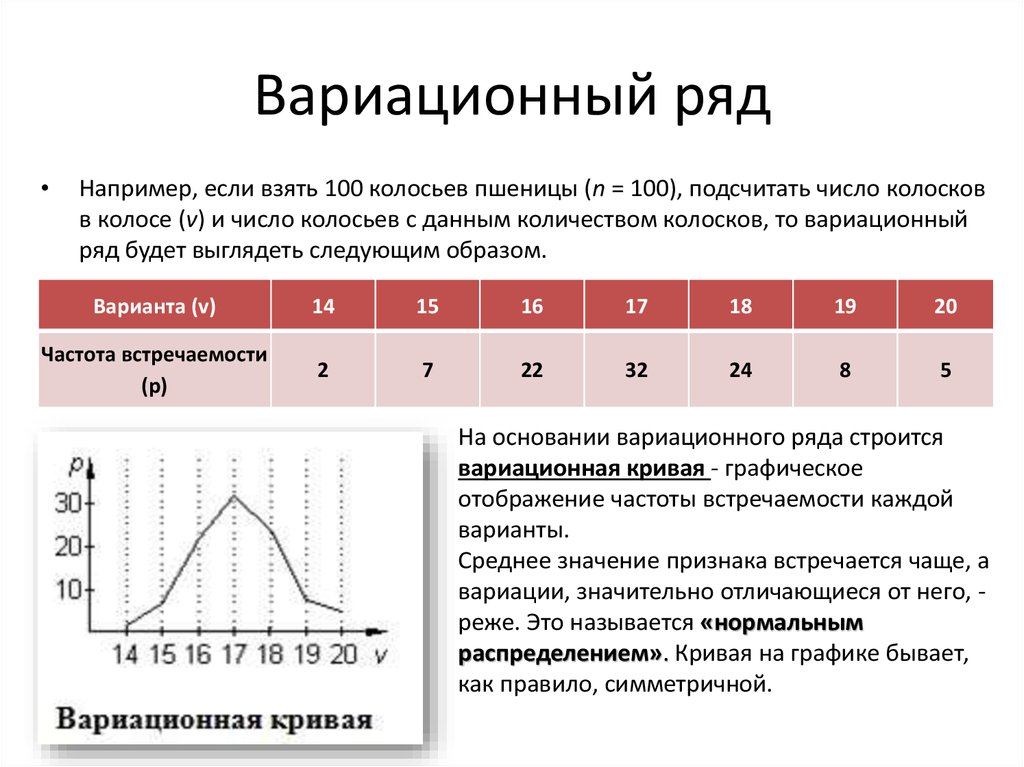
Если при графическом изображении вариационного ряда в виде кумуляты оси поменять местами, то получится огива.
Этапы проведения группировки:
число групп определяется числом разновидностей признака
число групп определяется числом разновидностей признака
число групп определяется числом интервалов, на которые разбивается весь диапазон изменения признака
Перед тем, как рассчитать величину интервала, целесообразно проанализировать характер варьирования группировочного признака, с этой целью стоят ранжированный ряд распределения.
Ранжированный ряд – это группировочный признак, расположенный в порядке возрастания.
Если группировочный
признак изменяется скачкообразно, то
число групп и их границы выделяются
логическим путем. А, если группировочный
признак изменяется плавно, то число
групп определяется математическим
способом, предложенным американским
ученым Стэрджессом.
n=2lg(N), где N число единиц совокупности, используется при N<50.
n=1+3.322lg(N), если число единиц совокупности превышает 50 единиц.
Полученные значения n необходимо округлить до наибольшего целого значения.
Интервал – это разница между максимальным и минимальным значениями признака в каждой группе.
ИНТЕРВАЛЫ
Равные интервалы определяются по формуле:
где xmax, xmin –максимальное и минимальное значение признака в совокупности; n – число групп;Существуют следующие правила округления шага интервала:
если величина h имеет один знак до запятой, то ее округляют до десятых;
если величина h имеет два знака до запятой, то ее округляют до целого числа;
если величина h имеет три знака до запятой, то ее округляют до числа, кратного 50 или 100, и т.
 д.
д.
Дискретный вариационный ряд и его характеристики — классификация, дисперсия, стандартное отклонение выборки
- Классификация рядов распределения
- Дискретный вариационный ряд, полигон частот и кумулята
- Выборочная средняя, мода и медиана
- Степень асимметрии вариационного ряда
- Выборочная дисперсия и СКО
- Исправленная выборочная дисперсия, стандартное отклонение выборки и коэффициент вариации
- Алгоритм исследования дискретного вариационного ряда
- Примеры
п.1. Классификация рядов распределения
Статистический ряд распределения – это количественное распределение единиц совокупности на однородные группы по некоторому варьирующему признаку.
В зависимости от природы признака различают атрибутивные и вариационные ряды.
Атрибутивный ряд распределения построен на качественном признаке.
Вариационный ряд распределения построен на количественном признаке.
Например:
Качественными признаками, которые не поддаются измерению, являются: профессия, пол, национальность и т. п.
п.
Количественными признаками, которые можно подсчитать или измерить, являются: количество людей в группе, число повторений в опыте, возраст, вес, рост, скорость, температура и т.п.
По упорядоченности вариационные ряды делятся на упорядоченные (ранжированные) и неупорядоченные. Упорядочить ряд можно по возрастанию или убыванию исследуемого признака.
По характеру непрерывности признака вариационные ряды делятся на дискретные и интервальные.
Например:
Дискретными признаками, которые принимают отдельные значения, являются: количество людей в группе, число детей в семье, количество домов, число опытов и т.п.
Непрерывными признаками, которые могут принимать любые значения в интервале, являются: возраст, вес, рост, скорость, температура и т.п.
Варианты – это отдельные значения признака, которые он принимает в вариационном ряду.
Частоты – это численности отдельных вариант.
Например:
| Оценка, \(x_i\) | 2 | 3 | 4 | 5 | Всего |
| К-во учеников, \(f_i\) | 3 | 15 | 10 | 5 | 33 |
В данном ряду признак – это оценка, варианты признака \(x_i\) – это множество {2;3;4;5}, частоты \(f_i\) – это количество учеников, получивших каждую из оценок. k f_i\)
k f_i\)
Полигон частот – это ломаная, которая соединяет точки \((x_i,f_i)\).
Например:
| Для распределения учеников по оценкам из нашего примера получаем такой полигон: |
Относительная частота варианты \(x_i\) — это отношение частоты \(f_i\) к общему количеству исходов: $$ w_i=\frac{f_i}{N},\ \ i=\overline{1,k} $$ Относительная частота \(w_i\) является эмпирической оценкой вероятности варианты \(x_i\) в исследуемом ряду.
Полигон относительных частот – это ломаная, которая соединяет точки \((x_i,w_i)\).
Полигон относительных частот является эмпирическим законом распределения исследуемого признака.
Накопленные относительные частоты – это суммы: $$ S_1=w_1,\ \ S_i=S_{i-1}+w_i,\ \ i=\overline{2,k} $$ Кумулята – это ломаная, которая соединяет точки \((x_i,S_i)\).
Ступенчатая кривая \(F(x_i)\), построенная по точкам \((x_i,S_i)\), является эмпирической функцией распределения исследуемого признака.
Например:
Проведем необходимые расчеты и построим полигон относительных частот, кумуляту и эмпирическую функцию распределения учеников по оценкам.
| Оценка, \(x_i\) | 2 | 3 | 4 | 5 | Всего |
| К-во учеников, \(f_i\) | 3 | 15 | 10 | 5 | 33 |
| \(w_i\) | 0,0909 | 0,4545 | 0,3030 | 0,1515 | 1 |
| \(S_i\) | 0,0909 | 0,4545 | 0,8485 | 1 | — |
Полигон относительных частот (эмпирический закон распределения)
Кумулята (красная ломаная) и эмпирическая функция распределения (ступенчатая синяя кривая).
Эмпирическая функция распределения: $$ F(x)= \begin{cases} 0,\ x\leq 2\\ 0,0909,\ 2\lt x\leq 3\\ 0,5455,\ 3\lt x\leq 4\\ 0,8485,\ 4\lt x\leq 5\\ 1,\ x\gt 5 \end{cases} $$
п.
 k x_iw_i $$
k x_iw_i $$Мода дискретного вариационного ряда – это варианта с максимальной частотой: $$ M_o=x*,\ \ f(x*)=\underset{i=\overline{1,k}}{max}f_i $$ Мод может быть несколько. Тогда говорят, что ряд мультимодальный.
На полигоне частот мода – это абсцисса самой высокой точки.
На графике кумуляты медиана – это абсцисса первой точки слева, ордината которой превысила 0,5.
Например:
1) Найдем выборочную среднюю для распределения учеников по оценкам:
| Оценка, \(x_i\) | 2 | 3 | 4 | 5 | Всего |
| К-во учеников, \(f_i\) | 3 | 15 | 10 | 5 | 33 |
| \(x_if_i\) | 6 | 45 | 40 | 25 | 116 |
$$ X_{cp}=\frac{6+45+40+25}{33}=\frac{116}{33}\approx 3,5 $$ Средняя оценка за контрольную – 3,5.
2) Найдем моду. Максимальная частота – 15 человек – у троечников. Значит: \(M_o=3\).
Значит: \(M_o=3\).
3) Найдем медиану. Общее количество измерений N=33 — нечетное.
Смотрим на ряд слева направо. Сначала у нас идет 3 двоечника, затем 15 троечников.
Вместе их 18, и 17-й человек в ряду — троечник. Группа троечников является медианной: \(M_e=3\).
Также, медиану можно найти по графику кумуляты. (3;0,5455) – это первая слева точка, в которой ордината больше 0,5. Значит, медиана равна абсциссе этой точки, т.е. \(M_e=3\).
п.4. Степень асимметрии вариационного ряда
В рядах с асимметрией или выбросами выборочная средняя не отражает в полной мере особенности исследуемого признака. Типичный случай – значение среднего уровня доходов в странах с высоким индексом Джини, где 5% населения получает 95% доходов. Или анекдотичный случай со «средней температурой по больнице».
Поэтому, кроме средней, в статистическом исследовании всегда следует определять моду и медиану.
Мода, медиана и выборочная средняя совпадут, если вариационный ряд является симметричным: $$ X_{cp}=M_o=M_e $$ Если вершина распределения сдвинута влево и правая часть ветви длиннее левой (длинный правый хвост), такая асимметрия называется правосторонней. При правосторонней асимметрии: $$ M_o\lt M_e\lt X_{cp} $$ Если вершина распределения сдвинута вправо и левая часть ветви длиннее правой (длинный левый хвост), такая асимметрия называется левосторонней. При левосторонней асимметрии: $$ M_o\gt M_e\gt X_{cp} $$ Для умеренно асимметричных рядов (по Пирсону) модуль разности между модой и средней не более 3 раз превышает модуль разности между медианой и средней: $$ \frac{|M_o-X_{cp}|}{|M_e-X_{cp}|}\geq 3 $$
При правосторонней асимметрии: $$ M_o\lt M_e\lt X_{cp} $$ Если вершина распределения сдвинута вправо и левая часть ветви длиннее правой (длинный левый хвост), такая асимметрия называется левосторонней. При левосторонней асимметрии: $$ M_o\gt M_e\gt X_{cp} $$ Для умеренно асимметричных рядов (по Пирсону) модуль разности между модой и средней не более 3 раз превышает модуль разности между медианой и средней: $$ \frac{|M_o-X_{cp}|}{|M_e-X_{cp}|}\geq 3 $$
Например:
Для распределения учеников по оценкам мы получили \(X_{cp}=3,5;\ M_o=3;\ M_e=3\).
Т.к. средняя оказалась больше моды и медианы, наше распределение имеет правостороннюю асимметрию (что видно на полигоне частот – правый хвост длиннее).
При этом \(\frac{|M_o-X_{cp}|}{|M_e-X_{cp}|}=\frac{0,5}{0,5}=1\lt 3\), т.е. распределение умеренно асимметрично.
п.5. Выборочная дисперсия и СКО
Выборочная дисперсия дискретного вариационного ряда определяется как средняя взвешенная для квадрата отклонения от средней: \begin{gather*} D=\frac{(x_1-X_{cp})^2 f_1+(x_2-X_{cp})^2 f_2+.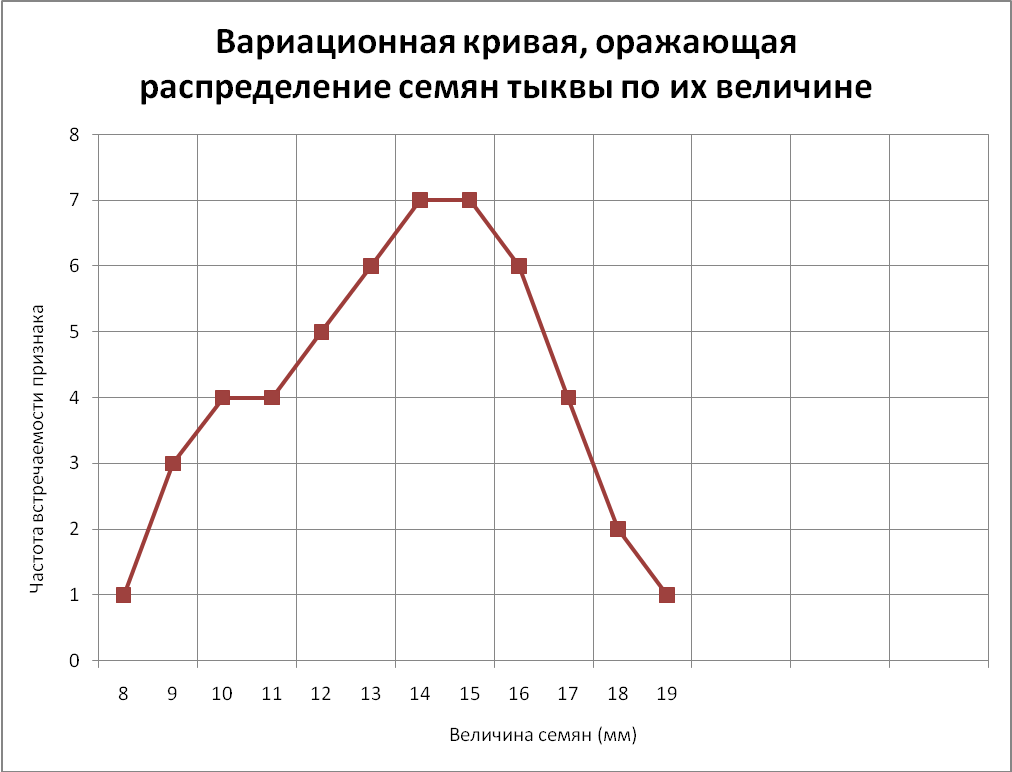 2f_i\)
2f_i\)
Шаг 2. Построить полигон относительных частот (эмпирический закон распределения) и график кумуляты с эмпирической функцией распределения. Записать эмпирическую функцию распределения.
Шаг 3. Найти выборочную среднюю, моду и медиану. Проанализировать симметрию распределения.
Шаг 4. Найти выборочную дисперсию и СКО.
Шаг 5. Найти исправленную выборочную дисперсию, стандартное отклонение и коэффициент вариации. Сделать вывод об однородности выборки.
п.8. Примеры
Пример 1. На площадке фриланса была проведена выборка из 100 фрилансеров и подсчитано количество постоянных заказчиков, с которыми они работают.
В результате было получено следующее распределение:
| Число постоянных заказчиков | 0 | 1 | 2 | 3 | 4 | 5 |
| Число фрилансеров | 22 | 35 | 27 | 11 | 3 | 1 |
Исследуйте полученный вариационный ряд. 2}\approx 1,109 $$ Коэффициент вариации: $$ V=\frac{s}{X_{cp}}\cdot 100\text{%}=\frac{1,109}{1,39}\cdot 100\text{%}\approx 79,8\text{%}\gt 33\text{%} $$ Представленная выборка неоднородна. Полученное значение средней \(X_{cp}=1,39\) не может быть распространено на генеральную совокупность всех фрилансеров.
2}\approx 1,109 $$ Коэффициент вариации: $$ V=\frac{s}{X_{cp}}\cdot 100\text{%}=\frac{1,109}{1,39}\cdot 100\text{%}\approx 79,8\text{%}\gt 33\text{%} $$ Представленная выборка неоднородна. Полученное значение средней \(X_{cp}=1,39\) не может быть распространено на генеральную совокупность всех фрилансеров.
типов статистических рядов — GeeksforGeeks
Что такое статистические ряды?
Упорядочивание секретных данных в некотором логическом порядке, например, по времени появления, размеру или некоторым другим измеримым или неизмеримым характеристикам, известно как Статистический ряд. Эти серии подготовлены для надлежащего представления собранных и классифицированных данных в упорядоченном виде. Например, , если данные, содержащие вес 50 учащихся в классе, расположить в систематическом порядке, они будут известны как статистические ряды.
Типы статистических рядов
Статистические ряды можно классифицировать По признакам и по построению:
А.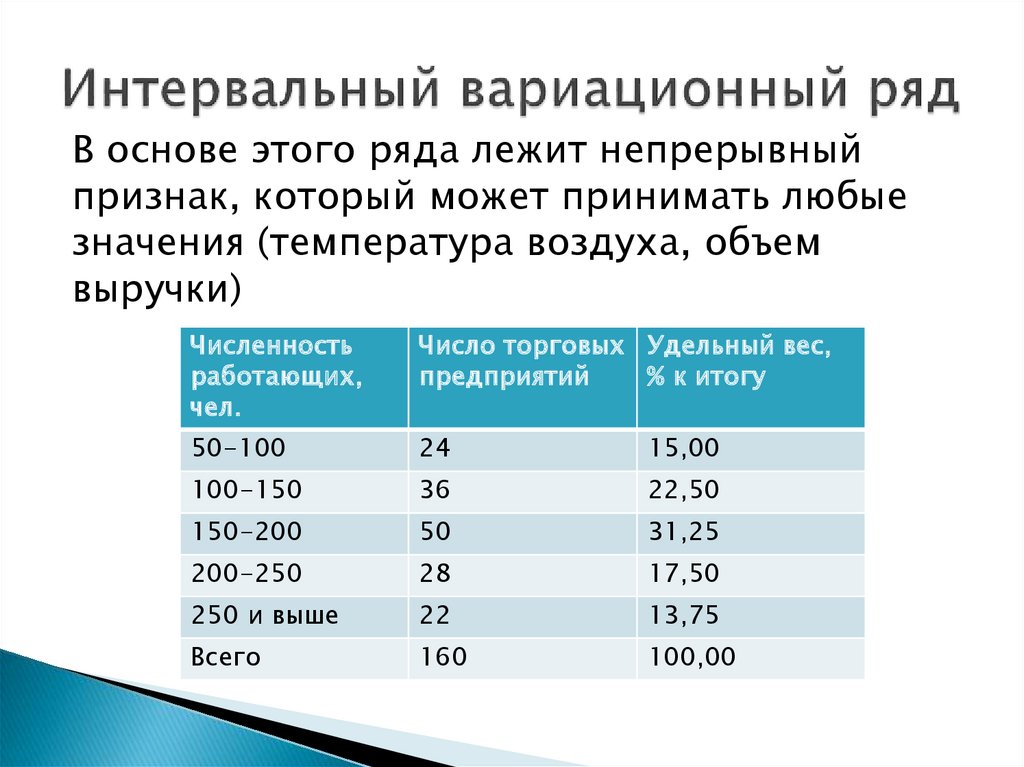 По признакам
По признакам качественные характеристики элементы, статистические ряды бывают трех видов; а именно, временной ряд , пространственный ряд, ряд условий и .
1. Временной ряд:Если различные значения, принимаемые переменной за определенный период времени, расположены в хронологическом порядке, то полученный ряд называется временным рядом. Проще говоря, временной ряд — это статистический ряд, в котором данные представлены в единицах времени; т. е. день, месяц, неделя или год.
Пример:
Ниже представлена численность населения Дели-НКР в 2010-2018 годах.
Это временной ряд, поскольку данные расположены в соответствии с единицей времени; то есть год.
2. Пространственный ряд:
Если данные расположены в соответствии с местоположением или географическим соображением, то они называются Пространственными рядами. В этом виде статистических рядов фактор времени остается постоянным, а место изменяется.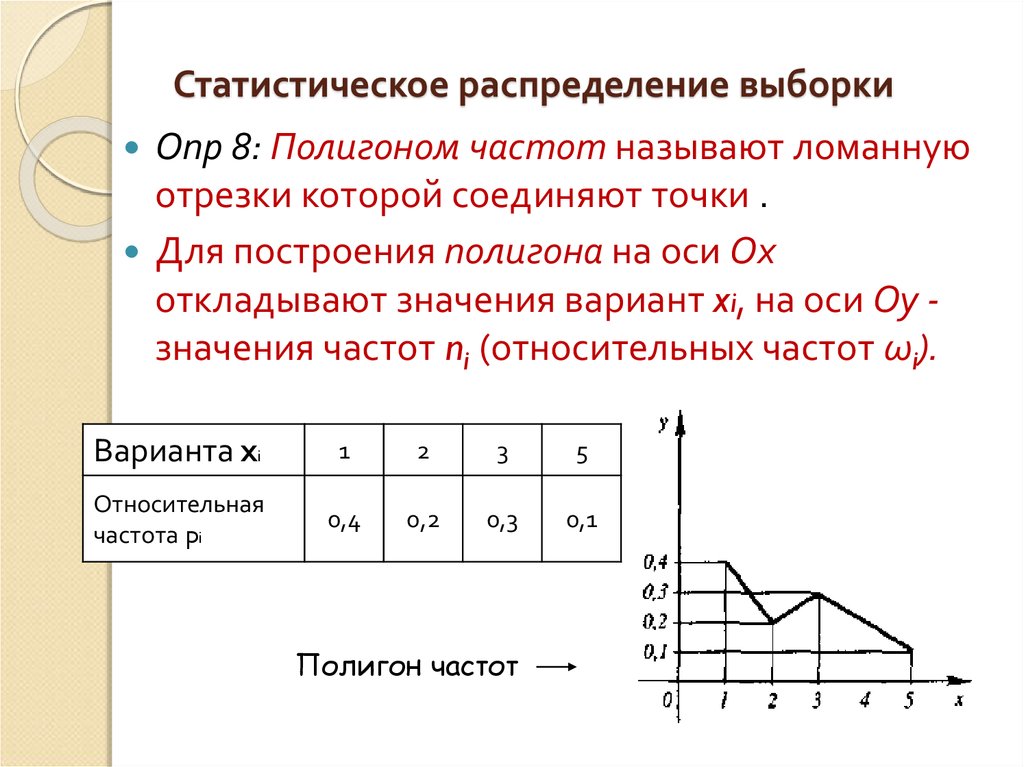
Пример:
Ниже представлено соотношение полов в 6 различных штатах Индии по данным переписи 2011 года. следовательно, это пространственный ряд.
3. Ряд условий:
Если данные ряда классифицируются в соответствии с изменениями, происходящими при определенных условиях, то он называется рядом условий.
Пример:
В следующей таблице показано распределение 40 учеников в классе по возрасту.
Это ряд условий, поскольку данные расположены на основе возраста учащихся
B. На основе построения
Данные могут быть организованы в виде статистических рядов на основе построения в следующем типы:
1. Индивидуальная серия: Серия, в которой элементы перечислены по отдельности, известна как индивидуальная серия. Проще говоря, каждому элементу присваивается отдельное значение измерения. Например, , если вес 10 учеников класса указан индивидуально, то результирующая серия будет индивидуальной серией. Два типа индивидуальных серий: Неорганизованная индивидуальная серия и Организованная индивидуальная серия.
Два типа индивидуальных серий: Неорганизованная индивидуальная серия и Организованная индивидуальная серия.
i) Неорганизованная индивидуальная серия: Серия с необработанными данными или неупорядоченной массой данных известна как неорганизованная серия. Необработанные данные — это данные в исходной форме. Проще говоря, когда исследователь собирает данные и не систематизирует их, собранные данные будут известны как неорганизованные данные. Данные, представленные в виде неорганизованных рядов, не дают исследователю никакой полезной информации; вместо этого это сбивает их с толку.
Пример:
Ниже приведены оценки, полученные 10 учащимися в классе:
В приведенной выше таблице показаны неорганизованные данные в исходном или необработанном виде.
ii) Организованная индивидуальная серия: Серия с упорядоченно расположенными необработанными данными известна как Организованная индивидуальная серия.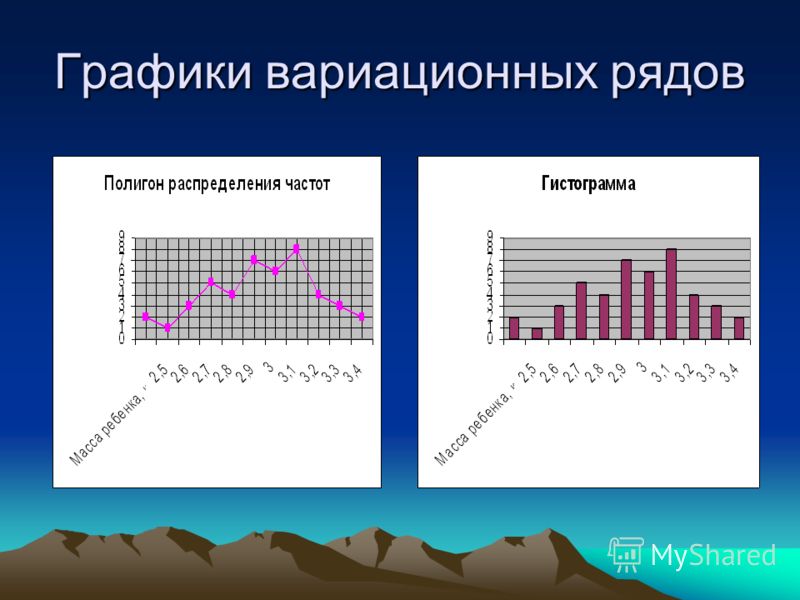 Есть два способа представить организованные отдельные серии; а именно, в соответствии с серийным номером и в соответствии с порядком величины (по возрастанию или по убыванию).
Есть два способа представить организованные отдельные серии; а именно, в соответствии с серийным номером и в соответствии с порядком величины (по возрастанию или по убыванию).
- В соответствии с серийным номером: Отдельные серии могут быть организованы в соответствии с серийным номером. Например, , Оценки, полученные 10 учащимися, расположенные в порядковом номере, показаны в таблице ниже:
- В соответствии с порядком величины (по возрастанию или по убыванию): Отдельная серия может располагаться в порядке возрастания или убывания. Расположение необработанных данных в порядке возрастания или убывания величины известно как Массив, Массивы, Массив данных, или Массив фигур. Например, Оценки, полученные 10 учащимися в порядке возрастания и убывания, показаны в таблице ниже:
количество наблюдений за исследованием велико , размещение данных в отдельных рядах не является решением.
 В этом случае дискретные ряды — гораздо лучший способ представления данных. Это ряд, в котором отдельные значения отличаются друг от друга на определенную величину. В этом ряду частотного распределения различные значения переменных показаны с соответствующими частотами. Классификация данных для дискретной переменной известна как Массив частот. Дискретная переменная не принимает дробное значение, а принимает только определенные целые значения.
В этом случае дискретные ряды — гораздо лучший способ представления данных. Это ряд, в котором отдельные значения отличаются друг от друга на определенную величину. В этом ряду частотного распределения различные значения переменных показаны с соответствующими частотами. Классификация данных для дискретной переменной известна как Массив частот. Дискретная переменная не принимает дробное значение, а принимает только определенные целые значения.Как построить дискретное частотное распределение с использованием подсчетных меток
Метод подсчетных столбцов или подсчетных меток используется исследователем для подсчета количества наблюдений или частоты каждого значения переменной. Шаги, связанные с построением дискретного частотного распределения с использованием контрольных меток, следующие:
- Подготовьте таблицу с тремя столбцами с заголовками Переменная, Контрольные метки и Частота.
- Первый столбец состоит из всех возможных значений переменной.

- Второй столбец включает в себя контрольную метку, обозначаемую | для каждого наблюдения против его соответствующего значения. Если конкретное значение встречается в пятый раз, мы ставим крест на счетной метке (
||||), разрезая четыре контрольных столбца и считая отрезанную линию пятым числом. Для шестого элемента мы поместим еще одну полосу подсчета, оставив немного места. - Третий столбец содержит общее количество баллов, соответствующих каждому значению переменной.
Пример:
Представить оценки 22 учеников класса в виде дискретного частотного распределения.
Решение:
В первом столбце записанные значения (баллы) будут 10, 15, 18, 20 и 22. произошло. Наконец, в третьем столбце будет записано подсчитанное количество контрольных отметок, соответствующих различным значениям. Таким образом, таблица распределения частот будет следующей:
Из приведенной выше таблицы мы можем констатировать, что из 22 студентов 6 студентов получили 10 баллов, 4 студента получили 15 баллов, 2 студента получили 18 баллов, 5 студентов получили 20 баллов и 5 студентов получили 22 балла.
3. Непрерывный ряд:Распределение относительной частоты:
Иногда фактическая частота выражается в процентах от общего числа наблюдений. В таких случаях получаются относительные частоты.
Пример:
Преобразовать данные об оценках, полученных 22 учениками класса в тесте, в виде дискретных рядов. Кроме того, рассчитайте относительную частоту.
Решение:
Дискретный ряд не может принимать никаких значений в интервале; поэтому в тех случаях, когда необходимо представить непрерывные переменные с диапазоном значений различных элементов заданных данных, используется непрерывный ряд. В этом ряду измерения являются только приближениями, и эти приближения выражаются в виде интервалов классов. Занятия формируются от начала до конца, без перерывов.
Другие названия непрерывных рядов: Частотное распределение, Групповое частотное распределение, Серии с интервалами классов, и Серии сгруппированных данных.
Существуют различные типы непрерывной серии (Ссылка) ; а именно, эксклюзивная серия, инклюзивная серия, открытое распределение, кумулятивная серия частот, серия с равными и неравными интервалами классов и серия со средним значением.
Важные термины для непрерывных серий
Различные термины, используемые в непрерывных сериях, следующие:
i) Класс: Класс в непрерывном ряду относится к группе номеров, в которые помещаются элементы. Например, 0-5, 5-10, 10-15, 15-20, 20-25 и т. д. Исследователю важно четко определить класс, чтобы не создавать путаницы . Кроме того, классы должны быть исчерпывающими и взаимоисключающими. Причина этого в том, что он гарантирует, что значение переменной входит только в один класс и не повторяется.
ii) Количество классов: Решение о количестве классов данных обычно зависит от суждения отдельного исследователя.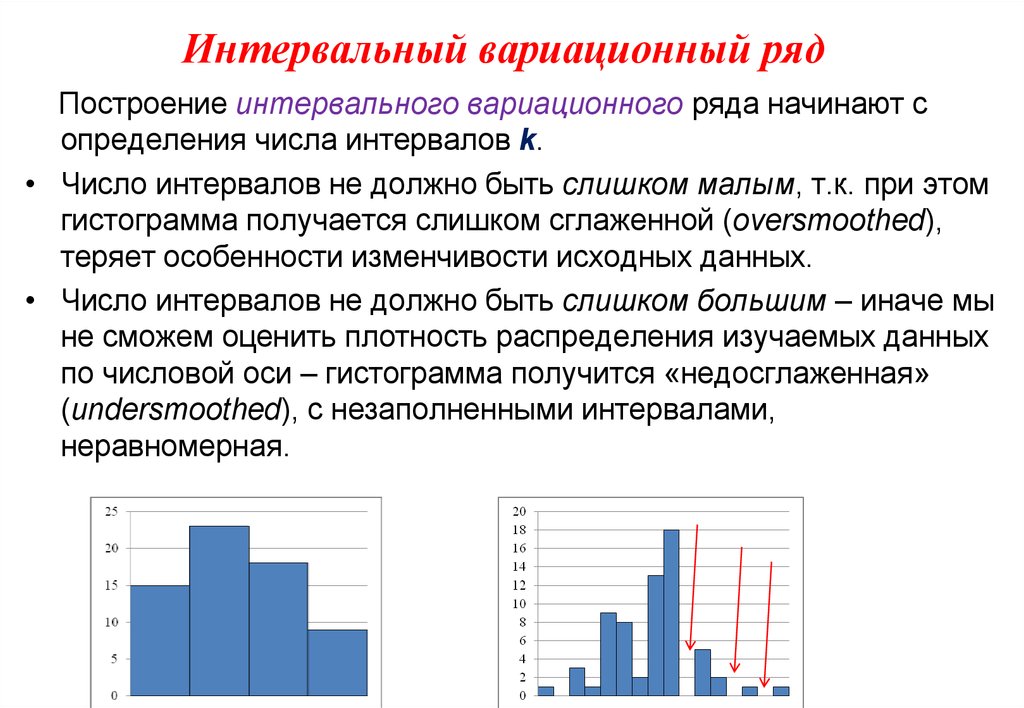 Несмотря на то, что не существует строгого правила относительно количества классов, это число не должно быть очень маленьким или очень большим и должно составлять от 5 до 15. Если количество классов меньше 5, то каждый элемент данных будет упомянут. правильно. Точно так же, если количество классов будет более 15, то это станет трудным и сложным в выполнении вычислений.
Несмотря на то, что не существует строгого правила относительно количества классов, это число не должно быть очень маленьким или очень большим и должно составлять от 5 до 15. Если количество классов меньше 5, то каждый элемент данных будет упомянут. правильно. Точно так же, если количество классов будет более 15, то это станет трудным и сложным в выполнении вычислений.
iii) Ограничения класса: Предел класса — это наименьшее и максимальное значение переменных внутри класса. В непрерывном ряду предел класса формируется двумя числами, между которыми расположен каждый класс. Наименьшее значение класса известно как Нижний предел или l 1 ; , однако наивысшее значение класса известно как Верхний предел или l 2 . Например, , если класс 5-10, то 5 — нижний предел, а 10 — верхний предел. Если нижняя граница класса равна 0 или кратна 5, это становится удобным для исследователя. Кроме того, следует убедиться, что ограничения класса являются целыми числами и что каждый элемент заданных данных включен в эти ограничения.
Кроме того, следует убедиться, что ограничения класса являются целыми числами и что каждый элемент заданных данных включен в эти ограничения.
iv) Интервал класса: Это разница между нижним пределом и верхним пределом класса. Интервал класса ряда обычно обозначается i или c. Следовательно, в символическом выражении
Интервал класса (i или c) = l 2 – l 1
Другие названия интервала класса: Величина, Размер, или Длина класса.
v) Ширина интервалов классов: Во время построения частотного распределения предполагается, что ширина каждого интервала классов равна по размеру. Формула для определения размера или ширины интервала каждого класса выглядит следующим образом:
Прежде чем принимать решение о ширине различных интервалов классов, необходимо принять во внимание следующие моменты: 15 и т. д., легко.
д., легко.
vi) Диапазон: Это разница между нижним пределом интервала первого класса и верхним пределом интервала последнего класса. Например, , если классы распределения 0-5, 5-10, 10-15, ………….до 45-50, тогда диапазон будет 50 – 0 = 50.
vii) Mid-Point или Mid-Value: Это центральная точка интервала класса. Формула для определения средней точки интервала класса выглядит следующим образом:
Например, середина интервала класса 30-40 будет
viii) Частота: Это количество элементов или наблюдений, попадающих в определенный интервал класса.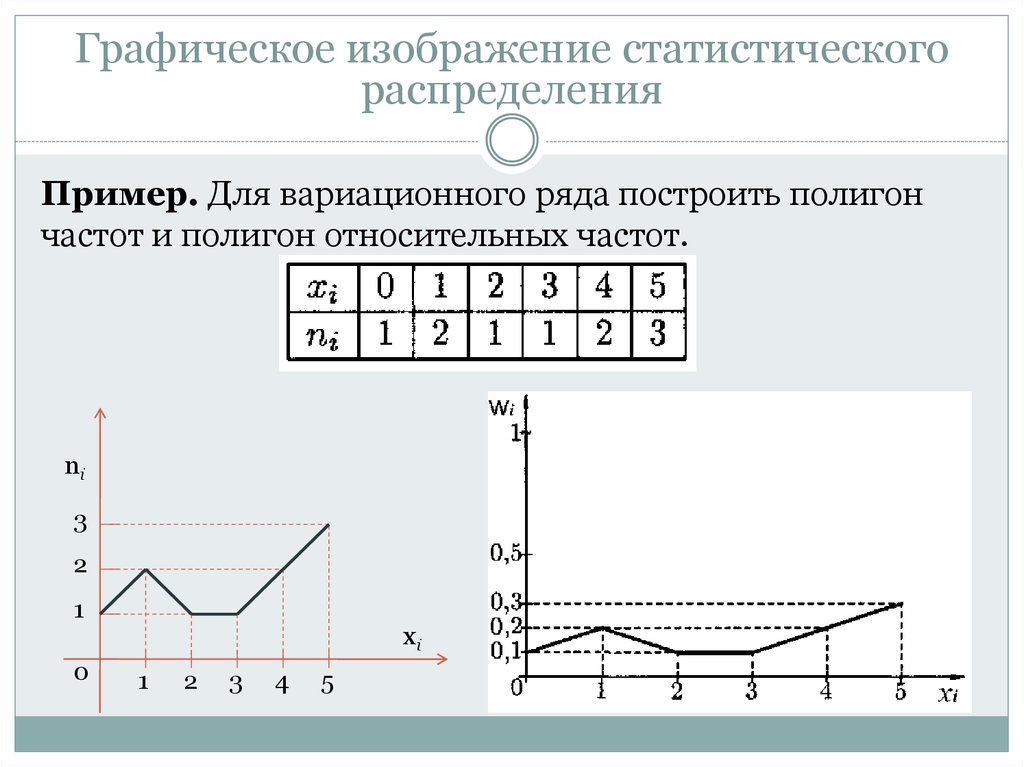 Например, , если в классе 20 учеников (показывают оценки) 25-30, то частота будет 20. Это означает, что есть 20 учеников, которые набрали оценки между 25-30.
Например, , если в классе 20 учеников (показывают оценки) 25-30, то частота будет 20. Это означает, что есть 20 учеников, которые набрали оценки между 25-30.
ix) Частотное распределение: Таблица, показывающая, как различные значения переменной распределяются по разным классам вместе с соответствующими им частотами классов, называется частотным распределением. Проще говоря, это таблица, которая всесторонне классифицирует необработанные данные количественной переменной.
x) Частота класса: Количество наблюдений, соответствующих определенному классу. Она также известна как частота этого класса и обозначается f. Сумма всех частот известна как N или ∑f. Например, если 20 учащихся набрали от 30 до 40 баллов, то частота занятий будет равна 20. классы 0-10, 10-20 и так далее.
Решение:
Шаги для построения таблицы распределения частот следующие:
- Первый столбец таблицы будет включать интервалы классов, начиная с 0-10 до 60-70, как значение наибольшего наблюдения.
 равно 69.
равно 69. - Второй столбец таблицы будет включать подсчет баллов.
- Третий столбец таблицы будет включать частоту появления путем подсчета меток, соответствующих различным значениям.
Построение скрытой сети для одномерных временных рядов на основе вариационного автоматического кодирования
- Список журналов
- Энтропия (Базель)
- PMC8394240
Являясь библиотекой, NLM предоставляет доступ к научной литературе. Включение в базу данных NLM не означает одобрения или согласия с содержание NLM или Национальных институтов здравоохранения. Узнайте больше о нашем отказе от ответственности.
Энтропия (Базель). 2021 авг. ; 23(8): 1071.
; 23(8): 1071.
Опубликовано в сети 18 августа 2021 г. doi: 10.3390/e23081071
, 1, * , 2, 90 374 3 , 1 , 1 и 1
Клаудиа Сабо, академический редактор
Информация об авторе Примечания к статье Информация об авторских правах и лицензиях Отказ от ответственности
- Заявление о доступности данных новые средства для понимания и анализа временных рядов. В этой работе, используя Variational Auto-Encode (VAE), мы исследовали построение скрытых сетей для одномерных временных рядов. Сначала мы обучили VAE для получения пространства скрытых распределений вероятностей временных рядов, а затем разложили многомерное гауссово распределение на несколько одномерных гауссовских распределений. Путем измерения расстояния между одномерными гауссовскими распределениями на статистическом многообразии наконец была достигнута конструкция скрытой сети. Экспериментальные результаты показывают, что латентная сеть может эффективно сохранять исходную информацию временного ряда и обеспечивать новую структуру данных для последующих задач.

Ключевые слова: временные ряды, комплексная сеть, статистическое многообразие, латентное пространство
Анализ наблюдаемых временных рядов всегда был фундаментальной проблемой, как в естественных, так и в социальных науках. В зависимости от области применения и решаемой задачи существуют различные методы анализа временных рядов, такие как частотно-временной анализ [1], классификация [2], рекурсивные графики [3], прогнозирование дорожно-транспортных происшествий [4]. и анализ хаотических временных рядов [5]. В последние годы, когда объем данных и сложность систем увеличились, были предложены новые методы, позволяющие справиться с такими ситуациями. Например, глубокое обучение было успешно применено для классификации [6] и прогнозирования временных рядов благодаря его превосходной способности автоматически извлекать признаки [7,8].
В последнее десятилетие преобразование временных рядов в сложные сети и реализация анализа временных рядов в контексте сложных систем стали важным подходом.
 Преобразование временных рядов в сложные сети представляет собой характеристики временных рядов, т. е. обеспечивает новую форму данных для анализа временных рядов. Классические подходы сосредоточены в основном на эволюционных свойствах временных рядов. По мере увеличения сложности системы недостаточно рассматривать только эволюционные свойства. На самом деле взаимодействие между различными компонентами системы или временного ряда обычно приводит к увеличению сложности [9].]. Следовательно, нам необходимо понимать такие взаимодействия, что является основной мотивацией для преобразования временных рядов в сложные сети. Более того, преобразование позволяет анализировать временные ряды методами из области сложных систем, что также дает новые способы характеристики временных рядов.
Преобразование временных рядов в сложные сети представляет собой характеристики временных рядов, т. е. обеспечивает новую форму данных для анализа временных рядов. Классические подходы сосредоточены в основном на эволюционных свойствах временных рядов. По мере увеличения сложности системы недостаточно рассматривать только эволюционные свойства. На самом деле взаимодействие между различными компонентами системы или временного ряда обычно приводит к увеличению сложности [9].]. Следовательно, нам необходимо понимать такие взаимодействия, что является основной мотивацией для преобразования временных рядов в сложные сети. Более того, преобразование позволяет анализировать временные ряды методами из области сложных систем, что также дает новые способы характеристики временных рядов.Преобразование временного ряда в сложную сеть обычно включает три этапа: извлечение компонентов временного ряда для формирования узлов сети, определение метрики ребер и формирование сети в соответствии с определенными критериями.
 Для выделения узлов сети существуют разные подходы для разных типов временных рядов. В случае одномерных временных рядов временной ряд обычно разбивается на подсегменты, которые соответствуют узлам сети [10,11]. Лакаса и др. напрямую использовали каждую точку временного ряда как узел, формируя так называемый граф видимости [12]. В переходных сетях Kulp et al. предложил сопоставить временной ряд со скрытой цепью Маркова, где каждое состояние действует как узел [13]. В случае многомерных временных рядов принято рассматривать каждую переменную как узел [14]. На основе информационной геометрии и теории дифференциальной геометрии [15,16] сложные сети временных рядов могут быть построены на римановых многообразиях [17]. Как только узлы определены, следующее, что нужно решить, — это отношения между узлами, то есть, как определить ребра между узлами. Как правило, подходящая метрика ребра выбирается в соответствии с характеристиками узлов. Например, в случае подсегментов как узлов для определения ребер можно рассматривать коэффициент корреляции или евклидово расстояние [10]; в [13] в качестве реберной метрики использовалась вероятность перехода; а в графе видимости для определения ребер использовалась стратегия ландшафта [12].
Для выделения узлов сети существуют разные подходы для разных типов временных рядов. В случае одномерных временных рядов временной ряд обычно разбивается на подсегменты, которые соответствуют узлам сети [10,11]. Лакаса и др. напрямую использовали каждую точку временного ряда как узел, формируя так называемый граф видимости [12]. В переходных сетях Kulp et al. предложил сопоставить временной ряд со скрытой цепью Маркова, где каждое состояние действует как узел [13]. В случае многомерных временных рядов принято рассматривать каждую переменную как узел [14]. На основе информационной геометрии и теории дифференциальной геометрии [15,16] сложные сети временных рядов могут быть построены на римановых многообразиях [17]. Как только узлы определены, следующее, что нужно решить, — это отношения между узлами, то есть, как определить ребра между узлами. Как правило, подходящая метрика ребра выбирается в соответствии с характеристиками узлов. Например, в случае подсегментов как узлов для определения ребер можно рассматривать коэффициент корреляции или евклидово расстояние [10]; в [13] в качестве реберной метрики использовалась вероятность перехода; а в графе видимости для определения ребер использовалась стратегия ландшафта [12]. На заключительном этапе построения сети обычно необходимо определить порог ребер, т. е. ребра больше порога сохраняются, а ребра меньше порога отбрасываются.
На заключительном этапе построения сети обычно необходимо определить порог ребер, т. е. ребра больше порога сохраняются, а ребра меньше порога отбрасываются.Предыдущие исследования были сосредоточены на определении узлов и ребер вручную, что является сложной задачей, особенно идентификация узлов. Например, при сегментировании временного ряда необходимо заранее определить многочисленные параметры, такие как длина подсегмента, длина скользящего окна и скользящие шаги, что делает оптимизацию модели сложной задачей. Кроме того, временные ряды имеют большую размерность и обычно содержат шум. Следовательно, существует острая необходимость в использовании сжатых и эффективных скрытых функций для представления временных рядов. Чтобы решить эти проблемы, на основе вариационного автоматического кодирования (VAE) [18] мы предлагаем в этой статье сначала отобразить одномерный временной ряд в пространство скрытых распределений вероятностей, а затем выполнить построение скрытых сетей. Основным преимуществом нашего метода является то, что узлы скрытой сети могут быть извлечены автоматически, а также метод теоретически нечувствителен к шуму.

В этом разделе мы сначала вводим архитектуру модели, а затем разрабатываем обучение VAE и метод построения скрытой сети соответственно.
2.1. Постановка задачи и структура предлагаемой модели
При заданном наборе данных с метками D={(xk,ck)}k=1K состоит из K одномерных временных рядов xk вместе с их метками классов ck, где xk — последовательность действительных числовых значений. значений и его длина равна Nk, то есть xk=(x1,x2…xNk). Для проверки эффективности реконструкции сети здесь используются одномерные временные ряды с метками классов. Фактически для самой реконструкции сети метки классов не нужны. Кроме того, не требуется, чтобы временные ряды были одинаковой длины.
Каркас предлагаемой модели показан на , который состоит из двух основных частей: процесс обучения VAE и процесс построения латентной сети. Общепринятой практикой является использование рекуррентных нейронных сетей (RNN), долговременной кратковременной памяти (LSTM) и Gated Recurrent Units (GRU) для работы с временными рядами [19].
 Как показано в верхней части, здесь мы выбрали LSTM для реализации кодирования и декодирования в VAE. Мотивацией для использования VAE здесь была его способность автоматически извлекать особенности временного ряда и генерировать скрытое пространство. Важно отметить, что это скрытое пространство определяется распределениями вероятностей, а не векторным пространством. Таким образом, VAE относится к генеративным моделям, которые обычно используются для генерации новых данных, а не с использованием скрытых переменных для реализации последующих задач, таких как классификация или регрессия. Некоторые исследования, использующие скрытые переменные для реализации последующих задач, обычно используют либо выборочный латентный вектор, либо латентное распределение в качестве представления входных данных. Когда используется скрытое распределение, также обычно используется только средний вектор и игнорируется вектор стандартного отклонения.
Как показано в верхней части, здесь мы выбрали LSTM для реализации кодирования и декодирования в VAE. Мотивацией для использования VAE здесь была его способность автоматически извлекать особенности временного ряда и генерировать скрытое пространство. Важно отметить, что это скрытое пространство определяется распределениями вероятностей, а не векторным пространством. Таким образом, VAE относится к генеративным моделям, которые обычно используются для генерации новых данных, а не с использованием скрытых переменных для реализации последующих задач, таких как классификация или регрессия. Некоторые исследования, использующие скрытые переменные для реализации последующих задач, обычно используют либо выборочный латентный вектор, либо латентное распределение в качестве представления входных данных. Когда используется скрытое распределение, также обычно используется только средний вектор и игнорируется вектор стандартного отклонения.Открыть в отдельном окне
Каркас модели. Структура состоит из процесса обучения VAE (, верхняя часть ) и процесса построения сети (, нижняя часть ).

В отличие от предыдущих стратегий, мы использовали всю вероятностную информацию для создания скрытой сети, т. е. включая среднее значение и стандартное отклонение. Как показано в нижней части, входной временной ряд сначала преобразуется в вектор среднего значения Zμ∈ℝM и вектор стандартного отклонения Zσ∈ℝM с использованием обученного кодировщика. i -й элемент в Zµ и Zσ вместе образуют одномерное гауссово распределение вероятностей N(µi,σi2). Согласно концепции информационной геометрии [15], распределения вероятностей лежат на статистическом многообразии, определяемом симметричными положительно определенными (SPD) матрицами. Наконец, мы получаем сеть, рассматривая N(µi,σi2) (i=1,2,…,M) как узлы, а расстояние между ними – как ребра.
2.2. VAE Triang Process
Структура VAE частично упоминается в [19]. Как показано на рисунке, VAE состоит из четырех компонентов: кодировщик, кодер-латентный, латентный-декодер и декодер.
Кодер передает серию входных векторов xk в LSTM для получения выходного вектора houtenc, который передается на следующий уровень;
Функция encoder-to-latent заключается в отображении houtenc в скрытое пространство, т.
 е. вектора среднего Zμ и вектора стандартного отклонения Zσ, с использованием линейного слоя;
е. вектора среднего Zμ и вектора стандартного отклонения Zσ, с использованием линейного слоя;На этапе латентного к декодеру выборочные латентные векторы проходят через линейный уровень для получения начального состояния декодера h0dec; 9к.
Функция потерь VAE состоит из двух компонентов, а именно ошибки восстановления и члена регуляризации. Ошибка реконструкции использует потерю MSE, в то время как член регуляризации (KL-дивергенция) делает скрытое пространство более похожим на распределение Гаусса. Функция потерь может быть выражена как:
ℒ(θ;xk)=−DKL(q(Z|xk)ǁp(Z))+Eq(Z|xk)[logpθ(xk|Z)]
(1 )
где DKL — KL-дивергенция, θ — параметры модели; p — распределение вероятностей декодера, q — его приближение. Используя «трюк репараметризации», передискретизированный вектор имеет вид Z=µ+σϵ с ϵ~N(0,1). В конце концов, функция потерь переформулируется следующим образом:
ℒ(θ;xk)≈∑m=1M(1+log((σkm)2)−(µkm)2−(σkm)2)+1L∑l=1Llogp(xk|Zkl)
(2)
где M — размерность Zμ, а L — количество выбранных векторов Z.
 Здесь мы сосредоточимся на архитектуре модели, а детали LSTM и VAE можно найти в [18,20].
Здесь мы сосредоточимся на архитектуре модели, а детали LSTM и VAE можно найти в [18,20].2.3. Построение сети на коллекторе
После обучения VAE мы можем использовать его для кодирования заданного временного ряда, чтобы получить пространство скрытых распределений вероятностей. В скрытом пространстве мы используем одномерное гауссово распределение вероятностей N(µi,σi2) в качестве узла, а затем измеряем расстояния между различными распределениями в качестве ребер для формирования сети. Некоторые классические методы можно использовать непосредственно для измерения расстояния между распределениями Гаусса, такие как дивергенция Кульбака-Лейблера или расстояние Бхаттачарьи [21]. Здесь мы использовали геодезическое расстояние для измерения сходства между распределениями вероятностей на статистическом многообразии, образованном SPD-матрицами. Используя геодезические расстояния, можно не только построить сеть, но и многообразие может также обеспечить удобную структуру и свойства для последующих задач, таких как классификация, регрессия и уменьшение размерности [22].

Согласно теории информационной геометрии [23], пространство D-мерных гауссовских распределений может быть вложено в пространство (D+1)×(D+1)-мерных SPD-матриц, которое образует многообразие. Для многомерного гауссовского распределения N(µ,Σ) это вложение определяется как:
P=(detΣ)−2/(D+1)[Σ+µµTµµT1]
(3)
где P — матрица SPD, локализованная на многообразии и соответствующая многомерному гауссову распределению. Для измерения матриц расстояний Pi и Pj введем геодезическое расстояние на многообразии следующим образом [22]:
d(Pi,Pj)=tr(log2(Pi−12PjPi−12))
(4)
Рассматривая одномерное гауссово распределение N(µi,σi2), P представляет собой 2×2-мерную SPD-матрицу:
Pi=σi−1[σi+µi2µiµi1]
(5)
Предположим, что временной ряд xk сжимается кодером до M-мерного гауссова распределения, т. е. Zµ∈ℝM и Zσ∈ℝM. С помощью (4) можно вычислить расстояния между парами одномерных распределений, образующих взвешенную матрицу смежности Ak=(ai,jk)M×M, где ai,jk=d(Pi,Pj).
 В некоторых случаях, чтобы выявить топологию сети, некоторые ребра можно удалить, задав порог τ, чтобы матрица смежности Ak преобразовалась в:
В некоторых случаях, чтобы выявить топологию сети, некоторые ребра можно удалить, задав порог τ, чтобы матрица смежности Ak преобразовалась в:A¯k={ai,jk если ai,jk>τ0 иначе
(6)
Итак, мы получили скрытую сеть Ak временного ряда xk. То есть мы преобразовали временной ряд в сеть в скрытом пространстве, которая является представлением временного ряда. Сеть можно использовать для изучения взаимодействий внутри скрытых переменных или в качестве новых функций для последующих задач, таких как кластеризация и классификация.
Для проверки разумности сети Ak дополнительно построим сеть B, где Ak используется в качестве узла. То есть B представляет собой сеть сетей. Используя метку класса ck для xk, мы можем проверить разумность сети Ak по топологии сети B. Для построения B необходимо расстояние между метриками Ak. Однако Ak не является SPD-матрицей, поэтому мы не можем напрямую применить (4) для вычисления расстояния. Следовательно, мы вводим лапласиан графа для преобразования Ak в SPD-матрицу следующим образом:
Lk=(Dk−Ak)+λI
(7)
где Dk=diag(∑jai,jk) — матрица степеней Ak, λ>0 — параметр регуляризации, а I — единичная матрица.
 Теперь у нас есть две стратегии построения сети B. Первая — построить сеть непосредственно на многообразии. В этой стратегии расстояние между Lk вычисляется с использованием (4) для формирования матрицы смежности, т. е. B=(bi,j)K×K, где bi,j=d(Li,Lj) и K — количество временной ряд хк. Другая стратегия состоит в том, чтобы спроецировать Lk на касательное пространство многообразия, а затем построить сеть в касательном пространстве. Пусть M∈ℳ — реперная точка, определяемая как среднее SPD-матриц, и тогда соответствие многообразия ℳ касательному пространству TM в M может быть определено логарифмическим отображением logM: ℳ↦TM [22]:
Теперь у нас есть две стратегии построения сети B. Первая — построить сеть непосредственно на многообразии. В этой стратегии расстояние между Lk вычисляется с использованием (4) для формирования матрицы смежности, т. е. B=(bi,j)K×K, где bi,j=d(Li,Lj) и K — количество временной ряд хк. Другая стратегия состоит в том, чтобы спроецировать Lk на касательное пространство многообразия, а затем построить сеть в касательном пространстве. Пусть M∈ℳ — реперная точка, определяемая как среднее SPD-матриц, и тогда соответствие многообразия ℳ касательному пространству TM в M может быть определено логарифмическим отображением logM: ℳ↦TM [22]:yk=logM(Lk)=M12log(M−12LkM−12)M12
(8)
Поскольку TM является векторным пространством, мы можем вычислить расстояние между yk, используя соответствующую метрику D(,) в евклидовой пространство для формирования матрицы смежности, т. е. B=(bi,j)K×K, где bi,j=D(yi,yj). В данном исследовании мы выбрали вторую стратегию построения сети B. Причина в том, что TM является евклидовым пространством, что облегчает применение некоторых классических алгоритмов.

В этом эксперименте мы использовали набор данных электрокардиограммы (ЭКГ) под названием ECG5000 из архива UCR [24], где обучающая и тестовая выборки содержат в общей сложности 5000 образцов. Сначала мы объединили обучающий и тестовый наборы данных, а затем 4500 случайно выбранных данных ЭКГ были использованы для обучения VAE, а еще 500 были использованы для построения латентной сети. Этот набор данных имеет пять классов с длиной выборки 140, и метки классов использовались для оценки производительности построения сети. Некоторые образцы показаны на а, где каждая последовательность соответствует одному сердечному сокращению. Важно отметить, что выборки в каждом классе сильно несбалансированы, что продемонстрировано в б. Видно, что преобладали первый и второй классы выборок, а остальные три категории были немногочисленны.
Открыть в отдельном окне
Набор данных ЭКГ5000. ( a ) Три образца в каждом классе были выбраны случайным образом для презентации.
 Горизонтальная и вертикальная оси обозначают класс и образец соответственно. ( b ) Процент размера выборки в каждом классе от общей выборки.
Горизонтальная и вертикальная оси обозначают класс и образец соответственно. ( b ) Процент размера выборки в каждом классе от общей выборки.Из-за симметрии VAE LSTM как в кодере, так и в декодере был одним уровнем; каждый слой имел 96 скрытых единиц, а размерность скрытых векторов Zμ и Zσ была равна 20. Скорость обучения была установлена на 0,0005, и Адам использовался для обновления весов. После того, как VAE был обучен, мы использовали его кодировщик для получения представления тестовых данных, то есть пространства скрытых распределений вероятностей. Результат скрытого пространства, соответствующий последовательности из класса 1, показан на .
Открыть в отдельном окне
Распределение скрытой вероятности последовательности. Разные цвета обозначают разные одномерные распределения Гаусса: N(µi,σi2), где µi и σi2 происходят от i -го элемента скрытых векторов Zµ и Zσ соответственно.
Как видно из , разные N имеют разные средние значения и стандартные отклонения.
 Для временного ряда xk мы использовали (4) и (5) для вычисления расстояний между N, формируя таким образом матрицу смежности Ak. Чтобы выделить топологию сети, мы использовали (6) для удаления большинства ребер. На самом деле, как определить соответствующий порог τ в (6) было открытой проблемой при построении сложных сетей. Здесь мы сохранили 20% краев на основе эмпирических значений и эффектов визуализации. Примеры скрытых сетей, соответствующих разным временным рядам, показаны на рис.
Для временного ряда xk мы использовали (4) и (5) для вычисления расстояний между N, формируя таким образом матрицу смежности Ak. Чтобы выделить топологию сети, мы использовали (6) для удаления большинства ребер. На самом деле, как определить соответствующий порог τ в (6) было открытой проблемой при построении сложных сетей. Здесь мы сохранили 20% краев на основе эмпирических значений и эффектов визуализации. Примеры скрытых сетей, соответствующих разным временным рядам, показаны на рис.Открыть в отдельном окне
Скрытые сети одномерных временных рядов ЭКГ разных классов. Каждый узел представляет собой одномерное распределение Гаусса, а ребра указывают расстояние между узлами. Цветная полоса обозначает вес ребра.
Каждая сеть соответствует временному ряду, принадлежащему к другому классу. Преобразование временных рядов в сети обеспечивает новую структуру данных для анализа временных рядов. Скрытые сети могут фиксировать взаимодействие неявных переменных во временных рядах, что является мотивацией для построения сети.
 Следовательно, скрытые сети могут предоставлять новые структуры данных для добычи и анализа временных рядов. После того, как скрытая сеть будет создана, мы можем использовать многочисленные методы из области науки о сложных сетях, чтобы охарактеризовать временной ряд. Например, топологическая статистика сети извлекается для формирования новых признаков для анализа временных рядов, таких как классификация стадий сна [25] и анализ сейсмических последовательностей [26]. Кроме того, графовые нейронные сети (GNN) в последнее время быстро развиваются и успешно используются во многих областях [27]. Предпосылкой для применения этого мощного инструмента является то, что входные данные должны быть графически структурированы. В большинстве случаев временные ряды не имеют явной графовой структуры. Таким образом, предлагаемая скрытая сеть обеспечивает условия для использования GNN для анализа временных рядов.
Следовательно, скрытые сети могут предоставлять новые структуры данных для добычи и анализа временных рядов. После того, как скрытая сеть будет создана, мы можем использовать многочисленные методы из области науки о сложных сетях, чтобы охарактеризовать временной ряд. Например, топологическая статистика сети извлекается для формирования новых признаков для анализа временных рядов, таких как классификация стадий сна [25] и анализ сейсмических последовательностей [26]. Кроме того, графовые нейронные сети (GNN) в последнее время быстро развиваются и успешно используются во многих областях [27]. Предпосылкой для применения этого мощного инструмента является то, что входные данные должны быть графически структурированы. В большинстве случаев временные ряды не имеют явной графовой структуры. Таким образом, предлагаемая скрытая сеть обеспечивает условия для использования GNN для анализа временных рядов.Скрытые сети представляют собой временные ряды; таким образом, разные классы сетей обычно имеют разные топологии.
 В , мы не можем визуально различить эту разницу с большой уверенностью из-за сложности сетевых подключений. Чтобы проверить правдоподобие нашего метода, используя (7) и (8), мы построили новую сеть B на основе скрытой сети A, а затем оценили конструкцию A в сочетании с метками классов. Результаты для сети B показаны на .
В , мы не можем визуально различить эту разницу с большой уверенностью из-за сложности сетевых подключений. Чтобы проверить правдоподобие нашего метода, используя (7) и (8), мы построили новую сеть B на основе скрытой сети A, а затем оценили конструкцию A в сочетании с метками классов. Результаты для сети B показаны на .Открыть в отдельном окне
Сеть B сети A. Метка класса определяет цвет узла, а цветная полоса обозначает вес (евклидово расстояние) ребер.
можно рассматривать как вложенную сеть, т. е. каждый узел в сети также представляет собой сеть. Как видно на рисунке, узлы класса 1 и класса 2 четко образуют два кластера. Эта топология указывает на то, что сеть А сохраняет информацию исходного временного ряда, позволяя образцам с похожими атрибутами группироваться вместе, что также подтверждает эффективность сети А. Однако следует также отметить, что другие три класса узлов неэффективны. отличающиеся друг от друга. Это явление в основном связано с двумя факторами.
 Первая причина — низкая отличимость этих трех классов образцов от двух других классов, особенно последовательностей класса 2 и класса 4 (см. а). Вторая причина заключается в том, что процент выборок в этих трех классах слишком низок (см. b), что влияет на обучение VAE.
Первая причина — низкая отличимость этих трех классов образцов от двух других классов, особенно последовательностей класса 2 и класса 4 (см. а). Вторая причина заключается в том, что процент выборок в этих трех классах слишком низок (см. b), что влияет на обучение VAE.На основе обученного VAE в нашей работе реализовано построение латентных сетей для одномерных временных рядов. Мы обнаружили, что VAE может эффективно извлекать признаки одномерных временных рядов и получать промежуточные представления. Кроме того, построенные скрытые сети могут эффективно сохранять информацию исходных данных и предоставлять новые структуры данных и инструменты анализа для анализа временных рядов. Основное преимущество нашей работы перед традиционными методами заключается в том, что нет необходимости вручную идентифицировать узлы сети благодаря способности VAE автоматически извлекать признаки временного ряда и выводить скрытое представление. Кроме того, предлагаемый подход представляет собой неконтролируемую модель, поэтому построенная латентная сеть не ограничивается конкретной нисходящей задачей, а может предоставлять новые структуры данных для разных задач.

Концептуализация, JS; программное обеспечение, З.В. и С.К.; курирование данных, HN; написание — подготовка первоначального проекта, JS; написание — обзор и редактирование, ZW; визуализация, З.Т. Все авторы прочитали и согласились с опубликованной версией рукописи.
Это исследование финансировалось Национальным фондом естественных наук Китая, номер гранта 62066017. ассоциированный комитет по этике.
От всех участников исследования было получено информированное согласие.
Данные, представленные в этом исследовании, доступны на сайте www.cs.ucr.edu/~eamonn/time_series_data/ (по состоянию на 17 августа 2021 г.).
Авторы заявляют об отсутствии конфликта интересов. Спонсоры не участвовали в разработке исследования; при сборе, анализе или интерпретации данных; при написании рукописи; или в решении опубликовать результаты.
Примечание издателя: MDPI сохраняет нейтралитет в отношении юрисдикционных претензий в опубликованных картах и институциональной принадлежности.

1. Фам Т.Д. Время-частота-время-пространство LSTM для надежной классификации физиологических сигналов. науч. 2021; 11:6936. doi: 10.1038/s41598-021-86432-7. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
2. Сунь Дж., Ян Ю., Лю Ю., Чен С., Рао В., Бай Ю. Одномерная классификация временных рядов с использованием информационной геометрии. Распознавание образов. 2019;95:24–35. doi: 10.1016/j.patcog.2019.05.040. [CrossRef] [Google Scholar]
3. Марван Н., Романо М.К., Тиль М., Куртс Дж. Рекуррентные графики для анализа сложных систем. физ. Представитель 2007; 438: 237–329.. doi: 10.1016/j.physrep.2006.11.001. [CrossRef] [Google Scholar]
4. Попеску Т. Д. Анализ временных рядов для оценки и прогнозирования дорожно-транспортных происшествий — тематические исследования. ВСЕАС Транс. Мат. 2020;19:177–185. doi: 10.37394/23206.2020.19.17. [CrossRef] [Google Scholar]
5. Цай Р.С., Чен Р. Нелинейный анализ временных рядов. Уайли; Хобокен, Нью-Джерси, США: 2018.
 [Google Scholar]
[Google Scholar]6. Zhang X., Gao Y., Lin J., Lu C.-T. TapNet: многомерная классификация временных рядов с прототипной сетью внимания. проц. Конф. АААИ. Артиф. Интел. 2020; 34: 6845–6852. дои: 10.1609/aaai.v34i04.6165. [CrossRef] [Google Scholar]
7. Лопес-Мартин М., Карро Б., Санчес-Эсгевильяс А. Метод прогнозирования типа трафика IoT на основе нейронных сетей с градиентным усилением. Футур. Генерал. вычисл. Сист. 2020;105:331–345. doi: 10.1016/j.future.2019.12.013. [CrossRef] [Google Scholar]
8. Лопес-Мартин М., Санчес-Эсгевильяс А., Эрнандес-Каллехо Л., Аррибас Дж.И., Карро Б. Аддитивная ансамблевая нейронная сеть с ограниченными взвешенными квантильными потерями для вероятностного прогнозирования электрической нагрузки . Датчики. 2021;21:2979. doi: 10.3390/s21092979. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
9. Митчелл М. Сложность: экскурсия с гидом. Издательство Оксфордского университета; Оксфорд, Великобритания: 2011. [Google Scholar]
10.
 Чжан Дж., Смолл М. Сложная сеть из псевдопериодических временных рядов: топология и динамика. физ. Преподобный Летт. 2006;96:238701. doi: 10.1103/PhysRevLett.96.238701. [PubMed] [CrossRef] [Google Scholar]
Чжан Дж., Смолл М. Сложная сеть из псевдопериодических временных рядов: топология и динамика. физ. Преподобный Летт. 2006;96:238701. doi: 10.1103/PhysRevLett.96.238701. [PubMed] [CrossRef] [Google Scholar]11. Доннер Р.В., Зоу Ю., Донгес Дж.Ф., Марван Н., Куртс Дж. Рекуррентные сети — новая парадигма нелинейного анализа временных рядов. New J. Phys. 2010;12:033025. doi: 10.1088/1367-2630/12/3/033025. [Перекрестная ссылка] [Академия Google]
12. Лакаса Л., Луке Б., Баллестерос Ф., Луке Дж., Нуньо Дж. К. От временных рядов к сложным сетям: график видимости. проц. Натл. акад. науч. США. 2008; 105:4972–4975. doi: 10.1073/pnas.0709247105. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
13. Kulp CW, Chobot JM, Freitas HR, Sprechini GD Использование порядковых переходных сетей для анализа данных ЭКГ. Хаос междисциплинарный. J. Нелинейные науки. 2016;26:073114. doi: 10.1063/1.4959537. [PubMed] [CrossRef] [Академия Google]
14. Цзян М., Гао С., Ан Х.
 , Ли Х., Сунь Б. Реконструкция сложной сети для характеристики изменяющегося во времени поведения причинно-следственной эволюции многомерных временных рядов. науч. Отчет 2017;7:10486. doi: 10.1038/s41598-017-10759-3. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
, Ли Х., Сунь Б. Реконструкция сложной сети для характеристики изменяющегося во времени поведения причинно-следственной эволюции многомерных временных рядов. науч. Отчет 2017;7:10486. doi: 10.1038/s41598-017-10759-3. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]15. Амари С.-И., Нагаока Х. Методы информационной геометрии. Том 191. Американское математическое общество; Провиденс, Род-Айленд, США: 2000. [Google Scholar]
16. Манейл Дж. Интегрирование гауссова через дифференцируемые топологические многообразия. ВСЕАС Транс. Мат. 2019;18:55–61. [Google Scholar]
17. Sun J., Yang Y., Xiong N.N., Dai L., Peng X., Luo J. Построение сложной сети многомерных временных рядов с использованием информационной геометрии. IEEE транс. Сист. Человек Киберн. Сист. 2019;49:107–122. doi: 10.1109/TSMC.2017.2751504. [CrossRef] [Google Scholar]
18. Кингма Д. П., Веллинг М. Автокодирование вариационных байесов; Материалы 2-й Международной конференции по представительствам в обучении, ICLR 2014 — Материалы конференции; Банф, AB, Канада.
 14–16 апреля 2014 г. [Google Scholar]
14–16 апреля 2014 г. [Google Scholar]19. Фабиус О., ван Амерсфорт Дж. Р. Вариационные рекуррентные автокодировщики; Материалы 3-й Международной конференции по представительствам в обучении, ICLR 2015 — Материалы семинара; Сан-Диего, Калифорния, США. 7–9 мая 2015 г. [Google Scholar]
20. Hochreiter S., Schmidhuber J. Долговременная кратковременная память. Нейронные вычисления. 1997; 9: 1735–1780. doi: 10.1162/neco.1997.9.8.1735. [PubMed] [CrossRef] [Google Scholar]
21. Нагино Г., Шозакаи М. Мера расстояния между распределениями Гаусса для различения стилей речи; Материалы INTERSPEECH 2006—ICSLP, Девятой международной конференции по обработке разговорной речи; Питтсбург, Пенсильвания, США. 17–21 сентября 2006 г.; стр. 657–660. [Академия Google]
22. Тузель О., Порикли Ф., Меер П. Обнаружение пешеходов с помощью классификации на римановых многообразиях. IEEE транс. Анальный узор. Мах. Интел. 2008; 30: 1713–1727. doi: 10.1109/TPAMI.2008.75. [PubMed] [CrossRef] [Google Scholar]
23.
 Ловрич М., Мин-Оо М., Рух Е.А. Многомерные нормальные распределения, параметризованные как риманово симметричное пространство. Дж. Мультивар. Анальный. 2000;74:36–48. doi: 10.1006/jmva.1999.1853. [CrossRef] [Google Scholar]
Ловрич М., Мин-Оо М., Рух Е.А. Многомерные нормальные распределения, параметризованные как риманово симметричное пространство. Дж. Мультивар. Анальный. 2000;74:36–48. doi: 10.1006/jmva.1999.1853. [CrossRef] [Google Scholar]24. Chen Y., Keogh E., Hu B., Begum N., Bagnall A., Abdullah Mueen G.B. Архив классификации временных рядов UCR. [(по состоянию на 17 августа 2021 г.)]; Доступно на сайте: www.cs.ucr.edu/~eamonn/time_series_data/
25. Zhu G., Li Y., Wen P. Анализ и классификация стадий сна на основе графиков разностной видимости одноканального сигнала ЭЭГ. IEEE J. Биомед. Информ о здоровье. 2014; 18:1813–1821. doi: 10.1109/JBHI.2014.2303991. [PubMed] [CrossRef] [Google Scholar]
26. Телеска Л., Ловалло М. Анализ сейсмических последовательностей с использованием метода графа видимости. Еврофиз. лат. 2012;97:50002. doi: 10.1209/0295-5075/97/50002. [CrossRef] [Google Scholar]
27. Zhou J., Cui G., Hu S., Zhang Z., Yang C., Liu Z., Wang L., Li C., Sun M. Граф нейронных сетей: Обзор методов и приложений.


 д.
д.
 равно 69.
равно 69.
 Преобразование временных рядов в сложные сети представляет собой характеристики временных рядов, т. е. обеспечивает новую форму данных для анализа временных рядов. Классические подходы сосредоточены в основном на эволюционных свойствах временных рядов. По мере увеличения сложности системы недостаточно рассматривать только эволюционные свойства. На самом деле взаимодействие между различными компонентами системы или временного ряда обычно приводит к увеличению сложности [9].]. Следовательно, нам необходимо понимать такие взаимодействия, что является основной мотивацией для преобразования временных рядов в сложные сети. Более того, преобразование позволяет анализировать временные ряды методами из области сложных систем, что также дает новые способы характеристики временных рядов.
Преобразование временных рядов в сложные сети представляет собой характеристики временных рядов, т. е. обеспечивает новую форму данных для анализа временных рядов. Классические подходы сосредоточены в основном на эволюционных свойствах временных рядов. По мере увеличения сложности системы недостаточно рассматривать только эволюционные свойства. На самом деле взаимодействие между различными компонентами системы или временного ряда обычно приводит к увеличению сложности [9].]. Следовательно, нам необходимо понимать такие взаимодействия, что является основной мотивацией для преобразования временных рядов в сложные сети. Более того, преобразование позволяет анализировать временные ряды методами из области сложных систем, что также дает новые способы характеристики временных рядов. Для выделения узлов сети существуют разные подходы для разных типов временных рядов. В случае одномерных временных рядов временной ряд обычно разбивается на подсегменты, которые соответствуют узлам сети [10,11]. Лакаса и др. напрямую использовали каждую точку временного ряда как узел, формируя так называемый граф видимости [12]. В переходных сетях Kulp et al. предложил сопоставить временной ряд со скрытой цепью Маркова, где каждое состояние действует как узел [13]. В случае многомерных временных рядов принято рассматривать каждую переменную как узел [14]. На основе информационной геометрии и теории дифференциальной геометрии [15,16] сложные сети временных рядов могут быть построены на римановых многообразиях [17]. Как только узлы определены, следующее, что нужно решить, — это отношения между узлами, то есть, как определить ребра между узлами. Как правило, подходящая метрика ребра выбирается в соответствии с характеристиками узлов. Например, в случае подсегментов как узлов для определения ребер можно рассматривать коэффициент корреляции или евклидово расстояние [10]; в [13] в качестве реберной метрики использовалась вероятность перехода; а в графе видимости для определения ребер использовалась стратегия ландшафта [12].
Для выделения узлов сети существуют разные подходы для разных типов временных рядов. В случае одномерных временных рядов временной ряд обычно разбивается на подсегменты, которые соответствуют узлам сети [10,11]. Лакаса и др. напрямую использовали каждую точку временного ряда как узел, формируя так называемый граф видимости [12]. В переходных сетях Kulp et al. предложил сопоставить временной ряд со скрытой цепью Маркова, где каждое состояние действует как узел [13]. В случае многомерных временных рядов принято рассматривать каждую переменную как узел [14]. На основе информационной геометрии и теории дифференциальной геометрии [15,16] сложные сети временных рядов могут быть построены на римановых многообразиях [17]. Как только узлы определены, следующее, что нужно решить, — это отношения между узлами, то есть, как определить ребра между узлами. Как правило, подходящая метрика ребра выбирается в соответствии с характеристиками узлов. Например, в случае подсегментов как узлов для определения ребер можно рассматривать коэффициент корреляции или евклидово расстояние [10]; в [13] в качестве реберной метрики использовалась вероятность перехода; а в графе видимости для определения ребер использовалась стратегия ландшафта [12]. На заключительном этапе построения сети обычно необходимо определить порог ребер, т. е. ребра больше порога сохраняются, а ребра меньше порога отбрасываются.
На заключительном этапе построения сети обычно необходимо определить порог ребер, т. е. ребра больше порога сохраняются, а ребра меньше порога отбрасываются.
 Как показано в верхней части, здесь мы выбрали LSTM для реализации кодирования и декодирования в VAE. Мотивацией для использования VAE здесь была его способность автоматически извлекать особенности временного ряда и генерировать скрытое пространство. Важно отметить, что это скрытое пространство определяется распределениями вероятностей, а не векторным пространством. Таким образом, VAE относится к генеративным моделям, которые обычно используются для генерации новых данных, а не с использованием скрытых переменных для реализации последующих задач, таких как классификация или регрессия. Некоторые исследования, использующие скрытые переменные для реализации последующих задач, обычно используют либо выборочный латентный вектор, либо латентное распределение в качестве представления входных данных. Когда используется скрытое распределение, также обычно используется только средний вектор и игнорируется вектор стандартного отклонения.
Как показано в верхней части, здесь мы выбрали LSTM для реализации кодирования и декодирования в VAE. Мотивацией для использования VAE здесь была его способность автоматически извлекать особенности временного ряда и генерировать скрытое пространство. Важно отметить, что это скрытое пространство определяется распределениями вероятностей, а не векторным пространством. Таким образом, VAE относится к генеративным моделям, которые обычно используются для генерации новых данных, а не с использованием скрытых переменных для реализации последующих задач, таких как классификация или регрессия. Некоторые исследования, использующие скрытые переменные для реализации последующих задач, обычно используют либо выборочный латентный вектор, либо латентное распределение в качестве представления входных данных. Когда используется скрытое распределение, также обычно используется только средний вектор и игнорируется вектор стандартного отклонения.
 е. вектора среднего Zμ и вектора стандартного отклонения Zσ, с использованием линейного слоя;
е. вектора среднего Zμ и вектора стандартного отклонения Zσ, с использованием линейного слоя; Здесь мы сосредоточимся на архитектуре модели, а детали LSTM и VAE можно найти в [18,20].
Здесь мы сосредоточимся на архитектуре модели, а детали LSTM и VAE можно найти в [18,20].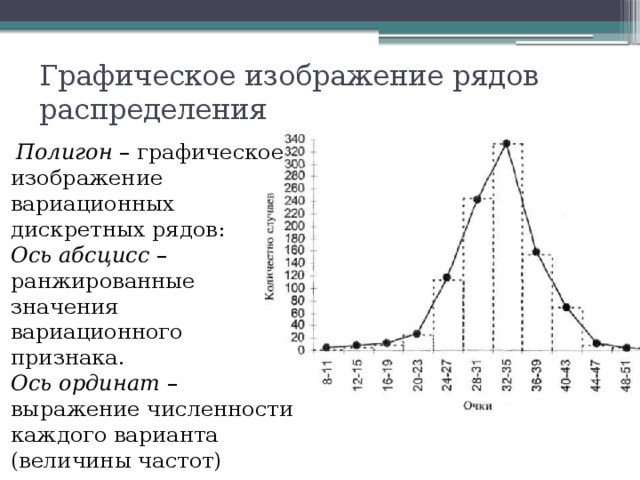
 В некоторых случаях, чтобы выявить топологию сети, некоторые ребра можно удалить, задав порог τ, чтобы матрица смежности Ak преобразовалась в:
В некоторых случаях, чтобы выявить топологию сети, некоторые ребра можно удалить, задав порог τ, чтобы матрица смежности Ak преобразовалась в: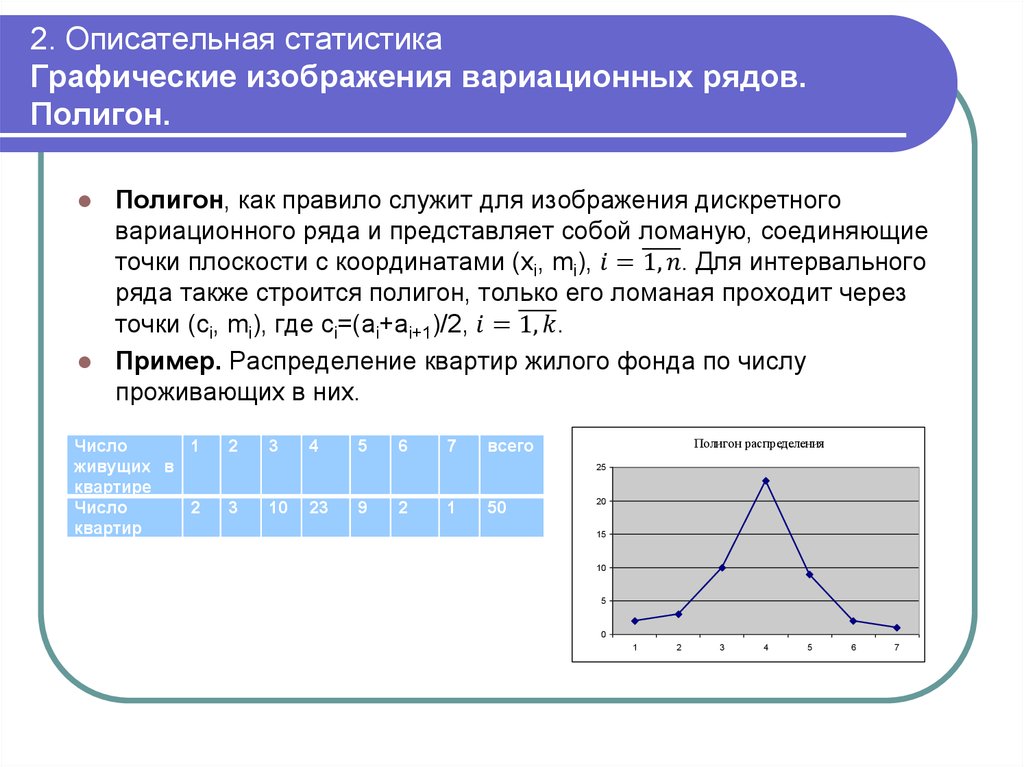 Теперь у нас есть две стратегии построения сети B. Первая — построить сеть непосредственно на многообразии. В этой стратегии расстояние между Lk вычисляется с использованием (4) для формирования матрицы смежности, т. е. B=(bi,j)K×K, где bi,j=d(Li,Lj) и K — количество временной ряд хк. Другая стратегия состоит в том, чтобы спроецировать Lk на касательное пространство многообразия, а затем построить сеть в касательном пространстве. Пусть M∈ℳ — реперная точка, определяемая как среднее SPD-матриц, и тогда соответствие многообразия ℳ касательному пространству TM в M может быть определено логарифмическим отображением logM: ℳ↦TM [22]:
Теперь у нас есть две стратегии построения сети B. Первая — построить сеть непосредственно на многообразии. В этой стратегии расстояние между Lk вычисляется с использованием (4) для формирования матрицы смежности, т. е. B=(bi,j)K×K, где bi,j=d(Li,Lj) и K — количество временной ряд хк. Другая стратегия состоит в том, чтобы спроецировать Lk на касательное пространство многообразия, а затем построить сеть в касательном пространстве. Пусть M∈ℳ — реперная точка, определяемая как среднее SPD-матриц, и тогда соответствие многообразия ℳ касательному пространству TM в M может быть определено логарифмическим отображением logM: ℳ↦TM [22]: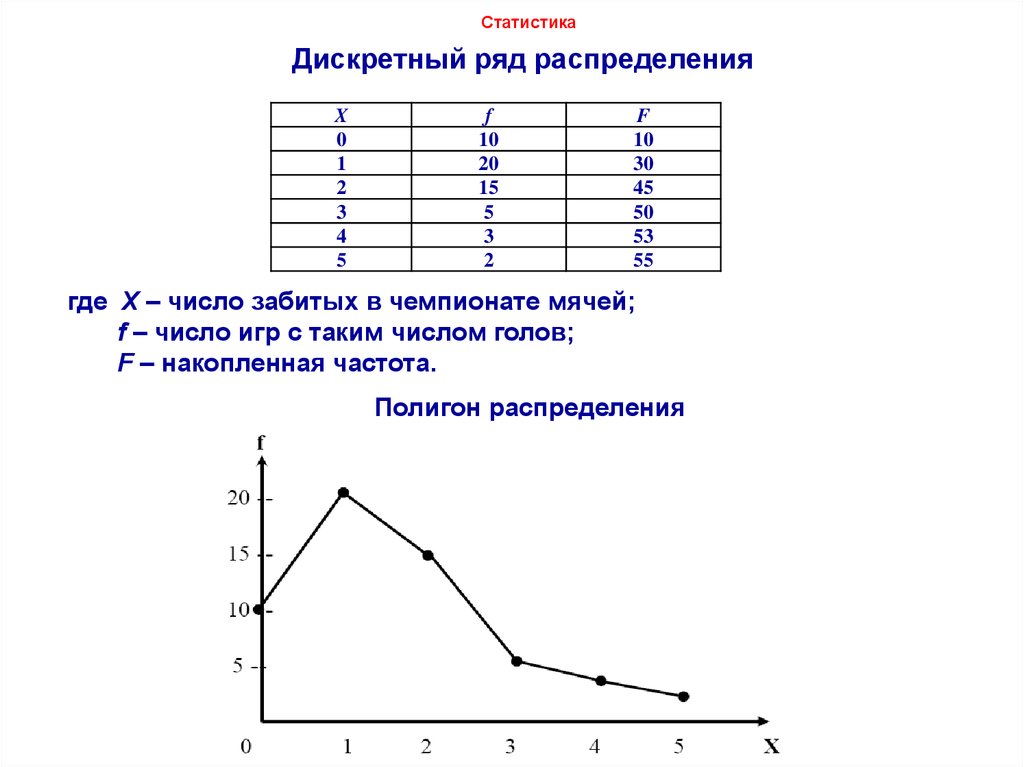
 Горизонтальная и вертикальная оси обозначают класс и образец соответственно. ( b ) Процент размера выборки в каждом классе от общей выборки.
Горизонтальная и вертикальная оси обозначают класс и образец соответственно. ( b ) Процент размера выборки в каждом классе от общей выборки.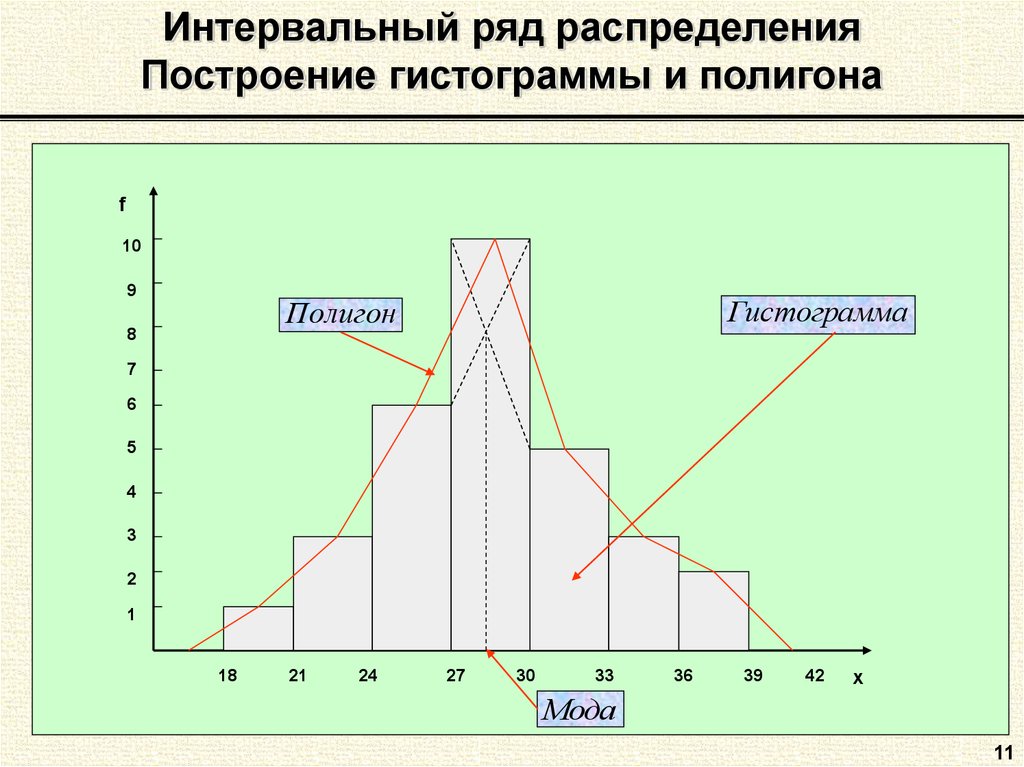 Для временного ряда xk мы использовали (4) и (5) для вычисления расстояний между N, формируя таким образом матрицу смежности Ak. Чтобы выделить топологию сети, мы использовали (6) для удаления большинства ребер. На самом деле, как определить соответствующий порог τ в (6) было открытой проблемой при построении сложных сетей. Здесь мы сохранили 20% краев на основе эмпирических значений и эффектов визуализации. Примеры скрытых сетей, соответствующих разным временным рядам, показаны на рис.
Для временного ряда xk мы использовали (4) и (5) для вычисления расстояний между N, формируя таким образом матрицу смежности Ak. Чтобы выделить топологию сети, мы использовали (6) для удаления большинства ребер. На самом деле, как определить соответствующий порог τ в (6) было открытой проблемой при построении сложных сетей. Здесь мы сохранили 20% краев на основе эмпирических значений и эффектов визуализации. Примеры скрытых сетей, соответствующих разным временным рядам, показаны на рис. Следовательно, скрытые сети могут предоставлять новые структуры данных для добычи и анализа временных рядов. После того, как скрытая сеть будет создана, мы можем использовать многочисленные методы из области науки о сложных сетях, чтобы охарактеризовать временной ряд. Например, топологическая статистика сети извлекается для формирования новых признаков для анализа временных рядов, таких как классификация стадий сна [25] и анализ сейсмических последовательностей [26]. Кроме того, графовые нейронные сети (GNN) в последнее время быстро развиваются и успешно используются во многих областях [27]. Предпосылкой для применения этого мощного инструмента является то, что входные данные должны быть графически структурированы. В большинстве случаев временные ряды не имеют явной графовой структуры. Таким образом, предлагаемая скрытая сеть обеспечивает условия для использования GNN для анализа временных рядов.
Следовательно, скрытые сети могут предоставлять новые структуры данных для добычи и анализа временных рядов. После того, как скрытая сеть будет создана, мы можем использовать многочисленные методы из области науки о сложных сетях, чтобы охарактеризовать временной ряд. Например, топологическая статистика сети извлекается для формирования новых признаков для анализа временных рядов, таких как классификация стадий сна [25] и анализ сейсмических последовательностей [26]. Кроме того, графовые нейронные сети (GNN) в последнее время быстро развиваются и успешно используются во многих областях [27]. Предпосылкой для применения этого мощного инструмента является то, что входные данные должны быть графически структурированы. В большинстве случаев временные ряды не имеют явной графовой структуры. Таким образом, предлагаемая скрытая сеть обеспечивает условия для использования GNN для анализа временных рядов. В , мы не можем визуально различить эту разницу с большой уверенностью из-за сложности сетевых подключений. Чтобы проверить правдоподобие нашего метода, используя (7) и (8), мы построили новую сеть B на основе скрытой сети A, а затем оценили конструкцию A в сочетании с метками классов. Результаты для сети B показаны на .
В , мы не можем визуально различить эту разницу с большой уверенностью из-за сложности сетевых подключений. Чтобы проверить правдоподобие нашего метода, используя (7) и (8), мы построили новую сеть B на основе скрытой сети A, а затем оценили конструкцию A в сочетании с метками классов. Результаты для сети B показаны на . Первая причина — низкая отличимость этих трех классов образцов от двух других классов, особенно последовательностей класса 2 и класса 4 (см. а). Вторая причина заключается в том, что процент выборок в этих трех классах слишком низок (см. b), что влияет на обучение VAE.
Первая причина — низкая отличимость этих трех классов образцов от двух других классов, особенно последовательностей класса 2 и класса 4 (см. а). Вторая причина заключается в том, что процент выборок в этих трех классах слишком низок (см. b), что влияет на обучение VAE.

 [Google Scholar]
[Google Scholar] Чжан Дж., Смолл М. Сложная сеть из псевдопериодических временных рядов: топология и динамика. физ. Преподобный Летт. 2006;96:238701. doi: 10.1103/PhysRevLett.96.238701. [PubMed] [CrossRef] [Google Scholar]
Чжан Дж., Смолл М. Сложная сеть из псевдопериодических временных рядов: топология и динамика. физ. Преподобный Летт. 2006;96:238701. doi: 10.1103/PhysRevLett.96.238701. [PubMed] [CrossRef] [Google Scholar] , Ли Х., Сунь Б. Реконструкция сложной сети для характеристики изменяющегося во времени поведения причинно-следственной эволюции многомерных временных рядов. науч. Отчет 2017;7:10486. doi: 10.1038/s41598-017-10759-3. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
, Ли Х., Сунь Б. Реконструкция сложной сети для характеристики изменяющегося во времени поведения причинно-следственной эволюции многомерных временных рядов. науч. Отчет 2017;7:10486. doi: 10.1038/s41598-017-10759-3. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]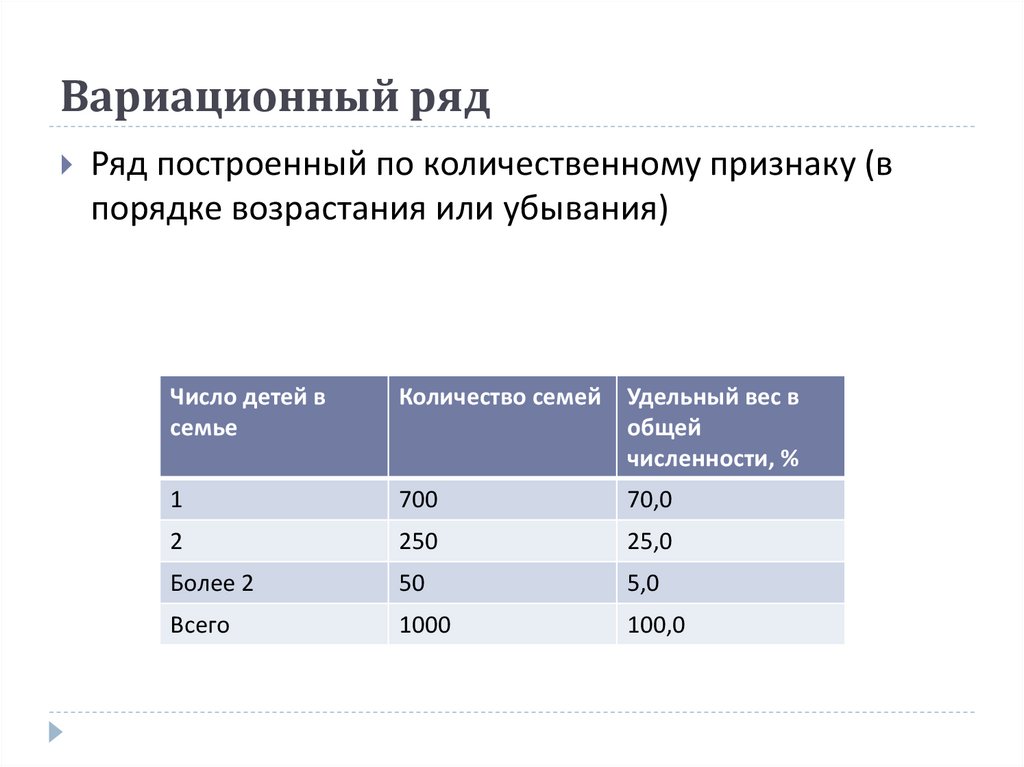 14–16 апреля 2014 г. [Google Scholar]
14–16 апреля 2014 г. [Google Scholar] Ловрич М., Мин-Оо М., Рух Е.А. Многомерные нормальные распределения, параметризованные как риманово симметричное пространство. Дж. Мультивар. Анальный. 2000;74:36–48. doi: 10.1006/jmva.1999.1853. [CrossRef] [Google Scholar]
Ловрич М., Мин-Оо М., Рух Е.А. Многомерные нормальные распределения, параметризованные как риманово симметричное пространство. Дж. Мультивар. Анальный. 2000;74:36–48. doi: 10.1006/jmva.1999.1853. [CrossRef] [Google Scholar]