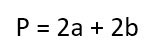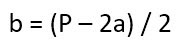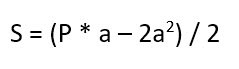Периметр через площадь формула: Как найти периметр если известна площадь 🚩 периметр через площадь 🚩 Математика

Как вычислить площадь по периметру

Инструкция

Прямоугольник.Задача: вычислите площадь прямоугольника, если известно, что его периметр равен 40, а длина b в 1,5 раза больше ширины a.

Решение.Используйте известную формулу периметра, он равен сумме всех сторон фигуры. В данном случае P = 2•a + 2•b. Из начальных данных задачи вы знаете, что b = 1,5•a, следовательно, P = 2•a + 2•1,5•a = 5•a, откуда a = 8. Найдите длину b = 1,5•8 = 12.

Запишите формулу для площади прямоугольника:S = a•b,Подставьте известные величины:S = 8•*12 = 96. Квадрат.Задача: найдите площадь квадрата, если периметр равен 36.

Решение.Квадрат – частный случай прямоугольника, где все стороны равны, следовательно, его периметр равен 4•a, откуда a = 8. Площадь квадрата определите по формуле S = a² = 64.

Треугольник.Задача: пусть дан произвольный треугольник ABC, периметр которого равен 29. Узнайте величину его площади, если известно, что высота BH, опущенная на сторону AC, делит ее на отрезки с длинами 3 и 4 см.

Решение.Для начала вспомните формулу площади для треугольника:S = 1/2•c•h, где c – основание и h – высота фигуры. В нашем случае основанием будет сторона AC, которая известна по условию задачи: AC = 3+4 = 7, осталось найти высоту BH.

Высота является перпендикуляром, проведенным к стороне из противоположной вершины, следовательно, она делить треугольник ABC на два прямоугольных треугольника. Зная это свойство, рассмотрите треугольник ABH. Вспомните формулу Пифагора, согласно которой:AB² = BH² + AH² = BH² + 9 → AB = √(h² + 9).В треугольнике BHC по тому же принципу запишите:BC² = BH² + HC² = BH² + 16 → BC = √(h² + 16).

Примените формулу периметра:P = AB + BC + ACПодставьте величины, выраженные через высоту:P = 29 = √(h² + 9) + √(h² + 16) + 7.

Решите уравнение:√(h² + 9) + √(h² + 16) = 22 → [замена t² = h² + 9]:√(t² + 7) = 22 — t, возведите обе стороны равенства в квадрат:t² + 7 = 484 – 44•t + t² → t≈10,84h² + 9 = 117,5 → h ≈ 10,42

Найдите площадь треугольника ABC:S = 1/2•7•10,42 = 36,47.

Что такое периметр и площадь — Topkin

Периметр – это геометрический термин, который часто встречается в задачах. Чтобы понять, что такое периметр, следует нарисовать произвольный многоугольник и вооружиться линейкой. В переводе с греческого языка этот термин обозначает «измеряю вокруг».

Как вычислить периметр

Периметр обозначается латинской буквой P. Его можно измерить в сантиметрах, миллиметрах, метрах или дециметрах. Чтобы узнать периметр, следует измерить длину всех сторон многоугольника. Полученные значения нужно сложить. Итоговая сумма и станет ответом на вопрос: «Чему равен периметр многоугольника».

Периметр – это длина линий, которые ограничивают замкнутую фигуру (квадрат, прямоугольник, треугольник и др.).

Например, перед вами многоугольник со сторонами 10, 12, 13 и 11 см. Складываем вышеназванные числа (10+12+13+11) и получаем сумму 46. Это и есть периметр многоугольника.

Для удобства вычисления периметра в геометрии существует ряд формул. Каждая формула соответствует определенной фигуре.

Периметр и площадь квадрата

Это сумма его четырех сторон. Как мы знаем, все стороны квадрата имеют равный размер. Поэтому мы можем узнать периметр квадрата, умножив длину его стороны на четыре:

P= a*4

P= a+a+a+a

Например, перед нами квадрат со стороной 10 см.

P= 10*4

P=40

Ответ: 40 см

P= 10+10+10+10

P=40

Ответ: 40 см

Чтобы разобраться, что такое периметр и площадь, следует уяснить, что периметр вычисляет длину контура фигуры, а площадь – размер всей ее поверхности.

Чтобы узнать площадь квадрата, необходимо воспользоваться простой формулой:

S= a*a

S=a²

S – это площадь, а – сторона квадрата.

Например, в задаче указано, что длина стороны квадрата составляет 10см.

S=10*10

S= 100см²

Ответ: 100см²

Периметр и площадь прямоугольника

Стороны прямоугольника, находящиеся друг напротив друга и имеющие одинаковую длину, называются противолежащими. Это длина и ширина, они условно обозначаются латинскими буквами a и b. Формула для вычисления периметра прямоугольника выглядит так:

P= (a+b)*2

Используя эту формулу, мы сначала находим сумму ширины и длины, а затем умножаем ее на два.

Например, перед нами прямоугольник, имеющий длину 6 см и ширину 2 см.

P= (6+2) * 2

P= 16

Ответ: 16 см

Чтобы узнать площадь прямоугольника, следует длину умножить на ширину. Формула выглядит так:

S= a*b

Например, в условиях задачи сказано, что прямоугольник имеет длину 5 см и ширину 2см. Меняем буквы a и b на указанные числа.

S= 5*2

S=10см²

Ответ: 10 см²

Периметр круга (длина окружности)

Каждый круг имеет центр. Расстояние от центра круга до любой точки, расположенной на окружности, имеет название радиус круга. Часто ученики путают понятия «круг» и «окружность» и пытаются определить площадь окружности. Это серьезная ошибка. Следует разделить в голове понятия «круг» и «окружность». У окружности нет и не может быть площади, у нее есть только длина.

Чтобы найти периметр круга, следует вычислить длину его окружности. Существует формула для нахождения длины окружности:

L = 2πr

L= 2πd

L – длина окружности

π – это число «пи», математическая константа. Она равна отношению длины окружности к длине ее диаметра. Древнее название числа «пи» – лудольфово число. Это число иррационально, его десятичное представление после точки никогда не заканчивается.

 π = 3.141 592 653 589 793 238 462 643 383 279 502

Для удобства вычислений обычно используют значение 3.14

R – это радиус окружности

D – Диаметр окружности

Итак, чтобы определить периметр круга, надо найти произведение радиуса и 2π. Если в задаче указан диаметр, то

Например, перед нами круг с радиусом 3 см. Найдем его периметр.

L= 2*3,14*3

L=6π

L=6*3.14

L = 18.84 см

P_к= 18,84 см

Ответ: 18.84 см

Отличие периметра от площади

Площадь – это размер поверхности фигуры, а периметр – это сумма ее границ.

Площадь всегда измеряется в квадратных единицах (см², м², мм²). Периметр измеряется в единицах длины – в сантиметрах, миллиметрах, метрах, дециметрах.

Периметр и площадь прямоугольника / Блог :: Бингоскул

Периметр — это сумма длин всех сторон многоугольника.

 

• Для вычисления периметра геометрических фигур используются специальные формулы, где периметр обозначается буквой «P». Название фигуры рекомендуется писать маленькими буквами под знаком «P», чтобы знать чей периметр ты находишь.
• Периметр измеряется в единицах длины: мм, см, м, км и т.д.

Отличительные особенности прямоугольника

• Прямоугольник – это четырехугольник.
• Все параллельные стороны равны
• Все углы = 90º.
• Например в повседневной жизни прямоугольник может встречаться в виде — книги, монитора, крышки от стола или двери.

 

Как вычислить периметр прямоугольника

Существует 2 способа его нахождения:

 

• 1 способ. Складываем все стороны. P = a + а + b + b
• 2 способ. Сложить ширину и длину, и умножить на 2. P = (a + b) · 2. ИЛИ Р = 2 · а + 2 · b. Стороны прямоугольника, которые лежат друг против друга (противолежащие), называются длиной и шириной.

 

«a» — длина прямоугольника, более длинная пара его сторон.

«b» — ширина прямоугольника, более короткая пара его сторон.

Пример задачи на подсчет периметра прямоугольника:

Вычислите периметр прямоугольника, есть его ширина равна 3 см., а длина — 6.

 

 

Запомни формулы вычисления периметра прямоугольника!

 

Формулы  периметра прямоугольника

 

Полупериметр — это сумма одной длины и одной ширины.

• Полупериметр прямоугольника — когда выполняешь первое действие в скобках – (a+b).
• Чтобы из полупериметра получить периметр, нужно его увеличить в 2 раза, т.е. умножить на 2.

Как найти площадь прямоугольника

Формула площади прямоугольника S= a*b

 

Если в условии известна длина одной стороны и длина диагонали, то площадь найти можно, используя в таких задачах, теорему Пифагора, она позволяет найти длину стороны прямоугольного треугольника если известны длины двух других сторон.

• Теорема Пифагора: a² + b² = c², где a и b – стороны треугольника, а с – гипотенуза, самая длинная сторона.

Помни!

1. Все квадраты – прямоугольники, но не все прямоугольники – квадраты. Так как:
   • Прямоугольник — это четырехугольник со всеми прямыми углами.
   • Квадрат — прямоугольник, у которого все стороны равны.
2. Если ты находишь площадь, ответ всегда будет в квадратных единицах (мм², см², м², км² и т.д.)

---

 

Смотри также: Основные формулы по математике

 

Решай задание 8 по математике база с ответами

Калькулятор вычисления периметра и площади геометрических фигур

Определение периметра и площади геометрических фигур — важная задача, которая возникает при решении многих практических или бытовых задач. Если вам требуется поклеить обои, установить забор, рассчитать расход краски или кафеля, то вам обязательно придется иметь дело с геометрическими расчетами.

Для решения перечисленных бытовых вопросов вам потребуется работать с самыми разными геометрическими фигурами. Мы представляем вам каталог онлайн-калькуляторов, которые позволяют вычислить параметры наиболее популярных плоских фигур. Рассмотрим их.

Круг

Окружность — это множество точек на плоскости, которые равноудалены от центра на некоторое расстояние, называемое радиусом. Многие считают круг и окружность синонимами, однако это не так. Круг — это часть плоскости, ограниченная окружностью. Вы можете отыскать периметр и площадь круга, но у окружности найти можно только длину, так как она представляет собой кривую, не имеющую площади. Длина окружности или периметр круга находятся по простой формуле:

l = 2 pi × R,

где R – радиус фигуры.

Площадь круга рассчитывается согласно следующему выражению:

S = pi R²

Круги часто встречаются в реальной жизни. В основном это основания цилиндрических и конических деталей, а также просто круглые поверхности, например, круглые столики, диски, грампластинки или катушки. Вид окружности имеют колеса, обручи или кольца. В трехмерной реальности окружность превращается в сферу, а круг — в шар. Форму этих геометрических тел имеют многие реальные и природные объекты. Благодаря своей эффективности круг охватывает максимальную площадь при минимальном периметре. Именно поэтому форму шара имеют капли, снежные комья, метеориты или планеты.

Треугольник

Треугольник — первая гармоничная фигура на плоскости, ограниченная тремя отрезками. Свойства треугольника известны людям с античных времен: изучение фигуры стартовало в Древнем Египте и не завершено до сих пор. Огромный вклад в изучение свойств фигуры внесли Евклид, Эйлер и Лобачевский, но даже сегодня продолжается работа над поиском замечательных точек треугольника, которых на данный момент найдено более 6 тысяч. Для определения периметра фигуры достаточно сложить длины всех сторон треугольника по формуле:

P = a + b + c,

где a, b, c – стороны.

Для вычисления площади треугольника используется 5 различных формул плюс нахождение площади через определенный интеграл. Самое простое выражение для вычисления площади:

S = 0,5 a × h,

где a — сторона треугольника, h — его высота.

Наш калькулятор позволяет отыскать площадь или периметр треугольника, зная разные комбинации нескольких параметров, таких как углы, стороны или радиусы связанных окружностей.

Треугольники не слишком распространены в реальной повседневности. В природе они практически не встречаются, за исключением кристаллических решеток некоторых молекул или формы ушей у рыси. А вот в технике, геометрии и прикладных науках треугольник — царь и бог. Наибольшее применение находит следующий тип фигуры.

Прямоугольный треугольник

Прямоугольный треугольник — особая вариация фигуры, у которой две стороны обязательно образуют прямой угол. Эти стороны называются катетами, а противолежащая им сторона — гипотенузой. Соотношение катетов и гипотенузы лежит в основе евклидовой геометрии — эти соотношения определяются теоремой Пифагора. Изучение свойств прямоугольного треугольника положило начало одному из важных разделов математики — тригонометрии, которая используется в самых разных прикладных сферах от компьютерных игр до океанографии.

Формулы для вычисления периметра и площади прямоугольного треугольника ничем не отличаются от формул для обычных вариаций данной фигуры или вытекают из них.

Трапеция

Трапеция, как и слово трапеза, по-гречески означают «стол». Это плоская фигура, ограниченная четырьмя прямыми, две из которых параллельны, а две — нет. По сути, это выпуклый четырехугольник, поэтому параллелограмм и прямоугольник считаются частными случаями трапеции. В общем случае все стороны трапеции имеют разную длину, и для вычисления периметра используется формула:

P = a + b + c + d,

a, b, c и d – стороны четырехугольника.

Площадь фигуры определяется как:

S = 0,5 (a + b) × h,

где a и b – параллельные стороны трапеции, h – высота.

Трапеция очень часто встречается в рукотворном мире. Грани многих предметов имеют вид этого четырехугольника, а буквально трапецеидальную форму имеют такие объекты как автомобильные окна, паруса, скаты крыш или юбки.

Параллелограмм

Параллелограмм — это элегантный четырехугольник, пары сторон которого параллельны друг другу. Любой четырехугольник становится параллелограммом, если его противолежащие стороны параллельны, диагонали в точке пересечения разделяются пополам, а противоположные углы равны. Для вычисления периметра параллелограмма используется простая формула, которая иллюстрирует сумму попарно равных сторон:

P = 2 (a + b).

Площадь параллелограмма не зависит от величины его углов, и находится по следующей формуле:

S = a × h.

Параллелограммы часто встречаются в реальной жизни: это грани многих призматических объектов, очертания полей, спортивных площадок или клумб. Форму параллелограммов имеют практически все отделочные материалы: плитка, кафель, гипсокартон, паркет. Такое разнообразие обусловлено тем, что частными случаями параллелограмма являются прямоугольник, ромб и квадрат, формулы для определения периметров и площадей которых аналогичны или выводятся из теоремы Пифагора.

Частные случаи

Ромб — четырехугольник с одинаковыми сторонами. Параллелограмм становится ромбом в случаях, если его диагонали пересекаются под углом 90 градусов и являются биссектрисами своих углов.

Прямоугольник — это параллелограмм с прямыми углами. Кроме того, параллелограмм считается прямоугольником, если его стороны и диагонали отвечают условиям теоремы Пифагора.

Квадрат — это параллелограмм, у которого все стороны равны и все углы равны. Диагонали квадрата полностью повторяют свойства диагоналей прямоугольника и ромба, что делает квадрат уникальной фигурой, которая характеризуется максимальной симметрией.

Многоугольник

Правильный полигон — это выпуклая фигура на плоскости, которая имеет равные стороны и равные углы. В зависимости от количества сторон многоугольники имеют собственные названия:

И так далее. Геометры шутят, что круг — это многоугольник с бесконечным количеством углов. Наш калькулятор запрограммирован на определение периметров и площадей только правильных многоугольников. Он использует общие формулы для всех правильных полигонов. Для вычисления периметра используется формула:

P = n × a,

где n – количество сторон многоугольника, a – длина стороны.

Для определения площади используется выражение:

S = n/4 × a² × ctg(pi/n).

Подставляя соответствующее n, мы можем подобрать формулу для любого правильного многоугольника, к которым также относятся равносторонний треугольник и квадрат.

Многоугольники имеют большое распространение в реальной жизни. Так форму пятиугольника имеет здание министерства обороны США — Пентагон, гексагона — пчелиные соты или кристаллы снежинки, октагона — дорожные знаки. Кроме того, многие простейшие, например радиолярии, имеют форму правильных полигонов.

Примеры из реальной жизни

Давайте рассмотрим пару примеров использования нашего калькулятора в реальных расчетах.

Покраска забора

Покраска поверхностей и расчет краски — это одни из самых очевидных бытовых задач, в которых требуются минимальные математические расчеты. Если нам нужно покрасить забор, высота которого составляет 1,5 метра, а длина 20 метров, то сколько потребуется банок краски? Для этого нужно узнать суммарную площадь забора и расход лакокрасочных материалов на 1 квадратный метр. Мы знаем, что расход эмали составляет 130 грамм на метр. Теперь определим площадь забора, используя калькулятор для вычисления площади прямоугольника. Она составит S = 30 квадратных метров. Естественно, что забор мы будем красить с обеих сторон, поэтому площадь для покраски увеличится до 60 квадратов. Тогда нам понадобится 60 × 0,13 = 7,8 килограмм краски или три стандартных банки по 2,8 килограмма.

Отделка бахромой

Пошив одежды — еще одна отрасль, в которой необходимы обширные геометрические познания. Пусть нам надо отделать бахромой платок, который представляет собой равнобедренную трапецию со сторонами 150, 100, 75 и 75 см. Для вычисления расхода бахромы нам потребуется узнать периметр трапеции. В этом нам и пригодится онлайн-калькулятор. Введем эти данные ячейки и получим ответ:

P = 400

Таким образом, нам понадобится 4 м бахромы для отделки платка.

Заключение

Плоские фигуры составляют реальный мир вокруг. Мы часто задавались в школе вопросом, пригодится ли нам геометрия в будущем? Выше приведенные примеры показывают, что математика постоянно используется в повседневной жизни. И если площадь прямоугольника для нас привычна, то вычислить площадь додекагона может оказаться трудной задачей. Используйте наш каталог калькуляторов для решения школьных заданий или бытовых вопросов.

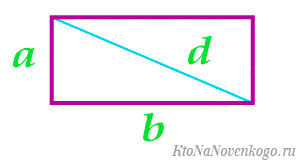
Площадь прямоугольника — как ее найти по основной формуле, а также через диагональ и периметр

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru.

Сегодня мы расскажем, как вычислять площадь прямоугольника.

Различные формулы вычисления площади (а их действительно немало), изучают в 8 классе школы.

Что такое площадь прямоугольника

Но для начала давайте все-таки дадим основные определения:

Прямоугольник – это геометрическая фигура, относящаяся к категории четырехугольников. Ее отличительная особенность в том, что противоположные стороны лежат на параллельных прямых (то есть параллельны друг другу) и равны.

Прямоугольник является параллелограммом (что это такое?) и выглядит вот так:

А частным случаем прямоугольника, если у него все стороны равны между собой, является квадрат.

Площадь любой геометрической фигуры, формально говоря, это ее размер. Другими словами, размер того пространства, которое находится внутри границ фигуры.

В отношении четырехугольников применимо еще понятие «квадратура». С его помощью показывали, сколько квадратов вместится внутрь фигуры.

Собственно, отсюда и пошло современное обозначение площадей, когда речь идет о габаритах помещения или какой-то территории. Мы часто слышим «столько-то квадратных метров (миллиметров, сантиметров, километров)» или просто «столько-то квадратов».

Для площади геометрических фигур действуют определенные правила:

1. Она не может быть отрицательной.
2. У равных фигур всегда равные площади.
3. Если две фигуры не пересекаются друг с другом, то их общая площадь равна сумме площадей фигур по отдельности.
4. Если одна фигура вписана в другую, то ее площадь всегда меньше, чем у второй.

Обычно фигуры, которые имеют равные площади, называют «равновеликими».

Как найти площадь прямоугольника

Площадь прямоугольника вычисляется по очень простой формуле – надо лишь перемножить его стороны.

Возьмем, к примеру, такой прямоугольник:

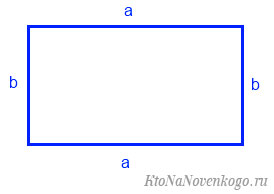
Площадь геометрической фигуры обычно обозначается латинской буквой «S». И тогда формула для конкретного примера будет:

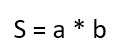
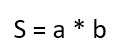
Например, если мы имеем прямоугольник со сторонами 2 и 3 сантиметра, то его площадь составит 2 * 3 = 6 сантиметров.

Но бывают случаи, когда неизвестны размеры сторон прямоугольника, а площадь вычислить все равно надо. Для этого существуют более сложные формулы.

Формула площади прямоугольника через периметр

Если известна длина только одной стороны, но известен еще и периметр прямоугольника.

В этом случае есть два варианта.

1. Первый — вычислить длину второй стороны. Для этого надо вспомнить, что периметр (обозначается буквой «Р») считается по формуле:

   И тогда обратные расчеты выглядят вот так:

   Ну а после того, как станет известна длина второй стороны прямоугольника, можно прибегнуть к классической формуле.
2. Ну и второй вариант – воспользоваться сразу готовой формулой:

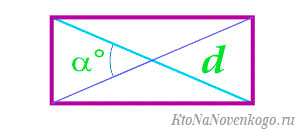
Площадь прямоугольника через диагональ

1. Известна одна сторона и длина диагонали.

   Тут опять же есть два варианта. В первом случае вычисляем длину второй стороны, используя теорему Пифагора.

   

   Второй вариант – опять же сразу прибегнуть к готовой формуле:

   

2. Если известны длина диагоналей и угол между ними.

   

   В этом случае стоит воспользоваться вот такой формулой:

   

Вот и все, что нужно знать о вычислении площади прямоугольников.

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Использую для заработка

Рубрика: ЧАстые ВОпросы

Периметр и площадь геометрических фигур

Существует много плоских геометрических фигур: точка, линия (прямая или кривая), отрезок, угол, ломаная и т. д.:

Если внимательно посмотреть на все эти фигуры, то можно выделить две из них, которые образованы замкнутыми линиями (окружность и треугольник). Эти фигуры имеют своего рода границу, отделяющую то что находится внутри, от того что находится снаружи. То есть граница делит плоскость на две части: внутреннюю и внешнюю область относительно фигуры, к которой она относится:

Периметр

Периметр – это замкнутая граница плоской геометрической фигуры, отделяющая её внутреннюю область от внешней.

Периметр есть у любой замкнутой геометрической фигуры:

На рисунке периметры выделены красной линией. Обратите внимание, что периметр окружности часто называют длиной.

Периметр измеряется в единицах измерения длины:  мм,  см,  дм,  м,  км.

У всех многоугольников нахождение периметра сводится к сложению длин всех сторон, то есть периметр многоугольника всегда равен сумме длин его сторон. При вычислении периметр часто обозначают большой латинской буквой P:

Площадь

Площадь – это часть плоскости, занимаемая замкнутой плоской геометрической фигурой.

Любая плоская замкнутая геометрическая фигура имеет определённую площадь. На чертежах площадью геометрических фигур является внутренняя область, то есть та часть плоскости, которая находится внутри периметра.

Измерить площадь фигуры — значит найти, сколько раз в данной фигуре помещается другая фигура, принятая за единицу измерения. Обычно за единицу измерения площади принимается квадрат, у которого сторона равна единице измерения длины: миллиметру, сантиметру, метру и т. д.

На рисунке изображён квадратный сантиметр. Квадратный сантиметр — квадрат, у которого каждая сторона имеет длину 1 см:

Площадь измеряется в квадратных единицах измерения длины. К единицам измерения площади относятся:  мм²,  см²,  м²,  км²  и т. д.

Таблица перевода квадратных единиц

	мм2	см2	дм2	м2	ар (сотка)	гектар (га)	км2
мм2	1 мм2	0,01 см2	10-4 дм2	10-6 м2	10-8 ар	10-10 га	10-12 км2
см2	100 мм2	1 см2	0,01 дм2	10-4 м2	10-6 ар	10-8 га	10-10 км2
дм2	104 мм2	100 см2	1 дм2	0,01 м2	10-4 ар	10-6 га	10-8 км2
м2	106 мм2	104 см2	100 дм2	1 м2	0,01 ар	10-4 га	10-6 км2
ар	108 мм2	106 см2	104 дм2	100 м2	1 ар	0,01 га	10-4 км2
га	1010 мм2	108 см2	106 дм2	104 м2	100 ар	1 га	0,01 км2
км2	1012 мм2	1010 см2	108 дм2	106 м2	104 ар	100 га	1 км2

104 = 10 000	10-4 = 0,000 1
106 = 1 000 000	10-6 = 0,000 001
108 = 100 000 000	10-8 = 0,000 000 01
1010 = 10 000 000 000	10-10 = 0,000 000 000 1
1012 = 1 000 000 000 000	10-12 = 0,000 000 000 001

Как найти периметр зная площадь – онлайн калькулятор геометрических фигур

Как найти периметр прямоугольника, зная только его площадь?

В общем случае эта задача не имеет решения, поскольку одной и той же площади могут соответствовать совершенно разные стороны. Однако, возможны случаи когда и такая задача имеет конкретные решения. Частный случай — когда прямоугольник квадрат. Тогда площадь равна квадрату его стороны, а все стороны равны между собой. Берем корень из площади и получаем значение стороны квадрата, умножаем на 4 — вот и периметр. Так же можно решить такую задачу если по условию стороны имеют целочисленное значение, просто методом подбора, который впрочем может дать более одного варианта ответа, но не очень много. Поскольку площадь прямоугольника это АхВ, то отношение сторон выражается как А=S/B и любые целые значения В, при которых А также получится целым будут вариантами ответа. Соответственно периметр, удвоенная сумма этих сторон, также будет разным.

в избранное ссылка отблагодарить

По одной только площади вычислить периметр прямоугольника не возможно.Нужны ещё дополнительные сведения. А это. или одна из сторон прямоугольника, или соотношение сторон прямоугольника.Есть даже такая задача: у какого прямоугольника заданной площади максимальный периметр?А чтобы представить формулу периметра по соотношению сторон, то рассмотрим:

Пусть соотношение сторон прямоугольника ав=к.Пусть известно значение а.Тогда в= ак.

Площадь S = а*в=а*ак.Откуда а=√(к*S ). р= 2(а+в)=2(а+ак)=2a(k+1)/k =2√(k*S)(k+1)/k=2√S(k+1)

А максимальный периметр при одинаковой площади прямоугольника — у прямоугольника с равными сторонами. то есть у квадрата.

К сожалению, придётся разочаровать тех, кто надеется, что, зная площадь прямоугольника, возможно найти его периметр. Не имея данных о длине хотя бы одной стороны сделать это невозможно.

Периметр прямоугольника – это сумма всех его сторон, так как противоположные стороны у него равны, то формула периметра Р=2 х (а+в). Зная же площадь (произведение сторон S=а х в) можно понять, что у нас в наличии два уравнения с тремя неизвестными (а, в и Р) и одним известным — S. Для решения этой системы уравнений не хватает ещё одного заданного параметра – одной из сторон.

в избранное ссылка отблагодарить

ПРОЕКТИРОВАНИЕ ВОДЫ И САНИТАЦИИ

E-mail: [email protected]

Время работы: Пн-Пт с 9-00 до 18-00 (без обеда)

Расчет геометрических фигур

Геометрические изображения представляют собой замкнутые множества точек на плоскости или в пространстве, которые ограничены конечным числом строк.

Они могут быть линейными (1D), плоскими (2D) или пространственными (3D).

Каждое тело, имеющее форму, представляет собой набор геометрических изображений.

Каждая картина может быть описана математической формулой разного уровня сложности.

Исходя из простого математического выражения, сумма набора математических выражений.

Основными математическими параметрами геометрических фигур являются радиусы, длины граней или граней и углы между ними.

Ниже приведены основные геометрические формы, наиболее часто используемые в расчетах, формулах и ссылках на компьютерные программы.

Линейные геометрические фигуры

1. Точка

Цель — основной объект измерения.

Главной и единственной математической характеристикой точки является ее координата.

Рассчитать расстояние между точками

2. Линия

Линия представляет собой тонкий пространственный объект с конечной длиной и представляет собой цепочку точек, связанных друг с другом. Основным математическим свойством линии является длина.

Вычислить длину линии

третий

луч

Лед — это тонкий пространственный объект, который имеет бесконечную длину и представляет собой цепочку точек, связанных друг с другом. Основными математическими характеристиками луча являются координаты его источника и направления.

Плоские геометрические фигуры

первый

круг

Круг представляет собой геометрический локус точек на плоскости, расстояние от которого центр не превышает заданное число, которое называется радиусом этого круга. Основной математической особенностью круга является радиус.

Расчет площади круга (круга)
Вычисление длины круга (круга)

второй

рынок

Квадрат — это четырехугольник, в котором все углы и все стороны одинаковы. Основным математическим свойством квадрата является длина его стороны.

Вычислить квадрат квадрата
Вычисление квадрата квадрата

третий

прямоугольник

Прямоугольник представляет собой четырехугольник со всеми углами, равными 90 градусам (прямые линии). Основными математическими характеристиками прямоугольника являются длины его сторон.

Вычисление поверхности прямоугольника
Вычисление периметра прямоугольника

четвёртая

треугольник

Треугольник представляет собой геометрическое изображение, образованное тремя сегментами, которые соединяют три точки (треугольные токи), которые не лежат на одной линии. Основными математическими характеристиками треугольника являются длины стороны и высота.

Расчет поверхности треугольника
Вычисление треугольника треугольника

пятые

Калькулятор для расчета окружности и области геометрической формы

Trapezij

Трапеция — это четырехугольник с двумя сторонами, параллельный, а другой не параллельный. Основными математическими характеристиками трапеции являются длины сторон и высота.

Расчет трапецеидальной области
Расчет окружности трапеции

6. Параллелограмма

Параллелограмм — это четырехугольник, противоположные стороны которого параллельны.

Основными математическими характеристиками параллелограмма являются длины его сторон и высота.

Вычисление поверхности параллелограмма
Вычисление границы параллелограмма

седьмые

ромб

Римба — четырехугольник со всеми сторонами, а углы его точек не равны 90 градусам. Основными математическими особенностями ромба являются длина его бока и его высота.

Расчет площади алмаза
Расчет периметра алмаза

восьмых

эллипс

Эллипс является замкнутой кривой на плоскости, которая может быть представлена ​​в виде ортогонального проектора отрезка окружности цилиндра к плоскости. Основными математическими характеристиками круга являются длина его полупроводников.

Расчет поверхности эллипса

3D-геометрия

первый

Балон

Сфера — это геометрическое тело, представляющее собой совокупность всех точек пространства, расположенных от центра на некотором расстоянии. Основной математической характеристикой шара является его радиус.

Вычисление объема шара
Вычислить площадь поверхности сферы

второй

Sfera

Сфера — это оболочка геометрического тела, представляющая собой совокупность всех точек пространства, которые находятся от центра на некотором расстоянии. Основной математической характеристикой сферы является ее радиус.

Расчет объема
Расчет площади поверхности сферы

3. Куб

Куб — это геометрическое тело, которое является правильным многоугольником, чья линия является квадратом.

Основной математической характеристикой куба является длина его ребра.

Вычисление объема куба
Расчет поверхности куба

4. Параллелепипед

Paralelepiped — это геометрическое тело, которое является полимером с шестью гранями и каждым прямоугольником. Основными математическими свойствами параллелепипеда являются длины ребер.

Вычисление объема параллелепипеда
Расчет поверхностей параллелепипеда

пятые

призма

Призма — многогранник, два графика которого являются одинаковыми многоугольниками, лежащими в параллельных плоскостях, а остальные грани — параллелограммы, которые имеют обычные стороны с этими многоугольниками. Основными математическими характеристиками призмы являются основная поверхность и высота.

Вычисление количества призмы

шестые

шишка

Конус представляет собой геометрическое число, полученное объединением всех лучей, происходящих из одного вершинного конуса и проходящих через плоскую поверхность. Основными математическими характеристиками конуса являются радиус основания и высоты.

Расчет объема конуса
Расчет поверхностей конуса

седьмые

пирамида

Пирамида — многогранник, основой которого является произвольный многоугольник, а боковые грани — треугольники, имеющие общую цепочку. Основными математическими характеристиками пирамиды являются основная поверхность и высота.

Расчет объема пирамиды

восьмых

цилиндр

Цилиндр представляет собой геометрическое число, ограниченное цилиндрической поверхностью и двумя параллельными плоскими плоскостями. Основными математическими характеристиками цилиндра являются радиус основания и высоты.

Объемный расчет
Расчет поверхностей цилиндра

На этой странице показаны все геометрические фигуры, которые наиболее часто встречаются в геометрии, чтобы представлять объект или его часть на плоскости или во Вселенной.

Длина круга и окружности

Сегодня мы познакомимся с такими определениями, как круг, радиус, диаметр и объем.. В этой статье мы рассмотрим геометрическое изображение, которое не содержит прямых линий, но изогнуто: круг. Мы выполняем некоторые свойства этих чисел. Представьте точку \ (P \) с точным местоположением, затем перетащите все возможные точки, которые находятся на одном и том же фиксированном расстоянии r от точки \ (P \).

Если мы перетаскиваем все точки, находящиеся на расстоянии \ (г \) из \ (Р \), то в итоге получим круг.

                                                                                                               

Таким образом, окружность — это серия всех точек, одинаково отдаленных (то есть все на одном расстоянии) от центральной точки.

Площадь и дальность

Расстояние r от центра к периферии называется радиусом. Если умножить радиус на \ (2 \), получим диаметр круга. 

                                                                                                              

Объем круга

Как и в случае треугольников и прямоугольников, мы можем попытаться получить формулы для области и «периметр» круглый.

Но такое понятие, как «периметр», круг нет. Существует определение длины круга. Однако расчет вычислительной схемы не так прост, как вычисление периметра прямоугольника или треугольника.

Очевидно, что, увеличивая диаметр или радиус, круг становится больше и, следовательно, объем увеличивается.

Если мы разделим любой круг по диаметру, получится постоянное число π. История π чисел была проведена параллельно с развитием всей математики и стала стандартной после работы Леонардо Эйлер в 1737 г. Эта константа примерно равна (3,14593 \). Точное значение \ (π \) неизвестно, pi — иррациональное число — неповторимое десятичное число, которое не может быть выражено как часть интегрированного счетчика и знаменателей.

Мы находим, что длина круга, деленная на диаметр, является постоянным числом π.

Диаметр вдвое превышает радиус, поэтому его можно использовать для замены. Таким образом, окружность круга может быть рассчитана, если мы знаем радиус круга или его диаметр. Для большинства вычислений, требующих правильного ответа, \ (π \) равно \ (3,14 \). Диапазон рассчитывается по формуле:

\ (2πr \)

Например, если окружность имеет радиус \ (3 \), то ее диапазон равен \ (6π \).

Диапазон круга рассчитывается с использованием уравнения:

\ (πr ^ 2 \)

Если круг имеет диаметр \ (6 \) сантиметров.

Какова его область? Радиус равен \ (3 \), поэтому поверхность \ (πr ^ 2-9π \) \ (cm ^ 2 \)

Подпишитесь на бесплатную пробную версию здесь и узнайте, что вы не понимаете.

Дополнительные уроки и задания по математике с преподавателями нашей интернет-школы «Альфа». Зарегистрируйтесь сейчас в пробной аптеке!

Зарегистрируйтесь для бесплатного тестирования знаний!

Как найти площадь, зная периметр Площадь и периметр фигуры являются основными ее геометрическими параметрами. Их нахождение и описание с учетом известных величин составляет значительную долю в обучающем процессе. как найти периметр по площади В общем смысле периметр – это длина всех границ фигуры. Для прямоугольника он равен сумме длин его сторон. А площадь представляет собой всю внутреннюю часть фигуры, измеренной в определенных единицах. Согласно свойствам фигур, а также формулам площади и периметра, можно найти соотношения между этими параметрами фигуры и выразить одно значение из другого. Для определения площади прямоугольника с известным периметром необходимо дополнительно знать одну его сторону. Инструкция

© CompleteRepair.Ru

Площадь — это стороны, перемноженные друг на друга То есть если принять допуск, что стороны все равны, то взять корень из площади — это будет одна сторона, и умножить на 4 — это периметр (в вашем случае примерно 10 метров)

напрашивается: корень квадратный и умножить на 4 стороны комнаты..

. но это не совсем правильно.. . Чем квадратнее прямоугольник — тем его периметр меньше.. . должн ещё что-то быть известно…

Допустим ваша ванная 1,5 м *4 м=6 м.

кв. Периметр тогда 1,5+1,5+4+4=11 м, если 2*3=6кв. м, 2+2+3+3=10 м, если 6*1=6 кв. м, то 6+6+1+1=14 м. О какой формуле может идти речь?

Сейчас Вы можете купить плитку только на пол.

Корень из 6.05 умнож на 4 и умнож на высоту 2.8плюс 10 процентов на резку, брак и т. д.

не сдан, но строители работают-подойди к прорабу может твою квартиру покажет может такуюжетебе главное или длину узнать или ширину я думаю где то 3Х2))

Одно из двух; 1.

либо память у вас девичья. 2 либо старческий маразм.

Как найти площадь, зная периметр

По секрету скажу. что раньше за попытки памятью подсказывать наличие подобных формул, могли закрыть и проколоть на предмет осеннего обострения шизофрениии.

не делайте этого. Плитка сейчас разных размеров, зная размеры стен, можно оптимально выбрать, чтоб было поменьше подрезки

Войдите, чтобы написать ответ

Площадь и периметр

Площадь:

Объем пространства внутри границы двухмерной фигуры, такой как треугольник или круг.

Периметр:

Периметр — это расстояние вокруг двухмерной формы, такой как квадрат, прямоугольник или треугольник.

Формулы

Квадрат:

Квадрат — это четырехсторонний многоугольник, в котором длины всех четырех сторон будут равны, а каждый угол при вершине будет прямым углом или 90 ° , как показано ниже.

Если задана длина стороны:

Площадь квадрата = ²

Если задана длина диагонали:

Площадь квадрата = 1/2 ⋅ d ²

Периметр квадрата = 4a

Прямоугольник:

Прямоугольник — это четырехсторонний многоугольник, в котором длины противоположных сторон будут равны, а угол каждой вершины будет равен 90 ° или прямому углу, как показано ниже.

Площадь прямоугольника = l ⋅ w

Периметр прямоугольника = 2 (l + w)

Равносторонний треугольник:

Равносторонний треугольник представляет собой трехсторонний многоугольник, длина которого равна все три стороны будут равны, а угол каждой вершины будет 60 °, как показано ниже.

Площадь равностороннего треугольника = √3 / 4 ⋅ a ²

Периметр равностороннего треугольника = 3a

Масштабный треугольник:

Масштабный треугольник — это трехсторонний многоугольник, в котором все три стороны будут иметь неодинаковую длину, и размеры всех трех углов будут разными, как показано ниже.

Площадь масштабного треугольника = √ [s (sa) (sb) (sc)

, где s = (a + b + c) / 2

Периметр масштабного треугольника = a + b + c

Четырехугольник:

Четырехугольник — это четырехсторонний многоугольник, как показано ниже.

Площадь четырехугольника = 1/2 ⋅ d ⋅ (h ₁ + h ₂ )

Периметр четырехугольника = a + b + c + d

Параллелограмм :

Параллелограмм — это четырехсторонний многоугольник, противоположные стороны которого равны и параллельны, как показано ниже.

Площадь параллелограмма = b ⋅ h

Периметр параллелограмма = 2 (a + b)

Ромб :

Ромб — четырехсторонний многоугольник, длина которого равна четыре стороны будут равны, а противоположные стороны будут параллельны, как показано ниже.

Площадь ромба = 1/2 ⋅ d ₁ ⋅ d ₂

Периметр ромба = 4a

Трапеция в форме четырехугольника:

многоугольник, у которого есть пара противоположных сторон, параллельных, как показано ниже.

Площадь трапеции = 1/2 ⋅ h ⋅ (a + b)

Периметр трапеции = a + b + c + d

Круг:

Круг круглая плоская фигура, граница (окружность) которой состоит из точек, равноудаленных от фиксированной точки (центра). Расстояние между центром и любой точкой на окружности называется радиусом (r).

Площадь круга = ∏ r ²

Периметр круга = 2 ∏ r

Полукруг:

Полукруг или полукруг его окружности, как показано ниже.

Площадь полукруга = ∏ r ² /2

Периметр полукруга = ∏ r + 2r

Квадрант:

Квадрант: 9000 четверть круга.

Площадь квадранта = ∏ r ² /4

Периметр квадранта = ∏ r / 2 + 2r

Сектор круга5:

сектор круга — это часть внутренней части круга, заключенная в дугу и два радиуса.

Площадь сектора = θ / 360 ° ⋅ ∏r ²

Длина дуги AB = θ / 36 0 ° ⋅ 2∏r

Периметр а Сектор = ( θ / 36 0 ° ⋅ 2∏r) + 2r

Правильный многоугольник:

Правильный многоугольник — это многоугольник, который является равноугольным (все внутренние углы равны по размеру) и равносторонним ( все стороны имеют одинаковую длину).

Площадь = 1/2 ⋅ (Апофема x Периметр)

Периметр = Число сторон ⋅ Длина каждой стороны

Если вы хотели бы иметь проблемы по площади и периметру,

Нажмите здесь

Кроме того, что описано в этом разделе, если вам нужны другие математические данные, воспользуйтесь нашим пользовательским поиском Google здесь.

Вы также можете посетить следующие веб-страницы, посвященные различным вопросам математики.

ЗАДАЧИ СО СЛОВАМИ

Задачи со словами HCF и LCM

Задачи со словами на простых уравнениях

Задачи со словами на линейных уравнениях

Задачи со словами на квадратных уравнениях

Задачи со словами

Проблемы со словами в поездах

Проблемы со словами по площади и периметру

Проблемы со словами по прямому и обратному изменению

Проблемы со словами по цене за единицу

Проблемы со словами по скорости за единицу

задачи по сравнению ставок

Преобразование обычных единиц в текстовые задачи

Преобразование метрических единиц в текстовые задачи

Word задачи по простому проценту

Word задачи по сложным процентам

ngles

Проблемы с дополнительными и дополнительными углами в словах

Проблемы со словами с двойными фактами

Проблемы со словами в тригонометрии

Проблемы со словами в процентах

Проблемы со словами

Задачи

Задачи с десятичными словами

Задачи со словами о дробях

Задачи со словами о смешанных фракциях

Одношаговые задачи с уравнениями со словами

Проблемы со словами с линейным неравенством

Задачи

Проблемы со временем и рабочими словами

Задачи со словами на множествах и диаграммах Венна

Задачи со словами на возрастах

Теорема Пифагора задачи со словами

Процент числового слова проблемы

Проблемы со словами при постоянной скорости

Проблемы со словами при средней скорости

Проблемы со словами при сумме углов треугольника 180 градусов

ДРУГИЕ ТЕМЫ

Сокращения прибыли и убытков

Сокращение в процентах

Сокращение в таблице времен

Сокращение времени, скорости и расстояния

Сокращение соотношения и пропорции

Область и диапазон рациональных функций

Область и диапазон рациональных функций

функции с отверстиями

Графики рациональных функций

Графики рациональных функций с отверстиями

Преобразование повторяющихся десятичных знаков в дроби

Десятичное представление рациональных чисел

Поиск корня из длинного квадрата видение

Л.Метод CM для решения временных и рабочих задач

Преобразование задач со словами в алгебраические выражения

Остаток при делении 2 в степени 256 на 17

Остаток при делении в степени 17 на 16

Сумма всех трехзначных чисел, делимых на 6

Сумма всех трехзначных чисел, делимых на 7

Сумма всех трехзначных чисел, делимых на 8

Сумма всех трехзначных чисел, образованных с использованием 1, 3 , 4

Сумма всех трех четырехзначных чисел, образованных ненулевыми цифрами

Сумма всех трех четырехзначных чисел, образованных с использованием 0, 1, 2, 3

Сумма всех трех четырехзначных чисел числа, образованные с использованием 1, 2, 5, 6

.

Формулы площади и периметра (видео) для прямоугольников, квадратов и кругов

Площадь и периметр — формулы для прямоугольников, квадратов и кругов

Вы можете использовать площадь квадрата или круга, чтобы найти периметр (или длину окружности) фигуры. С прямоугольниками, если вы знаете только площадь и длину одной стороны, вы можете найти периметр. Вы даже можете узнать длину сторон прямоугольника, если знаете площадь и периметр. Никаких уловок; просто математика!

1. Видео
2. Определения
3. Как найти площадь и периметр

Площадь и окружность круга

Периметр и площадь квадрата

Площадь и периметр прямоугольника

Определения

1. Площадь — замкнутое пространство внутри двухмерной формы.Форма может быть многоугольником, например треугольником, квадратом или прямоугольником. Также это может быть криволинейная форма, например круг. Площадь , всегда , измеряется в квадратных единицах.
2. Периметр — это расстояние вокруг двухмерной формы. Для многоугольников периметр можно найти, используя только сложение, добавляя расстояния при перемещении по форме.
3. Окружность — это набор всех точек на плоскости, находящихся на одинаковом расстоянии от данной точки. Этот набор точек замыкается во внутреннем пространстве, в области круга.Периметр круга называется его окружностью .

Как найти площадь и периметр

Формулы периметра

Формулы периметра

Форма	Формула	Переменные
Площадь	P = 4 с	с — длина любой стороны.
Прямоугольник	P = 2L + 2W	L и W — длина сторон (длина и ширина).
Треугольник	а + б + в	a, b и c — длина сторон.
Прямой треугольник	P = а + Ь + а2 + Ь2	a и b — длины двух ножек.
Круг	P = C = 2πr = πd	r — радиус, d — диаметр.

Формулы площади

Формулы площади

Форма	Формула	Переменные
Площадь	А = с2	с — длина любой стороны.
Прямоугольник	А = LW	L и W — длина сторон (длина и ширина).
Треугольник	А = 12 ч	b — основание, h — высота.
Треугольник	A = s (s-a) (s-b) (s-c) s = a + b + c2	a, b и c — длины сторон, а s — полупериметр.
Параллелограмм	A = bh	b — длина основания, а h — высота.
Трапеция	А = b1 + b22 ч	b1 и b2 — длины параллельных сторон, а h — высота (расстояние) между параллелями.
Круг	А = πr2	r — радиус.

Определение периметра из площади включает изменение единиц измерения с квадратных (двумерных) единиц площади на линейные (одномерные) единицы периметра. При форматировании окончательного ответа не забудьте «не квадрат» единиц измерения, но сохраните ту же систему: см, мм, м, фут, ярд и т. Д.

Площадь и окружность круга

На протяжении тысячелетий математики знали, что длина окружности связана с диаметром круга благодаря константе π, которая представляет собой строчную греческую букву «пи». В математике оно имеет значение, которое никогда не заканчивается и никогда не повторяется, а начинается с 3,1415926535. Для повседневной математики мы обычно используем 3,1415 или даже только 3,14.

Формула площади и окружности круга

Для C = длина окружности, r = радиус и D = диаметр окружности:

С = 2π × r

.

Формулы периметра, периметр

Периметр (P): Расстояние вокруг внешней части фигуры.

Стандартное обозначение для периметра — P

.

Периметр треугольника

Р = а + Ь + с

Периметр квадрата

У квадратов четыре равные стороны.
Пусть длина стороны будет a.
Периметр квадрата равен P = a + a + a + a или:

P = 4 ⋅ a

Периметр прямоугольника

Пусть длина и ширина прямоугольника равны a и b.
Сумма длин сторон равна P = a + b + a + b или:

P = 2 ⋅ a + 2 ⋅ b

Периметр параллелограмма

Поскольку противоположные стороны палалелограммы равны по длине, ее периметр равен P = a + b + a + b. или:

P = 2 ⋅ a + 2 ⋅ b

Как мы видим, периметр параллелограмма равен периметру прямоугольника.

Периметр ромба

P = 4 ⋅ a

Периметр равнобедренной трапеции

Пусть a и b — длины параллельных сторон.Так как он равнобедренный, две другие стороны равны по длине, и пусть c будет их длиной.

P = a + b + c + c = a + b + 2 ⋅ c

Периметр равностороннего треугольника

Как мы знаем, равносторонние треугольники имеют 3 равные стороны. Итак, если длина стороны равна тогда формула периметра P = a + a + a

P = 3 ⋅ a

Окружность круга

$ C = d \ cdot \ pi = 2 \ cdot r \ cdot \ pi $

$ \ pi = 3.14 $
r — радиус.
d — диаметр.

Правильный многоугольник

$ P = 2nb \ sin \ frac {\ pi} {n} $

n — количество ребер (вершин).
$ \ pi = 3,14159265359 $

.

Список формул площади и формул периметра всех геометрических фигур

Формулы измерения: Измерение — это раздел математики, который занимается измерением площади, периметра и объема различных геометрических форм. Это одна из самых важных глав математики в средней школе. Он находит огромное практическое применение в нашей повседневной жизни. По этой причине передовые концепции, связанные с измерением, рассматриваются в более высоких классах. Это также важная тема для конкурсных экзаменов, таких как олимпиады и NTSE.Задачи измерения также задаются на различных государственных экзаменах, таких как SSC, банковское дело, страхование и т. Д. Поэтому важно, чтобы каждый понимал и запоминал различные формулы измерения всех геометрических фигур.

В этой статье мы предоставим вам формулы площади и периметра всех основных геометрических форм, таких как квадрат, прямоугольник, ромб, четырехугольник, круг, эллипс и т. Д.

ВЫБЕРИТЕ ФОРМУЛЫ МАТЕРИАЛОВ ДЛЯ КЛАССА 8 ЗДЕСЬ

Формулы измерения: формулы площади и формулы периметра

Прежде чем попасть в список формул измерения, т.е. формулы площади и формулы периметра всех основных геометрических фигур, давайте взглянем на определение «площадь» и «периметр» .

Что такое площадь геометрической фигуры?

Площадь замкнутой геометрической фигуры — это в основном размер или протяженность двухмерной поверхности фигуры.

Что такое периметр геометрической фигуры?

Периметр замкнутой геометрической фигуры — это общая длина границы фигуры.

Давайте теперь рассмотрим формулы площади и периметра обычных f = геометрических фигур.

Формулы площади общих геометрических фигур

В таблице ниже показаны формулы площади общих геометрических фигур:

Геометрические формы	Формулы площади	Переменные
Площадь квадрата	Площадь = axa = a 2	a = Длина каждой стороны квадрата
Площадь прямоугольника	Площадь = lxb	l = длина прямоугольника b = ширина прямоугольника
Площадь треугольника	Площадь = (bxh) / 2	b = длина основания треугольник h = Высота треугольника
Площадь круга	πr 2	π = 22/7 = 3.14159 (приблизительно) r = Радиус окружности
Площадь параллелограмма	Площадь = bxh	b = Основание параллелограмма h = Высота параллелограмма
Площадь трапеции	Площадь = { (a + b) xh} / 2	a + b = сумма длин двух параллельных сторон трапеции, т. е. основания 1 и основания 2 h = расстояние по перпендикуляру между двумя параллельными сторонами
Площадь ромба	Площадь = (pxq) / 2	p = Длина 1-й диагонали q = Длина второй диагонали pq = Произведение двух диагоналей
Площадь эллипса	Площадь = πab	a = Большой радиус b = Малый радиус

Формулы периметра общих геометрических фигур

Формулы периметра общих геометрических фигур:

Геометрические формы	Формулы периметра	Переменные
Периметр квадрата	Периметр = 4a	a = Длина каждой стороны квадрата
Периметр прямоугольника		Периметр = 2 (l + b)	l = Длина прямоугольника b = Ширина прямоугольника
Периметр треугольника	Периметр = a + b + c	a, b и c — длины трех сторон треугольника
Периметр окружности	Периметр = πd = 2πr	π = 22/7 = 3.14159 (приблизительно) r = радиус окружности d = диаметр окружности
Периметр параллелограмма	Периметр = 2 (l + b)	l = длина параллелограмма b = ширина параллелограмма
Периметр трапеции	Периметр = a + b + c + d	a, b, c, d — длины четырех сторон трапеции
Периметр ромба	Периметр = 4a	a = Длина каждой стороны ромба
Периметр воздушного змея	Периметр = 2a + 2b	a = Длина каждой стороны первой пары b = Длина каждой стороны второй пары

Формулы для дополнительных площадей и параметров

Некоторые дополнительные формулы для расчета площади и периметров приведены ниже:

Площадь треугольника заданных сторон — a, b, c	Площадь = √ [s (s — a) (s — b) (s — c)]	s = Полупериметр треугольник = (a + b + c) / 2
Площадь равнобедренного треугольника	Площадь = (основание x высота) / 2 основание = b высота = √ (a 2 — b 2 /4)	a = Длина каждой из равных сторон равнобедренного треугольника b = Длина основания
Периметр равнобедренного треугольника	Периметр = 2a + b	a = Длина каждой из равных сторон равнобедренного треугольника b = Длина основания
Площадь равностороннего треугольника	Площадь = (√3 xa 2 ) / 4	a = Длина каждой стороны равностороннего треугольника
Периметр равностороннего треугольника	Периметр r = 3a	a = Длина каждой стороны равностороннего треугольника
Периметр полукруга	Периметр = πr + d = 3πr	r = Радиус окружности d = 2r = Диаметр окружности
Площадь полукруга	Площадь = (πr 2 ) x (1/2)	r = Радиус окружности

Итак, теперь вы знаете об общих формулах измерения, которые должны быть у вас под рукой.Запомните их наизусть. Убедитесь, что вы знаете, что означают переменные в формулах площади и формулах периметра. Решите достаточное количество практических вопросов, чтобы освоить приложение.

В Embibe вы можете решать вопросы практики измерения бесплатно:

Часто задаваемые вопросы по периметру и площади

Студенты могут найти некоторые общие часто задаваемые вопросы по теме ниже:

Q1: Какова формула измерения?

Ответ: Измерение обычно называют изучением геометрии, и формулы, которые подпадают под него, включают вычисление площади и периметра различных типов фигур.Список формул можно найти в этой статье.

Q2: Как мы можем запомнить формулы измерения?

Ответ: Лучший способ запомнить формулы измерения — это понять концепции площади и периметра, а затем вы можете использовать таблицы формул, представленные в этой статье. Вы можете либо распечатать страницу, либо добавить ее в закладки, когда вам это нужно.

Q3: Какой самый простой способ выучить формулы измерения?

Ответ: Самый простой способ изучить формулы измерения — это взять распечатку формул, представленных в этой статье, и прикрепить их рядом со своим учебным столом, чтобы вы могли их пересматривать, когда захотите, или вы можете добавить эту страницу в закладки и посетить доработка.

СКАЧАТЬ РЕШЕНИЯ NCERT ДЛЯ МАТЕРИАЛОВ КЛАССА 8 ЗДЕСЬ

Мы надеемся, что этот подробный список формул измерения вам поможет. Если у вас есть какие-либо вопросы, не стесняйтесь спрашивать в разделе комментариев ниже. Мы свяжемся с вами в ближайшее время.

2123 Просмотры.

No related posts.