формулы cos, sin, tg, ctg
Основные формулы тригонометрии — это формулы, устанавливающие связи между основными тригонометрическими функциями. Синус, косинус, тангенс и котангенс связаны между собой множеством соотношений. Ниже приведем основные тригонометрические формулы, а для удобства сгруппируем их по назначению. С использованием данных формул можно решить практически любую задачу из стандартного курса тригонометрии. Сразу отметим, что ниже приведены лишь сами формулы, а не их вывод, которому будут посвящены отдельные статьи.
Основные тождества тригонометрии
Тригонометрические тождества дают связь между синусом, косинусом, тангенсом и котангенсом одного угла, позволяя выразить одну функцию через другую.
Тригонометрические тождестваsin2a+cos2a=1tgα=sinαcosα, ctgα=cosαsinαtgα·ctgα=1tg2α+1=1cos2α, ctg2α+1=1sin2α
Эти тождества напрямую вытекают из определений единичной окружности, синуса (sin), косинуса (cos), тангенса (tg) и котангенса (ctg).
Формулы приведения
Формулы приведения позволяют переходить от работы с произвольными и сколь угодно большими углами к работе с углами в пределах от 0 до 90 градусов.
Формулы приведенияsinα+2πz=sinα, cosα+2πz=cosαtgα+2πz=tgα, ctgα+2πz=ctgαsin-α+2πz=-sinα, cos-α+2πz=cosαtg-α+2πz=-tgα, ctg-α+2πz=-ctgαsinπ2+α+2πz=cosα, cosπ2+α+2πz=-sinαtgπ2+α+2πz=-ctgα, ctgπ2+α+2πz=-tgαsinπ2-α+2πz=cosα, cosπ2-α+2πz=sinαtgπ2-α+2πz=ctgα, ctgπ2-α+2πz=tgαsinπ+α+2πz=-sinα, cosπ+α+2πz=-cosαtgπ+α+2πz=tgα, ctgπ+α+2πz=ctgαsinπ-α+2πz=sinα, cosπ-α+2πz=-cosαtgπ-α+2πz=-tgα, ctgπ-α+2πz=-ctgαsin3π2+α+2πz=-cosα, cos3π2+α+2πz=sinαtg3π2+α+2πz=-ctgα, ctg3π2+α+2πz=-tgαsin3π2-α+2πz=-cosα, cos3π2-α+2πz=-sinαtg3π2-α+2πz=ctgα, ctg3π2-α+2πz=tgα
Формулы приведения являются следствием периодичности тригонометрических функций.
Тригонометрические формулы сложения
Формулы сложения в тригонометрии позволяют выразить тригонометрическую функцию суммы или разности углов через тригонометрические функции этих углов.
sinα±β=sinα·cosβ±cosα·sinβcosα+β=cosα·cosβ-sinα·sinβcosα-β=cosα·cosβ+sinα·sinβtgα±β=tgα±tgβ1±tgα·tgβctgα±β=-1±ctgα·ctgβctgα±ctgβ
На основе формул сложения выводятся тригонометрические формулы кратного угла.
Формулы кратного угла: двойного, тройного и т.д.
Формулы двойного и тройного углаsin2α=2·sinα·cosαcos2α=cos2α-sin2α, cos2α=1-2sin2α, cos2α=2cos2α-1tg2α=2·tgα1-tg2α сtg2α=сtg2α-12·сtgα sin3α=3sinα·cos2α-sin3α, sin3α=3sinα-4sin3αcos3α=cos3α-3sin2α·cosα, cos3α=-3cosα+4cos3αtg3α=3tgα-tg3α1-3tg2αctg3α=ctg3α-3ctgα3ctg2α-1
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать заданиеФормулы половинного угла
Формулы половинного угла в тригонометрии являются следствием формул двойного угла и выражают соотношения между основными функциями половинного угла и косинусом целого угла.
sin2α2=1-cosα2cos2α2=1+cosα2tg2α2=1-cosα1+cosαctg2α2=1+cosα1-cosα
Формулы понижения степени
Формулы понижения степениsin2α=1-cos2α2cos2α=1+cos2α2sin3α=3sinα-sin3α4cos3α=3cosα+cos3α4sin4α=3-4cos2α+cos4α8cos4α=3+4cos2α+cos4α8
Часто при расчетах действовать с громоздктми степенями неудобно.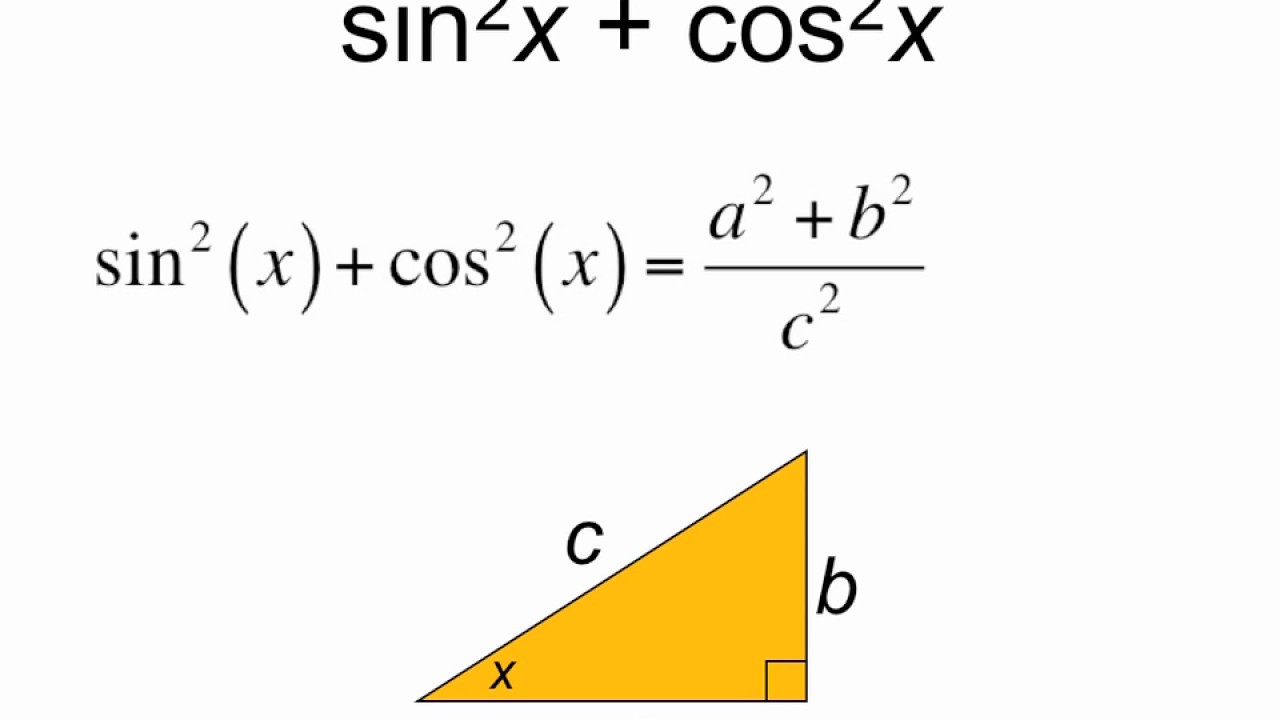 Формулы понижения степени позволяют понизить степень тригонометрической функции со сколь угодно большой до первой. Приведем их общий вид:
Формулы понижения степени позволяют понизить степень тригонометрической функции со сколь угодно большой до первой. Приведем их общий вид:
для четных n
sinnα=Cn2n2n+12n-1∑k=0n2-1(-1)n2-k·Ckn·cos((n-2k)α)cosnα=Cn2n2n+12n-1∑k=0n2-1Ckn·cos((n-2k)α)
для нечетных n
sinnα=12n-1∑k=0n-12(-1)n-12-k·Ckn·sin((n-2k)α)cosnα=12n-1∑k=0n-12Ckn·cos((n-2k)α)
Сумма и разность тригонометрических функций
Разность и сумму тригонометрических функций можно представить в виде произведения. Разложение на множители разностей синусов и косинусов очень удобно применять при решении тригонометрических уравнений и упрощении выражений.
Сумма и разность тригонометрических функцийsinα+sinβ=2sinα+β2·cosα-β2sinα-sinβ=2sinα-β2·cosα+β2cosα+cosβ=2cosα+β2·cosα-β2cosα-cosβ=-2sinα+β2·sinα-β2, cosα-cosβ=2sinα+β2·sinβ-α2
Произведение тригонометрических функций
Если формулы суммы и разности функций позволяют перейти к их произведению, то формулы произведения тригонометрических функций осуществляют обратный переход — от произведения к сумме. Рассматриваются формулы произведения синусов, косинусов и синуса на косинус.
Рассматриваются формулы произведения синусов, косинусов и синуса на косинус.
sinα·sinβ=12·(cos(α-β)-cos(α+β))cosα·cosβ=12·(cos(α-β)+cos(α+β))sinα·cosβ=12·(sin(α-β)+sin(α+β))
Универсальная тригонометрическая подстановка
Все основные тригонометрические функции — синус, косинус, тангенс и котангенс, — могут быть выражены через тангенс половинного угла.
sinα=2tgα21+tg2α2cosα=1-tg2α21+tg2α2tgα=2tgα21-tg2α2ctgα=1-tg2α22tgα2
| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) ) |
|
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | sin(45 град. ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. |
|
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) ) |
|
| 23 | Найти точное значение | arctan(- квадратный корень 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) ) |
|
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) ) |
|
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) ) |
|
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град.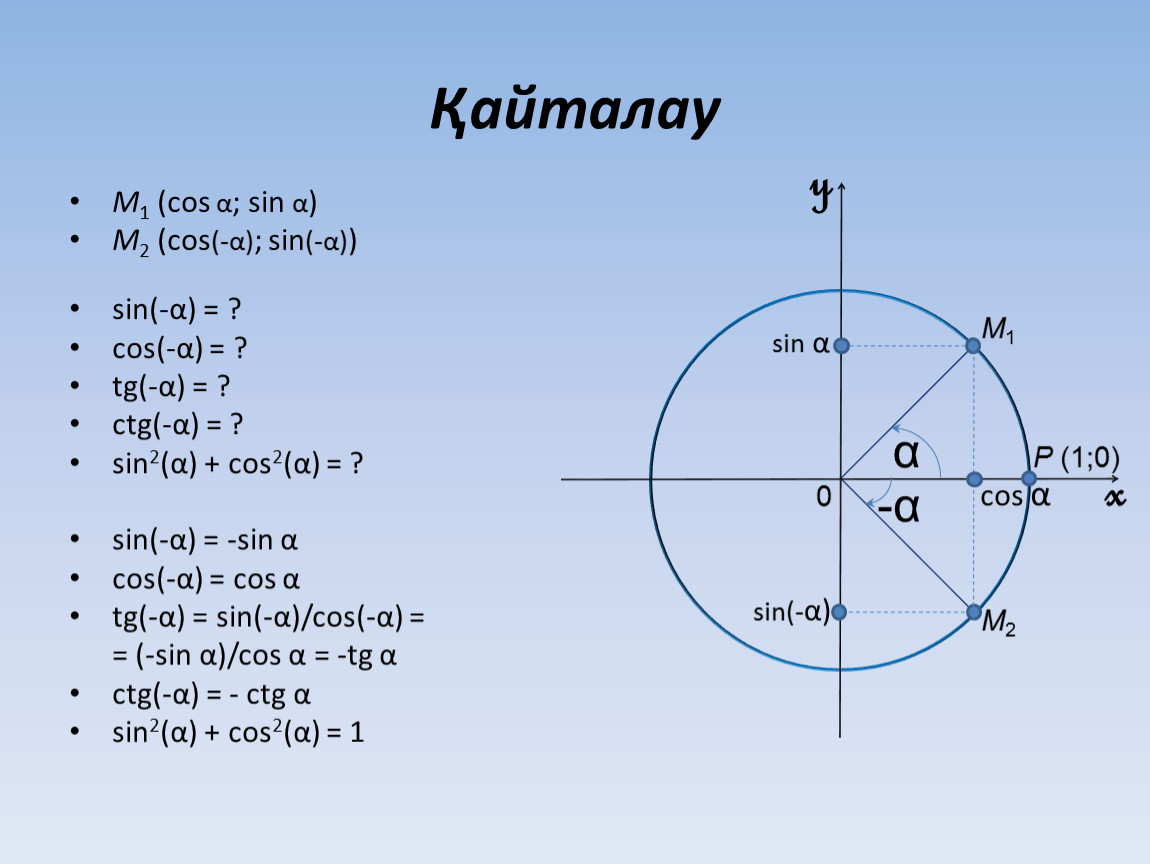 ) ) |
|
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) ) |
|
| 77 | Найти точное значение | arctan(-( квадратный корень 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) ) |
|
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град.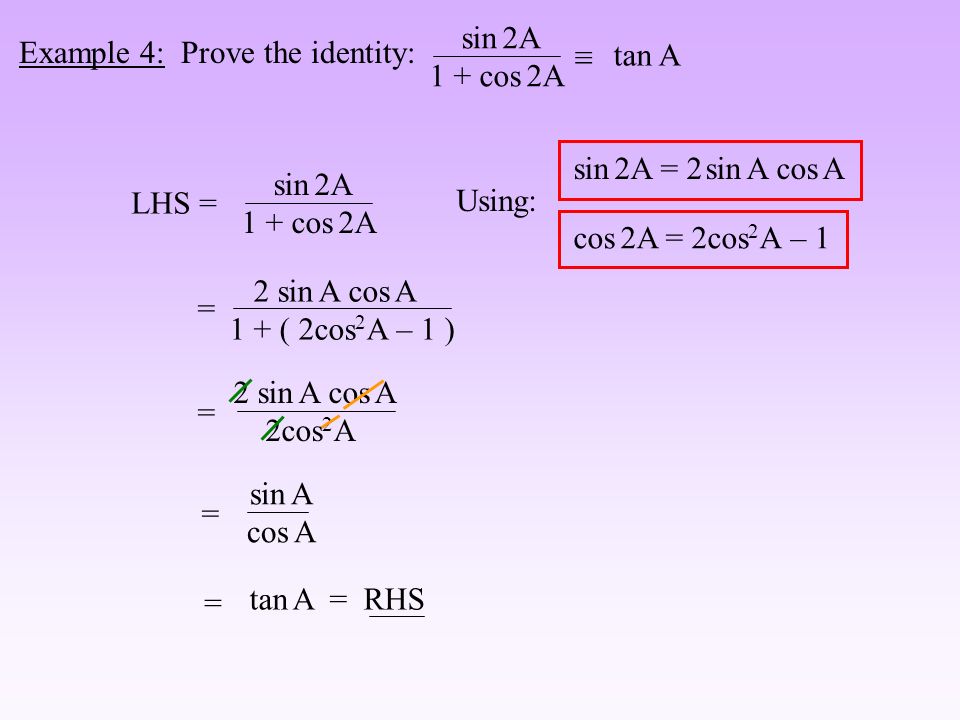 ) ) |
|
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
Четверть числовой окружности
Если посмотреть на числовую окружность, то можно заметить, что оси абсцисс и ординат разбивают ее на четыре части. Эти части называют четвертями и нумеруют в том порядке как их проходят, двигаясь в положительном направлении (против часовой стрелки).
|
\((\)\(\frac{π}{2}\)\(;π)\)- вторая четверть |
\((0;\)\(\frac{π}{2}\)\()\) — первая четверть |
|
|
|
|
|
|
\((π;\)\(\frac{3π}{2}\)\()\) — третья четверть |
\((\)\(\frac{3π}{2}\)\(;2π)\) — четвертая четверть |
Почему так важно определять какой четверти принадлежит угол?
Дело в том, что каждая четверть уникальна в плане знаков тригонометрических функций.
Например, для любого угла из второй четверти — синус положителен, а косинус, тангенс
и котангенс отрицательны. 2a=0,64\)
2a=0,64\)
\(\sina=0,8\) или \(\sina=-0,8\)
У нас два ответа, и оба нам подходят. Но у угла не может быть два синуса! Один лишний! А какой?
Вот тут нам и поможет знание о четвертях: обратите внимание, что у нас в условии есть двойное неравенство \(π<a<\) \(\frac{3π}{2}\), то есть угол \(a\) такой, что больше \(π\), но меньше \(\frac{3π}{2}\).
Значит он лежит в третьей четверти. А в третьей четверти синус отрицателен. Поэтому верный ответ: \(-0,8\).
Ответ: \(\sina=-0,8\).
Про непостоянство четвертей:
Важно понимать, что, например, первой четверти принадлежат не только углы от \(0\) до \(\frac{π}{2}\), но и углы от \(2π\) до \(\frac{5π}{2}\), и от \(4π\) до \(\frac{9π}{2}\), и от \(6π\) до \(\frac{13π}{2}\) и так далее. Ведь как только мы заканчиваем полный оборот – кончается четвертая четверть и опять начинается первая.
Ведь как только мы заканчиваем полный оборот – кончается четвертая четверть и опять начинается первая.
Кроме того, нужно помнить, что углы могут откладываться в отрицательную сторону (по часовой стрелке), и тогда мы попадем в первую четверть только в конце круга. Ведь сначала мы пройдем четвертую четверть, потом в третью и т.д.
|
\((-π;-\)\(\frac{3π}{2}\)\()\)- вторая четверть |
\((-\)\(\frac{3π}{2}\)\(;-2π)\) — первая четверть |
|
|
|
|
|
|
\((-\)\(\frac{π}{2}\)\(;-π)\) — третья четверть |
\((0;-\)\(\frac{π}{2}\)\()\) — четвертая четверть |
Ну и, конечно, мы можем в отрицательную сторону делать обороты, так же как и в положительную.
Смотрите также:
Числовая окружность (шпаргалка)
Тригонометрическая таблица с кругом
Как обозначать точки на числовой окружности
Скачать статью
Тригонометрические выражения и тригонометрические формулы [wiki.eduVdom.com]
subjects:mathematics:тригонометрические_выражения_и_формулы
Отметим на координатной оси Ох справа от точки О точку А и построим окружность с центром в точке О и радиусом ОА (так называемым начальным радиусом).
Окружность с центром в точке О и радиусом ОА
Рис.1
Пусть при повороте на угол a против часовой стрелки начальный радиус ОА переходит в радиус ОВ.
Тогда:
Синусом (sin α) угла α называется отношение ординаты точки В к длине радиуса.
Косинусом (cos α) угла α называется отношение абсциссы точки В к длине радиуса.

Тангенсом (tg α) угла α называется отношение ординаты точки В к ее абсциссе.
Котангенсом (ctg α) угла α называется отношение абсциссы точки В к ее ординате.
Секанс определяется как sec α = 1/(cos α)
Косеканс определяется как cosec α = 1/(sin α)
В западной литературе тангенс, котангенс и косеканс обозначаются tan x, cot x, csc x
Если координаты точки В равны x и y, то:
$$\sin{\alpha} = \frac{y}{R}\;;\; \cos{\alpha} = \frac{x}{R}\;;\; {\rm tg}\, \alpha = \frac{y}{x}\;;\; {\rm ctg}\, \alpha = \frac{x}{y}$$
Таблица значений sin α, cos α, tg α, ctg α
Приведем таблицу значений тригонометрических функций некоторых углов (прочерк сделан, когда выражение не имеет смысла):
| Таблица значений sin α, cos α, tg α, ctg α | ||||||||
| 0º | 30º | 45º | 60º | 90º | 180º | 270º | 360º | |
|---|---|---|---|---|---|---|---|---|
| 0 рад | $\frac{\pi}{6}$ | $\frac{\pi}{4}$ | $\frac{\pi}{3}$ | $\frac{\pi}{2}$ | $\pi$ | $\frac{3\pi}{2}$ | $2\pi$ | |
| $\sin \alpha$ | 0 | $\frac{1}{2}$ | $\frac{\sqrt{2}}{2}$ | $\frac{\sqrt{3}}{2}$ | 1 | 0 | -1 | 0 |
| $\cos \alpha$ | 1 | $\frac{\sqrt{3}}{2}$ | $\frac{\sqrt{2}}{2}$ | $\frac{1}{2}$ | 0 | -1 | 0 | 1 |
| $\textrm{tg}\, \alpha$ | 0 | $\frac{1}{\sqrt{3}}$ | 1 | $\sqrt{3}$ | — | 0 | — | 0 |
| $\textrm{ctg}\, \alpha$ | — | $\sqrt{3}$ | 1 | $\frac{1}{\sqrt{3}}$ | 0 | — | 0 | — |
Свойства sin, cos, tg и ctg
Свойства синуса (sin), косинуса (cos), тангенса(tg) и котангенса(ctg):
Определение знака
Если α-угол I или II координатной четверти, то sin α > 0;
Если α-угол III или IV координатной четверти, то sin α < 0;
Если α-угол I или IV координатной четверти, то cos α > 0;
Если α-угол II или III координатной четверти, то cos α < 0;
Если α-угол I или III координатной четверти, то tg α > 0 и ctg α > 0;
Если α-угол II или IV координатной четверти, то tg α < 0 и ctg α < 0.

Синус, тангенс и котангенс — нечетные функции; косинус — четная функция.
Для чётной функции справедливо равенство: y(-x) = y(x). Примеры чётных функций: y = cos(x), y = x2.
Для НЕчётной функции справедливо равенство: y(-x) = -y(x). Примеры НЕчётных функций: y = sin(x), y = x.
При изменении угла на целое число оборотов значения тригонометрических функций не меняются.
1 радиан — это мера центрального угла, которому соответствует длина дуги, равная длине радиуса окружности.
Связь радианов с градусами: $1° =\frac{\pi}{180}\text{рад; 1 рад }=\frac{180°}{\pi}$.
Основные тригонометрические тождества
Формулы приведения
| X | $\frac{\pi}{2}-\alpha$ | $\frac{\pi}{2}+\alpha$ | $\pi-\alpha$ | $\pi+\alpha$ | $\frac{3\pi}{2}-\alpha$ | $\frac{3\pi}{2}+\alpha$ | $2\pi-\alpha$ | $2\pi+\alpha$ |
|---|---|---|---|---|---|---|---|---|
| sin x | cos α | cos α | sin α | -sin α | -cos α | -cos α | -sin α | sin α |
| cos x | sin α | -sin α | -cos α | -cos α | -sin α | sin α | cos α | cos α |
| tg x | ctg α | -ctg α | -tg α | tg α | ctg α | -ctg α | -tg α | tg α |
| ctg x | tg α | -tg α | -ctg α | ctg α | tg α | -tg α | -ctg α | ctg α |
Формулы сложения
Формулы двойного угла
Формулы двойного угла или двойного аргумента:
Формулы половинного аргумента
Формулы половинного аргумента (для sin и cos — формулы понижения степени):
Формулы суммы и разности
Формулы произведения
Соотношения между sin x, cos x и tg(x/2)
Один из способов использования: свести всё к tg(x/2) и путём замены получить обычное алгебраическое выражение.
Простейшие тригонометрические уравнения
Дополнительно
subjects/mathematics/тригонометрические_выражения_и_формулы.txt · Последние изменения: 2021/03/24 18:37 — ¶
Таблица тригонометрических значений углов: синус, косинус, тангенс, котангенс
Ниже представлена таблица со значениями синусов (sin), косинусов (cos), тангенсов (tg) и котангенсов (ctg) углов от 0 до 360 градусов (или от 0 до 2π).
| α° | α | sin α | cos α | tg α | ctg α |
| 0° | 0 | 0 | 1 | 0 | — |
| 30° | π/6 | 1/2 | √3/2 | 1/√3 | √3 |
| 45° | π/4 | √2/2 | √2/2 | 1 | 1 |
| 60° | π/3 | √3/2 | 1/2 | √3 | 1/√3 |
| 90° | π/2 | 1 | 0 | — | 0 |
| 120° | 2π/3 | √3/2 | -1/2 | -√3 | -1/√3 |
| 135° | 3π/4 | √2/2 | -√2/2 | -1 | -1 |
| 150° | 5π/6 | 1/2 | -√3/2 | -1/√3 | -√3 |
| 180° | π | 0 | -1 | 0 | — |
| 210° | 7π/6 | -1/2 | -√3/2 | 1/√3 | √3 |
| 225° | 5π/4 | -√2/2 | -√2/2 | 1 | 1 |
| 240° | 4π/3 | -√3/2 | -1/2 | √3 | 1/√3 |
| 270° | 3π/2 | -1 | 0 | — | 0 |
| 300° | 5π/3 | -√3/2 | 1/2 | -√3 | -1/√3 |
| 315° | 7π/4 | -√2/2 | √2/2 | -1 | -1 |
| 330° | 11π/6 | -1/2 | √3/2 | -1/√3 | -√3 |
| 360° | 2π | 0 | 1 | 0 | — |
microexcel. ru
ru
Sin Cos Tan: Введение в тригонометрию
На колесе есть две точки, где вы будете находиться на нужной высоте (две красные точки на рисунке). Следовательно, существует два нужных нам угла α
1 и α2. Обратите внимание на два прямоугольных треугольника, выделенных зелёным цветом. Они одинаковые, так как являются зеркальным отображением друг друга. Давайте так же зеркально отобразим правый треугольник, но уже «вверх». Этот треугольник, выделенный красным цветом, имеет гипотенузу равную 1 (радиус колеса) и противолежащий катет (высота над центром) равный 1/2. В силу того, что все три треугольника одинаковые, они имеют одинаковые острые углы. Давайте найдём острый угол красного треугольника, при котором его синус равен 1/2. Поступим также, как древние астрономы, и заглянем в таблицу значений синуса для различных углов. Итак, sin α = 1/2 при = 30°. Интуитивно понятно, что наши три угла и значения их синусов связаны. Но как?
Но как?
Полный круг составляет 360°. Разделим его на четыре четверти по 90° и пронумеруем их. Первая точка находится в третьей четверти. Так как две четверти в общем дают 180°, а угол α = 30°, то искомый угол α 1 = 210°. Нашли первый угол. Вторая точка находится в четвертой четверти. Три четверти в общем дают 270°, но прибавлением 30° тут не отделаешся, так как нужно прибавить угол β, а не угол α. Так как угол α + β= 90°, то угол β = 90°− 30°=60°. И второй искомый угол равен 270°+ 60°=330°. Остался один маленький ньюанс. Помните, как мы говорили о том, что тригонометрические функции описывают повторяющиеся процессы? Если наше колесо не остановится после того, как совершит полный оборот в 360°, то с каждым новым оборотом вы будет проходить через две точки, находящиеся на уровне –1/2. Эти точки определяются простым прибавлением 360° к найденным нами углам.
При этом n – любое целое число, то есть, на нашем примере это количество оборотов колеса. Стоит заметить, что число n может быть и отрицательным, если колесо крутится в обратную сторону.
Стоит заметить, что число n может быть и отрицательным, если колесо крутится в обратную сторону.
Равенстно sin α=−1/2 мы решили. Перейдем к неравенству sin α ≥ −1/2. Если для решения равенства мы нашли значения углов, при которых наша высота над центром колеса равна −1/2, то для решения неравенства нам нужно найти все углы, при которых наша высота больше либо равна −1/2. Помните мы говорили о том, что угол может быть отрицательным? Сейчас нам это пригодится. Определим угол α2 не как 330°, а как −30° (330°−360°) На рисунке эта область выделена зелёным цветом.
Для того, чтобы правильно записать решение неравенства, обратите внимание на рисунок синусоиды и прямой y=−1/2(высота). Нас интересуют области синусоиды, которые выше прямой y=−1/2. На рисунке они заштрихованы красным цветом. Обратите внимание на точки, которые выделяют эти отрезки. Это те же точки, которые мы получили при решении равенства sin α=−1/2 и они повторяются каждые 360°.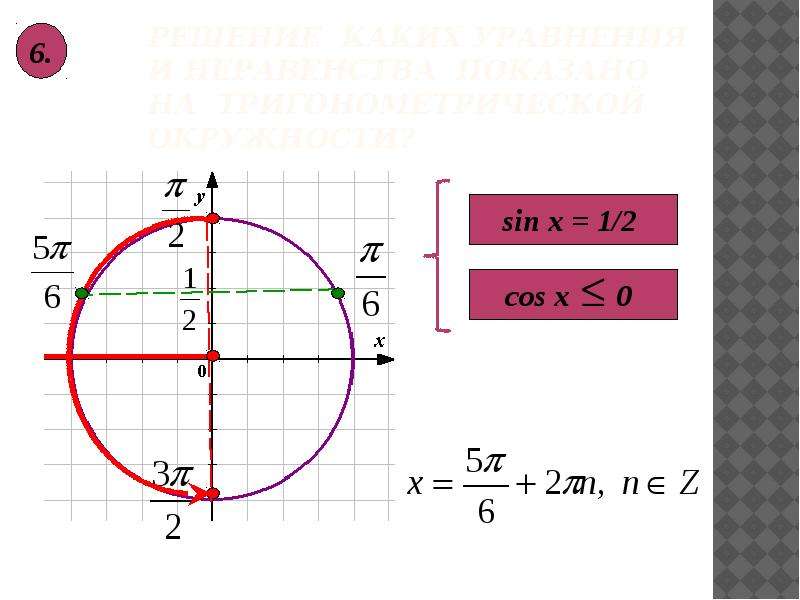 Ответ можно записать так:
Ответ можно записать так:
Дело осталось за малым. Во-первых, вспомнить, что математики обозначают 180° как π, когда записывают формулы с углами, и переписать решение так:
Во-вторых, произвести обратную замену α на 3x − π/4.
Путём нехитрых алгебраических преобразований, а именно прибавления π/4 и деления на 3 ко всем частям неравенства, получаем:
Ответ:
Миссия выполнена! -1x как алгебраическое выражение в x.
Привет, безмятежность!
Это отличная задача! У вас есть: sin (sin -1 x — cos -1 x). Всякий раз, когда у вас есть что-то вроде греха (A — B), часто бывает полезна формула для синуса разности двух углов:
sin (A — B) = sin (A) cos (B) — sin (B) cos (A)
В данном случае имеем:
sin (sin -1 x — cos -1 x) = sin (sin -1 x) cos (cos -1 x) — sin (cos -1 x) cos (sin -1 х)
Выглядит грязно! Во-первых, обратите внимание, что sin (sin -1 x) и cos (cos -1 x) равны x, потому что вы берете обратные функции. Таким образом, оно уменьшено до:
Таким образом, оно уменьшено до:
x * x — sin (cos -1 x) cos (sin -1 x)
Теперь, следующую часть сложно объяснить на этой доске сообщений, но оказывается, что и cos (sin -1 x), и sin (cos -1 x) равны √ (1-x 2 ) . Это * гораздо легче увидеть * на диаграмме, но я включил алгебраическое доказательство внизу вместо рисунка. Итак, вставка √ (1-x 2 ) в то, что у нас есть, дает:
x * x — √ (1-x 2 ) * √ (1-x 2 )
х 2 — (1-х 2 )
2x 2 — 1
Вуаля.Теперь, если вы хотите понять, почему sin (cos -1 x) = √ (1-x 2 ) уродливым способом без рисунка, продолжайте ниже.
======================
Мы пытаемся найти значение A:
A = sin (cos -1 x). Пусть θ = cos -1 x. Тогда, подставляя, получаем A = sin (θ).
Тогда, подставляя, получаем A = sin (θ).
Давайте немного посмотрим на θ = cos -1 x. Это означает, что x = cos (θ).
Но если A = sin (θ) и x = cos (θ), и поскольку sin 2 (θ) + cos 2 (θ) = 1, это означает, что A 2 + x 2 = 1 .Таким образом, A = √ (1-x 2 )
=======================
косинусов
Затем рассмотрим углы 30 ° и 60 °. В прямоугольном треугольнике 30 ° -60 ° -90 ° отношения
сторон равны 1: √3: 2. Отсюда следует, что
sin 30 ° = cos 60 ° = 1/2, и
sin 60 ° = cos 30 ° = √3 / 2.
В прямоугольном треугольнике 30 ° -60 ° -90 ° отношения
сторон равны 1: √3: 2. Отсюда следует, что
sin 30 ° = cos 60 ° = 1/2, и
sin 60 ° = cos 30 ° = √3 / 2.
Эти выводы занесены в эту таблицу.
| Угол | градусов | Радианы | косинус | синус | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 90 ° | π /2 | 0 | /3 | 1/2 | √3 / 2 | |||||||||
| 45 ° | π /4 | √2 / 2 | √2 / 2 | |||||||||||
| π /6 | √3 / 2 | 1/2 | ||||||||||||
| 0 ° | 0 | 1 | 0 |
Упражнения
Все эти упражнения относятся к прямоугольным треугольникам со стандартной маркировкой. 30. b = 2,25 метра и cos A = 0,15. Найдите a и c.
33. b = 12 футов и cos B = 1/3. Найдите c и a.
35. b = 6,4, c = 7,8. Найдите A, и a.
36. A = 23 ° 15 ‘, c = 12.15. Найдите a, и b.
Подсказки
30. Косинус A связывает b с гипотенузой c, , поэтому вы можете сначала вычислить c. Как только вы узнаете b и c, , вы сможете найти a по теореме Пифагора.
33. Вы знаете b и cos B. К сожалению, cos B — это отношение двух сторон, которых вы не знаете, а именно a / c. Тем не менее, это дает вам уравнение, с которым можно работать: 1/3 = a / c. Тогда c = 3 a. Из теоремы Пифагора тогда следует, что a 2 + 144 = 9 a 2 . Вы можете решить это последнее уравнение для a , а затем найти c.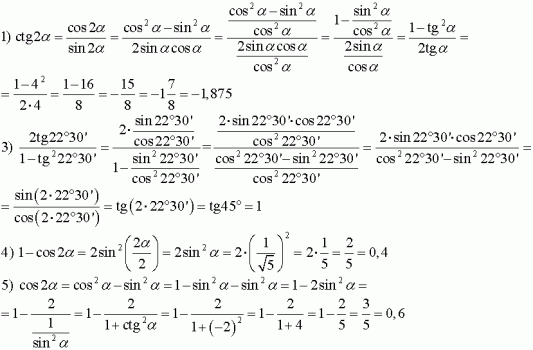
35. b и c дают A, по косинусам и a по теореме Пифагора.
36. A и c дают a по синусам и b по косинусам.
ответы
30. c = b / cos A = 2,25 / 0,15 = 15 метров; a = 14,83 метра.
33. 8 a 2 = 144, поэтому a 2 = 18. Следовательно, a составляет 4,24 ‘или 4’3 дюйма.
c = 3 a , что равно 12.73 ‘или 12’9 «.
35. cos A = b / c = 6,4 / 7,8 = 0,82. Следовательно, A = 34,86 ° = 34 ° 52 ‘, или около 35 °.
a 2 = 7,8 2 — 6,4 2 = 19,9, поэтому a составляет около 4,5.
36. a = c sin A = 12,15 sin 23 ° 15 ‘= 4,796.
b = c cos A = 12,15 cos 23 ° 15 ‘= 11. 17.
17.
Обратные тригонометрические функции
Вы изучили, как тригонометрические функции грех ( Икс ) , потому что ( Икс ) , а также загар ( Икс ) может использоваться, чтобы найти неизвестную длину стороны прямоугольного треугольника, если известны длина одной стороны и величина угла.
В обратные тригонометрические функции грех — 1 ( Икс ) , потому что — 1 ( Икс ) , а также загар — 1 ( Икс ) , используются для нахождения неизвестной меры угла прямоугольного треугольника, когда известны две длины сторон.
Пример 1:
Основание лестницы размещено
3
в футах от
10
-стена высотой до стопы, так чтобы верх лестницы совпадал с верхом стены.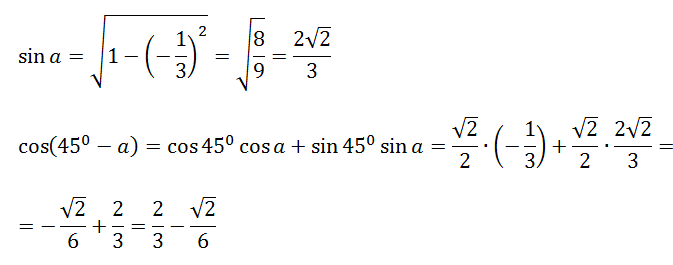 Каков угол между лестницей и землей?
Каков угол между лестницей и землей?
Здесь у нас есть прямоугольный треугольник, длина двух катетов которого нам известна, то есть сторон, противоположных и прилегающих к углу. Итак, мы используем функцию обратной касательной.Если вы введете это значение в калькулятор, установленный в режим «градус», вы получите
загар — 1 ( 10 3 ) ≈ 73,3 °
Если у вас установлен калькулятор в радианах, вы получите
загар — 1 ( 10 3 ) ≈ 1,28
Если вы запомнили отношения длин сторон, которые встречаются в
45
—
45
—
90
а также
30
—
60
—
90
треугольников, вы, вероятно, сможете найти некоторые значения обратных тригонометрических функций без использования калькулятора.
Пример 2:
Находить потому что — 1 ( 3 2 ) .
Вы можете вспомнить, что в 30 — 60 — 90 треугольник, если гипотенуза имеет длину 1 , то длинная нога имеет длину 3 2 . Поскольку косинус — это отношение смежной стороны к гипотенузе, значение обратного косинуса равно 30 ° , или около 0.52 радианы.
потому что — 1 ( 3 2 ) знак равно 30 °
Графики обратных тригонометрических функций
Все тригонометрические функции
периодические функции
. Таким образом, графики ни одного из них не проходят
Горизонтальная линия
Тест и так нет
1
—
к
—
1
. Это означает, что ни у одного из них нет обратного, если только
домен
каждого ограничено, чтобы сделать каждый из них
1
—
к
—
1
.
Это означает, что ни у одного из них нет обратного, если только
домен
каждого ограничено, чтобы сделать каждый из них
1
—
к
—
1
.
Поскольку графики периодические, если мы выберем подходящую область, мы сможем использовать все значения диапазон .
Если мы ограничим область ж ( Икс ) знак равно грех ( Икс ) к [ — π 2 , π 2 ] мы сделали функцию 1 — к — 1 .Диапазон [ — 1 , 1 ] .
(Хотя есть много способов ограничить домен для получения 1 — к — 1 функция это согласованный используемый интервал.)
Обозначим
обратная функция
в виде
у
знак равно
грех
—
1
(
Икс
)
. Читается
у
инверсия синуса
Икс
и означает
у
— угол действительного числа, значение синуса которого равно
Икс
.Будьте осторожны с используемыми обозначениями. Надстрочный индекс «
—
1
”НЕ является показателем. Чтобы избежать этого обозначения, в некоторых книгах используется обозначение
у
знак равно
Arcsin
(
Икс
)
вместо.
Читается
у
инверсия синуса
Икс
и означает
у
— угол действительного числа, значение синуса которого равно
Икс
.Будьте осторожны с используемыми обозначениями. Надстрочный индекс «
—
1
”НЕ является показателем. Чтобы избежать этого обозначения, в некоторых книгах используется обозначение
у
знак равно
Arcsin
(
Икс
)
вместо.
Чтобы построить график, обратный синусоидальной функции, помните, что график — это отражение над линией. у знак равно Икс функции синуса.
Обратите внимание, что домен теперь является диапазоном, а диапазон теперь является доменом.Поскольку домен ограничен, все положительные значения будут давать 1 ул угол квадранта и все отрицательные значения дадут 4 th угол квадранта.
Точно так же мы можем ограничить области определения функций косинуса и касательной, чтобы сделать их
1
—
к
—
1
.
Область определения функции обратного косинуса: [ — 1 , 1 ] и диапазон [ 0 , π ] .Это означает, что положительное значение даст 1 ул угол квадранта и отрицательное значение даст 2 nd угол квадранта.
Область определения функции обратной касательной: ( — ∞ , ∞ ) и диапазон ( — π 2 , π 2 ) .Функция, обратная касательной, даст значения в 1 ул а также 4 th квадранты.
Тот же процесс используется для нахождения обратных функций для остальных тригонометрических функций — котангенса, секанса и косеканса.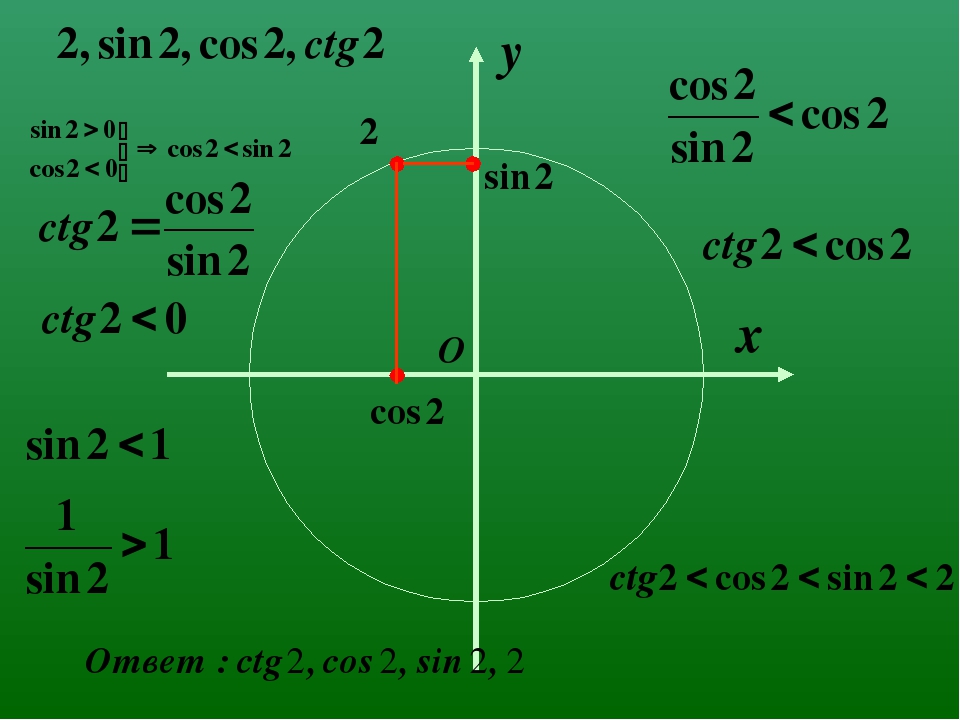
Функция | Домен | Диапазон |
|---|---|---|
грех — 1 ( Икс ) | [ — 1 , 1 ] | [ — π 2 , π 2 ] |
потому что — 1 ( Икс ) | [ — 1 , 1 ] | [ 0 , π ] |
загар — 1 ( Икс ) | ( — ∞ , ∞ ) | ( — π 2 , π 2 ) |
детская кроватка — 1 ( Икс ) | ( — ∞ , ∞ ) | ( 0 , π ) |
сек — 1 ( Икс ) | ( — ∞ , — 1 ] ∪ [ 1 , ∞ ) | [ 0 , π 2 ) ∪ ( π 2 , π ] |
csc — 1 ( Икс ) | ( — ∞ , — 1 ] ∪ [ 1 , ∞ ) | [ — π 2 , 0 ) ∪ ( 0 , π 2 ] |
Тригонометрических идентичностей
| Тригонометрические идентичности |
| (Математика | Триггер | Личности) |
| sin (тета) = кондиционер | csc (theta) = 1 / sin (theta) = c / a |
| cos (тета) = b / c | сек (тета) = 1 / cos (тета) = c / b |
| загар (тета) = грех (тета) / соз (тета) = а / Ь | кроватка (тета) = 1 / загар (тета) = b / a |
sin (-x) = -sin (x)
csc (-x) = -csc (x)
cos (-x) = cos (x)
sec (-x) = sec (x)
tan (-x ) = -тан (x)
детская кроватка (-x) = -колыбельная (x)
| sin ^ 2 (x) + cos ^ 2 (x) = 1 | загар ^ 2 (x) + 1 = сек ^ 2 (x) | детская кроватка ^ 2 (x) + 1 = csc ^ 2 (x) | |
| грех (x y) = sin x cos y cos х грех у | |||
| cos (x y) = cos x уютный грех х грех у | |||
загар (x y) = (загар х загар у) / (1 загар х загар у)
sin (2x) = 2 sin x cos x
cos (2x) = cos ^ 2 (x) — sin ^ 2 (x) = 2 cos ^ 2 (x) — 1 = 1-2 грех ^ 2 (х)
загар (2x) = 2 загар (x) / (1 — загар ^ 2 (x))
sin ^ 2 (x) = 1/2 — 1/2 cos (2x)
cos ^ 2 (x) = 1/2 + 1/2 cos (2x)
sin x — грех y = 2 sin ((x — y) / 2) cos ((x + y) / 2)
cos x — cos y = -2 sin ((x — y) / 2) sin ((x + y) / 2)
| угол | 0 | 30 | 45 | 60 | 90 |
|---|---|---|---|---|---|
| sin ^ 2 (а) | 0/4 | 1/4 | 2/4 | 3/4 | 4/4 |
| cos ^ 2 (а) | 4/4 | 3/4 | 2/4 | 1/4 | 0/4 |
| желто-коричневый ^ 2 (а) | 0/4 | 1/3 | 2/2 | 3/1 | 4/0 |
Данный треугольник abc с углами A, B, C; a противоположно A, b напротив B, c напротив C:
a / sin (A) = b / sin (B) = c / sin (C) (Закон Синусов)
| (Закон косинусов) |
(a — b) / (a + b) = tan [(A-B) / 2] / tan [(A + B) / 2] (Закон касательных)
Обратный косинус и обратный синус
Обратный косинус и обратный синус
Стандартные триггерные функции являются периодическими, то есть они повторяются. Следовательно, одно и то же выходное значение появляется для нескольких входных значений функции. Это делает невозможным построение обратных функций. Для решения уравнений, включающих триггерные функции, обязательно наличие обратных функций. Таким образом, математики должны ограничить функцию триггера, чтобы создать эти инверсии.
Следовательно, одно и то же выходное значение появляется для нескольких входных значений функции. Это делает невозможным построение обратных функций. Для решения уравнений, включающих триггерные функции, обязательно наличие обратных функций. Таким образом, математики должны ограничить функцию триггера, чтобы создать эти инверсии.
Чтобы определить обратную функцию, исходная функция должна быть взаимно однозначно . Для существования взаимно однозначного соответствия (1) каждое значение в домене должно соответствовать ровно одному значению в диапазоне, и (2) каждое значение в диапазоне должно соответствовать ровно одному значению в домене.Первое ограничение распространяется на все функции; второй нет. Например, синусоидальная функция не удовлетворяет второму ограничению, поскольку одно и то же значение в диапазоне соответствует многим значениям в домене (см. Рисунок 1).
Рисунок 1
Функция синуса не является взаимно однозначной.
Чтобы определить обратные функции для синуса и косинуса, области этих функций ограничены. Ограничение, которое накладывается на значения области значений функции косинуса, составляет 0 ≤ x ≤ π (см. Рисунок 2).Эта ограниченная функция называется косинусом. Обратите внимание на заглавную букву «C» в косинусе.
Рисунок 2
График функции ограниченного косинуса.
Функция обратного косинуса определяется как функция, обратная ограниченной функции косинуса Cos −1 (cos x ) = x ≤ x ≤ π. Следовательно,
Рисунок 3
График функции обратного косинуса.
Тождества для косинуса и обратного косинуса:
Развитие функции обратного синуса аналогично развитию функции косинуса. Ограничение, которое накладывается на значения домена синусоидальной функции, составляет
. Эта ограниченная функция называется синусом (см. Рисунок 4). Обратите внимание на заглавную букву «S» в синусе.
Рисунок 4). Обратите внимание на заглавную букву «S» в синусе.
Рисунок 4
График ограниченной синусоидальной функции.
Обратная функция синуса (см. Рисунок 5) определяется как обратная функция ограниченной синусоиды y = Sin x ,
Рисунок 5
График функции обратной синусоиды.
Следовательно,
Идентичности для синуса и обратного синуса:
Графики функций y = Cos x и y = Cos −1 x являются отражениями друг друга относительно линии y = x . Графики функций y = Sin x и y = Sin −1 x также являются отражениями друг друга относительно линии y = x (см. Рисунок 6).
Рисунок 6
Симметрия обратных синуса и косинуса.
Пример 1: Используя рисунок 7, найдите точное значение Cos −1 .
Рисунок 7
Чертеж для примера 1.
Таким образом, y = 5π / 6 или y = 150 °.
Пример 2: Используя рисунок 8, найдите точное значение Sin −1 .
Рисунок 8
Рисунок для примера 2.
Таким образом, y = π / 4 или y = 45 °.
Пример 3: Найдите точное значение cos (Cos −1 0,62).
Используйте тождество косинус-обратный косинус:
Обратный синус, косинус и тангенс. Как SOHCAHTOA может рассчитывать углы. Как использовать эти функции …
Обратный путь SOHCAHTOA против суммы внутренних углов
Сравните этот метод с проверенной теоремой о том, что сумма внутренних углов треугольника равна 180 °.
Что такое степень измерения LNM?
Внутренний угол Sum Way Поскольку общая величина внутренних углов треугольника составляет 180 градусов, мы можем проверить меру LNM.
180 ° -16 ° — 90 ° = 74 °
В качестве альтернативы, вы можете использовать инверсию одной из функций SOHCAHTOA, в данном случае инверсию синуса (sin -1 )! Чтобы найти угол прямоугольного треугольника, нам нужно знать только длину двух сторон! Затем используйте те же соотношения SOHCAHTOA — только по-другому См. Пример ниже.
Обратный путь SOHCAHTOAsin -1 (73,24 / 76,19) = 74 °
YouTube Vid: как рассчитать обратный SOHCAHTOA
Хорошее видео о том, как использовать ваш TI-Graphing Calculator для вычисления обратного синуса, косинуса или тангенса.
Сравните синус с обратным синусом.
Общая разница: синус — это отношение двух фактических сторон прямоугольного треугольника (противоположная гипотенуза ) грех (B) = AC / ABИнверсия или sin -1 — это операция, которая использует те же две стороны прямоугольного треугольника , что и синус (противоположный гипотенузе), чтобы найти меру угла (в данном случае b) sin -1 (AC / AB) = Измерьте угла B
Ключевое различие : Хотя и синус, и обратный синус включают противоположную сторону и гипотенузу прямоугольного треугольника, результаты этих двух операций очень, очень разные.Одна операция (синус) находит соотношение этих двух сторон; другая операция, инверсия синуса, фактически вычисляет величину угла (B в приведенном выше примере) с использованием противоположной стороны и гипотенузы.
Задача 1
Используйте обратный синус, косинус или тангенс, чтобы вычислить меру затененного угла слева.
Измерение угла
Задача 2
Используйте обратный синус, косинус или тангенс, чтобы вычислить меру затененного угла слева.
Измерение углаЗадача 3
Какова мера заштрихованного угла слева?
Измерение углаЗадача 4
Поскольку вы знаете все 3 стороны, вы можете использовать любое из следующего:
= sin -1 (7/25) = 16. 3 °
3 ° = cos -1 (6/15) = 16,3 °
= tan -1 (7/24) = 16,3 °
Задача 5
Поскольку вы знаете все 3 стороны, вы можете использовать любое из следующего:
= sin -1 (8/10) = 53.13 °= cos -1 (6/10) = 53,13 °
= tan -1 (8/6) = 53,13 °
Пример 2.
 1, 11 — Найдите значение tan-1 (1) + cos-1 (-1/2) + sin-1 (-1/2)
1, 11 — Найдите значение tan-1 (1) + cos-1 (-1/2) + sin-1 (-1/2)Последнее обновление: 12 мая 2021 г., Teachoo
Выписка
Пр. 2.1, 11 (метод 1)
Найдите значение tan − 1 (1) + cos − 1 (−1/2) + sin-1 (−1/2) Решение tan − 1 (1) Пусть y = tan − 1 (1)
загар у = 1
загар у = загар (𝝅 / 𝟒)
∴ y = 𝝅 / 𝟒 Поскольку диапазон tan − 1 равен (−π / 2, π / 2)
Следовательно, главное значение 𝝅 / 𝟒 Решение cos − 1 ((−𝟏) / 𝟐) Пусть y = cos − 1 ((−1) / 2) у = 𝜋 — cos − 1 (1/2)
у = 𝜋 — 𝝅 / 𝟑
у = 𝟐𝝅 / 𝟑
Поскольку диапазон cos − 1 равен [0, 𝜋]
Следовательно, главное значение равно 2π / 3 Мы знаем это
cos − 1 (−x) = 𝜋 — cos −1 x
Поскольку cos 𝜋 / 3 = 1/2
𝜋 / 3 = cos − 1 (1/2) Решение sin − 1 ((−𝟏) / 𝟐) Пусть y = sin − 1 ((−1) / 2) у = — грех − 1 (1/2)
у = (−𝝅) / 𝟔 Поскольку диапазон sin − 1 находится между [(−𝜋) / 2 «,» 𝜋 / 2]
Следовательно, главное значение равно (−𝝅) / 𝟔
Мы знаем это
sin − 1 (−x) = — грех − 1 x
Поскольку sin 𝜋 / 6 = 1/2
𝜋 / 6 = грех − 1 (1/2)
Теперь у нас есть
tan − 1 (1) = π / 4, cos − 1 ((−1) / 2) = 2π / 3, sin − 1 ((−1) / 2) = (−π) / 6 Находка
tan − 1 (1) + cos − 1 ((−𝟏) / 𝟐) + sin − 1 ((−𝟏) / 𝟐)
= π / 4 + 2π / 3 — π / 6
= (3 × π + 4 × (2π) — 2 (π)) / 12
= (3π + 8π — 2π) / 12
= 9π / 12
= 𝟑𝛑 / 𝟒
Пр. 2.1, 11 (метод 2)
Найдите значение tan − 1 (1) + cos − 1 (−1/2) + sin-1 (−1/2) Решение tan − 1 (1) Пусть y = tan − 1 (1)
загар у = 1
загар у = загар (𝝅 / 𝟒)
∴ y = 𝝅 / 𝟒 Поскольку диапазон tan − 1 равен (−π / 2, π / 2)
Следовательно, главное значение 𝝅 / 𝟒 Решение cos − 1 ((−𝟏) / 𝟐) Пусть y = cos − 1 ((−1) / 2)
cos y = (−1) / 2
cos y = cos (𝟐𝝅 / 𝟑) Поскольку диапазон cos − 1 равен [0, 𝜋] Следовательно, главное значение равно 2π / 3. Грубый
Мы знаем это
cos 60 ° = 1/2
θ = 60 ° = 60 × 𝜋 / 180 = 𝜋 / 3 Поскольку (−1) / 2 отрицательно
Главное значение — θ
я.е. π −𝜋 / 3 = 2𝜋 / 3 Решение sin − 1 ((−𝟏) / 𝟐) Пусть y = sin − 1 ((−1) / 2)
грех у = (-1) / 2
грех у = грех ((−𝝅) / 𝟔) Поскольку диапазон sin − 1 находится между [(−𝜋) / 2 «,» 𝜋 / 2] Следовательно, главное значение равно (−𝝅) / 𝟔
Грубый
Мы знаем это
грех 30 ° = 1/2
θ = 30 ° = 30 × 𝜋 / 180 = 𝜋 / 6 Поскольку (−1) / 2 отрицательно
Главное значение — −θ, т.е.
2.1, 11 (метод 2)
Найдите значение tan − 1 (1) + cos − 1 (−1/2) + sin-1 (−1/2) Решение tan − 1 (1) Пусть y = tan − 1 (1)
загар у = 1
загар у = загар (𝝅 / 𝟒)
∴ y = 𝝅 / 𝟒 Поскольку диапазон tan − 1 равен (−π / 2, π / 2)
Следовательно, главное значение 𝝅 / 𝟒 Решение cos − 1 ((−𝟏) / 𝟐) Пусть y = cos − 1 ((−1) / 2)
cos y = (−1) / 2
cos y = cos (𝟐𝝅 / 𝟑) Поскольку диапазон cos − 1 равен [0, 𝜋] Следовательно, главное значение равно 2π / 3. Грубый
Мы знаем это
cos 60 ° = 1/2
θ = 60 ° = 60 × 𝜋 / 180 = 𝜋 / 3 Поскольку (−1) / 2 отрицательно
Главное значение — θ
я.е. π −𝜋 / 3 = 2𝜋 / 3 Решение sin − 1 ((−𝟏) / 𝟐) Пусть y = sin − 1 ((−1) / 2)
грех у = (-1) / 2
грех у = грех ((−𝝅) / 𝟔) Поскольку диапазон sin − 1 находится между [(−𝜋) / 2 «,» 𝜋 / 2] Следовательно, главное значение равно (−𝝅) / 𝟔
Грубый
Мы знаем это
грех 30 ° = 1/2
θ = 30 ° = 30 × 𝜋 / 180 = 𝜋 / 6 Поскольку (−1) / 2 отрицательно
Главное значение — −θ, т.е.


