Площадь параллелограмма s. Периметр и площадь параллелограмма
Площадь геометрической фигуры — численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.
Формулы площади треугольника
- Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты - Формула площади треугольника по трем сторонам и радиусу описанной окружности
- Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности. где S — площадь треугольника,
— длины сторон треугольника,
— высота треугольника,
— угол между сторонами и,
— радиус вписанной окружности,
R — радиус описанной окружности,
Формулы площади квадрата
- Формула площади квадрата по длине стороны
Площадь квадрата равна квадрату длины его стороны.
- Формула площади квадрата по длине диагонали
Площадь квадрата равна половине квадрата длины его диагонали.S = 1 2 2 где S — Площадь квадрата,
— длина стороны квадрата,
— длина диагонали квадрата.
Формула площади прямоугольника
- Площадь прямоугольника равна произведению длин двух его смежных сторон
где S — Площадь прямоугольника,
— длины сторон прямоугольника.
Формулы площади параллелограмма
- Формула площади параллелограмма по длине стороны и высоте
Площадь параллелограмма - Формула площади параллелограмма по двум сторонам и углу между ними
Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.a · b · sin α
где S — Площадь параллелограмма,
— длины сторон параллелограмма,
— длина высоты параллелограмма,
— угол между сторонами параллелограмма.
Формулы площади ромба
- Формула площади ромба по длине стороны и высоте
Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты. - Формула площади ромба по длине стороны и углу
Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба. - Формула площади ромба по длинам его диагоналей
Площадь ромба равна половине произведению длин его диагоналей. где S — Площадь ромба,
— длина стороны ромба,
— длина высоты ромба,
— угол между сторонами ромба,
Формулы площади трапеции
- Формула Герона для трапеции
Где S — Площадь трапеции,
— длины основ трапеции,
— длины боковых сторон трапеции,
Параллелограмм представляет собой четырехугольную фигуру, у которой противолежащие стороны попарно параллельны и попарно равны.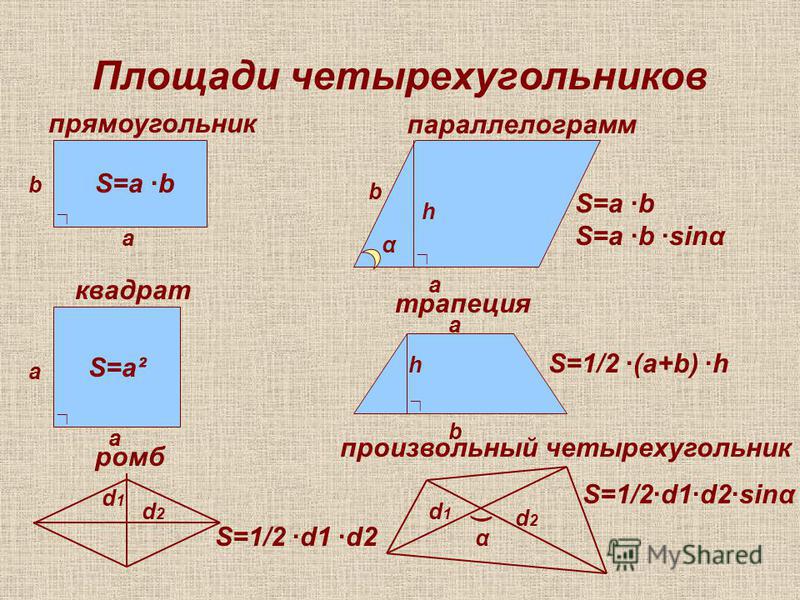
Равны у него также и противоположные углы, а точка пересечения диагоналей параллелограмма делит их пополам, являясь при этом центром симметрии фигуры. Частными случаями параллелограмма являются такие геометрические фигуры как квадрат, прямоугольник и ромб. Площадь параллелограмма может быть найдена различными способами, в зависимости от того, какими исходными данными сопровождается постановка задачи.
Ключевой характеристикой параллелограмма, очень часто используемой при нахождении его площади, является высота. Высотой параллелограмма принято называть перпендикуляр, опущенный из произвольной точки противоположной стороны к отрезку прямой, образующей данную сторону.
- В самом простом случае площадь параллелограмма определяется как произведение его основания на высоту.
S = DC ∙ h
где S — площадь параллелограмма;
a — основание;
h — высота, проведенная к данному основанию.Данную формулу очень легко понять и запомнить, если взглянуть на следующий рисунок.
Как видно из данного изображения, если слева от параллелограмма отрезать воображаемый треугольник и присоединить его справа, то в результате мы получим прямоугольник. А как известно, площадь прямоугольника находится перемножением его длины на высоту. Только в случае параллелограмма длина будет являться основанием, а высота прямоугольника — высотой параллелограмма, опущенной на данную сторону.
- Площадь параллелограмма может быть также найдена в результате перемножения длин двух смежных оснований и синуса угла между ними:
где AD, AB — смежные основания, образующие точку пересечения и угол а между собой;
α — угол между основаниями AD и AB. - Также площадь параллелограмма можно найти разделив пополам произведение длин диагоналей параллелограмма на синус угла между ними.
S = ½∙AC∙BD∙sinβ
где AC, BD — диагонали параллелограмма;
β — угол между диагоналями. - Существует также формула для нахождения площади параллелограмма через радиус вписанной в него окружности. Она записывается следующий образом:
Она записывается следующий образом:Параллелограммом называют четырехугольник у которого противоположные стороны параллельны между собой. Основные задачи в школе по данной теме заключаются в вычислении площади параллелограмма, его периметра, высоты, диагоналей. Указанные величины и формулы для их вычисления будут приведены ниже.
Свойства параллелограмма
Противоположные стороны параллелограмма как и противоположные углы равны между собой:
AB=CD, BC=AD
,
Диагонали параллелограмма в точке пересечения делятся на две равные части:
АО=OC, OB=OD.
Углы прилегающие к любой стороне (соседние углы) в сумме равны 180 градусов.
Каждая из диагоналей параллелограмма делит его на два одинаковые по площади и геометрическими размерами треугольники.
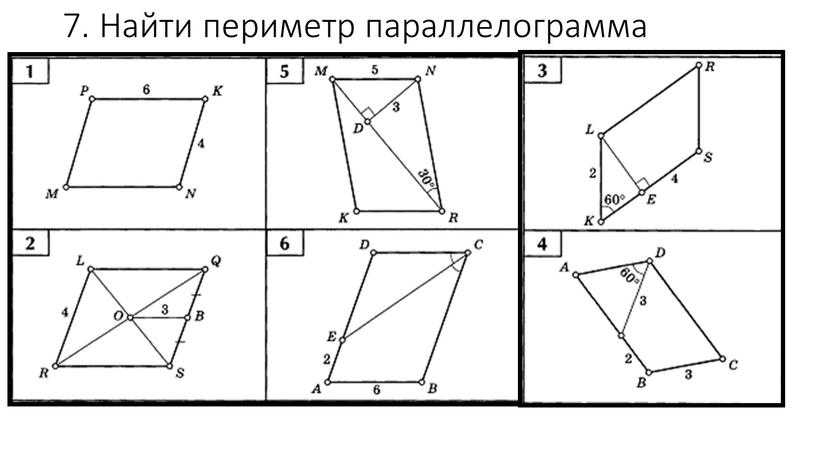
Еще одно замечательное свойство которое часто применяют при решении задач состоит в том, что сумма квадратов диагоналей в параллелограмме равна сумме квадратов всех сторон:
AC^2+BD^2=2*(AB^2+BC^2)
.
Основные признаки параллелограммов:
1. Четырехугольник у которого противоположные стороны попарно параллельны является параллелограммом.
2. Четырехугольник с равными противоположными сторонами является параллелограммом.
3. Четырехугольник с равными и параллельными противоположными сторонами является параллелограммом.
4. Если диагонали четырехугольника в точке пересечения делятся пополам то это параллелограмм.
5. Четырехугольник у которого противоположные углы попарно равны является параллелограммом
Биссектрисы параллелограмма
Биссектрисы противоположных углов в параллелограмме могут быть параллельными или совпадать.
Биссектрисы соседних углов (прилегающие к одной стороне) пересекаются под прямым углом (перпендикулярные).
Высота параллелограмма
Высота параллелограмма — это отрезок который проведен с угла перпендикулярно к основанию. Из этого следует что из каждого угла можно провести две высоты.
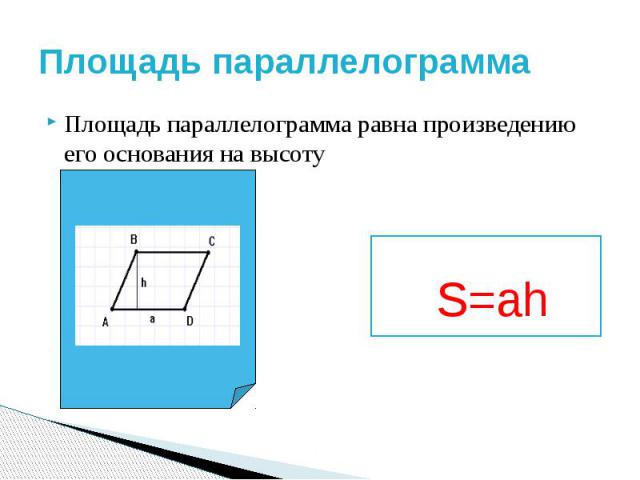
Формула площади параллелограмма
Площадь параллелограмма
равна произведению стороны на высоту проведенную к ней.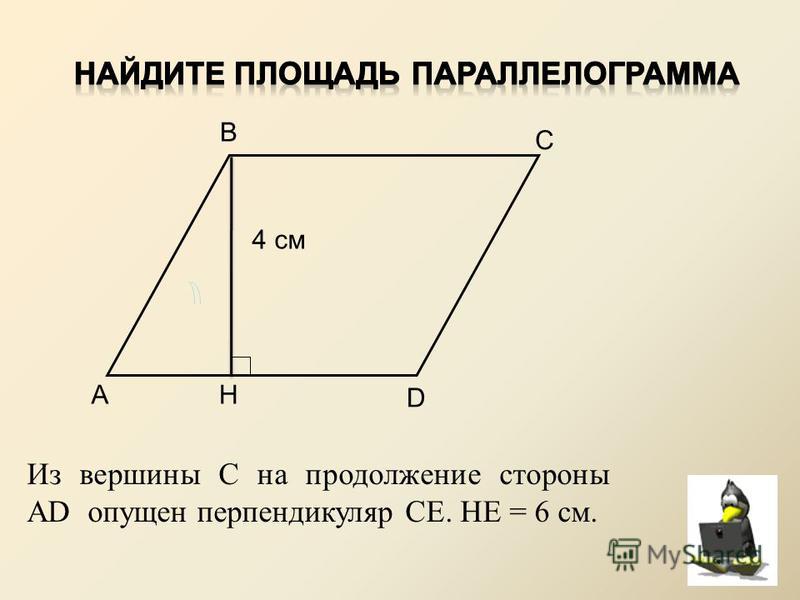
Формула площади следующая
Вторая формула не менее популярная при вычислениях и определяется так: площадь параллелограмма равна произведению соседних сторон на синус угла между ними
На основе приведенных формул Вы будете знать как вычислить площадь параллелограмма.
Периметр параллелограмма
Формула для вычисления периметру параллелограмма имеет вид
то есть периметр равен удвоенному значению суммы сторон. Задачи на параллелограмм будут рассмотрены в соседних материалах, а пока изучайте формулы. Большинство задач по вычислению сторон, диагоналей параллелограмма достаточно просты и сводятся к знанию теоремы синусов и теоремы Пифагора.
Площадь параллелограмма. В очень многих задачах по геометрии связанных с вычислением площадей, в том числе и заданиях на ЕГЭ, используются формулы площади параллелограмма и треугольника. Их существует несколько, здесь мы их с вами рассмотрим.
Перечислять эти формулы было бы слишком просто, этого добра и так хватает в справочниках и на различных сайтах.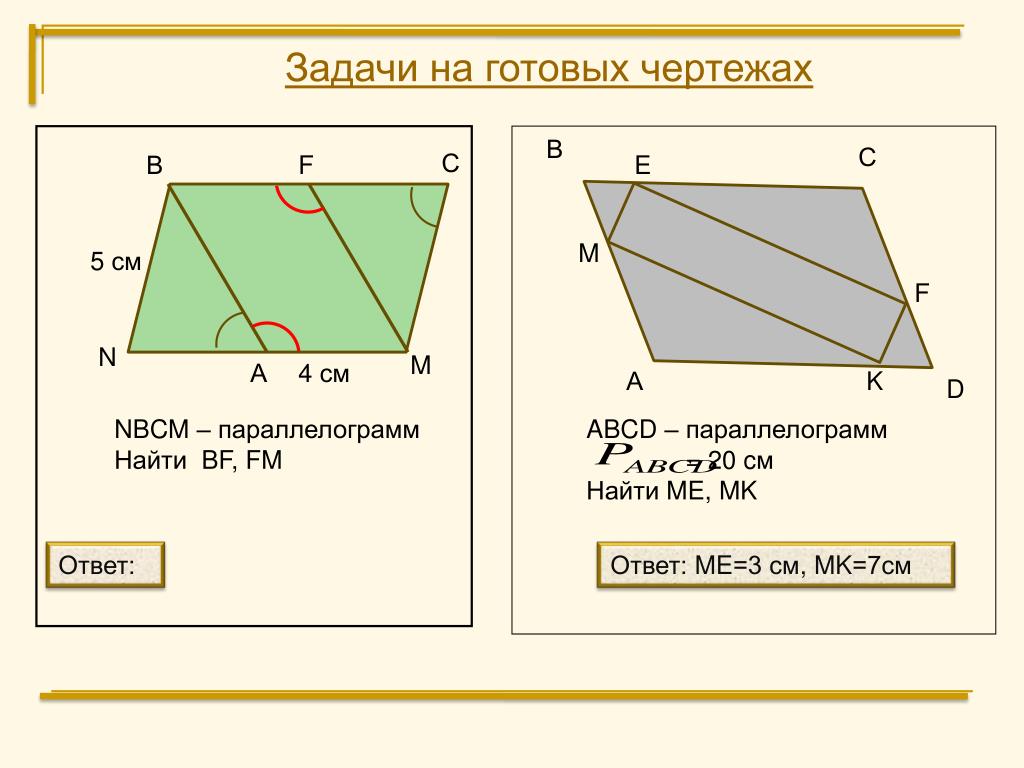
Мне хотелось бы донести суть — чтобы вы их не зубрили, а понимали и легко могли вспомнить в любой момент. После изучения материала статьи вы поймёте, что формулы эти учить совсем не нужно. Объективно говоря, они так часто встречаются при решениях, что откладываются в памяти надолго.
1. Итак, давайте рассмотрим параллелограмм. Определение гласит:
Почему так? Всё просто! Чтобы показать наглядно в чём смысл формулы, выполним некоторые дополнительные построения, а именно построим высоты:
Площадь треугольника (2) равна площади треугольника (1) — второй признак равенства прямоугольных треугольников «по катету и гипотенузе». Теперь мысленно «отрежем» второй и перенесём его наложив на первый — получим прямоугольник, площадь которого будет равна площади исходного параллелограмма:
Площадь прямоугольника, как известно, равна произведению его соседних сторон. Как видно по эскизу, одна сторона полученного прямоугольника равна стороне параллелограмма, а другая его высоте параллелограмма.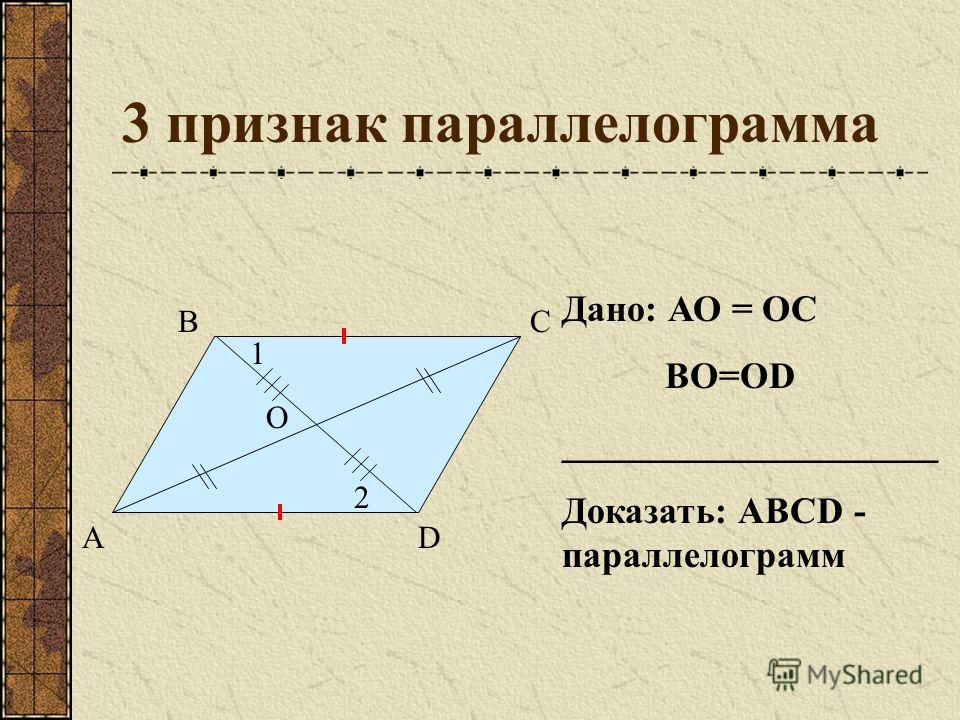
Поэтому и получаем формулу площади параллелограмма S = a∙h
a
2. Продолжим, ещё одна формула его площади. Имеем:
Площадь параллелограмма формула
Обозначим стороны как a и b, угол между ними γ «гамма», высота h a. Рассмотрим прямоугольный треугольник:
Параллелограмм – это четырехугольник, у которого стороны попарно параллельны.
В этой фигуре противоположные стороны и углы равны между собой. Диагонали параллелограмма пересекаются в одной точке и делятся ей пополам. Формулы площади параллелограмма позволяют найти значение через стороны, высоту и диагонали. Параллелограмм также может быть представлен в частных случаях. Ими считаются прямоугольник, квадрат и ромб.
Для начала рассмотрим пример расчета площади параллелограмма по высоте и стороне, к которой она опущена.
Этот случай считается классическим и не требует дополнительного разбирательства. Лучше рассмотрим формулу вычисления площади через две стороны и угол между ними.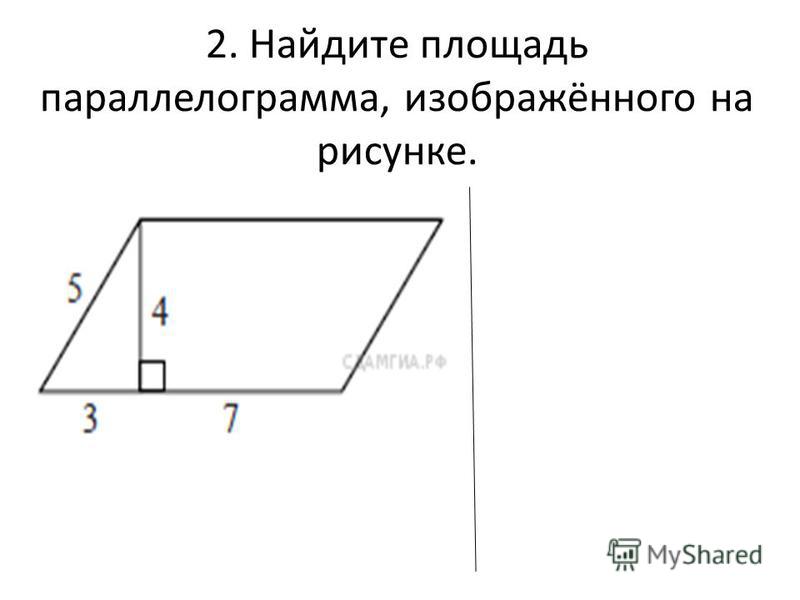
Этот же способ применяется в расчете . Если даны стороны и угол между ними, то площадь рассчитывается так:
Допустим, дан параллелограмм со сторонами a
= 4 см, b
= 6 см. Угол между ними α
= 30°. Найдем площадь:
Площадь параллелограмма через диагонали
Формула площади параллелограмма через диагонали позволяет быстро найти значение.
Для вычислений понадобится величина угла, расположенного между диагоналями.
Рассмотрим пример расчета площади параллелограмма через диагонали. Пусть дан параллелограмм с диагоналями D
= 7 см, d
= 5 см. Угол, лежащий между ними α
=30°. Подставим данные в формулу:
Пример расчета площади параллелограмма через диагональ дал нам прекрасный результат – 8,75.
Зная формулу площади параллелограмма через диагональ можно решать множество интересных задач. Давайте рассмотрим одну из них.
Задача: Дан параллелограмм с площадью 92 кв. см. Точка F
расположена на середине его стороны ВС
. Давайте найдем площадь трапеции ADFB
, которая будет лежать в нашем параллелограмме.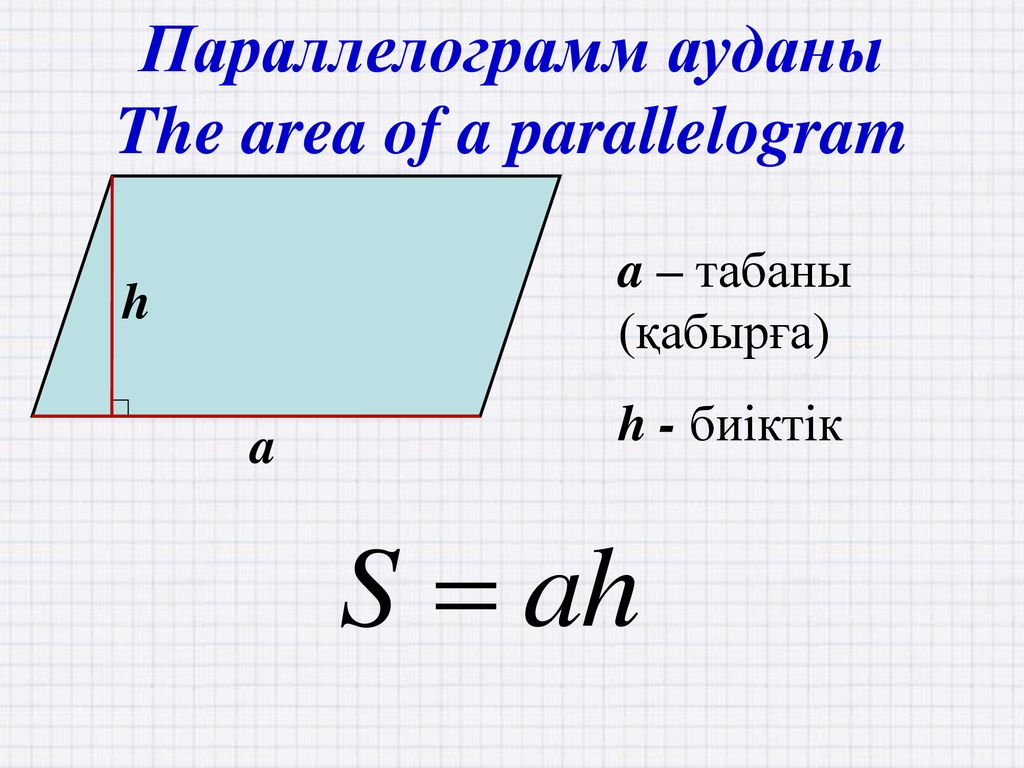
Для начала нарисуем все, что получили по условиям.
Приступаем к решению:
По нашим условиям ah
=92, а соответственно, площадь нашей трапеции будет равняться
Как найти площадь параллелограмма abcd формула. Периметр и площадь параллелограмма
Площадь геометрической фигуры — численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.
Формулы площади треугольника
- Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты - Формула площади треугольника по трем сторонам и радиусу описанной окружности
- Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности. где S — площадь треугольника,
— длины сторон треугольника,
— высота треугольника,
— угол между сторонами и,
— радиус вписанной окружности,
R — радиус описанной окружности,
Формулы площади квадрата
- Формула площади квадрата по длине стороны
Площадь квадрата равна квадрату длины его стороны. - Формула площади квадрата по длине диагонали
Площадь квадрата равна половине квадрата длины его диагонали.S =1 2 2 где S — Площадь квадрата,
— длина стороны квадрата,
— длина диагонали квадрата.
Формула площади прямоугольника
- Площадь прямоугольника равна произведению длин двух его смежных сторон
где S — Площадь прямоугольника,
— длины сторон прямоугольника.
Формулы площади параллелограмма
- Формула площади параллелограмма по длине стороны и высоте
Площадь параллелограмма - Формула площади параллелограмма по двум сторонам и углу между ними
Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.a · b · sin α
где S — Площадь параллелограмма,
— длины сторон параллелограмма,
— длина высоты параллелограмма,
— угол между сторонами параллелограмма.
Формулы площади ромба
- Формула площади ромба по длине стороны и высоте
Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты. - Формула площади ромба по длине стороны и углу
Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба. - Формула площади ромба по длинам его диагоналей
Площадь ромба равна половине произведению длин его диагоналей. где S — Площадь ромба,
— длина стороны ромба,
— длина высоты ромба,
— угол между сторонами ромба,
1 , 2 — длины диагоналей.
Формулы площади трапеции
- Формула Герона для трапеции
Где S — Площадь трапеции,
— длины основ трапеции,
— длины боковых сторон трапеции,
Как в евклидовой геометрии точка и прямая — главные элементы теории плоскостей, так и параллелограмм является одной из ключевых фигур выпуклых четырехугольников. Из него, как нитки из клубка, втекают понятия «прямоугольника», «квадрата», «ромба» и других геометрических величин.
Вконтакте
Определение параллелограмма
Выпуклый четырехугольник, состоящий из отрезков, каждая пара из которых параллельна, известен в геометрии как параллелограмм.
Как выглядит классический параллелограмм изображает четырехугольник ABCD. Стороны называются основаниями (AB, BC, CD и AD), перпендикуляр, проведенный из любой вершины на противоположную этой вершине сторону, — высотой (BE и BF), линии AC и BD — диагоналями.
Внимание! Квадрат, ромб и прямоугольник — это частные случаи параллелограмма.
Стороны и углы: особенности соотношения
Ключевые свойства, по большому счету, предопределены самим обозначением , их доказывает теорема. Эти характеристики следующие:
- Стороны, которые являются противоположными, — попарно одинаковые.
- Углы, расположенные противоположно друг другу — попарно равны.
Доказательство: рассмотрим ∆ABC и ∆ADC, которые получаются вследствие разделения четырехугольника ABCD прямой AC. ∠BCA=∠CAD и ∠BAC=∠ACD, поскольку AC для них общая (вертикальные углы для BC||AD и AB||CD, соответственно). Из этого следует: ∆ABC = ∆ADC (второй признак равенства треугольников).
Отрезки AB и BC в ∆ABC попарно соответствуют линиям CD и AD в ∆ADC, что означает их тождество: AB = CD, BC = AD. Таким образом, ∠B соответствует ∠D и они равны. Так как ∠A=∠BAC+∠CAD, ∠C=∠BCA+∠ACD, которые так же попарно одинаковые, то ∠A = ∠C. Свойство доказано.
Характеристики диагоналей фигуры
Основной признак этих линий параллелограмма: точка пересечения разделяет их пополам.
Доказательство: пусть т. Е — это точка пересечения диагоналей AC и BD фигуры ABCD. Они образуют два соизмеримых треугольника — ∆ABE и ∆CDE.
AB=CD, так как они противоположные. Согласно прямых и секущей, ∠ABE = ∠CDE и ∠BAE = ∠DCE.
По второму признаку равенства ∆ABE = ∆CDE. Это означает, что элементы ∆ABE и ∆CDE: AE = CE, BE = DE и при этом они соразмерные части AC и BD. Свойство доказано.
Особенности смежных углов
У смежных сторон сумма углов равна 180° , поскольку они лежат по одну сторону параллельных линий и секущей. Для четырехугольника ABCD:
∠A+∠B=∠C+∠D=∠A+∠D=∠B+∠C=180º
Свойства биссектрисы:
- , опущенные на одну сторону, являются перпендикулярными;
- противолежащие вершины имеют параллельные биссектрисы;
- треугольник, полученный проведением биссектрисы, будет равнобедренным.
Определение характерных черт параллелограмма по теореме
Признаки этой фигуры вытекают из ее основной теоремы, которая гласит следующее: четырехугольник считается параллелограммом в том случае, если его диагонали пересекаются, а эта точка разделяет их на равные отрезки.
Доказательство: пусть в т. Е прямые AC и BD четырехугольника ABCD пересекаются. Так как ∠AED = ∠BEC, а AE+CE=AC BE+DE=BD, то ∆AED = ∆BEC (по первому признаку равенства треугольников). То есть ∠EAD = ∠ECB. Они также являются внутренними перекрестными углами секущей AC для прямых AD и BC. Таким образом, по определению параллельности — AD || BC. Аналогичное свойство линий BC и CD выводится также. Теорема доказана.
Вычисление площади фигуры
Площадь этой фигуры находится несколькими методами, одним из самых простых: умножения высоты и основания, к которому она проведена.
Доказательство: проведем перпендикуляры BE и CF из вершин B и C. ∆ABE и ∆DCF — равные, поскольку AB = CD и BE = CF. ABCD — равновеликий с прямоугольником EBCF, так как они состоят и соразмерных фигур: S ABE и S EBCD , а также S DCF и S EBCD . Из этого следует, что площадь этой геометрической фигуры находится так же как и прямоугольника:
S ABCD = S EBCF = BE×BC=BE×AD.
Для определения общей формулы площади параллелограмма обозначим высоту как hb , а сторону — b . Соответственно:
Другие способы нахождения площади
Вычисления площади через стороны параллелограмма и угол , который они образуют, — второй известный метод.
,
Sпр-ма — площадь;
a и b — его стороны
α — угол между отрезками a и b.
Этот способ практически основывается на первом, но в случае, если неизвестна. всегда отрезает прямоугольный треугольник, параметры которого находятся тригонометрическими тождествами, то есть . Преобразуя соотношение, получаем . В уравнении первого способа заменяем высоту этим произведением и получаем доказательство справедливости этой формулы.
Через диагонали параллелограмма и угол, который они создают при пересечении, также можно найти площадь.
Доказательство: AC и BD пересекаясь, образуют четыре треугольника: ABE, BEC, CDE и AED. Их сумма равна площади этого четырехугольника.
Площадь каждого из этих ∆ можно найти за выражением , где a=BE, b=AE, ∠γ =∠AEB. Поскольку , то в расчетах используется единое значение синуса. То есть . Поскольку AE+CE=AC= d 1 и BE+DE=BD= d 2 , формула площади сводится до:
.
Применение в векторной алгебре
Особенности составляющих частей этого четырехугольника нашли применение в векторной алгебре, а именно: сложении двух векторов. Правило параллелограмма утверждает, что если заданные векторы и не коллинеарны, то их сумма будет равна диагонали этой фигуры, основания которой соответствуют этим векторам.
Доказательство: из произвольно выбранного начала — т. о. — строим векторы и . Далее строим параллелограмм ОАСВ, где отрезки OA и OB — стороны. Таким образом, ОС лежит на векторе или сумме .
Формулы для вычисления параметров параллелограмма
Тождества приведены при следующих условиях:
- a и b, α — стороны и угол между ними;
- d 1 и d 2 , γ — диагонали и в точке их пересечения;
- h a и h b — высоты, опущенные на стороны a и b;
| Параметр | Формула |
| Нахождение сторон | |
| по диагоналям и косинусу угла между ними | |
| по диагоналям и стороне | |
| через высоту и противоположную вершину | |
| Нахождение длины диагоналей | |
| по сторонам и величине вершины между ними | |
Параллелограммом называют четырехугольник у которого противоположные стороны параллельны между собой. Основные задачи в школе по данной теме заключаются в вычислении площади параллелограмма, его периметра, высоты, диагоналей. 2)
.
Основные признаки параллелограммов:
1. Четырехугольник у которого противоположные стороны попарно параллельны является параллелограммом.
2. Четырехугольник с равными противоположными сторонами является параллелограммом.
3. Четырехугольник с равными и параллельными противоположными сторонами является параллелограммом.
4. Если диагонали четырехугольника в точке пересечения делятся пополам то это параллелограмм.
5. Четырехугольник у которого противоположные углы попарно равны является параллелограммом
Биссектрисы параллелограмма
Биссектрисы противоположных углов в параллелограмме могут быть параллельными или совпадать.
Биссектрисы соседних углов (прилегающие к одной стороне) пересекаются под прямым углом (перпендикулярные).
Высота параллелограмма
Высота параллелограмма
— это отрезок который проведен с угла перпендикулярно к основанию. Из этого следует что из каждого угла можно провести две высоты.
Формула площади параллелограмма
Площадь параллелограмма
равна произведению стороны на высоту проведенную к ней. Формула площади следующая
Вторая формула не менее популярная при вычислениях и определяется так: площадь параллелограмма равна произведению соседних сторон на синус угла между ними
На основе приведенных формул Вы будете знать как вычислить площадь параллелограмма.
Периметр параллелограмма
Формула для вычисления периметру параллелограмма имеет вид
то есть периметр равен удвоенному значению суммы сторон. Задачи на параллелограмм будут рассмотрены в соседних материалах, а пока изучайте формулы. Большинство задач по вычислению сторон, диагоналей параллелограмма достаточно просты и сводятся к знанию теоремы синусов и теоремы Пифагора.
При решении задач по данной теме кроме основных свойств параллелограмма и соответственных формул можно запомнить и применять следующее:
- Биссектриса внутреннего угла параллелограмма отсекает от него равнобедренный треугольник
- Биссектрисы внутренних углов прилежащие к одной из сторон параллелограмма взаимно перпендикулярные
- Биссектрисы, выходящие из противоположных внутренних углов параллелограмма, параллельные между собой либо лежат на одной прямой
- Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон
- Площадь параллелограмма равна половине произведения диагоналей на синус угла между ними
Рассмотрим задачи, при решении которых используются данные свойства.
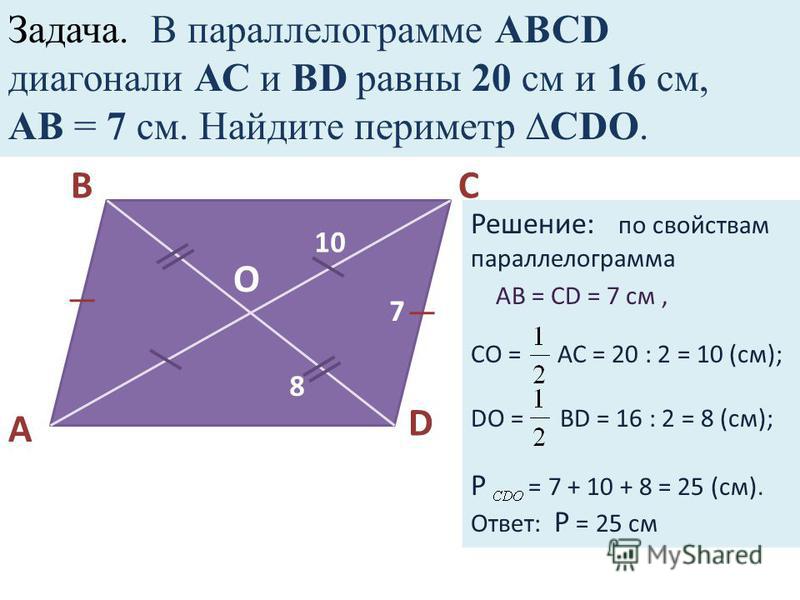
Задача 1.
Биссектриса угла С параллелограмма АВСD пересекает сторону АD в точке М и продолжение стороны АВ за точку А в точке Е. Найдите периметр параллелограмма, если АЕ = 4, DМ = 3.
Решение.
1. Треугольник СМD равнобедренный. (Свойство 1). Следовательно, СD = МD = 3 см.
2. Треугольник ЕАМ равнобедренный.
Следовательно, АЕ = АМ = 4 см.
3. АD = АМ + МD = 7 см.
4. Периметр АВСD = 20 см.
Ответ. 20 см.
Задача 2.
В выпуклом четырёхугольнике АВСD проведены диагонали. Известно, что площади треугольников АВD, АСD, ВСD равны. Докажите, что данный четырёхугольник является параллелограммом.
Решение.
1. Пусть ВЕ – высота треугольника АВD, СF – высота треугольника АCD. Так как по условию задачи площади треугольников равны и у них общее основание АD, то высоты этих треугольников равны. ВЕ = СF.
2. ВЕ, СF перпендикулярны АD. Точки В и С расположены по одну сторону относительно прямой АD. ВЕ = СF. Следовательно, прямая ВС || AD. (*)
3. Пусть АL – высота треугольника АСD, BK – высота треугольника BCD. Так как по условию задачи площади треугольников равны и у них общее основание СD, то высоты этих треугольников равны. АL = BK.
4. АL и BK перпендикулярны СD. Точки В и А расположены по одну сторону относительно прямой СD. АL = BK. Следовательно, прямая АВ || СD (**)
5. Из условий (*), (**) вытекает – АВСD параллелограмм.
Ответ. Доказано. АВСD – параллелограмм.
Задача 3.
На сторонах ВС и СD параллелограмма АВСD отмечены точки М и Н соответственно так, что отрезки ВМ и НD пересекаются в точке О;
Решение.
1. В треугольнике DОМ
2. В прямоугольном треугольнике DНС
(
Тогда (Так как в прямоугольном треугольнике катет, который лежит против угла в 30 о, равен половине гипотенузы).
Но СD = АВ. Тогда АВ: НD = 2: 1.
3.
4.
Ответ: АВ: НD = 2: 1,
Задача 4.
Одна из диагоналей параллелограмма длиною 4√6, составляет с основанием угол 60 о, а вторая диагональ составляет с тем же основанием угол 45 о. Найти вторую диагональ.
Решение.
1. АО = 2√6.
2. К треугольнику АОD применим теорему синусов.
АО/sin D = OD/sin А.
2√6/sin 45 о = OD/sin 60 о.
ОD = (2√6sin 60 о) / sin 45 о = (2√6 · √3/2) / (√2/2) = 2√18/√2 = 6.
Ответ: 12.
Задача 5.
У параллелограмма со сторонами 5√2 и 7√2 меньший угол между диагоналями равен меньшему углу параллелограмма. Найдите сумму длин диагоналей.
Решение.
Пусть d 1 , d 2 – диагонали параллелограмма, а угол между диагоналями и меньший угол параллелограмма равен ф.
1. Посчитаем двумя разными
способами его площадь.
S ABCD = AB · AD · sin A = 5√2 · 7√2 · sin ф,
S ABCD = 1/2 AС · ВD · sin AОВ = 1/2 · d 1 d 2 sin ф.
Получим равенство 5√2 · 7√2 · sin ф = 1/2d 1 d 2 sin ф или
2 · 5√2 · 7√2 = d 1 d 2 ;
2. Используя соотношение между сторонами и диагоналями параллелограмма запишем равенство
(АВ 2 + АD 2) · 2 = АС 2 + ВD 2 .
((5√2) 2 + (7√2) 2) · 2 = d 1 2 + d 2 2 .
d 1 2 + d 2 2 = 296.
3. Составим систему:
{d 1 2 + d 2 2 = 296,
{d 1 + d 2 = 140.
Умножим второе уравнение системы на 2 и сложим с первым.
Получим (d 1 + d 2) 2 = 576. Отсюда Id 1 + d 2 I = 24.
Так как d 1 , d 2 – длины диагоналей параллелограмма, то d 1 + d 2 = 24.
Ответ: 24.
Задача 6.
Стороны параллелограмма 4 и 6. Острый угол между диагоналями равен 45 о. Найдите площадь параллелограмма.
Решение.
1. Из треугольника АОВ, используя теорему косинусов, запишем соотношение между стороной параллелограмма и диагоналями.
АВ 2 = АО 2 + ВО 2 2 · АО · ВО · cos АОВ.
4 2 = (d 1 /2) 2 + (d 2 /2) 2 – 2 · (d 1 /2) · (d 2 /2)cos 45 о;
d 1 2 /4 + d 2 2 /4 – 2 · (d 1 /2) · (d 2 /2)√2/2 = 16.
d 1 2 + d 2 2 – d 1 · d 2 √2 = 64.
2. Аналогично запишем соотношение для треугольника АОD.
Учтем, что
Получим уравнение d 1 2 + d 2 2 + d 1 · d 2 √2 = 144.
3. Имеем систему
{d 1 2 + d 2 2 – d 1 · d 2 √2 = 64,
{d 1 2 + d 2 2 + d 1 · d 2 √2 = 144.
Вычитая из второго уравнения первое, получим 2d 1 · d 2 √2 = 80 или
d 1 · d 2 = 80/(2√2) = 20√2
4. S ABCD = 1/2 AС · ВD · sin AОВ = 1/2 · d 1 d 2 sin α = 1/2 · 20√2 · √2/2 = 10.
Примечание: В этой и в предыдущей задаче нет надобности, решать полностью систему, предвидя то, что в данной задаче для вычисления площади нам нужно произведение диагоналей.
Ответ: 10.
Задача 7.
Площадь параллелограмма равна 96, а его стороны равны 8 и 15. Найдите квадрат меньшей диагонали.
Решение.
1. S ABCD = AВ · АD · sin ВAD. Сделаем подстановку в формулу.
Получим 96 = 8 · 15 · sin ВAD. Отсюда sin ВAD = 4 / 5 .
2. Найдём cos ВАD. sin 2 ВAD + cos 2 ВАD = 1.
(4 / 5) 2 + cos 2 ВАD = 1. cos 2 ВАD = 9 / 25 .
По условию задачи мы находим длину меньшей диагонали. Диагональ ВD будет меньшей, если угол ВАD острый. Тогда cos ВАD = 3 / 5.
3. Из треугольника АВD по теореме косинусов найдём квадрат диагонали ВD.
ВD 2 = АВ 2 + АD 2 – 2 · АВ · ВD · cos ВАD.
ВD 2 = 8 2 + 15 2 – 2 · 8 · 15 · 3 / 5 = 145.
Ответ: 145.
Остались вопросы? Не знаете, как решить геометрическую задачу?
Чтобы получить помощь репетитора – зарегистрируйтесь .
Первый урок – бесплатно!
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Нахождение площади и периметра параллелограмма
Нахождение площади и периметра периметр следующих параллелограммов:
Задача 1:
Решение:
Из фигурка,
Основание параллелограмм (b) = 11 см
Высота параллелограмм (h) = 3 см
Тогда
Площадь параллелограмма
= b x h кв. единиц.
Площадь = 11 x 3
Итак, площадь параллелограмма = 33 кв. см.
Периметр параллелограмма = сумма длин четырех стороны.
= 11 см + 4 см + 11 см + 4 см
Итак, периметр параллелограмма = 30 см
Задача 2 :
Решение: фигурка,
Основание параллелограмм (b) = 7 см
Высота параллелограмм (h) = 10 см
Тогда
Площадь параллелограмма = b x h кв. единиц.
Площадь = 7 х 10
Итак, площадь параллелограмма = 70 кв. см.
Периметр параллелограмма = сумма длин четырех стороны.
= 13 см + 7 см + 13 см + 7 см
= 40 см
Задача 3 :
Найди пропажу ценности.
Решение:
(i)
Основание параллелограмма (b) = 18 см
Высота параллелограмм (h) = 5 см
Тогда
Площадь параллелограмма = b x h кв. единиц.
Площадь = 18 x 5
Итак, площадь параллелограмма =
90 кв. см.
(ii)
Основание параллелограмма (b) = 8 м
Площадь параллелограмма = 56 кв. м
Тогда
Площадь параллелограмма = b x h кв. единиц.
56 = 8 х ч
56/8 = ч
7 м = ч
Итак, высота параллелограмма (ч) = 7 м
(iii)
Высота параллелограмма (h) = 17 мм
Площадь параллелограмма = 221 кв. мм
Площадь параллелограмма = b x h кв. единиц.
221 = б х 17
221/17 = б
13 мм = b
Итак, основание параллелограмма (b) = 13 мм.
Задача 4 :
Суреш выиграл кубок в форме параллелограмма в шахматный турнир государственного уровня. Он знает, что площадь трофея 735 кв. см, а его основание 21 см. какая высота трофея?
Решение:
Дано,
Основание трофея (b) = 21 см
Площадь трофея = 735 кв.см
Площадь параллелограмм = b x h кв. единиц.
735 = 21 x ч
735/21 = ч
35 см = h
Итак, высота трофеев (ч) = 35 см
Задача 5 :
У Джанаки есть кусок ткани в форме
параллелограмм. Его высота 12 м, а основание 18 м. Она режет ткань
на четыре равных параллелограмма, разрезав параллельные стороны через его середину.
точки. Найдите площадь каждого нового параллелограмма.
Решение:
Дано,
Основание параллелограмма (b) = 18 м
Высота параллелограмма (h) = 12 м
Площадь параллелограмма = b x h кв. единиц.
= 18 м x 12 м
= 216 м 2
Так как она разрезает ткань на четыре равных параллелограмма,
= 216/4
= 54 м 2
Итак, площадь каждого нового параллелограмма = 54 м 2 .
Задача 6 :
Земля имеет форму параллелограмма. Высота параллелограмма 14 метров, а соответствующее основание на 8 метров длиннее его высоты. Узнать стоимость выравнивания грунта по тарифу от $15 за кв.м.
Решение :
Дано,
Основание параллелограмма (b) = 8 м
Поскольку основание на 8 метров длиннее высоты,
Теперь основание = (14 + 8) = 22 м параллелограмм (h) = 14 м
Площадь параллелограмма
= b x h кв. единиц.
= 22 м х 14 м
= 308 м 2
Стоимость выравнивания 1 м 2 = 15 за кв.м.
Стоимость выравнивания 308 м 2 = 308 х 15
= 4 620 $
Итак, стоимость выравнивания земли = $ 4,620
Пожалуйста, отправьте ваш отзыв на [email protected]
Мы всегда ценим ваши отзывы.
©Все права защищены. onlinemath5all.com
Видео-вопрос: нахождение периметра и площади параллелограмма на координатной сетке
Стенограмма видео
Параллелограмм имеет вершины в точках 𝐴, 𝐵, 𝐶 и 𝐷 с отрицательными координатами один, один; один три; три, отрицательный; и один, отрицательное три, соответственно. Вычислите периметр параллелограмма 𝐴𝐵𝐶𝐷. Дайте свое решение с точностью до одного десятичного знака. Проведя через вершины параллелограмма прямоугольник или иначе, вычислить площадь параллелограмма 𝐴𝐵𝐶𝐷.
В этом вопросе нам даны четыре координаты четырех вершин параллелограмма. Поскольку это относительно простые координаты, возможно, самым разумным будет нанести их на график. Итак, давайте возьмем сетку и нанесем на нее эти четыре точки. Итак, здесь у нас есть 𝐴 при минусе один, один; 𝐵 в час, три; 𝐶 в три, минус один; и 𝐷 в один, минус три. Затем мы можем соединить эти четыре вершины, чтобы создать параллелограмм 𝐴𝐵𝐶𝐷. Мы также можем заметить, что это параллелограмм, поскольку это четырехугольник, у которого противоположные стороны параллельны. Это также хорошая проверка того, что мы правильно нанесли эти точки.
Давайте теперь посмотрим на первую часть этого вопроса, которая просит нас вычислить периметр параллелограмма. Мы можем вспомнить, что периметр фигуры определяется расстоянием вокруг внешнего края. К сожалению, с этим параллелограммом это не так просто, как если бы стороны были заданы как горизонтальные или вертикальные линии. Однако мы все еще можем вычислить периметр этого параллелограмма, найдя длины сторон. Возьмем эту длину 𝐴𝐵. Мы могли бы решить это, используя теорему Пифагора, или мы могли бы использовать формулу, применяющую теорему Пифагора.
Эта формула позволяет найти расстояние между двумя координатами 𝑥 меньше единицы, 𝑦 меньше единицы и 𝑥 меньше двух, 𝑦 меньше двух. Расстояние дается как квадратный корень из 𝑥 меньше двух минус 𝑥 меньше единицы в квадрате плюс 𝑦 меньше двух минус 𝑦 меньше единицы в квадрате. Мы можем принять координату 𝐴 за наши 𝑥 подчиненные единицы, 𝑦 подчиненные значения, а координату 𝐵 за 𝑥 подчиненные два, 𝑦 подчиненные два значения. Затем мы подставляем эти значения в формулу, чтобы найти расстояние 𝐴𝐵.
Итак, 𝐴𝐵 равно квадратному корню из одного вычесть минус один в квадрате плюс три вычесть один в квадрате. Упрощая это, если мы посмотрим на первый набор круглых скобок, одно вычитание отрицательной единицы эквивалентно одному плюс один, что равно двум. А во втором наборе скобок из трех вычесть один тоже будет два. Итак, нам нужно извлечь квадратный корень из двух в квадрате плюс два в квадрате. Тогда, поскольку два в квадрате равно четырем, у нас есть четыре плюс четыре, что равно восьми. Итак, 𝐴𝐵 равно квадратному корню из восьми.
Хотя окончательный ответ на эту часть вопроса требуется с точностью до одного десятичного знака, мы сохраним его в форме квадратного корня как квадратный корень из восьми. Поскольку мы знаем, что это параллелограмм, то это означает, что противоположные стороны равны. Итак, длина 𝐶𝐷 также равна квадратному корню из восьми. Затем мы можем использовать эту же формулу для определения длины 𝐴𝐷. Неважно, какую координату мы обозначаем значениями 𝑥 sub one, 𝑦 sub one. Итак, давайте сделаем так, чтобы на этот раз 𝐷 имел значения 𝑥 sub two, 𝑦 sub two. Подставив эти значения в формулу, чтобы найти длину 𝐴𝐷, мы получим 𝐴𝐷, равное квадратному корню из одного вычесть минус один в квадрате плюс минус три вычесть один в квадрате.
Если упростить, то 𝐴𝐷 равно квадратному корню из двух в квадрате плюс минус четыре в квадрате. Мы знаем, что два в квадрате равно четырем, а отрицательные четыре в квадрате равны 16. Итак, сложив их вместе, мы получим 20, а извлечение квадратного корня даст нам корень 20. Итак, теперь мы обнаружили, что длина 𝐴𝐷, а также длина 𝐵𝐶 можно задать как корень 20. Обратите внимание, что все эти длины будут заданы в единицах длины.
Наконец, чтобы ответить на этот вопрос, нам нужно вычислить периметр. Мы знаем, что есть две стороны, длина которых равна 8 единицам корня, и две стороны, длина которых равна 20 единицам длины. Поскольку нам нужно дать ответ с точностью до одного десятичного знака, мы можем использовать наш калькулятор, чтобы получить значение 14,6011 и так далее. Затем нам нужно проверить нашу вторую десятичную цифру, чтобы увидеть, является ли она пятью или больше, что означает, что наш ответ сводится к 14,6. Следовательно, 𝐴𝐵𝐶𝐷 имеет периметр 14,6. Нам не дали никаких единиц в вопросе, но если бы нам нужно было их указать, это были бы единицы длины.
Теперь освободим место, чтобы ответить на вторую часть этого вопроса. В этом вопросе нас просят найти площадь параллелограмма 𝐴𝐵𝐶𝐷. Возможно, вы помните, что для нахождения площади параллелограмма мы вычисляем основание, умноженное на высоту перпендикуляра. Допустим, мы взяли за основу длину 𝐴𝐷. Чтобы использовать эту формулу, нам нужно вычислить длину перпендикуляра от 𝐶 до 𝐴𝐷. Поскольку это выглядит довольно сложно, давайте еще раз посмотрим на эту часть вопроса.
На самом деле нам дали подсказку провести прямоугольник через вершины параллелограмма. Итак, давайте посмотрим, как это выглядит. Здесь у нас есть прямоугольник. Мы знаем, что у него четыре прямых угла, и мы также знаем, что противоположные стороны параллельны и конгруэнтны. Но как это поможет нам найти площадь параллелограмма? Давайте сделаем еще один шаг и разделим этот прямоугольник и параллелограмм внутри него на две равные части.
Если мы заштрихуем левую сторону этого параллелограмма, мы на самом деле создадим другую фигуру — треугольник. И мы должны помнить, что площадь треугольника равна половине, умноженной на основание, умноженное на высоту перпендикуляра. Чтобы вычислить площадь этого треугольника слева, треугольника 𝐴𝐵𝐷, основание будет равно 𝐵𝐷. Считая квадраты в сетке, длина 𝐵𝐷 может быть равна шести единицам длины.