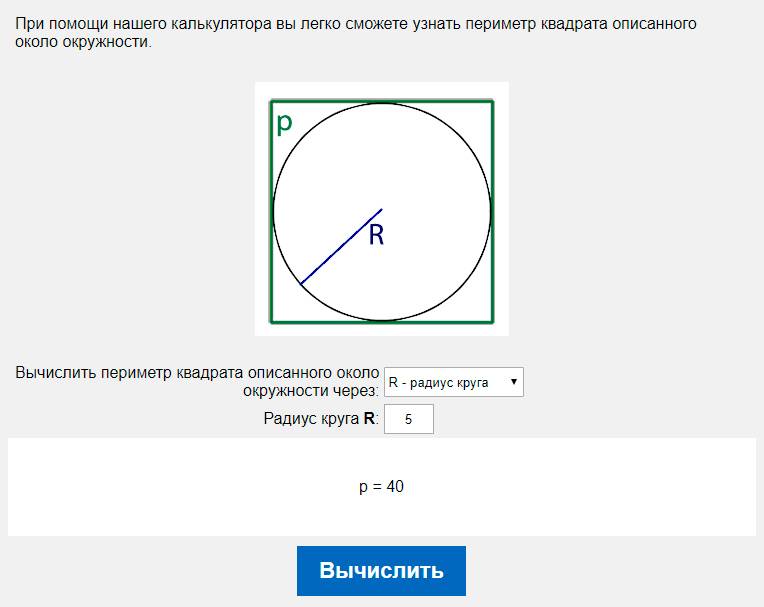
как посчитать через диаметр или радиус, формула расчета
Содержание:
- Периметр круга — что это, определение
-
Как рассчитать периметр круга или длину окружности
- Через радиус
- Через диаметр
- Примеры решения задач
Содержание
- Периметр круга — что это, определение
-
Как рассчитать периметр круга или длину окружности
- Через радиус
- Через диаметр
- Примеры решения задач
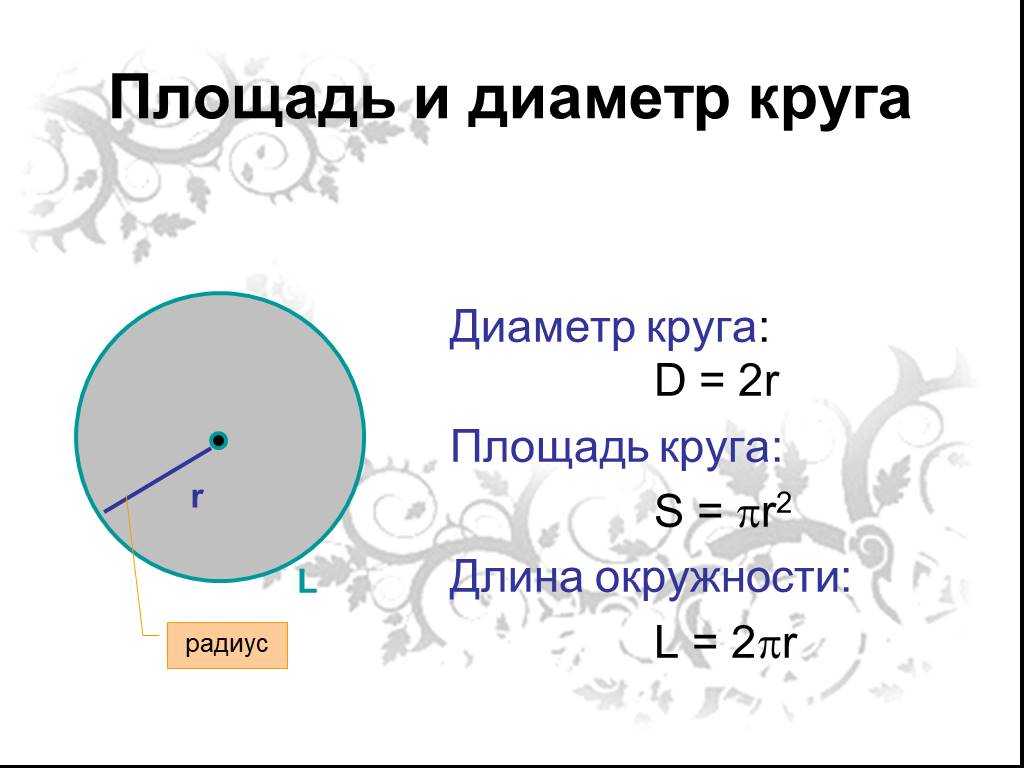
Периметр круга — что это, определение
Определение
Круг — это геометрическое множество точек на плоскости, расстояние от которых до данной точки, называемой центром круга, не превосходит заданного неотрицательного числа.
Оределение
Окружность — замкнутая кривая на плоскости, все точки которой равноудалены от центра окружности.
Эти определения плотно связаны друг с другом. Круг — это часть плоскости, ограниченная окружностью. Окружность — это граница круга.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Определение
Радиус — расстояние от центра окружности до любой ее точки. Это отрезок, который соединяет центр круга с его границей.
Определение
Диаметр — это отрезок, соединяющий две точки окружности и проходящий через ее центр. Он равен двум радиусам.
Определение
Периметр — это длина окружности, ограничивающей круг.
Понятия «периметр круга» и «длина окружности» считаются синонимичными.
Как рассчитать периметр круга или длину окружности
Чтобы вычислить периметр круга, необходимо ввести постоянную величину — число Пи. Оно равно отношению длины окружности к ее диаметру. Это отношение идентично для всех окружностей и равно \(\pi=3,14159…\)
Чтобы произвести расчет периметра круга, достаточно помнить это число до двух знаков после запятой:
\(\pi=3,14\)
Помимо этого, для вычисления необходимо знать длину радиуса или диаметра.
Через радиус
Длину окружности L можно найти по формуле через радиус:
\(L=2\pi R\)
где \(\pi \) — число Пи, R — радиус.
Через диаметр
Длину окружности L можно найти по формуле через диаметр. Поскольку диаметр D равен двум радиусам:
\(L=\pi D\)
Примеры решения задач
Задача
Каков периметр круга, если его радиус равен 0,5 см?
Решение
По формуле, \(L= 2\pi R\).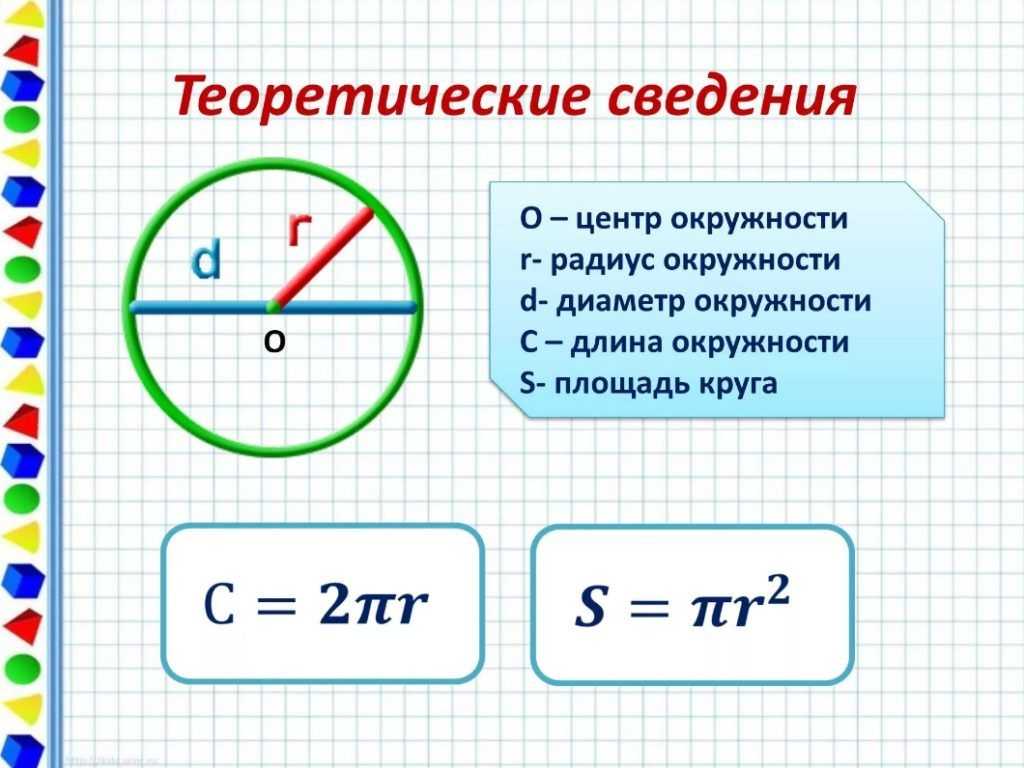
Отсюда:
\(L=2\pi R=2\cdot0,5\pi=\pi\approx3,14\)
Ответ: 3,14 см.
Задача
Какова длина окружности, если ее диаметр равен 2 см?
Решение
По формуле, \(L=\pi D\). Отсюда:
\(L=\pi D=\pi\cdot2\approx3,14\cdot2=6,28\)
Ответ: 6,28 см.
Насколько полезной была для вас статья?
Рейтинг: 3.00 (Голосов: 2)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Поиск по содержимому
Формула периметра круга
- Главная
- Справочник
- Геометрия
- Формулы периметра
- Формула периметра круга
- Формула периметра круга
- Длина окружности (периметр круга)
Определение круга часто звучит, как часть плоскости, которая ограничена окружностью. Окружность круга является плоской замкнутой кривой. Все точки, расположенные на кривой, удалены от центра круга на одинаковое расстояние.
В круге его длина и периметр одинаковы. Соотношение длины любой окружности и ее диаметра постоянное и обозначается числом π = 3,1415.
Определение периметра круга
Периметр круга радиуса r равен удвоенному произведению радиуса r на число π(~3.1415)
Формула периметра круга
Периметр круга радиуса \(r\) :
\[ \LARGE{P} = 2 \cdot \pi \cdot r \]
или
\[ \LARGE{P} = \pi \cdot d \]
где
\( P \) – периметр (длина окружности).
\( r \) – радиус.
\( d \) – диаметр.
Окружностью будем называть такую геометрическую фигуру, которая будет состоять из всех таких точек, которые находятся на одинаковом расстоянии от какой-либо заданной точки.
Центром окружности будем называть точку, которая задается в рамках определения 1.
Радиусом окружности будем называть расстояние от центра этой окружности до любой ее точки.
0}{n}}=\frac{2τ}{2τ’} \)
Получаем, что отношение \( \frac{ρ}{ρ’}=\frac{2τ}{2τ’} \) будет верным независимо от значения числа сторон вписанных правильных многоугольников. То есть
\( \lim_{n\to\infty}(\frac{ρ}{ρ’})=\frac{2τ}{2τ’} \)
С другой стороны, если бесконечно увеличивать число сторон вписанных правильных многоугольников (то есть \( n→∞ \) ), будем получать равенство:
\( lim_{n\to\infty}(\frac{ρ}{ρ’})=\frac{C}{C’} \)
Из последних двух равенств получим, что
\( \frac{C}{C’}=\frac{2τ}{2τ’} \)
То есть
\( \frac{C}{2τ}=\frac{C’}{2τ’} \)
Видим, что отношение длины окружности к его удвоенному радиусу всегда одно и тоже число, независимо от выбора окружности и ее параметров, то есть
\( \frac{C}{2τ}=const \)
Эту постоянную принять называть числом «пи» и обозначать \( π \) . Приближенно, это число будет равняться \( 3,14 \) (точного значения этого числа нет, так как оно является иррациональным числом). Таким образом
\( \frac{C}{2τ}=π \)
Окончательно, получим, что длина окружности (периметр круга) определяется формулой
\( C=2πτ \)
В вашем браузере отключен Javascript.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Формулы периметра Математика Тригонометрия Формулы Геометрия Теория 8013
Периметр формулы круга — Что такое периметр формулы круга? Примеры
Формула периметра круга используется для нахождения периметра круга. Периметром круга является его граница или длина полной дуги периферии круга. Термин, обозначающий периметр круга, называется его окружностью. Следовательно, периметр круга говорит нам об окружности круга, поэтому он также известен как формула окружности круга. Давайте узнаем больше о периметре формулы круга вместе с решенными примерами.
Формула периметра круга??
Формула периметра окружности состоит из трех компонентов: двух констант и одной переменной, представляющей собой радиус окружности. Формула для вычисления периметра круга или формулы окружности может быть представлена следующим образом:
Формула периметра круга
Периметр круга = 2 π r = π D единиц
где,
- r = радиус круга
- D = диаметр окружности.
Хотите найти сложные математические решения за считанные секунды?
Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.
Заказать бесплатный пробный урок
Примеры по формуле периметра окружности
Давайте решим несколько интересных задач, используя формулу периметра окружности.
Пример 1: Используя формулу для определения периметра круга, рассчитайте длину окружности круга диаметром 7 дюймов (Используйте значение π как 22/7)?
Решение:
Чтобы найти: Периметр круга
Дано: Диаметр круга = 7 в
Используя формулу периметра круга,
Периметр круга = π D
Периметр или длина окружности = 22 /7 × 7
= 22 дюйма
Ответ: Периметр круга или длина окружности = 22 дюйма. в.
Решение:
Чтобы найти: Радиус окружности
Дано: Длина окружности = 110 в
Используя формулу периметра окружности,
Периметр круга или окружности = 2 π r
2 π r = 110
2 × 22/7 × r = 110
r = 110 × 7 / 44
r = 17,5
3 Radius:2 9 окружности = 17,5 дюймов.
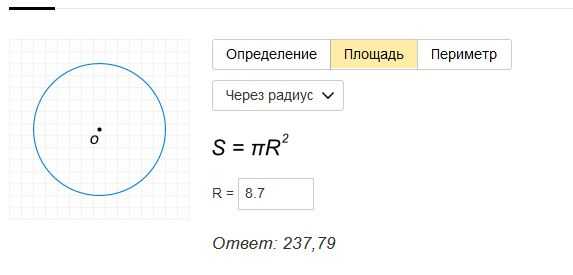
Пример 3: Радиус окружности равен 7 дюймов. Используя формулу периметра окружности, рассчитайте длину окружности.
Решение:
Найти: Периметр круга
Дано: r = 7 в
Формула периметра круга = 2 π r
C = 2 × (22/7) × (7)
Ответ: Длина окружности 44 дюйма.
Часто задаваемые вопросы о формуле периметра круга
Что такое формула периметра круга для полукруга?
Полукруг означает половину полного круга. Он включает в себя половину окружности и диаметр окружности. Следовательно, если периметр формулы круга равен 2 π r, то периметр полукруга равен 1/2 (2πr) + d = (π r + d) единиц.
Какова формула периметра круга, если известен диаметр?
Мы знаем, что формула периметра круга = 2 π r и D = 2r. Если диаметр задан, то формула периметра круга = π d, где d — диаметр, а π — константа со значением (3,14 или 22/7).
Какова формула периметра круга, если известен радиус?
Формула периметра круга, если задан радиус, составляет 2πr единиц, где r — радиус, а π — константа со значением (3,14 или 22/7).
Как рассчитать радиус по формуле периметра круга?
Формула периметра круга = 2πr единиц. Если мы знаем значение длины окружности или периметра круга, то, подставив значение в формулу, мы можем вычислить радиус. Следовательно, R = (периметр круга)/2π.
Калькулятор периметра круга
Создано Luis Hoyos
Отзыв от Wojciech Sas, PhD
Последнее обновление: 25 сентября 2022 г.
Содержание:- Формула периметра круга
- Как рассчитать периметр круга?
- Другие полезные инструменты помимо калькулятора периметра круга
- Часто задаваемые вопросы
Наш калькулятор периметра круга может очень помочь, если вы пытаетесь решить геометрические задачи. Одной из распространенных задач является нахождение периметра круга, также называемого его окружностью , которая измеряет длину линии, образующей эту геометрическую фигуру. Продолжайте читать, если хотите знать:
- Какова формула периметра круга.
- Как найти периметр круга, используя формулу периметра круга и наш калькулятор длины окружности.
- Каковы периметры четверти круга и полукруга.
🔎 Помните, что, как и в случае с остальными нашими инструментами, этот калькулятор длины окружности работает в обоих направлениях — он также является калькулятором длины окружности в радиус — и вы можете использовать его для преобразования длины окружности в радиус.
Формула периметра круга
Если вы не знаете, как найти длину окружности, наш калькулятор — самый быстрый вариант. Тем не менее, полезно понять, как работают уравнения, чтобы лучше интерпретировать результаты. Формула периметра круга:
p = 2πr ,
, где p — периметр круга, r — радиус, а π — константа, равная приблизительно 3,1415… 90 выразите периметр через диаметр ( d ), помня, что r=d/2 :
p = πd
💡 Число π есть константа, равная отношению длины окружности к диаметру (или удвоенному радиусу ).
Он всегда будет иметь одно и то же значение, независимо от размера круга.
Решение для π в приведенном выше уравнении приводит к указанному соотношению: π = p/(2r) .
Формулы периметра полукруга и четверти круга
Иногда нам нужно вычислить части круга вместо целого. Мы можем получить формулы для периметров 9Полуокружность 0035 и четверть окружности путем деления приведенного выше уравнения на 2 и 4 соответственно: круг?
Если вы хотите использовать калькулятор периметра круга, чтобы найти длину окружности, выполните следующие действия:
- Определите радиус вашего круга. Например, предположим, что это 7 см.
- Введите радиус в калькулятор, и вы узнаете длину окружности. В результате должно получиться 43,982 см.
- Чтобы перепроверить результат , введите радиус в формулу периметра круга:
p = 2 × π × (7 см) = 43,982 см.
Другие полезные инструменты помимо калькулятора периметра круга
Теперь, когда вы знаете, как найти периметр круга, не забывайте, что калькулятор длины окружности в радиус — не единственный наш инструмент для работы с круглыми объектами. Мы надеемся, что приведенные ниже калькуляторы помогут вам решить повседневные круговые задачи:
- Расчет круга: найти c, d, a, r;
- Калькулятор измерения окружности;
- Калькулятор формулы круга;
- Калькулятор радиуса окружности;
- Калькулятор длины окружности;
- Окружность к диаметру;
- Калькулятор диаметра круга;
- Калькулятор длины окружности и площади круга;
- Квадратный метр круга калькулятор; и
- Квадратный дюйм калькулятора круга.
Часто задаваемые вопросы
Как найти периметр четверти круга?
Чтобы найти периметр четверти круга:
- Запомните периметр обычного круга, который равен
p = 2πr.
