Периметр окружности формула через диаметр: Как найти периметр круга? Ответ на webmath.ru

Расчет длины окружности по диаметру. Формула периметра круга (длины окружности)

1) Периметр круга равен произведению радиуса на два пи (3.1415).

P — Периметр круга (длина окружности)

π — число пи (3.1415)

r — радиус круга (окружности)

Формулы трапеции

Трапеция — четырёхугольник, у которого две стороны параллельны (основания трапеции), а две другие — непараллельны (боковые стороны трапеции). Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.

Формула площади трапеции:

Площадь геометрической фигуры — часть поверхности, ограниченная замкнутым контуром данной фигуры. Величина площади трапеции выражается числом заключающихся в него квадратных единиц.

1) Площадь трапеции равна произведению полусуммы ее оснований на высоту (a, b, h).

S — площадь трапеции

a — длина 1-ого основания

b — длина 2-ого основания

h — длина высоты трапеции

См.

также: Программа для расчета площади трапеции.

Формула периметра трапеции:

Периметр геометрической фигуры — суммарная длина границ плоской геометрической фигуры. Периметр имеет ту же размерность величин, что и длина.

1) Периметр трапеции равен сумме 4-х её сторон (a, b, c, d).

P — периметр трапеции

a, c — длины оснований трапеции

b, d — длины боковых сторон трапеции

Формулы квадрата

Квадрат — правильный четырёхугольник, у которого все стороны и углы равны между собой. Может быть определён как прямоугольник, у которого две смежные стороны равны между собой, или как ромб, у которого все углы прямые. У квадрата есть две диагонали, соединяющие несмежные вершины.

Формулы площади квадрата:

Площадь геометрической фигуры — часть поверхности, ограниченная замкнутым контуром данной фигуры. Величина площади квадрата выражается числом заключающихся в него квадратных единиц.

1) Площадь квадрата равна квадрату длины его стороны (a).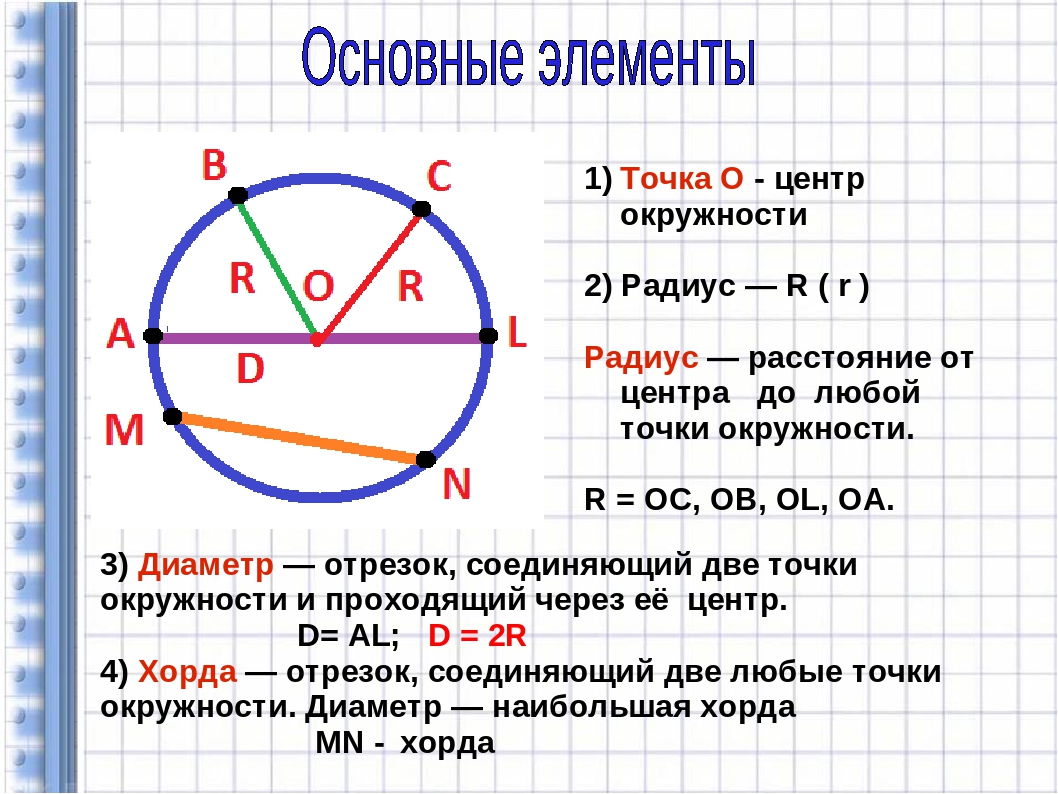

2) Площадь квадрата равна половине квадрата длины его диагонали (d).

S — площадь квадрата

a — длина стороны квадрата

d — длина диагонали квадрата

См. также: Программа для расчета площади квадрата.

Формулы периметра квадрата:

Периметр геометрической фигуры — суммарная длина границ плоской геометрической фигуры. Периметр имеет ту же размерность величин, что и длина.

1) Периметр квадрата равен сумме 4-х длин его сторон или произведению длины любой его стороны на четыре (так как у квадрат длины всех сторон равны).

2) Периметр квадрата равен произведению длины его диагонали на два корня из двух.

P — периметр квадрата

a — длина стороны квадрата

d — длина диагонали квадрата

Формулы прямоугольника

Прямоугольник — это четырёхугольник, у которого четыре прямых угла. Размеры прямоугольника задаются длинами его сторон, обозначаемых обычно a и b. Прямоугольник, все стороны которого равны (a = b) называется квадратом.

Окружность встречается в повседневной жизни не реже, чем прямоугольник. А у многих людей задача о том, как рассчитать длину окружности, вызывает затруднение. И все потому, что у нее нет углов. При их наличии все стало бы намного проще.

Что такое окружность и где она встречается?

Эта плоская фигура представляет собой некоторое количество точек, которые расположены на одинаковом удалении от еще одной, которая является центром. Это расстояние называется радиусом.

В повседневной жизни нечасто приходится вычислять длину окружности, кроме людей, которые являются инженерами и конструкторами. Они создают проекты механизмов, в которых используются, например, шестеренки, иллюминаторы и колеса. Архитекторы создают дома, имеющие круглые или арочные окна.

В каждом из этих и других случаях требуется своя точность. Причем высчитать длину окружности совершенно точно оказывается невозможно. Связано это с бесконечностью основного числа, имеющегося в формуле. «Пи» до сих пор уточняется. И используется чаще всего округленное значение. Степень точности выбирается такой, чтобы дать максимально верный ответ.

Обозначения величин и формулы

Теперь легко ответить на вопрос о том, как рассчитать длину окружности по радиусу, для этого потребуется такая формула:

Поскольку радиус и диаметр связаны друг с другом, то есть и другая формула для расчетов. Так как радиус в два раза меньше, то выражение немного видоизменится. И формула того, как рассчитать длину окружности, зная диаметр, будет следующей:

l = &pi- * d.

Как быть, если нужно вычислить периметр круга?

Просто вспомнить, что круг включает в себя все точки внутри окружности. А значит, его периметр совпадает с ее длиной. И после того, как рассчитать длину окружности, поставить знак равенства с периметром круга.

Кстати, и обозначения у них такие же. Это касается радиуса и диаметра, а периметром является латинская буква P.

Примеры заданий

Задача первая

Условие. Узнать длину окружности, радиус которой равен 5 см.

Решение. Здесь несложно понять, как рассчитать длину окружности. Нужно только воспользоваться первой формулой. Поскольку радиус известен, то потребуется только подставить значения и сосчитать. 2 умноженное на радиус, равный 5 см, даст 10. Осталось еще умножить его на значение &pi-. 3,14 * 10 = 31,4 (см).

Ответ: l = 31,4 см.

Задача вторая

Условие. Имеется колесо, длина окружности которого известна и равна 1256 мм. Необходимо вычислить его радиус.

Решение. В этом задании потребуется воспользоваться той же формулой. Но только известную длину нужно будет разделить на произведение 2 и &pi-. Получается, что произведение даст результат: 6,28. После деления остается число: 200. Это искомая величина.

Ответ: r = 200 мм.

Задача третья

Условие. Вычислить диаметр, если известна длина окружности, которая равна 56,52 см.

Решение. Аналогично предыдущей задаче потребуется разделить известную длину на значение &pi-, округленное до сотых. В результате такого действия получается число 18. Результат получен.

Ответ: d = 18 см.

Задача четвертая

Условие. Стрелки часов имеют длину 3 и 5 см. Нужно вычислить длины окружностей, которые описывают их концы.

Решение. Поскольку стрелки совпадают с радиусами окружностей, то потребуется первая формула. Ею нужно воспользоваться два раза.

Для первой длины произведение будет состоять из множителей: 2- 3,14 и 3. Итогом будет число 18,84 см.

Для второго ответа нужно перемножить 2, &pi- и 5. Произведение даст число: 31,4 см.

Ответ: l 1 = 18,84 см, l 2 = 31,4 см.

Задача пятая

Условие. Белка бегает в колесе диаметром 2 м. Какое расстояние она пробегает за один полный оборот колеса?

Решение. Это расстояние равно длине окружности. Поэтому нужно воспользоваться подходящей формулой. А именно перемножить значение &pi- и 2 м. Подсчеты дают результат: 6,28 м.

Ответ: Белка пробегает 6,28 м.

Периметром плоской геометрической фигуры называется суммарная длина всех составляющих ее сторон. У круга такая сторона всего одна, и ее протяженность обычно называют длиной окружности, а не периметром. В зависимости от известных параметров круга вычислять эту величину можно разными способами.

Спонсор размещения P&G Статьи по теме «Как определить периметр круга» Как найти периметр круга Как вычислить периметр окружности Как вычислить радиус круга

Инструкция

Для измерения периметра круга на местности используйте специальное устройство — курвиметр. Чтобы узнать с его помощью длину окружности, агрегат нужно просто прокатить по ней колесом. Такие же приборы, но гораздо меньших размеров, используются и для определения длины любых кривых линий, включая окружности, на чертежах и картах. Если нужно вычислить длину окружности (L) по известному диаметру (d), умножьте его на число Пи (3,1415926535897932384626433832795…), округлив количество знаков до нужной степени точности: L=d*?. Так как диаметр равен удвоенному радиусу (r), если известна эта величина, добавьте в формулу соответствующий множитель: L=2*r*?. Зная площадь круга (S), тоже можно вычислить длину окружности (L). Соотношение и этих двух величин выражается через число Пи, поэтому удвойте квадратный корень из произведения площади на эту математическую константу: L = 2*v(S*?). Если известна площадь (s) не всего круга, а лишь сектора с заданным центральным углом (?), то при вычислении длины окружности (L) исходите из формулы предыдущего шага. Если угол выражен в градусах, площадь сектора будет составлять?/360 от общей площади круга, которую можно выразить формулой s*360/?. Подставьте ее в приведенное выше равенство: L = 2*v((s*360/?)*?) = 2*v(s*360*?/?). Однако чаще для измерения центрального угла используют не градусы, а радианы. В этом случае площадь сектора будет составлять?/(2*?) от общей площади круга, а формула вычисления длины окружности приобретет такой вид: L = 2*v((s*2*?/?)*?) = 2*v(s*2*??/?) = 2*?*v(2*s/?).

Аналогичные пропорции применяйте и при вычислении длины окружности (L) по известным длине дуги (l) и соответствующему ей центральному углу (?) — в этом случае формулы будут проще. При центральном угле, выраженном в градусах, используйте такое тождество: L = l*360/?, а если он дан в радианах, формула должна быть такой: L = l*2*?/?. Как просто

Другие новости по теме:

Древними геометрами на основе многократных математических действий с кругом, окружностью и диаметром было выведено универсальное число Пи. Пи – это отношение длины окружности к ее радиусу с числовым значением приблизительно 3.14. Вам понадобится знания и умения математического счета Спонсор

Длиной окружности называют протяженность границы круга — простейшей плоской геометрической фигуры. По определению каждая точка этой границы находится на одинаковом расстоянии от центра, поэтому при заданной длине окружности эту границу можно найти только одним единственным способом. Из этого

Если все точки внутри периметра круга не выходят за пределы периметра треугольника и при этом периметр круга имеет всего по одной общей точке с каждой из сторон треугольника, то окружность называется вписанной в треугольник. Существует всего одно значение радиуса круга, при котором его можно

Вычисление площади круга и его частей относится к задачам по геометрии 9-го класса. Умение их решать вам может потребоваться не только для того, чтобы помочь вашему ребенку с геометрией, но и для выполнения технических задач на работе или в быту. Применяя формулу вычисления площади круга, можно,

Длину линии, ограничивающей внутреннее пространство плоской геометрической фигуры, обычно называют периметром. Однако применительно к кругу этот параметр фигуры не менее часто обозначают понятием «длина окружности». Свойства круга, связанные с длиной окружности, известны очень давно, а способы

Для решения поставленной задачи прежде всего необходимо ввести понятие числа П (Пи). Число П – математическая константа, выражающая отношение длины окружности к диаметру этой окружности. П – это бесконечная непериодическая десятичная дробь, её значение постоянно для любых окружностей и

Вычислить площадь окружности невозможно, ведь это линия, понятие площади для нее не определено. Зато можно вычислить площадь круга, ограниченного этой окружностью. Для решения задачи надо знать радиус. Спонсор размещения P&G Статьи по теме «Как вычислить площадь окружности» Как найти площадь

Знаете ли вы, что человек за всю свою жизнь забывает около 40% информации, которую он воспринимал. Из этого следует, что все запомнить, и тем более все знать очень тяжело, а порой даже нереально. К примеру, после того, как ученик закончил школу, а потом институт, допустим, по гуманитарной специальности, а не по технической (строительный или инженерный факультет), можно с большой вероятностью утверждать, что он уже давно забыл элементарную математику.

Вот вы помните, как найти высоту трапеции, как найти производную функции или же правильно построить график? Наверняка, нет. Редко кто сможет осилить такую задачу без дополнительной помощи. Возьмем, например, студента, который плохо изучал геометрию в школе, и просто забыл, как найти периметр круга. Эта статья пригодится тем, кто желает возобновить в памяти школьную программу математики. Зачастую такая необходимость возникает у родителей, к которым дети-школьники обращаются за помощью по домашнему заданию по геометрии, а также ученикам, которые сейчас изучают материал.

Необходимо:

— круг, периметр которого нужно найти;
— школьный циркуль и линейка;
— листок бумаги и карандаш;
— калькулятор.

Инструкция:

• Найти периметр круга – это аналогичное задание вычислению длины окружности. Для начала потребуется измерять его радиус . Для этого нужно воспользоваться циркулем. Одну его ножку ставим в центр круга, а вторую на любую точку окружности. Поскольку окружность представляет собой совокупность всех равно-отдаленных точек от центра, то куда именно станет вторая ножка циркуля — роли не играет, поскольку везде будет одинаковое расстояние.
• Если же под рукой нет циркуля, то можно узнать диаметр круга при помощи линейки. Для этого измеряем длину, положив линейку так, чтобы она проходила через центр круга. Расстояние, которое мы получим, будет диаметром . Он равен двум радиусам, поэтому формула, приведенная немного дальше, остается актуальной.
• Если центр круга не обозначен, то линейкой измеряем самое большое расстояние от одной точки окружности к другой. При таком способе расчета, полученный периметр круга будет числом неточным, так как диаметр мы могли определить не совсем точно. Полученное расстояние измеряем на линейке, приложив к ней циркуль. Результат записываем на листе бумаги. Это и есть радиус нашей окружности.
• Чтобы узнать периметр круга, нужно воспользоваться формулой . Она очень проста: радиус нашей окружности умножается на два, после чего умножается на число Пи , которое является постоянным и равняется значению 3,14 . Рассчитали его еще древние математики, а последующие поколения успешно применяют в вычислениях уже не одну тысячу лет, поэтому в его правильности можно не сомневаться. После того, как мы проведем расчеты, получим число, которое и является искомым.
• Для окружностей больших размеров алгоритм и инструкция по измерению остается прежней, вот только линейка и циркуль заменяются строительной рулеткой, и специальными программами для расчетов.

Мне нужна помощь в определении окружности и площади кругов.

Площадь кругов

Кортни Т.

спросил 09.01.13

Мне нужна помощь в этом, мой учитель математики не очень хороший учитель, когда дело доходит до обучения. Пожалуйста, объясните мне это. Это > π < является символом пи . Спасибо!

Решите, используя:        C = 2πr = πd   или      A = πr ²

1. Какова длина окружности с радиусом 6?
2. Длина окружности равна 24π. Каков радиус?
3. Если длина окружности 32π, какова площадь?
4. Какова площадь круга с радиусом 5?
5. Площадь круга равна 169π. Каков радиус?
6. Площадь круга равна 100π. Если радиус удвоится, какова будет новая площадь?

 

Подписаться І 7

Еще

Отчет

7 ответов от опытных наставников

Лучший Новейшие Самый старый

Автор: Лучшие новыеСамые старые

Джонни Р. ответил 02.03.13

Репетитор

4,8 (166)

Исключительный репетитор по математике и бухгалтерскому учету

См. таких репетиторов

Смотрите таких репетиторов

Кортни , чтобы решить их, вы должны подставить формулу для каждого.

Понятия, которые нужно запомнить .
• Окружность — это площадь за пределами круга.
• Радиус — это прямая линия из центра окружности, конечная точка которой лежит на окружности.
• Диаметр — это прямая линия, проходящая через центр окружности, обе конечные точки которой лежат на окружности. Следовательно, диаметр в два раза больше длины или расстояния радиуса.
• пи π символизирует отношение — отношение относительного размера окружности круга к его диаметру. Числовое значение π равно 3,14

Начнем с того, что мы знаем, и определим, что мы хотим знать.

• Мы знаем, что длина окружности в 2 раза больше радиуса, умноженного на π. = 2 (3,14) умножить на радиус или (6,28 умножить на радиус).
• Мы знаем, что длина окружности равна π, умноженному на диаметр, или (3,14 x диаметр).
• Мы знаем, что площадь круга равна π, умноженному на квадрат радиуса, или (3,14 x r ² ).

Начнем с числа 1.

1. Длина окружности равна «2 πr». Мы знаем, что 2 π = 6,28. Радиус равен 6.
Уравнение будет 6,28 x 6 = 37,68
2. Длина окружности равна «2 πr». Если длина окружности равна 24 π, то наше уравнение будет «24 π = 2 πr». Чтобы упростить, разделите обе части на π, чтобы исключить. Уравнение становится 24 = 2r. 12= r (радиус).
3. Площадь равна πr ² . Длина окружности равна «2 πr». Если длина окружности равна 32 π, то наше уравнение будет «32 π = 2 πr». Чтобы упростить, разделите обе части на π, чтобы исключить. Уравнение становится 32 = 2r. 16= r (радиус).
Подставим 16 вместо r в нашу формулу и 3,14 вместо π, и мы получим
A = 3,14 (16 ² ) = 3,14 x 256 = 803,84

. в состоянии вычислить окончательное 3.

 

Голосовать за 0 голос против

Подробнее

Отчет

Джереми Э. ответил 10.01.13

Репетитор

Новое в Византе

Терпеливый, эффективный репетитор по математике, естественным наукам и истории

Смотрите таких репетиторов

Смотрите таких репетиторов

C = 2πr = πd или A = πr2

Какова длина окружности с радиусом 6? 12π
Длина окружности равна 24π. Каков радиус? 12
Если длина окружности 32π, какова площадь? 18
Какова площадь круга с радиусом 5? 25π
Площадь круга равна 169π. Каков радиус? 13
Площадь круга равна 100π. Если радиус удвоится, какова будет новая площадь? №400

Голосовать за 0 голос против

Подробнее

Отчет

Стив П. ответил 09.01.13

Репетитор

5,0 (136)

Позитивный, ориентированный на достижения репетитор, специализирующийся на физике

Смотрите таких репетиторов

Смотрите таких репетиторов

Для каждого вопроса необходимо:

1) Решите, какую формулу использовать.
2) Подставьте каждое данное число в нужное место в формуле.
3) Решить.

Вот как сделать #1:

Требуется длина окружности, поэтому используйте формулу C = 2*pi*r.

Подставьте «6» для радиуса: C = 2*pi*6

Решите:  C = 12*pi

Голосовать за 0 голос против

Подробнее

Отчет

Келли Х. ответил 09.01.13

Репетитор

5,0 (90)

Репетитор по математике и естествознанию — Технологический институт Джорджии

Смотрите таких репетиторов

Посмотреть таких репетиторов

Привет, Кортни,

1. Поскольку радиус равен 6, тогда r = 6, а длина окружности C = 2*pi*6 или 12*pi

2. Длина окружности равна 24pi, поэтому она должна равняться уравнению для длины окружности или 24pi = 2*пи*г; Вы можете разделить обе части уравнения на 2pi, тогда r = 12

3. Решите так же, как в вопросе 2, разделите на 2pi, чтобы получить r = 16, а затем подставьте в уравнение для площади. A = pi*(16) ² = 256pi

4. Подставьте 5 для радиуса; А = пи * (5) ² = 25pi

5.  если площадь равна 169pi, установите это значение равным уравнению для площади, так что 169pi = pi*r ² . Сначала разделите обе части уравнения на число пи, тогда r ² = 169, а затем извлеките квадратный корень из 169, чтобы получить r = 13.

6. Сначала решите радиус, как в вопросе 5, чтобы получить r = 10. Теперь удвойте радиус (20) и подставьте в уравнение площади A = pi*(20) ² = 400pi

Надеюсь, это поможет!

Голосовать за 0 голос против

Подробнее

Отчет

Кевин С. ответил 09.01.13

Репетитор

5 (4)

Смотрите таких репетиторов

Смотрите таких репетиторов

Окружность круга — это расстояние по его внешней стороне (представьте, что вы идете по внешней стороне круглого бассейна). Длина окружности равна π, умноженному на удвоенный радиус (расстояние от центра круга до внешней стороны) или диаметр (расстояние от одной стороны круга до другой, проходящее через центр круга).

Исходя из этого,

1 : C = 2πr = 2π(6) = 12π

2: 24π = 2πr Разделите каждую сторону на 2π, и у вас останется r = (24π)/(2π) или r = 12

3: Следуйте примеру из пункта 2. Как только вы найдете r, возведите его в квадрат, затем умножьте на π, и вы получите площадь.

4: A = πr ² = π(5) ² = 25π

5: A = 169π, поэтому 169π = πr ² . Разделите обе части на π (в результате у вас останется r ² в правой части), затем извлеките квадратный корень из обеих частей.

6: Следуйте шагам задачи 5, чтобы определить радиус круга площадью 100π. Затем возведите радиус в два раза и определите новую площадь (Подсказка: это A’ = π(2r) ² )

Голосовать за 0 голос против

Подробнее

Отчет

Дэниел К. ответил 09.01.13

Репетитор

4. 9 (45)

Опытный и энергичный репетитор Колледжа Уильямс

Смотрите таких репетиторов

Смотрите таких репетиторов

π — это просто отношение диаметра d (или удвоенного радиуса r) круга к его длине окружности. Другими словами, окружность диаметром 1 или радиусом 1/2 будет иметь длину окружности π. π также представляет собой отношение r в квадрате (r умножить на r) к площади круга, а это означает, что круг с радиусом 1 будет иметь площадь π. Давайте рассмотрим некоторые из ваших вопросов.

1) Здесь нам дали, что радиус равен 6. Теперь мы просто подставляем это в наше уравнение для длины окружности и находим длину окружности 12π или около 37,7.

2) Теперь у нас есть длина окружности и нам нужен радиус, поэтому мы перестраиваем наше уравнение окружности, чтобы найти r. Мы делаем это, разделив обе части на 2π, чтобы получить: r = C/2π. Теперь мы просто подставляем нашу длину окружности 24π, чтобы получить 24π/2π или 12.  

3) Мы можем решить это уравнение в три шага. Сначала мы используем уравнение из задачи 2 для решения радиуса. Это даст нам 16 как r. Теперь подставим 16 в наше уравнение A = π(r-квадрат), чтобы получить площадь 256π.

 

Как видите, все эти вопросы можно решить, перейдя от того, что вам дано (будь то радиус, площадь или длина окружности), к тому, что вам нужно решить. Посмотрите, сможете ли вы самостоятельно решить следующие три задачи, используя то, что я объяснил. Для числа 6 вам нужно найти первоначальный радиус, удвоить его, а затем найти новую площадь. Надеюсь, это поможет!

Голосовать за 0 голос против

Подробнее

Отчет

Билл Ф. ответил 09.01.13

Репетитор

5 (1)

Опытный преподаватель и репетитор в Раунд-Рок, Техас

Смотрите таких репетиторов

Смотрите таких репетиторов

Хорошо, Кортни, это несложно:  

Мы знаем, что 2 r = 1 d (диаметр в два раза больше радиуса), верно?

И вы можете вспомнить или легко найти, что пи (∏) = приблизительно 3,14

1. У нас есть C = 2∏r, или ∏d. Теперь просто подставим то, что мы знаем: 2*∏*r = 2*3,14*6 = 37,68

2. Если C — 2∏r, то C/2∏ = r, или r = C/2∏: r = 32∏/2∏ = 16

3. Если C = 32∏, то r = 16∏. A=∏r ²  :  A = (∏)(16∏) ²  = 256∏ ³ . Если мы умножим это, = 7 925,54

Теперь я знаю, что вы можете сделать все остальное!

Голосовать за 0 голос против

Подробнее

Отчет

Все еще ищете помощи? Получите правильный ответ, быстро.

Задайте вопрос бесплатно

Получите бесплатный ответ на быстрый вопрос.
Ответы на большинство вопросов в течение 4 часов.

ИЛИ

Найдите онлайн-репетитора сейчас

Выберите эксперта и встретьтесь онлайн. Никаких пакетов или подписок, платите только за то время, которое вам нужно.

3.2.3: Отношение площади к окружности

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

38175

• Иллюстративная математика
• OpenUp Resources

Lesson

Давайте переставим круги, чтобы вычислить их площади.

Упражнение \(\PageIndex{1}\): Орошение поля

Круглое поле представляет собой квадрат со стороной 800 м. Оцените площадь поля.

Рисунок \(\PageIndex{1}\): Квадрат, где расстояние по вертикали обозначено как 800 метров. Внутри квадрата рисуется максимально возможная окружность с отрезком, который начинается от центра окружности до точки на краю окружности. 9{2}\)

Упражнение \(\PageIndex{2}\): Создание многоугольника из круга

Учитель даст вам круглый предмет, маркер и два листа бумаги разных цветов.

Следуйте этим инструкциям, чтобы создать визуальное представление:

1. Используя толстый маркер, обведите круг в двух разных местах на одном листе бумаги.
2. Вырежьте оба круга по маркерной линии.
3. Сложите и разрежьте один из кругов на четыре части.
4. Расположите четверти так, чтобы прямые стороны были рядом друг с другом, а изогнутые края были попеременно сверху и снизу. Сделайте паузу, чтобы учитель мог просмотреть вашу работу.
5. Сложите и разрежьте четверти пополам, чтобы получились восьмые. Расположите восьмые рядом друг с другом, как вы это делали с четвертыми.
6. Если ваши части все еще достаточно велики, повторите предыдущий шаг, чтобы сделать шестнадцатые.
7. Приклейте оставшийся круг и новую фигуру на лист бумаги другого цвета.

После того, как вы закончите склеивать фигуры, ответьте на следующие вопросы.

1. Как соотносятся площади двух фигур?
2. На какой многоугольник больше всего похожа форма, состоящая из частей круга?
3. Как найти площадь этого многоугольника?

Упражнение \(\PageIndex{3}\): создание другого многоугольника из круга

Представьте себе круг, состоящий из колец, которые могут сгибаться, но не растягиваться.

Рисунок \(\PageIndex{2}\)

Посмотрите анимацию.

1. На какой многоугольник похожа новая форма?
2. Как площадь многоугольника соотносится с площадью круга?
3. Как найти площадь многоугольника?
4. Покажите, подробно по шагам, как можно найти площадь многоугольника с точки зрения размеров окружности. Покажите свое мышление. Организуйте его так, чтобы за ним могли следить другие.
5. После того, как вы закончите, обменяйтесь бумагами с напарником и проверьте работу друг друга. Если вы не согласны, постарайтесь прийти к соглашению. Обсуждать:
   • Вы согласны или не согласны с каждым шагом?
   • Можно ли сделать объяснение более понятным?
6. Верните работу вашего партнера и пересмотрите свое объяснение на основе полученных отзывов.

Упражнение \(\PageIndex{4}\): Мозаика таблицы

Елена хочет выложить мозаикой верхнюю часть круглого стола. Диаметр столешницы 28 дюймов. Какова его площадь?

Готовы ли вы к большему?

В коробке 20 квадратных плиток со стороной 2 дюйма. Сколько коробок плитки понадобится Елене, чтобы выложить плиткой стол? 9{2}\)

(Помните, что когда у нас есть, мы можем написать и сказать « в квадрате ».)

Это означает, что если мы знаем радиус, мы можем найти площадь. Например, если окружность имеет радиус 10 см, то площадь равна примерно \((3.14)\cdot 100\), что равно 314 см ² .

Если мы знаем диаметр, мы можем вычислить радиус, а затем найти площадь. {2}\)?

Упражнение \(\PageIndex{6}\)

Длина окружности примерно 76 см. Оцените радиус, диаметр и площадь круга.

Упражнение \(\PageIndex{7}\)

Джада рисует круглый стол диаметром 37 дюймов. Какова площадь стола?

Упражнение \(\PageIndex{8}\)

В карусели Национальной аллеи есть 4 круга лошадей. Киран едет по внутреннему кольцу радиусом 9 футов. Май едет по внешнему кольцу, которое находится на 8 футов дальше от центра, чем внутреннее кольцо.

1. За один оборот карусели, насколько дальше проходит Май, чем Киран?
2. Один оборот карусели занимает 12 секунд. Насколько быстрее Май движется, чем Киран?

(Из модуля 3.1.4)

Упражнение \(\PageIndex{9}\)

Вот диаметры четырех монет:

монета	пенни	никель	десять центов	квартал
диаметр	\(1,9\) см	\(2. No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт