Как рассчитать площадь по периметру. Калькулятор вычисления периметра и площади геометрических фигур
При решении, необходимо принять во внимание, что решить задачу о нахождении площади прямоугольника только из длины его сторон нельзя .
В этом несложно убедиться. Пусть периметр прямоугольника будет равен 20 см. Это будет верно, если его стороны 1 и 9, 2 и 8, 3 и 7 см. Все эти три прямоугольника будут иметь одинаковый периметр, равный двадцати сантиметрам. (1 + 9) * 2 = 20 точно также как и (2 + 8) * 2 = 20 см.
Как видно, мы можем подобрать бесконечное количество вариантов размеров сторон прямоугольника, периметр которого будет равен заданному значению.
Площадь прямоугольников с заданным периметром 20 см, но с различными сторонами будет различна. Для приведенного примера — 9, 16 и 21 квадратных сантиметров соответственно.
S 1 = 1 * 9 = 9 см 2
S 2 = 2 * 8 = 16 см 2
S 3 = 3 * 7 = 21 см 2
Как видим, вариантов площади фигуры при заданном периметре — бесконечное количество.
Таким образом, для того, чтобы вычислить площадь прямоугольника из его периметра, нужно обязательно знать либо соотношение его сторон, либо длину одной из них. Единственной фигурой, которая имеет однозначную зависимость своей площади от периметра, является круг. Только для круга и возможно решение.
В этом уроке:
- Задача 4. Изменение длины сторон при сохранении площади прямоугольника
Задача 1. Найти стороны прямоугольника из площади
Периметр прямоугольника равен 32 сантиметрам, а сумма площадей квадратов, построенных на каждой из его сторон — 260 квадратных сантиметров. Найдите стороны прямоугольника.
Решение.
2(x+y)=32
Согласно условию задачи, сумма площадей квадратов построенных на каждой из его сторон (квадратов, соответственно, четыре) будет равна
x+y=16
x=16-y
2(16-y) 2 +2y 2 =260
2(256-32y+y 2)+2y 2 =260
512-64y+4y 2 -260=0
4y 2 -64y+252=0
D=4096-16×252=64
x 1 =9
x 2 =7
Теперь примем во внимание, что исходя из того, что x+y=16 (см.
 выше) при x=9, то y=7 и наоборот, если x=7, то y=9
выше) при x=9, то y=7 и наоборот, если x=7, то y=9 Ответ : Стороны прямоугольника равны 7 и 9 сантиметров
Задача 2. Найти стороны прямоугольника из периметра
Периметр прямоугольника 26 см, а сумма площадей квадратов, построенных на двух его смежных сторонах, равна 89 кв. см. Найдите стороны прямоугольника.
Решение.
Обозначим стороны прямоугольника как x и y.
Тогда периметр прямоугольника равен:
2(x+y)=26
Сумма площадей квадратов построенных на каждой из его сторон (квадратов, соответственно, два и это квадраты ширины и высоты, поскольку стороны смежные) будет равна
x 2 +y 2 =89
Решаем полученную систему уравнений. Из первого уравнения выводим, что
y=13-y
Теперь выполняем подстановку во второе уравнение, заменяя x его эквивалентом.
(13-y) 2 +y 2 =89
169-26y+y 2 +y 2 -89=0
2y 2 -26y+80=0
Решаем полученное квадратное уравнение.
D=676-640=36
x 1 =5
x 2 =8
Теперь примем во внимание, что исходя из того, что x+y=13 (см.
 выше) при x=5, то y=8 и наоборот, если x=8, то y=5
выше) при x=5, то y=8 и наоборот, если x=8, то y=5 Ответ: 5 и 8 см
Задача 3. Найти площадь прямоугольника из пропорции его сторон
Найти площадь прямоугольника если его периметр равен 26 см а стороны пропорциональны как 2 к 3.
Решение.
Обозначим стороны прямоугольника через коэффициент пропорциональности x.
Откуда длина одной стороны будет равна 2x, другой — 3х.
Тогда:
2(2x+3x)=26
2x+3x=13
5x=13
x=13/5
Теперь, исходя из полученных данных, определим площадь прямоугольника:
2x*3x=2*13/5*3*13/5=40,56 см 2
Длина прямоугольника увеличена на 25%. На сколько процентов надо уменьшить ширину, чтобы его площадь не изменилась?
Решение .
Площадь прямоугольника равна
S = ab
В нашем случае один из множителей увеличился на 25%, что означает a 2 = 1,25a . Таким образом, новая площадь прямоугольника должна быть равна
S 2 = 1,25ab
Таким образом, для того, чтобы вернуть площадь прямоугольника к начальному значению, то
S 2 = S / 1.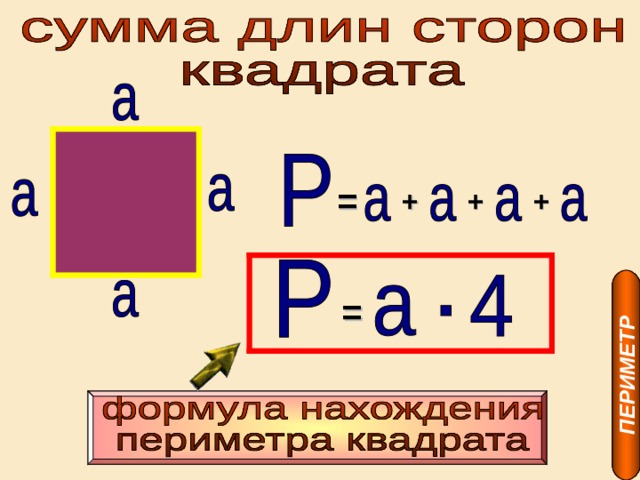 25
25
S 2 = 1,25ab / 1.25
Поскольку новый размер а изменять нельзя, то
S 2 = (1,25a) b / 1.25
1 / 1,25 = 0,8
Таким образом, величину второй стороны нужно уменьшить на (1 — 0,8) * 100% = 20%
Ответ : ширину нужно уменьшить на 20%.
Как вычислить площадь фигуры зная ее периметр? и получил лучший ответ
Ответ от Ёемен Аркадьевич[гуру]
В Компас 3D нанести план и автоматически посчитать площадь. По периметру площадь произвольного многоугольника не посчитать. Все равно придется разбивать на отдельные фигуры.
Будут вопросы — пиши в агент.
Ответ от Ѐамис Ш [новичек]
..
Ответ от Kiss(RUSS фор всех) ки (я) [гуру]
1.выбрать центр
2.измерить расстояние от центра до углов
3.измерить стороны вашего многоугольника
4.вычислить периметры получившихся N треугольников
5.вычислить площади всех треугольников, используя формулу Герона-через полупериметр.
6.суммировать все площади
7.выбрать мой ответ лучшим.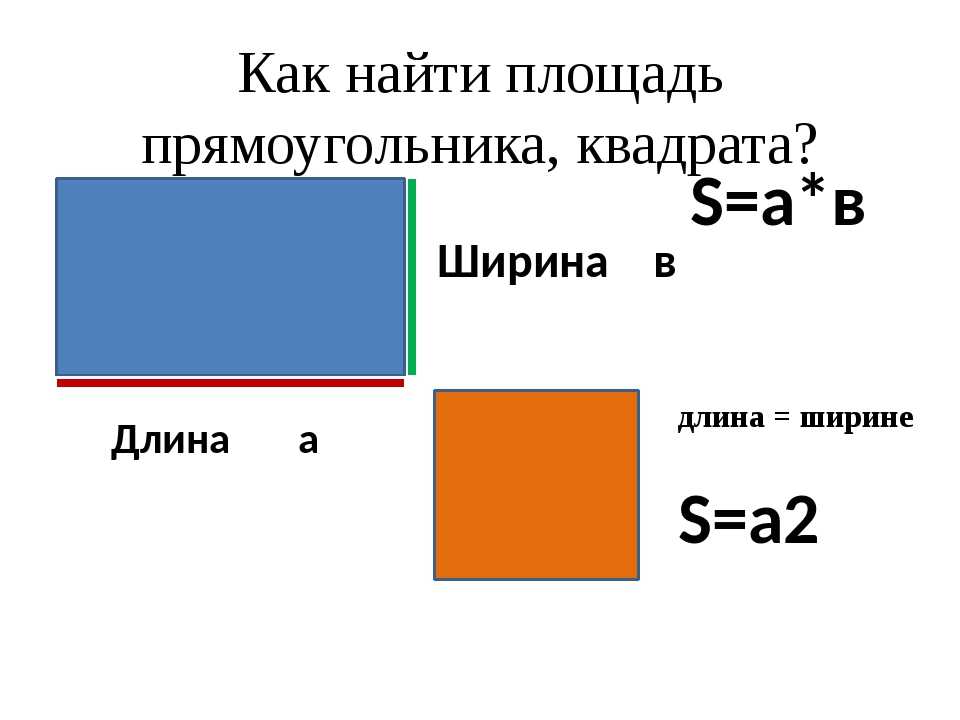
8.все
Ответ от Semrid [гуру]
попробуй разделить периметр на 4 и потом перемножить полученное друг на друга
Ответ от ScrAll [гуру]
Или разбиваешь на треугольники.
Половина основания на высоту…
Ответ от Алексей Зайцев [гуру]
Проще и безошибочнее начертить эскизик — вид сверху с размерами. Затем по этому эскизику площадь разделить на прямоугольники, посчитать и просуммировать их площади
Ответ от Мария Кемпель [активный]
нереально
Ответ от Nemo [гуру]
Нереально. По периметру вычисляется площадь только ПРАВИЛЬНЫХ фигур. Советую кусочным способом
Ответ от Djon [гуру]
лучше всего разбить сложную фигуру на несколько простых, и посчитать площадь отдельно, затем сложить
Ответ от Lavavoth [гуру]
Нереально.. . Лучше выложи план зала, есть другие способы подсчета, но нужно видеть план.
Ответ от 3 ответа [гуру]
Привет! Вот подборка тем с ответами на Ваш вопрос: Как вычислить площадь фигуры зная ее периметр?
Петя хочет нарисовать фигуру, у которой периметр 12 см, а площадь 12 кв.
максимальная площадь по периметру у фигуры — Круг.
Если площадь круга с длинной окружности 12
Определение периметра и площади геометрических фигур — важная задача, которая возникает при решении многих практических или бытовых задач. Если вам требуется поклеить обои, установить забор, рассчитать расход краски или кафеля, то вам обязательно придется иметь дело с геометрическими расчетами.
Для решения перечисленных бытовых вопросов вам потребуется работать с самыми разными геометрическими фигурами. Мы представляем вам каталог онлайн-калькуляторов, которые позволяют вычислить параметры наиболее популярных плоских фигур. Рассмотрим их.
Круг
Частные случаи
Четырехугольник с одинаковыми сторонами. Параллелограмм становится ромбом в случаях, если его диагонали пересекаются под углом 90 градусов и являются биссектрисами своих углов.
Это параллелограмм с прямыми углами. Кроме того, параллелограмм считается прямоугольником, если его стороны и диагонали отвечают условиям теоремы Пифагора.
Это параллелограмм, у которого все стороны равны и все углы равны. Диагонали квадрата полностью повторяют свойства диагоналей прямоугольника и ромба, что делает квадрат уникальной фигурой, которая характеризуется максимальной симметрией.
Многоугольник
Правильный полигон — это выпуклая фигура на плоскости, которая имеет равные стороны и равные углы. В зависимости от количества сторон многоугольники имеют собственные названия:
- — пентагон;
- — гексагон;
- восемь — октагон;
- двенадцать — додекагон.
И так далее. Геометры шутят, что круг — это многоугольник с бесконечным количеством углов. Наш калькулятор запрограммирован на определение периметров и площадей только правильных многоугольников. Он использует общие формулы для всех правильных полигонов. Для вычисления периметра используется формула:
где n – количество сторон многоугольника, a – длина стороны.
Для определения площади используется выражение:
S = n/4 × a 2 × ctg(pi/n).
Подставляя соответствующее n, мы можем подобрать формулу для любого правильного многоугольника, к которым также относятся равносторонний треугольник и квадрат.
Многоугольники имеют большое распространение в реальной жизни. Так форму пятиугольника имеет здание министерства обороны США — Пентагон, гексагона — пчелиные соты или кристаллы снежинки, октагона — дорожные знаки. Кроме того, многие простейшие, например радиолярии, имеют форму правильных полигонов.
Примеры из реальной жизни
Давайте рассмотрим пару примеров использования нашего калькулятора в реальных расчетах.
Покраска забора
Покраска поверхностей и расчет краски — это одни из самых очевидных бытовых задач, в которых требуются минимальные математические расчеты. Если нам нужно покрасить забор, высота которого составляет 1,5 метра, а длина 20 метров, то сколько потребуется банок краски? Для этого нужно узнать суммарную площадь забора и расход лакокрасочных материалов на 1 квадратный метр. Мы знаем, что расход эмали составляет 130 грамм на метр. Теперь определим площадь забора, используя калькулятор для вычисления площади прямоугольника. Она составит S = 30 квадратных метров. Естественно, что забор мы будем красить с обеих сторон, поэтому площадь для покраски увеличится до 60 квадратов. Тогда нам понадобится 60 × 0,13 = 7,8 килограмм краски или три стандартных банки по 2,8 килограмма.
Теперь определим площадь забора, используя калькулятор для вычисления площади прямоугольника. Она составит S = 30 квадратных метров. Естественно, что забор мы будем красить с обеих сторон, поэтому площадь для покраски увеличится до 60 квадратов. Тогда нам понадобится 60 × 0,13 = 7,8 килограмм краски или три стандартных банки по 2,8 килограмма.
Отделка бахромой
Пошив одежды — еще одна отрасль, в которой необходимы обширные геометрические познания. Пусть нам надо отделать бахромой платок, который представляет собой равнобедренную трапецию со сторонами 150, 100, 75 и 75 см. Для вычисления расхода бахромы нам потребуется узнать периметр трапеции. В этом нам и пригодится онлайн-калькулятор. Введем эти данные ячейки и получим ответ:
Таким образом, нам понадобится 4 м бахромы для отделки платка.
Заключение
Плоские фигуры составляют реальный мир вокруг. Мы часто задавались в школе вопросом, пригодится ли нам геометрия в будущем? Выше приведенные примеры показывают, что математика постоянно используется в повседневной жизни. И если площадь прямоугольника для нас привычна, то вычислить площадь додекагона может оказаться трудной задачей. Используйте наш каталог калькуляторов для решения школьных заданий или бытовых вопросов.
И если площадь прямоугольника для нас привычна, то вычислить площадь додекагона может оказаться трудной задачей. Используйте наш каталог калькуляторов для решения школьных заданий или бытовых вопросов.
Геометрия постигает свойства и колляции двумерных и пространственных фигур. Числовыми величинами, характеризующими такие конструкции, являются площадь и периметр, вычисление которых производится по знаменитым формулам либо выражается одно через другое.
Инструкция
1. Прямоугольник.Задача: вычислите площадь прямоугольника, если вестимо, что его периметр равен 40, а длина b в 1,5 раза огромнее ширины a.
2. Решение.Используйте знаменитую формулу периметра, он равен сумме всех сторон фигуры. В данном случае P = 2 a + 2 b. Из исходных данных задачи вы знаете, что b = 1,5 a, следственно, P = 2 a + 2 1,5 a = 5 a, откуда a = 8. Обнаружьте длину b = 1,5 8 = 12.
3. Запишите формулу для площади прямоугольника:S = a b,Подставьте вестимые величины:S = 8 *12 = 96.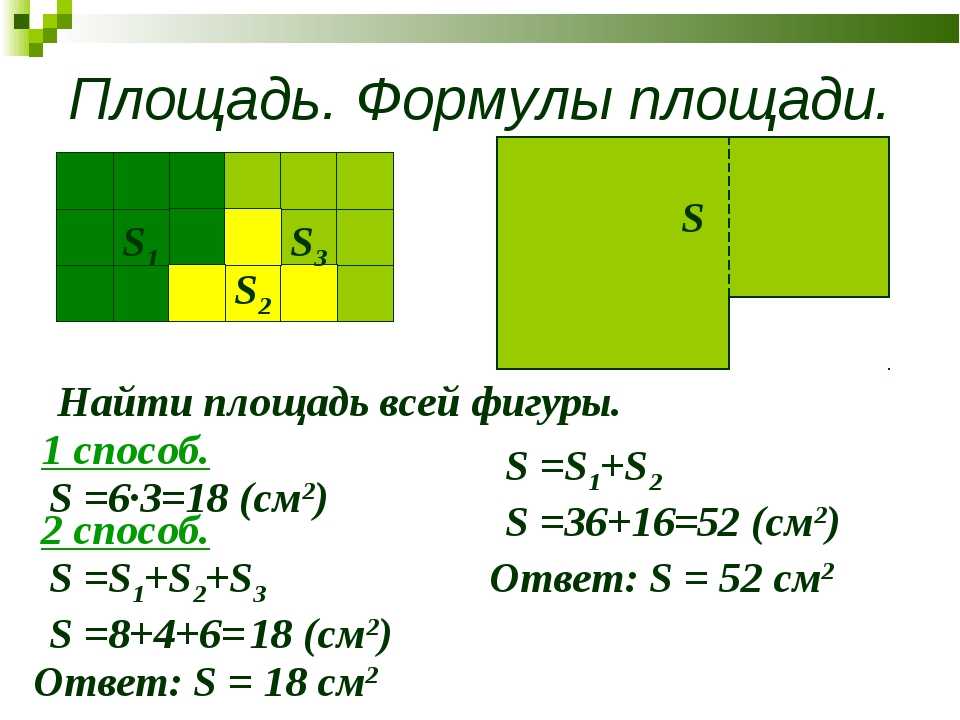
4. Квадрат.Задача: обнаружьте площадь квадрата, если периметр равен 36.
5. Решение.Квадрат – частный случай прямоугольника, где все стороны равны, следственно, его периметр равен 4 a, откуда a = 8. Площадь квадрата определите по формуле S = a? = 64.
6. Треугольник.Задача: пускай дан произвольный треугольник ABC, периметр которого равен 29. Узнайте величину его площади, если знаменито, что высота BH, опущенная на сторону AC, делит ее на отрезки с длинами 3 и 4 см.
7. Решение.Для начала припомните формулу площади для треугольника:S = 1/2 c h, где c – основание и h – высота фигуры. В нашем случае основанием будет сторона AC, которая знаменита по условию задачи: AC = 3+4 = 7, осталось обнаружить высоту BH.
8. Высота является перпендикуляром, проведенным к стороне из противоположной вершины, следственно, она разделять треугольник ABC на два прямоугольных треугольника. Зная это качество, разглядите треугольник ABH. Припомните формулу Пифагора, согласно которой:AB? = BH? + AH? = BH? + 9 ? AB = ?(h? + 9).В треугольнике BHC по тому же тезису запишите:BC? = BH? + HC? = BH? + 16 ? BC = ?(h? + 16).
Припомните формулу Пифагора, согласно которой:AB? = BH? + AH? = BH? + 9 ? AB = ?(h? + 9).В треугольнике BHC по тому же тезису запишите:BC? = BH? + HC? = BH? + 16 ? BC = ?(h? + 16).
9. Примените формулу периметра:P = AB + BC + ACПодставьте величины, выраженные через высоту:P = 29 = ?(h? + 9) + ?(h? + 16) + 7.
10. Решите уравнение:?(h? + 9) + ?(h? + 16) = 22 ? [замена t? = h? + 9]:?(t? + 7) = 22 – t, возведите обе стороны равенства в квадрат:t? + 7 = 484 – 44 t + t? ? t?10,84h? + 9 = 117,5 ? h ? 10,42
11. Обнаружьте площадь треугольника ABC:S = 1/2 7 10,42 = 36,47.
Периметр и площадь прямоугольника
Можно ли найти площадь из периметра?
При решении, необходимо принять во внимание, что решить задачу о нахождении площади прямоугольника только из длины его сторон нельзя.
В этом несложно убедиться. Пусть периметр прямоугольника будет равен 20 см. Это будет верно, если его стороны 1 и 9, 2 и 8, 3 и 7 см. Все эти три прямоугольника будут иметь одинаковый периметр, равный двадцати сантиметрам. ( 1 + 9 ) * 2 = 20 точно также как и ( 2 + 8 ) * 2 = 20 см.
Все эти три прямоугольника будут иметь одинаковый периметр, равный двадцати сантиметрам. ( 1 + 9 ) * 2 = 20 точно также как и ( 2 + 8 ) * 2 = 20 см.
Как видно, мы можем подобрать бесконечное количество вариантов размеров сторон прямоугольника, периметр которого будет равен заданному значению.
Площадь прямоугольников с заданным периметром 20 см, но с различными сторонами будет различна. Для приведенного примера — 9, 16 и 21 квадратных сантиметров соответственно.
S1 = 1 * 9 = 9 см2
S2 = 2 * 8 = 16 см2
S3= 3 * 7 = 21 см2
Как видим, вариантов площади фигуры при заданном периметре — бесконечное количество.
Таким образом, для того, чтобы вычислить площадь прямоугольника из его периметра, нужно обязательно знать либо соотношение его сторон, либо длину одной из них. Единственной фигурой, которая имеет однозначную зависимость своей площади от периметра, является круг. Только для круга и возможно решение.
Единственной фигурой, которая имеет однозначную зависимость своей площади от периметра, является круг. Только для круга и возможно решение.
В этом уроке:
-
Задача 1. Найти стороны прямоугольника из площади
- Задача 2. Найти стороны прямоугольника из периметра
- Задача 3. Найти площадь прямоугольника из пропорции его сторон
- Задача 4. Изменение длины сторон при сохранении площади прямоугольника
Задача 1. Найти стороны прямоугольника из площади
Периметр прямоугольника равен 32 сантиметрам, а сумма площадей квадратов, построенных на каждой из его сторон — 260 квадратных сантиметров. Найдите стороны прямоугольника.Решение.
Обозначим стороны прямоугольника как x и y.
Тогда периметр прямоугольника равен:
2(x+y)=32
Согласно условию задачи, сумма площадей квадратов построенных на каждой из его сторон (квадратов, соответственно, четыре) будет равна
2x2+2y2=260
Решаем полученную систему уравнений.
 Из первого уравнения выводим, что
Из первого уравнения выводим, что x+y=16
x=16-y
Теперь выполняем подстановку во второе уравнение, заменяя x его эквивалентом.
2(16-y)2+2y2=260
2(256-32y+y2)+2y2=260
512-64y+4y2-260=0
4y2-64y+252=0
Решаем полученное квадратное уравнение.
D=4096-16×252=64
x1=9
x2=7
Теперь примем во внимание, что исходя из того, что x+y=16 (см. выше) при x=9, то y=7 и наоборот, если x=7, то y=9
Ответ: Стороны прямоугольника равны 7 и 9 сантиметров
Задача 2. Найти стороны прямоугольника из периметра
Периметр прямоугольника 26 см, а сумма площадей квадратов, построенных на двух его смежных сторонах, равна 89 кв. см. Найдите стороны прямоугольника.
Решение.
Обозначим стороны прямоугольника как x и y.
Тогда периметр прямоугольника равен:
2(x+y)=26
Сумма площадей квадратов построенных на каждой из его сторон (квадратов, соответственно, два и это квадраты ширины и высоты, поскольку стороны смежные) будет равна
x2+y2=89
Решаем полученную систему уравнений. Из первого уравнения выводим, что
Из первого уравнения выводим, что
x+y=13
y=13-y
Теперь выполняем подстановку во второе уравнение, заменяя x его эквивалентом.
(13-y)2+y2=89
169-26y+y2+y2-89=0
2y2-26y+80=0
Решаем полученное квадратное уравнение.
D=676-640=36
x1=5
x2=8
Теперь примем во внимание, что исходя из того, что x+y=13 (см. выше) при x=5, то y=8 и наоборот, если x=8, то y=5
Ответ: 5 и 8 см
Задача 3. Найти площадь прямоугольника из пропорции его сторон
Найти площадь прямоугольника если его периметр равен 26 см а стороны пропорциональны как 2 к 3.
Решение.
Обозначим стороны прямоугольника через коэффициент пропорциональности x.
Откуда длина одной стороны будет равна 2x, другой — 3х.
Тогда:
2(2x+3x)=26
2x+3x=13
5x=13
x=13/5
Теперь, исходя из полученных данных, определим площадь прямоугольника:
2x*3x=2*13/5*3*13/5=40,56 см2
Решение.
Площадь прямоугольника равна
S = ab
В нашем случае один из множителей увеличился на 25%, что означает a2 = 1,25a . Таким образом, новая площадь прямоугольника должна быть равна
S2 = 1,25ab
Таким образом, для того, чтобы вернуть площадь прямоугольника к начальному значению, то
S2 = S / 1.25
S2 = 1,25ab / 1.25
поскольку новый размер а изменять нельзя, то
S2 = (1,25a) b / 1. 25
25
1 / 1,25 = 0,8
Таким образом, величину второй стороны нужно уменьшить на ( 1 — 0,8 ) * 100% = 20%
Ответ: ширину нужно уменьшить на 20%.
0
Периметр прямоугольника | Описание курса | Тригонометрия
Периметр, площадь и объем — Помощник для школьников Спринт-Олимпик.ру
Данный материал содержит геометрические фигуры с измерениями. Приведённые измерения являются приблизительными и могут не совпадать с измерениями в реальной жизни.
Содержание
- Периметр геометрической фигуры
- Площадь геометрической фигуры
- Площадь прямоугольника
- Площадь квадрата
- Обозначения
- Перевод единиц измерения площади
- Единицы измерения площади земельных участков
- Прямоугольный параллелепипед и куб
- Объём геометрической фигуры
- Кубический дециметр. Кубический метр
- Перевод единиц измерения объёма
- Таблица квадратов
- Таблица кубов
- Задания для самостоятельного решения
Периметр геометрической фигуры
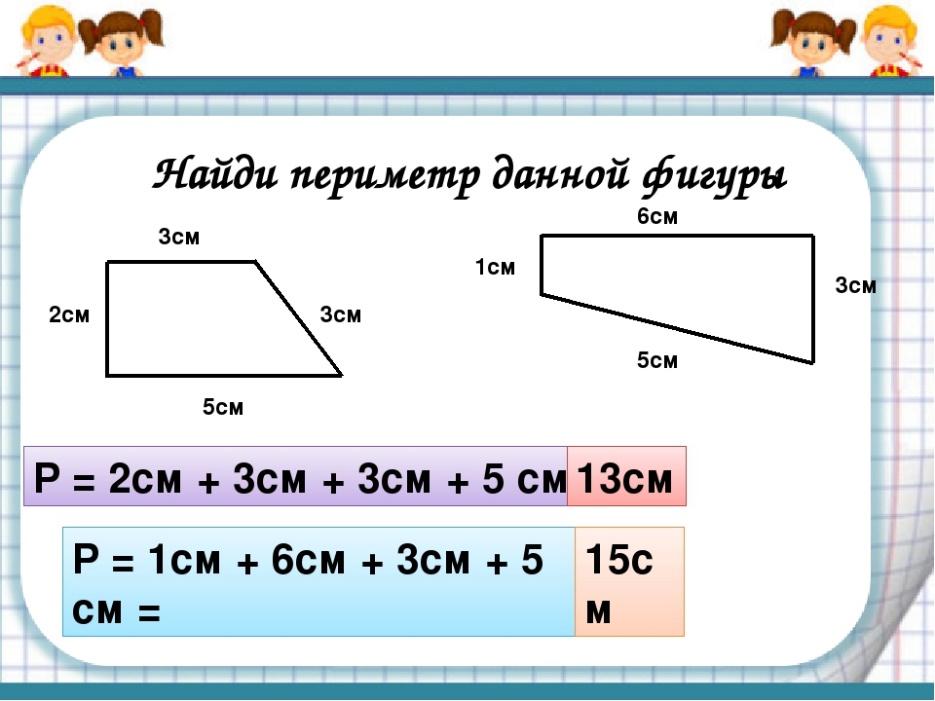
Периметр геометрической фигуры — это сумма всех её сторон.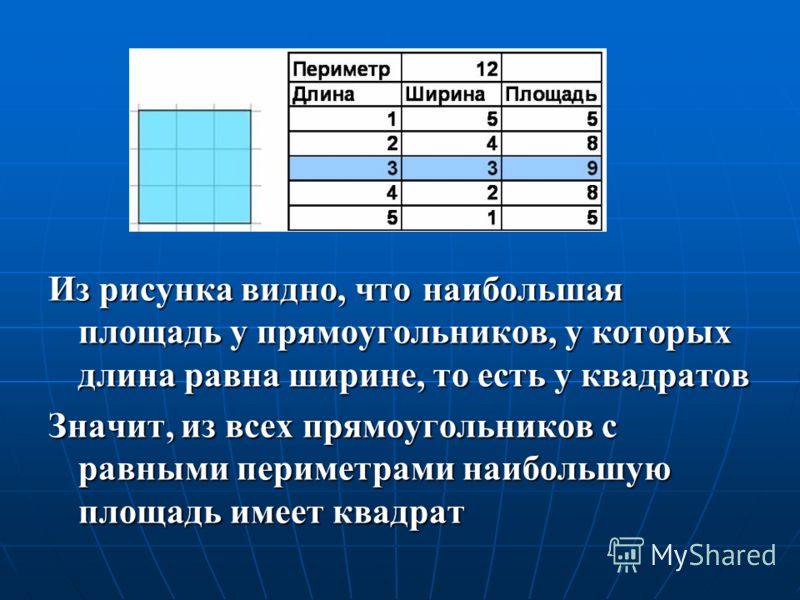 Чтобы вычислить периметр, нужно измерить каждую сторону и сложить результаты измерений.
Чтобы вычислить периметр, нужно измерить каждую сторону и сложить результаты измерений.
Вычислим периметр следующей фигуры:
Это прямоугольник. Детальнее мы поговорим об этой фигуре позже. Сейчас просто вычислим периметр этого прямоугольника. Длина его равна 9 см, а ширина 4 см.
У прямоугольника противоположные стороны равны. Это видно на рисунке. Если длина равна 9 см, а ширина равна 4 см, то противоположные стороны будут равны 9 см и 4 см соответственно:
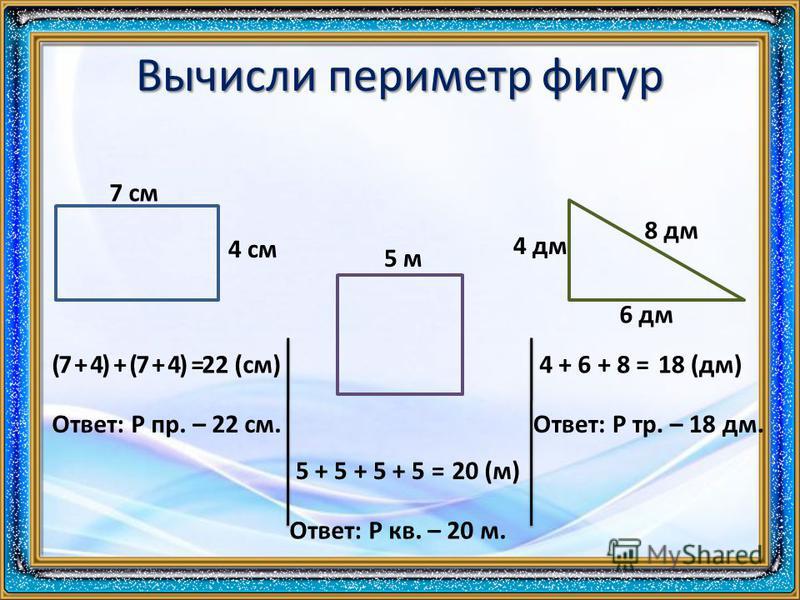
Найдём периметр. Для этого сложим все стороны. Складывать их можно в любом порядке, поскольку от перестановки мест слагаемых сумма не меняется. Периметр часто обозначается заглавной латинской буквой P (англ. perimeters). Тогда получим:
P = 9 см + 4 см + 9 см + 4 см = 26 см.
Поскольку у прямоугольника противоположные стороны равны, нахождение периметра записывают короче — складывают длину и ширину, и умножают её на 2, что будет означать «повторить длину и ширину два раза»
P = 2 × (9 + 4) = 18 + 8 = 26 см.
Квадрат это тот же прямоугольник, но у которого все стороны равны. Например, найдём периметр квадрата со стороной 5 см. Фразу «со стороной 5 см» нужно понимать как «длина каждой стороны квадрата равна 5 см»
Чтобы вычислить периметр, сложим все стороны:
P = 5 см + 5 см + 5 см + 5 см = 20 см
Но поскольку все стороны равны, вычисление периметра можно записать в виде произведения. Сторона квадрата равна 5 см, и таких сторон 4. Тогда эту сторону, равную 5 см нужно повторить 4 раза
P = 5 см × 4 = 20 см
Площадь геометрической фигуры
Площадь геометрической фигуры — это число, которое характеризует размер данной фигуры.
Следует уточнить, что речь в данном случае идёт о площади на плоскости. Плоскостью в геометрии называют любую плоскую поверхность, например: лист бумаги, земельный участок, поверхность стола.
Площадь измеряется в квадратных единицах. Под квадратными единицами подразумевают квадраты, стороны которых равны единице.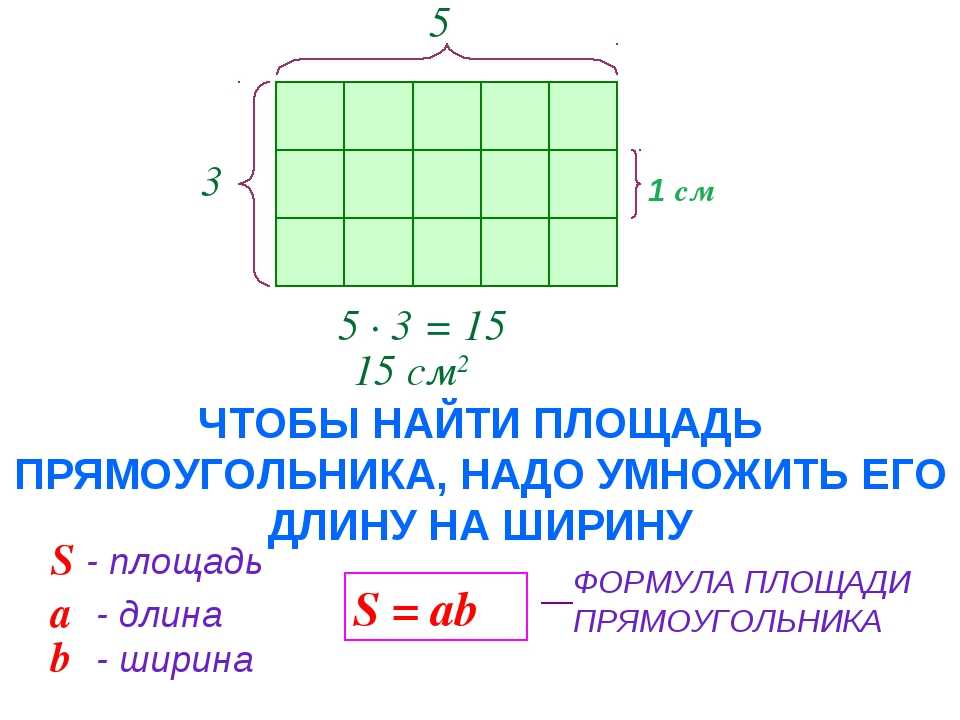 Например, 1 квадратный сантиметр, 1 квадратный метр или 1 квадратный километр.
Например, 1 квадратный сантиметр, 1 квадратный метр или 1 квадратный километр.
Измерить площадь какой-нибудь фигуры означает выяснить сколько квадратных единиц содержится в данной фигуре.
Например, площадь следующего прямоугольника равна трём квадратным сантиметрам:
Это потому что в данном прямоугольнике содержится три квадрата, каждый из которых имеет сторону, равную одному сантиметру:
Справа представлен квадрат со стороной 1 см (он в данном случае является квадратной единицей). Если посмотреть сколько раз этот квадрат входит в прямоугольник, представленный слева, то обнаружим, что он входит в него три раза.
Следующий прямоугольник имеет площадь, равную шести квадратным сантиметрам:
Это потому что в данном прямоугольнике содержится шесть квадратов, каждый из которых имеет сторону, равную одному сантиметру:
Допустим, потребовалось измерить площадь следующей комнаты:
Определимся в каких квадратах будем измерять площадь.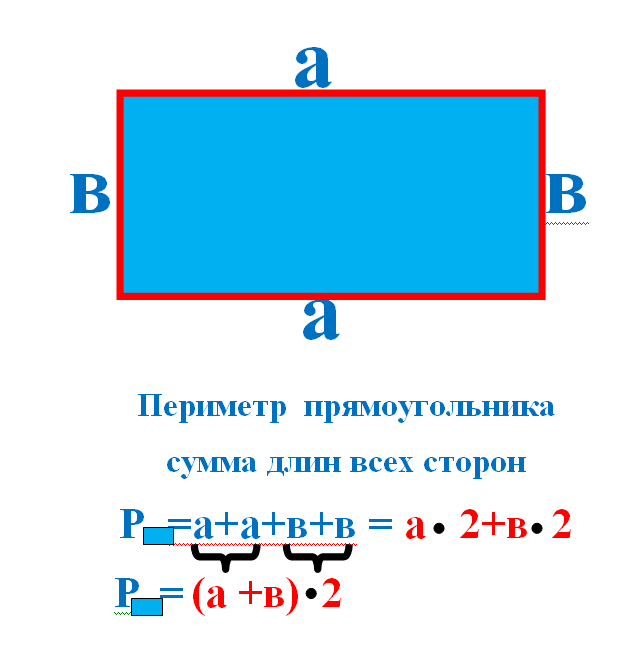 В данном случае площадь удобно измерить в квадратных метрах:
В данном случае площадь удобно измерить в квадратных метрах:
Итак, наша задача состоит в том, чтобы определить сколько таких квадратов со стороной 1 м содержится в исходной комнате. Заполним этим квадратом всю комнату:
Видим, что квадратный метр содержится в комнате 12 раз. Значит, площадь комнаты составляет 12 квадратных метров.
Площадь прямоугольника
В предыдущем примере мы вычислили площадь комнаты, последовательно проверив сколько раз в ней содержится квадрат, сторона которого равна одному метру. Площадь составила 12 квадратных метров.
Комната представляла собой прямоугольник. Площадь прямоугольника можно вычислить перемножив его длину и ширину.
Чтобы вычислить площадь прямоугольника, нужно перемножить его длину и ширину.
Вернёмся к предыдущему примеру. Допустим, мы измерили длину комнаты рулеткой и оказалось, что длина составила 4 метра:
Теперь измерим ширину. Пусть она составила 3 метра:
Умножим длину (4 м) на ширину (3 м).
4 × 3 = 12
Как и в прошлый раз получаем двенадцать квадратных метров. Это объясняется тем, что измерив длину, мы тем самым узнаём сколько раз можно уложить в эту длину квадрат со стороной, равной одному метру. Уложим четыре квадрата в эту длину:
Затем мы определяем сколько раз можно повторить эту длину с уложенными квадратами. Это мы узнаём, измерив ширину прямоугольника:
Площадь квадрата
Квадрат это тот же прямоугольник, но у которого все стороны равны. Например, на следующем рисунке представлен квадрат со стороной 3 см. Фраза «квадрат со стороной 3 см» означает, что все стороны равны 3 см
Площадь квадрата вычисляется таким же образом, как и площадь прямоугольника — длину умножают на ширину.
Вычислим площадь квадрата со стороной 3 см. Умножим длину 3 см на ширину 3 см
3 × 3 = 9
В данном случае требовалось узнать сколько квадратов со стороной 1 см содержится в исходном квадрате. В исходном квадрате содержится девять квадратов со стороной 1 см. Действительно, так оно и есть. Квадрат со стороной 1 см, входит в исходный квадрат девять раз:
Действительно, так оно и есть. Квадрат со стороной 1 см, входит в исходный квадрат девять раз:
Умножив длину на ширину, мы получили выражение 3 × 3, а это есть произведение двух одинаковых множителей, каждый из которых равен 3. Иными словами выражение 3 × 3 представляет собой вторую степень числа 3. А значит процесс вычисления площади квадрата можно записать в виде степени 32.
Поэтому вторую степень числа называют квадратом числа. При вычислении второй степени числа a, человек тем самым находит площадь квадрата со стороной a. Операцию возведения числа во вторую степень по другому называют возведением в квадрат.
Обозначения
Площадь обозначается заглавной латинской буквой S (англ. Square — квадрат). Тогда площадь квадрата со стороной a см будет вычисляться по следующему правилу
S = a2
где a — длина стороны квадрата. Вторая степень указывает на то, что происходит перемножение двух одинаковых сомножителей, а именно длины и ширины. Ранее было сказано, что у квадрата все стороны равны, а значит равны длина и ширина квадрата, выраженные через букву a.
Ранее было сказано, что у квадрата все стороны равны, а значит равны длина и ширина квадрата, выраженные через букву a.
Если задача состоит в том, чтобы определить сколько квадратов стороной 1 см содержится в исходном квадрате, то в качестве единиц измерения площади нужно указывать см2. Это обозначение заменяет словосочетание «квадратный сантиметр».
Например, вычислим площадь квадрат со стороной 2 см.
Значит, квадрат со стороной 2 см, имеет площадь, равную четырём квадратным сантиметрам:
Если задача состоит в том, чтобы определить сколько квадратов со стороной 1 м содержится в исходном квадрате, то в качестве единиц измерения нужно указывать м2. Это обозначение заменяет словосочетание «квадратный метр».
Вычислим площадь квадрата со стороной 3 метра
Значит, квадрат со стороной 3 м, имеет площадь равную девяти квадратным метрам:
Аналогичные обозначения используются при вычислении площади прямоугольника. Но длина и ширина прямоугольника могут быть разными, поэтому они обозначаются через разные буквы, например a и b. Тогда площадь прямоугольника, длиной a и шириной b вычисляется по следующему правилу:
Но длина и ширина прямоугольника могут быть разными, поэтому они обозначаются через разные буквы, например a и b. Тогда площадь прямоугольника, длиной a и шириной b вычисляется по следующему правилу:
S = a × b
Как и в случае с квадратом, единицами измерения площади прямоугольника могут быть см2, м2, км2. Эти обозначения заменяют словосочетания «квадратный сантиметр», «квадратный метр», «квадратный километр» соответственно.
Например, вычислим площадь прямоугольника, длиной 6 см и шириной 3 см
Значит, прямоугольник длиной 6 см и шириной 3 см имеет площадь, равную восемнадцати квадратным сантиметрам:
В качестве единицы измерения допускается использовать словосочетание «квадратных единиц». Например, запись S = 3 кв.ед означает, что площадь квадрата или прямоугольника равна трём квадратам, каждый из которых имеет единичную сторону (1 см, 1 м или 1 км).
Перевод единиц измерения площади
Единицы измерения площади можно переводить из одной единицы измерения в другую. Рассмотрим несколько примеров:
Рассмотрим несколько примеров:
Пример 1. Выразить 1 квадратный метр в квадратных сантиметрах.
1 квадратный метр это квадрат со стороной 1 м. То есть все четыре стороны имеют длину, равную одному метру.
Но 1 м = 100 см. Тогда все четыре стороны тоже имеют длину, равную 100 см
Вычислим новую площадь этого квадрата. Умножим длину 100 см на ширину 100 см или возведём в квадрат число 100
S = 1002 = 10 000 см2
Получается, что на один квадратный метр приходится десять тысяч квадратных сантиметров.
1 м2 = 10 000 см2
Это позволяет в будущем умножить любое количество квадратных метров на 10 000 и получить площадь, выраженную в квадратных сантиметрах.
Чтобы перевести квадратные метры в квадратные сантиметры, нужно количество квадратных метров умножить на 10 000.
А чтобы перевести квадратные сантиметры в квадратные метры, нужно наоборот количество квадратных сантиметров разделить на 10 000.
Например, переведём 100 000 см2 в квадратные метры. Рассуждать в этом случае можно так: «если 10 000 см2 это один квадратный метр, то сколько раз 100 000 см2 будут содержать по 10 000 см2»
100 000 см2 : 10 000 см2 = 10 м2
Другие единицы измерения можно переводить таким же образом. Например, переведём 2 км2 в квадратные метры.
Один квадратный километр это квадрат со стороной 1 км. То есть все четыре стороны имеют длину, равную одному километру. Но 1 км = 1000 м. Значит, все четыре стороны квадрата также равны 1000 м. Найдём новую площадь квадрата, выраженную в квадратных метрах. Для этого умножим длину 1000 м на ширину 1000 м или возведём в квадрат число 1000
S = 10002 = 1 000 000 м2
Получается, что на один квадратный километр приходится один миллион квадратных метров:
1 км2 = 1 000 000 м2
Это позволяет в будущем умножить любое количество квадратных километров на 1 000 000 и получить площадь, выраженную в квадратных метрах.
Чтобы перевести квадратные километры в квадратные метры, нужно количество квадратных километров умножить на 1 000 000.
Итак, вернёмся к нашей задаче. Требовалось перевести 2 км2 в квадратные метры. Умножим 2 км2 на 1 000 000
2 км2 × 1 000 000 = 2 000 000 м2
А чтобы перевести квадратные метры в квадратные километры, нужно наоборот количество квадратных метров разделить на 1 000 000.
Например, переведём 3 500 000 м2 в квадратные километры. Рассуждать в этом случае можно так: «если 1 000 000 м2 это один квадратный километр, то сколько раз 3 500 000 м2 будут содержать по 1 000 000 м2»
3 500 000 м2 : 1 000 000 м2 = 3,5 км2
Пример 2. Выразить 7 м2 в квадратных сантиметрах.
Умножим 7 м2 на 10 000
7 м2 = 7 м2 × 10 000 = 70 000 см2
Пример 3. Выразить 5 м2 13 см2 в квадратных сантиметрах.
5 м2 13 см2 = 5 м2 × 10 000 + 13 см2 = 50 013 см2
Пример 4. Выразить 550 000 см2 в квадратных метрах.
Выразить 550 000 см2 в квадратных метрах.
Узнаем сколько раз 550 000 см2 содержит по 10 000 см2. Для этого разделим 550 000 см2 на 10 000 см2
550 000 см2 : 10 000 см2 = 55 м2
Пример 5. Выразить 7 км2 в квадратных метрах.
Умножим 7 км2 на 1 000 000
7 км2 × 1 000 000 = 7 000 000 м2
Пример 6. Выразить 8 500 000 м2 в квадратных километрах.
Узнаем сколько раз 8 500 000 м2 содержит по 1 000 000 м2. Для этого разделим 8 500 000 м2 на 1 000 000 м2
8 500 000 м2 × 1 000 000 м2 = 8,5 км2
Единицы измерения площади земельных участков
Площади небольших земельных участков удобно измерять в квадратных метрах.
Площади более крупных земельных участков измеряются в арах и гектарах.
Ар (сокращённо: a) — это площадь равная ста квадратным метрам (100 м2). В виду частого распространения такой площади (100 м2) она стала использоваться, как отдельная единица измерения.
К примеру, если сказано, что площадь какого-нибудь поля составляет 3 а, то нужно понимать, что это три квадрата площадью 100 м2 каждый, то есть:
3 а = 100 м2 × 3 = 300 м2
В народе ар часто называют соткой, поскольку ар равен квадрату, площадью 100 м2. Примеры:
Примеры:
1 сотка = 100 м2
2 сотки = 200 м2
10 соток = 1000 м2
Гектар (сокращенно: га) — это площадь, равная 10 000 м2. К примеру, если сказано, что площадь какого-нибудь леса составляет 20 гектаров, то нужно понимать, что это двадцать квадратов площадью 10 000 м2 каждый, то есть:
20 га = 10 000 м2 × 20 = 200 000 м2
Прямоугольный параллелепипед и куб
Прямоугольный параллелепипед — это геометрическая фигура, состоящая из граней, ребер и вершин. На рисунке показан прямоугольный параллелепипед:
Желтым цветом показаны грани параллелепипеда, чёрным цветом — рёбра, красным — вершины.
Прямоугольный параллелепипед обладает длиной, шириной и высотой. На рисунке показано где длина, ширина и высота:
Параллелепипед, у которого длина, ширина и высота равны между собой, называется кубом. На рисунке показан куб:
Объём геометрической фигуры
Объём геометрической фигуры — это число, которое характеризует вместимость данной фигуры.
Объём измеряется в кубических единицах. Под кубическими единицами подразумевают кубы длиной 1, шириной 1 и высотой 1. Например, 1 кубический сантиметр или 1 кубический метр.
Измерить объём какой-нибудь фигуры означает выяснить сколько кубических единиц вмещается в данную фигуру.
Например, объём следующего прямоугольного параллелепипеда равен двенадцати кубическим сантиметрам:
Это потому что в данный параллелепипед вмещается двенадцать кубов длиной 1 см, шириной 1 см и высотой 1 см:
Объём обозначается заглавной латинской буквой V. Одна из единиц измерения объема это кубический сантиметр (см3). Тогда объём V рассмотренного нами параллелепипеда равен 12 см3
V = 12 см3
Объём любого параллелепипеда вычисляют следующим образом: перемножают его длину, ширину и высоту .
Объём прямоугольного параллелепипеда равен произведению его длины, ширины и высоты.
V = abc
где, a — длина, b — ширина, c — высота
Так, в предыдущем примере мы визуально определили, что объём параллелепипеда равен 12 см3. Но можно измерить длину, ширину и высоту данного параллелепипеда и перемножить результаты измерений. Мы получим тот же результат
Но можно измерить длину, ширину и высоту данного параллелепипеда и перемножить результаты измерений. Мы получим тот же результат
Объём куба вычисляется таким же образом, как и объём прямоугольного параллелепипеда — перемножают длину, ширину и высоту.
Например, вычислим объём куба, длина которого 3 см. У куба длина, ширина и высота равны между собой. Если длина равна 3 см, то равны этим же трём сантиметрам ширина и высота куба:
Перемножаем длину, ширину, высоту и получаем объём, равный двадцати семи кубическим сантиметрам:
V = 3 × 3 × 3 = 27 см³
Действительно, в исходный куб вмещается 27 кубиков длиной 1 см
При вычислении объёма данного куба мы перемножили длину, ширину и высоту. Получилось произведение 3 × 3 × 3. Это есть произведение трёх сомножителей, каждый из которых равен 3. Иными словами, произведение 3 × 3 × 3 является третьей степенью числа 3 и может быть записано в виде 33.
V = 33 = 27 см3
Поэтому третью степень числа называют кубом числа. При вычислении третьей степени числа a, человек тем самым находит объём куба, длиной a. Операцию возведения числа в третью степень по другому называют возведением в куб.
При вычислении третьей степени числа a, человек тем самым находит объём куба, длиной a. Операцию возведения числа в третью степень по другому называют возведением в куб.
Таким образом, объём куба вычисляется по следующему правилу:
V = a3
Где a — длина куба.
Кубический дециметр. Кубический метр
Не все объекты нашего мира удобно измерять в кубических сантиметрах. Например, объём комнаты или дома удобнее измерять в кубических метрах (м3). А объём бака, аквариума или холодильника удобнее измерять в кубических дециметрах (дм3).
Другое название одного кубического дециметра – один литр.
1 дм3 = 1 литр
Перевод единиц измерения объёма
Единицы измерения объёма можно переводить из одной единицы измерения в другую. Рассмотрим несколько примеров:
Пример 1. Выразить 1 кубический метр в кубических сантиметрах.
Один кубический метр это куб со стороной 1 м. Длина, ширина и высота этого куба равны одному метру.
Длина, ширина и высота этого куба равны одному метру.
Но 1 м = 100 см. Значит, длина, ширина и высота тоже равны 100 см
Вычислим новый объём куба, выраженный в кубических сантиметрах. Для этого перемножим его длину, ширину и высоту. Либо возведём число 100 в куб:
V = 1003 = 1 000 000 см3
Получается, что на один кубический метр приходится один миллион кубических сантиметров:
1 м3 = 1 000 000 см3
Это позволяет в будущем умножить любое количество кубических метров на 1 000 000 и получить объём, выраженный в кубических сантиметрах.
Чтобы перевести кубические метры в кубические сантиметры, нужно количество кубических метров умножить на 1 000 000.
А чтобы перевести кубические сантиметры в кубические метры, нужно наоборот количество кубических сантиметров разделить на 1 000 000.
Например, переведём 300 000 000 см3 в кубические метры. Рассуждать в этом случае можно так: «если 1 000 000 см3 это один кубический метр, то сколько раз 300 000 000 см3 будут содержать по 1 000 000 см3»
300 000 000 см3 : 1 000 000 см3 = 300 м3
Пример 2. Выразить 3 м3 в кубических сантиметрах.
Выразить 3 м3 в кубических сантиметрах.
Умножим 3 м3 на 1 000 000
3 м3 × 1 000 000 = 3 000 000 см3
Пример 3. Выразить 60 000 000 см3 в кубических метрах.
Узнаем сколько раз 60 000 000 см3 содержит по 1 000 000 см3. Для этого разделим 60 000 000 см3 на 1 000 000 см3
60 000 000 см3 : 1 000 000 см3 = 60 м3
Вместимость бака, банки или канистры измеряют в литрах. Литр это тоже единица измерения объема. Один литр равен одному кубическому дециметру.
1 литр = 1 дм3
Например, если вместимость банки составляет 1 литр, это значит что объём этой банки составляет 1 дм3. При решении некоторых задач может быть полезным умение переводить литры в кубические дециметры и наоборот. Рассмотрим несколько примеров.
Пример 1. Перевести 5 литров в кубические дециметры.
Чтобы перевести 5 литров в кубические дециметры, достаточно умножить 5 на 1
5 л × 1 = 5 дм3
Пример 2. Перевести 6000 литров в кубические метры.
Шесть тысяч литров это шесть тысяч кубических дециметров:
6000 л × 1 = 6000 дм3
Теперь переведём эти 6000 дм3 в кубические метры.
Длина, ширина и высота одного кубического метра равны 10 дм
Если вычислить объём этого куба в дециметрах, то получим 1000 дм3
V = 103= 1000 дм3
Получается, что одна тысяча кубических дециметров соответствует одному кубическому метру. А чтобы определить сколько кубических метров соответствуют шести тысячамл кубических дециметров, нужно узнать сколько раз 6 000 дм3 содержит по 1 000 дм3
6 000 дм3 : 1 000 дм3 = 6 м3
Значит, 6000 л = 6 м3.
Таблица квадратов
В жизни часто приходиться находить площади различных квадратов. Для этого каждый раз требуется возводить исходное число во вторую степень.
Квадраты первых 99 натуральных чисел уже вычислены и занесены в специальную таблицу, называемую таблицей квадратов.
Первая строка данной таблицы (цифры от 0 до 9) это единицы исходного числа, а первый столбец (цифры от 1 до 9) это десятки исходного числа.
Например, найдём квадрат числа 24 по данной таблице. Число 24 состоит из цифр 2 и 4. Точнее, число 24 состоит из двух десятков и четырёх единиц.
Итак, выбираем цифру 2 в первом столбце таблицы (столбце десятков), а цифру 4 выбираем в первой строке (строке единиц). Затем, двигаясь вправо от цифры 2 и вниз от цифры 4, найдём точку пересечения. В результате окажемся на позиции, где располагается число 576. Значит, квадрат числа 24 есть число 576
242 = 576
Таблица кубов
Как и в ситуации с квадратами, кубы первых 99 натуральных чисел уже вычислены и занесены в таблицу, называемую таблицей кубов.
Куб числа по таблице определяется таким же образом, как и квадрат числа. Например, найдём куб числа 35. Это число состоит из цифр 3 и 5. Выбираем цифру 3 в первом столбце таблицы (столбце десятков), а цифру 5 выбираем в первой строке (строке единиц). Двигаясь вправо от цифры 3 и вниз от цифры 5, найдём точку пересечения. В результате окажемся на позиции, где располагается число 42875. Значит, куб числа 35 есть число 42875.
В результате окажемся на позиции, где располагается число 42875. Значит, куб числа 35 есть число 42875.
353 = 42875
Задания для самостоятельного решения
Задача 1. Длина прямоугольника составляет 6 см, а ширина 2 см. Найдите периметр.
Решение
P = 2(a + b)
a = 6, b = 2
P = 2(6 + 2) = 12 + 4 = 16 см
Ответ: периметр прямоугольника равен 16 см.
Задача 2. Длина прямоугольника составляет 6 см, а ширина 2 см. Найдите площадь.
Решение
S = ab
a = 6, b = 2
S = 6 × 2 = 12 см2
Ответ: площадь равна 12 см2.
Задача 3. Площадь прямоугольника составляет 12 см2. Длина составляет 6 см. Найдите ширину прямоугольника.
Решение
S = ab
S = 12, a = 6, b = x
12 = 6 × x
x = 2
Ответ: ширина прямоугольника составляет 2 см.
Задача 4. Вычислите площадь квадрата со стороной 8 см
Решение
S = a2
a = 8
S = 82 = 64 см2
Ответ: площадь квадрата со стороной 8 см равна 64 см2
Задача 5. Вычислите объем прямоугольного параллелепипеда, длина которого 6 см, ширина 4 см, высота 3 см.
Решение
V = abc
a = 6, b = 4, c = 3
V = 6 × 4 × 3 = 72 см3.
Ответ: объем прямоугольного параллелепипеда, длина которого 6 см, ширина 4 см, высота 3 см равен 72 см3
Задача 6. Объем прямоугольного параллелепипеда составляет 200 см3. Найдите высоту параллелепипеда, если его длина равна 10 см, а ширина 5 см
Решение
V = abc
V = 200, a = 10, b = 5, c = x
200 = 10 × 5 × x
200 = 50x
x = 4
Ответ: высота прямоугольного параллелепипеда равна 4 см.
Задача 7. Площади земельного участка, засеянные пшеницей и льном, пропорциональны числам 4 и 5. На какой площади засеяна пшеница, если под льном засеяно 15 га
Решение
Число 4 отражает площадь, засеянную пшеницей. А число 5 отражает площадь, засеянную льном.
Сказано что площади, засеянные пшеницей и льном пропорциональны этим числам.
Проще говоря, во сколько раз изменяются числа 4 или 5, во сколько же раз изменится и площадь, которая засеяна пшеницей или льном. Льном засеяно 15 га. То есть число 5, которое отражает площадь, засеянную льном, изменилось в 3 раза.
Тогда число 4, которое отражает площадь засеянную пшеницей, нужно увеличить в три раза
4 × 3 = 12 га
Ответ: пшеницей засеяно 12 га.
Задача 8. Длина зернохранилища 42 м, ширина составляет длины, а высота – 0,1 длины. Определите сколько тонн зерна вмещает зернохранилище, если 1 м3 его весит 740 кг.
Решение
a — длина
b — ширина
c — высота
a = 42 м
b = м
c = 42 × 0,1 = 4,2 м
Определим объем зернохранилища:
V = abc = 42 × 30 × 4,2 = 5292 м3
Определите сколько тонн зерна вмещает зернохранилище:
5292 × 740 = 3916080 кг
Переведём килограммы в тонны:
Ответ: зернохранилище вмещает 3916,08 тонн зерна.
Задача 9. 12. Бассейн имеет форму прямоугольного параллелепипеда, длина которого равна 5,8 м, а ширина – 3,5 м. Две трубы наполняют его водой в течение 13 ч 32 мин., причём через одну из них вливается 25 л/мин, а через вторую – 0,75 этого количества. Определите высоту (глубину) бассейна.
Решение
Определим сколько литров в минуту вливается через вторую трубу:
25 л/мин × 0,75 = 18,75 л/мин
Определим сколько литров в минуту вливается в бассейн через обе трубы:
25 л/мин + 18,75 л/мин = 43,75 л/мин
Определим сколько литров воды будет залито в бассейн за 13 ч 32 мин
43,75 × 13 ч 32 мин = 43,75 × 812 мин = 35 525 л
1 л = 1 дм3
35 525 л = 35 525 дм3
Переведём кубические дециметры в кубические метры. Это позволит вычислит объем бассейна:
35 525 дм3 : 1000 дм3 = 35,525 м3
Зная объём бассейна можно вычислить высоту бассейна. Подставим в буквенное уравнение V=abc имеющиеся у нас значения. Тогда получим:
Тогда получим:
V = 35,525
a = 5.8
b = 3.5
c = x
35,525 = 5,8 × 3,5 × x
35,525 = 20,3 × x
x = 1,75 м
с = 1,75
Ответ: высота (глубина) бассейна составляет 1,75 м.
Предыдущая
Математика с нуляСтепень с целым показателем
СледующаяМатематика с нуляОдночлены
Оценить периметр и площадь полигона—ArcGIS Pro
Available with ArcGIS Pro Standard and Data Reviewer licenses.
Краткая информация
Проверка Оценить периметр и площадь полигона ищет полигональные объекты на основе значений периметра и площади всего полигона или его отдельных частей и сегментов.
Обзор
Назначение проверки Оценить периметр и площадь полигона — нахождение объектов, значения площади или периметра которых являются некорректными. Это может быть оценка всей геометрии объекта или его частей (сегментов).
При настройке в качестве правила ограничений уведомление об ошибке возвращается, если создается или изменяется объект, основанный на заданном диапазоне, который определяется правилом.
При настройке правила проверки для каждого объекта, который содержит значение измерения площади или периметра в рамках указанного диапазона.
Отраслевые сценарии
Эта проверка может использоваться в следующих случаях:
- При отображении объектов определенные типы сооружений, такие как навесы, должны иметь площадь меньше указываемого размера; в противном случае для них должен использоваться код другого типа сооружения.
- В случае топографических карт длины сегментов объектов должны быть больше определенного значения, что позволит обеспечить согласованность продуктов, полученных из разных источников данных.
Поддерживаемые рабочие процессы
Проверки ArcGIS Data Reviewer поддерживают множество методов для встраивания автоматического просмотра данных. Следующая таблица описывает поддерживаемые методы встраивания для этой проверки:
| Проверка | Ограничения | ||
|---|---|---|---|
Пакетное задание Reviewer | Правило атрибутов (проверка) | Да (ArcGIS Pro 2. | |
Да | Да (ArcGIS Pro 2.5 или более поздней версии) | ||
Синтаксис
| Параметр | Обязательный | Описание | Рабочий процесс |
|---|---|---|---|
Подтип | Нет |
Подтип, к которому применяется правило. | Ограничения |
Проверка | |||
Атрибут | Нет | Запрос, который определяет объект, к которому применяется правило. | Проверка |
Оценка | Да | Свойство геометрии, оцениваемое проверкой.
| Ограничения |
Проверка | |||
Тип | Да | Метод используется при оценке площади или периметра объекта.
| Ограничения |
Проверка | |||
Цель поиска | Да | Ошибочные условия, оцененные правилом. Любой объект, значения которого соответствуют заданным в правиле, возвращается как ошибка.
При выборе оператора с верхним и нижним граничными значениями требуется дополнительный ввод условий. | Ограничения |
Проверка | |||
Триггеры | Да | События редактирования, которые приведут к вступлению в силу правила.
| Ограничения |
Имя | Да | Уникальное название или имя для правила. Эта информация используется для поддержки сопоставимости требований к качеству данных, автоматического создания отчетов и корректировки рабочих процессов. | Ограничения |
Проверка | |||
Описание | Нет | Текст описания ошибки, когда найдены несовместимые объекты. Эта информация используется для обеспечения руководства при корректировке рабочих процессов. | Ограничения |
Проверка | |||
Важность | Нет | Степень серьезности ошибки, присваиваемая при обнаружении несовместимых объектов. Это значение указывает важность ошибки относительно других ошибок. Диапазон значений от 1 до 5, где 1 обозначает высший приоритет, а 5 – низший. | Проверка |
Теги | Нет | Тег правила. Эта информация используется в правиле рабочих процессов создания и управления для поддержки сопоставимости требований к качеству данных и создания отчетов. | Ограничения |
Проверка |
Примечания
При использовании проверки следует учитывать следующее:
- Объекты, найденные этой проверкой, отличаются в зависимости от того, оценивались ли целые объекты или их части и сегменты.
- Если проверка создается как правило атрибута (ограничения), поддержка наборов данных на основе географических систем координат ограничивается теми, которые используют Web Mercator (WKID 3857) или WGS 84 (WKID 4326).
- Параметр фильтра Атрибут ограничен операторами сравнения (=, <>, >, <, >=, <=) и логическими операторами (AND/OR, IN/NOT IN, LIKE/NOT LIKE, IS NULL).

Связанные разделы
Отзыв по этому разделу?
Изучение зависимостей площадей и периметров в четырехугольниках
- Авторы
- Руководители
- Файлы работы
- Наградные документы
Хакверди Елиз Уналовна 1
1Муниципальное бюджетное общеобразовательное учреждение «Средняя общеобразовательная школа №30»
Берговина Ю.Д. 1
1Муниципальное бюджетное общеобразовательное учреждение «Средняя общеобразовательная школа №30»
Автор работы награжден дипломом победителя III степени
Диплом школьникаСвидетельство руководителя
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
Введение
С понятием периметр и площадь я познакомилась в 3 классе. Эти важные понятия необходимы человеку на протяжении всей его жизни. Деятельность строителей, инженеров, земледельцев и представителей других профессий немыслима без прочных знаний по этой теме.
Эти важные понятия необходимы человеку на протяжении всей его жизни. Деятельность строителей, инженеров, земледельцев и представителей других профессий немыслима без прочных знаний по этой теме.
Актуальность темы. Понятия «площади» и «периметра» необходимы человеку в окружающей жизни постоянно, например – сделать ремонт в доме или красиво оформить клумбу на даче. И то и другое понятие связывают стороны многоугольников. Знание зависимостей между этими величинами очень важно для современного человека.
Цель проекта: установить некоторые зависимости между площадью и периметром, увидеть их применение в практических ситуациях.
Задачи:повторить понятия по теме исследования, а именно: «площадь фигуры» и «периметр фигуры»; провести необходимые исследования и опыты; сделать выводы о зависимости площадей и периметров; рассмотреть практическое применение полученных результатов.
Основнаячасть
Определение предмета исследования. Что нужно выяснить:
Как связаны периметры и площади прямоугольников?
Зависит ли площадь прямоугольника от его периметра?
Какой прямоугольник имеет наибольшую площадь при заданном периметре?
Если известен периметр прямоугольника, то нельзя ли однозначно установить его площадь?
Что можно сказать о зависимости площади квадрата от его периметра?
Проблема. Никаких зависимостей связывающих площади и периметры фигур мы пока не изучили.
Вот, самый простой пример, который задает проблему: «Есть два участка земли 80 м на 100 м и 50 м на 160 м. Вроде, площадь одинаковая – 8000 м 2, а первый участок выгоднее купить, чем второй, забор то на 60 м короче строить». С точки зрения математики, все ясно, а вот логически – странно, периметр это замкнутая воображаемая нить, и то, что внутри нее не должно меняться, как ее не крути. Почему есть разница в периметрах? Так все-таки, есть ли какие-то зависимости, или площадь и периметр никак не зависят друг от друга?
Почему есть разница в периметрах? Так все-таки, есть ли какие-то зависимости, или площадь и периметр никак не зависят друг от друга?
Гипотеза.Предполагаем, что некоторые зависимости существуют. С изменением длины одной из сторон прямоугольника при заданном периметре изменится и площадь этого прямоугольника. Можно даже предположить, что если площадь больше, то периметр больше. Если у одной фигуры больше периметр, чем у второй, то её площадь больше, меньше или по-разному?
Мы уже знаем:
Периметр – величина, равная сумме длин всех сторон многоугольника.
Площадь фигуры – величина, показывающая сколько места занимает фигура на плоскости.
Свойства площадей нам тоже известны:
Равные фигуры имеют равные площади.
Площадь всей фигуры равна сумме площадей ее частей.
За единицу площади принимают площадь квадрата, сторона которого равна единичному отрезку.
Проверка гипотезы.
Исследования начнем с простой и хорошо знакомой нам фигуры – прямоугольника.
Исследование №1.
Заполним таблицу, считая площадь одной клеточки равной 1 см 2
Таблица №1
|
№ |
Фигуры |
Площадь (S, см 2) |
Периметр (Р, см) |
|
1 |
1 |
4 |
|
|
2 |
2 |
6 |
|
|
3 |
3 |
8 |
|
|
4 |
4 |
10 |
|
|
5 |
4 |
8 |
|
|
6 |
5 |
12 |
|
|
7 |
6 |
14 |
|
|
8 |
6 |
10 |
|
|
9 |
7 |
16 |
|
|
10 |
8 |
12 |
|
|
11 |
8 |
18 |
|
|
12 |
9 |
20 |
|
|
13 |
9 |
12 |
|
|
14 |
10 |
22 |
|
|
15 |
10 |
14 |
Исследуя результаты измерений, делаем вывод, что не всегда увеличение площади означает, что периметр тоже увеличивается, например фигуры №3 и №5 или фигуры №4 и №8, или фигуры №6 и №10 и №13. Если периметры равны, то площади могут быть различны. (Приложение 1, стр.14-16)
Если периметры равны, то площади могут быть различны. (Приложение 1, стр.14-16)
Мы заметили, если периметр одного прямоугольника больше, то и его площадь больше чем у других, например фигуры №2 и №3 или фигуры №4 и №6. Однако, если периметр одного прямоугольника больше, то его площадь не всегда больше, например фигуры №6 и №8.
При одинаковом периметре и площади бывают разные! Отчего же так происходит?
Продолжим наблюдения.
Исследование №2.
Таблица №2
|
№ фигуры |
1 сторона (длина, см) |
2 сторона (ширина, см) |
Площадь (S, см 2) |
Периметр (Р, см) |
|
1 |
1 |
100 |
100 |
202 |
|
2 |
2 |
50 |
100 |
104 |
|
3 |
4 |
25 |
100 |
58 |
|
4 |
5 |
20 |
100 |
50 |
|
5 |
10 |
10 |
100 |
40 |
|
6 |
20 |
5 |
100 |
50 |
|
7 |
25 |
4 |
100 |
58 |
|
8 |
50 |
2 |
100 |
104 |
|
9 |
100 |
1 |
100 |
202 |
Замечаем, что при равных площадях периметры не равны, самый маленький периметр из всех прямоугольников с равными площадями – у квадрата. Вот какое замечательное свойство у квадрата! Оказывается, что среди всех прямоугольников одинаковой площади у квадрата самый маленький периметр!
Вот какое замечательное свойство у квадрата! Оказывается, что среди всех прямоугольников одинаковой площади у квадрата самый маленький периметр!
Какой же из всех прямоугольников заданного периметра имеет наибольшую площадь? Решение этой задачи было известно ещё математикам Древней Греции. Оно изложено в книге Евклида.
Исследование №3.
Таблица №3
|
№ фигуры |
1 сторона (длина, см) |
2 сторона (ширина, см) |
Площадь (S, см 2) |
Периметр (Р, см) |
|
1 |
1 |
49 |
49 |
100 |
|
2 |
2 |
48 |
96 |
100 |
|
3 |
5 |
45 |
225 |
100 |
|
4 |
10 |
40 |
400 |
100 |
|
5 |
20 |
30 |
600 |
100 |
|
6 |
25 |
25 |
625 |
100 |
Очевидно, можно сделать вывод, что при одинаковом периметре, самая выгодная площадь у квадрата. Запомним это замечательное свойство квадрата, заключать в своих границах наибольшую площадь при постоянном периметре. Отчего же возникают такие зависимости, в чем причина? Чтобы лучше разобраться в этом вопросе, проведем опыт.
Запомним это замечательное свойство квадрата, заключать в своих границах наибольшую площадь при постоянном периметре. Отчего же возникают такие зависимости, в чем причина? Чтобы лучше разобраться в этом вопросе, проведем опыт.
Опыт.
Я взяла четырехугольник – квадрат. Измерила его стороны, вычислила площадь и периметр. Разрезала фигуру пополам и составила новую фигуру (Приложение 2, стр.17). Результаты измерений занесла в таблицу №4.
Таблица №4
|
№ фигуры |
1 сторона (длина, см) |
2 сторона (ширина, см) |
Площадь (S, см 2) |
Периметр (Р, см) |
|
1 |
8 |
8 |
64 |
32 |
|
2 |
16 |
4 |
64 |
40 |
Таблица №5
|
1 фигура |
|
|
2 фигура |
Количество квадратиков не изменилось. Наблюдаем, что происходит со сторонами, когда периметр увеличивается. У фигуры появились дополнительные стороны, которые стали границами, это дополнительные 8+8=16 см, и исчезла граница 4+4=8 см. Итого: 16-8=8 см. Вот и дополнительные 8 см. Периметр увеличится.
Наблюдаем, что происходит со сторонами, когда периметр увеличивается. У фигуры появились дополнительные стороны, которые стали границами, это дополнительные 8+8=16 см, и исчезла граница 4+4=8 см. Итого: 16-8=8 см. Вот и дополнительные 8 см. Периметр увеличится.
Практические задачи.
А что можно сказать о зависимости площади квадрата от его периметра?
Задача №1. Если известен периметр квадрата, то можно ли однозначно установить его площадь?
Решим задачу для квадрата, периметр которого равен 40 см. Можно, поскольку по известному периметру можно вычислить сторону квадрата. А вычислив его сторону, можно потом вычислить площадь по этой найденной стороне.
1) 40 : 4 = 10 (см) – одна сторона
2) 10 • 10 = 100 (см 2) – площадь
Площадь квадрата однозначно зависит от его периметра, поскольку каждому значению периметра квадрата соответствует единственное значение площади.
Задача №2. Начертите какой-нибудь квадрат. Как надо изменить его стороны, чтобы построить квадрат, площадь которого была бы: 1) в 4 раза больше? 2) в 9 раз больше? 3) в 16 раз больше?
Проверим решение построением (Приложение 3, стр.18).
Таблица №6
|
№ |
Фигуры |
Вывод |
|
1 |
Стороны увеличить в 2 раза |
|
|
2 |
Стороны увеличить в 3 раза |
|
|
3 |
Стороны увеличить в 4 раза |
Задача №3. Начертите три прямоугольника, у одного из которых стороны имеют длину 7 см и 3 см, у второго соответственно 8 см и 2 см, а у третьего – 9 см и 1 см. Вычислите периметр и площадь каждого из этих прямоугольников. Сравните получившиеся периметры между собой и получившиеся площади между собой.
Начертите три прямоугольника, у одного из которых стороны имеют длину 7 см и 3 см, у второго соответственно 8 см и 2 см, а у третьего – 9 см и 1 см. Вычислите периметр и площадь каждого из этих прямоугольников. Сравните получившиеся периметры между собой и получившиеся площади между собой.
Проиллюстрируем на примере.
Первый прямоугольник: Р = (7 + 3) • 2 = 20 (см), S = 7 • 3= 21 (см 2).
Второй прямоугольник: Р = (8 + 2) • 2 = 20 (см), S = 8 • 2 = 16 (см 2).
Третий прямоугольник: Р = (9 + 1) • 2 = 20 (см), S = 9 • 1 = 9 (см 2).
Периметры прямоугольников равны, а площадь первого прямоугольника больше площади второго прямоугольника и площадь второго – больше площади третьего: 21 > 16 > 9 . Если известен периметр прямоугольника, то нельзя однозначно установить его площадь. Площадь прямоугольника не будет однозначно зависеть от его периметра.
А, что можно сказать о зависимости периметра квадрата от длины его стороны?
Задача №4. Может ли периметр квадрата не измениться, если длина стороны квадрата изменилась? Могут ли получиться разные значения периметра квадрата при одном и том же значении длины его стороны?
Таблица №7
|
Длина стороны квадрата α, см |
1 |
2 |
3 |
4 |
5 |
|
Периметр квадрата Р, см |
4 |
8 |
12 |
16 |
20 |
Из таблицы видно, что с изменением стороны квадрата изменяется и периметр. Периметр квадрата однозначно зависит от длины его стороны, поскольку периметр квадрата – 4 • α, то есть при изменении значения α, изменится значение выражения. Если изменить длину стороны квадрата, то это обязательно приведёт к изменению его периметра, то есть Р зависит от а.
Периметр квадрата однозначно зависит от длины его стороны, поскольку периметр квадрата – 4 • α, то есть при изменении значения α, изменится значение выражения. Если изменить длину стороны квадрата, то это обязательно приведёт к изменению его периметра, то есть Р зависит от а.
Если длина стороны квадрата увеличивается, то его периметр тоже увеличивается.
Если длина стороны квадрата уменьшается, то его периметр тоже уменьшается.
Заключение
Практические результаты и выводы, полученные мною, могут быть использованы при подготовке домашних заданий и в бытовых вопросах, постоянно возникающих в жизни. Мои исследования помогли узнать о том, что по известному периметру прямоугольника нельзя однозначно установить его площадь.
Потому, что у прямоугольников с одинаковым периметром могут быть разные площади, как выяснилось выше.
Я выяснила, что площадь квадрата однозначно зависит от его периметра, поскольку каждому значению периметра квадрата соответствует единственное значение площади.
Основные выводы.
Если периметры прямоугольников равны, то площади могут быть различны.
Не всегда увеличение площади прямоугольников означает, что периметр тоже увеличивается.
Если площади прямоугольников равны, то периметры могут быть различны.
Из всех прямоугольников с равными площадями наименьший периметр имеет квадрат.
Из всех прямоугольников с равными периметрами наибольшую площадь имеет квадрат.
Площадь квадрата однозначно зависит от его периметра.
Основные выводы я разместила на памятках-закладках (Приложение 4.1 и 4.2, стр.19-20)
Списокиспользованныхисточниковилитературы
А. Г. Мерзляк. Математика: 5 кл.: учебник для общеобразовательных организаций / А. Г. Мерзляк, В. Б. Полонский, М. С. Якир. − 2-е изд., перераб. — М.: Вентана-Граф, 2018
Г. Мерзляк, В. Б. Полонский, М. С. Якир. − 2-е изд., перераб. — М.: Вентана-Граф, 2018
М.И. Моро, М.А. Бантова, Г.В. Бельтюкова, Математика — 4 класс, учебник для общеобразовательных организаций, в двух частях, М: Просвещение, 2018 г.-148 с.
3. Я.И. Перельман, Занимательная геометрия, Изд.: Терра-Книжный клуб, 2008 г., 384 стр.
4. Я.И. Перельман: Занимательная геометрия на вольном воздухе и дома , Издательство: Центрополиграф, 2017 г.
5. М.Г. Нефедова, Рабочая тетрадь по математике, Периметр и площадь — 3-4 классы. М: Издательство «Экзамен», 2014 г.- 46 стр.
6. М.И. Башмаков, М.Г. Нефедова, Математика, 3 класс, учебник, АСТ-Астрель, Москва, 2010 г.
7. О.В. Узорова, М.Г. Нефедова: Математика. 4 класс. Простые и составные задачи площади и периметра, Тренинговая тетрадь, ФГОС: издательства АСТ, 2015 г.
Приложение 4.1
Приложение 4.2
Просмотров работы: 3338
Сложности изучения понятий «периметр» и «площадь» в начальной школе
Автор: Нагимова Мария Хайдаровна
Рубрика: 5. Педагогика общеобразовательной школы
Опубликовано в
XXII международная научная конференция «Педагогическое мастерство» (Казань, февраль 2022)
Дата публикации: 30.01.2022
Статья просмотрена: 174 раза
Скачать электронную версию
Библиографическое описание:Нагимова, М. Х. Сложности изучения понятий «периметр» и «площадь» в начальной школе / М. Х. Нагимова. — Текст : непосредственный // Педагогическое мастерство : материалы XXII Междунар. науч. конф. (г. Казань, февраль 2022 г.). — Казань : Молодой ученый, 2022. — С. 37-40. — URL: https://moluch.ru/conf/ped/archive/417/16937/ (дата обращения: 21.09.2022).
науч. конф. (г. Казань, февраль 2022 г.). — Казань : Молодой ученый, 2022. — С. 37-40. — URL: https://moluch.ru/conf/ped/archive/417/16937/ (дата обращения: 21.09.2022).
Почему дети путают понятия «периметр» и «площадь»? В курсе математики начальной школы понятие периметр изучается намного раньше, чем площадь. Дети постепенно учатся находить сумму длин сторон многоугольника, навык постепенно доходит до автоматизма. При нахождении периметра прямоугольника несколькими способами тоже всё проходит гладко. Но вдруг… наступает время изучения темы «Площадь фигур», и тут учащиеся начинают путаться. Что же делать, чтобы не было путаницы между этими понятиями?
При изучении темы «Периметр» необходимо увеличить количество практических задач. Лучше всего учащиеся усвоят материал тогда, когда сами походят по школьному участку с рулеткой и измерят периметр беседки, спортивной площадки, кабинета, библиотеки, коридора и т. д. Важно чтобы дети находили периметр в разных единицах длины.
д. Важно чтобы дети находили периметр в разных единицах длины.
Перед изучением темы «Площадь» нужно включить задания на нахождение периметра на каждом уроке.
На первых уроках изучения понятия «Площадь геометрических фигур» необходимо чередовать задания на нахождение периметра и площади.
Для более прочного усвоения можно использовать на уроках игру цвета. Формулы нахождения периметра записывать зеленым цветом, а площади — красным. Если постоянно акцентировать внимание на обозначение цветом, учащиеся привыкают к алгоритму и быстрее ориентируются в выборе формулы для выполнения заданий. Следует включать в работу с нахождением периметра и обратные задачи. Например, 1) Из проволоки длиной 9 см разные треугольники. Какой длины (в сантиметрах) могут быть стороны треугольника? Можно ли считать длины всех сторон проволоки периметром? Перед самым изучением темы «Площадь» дать такое задание: 2) Брат и сестра находили периметр пяти разных прямоугольников и получили 24 см. Какие размеры могли быть у этих прямоугольников? Начерти эти прямоугольники. Выполнить это задание необходимо на листочках, а затем, когда дети научатся находить площадь прямоугольника, нужно вернуться к этому заданию и уже найти площадь этих же прямоугольников.
Какие размеры могли быть у этих прямоугольников? Начерти эти прямоугольники. Выполнить это задание необходимо на листочках, а затем, когда дети научатся находить площадь прямоугольника, нужно вернуться к этому заданию и уже найти площадь этих же прямоугольников.
Конечно, не во всех УМК получится дать такие задания. Например, по учебнику И. И. Аргинской (система Л. В. Занкова) раздел «Площадь и её измерение» стоит в самом начале учебника за 3 класс. Естественно, здесь невозможно начать изучение темы с повторения темы нахождения периметра прямоугольника. Алгоритм методически будет такой же, как и в работе с другой любой величиной, но здесь уже есть возможность провести сравнение, потому что есть фигуры, которые имеют одномерность (через упражнение). На наглядном материале рассматриваем понятие «Площадь», где мы в жизни с этим встречались. С помощью заданий отрабатываем, вычленяем, классифицируем позиции, используем разные мерки, сравниваем, какие из них удобные, а какие неудобные. Далее направляем детей на то, что необходимо использовать какие-то одинаковые замеры, потому что разные мерки не дают правильной картины сравнения площадей прямоугольников с различными размерами. На практике в одном из заданий предлагается начертить прямоугольники на бумаге, вырезать их и попробовать наложить их друг на друга. Выигрышную позицию здесь сыграет выполнение задания на бумаге в клетку. Понятно, что клетка может служить меркой для измерения площади. На следующих уроках постепенно мерка размером в одну клетку, вытесняет все другие мерки. Здесь важно подвести детей к тому, что в геометрии нет единицы длины — 1 клетка, а есть единица длины — 1 сантиметр и именно квадрат со стороной 1 сантиметр может быть идеальной меркой для подсчета площади прямоугольника. Далее выводится формула нахождения площади прямоугольника.
Далее направляем детей на то, что необходимо использовать какие-то одинаковые замеры, потому что разные мерки не дают правильной картины сравнения площадей прямоугольников с различными размерами. На практике в одном из заданий предлагается начертить прямоугольники на бумаге, вырезать их и попробовать наложить их друг на друга. Выигрышную позицию здесь сыграет выполнение задания на бумаге в клетку. Понятно, что клетка может служить меркой для измерения площади. На следующих уроках постепенно мерка размером в одну клетку, вытесняет все другие мерки. Здесь важно подвести детей к тому, что в геометрии нет единицы длины — 1 клетка, а есть единица длины — 1 сантиметр и именно квадрат со стороной 1 сантиметр может быть идеальной меркой для подсчета площади прямоугольника. Далее выводится формула нахождения площади прямоугольника.
Полезно выполнить на сравнение площадей такое упражнение. Учитель вывешивает два прямоугольника разного цвета, но одинакового размера, Один из них разделен на 8 равных квадратов, а другой на 32 таких же квадрата. Учитель просит детей сначала сосчитать, на сколько квадратов разделен первый прямоугольник. Записывает результат счета на доске. Аналогичная работа проводится с другим прямоугольником. Затем дети по найденному числу квадратов сравнивают площади прямоугольников. Как правило, дети делают ошибочные выводы. Но неправильный вывод приводит к пониманию необходимости новых единиц для измерения площадей геометрических фигур.
Учитель просит детей сначала сосчитать, на сколько квадратов разделен первый прямоугольник. Записывает результат счета на доске. Аналогичная работа проводится с другим прямоугольником. Затем дети по найденному числу квадратов сравнивают площади прямоугольников. Как правило, дети делают ошибочные выводы. Но неправильный вывод приводит к пониманию необходимости новых единиц для измерения площадей геометрических фигур.
Для измерения площади линейные единицы не пригодны, нужны новые единицы — единицы площади.
Одним из эффективных заданий на показ разницы между понятиями периметр и площадь — это практическое задание на конструирование прямоугольника из проволоки и картона:
1) Согните проволоку в фигуру прямоугольной формы длиной 8 см и шириной 5 см.
2) Из картона вырежете прямоугольник длиной 8 см и шириной 5 см.
3) Сравните фигуру из проволоки с фигурой из картона. Что можете сказать? (на данном этапе дети могут ответить, что у них одинаковые размеры и форма)
4) Найдите периметр фигуры из проволоки (дети находят периметр прямоугольника любым способом).
5) Можно ли разогнуть фигуру из проволоки в линию? (дети видят, что фигура вышла «пустая», она не является плоской и её легко разогнуть). Можно ли также поступить с фигурой из картона? Почему?
6) Можно ли сказать о том, что периметр прямоугольника и длина линии равны? Почему?
7) Равны ли периметры этих фигур? Почему?
Это задание нужно обязательно давать кинестетикам. Ребенок должен потрогать проволоку, провести пальцами по всем сторонам прямоугольника и по всей длине линии. Также поступить с прямоугольником из картона — провести пальцами по всем сторонам и ладонью по всей поверхности фигуры. Так он быстрее поймет разницу между суммой длин сторон и площадью.
Чтобы отработать навык дифференциации понятий «Периметр» и «Площадь» целесообразно предложить задания на нахождение периметра и площади прямоугольника одновременно.
В целях систематизации знаний полезно провести обобщающую работу, в ходе которой учащиеся сами придумывают задания для одноклассников на нахождение площади и периметра и проверяют правильность их выполнения.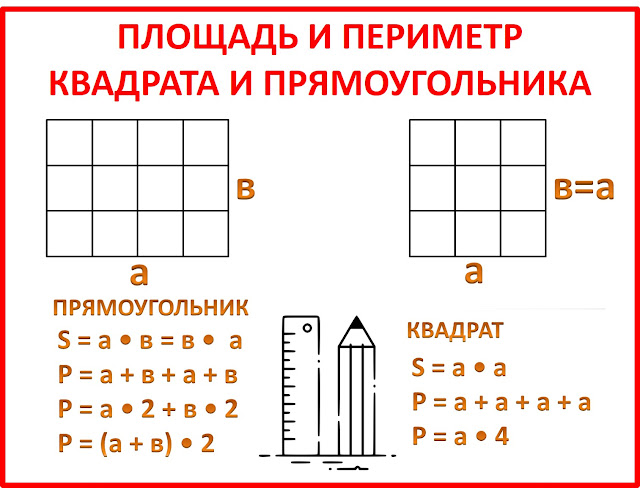 Данные можно зафиксировать на листах самооценки и оценки.
Данные можно зафиксировать на листах самооценки и оценки.
- Как издать спецвыпуск?
- Правила оформления статей
- Оплата и скидки
Разница между площадью и периметром
LearnPracticeDownload
Площадь и периметр — два важных понятия. Иногда термин «площадь» путают с «периметром». Они оба совершенно разные. Площадь определяется как количество пространства, занимаемого любой двумерной формой. Периметр определяет границу или контур плоской формы. Способы измерения площади и периметра совершенно разные. Давайте обсудим ключевые различия между этими двумя важными терминами.
| 1. | Определение области |
| 2. | Определение периметра |
| 3. | В чем разница между площадью и периметром |
| 4. | Формула площади и периметра |
5. | Решенные примеры по площади и периметру |
| 6. | Практические вопросы по площади и периметру |
| 7. | Часто задаваемые вопросы о разнице между площадью и периметром |
Определение области
Площадь определяется как пространство, занимаемое любой формой, объектом или плоской поверхностью. Общее количество квадратных единиц, которые могут вписаться в форму, объект или плоскую поверхность, определяет фактическую площадь. Концепцию нахождения площади можно легко понять, используя бумагу с квадратной сеткой. Общее количество единичных квадратов, заключенных в фигуру, дает площадь этой фигуры. Например, синий квадрат занимает 9квадратов, что означает, что площадь квадрата составляет 9 квадратных единиц. В реальной жизни мы используем понятие площади, чтобы определить площадь стены, которую нужно покрасить, размеры комнаты, площадь пола комнаты, которую нужно покрыть плиткой, газон во дворе и так далее.
Определение периметра
Слово «периметр» происходит от греческого слова «периметрон». «Пери» означает «вокруг», а «Метрон» означает «мера». Периметр фигуры рассчитывается путем сложения длин всех сторон или путем измерения внешней границы формы или объекта. Некоторые реальные способы использования периметра заключаются в том, чтобы знать размер фоторамки, длину газона и то, ради чего нам нужно поставить забор. Периметры малых объектов можно найти, обернув веревку или нить вокруг объекта, для которого нужно найти периметр. В случае многоугольников их периметр можно найти, сложив стороны многоугольника и выразив их в заданных единицах. На приведенном ниже рисунке показан периметр квадрата, который равен 20 единицам.
В чем разница между площадью и периметром?
В следующей таблице перечислены важные различия между площадью и периметром.
| Площадь | Периметр |
|---|---|
Площадь относится к пространству, занимаемому формой, объектом или поверхностью. | Периметр относится к мере длины контура или границы формы, объекта или поверхности. |
| Площадь измеряется в квадратных единицах. Например, если размеры указаны в дюймах, то площадь выражается в квадратных дюймах. | Периметр измеряется в линейных единицах. Например, если размеры указаны в дюймах, то периметр выражается в дюймах. |
| Пример: Площадь квадратного парка равна стороне парка × стороне парка или стороне 2 | Пример: Периметр квадратного парка равен сумме всех 4-х сторон парка или 4-х сторон. |
Формула площади и периметра
В приведенной ниже таблице перечислены некоторые важные формулы площади и периметра некоторых распространенных форм.
| Форма | Площадь (квадратные единицы ) | Периметр (шт. ) ) |
|---|---|---|
| Квадрат | сторона × сторона | 4 × стороны |
| Прямоугольник | длина × ширина | 2(длина + ширина) |
| Круг | 2πr | πr 2 |
| Равносторонний треугольник | сторона + сторона + сторона | (1/2) × основание × высота |
| Параллелограмм | 2 × (сумма двух параллельных сторон) | основание × высота |
| Ромб | 4 × стороны | (1/2) × диагональ 1 × диагональ 2 |
Темы, связанные с площадью и периметром
Ознакомьтесь с интересными статьями, посвященными площади и периметру.
- Площадь квадрата
- Площадь треугольника
- Площадь полукруга
- Площадь ромба
- Периметр треугольника
- Калькулятор площади квадрата
- Калькулятор периметра прямоугольника
Решенные примеры по площади и периметру
Пример 1: Найдите площадь и периметр квадрата со стороной 7 единиц.

Решение:
Площадь квадрата = (сторона × сторона) квадратных единиц. Сторона квадрата = 7 единиц (данные). Следовательно, площадь квадрата = 7 × 7 = 49квадратных единиц. Периметр квадрата = (4 × стороны) единиц. Сторона квадрата = 7 единиц. Следовательно, периметр квадрата = 4 × 7 = 28 единиц.
Пример 2: Длина прямоугольного ковра составляет 21 единицу. Его площадь составляет 210 кв. Найдите ширину ковра и периметр ковра.
Решение:
Площадь прямоугольника = (длина × ширина) квадратных единиц. Дано: длина прямоугольного ковра = 21 единица, а площадь = 210 квадратных единиц ⇒ 21 × ширина = 210 ⇒ ширина = 210/21. Таким образом, ширина прямоугольного ковра = 10 ед.
Периметр прямоугольника = 2 (длина + ширина) единиц. Дано: длина прямоугольного ковра = 21 единица и ширина прямоугольного ковра = 10 единиц. Подставляя значения длины и ширины в формулу получаем, периметр = 2 (21 + 10) = 2 (31) = 62 единицы.
 Следовательно, периметр прямоугольного ковра = 62 единицы.
Следовательно, периметр прямоугольного ковра = 62 единицы.Пример 3: Круглый сад радиусом 50 единиц должен быть огорожен. Найдите стоимость ограждения круглого сада, если для ограждения одного участка требуется 10 долларов. (Используйте значение π как 22/7)
Решение:
Чтобы рассчитать стоимость ограждения сада, мы сначала должны найти длину внешней границы сада. Чтобы найти это, найдем периметр круглого сада радиусом 50 единиц. Для круга длина окружности = 2πr единиц.
Дано: радиус = 50 единиц. Следовательно, окружность = 2 × (22/7) × 50 = 314,28 единиц. Стоимость ограждения 1 единицы сада = 10$. Следовательно, стоимость ограждения 314,28 ед. сада = 314,28 × 10 = 3142,8 9 долл.0003
перейти к слайдуперейти к слайдуперейти к слайду
Есть вопросы по основным математическим понятиям?
Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему стоит математика, с сертифицированными экспертами ourCuemath.
Забронировать бесплатный пробный урок
Практические вопросы по площади и периметру
перейти к слайдуперейти к слайдуперейти к слайду
Часто задаваемые вопросы о разнице между площадью и периметром
Как связаны площадь и периметр?
Площадь определяется как мера пространства, занимаемого любой поверхностью или объектом, тогда как периметр определяет длину границы объекта или формы.
Что такое единица измерения периметра и площади?
Периметр измеряется в линейных единицах, а площадь измеряется в квадратных единицах. Например, если длина и ширина прямоугольника равны 6 единицам и 4 единицам соответственно, то его периметр равен 20 единицам, а площадь прямоугольника равна 24 квадратным единицам.
Площадь окружности или периметр?
Периметр круга называется его окружностью.
В чем разница между периметром и окружностью?
Периметр измеряется путем вычисления длины границы поверхности или формы. Периметр круга обозначается термином «окружность». Длина окружности рассчитывается по формуле 2πr единиц.
Периметр круга обозначается термином «окружность». Длина окружности рассчитывается по формуле 2πr единиц.
Как вычислить площадь квадрата?
Площадь квадрата рассчитывается по формуле (сторона × сторона) квадратных единиц, если дана длина его стороны. Например, площадь квадрата со стороной 5 единиц равна 5 × 5, что равно 25 квадратным единицам.
В чем разница между площадью и периметром?
Площадь определяется как пространство или область, занимаемая фигурой, тогда как периметр определяется как граница или контур фигуры. Две фигуры с одинаковыми площадями могут иметь разное значение периметра. Площадь измеряется в квадратных единицах, тогда как периметр измеряется в линейных единицах.
Скачать БЕСПЛАТНЫЕ учебные материалы
Рабочие листы по площади и периметру
Рабочие листы по математике и
наглядный учебный план
1.1: Периметр и площадь — Математика LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 64049
Периметр
Периметр — это одномерное измерение, которое проводится вокруг внешней стороны замкнутой геометрической формы. Давайте начнем обсуждение концепции периметра с примера.
Давайте начнем обсуждение концепции периметра с примера.
Пошаговый пример
Рис. 1.
Рис. 2.
У Джозефа нет машины, поэтому он должен везде ездить на автобусе или ходить пешком. По понедельникам он должен ходить в школу, на работу и снова домой. Его маршрут изображен на рис. 1.
Очевидный вопрос в этой ситуации: «Сколько миль Джозеф проезжает по понедельникам»? Чтобы рассчитать каждое расстояние: 3 + 6 + 6 = 15.
Джозеф проходит 15 миль по понедельникам.
Еще один способ справиться с этой ситуацией — нарисовать фигуру, представляющую маршрут путешествия Джозефа и отмеченную расстоянием от одного места до другого.
Обратите внимание, что форма, созданная маршрутом Джозефа, представляет собой замкнутую геометрическую фигуру с тремя сторонами (треугольник) (см. рис. 2). Что мы можем спросить об этой форме: «Что такое периметр треугольника»?
Периметр означает «расстояние вокруг замкнутой фигуры или фигуры», и для вычисления мы добавляем каждую длину: 3 + 6 + 6 = 15
Наш вывод такой же, как и выше: Джозеф проходит 15 миль по понедельникам.
Однако мы смоделировали ситуацию с помощью геометрической формы, а затем применили определенную геометрическую концепцию ( периметр ) к вычислению расстояния, пройденного Джозефом.
Примечания по периметру
- Периметр — это одномерное измерение, представляющее расстояние вокруг замкнутой геометрической фигуры или формы (без зазоров).
- Чтобы найти периметр, сложите длины каждой стороны фигуры.
- Если есть единицы, включите их в окончательный результат. Единицы измерения всегда будут одномерными (например, футы, дюймы, ярды, сантиметры и т. д.)
Чтобы вычислить периметр, наши фигуры должны быть замкнуты. На рис. 3 показана разница между закрытой и открытой фигурой.
Рисунок 3.
Пример 1
Найдите периметр каждой из фигур ниже.
- Сложите длины каждой стороны.
- Иногда приходится делать предположения, если длины не помечены.
Растворы
- 12 шт.

- 40 футов
Пример 2
Как найти периметр этой более сложной формы?
Решение
Просто продолжайте добавлять эти длины сторон. 6 + 7 + 4 + 4 + 5 + 6 + 2 = 34 единицы
Если вы внимательно посмотрите на фигуры в предыдущих примерах, вы можете заметить некоторые способы записи каждого периметра в виде более явной формулы. Посмотрите, соответствуют ли результаты того, что мы сделали до сих пор, приведенным ниже формулам.
| Форма | Периметр | |
|---|---|---|
| Треугольник с длинами сторон: \(a, b, c \) | \(Р = а + б + с \) | |
| Квадрат со стороной \(a\): | \( Р = 4а \) | |
| Прямоугольник с длинами сторон \(a, b\): | \( Р = а + Ь + а + Ь \) \( Р = а + а + Ь + Ь \) \( Р = 2а + 2б \)
| |
Окружность
Возможно, вы понимаете, что мы еще не обсуждали расстояние вокруг очень важной геометрической формы: круга! Расстояние по окружности имеет специальное название, называемое окружность .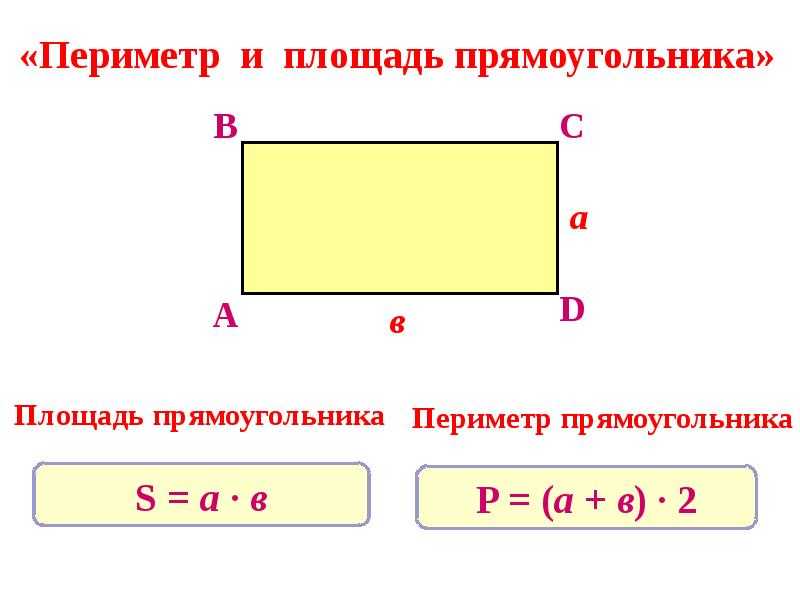 Чтобы найти длину окружности, мы используем эту формулу: \(C = 2\pi r\)
Чтобы найти длину окружности, мы используем эту формулу: \(C = 2\pi r\)
Рисунок 4.
В этой формуле \( \pi \) произносится как «пи» и определяется как длина окружности, деленная на ее диаметр: \( \pi = \frac{C}{d} \). Обычно мы заменяем \( \pi \) на приближение 3.14. Буква r представляет радиус окружности.
Давайте посмотрим, откуда взялась формула длины окружности. На рисунке 4 показана общая окружность с радиусом \( r \) .
Примечания о \(C = 2 \pi r \)
Помните, что в формуле при вычислении длины окружности \( C = 2 \pi r \) мы умножаем следующим образом обычно подставляя 3,14 вместо \( \pi \) :
C = 2 × 3,14 × r
Часто использование ( ) помогает облегчить просмотр различных частей формулы:
C = (2 )×(3.14)×( r )
Происхождение \(C = 2 \pi r \)
Как упоминалось ранее, специальное число \( \pi \) определяется как отношение длины окружности к ее диаметру. Мы можем записать это в виде уравнения: \( \pi = \frac{C}{d} \).
Мы можем записать это в виде уравнения: \( \pi = \frac{C}{d} \).
Из нашей предыдущей работы мы знаем, что для определения неизвестного \( C \) мы можем переместить \(d\) на другую часть уравнения, написав \(C = \pi d \) . Диаметр полностью проходит через середину круга, поэтому диаметр в два раза больше радиуса. Мы можем обновить \( C \) с точки зрения радиуса как \( C = \pi (2r) \). Немного изменив порядок записи наших частей, мы можем сказать, что \( C = 2 \pi r \) .
Воспользуемся формулой, чтобы найти длину окружности нескольких кругов.
Пример 3
Найдите длину окружности каждого из следующих кругов. Оставляйте свои ответы сначала в точной форме, а затем в округленной форме (с точностью до сотых). (Обратите внимание, что при указании радиуса его значение центрируется над сегментом радиуса. Когда указывается диаметр, его значение центрируется над сегментом диаметра.)
Решения
- Точное значение \(8\pi \) дюйм; округлено от точного ответа 25,13 дюйма; округлено с использованием 3,14 для \(\pi \) 25,12 в
- Точно \(12,44\pi \) м; округлено от точного ответа 39,08 м; округлено с использованием 3,14 для \( \pi \) 39,06 м
Точная форма против округленной формы
- \( \pi \) — число в точной форме.
 Он не округлый.
Он не округлый. - 3.14 представляет собой приближение округленной формы для \( \pi \).
Почему так важно, какую форму мы используем? Это важно, потому что, когда мы округляем, мы вносим ошибку в наш окончательный результат. Для этого класса эта ошибка обычно приемлема. Однако вы обнаружите, что в других предметах, таких как физика или химия, этот уровень точности имеет большое значение. Давайте посмотрим на пример разницы в формах.
Пример 4
Радиус Луны составляет около 1079 миль. Что такое окружность? Давайте решим это, используя как точную, так и округленную форму:
Точное решение
\(C = 2\pi r = 2 \pi (1079) = 2158 \pi \)
Округлить из точное решение , используйте кнопку \( \pi \) на калькуляторе, чтобы получить
\(2158 \pi \приблизительно 6779,56 \)
Округленное решение
\(C = 2\pi r = 2(3,14)(1079) \ ок 6776,12 \)
Обратите внимание, что наши окончательные результаты отличаются. Эта разница является ошибкой, создаваемой использованием 3.14 в качестве начального приближения для \pi . Выполняя домашнее задание и тесты, внимательно читайте указания по каждой задаче, чтобы понять, какую форму использовать.
Эта разница является ошибкой, создаваемой использованием 3.14 в качестве начального приближения для \pi . Выполняя домашнее задание и тесты, внимательно читайте указания по каждой задаче, чтобы понять, какую форму использовать.
Пример 5
Найдите длину окружности или периметра в каждой описанной ниже ситуации. Включите чертеж формы с включенной информацией. Используйте примеры, чтобы определить, какие фигуры нужно рисовать. Показать все работы. Как и в примерах, если единицы включены, единицы должны присутствовать в конечном результате. Округлите до десятых, если не указано иное.
- Найдите периметр квадрата со стороной 2,17 фута.
- Найдите периметр прямоугольника со сторонами 4,2 и 3,8.
- Найдите периметр треугольника со сторонами 2, 5, 7.
- Найдите длину окружности радиусом 6 дюймов. Представьте ответ в точной форме, а также вычислите, используя 3.14 для \( \pi \) . Присутствует округлая форма с точностью до десятых.

- Найдите длину окружности круга диаметром 14,8 дюйма. Представьте ответ в точной форме, а также вычислите, используя 3.14 для \( \pi \) . Присутствует округлая форма с точностью до десятых.
Решения
- 8,68 футов
- 16
- 14
- Точное \( 12 \pi \) дюймов, округленное 37,7 дюймов
- Точное \( 14,8\pi \) дюймов, округленное 46,5 дюймов
Пример 6
Нахождение расстояния вокруг нестандартных фигур
Основные формулы для периметра прямолинейных фигур и длины окружности помогут нам найти расстояние вокруг более сложных фигур. Найдите расстояние вокруг следующей фигуры. Округлите окончательный ответ до десятых и используйте 3.14 для \( \pi \).
Решение
34,7 дюйма
Пример 7
Применение периметра и окружности
Наши знания об основных геометрических фигурах можно применить для решения «реальных» задач.
Уолли хочет добавить забор к задней части своего дома, чтобы его дети могли безопасно играть (см.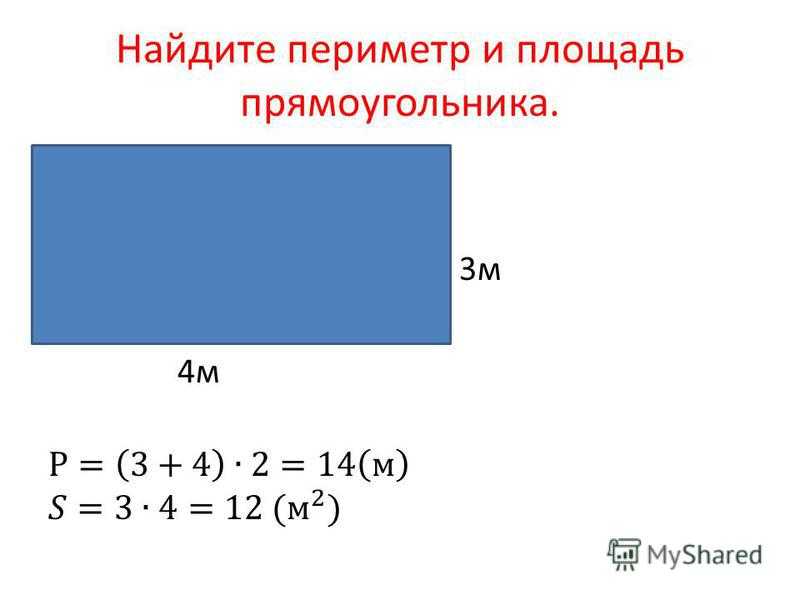 схему ниже). Он начал измерять свой двор, но отвлекся и забыл закончить измерение перед тем, как пойти в магазин. Если он помнит, что задняя стена его дома имеет длину 15 ярдов, достаточно ли у него информации, чтобы купить необходимое ему ограждение? Если да, то сколько футов он должен купить?
схему ниже). Он начал измерять свой двор, но отвлекся и забыл закончить измерение перед тем, как пойти в магазин. Если он помнит, что задняя стена его дома имеет длину 15 ярдов, достаточно ли у него информации, чтобы купить необходимое ему ограждение? Если да, то сколько футов он должен купить?
Решение
81 фут
Площадь
Давайте еще раз взглянем на задний двор Уолли из примера 7, чтобы ввести следующее понятие: площадь.
Пошаговый пример
Уолли успешно огородил свой двор, но теперь хочет добавить немного ландшафта и создать лужайку, как показано ниже.
Он направляется в местный магазин газонов и узнает, что для того, чтобы определить, сколько дерна ему нужно, он должен определить площадь участка, на который он хочет добавить траву. По пути домой он понимает, что если он разделит травяной участок на участки размером 1 фут на 1 фут, а затем посчитает их, то сможет определить площадь участка в квадратных футах. Вот информация, которую Уолли нарисовал, когда вернулся домой.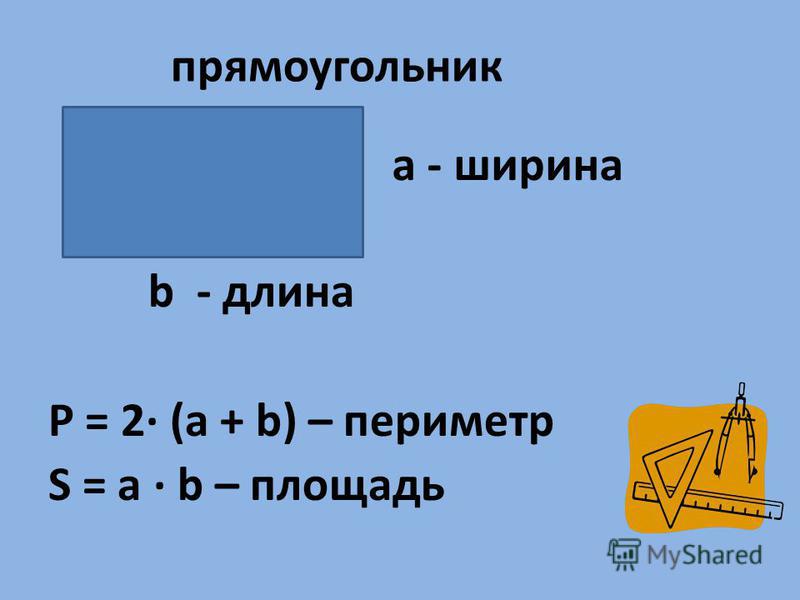
Уолли правильно определил, что площадь прямоугольной травянистой секции составляет 30 квадратных футов.
Примечания к площади
- Площадь — это двумерное измерение, представляющее объем пространства внутри двумерной формы.
- Чтобы найти площадь, подсчитайте количество единичных квадратов внутри фигуры.
- Если есть единицы, включите их в окончательный результат. Единицы измерения всегда будут двумерными (например, квадратные футы, квадратные ярды, квадратные мили и т. д.)
Пример 8
Найдите площадь каждой из фигур ниже.
- Не забудьте подсчитать единичные квадраты внутри фигуры.
- Есть ли здесь схема, которая облегчила бы нам работу?
Пример 9
Как найти площадь более сложных форм? Разбейте области на формы, которые мы узнаем, и сложите значения площади вместе.
Если вы внимательно посмотрите на фигуры в предыдущих примерах, вы можете заметить некоторые способы записи каждой области в виде более явной формулы. Посмотрите, соответствуют ли результаты того, что мы сделали до сих пор, приведенным ниже формулам. 92\)
Посмотрите, соответствуют ли результаты того, что мы сделали до сих пор, приведенным ниже формулам. 92\)
\(А=а\cточка б\)
(Вы также увидите это как \(A=\text{длина} \cdot \text{ширина} \))
Формулы площади для приведенных ниже фигур вывести сложнее, поэтому формулы приведены в таблице.
| Форма | Форма |
|---|---|
Треугольник с высотой h и основанием b \( A = \dfrac{1}{2}bh = \dfrac{bh}{2} \) Читается как «половина основания умноженная на высоту» Обратите внимание, что h — это расстояние по прямой линии от вершины треугольника непосредственно до другой стороны. На это указывает маленькое поле рядом с h . Читается как «пи умножить на радиус в квадрате» | |
Если ваш треугольник такой, как на рисунке слева, то высота нарисована и измерена за пределами треугольника. Формула площади такая же. |
Пример 10
Найдите площадь для каждой описанной ситуации. Создайте рисунок формы с включенной информацией. Показать все работы. Как и в примерах, если включены единицы измерения, они должны присутствовать и в конечном результате. Используйте 3,14 для \pi и округляйте ответы до десятых по мере необходимости.
- Найдите площадь прямоугольника, длина которого равна 12,9 метра, а высота составляет одну треть этой суммы.
- Найдите площадь треугольника с основанием \(24 \frac{1}{2} \) дюймов и высотой 7 дюймов.

- Найдите площадь круга радиусом \(2 \frac{1}{3} \) дюймов. Представьте ответ в точной форме, а также вычислите округленную форму, используя 3.14 для \( \pi \) . Присутствует округлая форма с точностью до десятых.
Solutions
- 55,5 м 2 или 55,5 квадратных метров (округлено)
- 85,8 дюйма 2 или 85,8 квадратных дюйма (округленные)
- Точное число 49/9 \( \pi \) в 2 , округленное 17,1 в 2
Пример 11
Найдите площадь для каждой описанной ситуации. Включите рисунок формы с включенной информацией. Показать все работы. Как и в примерах, если включены единицы, то единицы должны присутствовать в конечном результате. Округлите ответы до десятых, если не указано иное.
- Найдите площадь квадрата со стороной 4,2 фута.
- Найдите площадь прямоугольника со сторонами 4,2 и 3,8.
- Найдите площадь треугольника с высотой 7 дм и основанием 12 дм.

- Найдите площадь круга радиусом 6 дюймов. Представьте ответ в точной форме, а также вычислите, используя 3.14 для \( \pi \) . Присутствует округлая форма с точностью до десятых.
Решения
- 17,64 фута 2 или 17,64 квадратных фута
- 16,0
- 42 в 2 или 42 квадратных дюйма
- Точно 36\( \pi \) в 2 или 36\( \pi \) квадратных дюймов, округлено с использованием 3,14 для \( \pi \) 113,0 в 2 или 113,0 квадратных дюймов
Пример 12
Нахождение площади нестандартных фигур
Основные формулы площади помогут нам найти площадь более сложных фигур. Это та же проблема, для которой мы нашли периметр ранее. Найдите площадь заданной фигуры. Вычислите, используя 3,14 для \( \pi \) и округлите до десятых. 9 2
Пример 13
Применение площади и периметра
Мы можем объединить наши знания о площади/периметре для решения таких задач, как эта.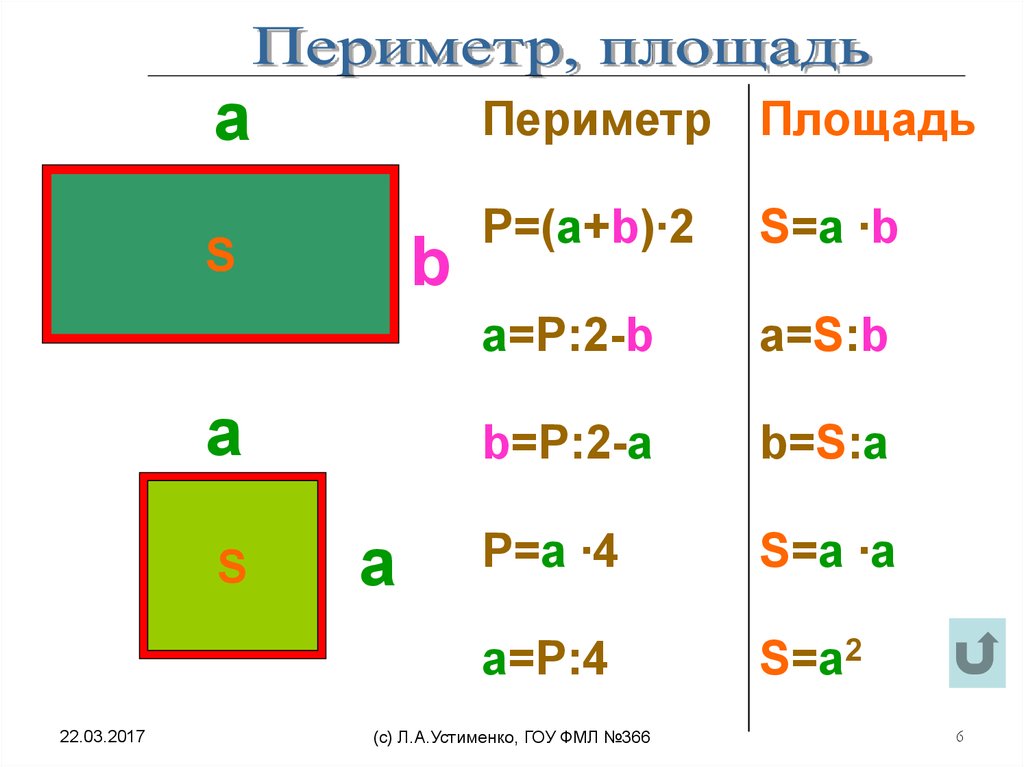
Уолли все еще ремонтирует свой дом, и ему нужно закончить проект пола. Он хочет купить достаточное количество бамбукового паркета, чтобы покрыть площадь пола в комнатах A, C и коридоре B, а также достаточное количество бамбуковой кромки для плинтусов во всех помещениях. Сколько квадратных футов полов и сколько футов плинтусов он должен купить?
Solution
256 футов 2 пол, 108 футов кромки
Контент под лицензией CC, совместно используемый ранее
- Рабочая тетрадь для учащихся по основам арифметики. Авторы : Донна Годе, Эми Вольпе и Дженифер Бохарт. Предоставлено : Общественный колледж Скоттсдейла. Расположен по адресу : https://sccmath.wordpress.com/. Лицензия : CC BY-SA: Attribution-ShareAlike
1.1: Perimeter and Area распространяется по недекларированной лицензии, автором, ремиксом и/или куратором является LibreTexts.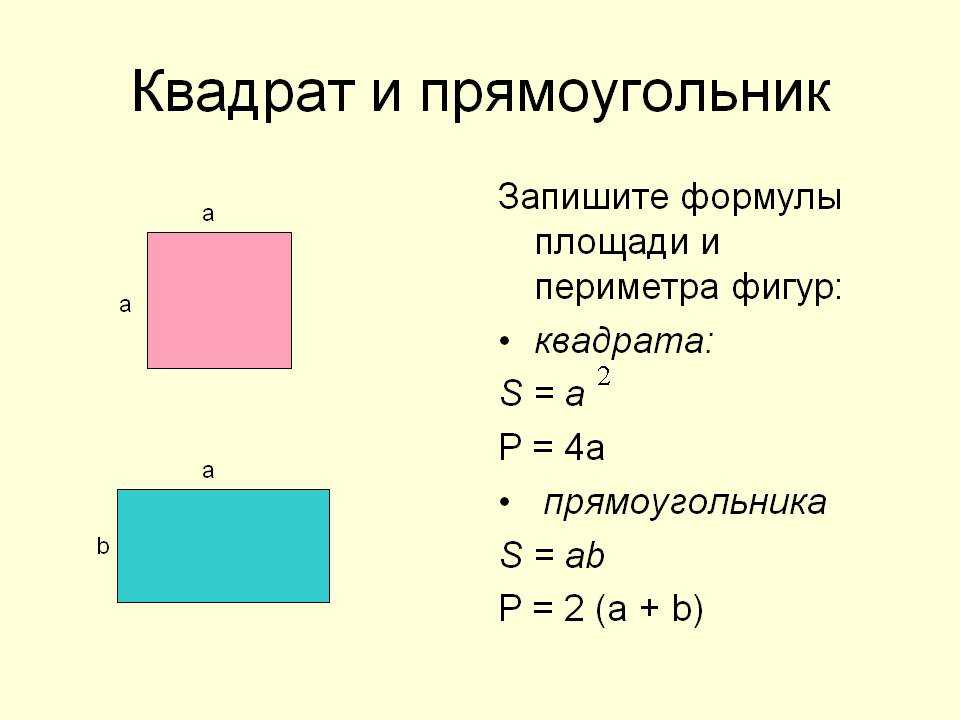
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Теги
- источник[1]-math-51600
- источник[2]-math-51600
- источник[21]-math-57198
- источник[22]-math-57198
Периметр и площадь — Преподавание с видом на горы
Мы закончили работу над единицами измерения периметра и площади несколько недель назад (как раз перед дробями!), но я так и не удосужился опубликовать некоторые интересные задания, которые мы проделали.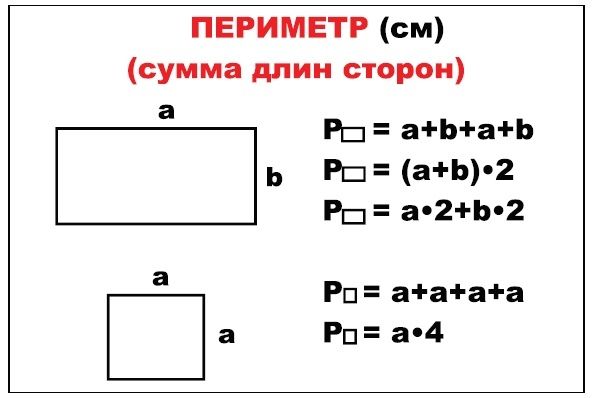 На самом деле это был обзор для моих детей, поэтому было забавно вытащить некоторые из более основанных на исследованиях занятий и посмотреть, как они отправляются в город. Перед тем, как в этом году мы начали работу над блоком периметра и площади, я разослал своим ученикам небольшой тизер через ClassDojo…
На самом деле это был обзор для моих детей, поэтому было забавно вытащить некоторые из более основанных на исследованиях занятий и посмотреть, как они отправляются в город. Перед тем, как в этом году мы начали работу над блоком периметра и площади, я разослал своим ученикам небольшой тизер через ClassDojo…
Они заметили каски и попались на крючок! Они не могли дождаться, когда придут в школу и увидят, что мы собираемся делать в этих касках.
Диаграммы привязки периметра и площади
Прошло несколько дней, прежде чем мы смогли по-настоящему погрузиться в работу, поэтому мы начали наш обзор с создания этой диаграммы привязки периметра и площади.
Нам нужно было узнать, как найти периметр и площадь обеих правильных неправильных фигур, поэтому есть два примера.
Книги по периметру и площади Урок врезки
Затем мы провели один из моих самых любимых уроков по периметру и площади. Я ЛЮБЛЮ это! Мы используем Спагетти и фрикадельки для всех от Мэрилин Бернс (Нажмите на название, чтобы увидеть мою партнерскую ссылку на Amazon!).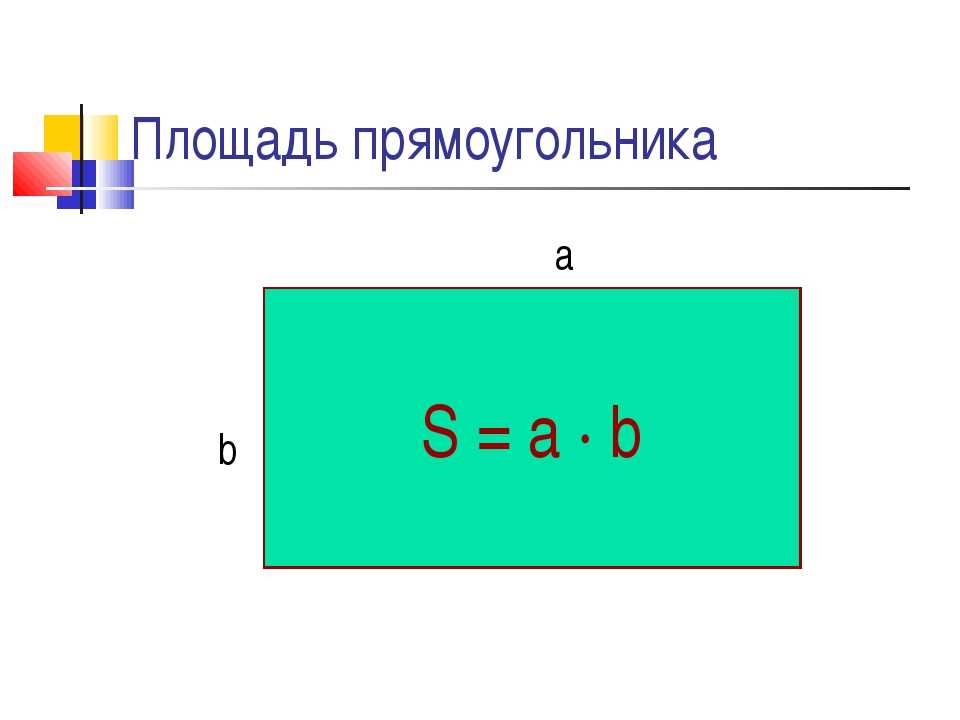 В книге рассказывается о том, как семья устраивает большой ужин из спагетти и должна придумать, как рассадить всех приглашенных всего на двух стульях. В веселой истории они пробуют несколько разных расстановок, и на протяжении всего пути мы составляем схему рассадки и сравниваем площадь и периметр. У всех детей есть 8 плиток (количество столов, которые у них есть), которыми они могут манипулировать, когда мы читаем историю, а затем записываем ее на бумаге. В Beacon Learning есть отличный бесплатный урок ( нажмите здесь ), который проведет вас через процесс обучения, а также предоставит вам рабочий лист, похожий на мою привязку выше. Я использовал этот урок с детьми в 3-5 классах, и у меня никогда не было ребенка, который бы НЕ любил его и не научился чему-то из него. В конце они ВОЮТ на персонажей рассказа, пытающихся объяснить им, как расставить стулья. Разговор о помолвке! В книге также есть отличные дополнения. В конце я всегда прошу своих учеников придумать, как они могут разместить 12, 16, 24 и т.
В книге рассказывается о том, как семья устраивает большой ужин из спагетти и должна придумать, как рассадить всех приглашенных всего на двух стульях. В веселой истории они пробуют несколько разных расстановок, и на протяжении всего пути мы составляем схему рассадки и сравниваем площадь и периметр. У всех детей есть 8 плиток (количество столов, которые у них есть), которыми они могут манипулировать, когда мы читаем историю, а затем записываем ее на бумаге. В Beacon Learning есть отличный бесплатный урок ( нажмите здесь ), который проведет вас через процесс обучения, а также предоставит вам рабочий лист, похожий на мою привязку выше. Я использовал этот урок с детьми в 3-5 классах, и у меня никогда не было ребенка, который бы НЕ любил его и не научился чему-то из него. В конце они ВОЮТ на персонажей рассказа, пытающихся объяснить им, как расставить стулья. Разговор о помолвке! В книге также есть отличные дополнения. В конце я всегда прошу своих учеников придумать, как они могут разместить 12, 16, 24 и т.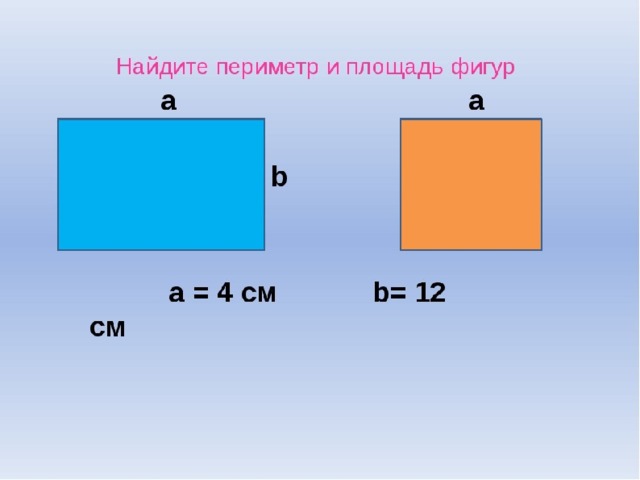 д. человек, и им это тоже нравится.
д. человек, и им это тоже нравится.
Математический проект по периметру и площади
Так как это отличная концепция из реальной жизни, к которой можно применить этот навык, я продолжаю работать над своим математическим проектом по периметру и площади.
В этом математическом проекте учащиеся должны построить свой собственный город. Они начинают с того, что выкладывают все это, затем «приближают» здания в отдельных управляемых заданиях. Я люблю это! Ознакомиться с проектом можно ЗДЕСЬ. Вот тут-то и пригодились каски! В этом году я решил купить им все каски в «Ориентал Трейдинг», так как им поручили быть градостроительами. Они были на седьмом небе от этих маленьких шляп и проекта, и мы были в восторге от него.
Этот же проект также включает ЦИФРОВУЮ ВЕРСИЮ для большей гибкости.
Еще Практика по периметру и площади
Неправильные формы
Это задание с каталожными карточками — еще одно из моих любимых занятий для детей старшего возраста. Я думаю, что первоначально я почерпнул какую-то версию этой идеи из журнала Mailbox Tips, а затем адаптировал ее на протяжении многих лет, чтобы она соответствовала моим потребностям. В нем столько всего интересного… взаимосвязь между площадью и периметром, нахождение недостающих измерений, добавочная площадь и т. д. И это так просто… просто достаньте несколько каталожных карточек для групп детей и попросите их найти разные комбинации карточек, чтобы составить разные фигуры. Я требую, чтобы одна из фигур была по ширине к ширине, а одна из фигур была по длине к длине, а затем остальные они могли настроить так, как они хотят. В конце концов они понимают, что даже если фигуры имеют одинаковую площадь, они могут иметь разный периметр. Опять же… это ОЧЕНЬ ценный урок, когда вы пытаетесь научить отсутствующим измерениям и площади неправильных форм. Они знают, что каждая учетная карточка имеет размер 3×5, поэтому независимо от (почти) того, как они ее составят, они должны быть в состоянии вычислить все длины сторон.
Я думаю, что первоначально я почерпнул какую-то версию этой идеи из журнала Mailbox Tips, а затем адаптировал ее на протяжении многих лет, чтобы она соответствовала моим потребностям. В нем столько всего интересного… взаимосвязь между площадью и периметром, нахождение недостающих измерений, добавочная площадь и т. д. И это так просто… просто достаньте несколько каталожных карточек для групп детей и попросите их найти разные комбинации карточек, чтобы составить разные фигуры. Я требую, чтобы одна из фигур была по ширине к ширине, а одна из фигур была по длине к длине, а затем остальные они могли настроить так, как они хотят. В конце концов они понимают, что даже если фигуры имеют одинаковую площадь, они могут иметь разный периметр. Опять же… это ОЧЕНЬ ценный урок, когда вы пытаетесь научить отсутствующим измерениям и площади неправильных форм. Они знают, что каждая учетная карточка имеет размер 3×5, поэтому независимо от (почти) того, как они ее составят, они должны быть в состоянии вычислить все длины сторон. Я не могу рекомендовать это занятие достаточно.
Я не могу рекомендовать это занятие достаточно.
Я также написал в блоге об использовании пентамино для обучения площади и периметра. Это еще один отличный практический урок для этого навыка, особенно если вы занимаетесь площадью и периметром неправильных форм! Вы можете прочитать больше об этой деятельности ЗДЕСЬ !
Опрокидывающие блоки
Использование этих красочных опрокидывающих блоков — еще один увлекательный способ отработать навыки периметра и площади . Каждый цветной блок состоит из шести вопросов. Когда учащийся вытягивает определенный цвет, вся его команда должна ответить на вопрос, соответствующий этому цвету. Так весело!
Candy Math
Кто не любит Skittles?? Вы можете использовать этот набор Candy Math Pack , чтобы практиковать периметр и площадь, а также десятки других математических навыков! Мне очень нравится использовать его в качестве математического центра, но он также подходит для подготовки к тестам или оценок.
Карточки с заданиями по периметру и площади
И, наконец… будет ли какое-либо из моих математических заданий завершенным без старого доброго набора карточек с заданиями? Конечно нет! Дети выполнили эти карточки с заданиями в качестве оценки. У меня даже есть несколько бонусных карточек, чтобы студенты могли показать, что они знают. Вы можете приобрести эти карточки с заданиями ЗДЕСЬ . Они также являются частью моего огромного набора периметра и площади .
Просмотры сообщений: 18,581
Рабочие листы по площади и периметру | Бесплатно
| Хотите помочь поддержать сайт и убрать рекламу? Станьте покровителем через patreon или сделайте пожертвование через paypal. |
Определение площади с помощью блоков
ссылка
Перетащите ⇄ для прокруткиНажмите, чтобы открыть 3md6Blocks (целиком) ★
Каждый рабочий лист содержит 10 задач на нахождение площади фигуры.
Каждый рабочий лист содержит 8 задач на нахождение площади фигуры.
Создать новый лист Один атта раз Флэш-карты Делиться Дистанционное обучение Выберите рабочий лист Версия 1 Версия 2 Версия 3 Версия 4 Версия 5 Версия 6 Версия 7 Версия 8 Версия 9 Версия 10Grab ’em AllCreate New Sheet 3md6Область поиска ★Каждый рабочий лист содержит 15 задач на нахождение площади прямоугольника.
Создать новый лист Один атта раз Флэш-карты Делиться Дистанционное обучение Выберите рабочий лист Версия 1 Версия 2 Версия 3 Версия 4 Версия 5 Версия 6 Версия 7 Версия 8 Версия 9 Версия 10Grab ’em AllCreate New Sheet 3md7bОбласть поиска ★ Каждый рабочий лист содержит 15 задач на нахождение площади прямоугольника.
Каждый рабочий лист содержит 10 задач на нахождение площади прямоугольника путем замощения.
Создать новый лист Один атта раз Флэш-карты Делиться Дистанционное обучение Выберите рабочий лист Версия 1 Версия 2 Версия 3 Версия 4 Версия 5 Версия 6 Версия 7 Версия 8 Версия 9 Версия 10Grab ’em AllCreate New Sheet Продолжающиеся узоры области ★Каждый рабочий лист содержит 10 задач на определение площади будущих сеток на основе шаблона.
Создать новый лист Один атта раз Флэш-карты Делиться Дистанционное обучение Выберите рабочий лист Версия 1 Версия 2 Версия 3 Версия 4 Версия 5 Версия 6 Версия 7 Версия 8 Версия 9 Версия 10Grab ’em AllCreate New Sheet 6g1. Нахождение площади прямоугольных треугольников с помощью сетки ★
Нахождение площади прямоугольных треугольников с помощью сетки ★Каждый рабочий лист содержит 9задачи с использованием сетки для нахождения площади прямоугольного треугольника.
Создать новый лист Один атта раз Флэш-карты Делиться Дистанционное обучение Выберите рабочий лист Версия 1 Версия 2 Версия 3 Версия 4 Версия 5 Версия 6 Версия 7 Версия 8 Версия 9 Версия 10Grab ’em AllCreate New SheetОпределение периметра с помощью блоков
ссылка
Перетащите ⇄ для прокруткиНажмите, чтобы открыть 3md6Периметр Блоки ★
Каждый рабочий лист содержит 8 задач на нахождение периметра фигуры.
Создать новый лист Один атта раз Флэш-карты Делиться Дистанционное обучение Выберите рабочий лист Версия 1 Версия 2 Версия 3 Версия 4 Версия 5 Версия 6 Версия 7 Версия 8 Версия 9 Версия 10Grab ’em AllCreate New SheetЧетырехугольники
ссылка
Перетащите ⇄ для прокруткиНажмите, чтобы открыть 3md7dПрямоугольная площадь ★
Каждый рабочий лист содержит 10 задач на нахождение площади прямолинейной фигуры.
Каждый рабочий лист содержит 12 задач на создание прямоугольников для заданной площади или периметра.
Создать новый лист Один атта раз Флэш-карты Делиться Дистанционное обучение Выберите рабочий лист Версия 1 Версия 2 Версия 3 Версия 4 Версия 5 Версия 6 Версия 7 Версия 8 Версия 9 Версия 10Grab ’em AllCreate New Sheet 3md8Rectangles — одинаковая площадь и разный периметр ★На каждом листе есть 5 задач на создание прямоугольника с одинаковой площадью, но разным периметром.
Создать новый лист Один атта раз Флэш-карты Делиться Дистанционное обучение Выберите рабочий лист Версия 1 Версия 2 Версия 3 Версия 4 Версия 5 Версия 6 Версия 7 Версия 8 Версия 9 Версия 10Grab ’em AllCreate New Sheet 3md8Rectangles — одинаковый периметр и разная площадь ★ На каждом листе есть 5 задач на создание прямоугольника с одинаковой площадью, но разным периметром.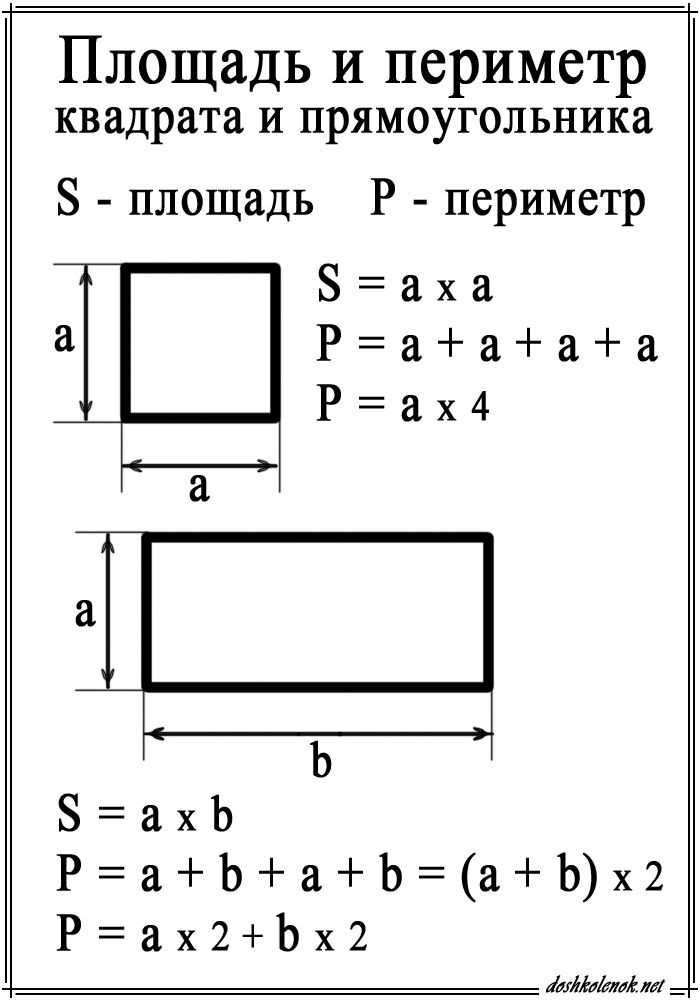
Каждый рабочий лист содержит 15 задач на нахождение площади и периметра прямоугольника.
Создать новый лист Один атта раз Флэш-карты Делиться Дистанционное обучение Выберите рабочий лист Версия 1 Версия 2 Версия 3 Версия 4 Версия 5 Версия 6 Версия 7 Версия 8 Версия 9Версия 10Grab ’em AllCreate New Sheet 7g1Нахождение ширины, высоты и площади масштабных прямоугольников ★Каждый рабочий лист содержит 8 задач на нахождение ширины, высоты и площади масштабированного прямоугольника.
Создать новый лист Один атта раз Флэш-карты Делиться Дистанционное обучение Выберите рабочий лист Версия 1 Версия 2 Версия 3 Версия 4 Версия 5 Версия 6 Версия 7 Версия 8 Версия 9 Версия 10Grab ’em AllCreate New Sheet Нахождение периметра и площади с помощью десятичных знаков ★ Каждый рабочий лист содержит 15 задач на нахождение площади и периметра четырехугольника с десятичными дробями.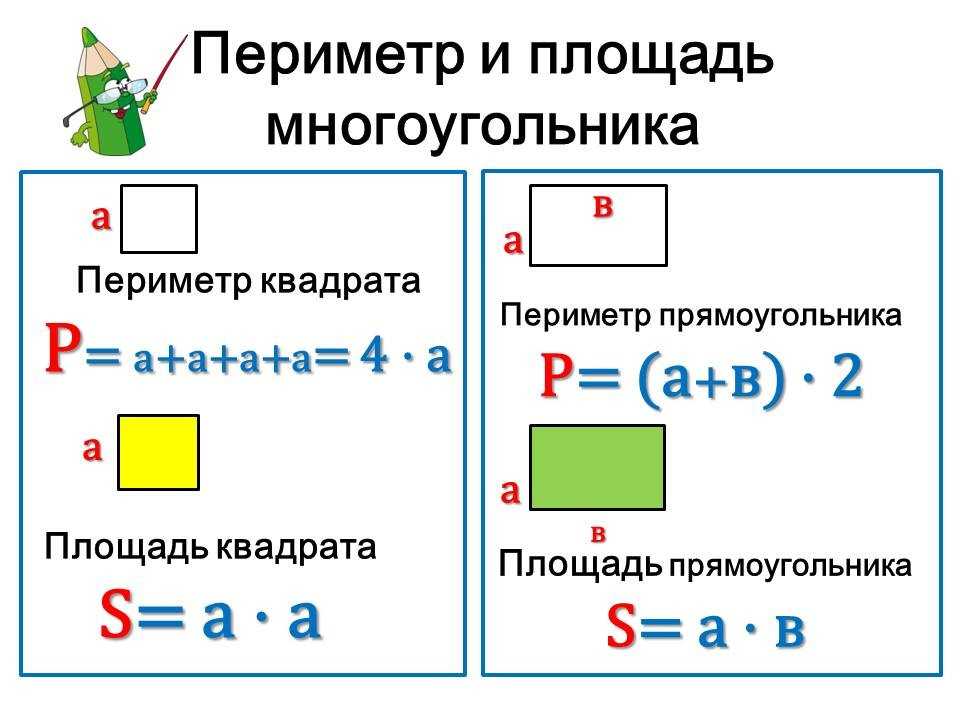
Каждый рабочий лист содержит 15 задач на определение значения пропущенной стороны.
Создать новый лист Один атта раз Флэш-карты Делиться Дистанционное обучение Выберите рабочий лист Версия 1 Версия 2 Версия 3 Версия 4 Версия 5 Версия 6 Версия 7 Версия 8 Версия 9 Версия 10Grab ’em AllCreate New Sheet Нахождение недостающей длины стороны прямоугольника с десятичными знаками ★Каждый рабочий лист содержит 15 задач на определение значения пропущенной стороны.
Создать новый лист Один атта раз Флэш-карты Делиться Дистанционное обучение Выберите рабочий лист Версия 1 Версия 2 Версия 3 Версия 4 Версия 5 Версия 6 Версия 7 Версия 8 Версия 9Версия 10Grab ’em AllCreate New Sheet Нахождение недостающей длины стороны прямоугольника с дробями ★ Каждый рабочий лист содержит 15 задач на нахождение недостающей стороны с дробными длинами сторон.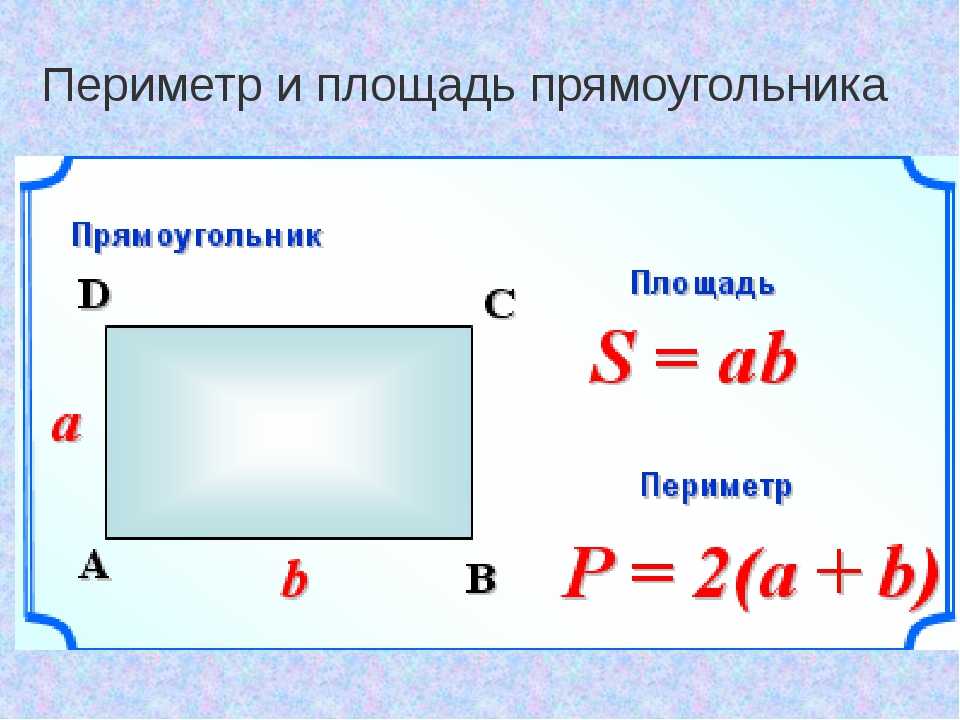
Треугольники
ссылка
Перетащите ⇄ для прокруткиНажмите, чтобы открыть 6g1Площадь треугольников (основание и высота) ★M
Каждый рабочий лист содержит 10 задач на нахождение площади треугольника по основанию и высоте.
Создать новый лист Один атта раз Флэш-карты Делиться Дистанционное обучение Выберите рабочий лист Версия 1 Версия 2 Версия 3 Версия 4 Версия 5 Версия 6 Версия 7 Версия 8 Версия 9Версия 10Grab ’em AllCreate New SheetКруги
ссылка
Перетащите ⇄ для прокруткиНажмите, чтобы открыть 7g4Площадь и длина окружности ★M
Каждый рабочий лист содержит 10 задач на нахождение площади и длины окружности.
Каждый рабочий лист содержит 10 задач на нахождение площади круга.
Создать новый лист Один атта раз Флэш-карты Делиться Дистанционное обучение Выберите рабочий лист Версия 1 Версия 2 Версия 3 Версия 4 Версия 5 Версия 6 Версия 7 Версия 8 Версия 9 Версия 10Grab ’em AllCreate New Sheet 7g4Диаметр окружности ★MКаждый рабочий лист содержит 10 задач на нахождение длины окружности.
Создать новый лист Один атта раз Флэш-карты Делиться Дистанционное обучение Настроить Выберите рабочий лист Версия 1 Версия 2 Версия 3 Версия 4 Версия 5 Версия 6 Версия 7 Версия 8 Версия 9 Версия 10Grab ’em AllCreate New SheetОпределение длины стороны
ссылка
Перетащите ⇄ для прокруткиНажмите, чтобы открыть 3md8Отсутствующая сторона (область) E ★
Каждый рабочий лист содержит 15 задач на нахождение недостающей стороны прямоугольника по заданной площади.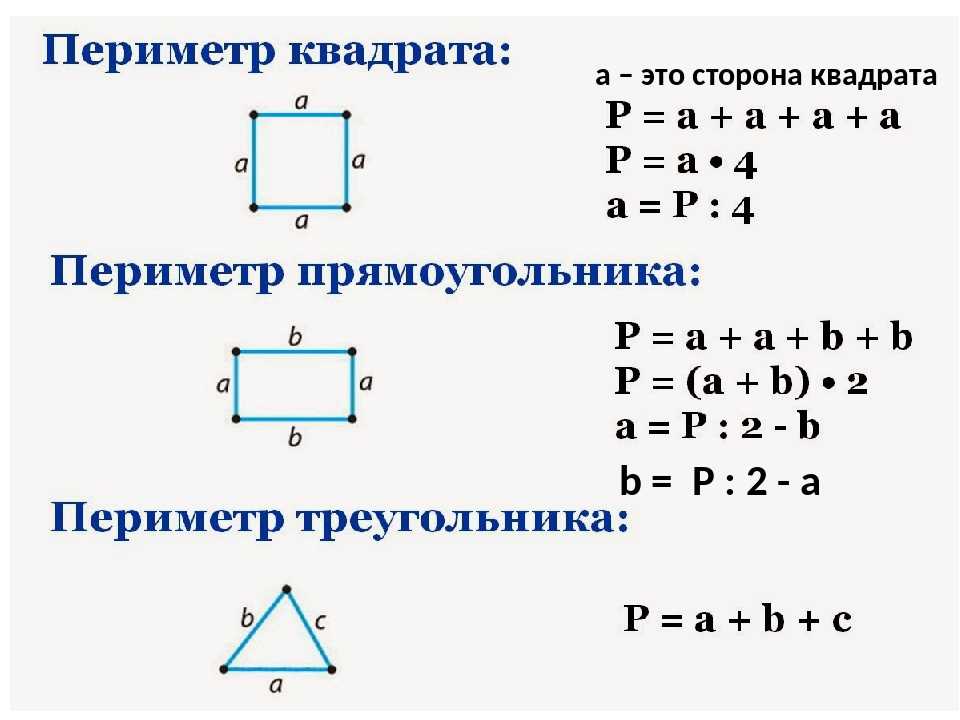
Каждый рабочий лист содержит 15 задач на нахождение недостающей стороны прямоугольника по заданному периметру.
Создать новый лист Один атта раз Флэш-карты Делиться Дистанционное обучение Выберите рабочий лист Версия 1 Версия 2 Версия 3 Версия 4 Версия 5 Версия 6 Версия 7 Версия 8 Версия 9 Версия 10Grab ’em AllCreate New Sheet Нахождение недостающей длины стороны прямоугольника ★MКаждый рабочий лист содержит 15 задач на определение значения пропущенной стороны.
Создать новый лист Один атта раз Флэш-карты Делиться Дистанционное обучение Выберите рабочий лист Версия 1 Версия 2 Версия 3 Версия 4 Версия 5 Версия 6 Версия 7 Версия 8 Версия 9Версия 10Grab ’em AllCreate New Sheet Нахождение недостающей длины стороны прямоугольника с десятичными дробями ★M Каждый рабочий лист содержит 15 задач на определение значения пропущенной стороны.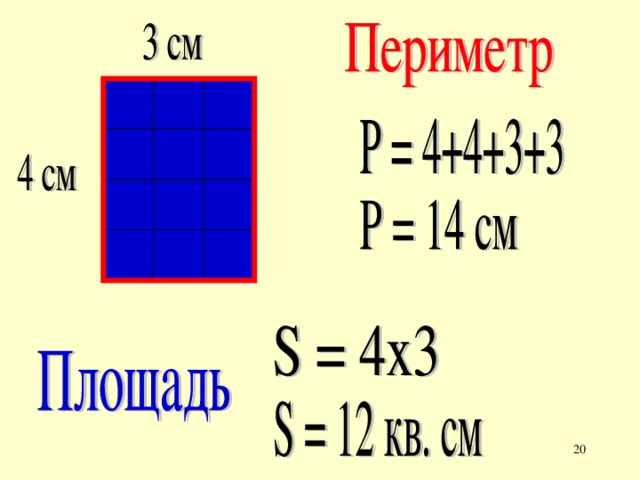
Каждый рабочий лист содержит 12 задач на нахождение недостающей стороны прямоугольного треугольника по заданной площади.
Создать новый лист Один атта раз Флэш-карты Делиться Дистанционное обучение Выберите рабочий лист Версия 1 Версия 2 Версия 3 Версия 4 Версия 5 Версия 6 Версия 7 Версия 8 Версия 9 Версия 10Grab ’em AllCreate New SheetПоиск площади и периметра (слова)
ссылка
Перетащите ⇄ для прокруткиНажмите, чтобы открыть 4md3Периметр — Площадь (Слова) ★M
Каждый рабочий лист содержит 10 задач на решение текстовых задач на площадь и периметр.
Создать новый лист Один атта раз Флэш-карты Делиться Дистанционное обучение Выберите рабочий лист Версия 1 Версия 2 Версия 3 Версия 4 Версия 5 Версия 6 Версия 7 Версия 8 Версия 9 Версия 10Grab ’em AllCreate New Sheet 6g4Нахождение площади поверхности ★ Каждый рабочий лист содержит 8 задач на определение площади поверхности фигуры.
Найдите площадь и периметр (если вы их потеряли) (Видео)
Если вам нужна помощь с периметром прямоугольника, введите здесь .
TranscriptFAQsPractice
Привет, ребята! Добро пожаловать в это видео о нахождении площади и периметра объекта.
Площадь и периметр помогают нам измерять двумерные фигуры.
Площадь измеряет поверхность объекта, а периметр измеряет длину внешней стороны объекта.
Допустим, у вас есть прямоугольный бассейн.
Вы хотите найти брезент, чтобы накрыть его, тогда вам нужно знать площадь поверхности бассейна (все синее).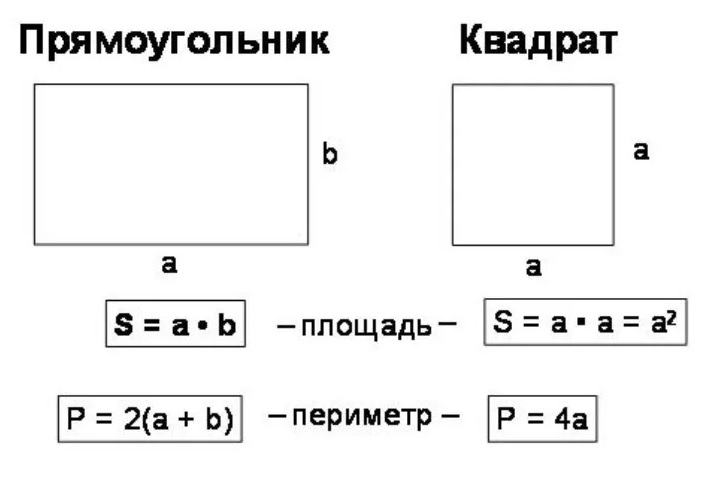 Но если вы хотите узнать расстояние, которое потребуется вам, чтобы обойти бассейн, вам нужно будет знать периметр.
Но если вы хотите узнать расстояние, которое потребуется вам, чтобы обойти бассейн, вам нужно будет знать периметр.
Теперь давайте посмотрим, как рассчитать каждый из них.
Как найти Периметр
Во-первых, периметр. Чтобы вычислить периметр любого многоугольника, достаточно сложить длины всех сторон.
В качестве примера возьмем наш прямоугольный бассейн. Допустим, что ширина 15 футов, а длина 7 футов.
Поскольку это прямоугольник, мы знаем, что параллельные стороны имеют одинаковую длину.
Итак, у нас есть вся необходимая информация. Теперь просто сложите все стороны.
Начнем с нашей формулы. Допустим, 15 равно \(a\), а 7 равно \(b\).
Итак, мы имеем \(P= a + a + b + b\).
Теперь давайте подставим наши числа. \(P=15\текст{футы}+15\текст{футы}+7\текст{футы}+7\текст{футы}\). Итак, складываем все это и получаем, что наш периметр равен 44 футам.
Мы можем даже упростить формулу периметра прямоугольника.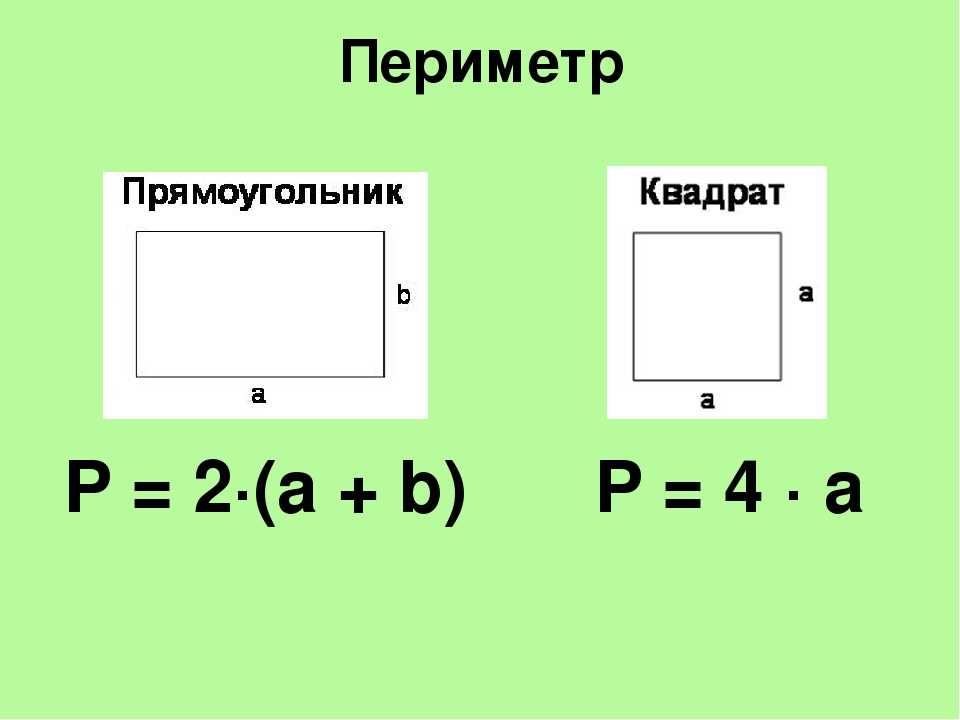 Поскольку мы знаем, что есть 4 стороны и что есть два набора одинаковых сторон (две стороны параллельны друг другу), мы можем упростить нашу формулу до \(P=2(a+b)\). Давайте попробуем и посмотрим, получится ли у нас то же самое.
Поскольку мы знаем, что есть 4 стороны и что есть два набора одинаковых сторон (две стороны параллельны друг другу), мы можем упростить нашу формулу до \(P=2(a+b)\). Давайте попробуем и посмотрим, получится ли у нас то же самое.
\(P=2(15\text{ футов}+7\text{ футов})=2(22\text{ футов})=44\text{ футов}\)
Итак, вы здесь можно увидеть, что мы действительно получаем то же самое.
Мы можем применить тот же принцип для нахождения периметра квадрата. Поскольку у квадрата четыре стороны одинакового размера, мы можем сказать, что периметр квадрата равен \(4\x a\).
Тот же принцип справедлив и для равностороннего треугольника. Все три стороны одинаковы, поэтому мы можем сказать \(P=3\times a\). У равнобедренного треугольника две стороны одинаковы, поэтому мы можем записать нашу формулу периметра как \(P=2a+b\).
Единственная фигура, периметр которой может показаться немного менее очевидным, это наш друг круг. Вы, ребята, возможно, слышали о термине окружность . Окружность — это то же самое, что и периметр круга.
Окружность — это то же самое, что и периметр круга.
Некоторых математиков может немного смутить термин, который вы используете, потому что технически периметр определяется как «сумма длин ребер замкнутой фигуры», а у круга нет ребер. Но определение окружности — это периметр круга. Итак, как бы вы ни предпочитали называть это, давайте посмотрим, как вы его найдете.
Чтобы найти длину окружности , умножьте диаметр на \(π\): (\(C=d\pi\)).
Хорошо, теперь по области.
Как найти площадь
Когда мы смотрели на периметр различных фигур, мы смогли упростить формулы. Давая нам разные формулы для разных форм, но придерживаясь определения сложения всех сторон.
Аналогично, при нахождении площади объекта формула будет разной для разных форм, но каждая формула представляет собой решение для нахождения площади поверхности объекта.
Итак, давайте посмотрим на различные формы и формулу площади, соответствующую каждой форме.
Хорошо, теперь давайте рассмотрим несколько примеров того, как найти площадь эллипса и площадь трапеции.
Допустим, у вас есть эллипс и \(a=6\) и \(b=4\). Теперь давайте подставим наши числа в формулу эллипса.
Допустим, у нас есть трапеция. Мы скажем, что наша высота равна 7, наша сторона \(a\) равна 8, а наша сторона \(b\) равна 5. Теперь мы делаем то же самое, что и в прошлый раз. . Мы просто подставляем наши числа в формулу площади. 92\)
Прямоугольник: \(A=lw\)
Треугольник: \(A=\frac{1}{2}bh\)
Параллелограмм: \(A=bh\)
Трапеция: \(A=1/ 2 (b_1+b_2)h\)
Q
Как найти периметр?
A
Найдите периметр, сложив длины каждой стороны фигуры.
пр. Чему равен периметр этой фигуры?
P = 4 + 7 + 3 + 13 + 7 + 20 = 54 в
Q
Как найти площадь треугольника?
А 92\)
Q
Как найти периметр прямоугольника?
A
Найдите периметр прямоугольника, умножив его длину на 2 и ширину на 2 и сложив значения, или добавив его длину и ширину, а затем умножив на 2.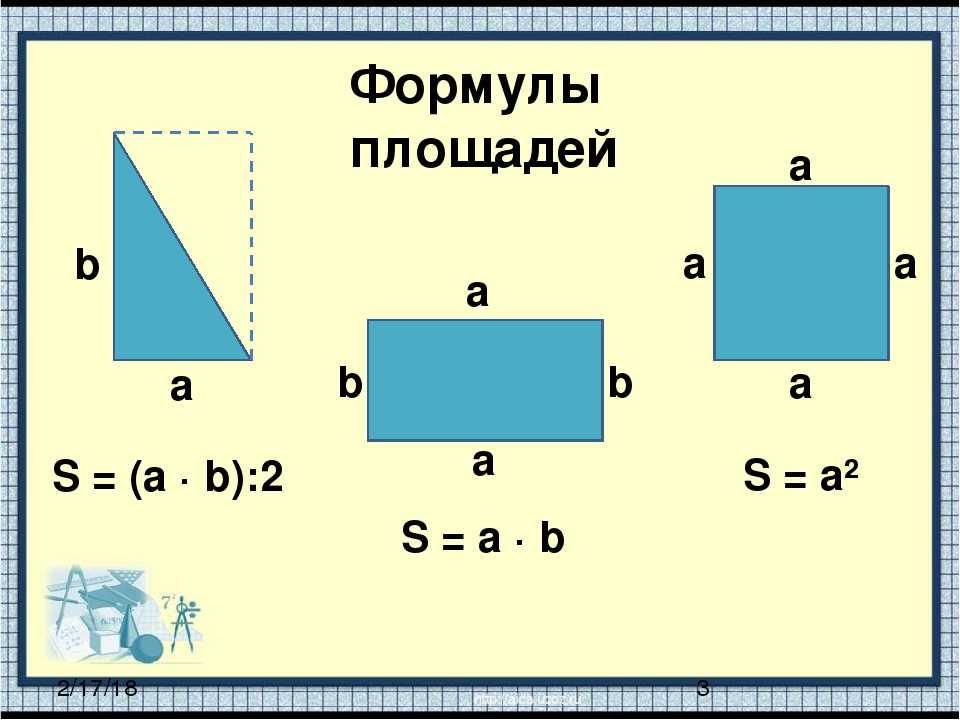
P = 2l + 2w или P = 2(д + ш)
Пр. Чему равен периметр этого прямоугольника?
P = 2(12) + 2(4) = 24 + 8 = 32 дюйма или P = 2(12 + 4) = 2(16) = 32 дюйма
Q
Как найти площадь круг? 92\)
Q
Как найти периметр треугольника?
A
Найдите периметр треугольника, сложив вместе длины всех трех сторон.
Практические вопросы
Вопрос №1:
Какова площадь этого прямоугольника?
52 см 2
133 см 2
47 см 2
154 см
3 4 9000 Ответить2\)
Скрыть ответ
Вопрос №3:
Каков периметр этого прямоугольника?
192 см
176 см
60 см
30 см
Показать Ответ
Ответ:
см. Правильный ответ. Формула периметра прямоугольника:
Правильный ответ. Формула периметра прямоугольника:
\(P=2(l+w)\) или
\(P=2l+2w\)
Длина 22см, ширина 8см.
\(P=2(22+8)=2(30)=60\text{см}\)
Скрыть ответ
Вопрос №4:
Каков периметр этого пятиугольника?
38 FT
26 FT
42 FT
59 FT
Показать ответ
Ответ:
Правильный ответ — 38 футов. вместе.
\(P=9+9+7+6+7=38\text{ ft}\)
Скрыть ответ
Вопрос №5:
По какой формуле находится периметр прямоугольника?
\(P=4s\)
\(P=2a+b+c\)
\(P=a+b+c\)
\(P=2l+2w\)
Показать ответ
Ответ:
Правильный ответ \(P=2l+2w\). Найдите периметр прямоугольника, удвоив длину и удвоив ширину, или сложив длину и ширину, а затем удвоив это число.
Найдите периметр прямоугольника, удвоив длину и удвоив ширину, или сложив длину и ширину, а затем удвоив это число.
Скрыть ответ
471797
Разница между площадью и периметром (со сравнительной таблицей)
Площадь и периметр — два жизненно важных фундаментальных понятия математики, которые часто понимаются вместе. Эти две концепции используются для измерения физического пространства объекта и составляют основу продвинутой математики. Под периметром часто понимается длина пути, охватывающего замкнутую фигуру, а под площадью понимается пространство, охватываемое замкнутой фигурой.
Обе концепции имеют практическое применение и используются в нашей повседневной жизни. В то время как площадь — это не что иное, как протяженность поверхности, периметр — это непрерывная линия, образующая границу замкнутой геометрической формы. Прочитайте статью, чтобы узнать основные различия между площадью и периметром.
Содержание: площадь и периметр
- Сравнительная таблица
- Определение
- Ключевые отличия
- Формулы
- Вывод
Сравнительная таблица
| Основание для сравнения | Площадь | Периметр |
|---|---|---|
| Значение | Площадь описывается как измерение поверхности объекта. | Периметр относится к контуру, который окружает замкнутую фигуру. |
| Обозначает | Пространство, занимаемое фигурой. | Обод или граница фигуры. |
| Измерение | Квадратные единицы | Линейные единицы |
| Размеры | Два | Один |
| Пример | Площадь, покрытая садом. | Длина забора, необходимая для ограждения сада. |
Определение площади
В математике площадь плоской поверхности определяется как площадь, занимаемая ею. Это физическая величина, которая указывает количество квадратных единиц, занимаемых двумерным объектом. Он используется, чтобы узнать, сколько места занимает плоская поверхность. Он измеряется в квадратных единицах, то есть в квадратных метрах, квадратных милях, квадратных дюймах и т. д.
Это физическая величина, которая указывает количество квадратных единиц, занимаемых двумерным объектом. Он используется, чтобы узнать, сколько места занимает плоская поверхность. Он измеряется в квадратных единицах, то есть в квадратных метрах, квадратных милях, квадратных дюймах и т. д.
Термин «площадь» имеет конечное практическое значение, например, в строительных проектах, сельском хозяйстве, архитектуре и т.д. Чтобы измерить площадь плоской поверхности, вам нужно посчитать количество квадратов, покрытых фигурой.
Например, : Предположим, вам нужно выложить плиткой пол комнаты, количество плиток, необходимое для покрытия всей комнаты, будет ее площадью.
Определение периметра
Периметр определяется как мера длины границы, окружающей замкнутую геометрическую фигуру. Термин «периметр» происходит от греческих слов «пери» и «метр», что означает вокруг и меру. В геометрии это подразумевает непрерывную линию, образующую путь вне двумерной формы.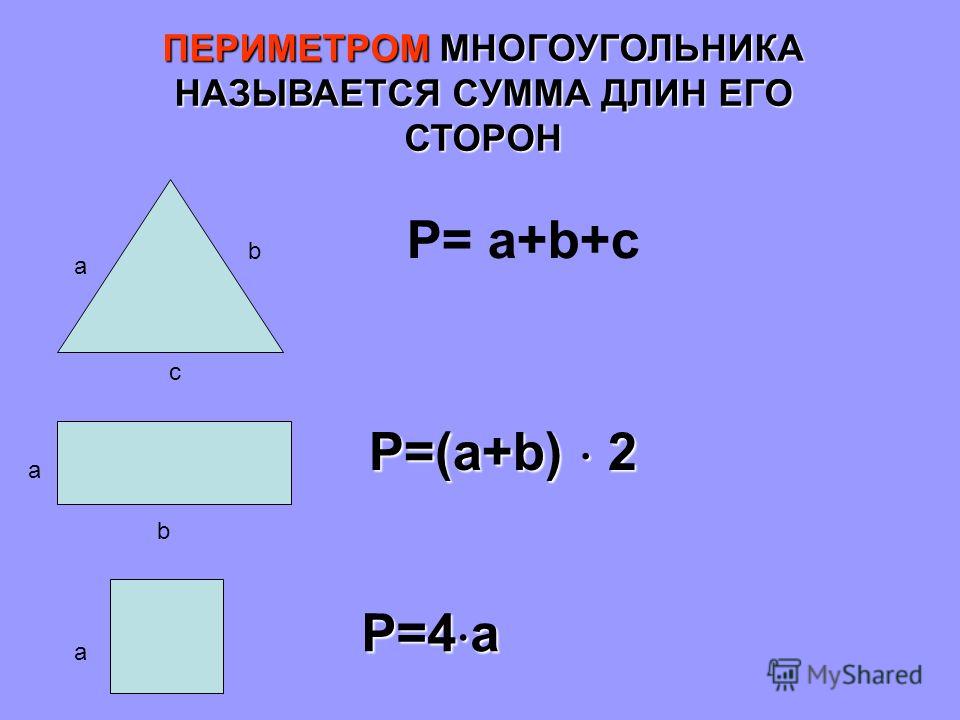
Проще говоря, периметр — это не что иное, как длина контура фигуры. Чтобы узнать периметр конкретного объекта, вы можете просто сложить длины сторон, чтобы получить его периметр. Периметр круга обычно называют его окружностью.
Например, : а. Предположим, вы намотали веревку вокруг квадрата, длина веревки будет его периметром.
б. Вы гуляете за пределами сада, пройденное расстояние будет периметром сада.
Ключевые различия между площадью и периметром
Существенные различия между площадью и периметром подробно описаны в следующих пунктах:
- Площадь описывается как измерение поверхности объекта. Периметр относится к контуру, который окружает замкнутую фигуру.
- .Area представляет пространство, занимаемое объектом. и наоборот, периметр указывает внешний край или границу формы.
- Площадь измеряется в квадратных единицах, т. е. в квадратных километрах, квадратных футах, квадратных дюймах и т. д.
 С другой стороны, периметр фигуры измеряется в линейных единицах, т. е. в километрах, дюймах, футах и т. д. 92
С другой стороны, периметр фигуры измеряется в линейных единицах, т. е. в километрах, дюймах, футах и т. д. 922πr = πd где r = радиус Треугольник 1/2 bh a+b+c где, b = основание
h = высота
a,b,c = длина сторонРомб (pq)/2 4a где a = сторона
p и q диагоналиПараллелограмм bh 2(a+b) где b = основание
h = высота
a = сторонаТрапеция ½(a+b) × h a+b+c+d где a = основание
b = основание
h = высота
c = сторона
d = сторонаЗаключение
Изучив вышеизложенные пункты, становится совершенно ясно, что эти два математических понятия различны, но вы можете использовать одно, чтобы понять другое. В то время как площадь просто означает «покрытое пространство», то есть внутри объекта, периметр относится к «расстоянию вокруг», то есть контуру формы.


 4 или более поздней версии)
4 или более поздней версии)
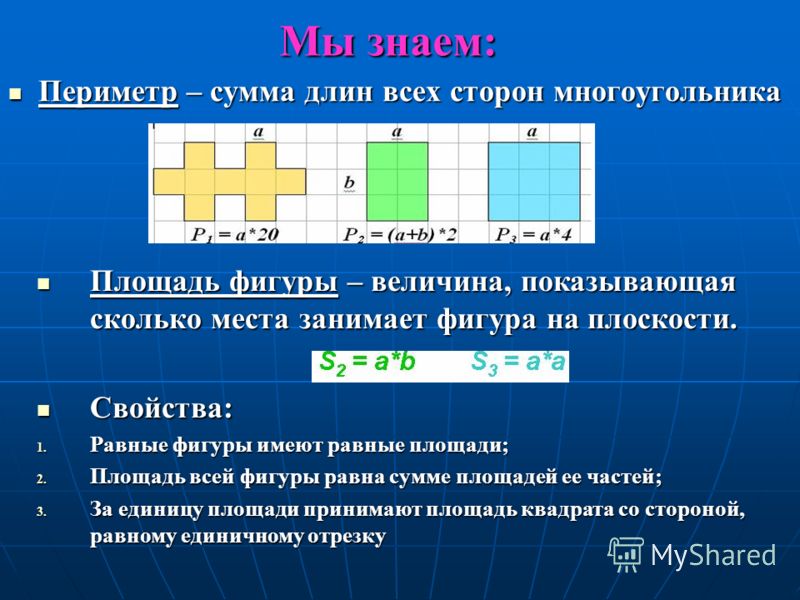


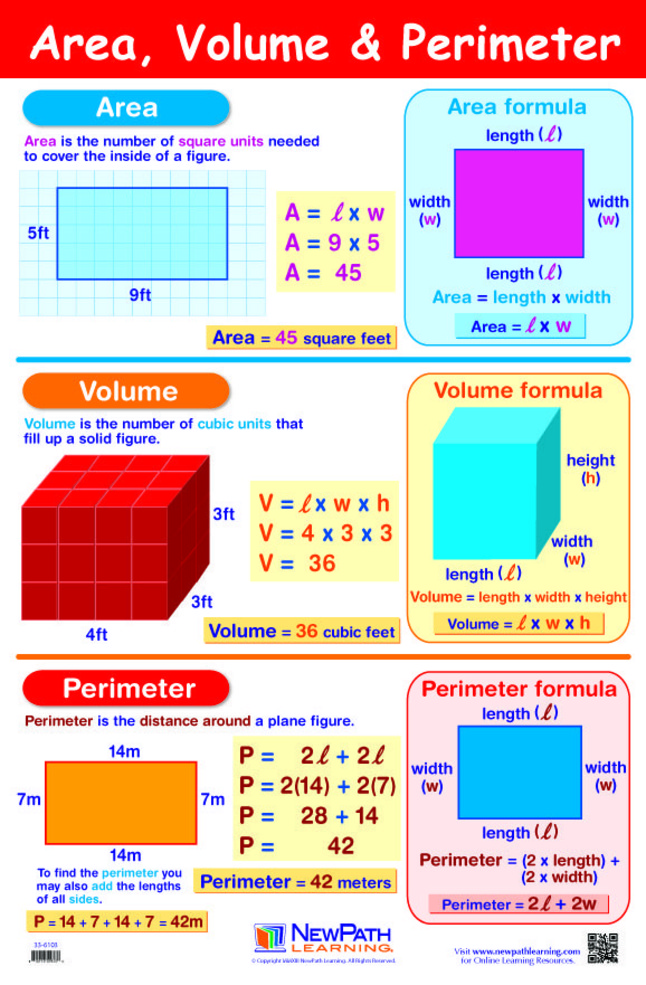

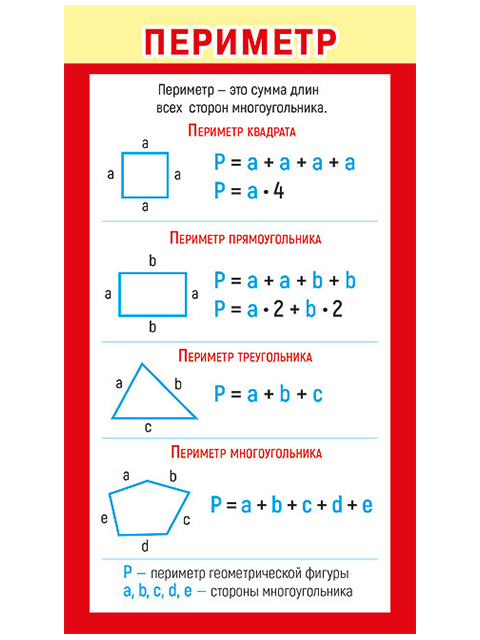

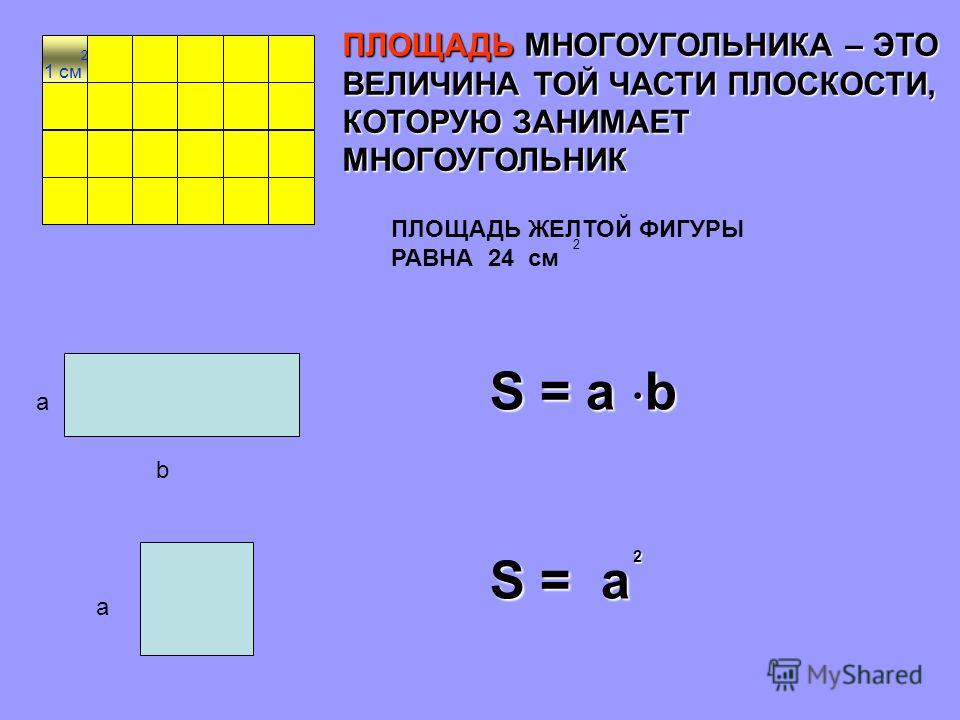
 Следовательно, периметр прямоугольного ковра = 62 единицы.
Следовательно, периметр прямоугольного ковра = 62 единицы.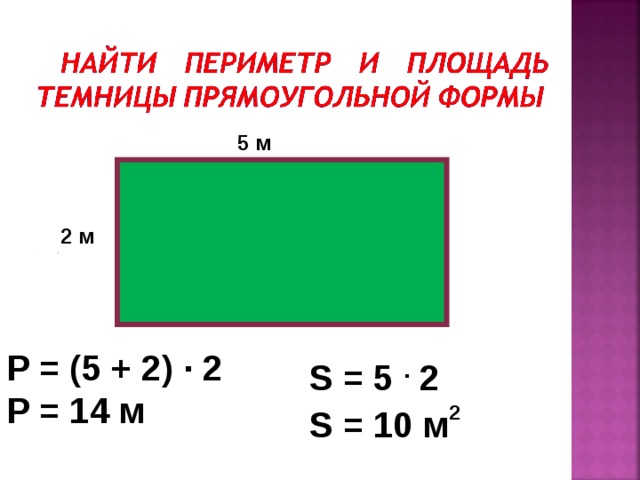
 Он не округлый.
Он не округлый.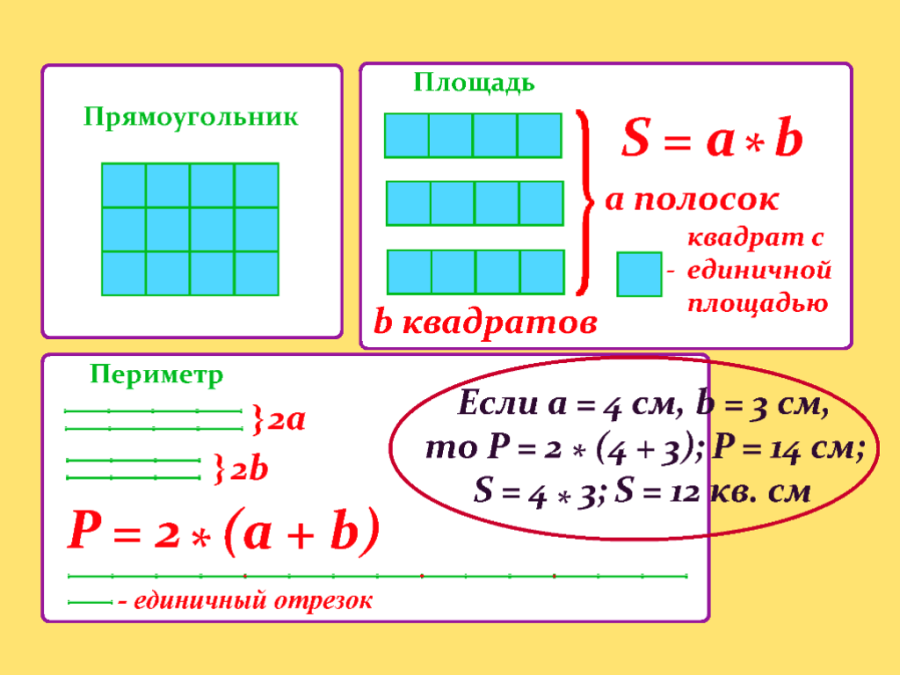
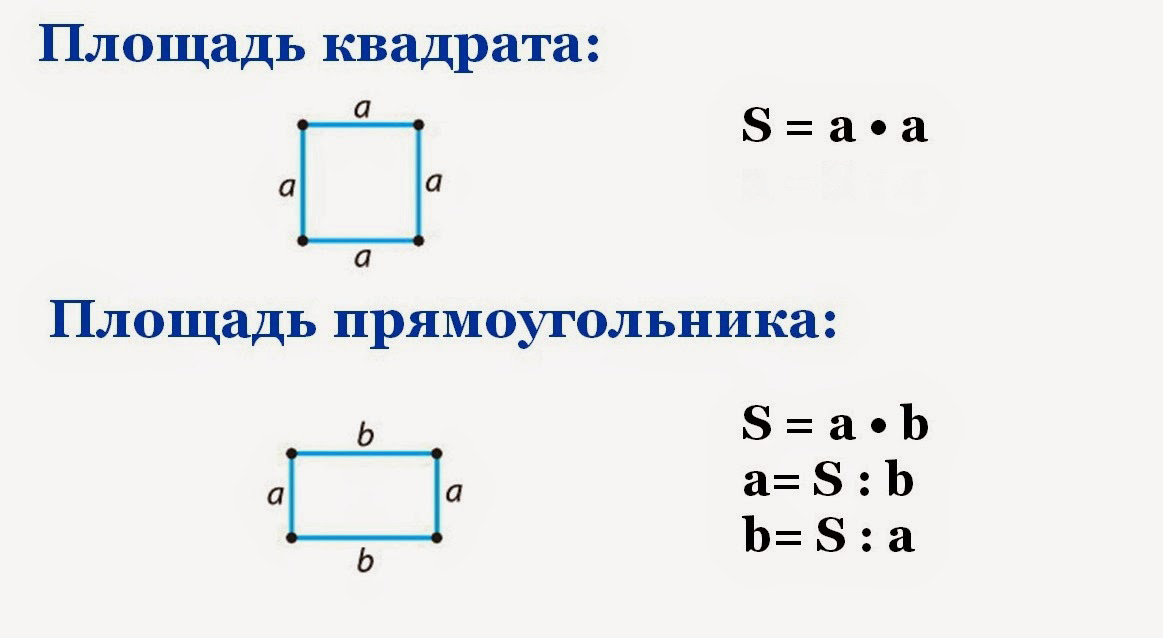 С точки зрения математики прямоугольник обозначает угол 90º (прямой). 92\)
С точки зрения математики прямоугольник обозначает угол 90º (прямой). 92\)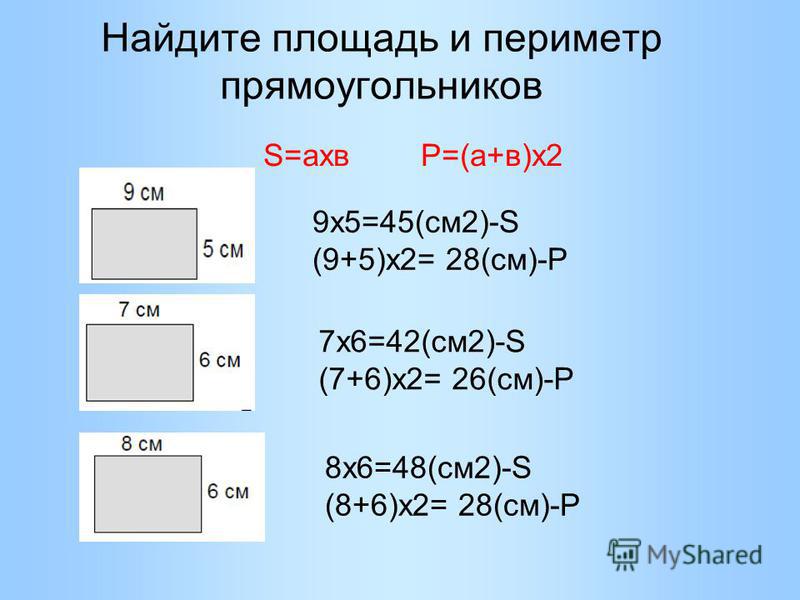
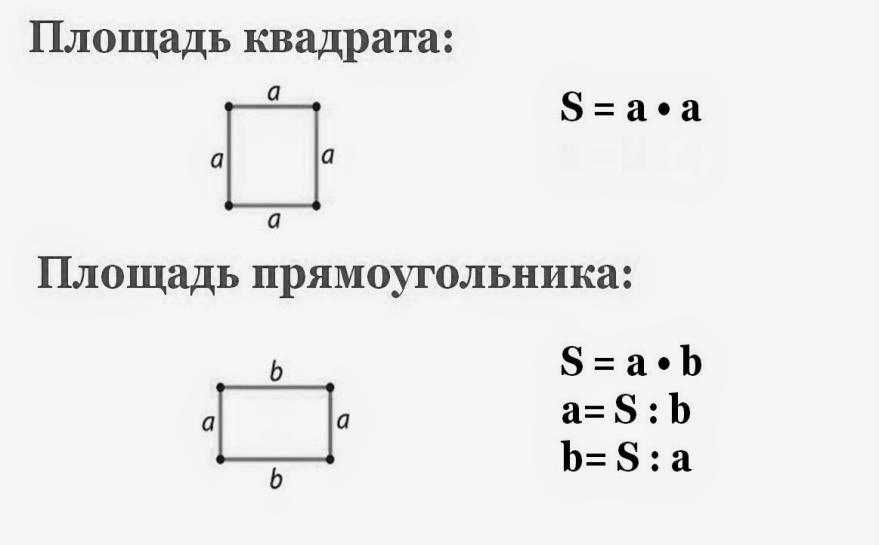
 С другой стороны, периметр фигуры измеряется в линейных единицах, т. е. в километрах, дюймах, футах и т. д. 92
С другой стороны, периметр фигуры измеряется в линейных единицах, т. е. в километрах, дюймах, футах и т. д. 92