Периметр прямокутного трикутника: Как найти периметр прямоугольного треугольника? Ответ на webmath.ru

Содержание

✅Як знайти периметр трикутника якщо відомі не всі сторони

✅ Периметр – це величина, що має на увазі довжину всіх сторін плоскої (двовимірної) геометричної фігури. Для різних геометричних фігур існують різні способи знаходження периметра.

У даній статті ви дізнаєтеся як знаходити периметр фігури різними способами, в залежності від відомих його граней.

Периметр – це величина, що має на увазі довжину всіх сторін плоскою (двовимірної) геометричної фігури. Для різних геометричних фігур існують різні способи знаходження периметра.

Можливі методи:

відомі всі три сторони рівнобедреного або будь-якого іншого трикутника;
як знайти периметр прямокутного трикутника при двох відомих його гранях;
відомі дві грані і кут, який розташований між ними (формула косинусів) без середньої лінії і висоти;

Перший метод: відомі всі сторони фігури

Зміст статті

1 Перший метод: відомі всі сторони фігури
2 Другий метод: прямокутний трикутник і дві відомі його боку
3 Третій метод: по обидва боки і кути між ними

Як знаходити периметра трикутника, коли відомі всі три грані, необхідно використовувати наступну формулу: P = a + b + c, де a, b, c – відомі довжини всіх сторін трикутника, P – периметр фігури.

Наприклад, відомі три сторони фігури: a = 24 см, b = 24 см, c = 24 см. Це правильна рівнобедрена фігура, щоб обчислити периметр користуємося формулою: P = 24 + 24 + 24 = 72 см.

Дана формула підходить до будь-якого трикутника, необхідно просто знати довжини всіх його сторін. Якщо хоча б одна з них невідома, необхідно скористатися іншими способами, про які ми поговоримо нижче.

Ще один приклад: a = 15 см, б = 13 см, c = 17 см. Обчислюємо периметр: P = 15 + 13 + 17 = 45 см.

Дуже важливо позначати одиницю виміру в отриманій відповіді. У наших прикладах довжини сторін вказані в сантиметрах (см), проте, існують різні завдання, в умовах яких присутні інші одиниці виміру.

Другий метод: прямокутний трикутник і дві відомі його боку

У тому випадку, коли в завданні, яке потрібно вирішити, дана прямокутна фігура, довжини двох граней якої відомі, а третя немає, необхідно скористатися теоремою Піфагора.

Теорема Піфагора описує співвідношення між гранями прямокутного трикутника.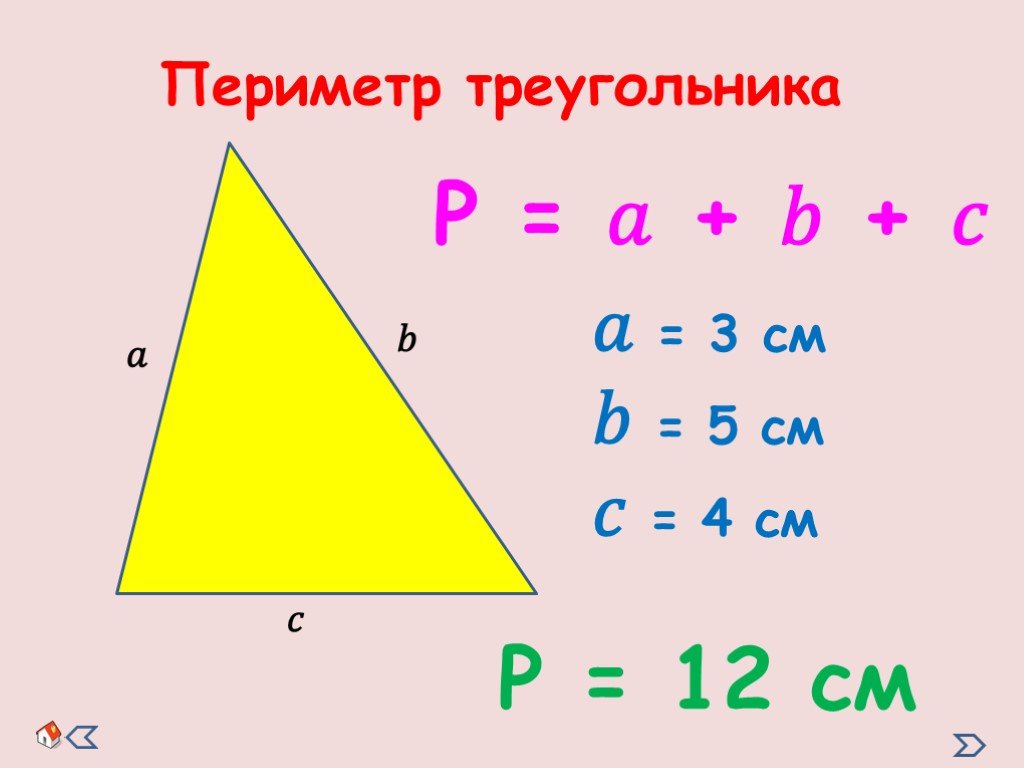 2 – (2 * a * b * cos (C)), де a, b, c – стандартно довжини граней, а A, B і С – це кути, які лежать навпроти відповідних граней трикутника. Тобто, A – кут, протилежний стороні a і так далі.

Уявімо, що описаний трикутник, сторони, а і б якого складають 100 см і 120 см відповідно, а кут, що лежить між ними, складає 97 градусів. Тобто а = 100 см, б = 120 см, C = 97 градусів.

Все, що потрібно зробити в даному випадку – це підставити всі відомі значення в теорему косинусів. Довжини відомих граней зводяться у квадрат, після чого відомі боку перемножуються між один одним і на два і множаться на косинус кута між ними. Далі, необхідно скласти квадрати граней і відняти від них другою отримане значення. З підсумкової величини витягується квадратний корінь – це буде третя, невідома до цього сторона.

Після того як всі три грані фігури відомі, залишилося скористатися вже полюбилася нам стандартної формулою пошуку периметра описуваної фігури з першого методу.

Як знайти периметр трикутника, якщо відомі не всі сторони.

Як знайти периметр трикутника якщо відомі не всі сторони Як виглядає прямокутний трикутник та його периметр

Прямокутним трикутником вважається такий трикутник, один із кутів якого дорівнює 90 градусам, а два інших є гострими кутами. Розрахунок периметратакого трикутникабуде залежним від кількості відомих про нього даних.

Вам знадобиться

Залежно від випадку, вміння двох з трьох сторін трикутника, а також одного з його гострих кутів.

Інструкція

1. Метод 1.Якщо відомі всі три сторони трикутника, то, самостійно від цього, прямокутний чи трикутник чи ні, його периметр буде розрахований так: P = a + b + c, де, можливий, c – гіпотенуза; a і b – катети.

2. Метод 2. Якщо у прямокутнику вести лише дві сторони, то, застосовуючи теорему Піфагора, периметр цього трикутникаможна розрахувати за формулою: P = v (a2 + b2) + a + b, або P = v (c2 — b2) + b + с.

3. Метод 3. Нехай у прямокутному трикутнику дані гіпотенуза c та гострий кут?, то виявити периметр можна буде таким чином: P = (1 + sin ? + cos ?) * с.

4. Метод 4. Дано, що у прямокутному трикутнику довжина одного з катета дорівнює a, а навпаки, його лежить гострий кут?. Тоді розрахунок периметрацього трикутникавестиметься за формулою:P = a*(1/tg ? + 1/sin ? + 1)

5. Метод 5. Нехай нам ведемо катет a і кут, що прилягає до нього?, тоді периметр буде розрахований так:P = a*(1/сtg ? + 1/cos ? + 1)

Відео на тему

Прямокутний трикутник – проста, але вкрай важлива для математики фігура. Знання про його властивості та вміння оперувати основними параметрами прямокутного трикутника дозволить вам впоратися як зі шкільними, так і реальними завданнями.

Геометрія прямокутного трикутника

Геометрично трикутник — це три точки, що не лежать на одній прямій, які з’єднані між собою відрізками. Прямокутний трикутник – фігура, дві сторони якої утворюють прямий кут. Ці сторони називаються катетами трикутника, а третя, найдовша сторона, називається гіпотенузи. Співвідношення квадратів катетів та гіпотенузи встановлює теорема Піфагора – одна з фундаментальних теорем евклідової геометрії.

Співвідношення гіпотенузи та катетів також поклали основу для цілого розділу математики – тригонометрії. Спочатку синуси і косинуси визначалися як функції кутів прямокутного трикутника, але в сучасному значеннітригонометричні функції розширено на всю числову вісь. Сьогодні тригонометрія використовується в багатьох сферах людської діяльності: від астрономії та океанографії до аналізу фінансових ринків та розробки комп’ютерних ігор.

Прямокутний трикутник насправді

Безпосередньо прямокутний трикутник зустрічається насправді кожному кутку, як і прямому, і у переносному сенсі. Форму прямокутного трикутника мають грані тетраедрів та призм, які насправді перетворюються на деталі машин, керамічну плитку або схилі дахів. Кутник — креслярський інструмент, з яким людина вперше зустрічається на уроці геометрії, має форму прямокутного трикутника і використовується в проектуванні, будівництві та столярній справі.

Периметр трикутника

Периметр – це чисельна оцінка довжин усіх сторін плоскої геометричної фігури.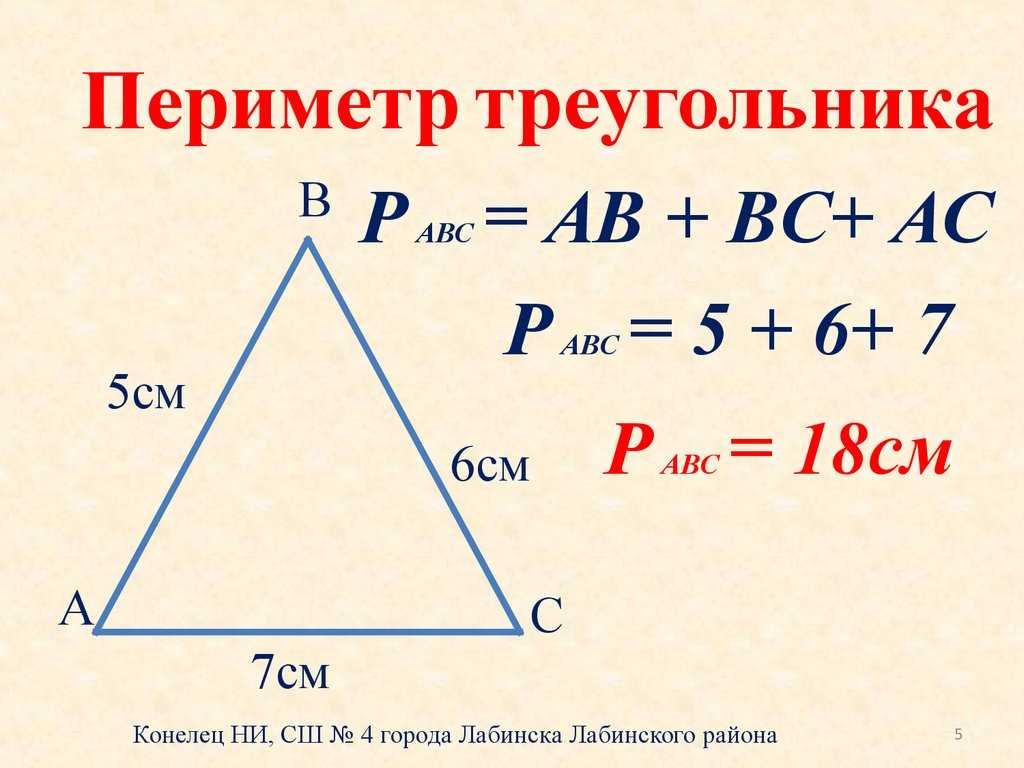 Периметр n-кутника перебуває як сума довжин n сторін. Для визначення периметра прямокутного трикутника використовується проста формула:

a та b – катети, c – гіпотенуза.

Обчислюючи периметр трикутника вручну, вам довелося б вимірювати всі три сторони, проводити додаткові тригонометричні операції або обчислення теореми Піфагора. Використовуючи онлайн-калькулятор, вам достатньо дізнатися наступні пари змінних:

два катети;
катет та кут;
гіпотенуза та кут.

У шкільних завданнях або на практиці вам буде задано вихідні дані, тому калькулятор дозволяє знайти периметр, знаючи різні пари параметрів. Крім того, інструмент автоматично розраховує решту атрибутів прямокутного трикутника, тобто довжини всіх сторін і величини всіх кутів. Розглянемо кілька прикладів.

Приклади з життя

Шкільне завдання

Нехай у шкільному завданні вам заданий прямокутний трикутник із довжиною катета рівним 5 см та прилеглим кутом, величина якого становить 60 градусів. Потрібно знайти периметр геометричної фігури. Онлайн-калькулятор супроводжується малюнком, на якому зображені сторони та кути прямокутного трикутника. Ми, що якщо катет a = 5 див, його прилеглий кут — це кут бета. Це важливий момент, оскільки якщо ви використовуєте для розрахунків кут альфа, результат буде неправильним. Вбиваємо ці дані у форму та отримуємо відповідь у вигляді:

Крім безпосередньо периметра, наша програма також визначила величину протилежного кута, а також довжину другого катета та гіпотенузи.

Облаштування клумби

Допустимо, ви хочете зробити огорожу для клумби, яка має форму прямокутного трикутника. Для цього вам необхідно дізнатися про периметр фігури. Звичайно, в реальності ви можете просто виміряти всі три сторони, але легко спростити собі завдання і виміряти лише два катети. Нехай вони мають довжину 8 та 15 метрів. Вбиваємо ці дані у форму калькулятора та отримуємо відповідь:

Отже, вам доведеться закупити матеріали для облаштування 40 метрів огорожі. Наш калькулятор також підрахував довжину гіпотенузи – 17 метрів. Числа 8, 15 та 17 складають піфагорову трійку – натуральні числа, які задовольняють умовам теореми Піфагора.

Висновок

Прямокутні трикутники набули широкого поширення у повсякденності, тому визначення площі або периметра геометричної фігури напевно стане вам у нагоді при вирішенні шкільних завдань або побутових питань.

Прямокутний трикутник — це окремий вид довільного трикутника. Як і будь-який інший трикутник, він має три сторони, але один з його кутів обов’язково повинен становити 90 градусів. Якщо ви визначили, що заданий трикутник є прямокутним, можна приступити до знаходження його основних величин. Однією з параметрів прямокутного трикутника є його периметр. Знаходженню периметра прямокутного трикутника присвячено багато завдань із геометрії. Перед тим як ми розглянемо основні способи знаходження периметра прямокутного трикутника, хотілося б нагадати, що периметр будь-якої геометричної фігури на площині дорівнює сумі довжин її сторін. Для всіх видів трикутників це твердження можна записати у вигляді наступного виразу:

де P – периметр трикутника;
a, b, c – сторони трикутника.

У прямокутному трикутнику, як уже було сказано вище, присутня відмінна особливість у вигляді одного з кутів, що становить 90 градусів. Дві сторони трикутника, що прилягають до цього кута, називають катетами. Протилежний прямому куту бік прийнято називати гіпотенузою.

Незвичайні властивості прямокутного трикутника було відкрито Піфагором, який виявив, що квадрат гіпотенузи прямокутного трикутника дорівнює сумі квадратів його катетів, що може бути записано у вигляді виразу:

Де P – периметр трикутника;

A, b, c – сторони трикутника.

Виходячи з теореми Піфагора з’явилася можливість визначати периметр прямокутного трикутника з його двох будь-яких сторін відомої довжини. Якщо відомі довжини катетів, то периметр трикутника визначається через знаходження величини гіпотенузи за формулою:

Якщо відомий тільки один з катетів і довжина гіпотенузи, то периметр трикутника визначається через знаходження величини катета, що бракує, за формулою:

Якщо у прямокутному трикутнику відома лише довжина гіпотенузи с і один із прилеглих до неї гострих кутів α, то периметр трикутника в даному випадку може бути визначений за формулою:

У тому випадку, коли умовами задачі задана довжина катета a і величина гострого кута α, що протилежить йому, то периметр прямокутного трикутника в даному випадку обчислюється за формулою:

Якщо ж заданий катет a з кутом β, що прилягає до нього, то периметр трикутника може бути розрахований на основі виразу:

P = a + b + c де, припустимо,

P = v(a2 + b2) + a + b, або

P = v (c2 — b2) + b + с.

P = (1 + sin? + cos?) * с.

P = a*(1/tg? + 1/sin? + 1)

P = a * (1 / сtg? + 1 / cos? + 1)

Інші новини по темі:

Як знайти периметр прямокутного трикутника

Прямокутним трикутником вважається такий трикутник, один із кутів якого дорівнює 90 градусам, а два інших є гострими кутами. Розрахунок периметра такого трикутника буде залежати від кількості відомих про нього даних.

Залежно від випадку, знання двох із трьох сторін трикутника, а також одного з його гострих кутів.

Спонсор розміщення P&G Статті по темі Як знайти периметр прямокутного трикутника Як знайти площу поверхні піраміди Як знайти периметр якщо відома площа Як знайти периметр рівностороннього трикутника

Спосіб 1. Якщо відомі всі три сторони трикутника, то, незалежно від того, прямокутний чи трикутник, його периметр буде розрахований так:

P = a + b + c де, припустимо,

Спосіб 2. Якщо у прямокутнику відомі лише дві сторони, то, використовуючи теорему Піфагора, периметр цього трикутника можна розрахувати за формулою:

P = v(a2 + b2) + a + b, або

P = v (c2 — b2) + b + с.

Спосіб 3. Нехай у прямокутному трикутнику дано гіпотенузу c та гострий кут?, то знайти периметр можна буде таким чином:

P = (1 + sin? + cos?) * с.

Спосіб 4. Дано, що у прямокутному трикутнику довжина одного з катета дорівнює a, а навпроти нього лежить гострий кут? Тоді розрахунок периметра цього трикутника вестиметься за формулою:

P = a*(1/tg? + 1/sin? + 1)

Спосіб 5. Нехай нам відомий катет a і кут, що прилягає до нього?, тоді периметр буде розрахований так:

P = a * (1 / сtg? + 1 / cos? + 1)

Інші новини по темі:

Площа та периметр – основні числові характеристики будь-яких геометричних фігур. Знаходження цих величин спрощується завдяки загальноприйнятим формулам, згідно з якими можна обчислити одне через інше з мінімумом або повною відсутністю додаткових початкових даних. Спонсор розміщення P&G

Рівносторонній трикутник поряд з квадратом є, мабуть, найпростішою та симетричною фігурою у планіметрії. Вочевидь, все співвідношення, справедливі для простого трикутника, правильні також і рівностороннього. Однак для правильного трикутника всі формули стають набагато простішими. Вам

Периметр трикутника, як і будь-якої іншої плоскої геометричної фігури, становить сума довжин, що обмежують його відрізків. Тому, щоб вирахувати довжину периметра, треба знати довжини його сторін. Але через те, що довжини сторін у геометричних фігурах пов’язані певними співвідношеннями з

Прямокутним вважається такий трикутник, у якого один із кутів прямий. Сторона трикутника, розташована навпроти прямого кута, називається гіпотенузою, а дві інші сторони – катетами. Щоб знайти довжини сторін прямокутного трикутника, можна скористатися кількома способами. Спонсор

Периметр будь-якої геометричної фігури, у тому числі трикутника, дорівнює сукупній довжині меж цієї фігури. Він позначається великою латинською літерою P і легко перебуває методом складання довжин всіх сторін цієї постаті. Спонсор розміщення P&G Статті на тему «Як обчислити периметр трикутника»

Трикутник — це багатокутник, що має три сторони та три кути. Як же вирахувати його периметр? Спонсор розміщення P&G Статті по темі «Як знаходити периметр трикутника» Як знайти периметр трикутника, заданого координатами своїх вершин Як знайти площу трикутника Як знайти довжину та ширину

Гіпотенуза – найдовша сторона прямокутного трикутника. Вона розташована протилежно до прямого кута. Спосіб знаходження гіпотенузи прямокутного трикутника залежить від того, якими вихідними даними ви маєте. Спонсор розміщення P&G Статті на тему «Як знайти гіпотенузу трикутника» Як

Прямокутний трикутник характеризується певними співвідношеннями між кутами та сторонами. Знаючи значення одних, можна обчислювати інші. І тому використовуються формули, засновані, своєю чергою, на аксіомах і теоремах геометрії. Спонсор розміщення P&G Статті на тему «Як визначити

Здавалося б, що може бути простіше, ніж обчислення площі та периметра трикутника – виміряв сторони, поставив цифри у формулу – і все. Якщо ви так вважаєте, значить, забули, що для цих цілей існує не дві прості формули, а набагато більше – для кожного виду трикутника – своя. Вам

Периметр трикутника – сума довжин його сторін. Знайти периметр трикутника часто потрібно як задачах початкової геометрії, і у складніших завданнях. При їх вирішенні відсутні величини знаходять з інших даних. Основні залежності периметра трикутника від інших вимірювань відображені в

Периметр – це величина, що має на увазі довжину всіх сторін плоскої (двовимірної) геометричної фігури. Для різних геометричних фігур є різні способи знаходження периметра.

У цій статті ви дізнаєтеся, як знаходити периметр фігури різними способами, залежно від відомих його граней.

Можливі методи:

відомі всі три сторони рівнобедреного або будь-якого іншого трикутника;
як знайти периметр прямокутного трикутника за двох відомих його гранях;
відомі дві грані та кут, який розташований між ними (формула косінусів) без середньої лінії та висоти.

Перший метод: відомі усі сторони фігури

Як знаходити периметри трикутника, коли відомі всі три грані, необхідно використовувати таку формулу: P = a + b + c де a, b, c – відомі довжини всіх сторін трикутника, P – периметр фігури.

Ця формула підходить до будь-якого трикутника.необхідно просто знати довжини всіх його сторін. Якщо хоча б одна з них невідома, необхідно скористатися іншими способами, про які ми поговоримо нижче.

Ще один приклад: a = 15 см, б = 13 см, c = 17 см. Обчислюємо периметр: P = 15 + 13 + 17 = 45 см.

Дуже важливо помічати одиницю виміру в отриманій відповіді. У прикладах довжини сторін зазначені в сантиметрах (см), проте, існують різні завдання, за умов яких присутні інші одиниці виміру.

Другий метод: прямокутний трикутник та дві відомі його сторони

У тому випадку, коли в завданні, яке потрібно вирішити, дана прямокутна фігура, довжини двох граней якої відомі, а третя ні, необхідно скористатися теоремою Піфагора.

Визначає співвідношення між гранями прямокутного трикутника. 2 – (2 * a * b * cos(C)), де a,b,c – стандартно довжини граней, а A,B і С – це кути, що лежать навпроти відповідних граней трикутника. Тобто A – кут, що протилежить стороні a і так далі.

Припустимо, що описаний трикутник, сторони а і б якого складають 100 см і 120 см відповідно, а кут, що лежить між ними, становить 97 градусів. Тобто а=100 см, б=120 см, C=97 градусів.

Все, що потрібно зробити в даному випадку — це підставити всі відомі значення теорему косінусів. Довжини відомих граней зводяться в квадрат, після чого відомі сторони перемножуються між один одним і два і множаться на косинус кута між ними. Далі, необхідно скласти квадрати граней і відібрати від них друге отримане значення. З підсумкової величини витягується квадратний корінь – це буде третя, невідома раніше сторона.

Після того як всі три грані фігури відомі, залишилося скористатися стандартною формулою пошуку периметра описуваної фігури з першого методу.

Однією з основних геометричних фігур є трикутник. Він утворюється при перетині трьох відрізків прямих. Дані відрізки прямих утворюють сторони фігури, а точки їх перетину називаються вершинами. Кожен школяр, вивчає курс геометрії, повинен вміти шукати периметр цієї постаті. Отримане вміння буде корисним для багатьох і дорослого життя, наприклад, знадобиться студенту, інженеру, будівельнику,

Існують різні способи знайти периметр трикутника. Вибір необхідної вам формули залежить від наявних вихідних даних. Щоб записати цю величину в математичній термінології використовують спеціальне позначення — Р. Розглянемо, що таке периметр, основні способи розрахунку для трикутних фігур різних видів.

Самим простим способомзнайти периметр фігури, якщо є дані всіх сторін. У цьому випадку використовується така формула:

Літерою «P» позначається сама величина периметра. У свою чергу «a», «b» і «c» — це довжини сторін.

Знаючи розмір трьох величин, достатньо буде отримати їхню суму, яка є периметром.

Альтернативний варіант

У математичних завданнях усі дані довжини рідко бувають відомі.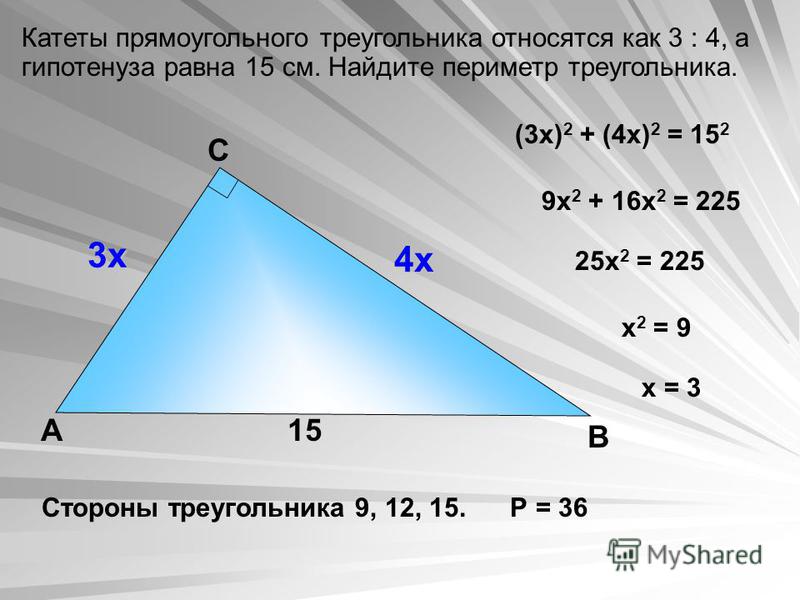 У разі рекомендується скористатися альтернативним способом пошуку потрібної величини. Коли в умовах зазначена довжина двох прямих, а також кут, що знаходиться між ними, розрахунок проводиться через третій пошук. Для пошуку цього числа необхідно добути квадратний корінь за такою формулою:

Периметр з обох боків

Для розрахунку периметра не обов’язково знати усі дані геометричної фігури. Розглянемо способи розрахунку з обох боків.

Рівнобедрений трикутник

Рівнобедренним називається такий трикутник, щонайменше двох сторін якого мають однакову довжину. Вони називаються бічними, а третя сторона – основою. Рівні прямі утворюють кут вершини. Особливістю в рівнобедреному трикутнику є наявність однієї осі симетрії. Вісь – вертикальна лінія, що виходить з вершинного кута і закінчується посередині основи. За своєю суттю вісь симетрії включає такі поняття:

бісектриса вершинного кута;
медіана до основи;
висота трикутника;
серединний перпендикуляр.

Щоб визначити периметр рівнобедреного виду трикутної фігури, Скористайтеся формулою.

В даному випадку вам необхідно знати лише дві величини: основу та довжину однієї сторони. Позначення «2а» має на увазі множення довжини бічної сторони на 2. До отриманої цифри потрібно додати величину основи — «b».

У винятковому випадку, коли довжина основи рівнобедреного трикутника дорівнює його бічній прямій, можна скористатися більш простим способом. Він виявляється у такій формулі:

Для отримання результату достатньо помножити число на три. Ця формула використовується у тому, щоб знайти периметр правильного трикутника.

Корисне відео: завдання на периметр труєгольника

Трикутник прямокутний

Головною відмінністю прямокутного трикутника з інших геометричних фігур цієї категорії є наявність кута 90°. За цією ознакою визначається вид фігури. Перш ніж визначити, як знайти периметр прямокутного трикутника, варто помітити, що дана величина для будь-якої плоскої геометричної фігури становить суму всіх сторін. Так і в цьому випадку найпростіший спосіб дізнатися результат – підсумовувати три величини.

У науковій термінології ті сторони, що прилягають до прямого кута, мають назву «катети», а протилежна до кута 90º – гіпотенуза. Особливості цієї постаті досліджувалися ще давньогрецьким вченим Піфагором. Відповідно до теорії Піфагора, квадрат гіпотенузи дорівнює сумі квадратів катетів.

На підставі цієї теореми виведена ще одна формула, яка пояснює, як знайти периметр трикутника з двох відомих сторін. Розрахувати периметр при зазначеній довжині катетів можна за допомогою наступного способу.

Щоб дізнатися периметр, маючи інформацію про розмір одного катета та гіпотенузи, потрібно визначити довжину другої гіпотенузи. З цією метою використовують такі формули:

Також периметр описаного виду фігури визначається без даних про розміри катетів.

Вам знадобиться довжина гіпотенузи, а також кут, що прилягає до неї. Знаючи довжину одного з катетів, якщо є кут, що прилягає до нього, периметр фігури розраховують за формулою:

Розрахунок через висоту

Розрахувати периметр таких категорій, як рівнобедрені та прямокутні трикутники, можна через показник їхньої середньої лінії. Як відомо, висота трикутника поділяє його основу навпіл. Таким чином, вона утворює дві прямокутні фігури. Далі, необхідний показник обчислюється з допомогою теореми Піфагора. Формула матиме такий вигляд:

Якщо відома висота та половина основи, використовуючи цей спосіб, ви отримаєте потрібне число без пошуку інших даних про фігуру.

Корисне відео: знаходження периметра трикутника

Патент США на сумку для сушки рук Боулеров Патент (Патент № 4,682,422, выданный 28 июля 1987 г.)

ПРЕДПОСЫЛКИ ИЗОБРЕТЕНИЯ влаги для предотвращения соскальзывания шара для боулинга с руки во время приближения к дорожке и подачи. Боулер обычно постоянно вытирает руку непосредственно перед тем, как взять шар для боулинга для подхода к дорожке и подачи. Это делается для того, чтобы предотвратить, насколько это возможно, любое выскальзывание мяча из пальцев и руки, чтобы можно было добиться правильного прохождения и размещения мяча на направляющих стрелках дорожки последовательным и точным образом. . В настоящее время используемые методы защиты рук от влаги включают использование вентилятора, обычно установленного на каждой дорожке, или мешков с канифолью. Хотя использование вентилятора-вентилятора дает некоторое преимущество при высыхании рук, это трудоемкая процедура, которая не может испарить всю влагу с руки, особенно когда боулеры спешат подойти к дорожке для доставки. . Мешок с канифолью обеспечивает лучшее высыхание рук, но это очень грязная процедура, поскольку частицы из внутренней части мешка улетучиваются и создают беспорядок на дорожке, что привело к тому, что многие заведения для боулинга запретили использование канифоли. сумки целиком. Настоящее изобретение относится к мешку для сушки рук игрока в боулер, который имеет, по меньшей мере, такой же хороший результат, как мешок для канифоли, но не создает всплывающих и загрязняющих мелких частиц мешка для канифоли.

СУЩНОСТЬ ИЗОБРЕТЕНИЯ

Таким образом, основная цель настоящего изобретения состоит в том, чтобы предоставить помощь игроку в боулер для сушки рук, которая не пачкается, быстро действует и безопасна в использовании.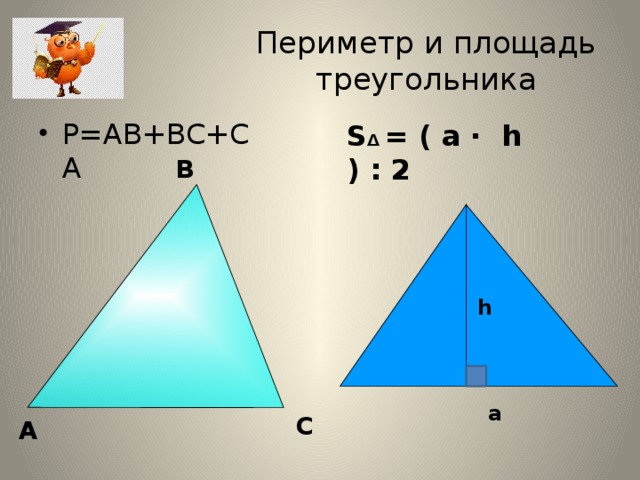

Еще одна цель настоящего изобретения состоит в том, чтобы предоставить такое вспомогательное средство для боулера в мелкопористом мешочке, которое позволяет легко использовать вспомогательное средство таким же образом, как в настоящее время используются обычные канифольные мешки, по крайней мере, не хуже, чем результат в виде канифольного мешка.

Еще одной целью настоящего изобретения является создание такого вспомогательного приспособления для боулера для сушки руки, которое легко захватывается рукой, плотно удерживается в нем и сжимается таким образом, чтобы повысить характеристики высыхания и испарения влаги приспособления для котелка.

Для достижения этих и других целей настоящее изобретение состоит из небольшого прямоугольного мешка, примерно четырех дюймов в длину и трех дюймов в ширину, в котором содержится составная серицитовая глина Фуллера. Сама сумка предпочтительно изготавливается из плоского трикотажа 32 калибра с 2 полосками, имеющего выход 4,10 унций/ярд, и предпочтительно из 100% полиэфирной пряжи плотностью от 20 до 40 денье.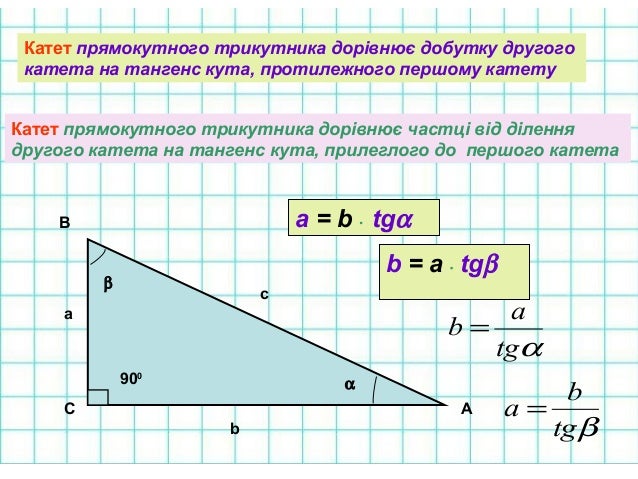 Было обнаружено, что это качество ткани обеспечивает наилучшее проникновение через нее глинистой пыли в надлежащих количествах, так что достаточное количество глины в виде частиц пыли может выйти через ткань, чтобы вызвать высыхание руки. но недостаточно, чтобы создать беспорядок неприглядного вида.

ПОДРОБНОЕ ОПИСАНИЕ ИЗОБРЕТЕНИЯ

Изобретение представляет собой комбинацию особого типа рыхлого, нелипкого глиняного состава, подробно описанного ниже, содержащегося в закрытом мешке, который позволяет частицам глины просачиваться через него, когда мешок встряхивают, так что частицы глины выделяются в виде тонкой пыли, которая быстро и эффективно высушивает руку пользователя, держащего и встряхивающего в ней мешок. Было обнаружено, что для обеспечения надлежащего выхода и выделения найденной глиняной пыли эффективно работает 2-полосная трикотажная ткань калибра 32, изготовленная из полиэфирной пряжи 100 калибра от 20 до 40. Эта ткань имеет выход примерно 4,10 унции на погонный ярд и обычно имеет ширину 60 дюймов. В предпочтительной форме изобретения размер мешка, служащего в качестве дозатора глиняной пыли, представляет собой закрытый мешок прямоугольной формы, имеющий длину 4 дюйма и ширину 3 дюйма, размеры которого, как было установлено, обеспечивают лучший размер захвата для рук разного размера, так что руки разного размера все еще могут захватывать и встряхивать мешок, а также позволяют глиняной пыли эффективно выделяться для сушки. Хотя в предпочтительном варианте осуществления указана ткань 32 размера, следует понимать, что могут использоваться другие размеры, предпочтительно в диапазоне от 28 размера до 36 размера трикотажа, трикотажа. Кроме того, размер пряжи предпочтительно находится в диапазоне от 15 денье до 45 денье. Кроме того, помимо полиэфира и любых их комбинаций могут быть использованы другие искусственные нити, причем искусственные нити предпочтительно имеют худшие характеристики влагопоглощения. Рыхлым, нелипким частицам глины, содержащимся в структуре мешка, позволяют выходить через пористую структуру трикотажного полотна 32 размера, при этом скорость их потока остается практически постоянной независимо от степени встряхивания или вибрации мешка. поскольку поры, через которые течет пыль, крошечные и расположены через равные промежутки, хотя продолжительность времени, в течение которого такие частицы пыли будут просачиваться, будет прямо пропорциональна количеству и силе сотрясения и вибрации мешка.

Саму сумку формируют, сначала беря прямоугольный кусок ткани длиной 7 дюймов и шириной 5 дюймов и складывая его таким образом, чтобы линия сгиба лежала параллельно двум его более коротким пятидюймовым сторонам. . После этого свернутый кусок сшивают по большей части его периметра, чтобы сшить загнутые верхний слой и нижний слой вместе по большей части его окружности, с небольшим отверстием, через которое высыпают рыхлые частицы глины, после в котором отверстие сшивается вместе, чтобы таким образом полностью закрыть сумку и образовать прямоугольную форму. Было обнаружено, что для мешка размером четыре дюйма на три дюйма, измеренного между линиями стежков, которые определяют внутреннюю, вместительную часть мешка, от 2,25 до 3,50 унций рыхлых частиц глины, подробно описанных ниже. , требуется для обеспечения влагопоглощающих свойств, необходимых для мешка, чтобы гарантировать, что через поры трикотажного полотна проходит достаточное количество мелкодисперсной сточной пыли для средней вибрации или встряхивания мешка, длящейся примерно от пяти до десяти секунд, например средний показатель определяется боулером-мужчиной.

Рыхлая глина, содержащаяся в трикотажном мешочке из трикотажной ткани, представляет собой фуллерову серицитовую глину и имеет следующий весовой состав:

Кремнезем (SiO 2 ): 80,40% O3 ): 9,48 %

Оксид железа (Fe 2 O 3 ): 0,88 %

Оксид кальция (CaO): 0,20 %

Оксид магния (MgO): 0,54 %

Натрий и оксид калия (R2): 0,15%

Смешанная вода: 8,35%

Земляная глина Фуллера представляет собой сорбирующую глину, которая избирательно собирает и концентрирует на твердых поверхностях определенные типы молекул, содержащихся в жидкости или газе. Существует два основных минеральных типа фуллеровой земли: аттапульгит и монтмориллонит. Монтмориллонит представляет собой: X y Al 2 (Al y Si 4 -y O 10 )(OH 2 ), где X обычно представляет собой Na, Mg или Al. . Тип Attapulgus представляет собой кристаллический гидратированный алюмосиликат магния, дающий большую площадь поверхности пористого материала, и состоит из:

SiO 2 : 55,03%

Al 2 O 3 : 10,24 %

Fe 2 O 3 : 3,53 %

MgO: 10,49 %

К. суб.2 О: 0,47%;

H 2 O, удаленный при 110°С, составляет 9,73%, а выше 150°С – 10,13%;

Любая форма фуллеровой земли может использоваться в настоящем изобретении в сочетании с серицитом, как указано ниже.

Серицит представляет собой чешуйчатую разновидность минерала мусковита со следующей формулой:

K Al 3 Si 3 O 10 (OH) 2 .

Серицитовая земля Фуллера является коммерчески доступным продуктом. Предпочтительный размер каждой частицы серицита составляет примерно от одной четверти до одной восьмой дюйма, что, как было обнаружено, обеспечивает получение мелких пылевидных частиц только после умеренного встряхивания и вибрации мешка-контейнера.