Периметр трапеции формула через площадь: Формулы трапеции, формулы для расчета площади и периметра трапеции

Содержание

Трапеция. Формулы, признаки и свойства трапеции

Навигация по странице: Определение трапеции Элементы трапеции Виды трапеций Основные свойства трапеции Стороны трапеции Средняя линия трапеции Высота трапеции Диагонали трапеции Площадь трапеции Периметр трапеции Окружность описанная вокруг трапеции Окружность вписанная в трапецию Другие отрезки трапеции

Определение.

Трапеция — это четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.

Параллельные стороны называются основами трапеции, а две другие боковыми сторонами

Так же, трапецией называется четырехугольник, у которого одна пара противоположных сторон параллельна, и стороны не равны между собой.

Элементы трапеции:

Основы трапеции — параллельные стороны
Боковые стороны — две другие стороны
Средняя линия — отрезок, соединяющий середины боковых сторон.

Виды трапеций:

Равнобедренная трапеция — трапеция, у которой боковые стороны равны
Прямоугольная трапеция — трапеция, у которой одна из боковых сторон перпендикулярна основам


Рис.1		Рис.2

Основные свойства трапеции

1. В трапецию можно вписать окружность, если сумма длин оснований равна сумме длин боковых сторон:

AB + CD = BC + AD

2. Средняя линия трапеции разделяет пополам любой отрезок, который соединяет основы, так же делит диагонали пополам:

AK = KB, AM = MC, BN = ND, CL = LD

3. Средняя линия трапеции параллельна основаниям и равна их полусумме:

m =	a + b
	2

4. Точка пересечения диагоналей трапеции и середины оснований лежат на одной прямой.

5. В трапеции её боковая сторона видна из центра вписанной окружности под углом 90°.

6. Каждая диагональ в точке пересечения делится на две части с таким соотношением длины, как соотношение между основаниями:

BC : AD = OC : AO = OB : DO

7. Диагонали трапеции d₁ и d₂ связаны со сторонами соотношением:

d₁² + d₂² = 2ab + c² + d²

Сторона трапеции

Формулы определения длин сторон трапеции:

1. Формула длины оснований трапеции через среднюю линию и другую основу:

a = 2m — b

b = 2m — a

2. Формулы длины основ через высоту и углы при нижнем основании:

a = b + h · (ctg α + ctg β)

b = a — h · (ctg α + ctg β)

3.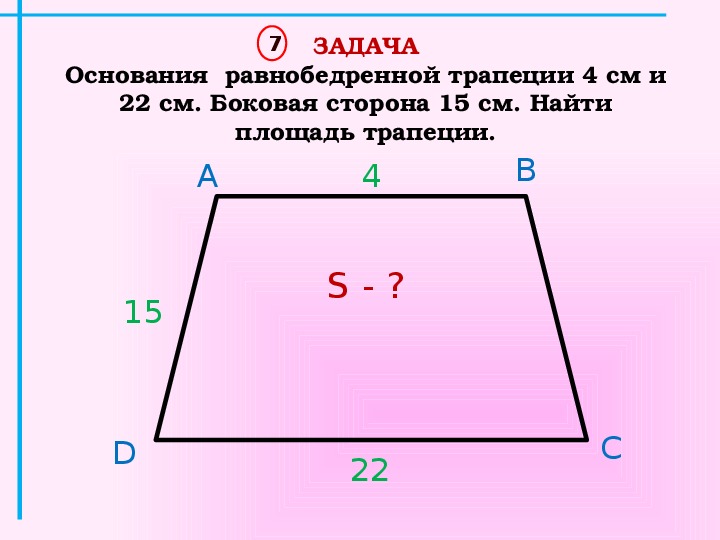 Формулы длины основ через боковые стороны и углы при нижнем основании:

a = b + c·cos α + d·cos β

b = a — c·cos α — d·cos β

4. Формулы боковых сторон через высоту и углы при нижнем основании:

с =	h	d =	h
	sin α		sin β

Средняя линия трапеции

Определение.

Средняя линия — отрезок, соединяющий середины боковых сторон трапеции.

Формулы определения длины средней линии трапеции:

1. Формула определения длины средней линии через длины оснований:

m =	a + b
	2

2. Формула определения длины средней линии через площадь и высоту:

m =	S
	h

Высота трапеции

Формулы определения длины высоты трапеции:

1. Формула высоты через сторону и прилегающий угол при основании:

h = c·sin α = d·sin β

2. Формула высоты через диагонали и углы между ними:

h =	sin γ ·	d₁ d₂	=	sin δ ·	d₁ d₂
		a + b			a + b

3. Формула высоты через диагонали, углы между ними и среднюю линию:

h =	sin γ ·	d₁ d₂	=	sin δ ·	d₁ d₂
		2m			2m

4. Формула высоты трапеции через площадь и длины оснований:

h =	2S
	a + b

5. Формула высоты трапеции через площадь и длину средней линии:

h =	S
	m

Диагонали трапеции

Формулы определения длины диагоналей трапеции:

1.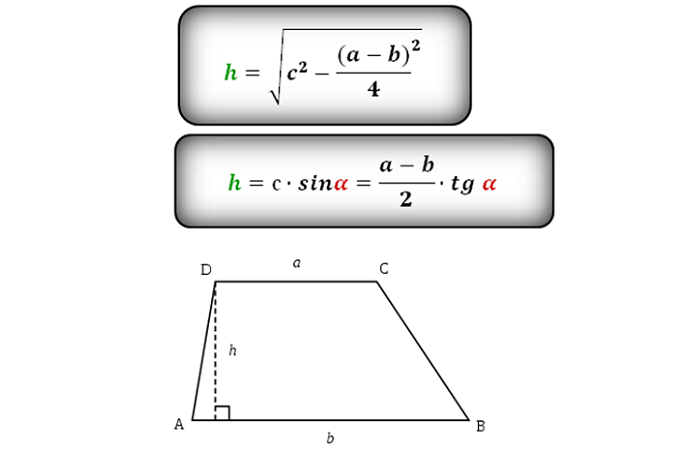 Формулы диагоналей по теореме косинусов:

d₁ = √a² + d² — 2ad·cos β

d₂ = √a² + c² — 2ac·cos α

2. Формулы диагоналей через четыре стороны:

d₁ =	√	d ² + ab —	a(d ² — c²)
			a — b

d₂ =	√	c² + ab —	a(c² — d ²)
			a — b

3. Формула длины диагоналей через высоту:

d₁ = √h² + (a — h · ctg β)² = √h² + (b + h · ctg α)²

d₂ = √h² + (a — h · ctg α)² = √h² + (b + h · ctg β)²

4. Формулы длины диагонали через сумму квадратов диагоналей:

d₁ = √c² + d ² + 2ab — d₂²

d₂ = √c² + d ² + 2ab — d₁²

Площадь трапеции

Формулы определения площади трапеции:

Формула площади через основания и высоту:

S =	(a + b)	· h
	2

2. Формула площади через среднюю линию и высоту:

S = m · h

3. Формула площади через диагонали и угол между ними:

S =	d₁d₂	· sin γ	=	d₁d₂	· sin δ
	2			2

4. Формула площади через четыре стороны:

S =	a + b	√	c² —	(	(a — b)² + c² — d ²	)	²
	2				2(a — b)

5. Формула Герона для трапеции

S =	a + b	√(p — a)(p — b)(p — a — c)(p — a — d)
	\|a — b\|

где

p =	a + b + c + d	— полупериметр трапеции.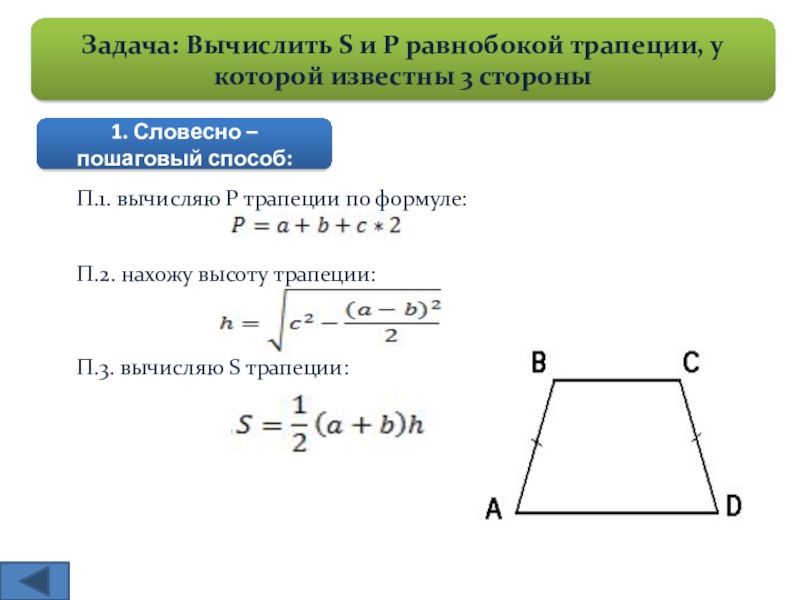
	2

Периметр трапеции

Формула определения периметра трапеции:

1. Формула периметра через основания:

P = a + b + c + d

Окружность описанная вокруг трапеции

Окружность можно описать только вокруг равнобедренной трапеции!!!

Формула определения радиуса описанной вокруг трапеции окружности:

1. Формула радиуса через стороны и диагональ:

R =	a·c·d₁
	4√p(p — a)(p — c)(p — d₁)

где

p =	a + c + d₁
	2

a — большее основание

Окружность вписанная в трапецию

В трапецию можно вписать окружность, если сумма длин оснований равна сумме длин боковых сторон:

a + b = c + d

Формула определения радиуса вписанной в трапецию окружности

1. Формула радиуса вписанной окружности через высоту:

r =	h
	2

Другие отрезки разносторонней трапеции

Формулы определения длин отрезков проходящих через трапецию:

1. Формула определения длин отрезков проходящих через трапецию:

KM = NL =	b	KN = ML =	a	TO = OQ =	a · b
	2		2		a + b

Все таблицы и формулы

Площадь трапеции: формулы, определения, элементы

Площадь трапеции, формулы расчета, определение,
способы найти площадь, нахождение площади
через величины и примеры площади трапеции.

Все формулы расчета площади трапеции
через основания и угол, периметр, радиус,
синус и две стороны, диагональ,
высоту, среднюю линию.

Площадь трапеции, можно измерить, в единицах
измерения в квадрате: мм², см², м² и км² и так далее.

Площадь трапеции через окружность вписанную можно
найти, зная радиус окружности вписанной в трапецию
и некоторые другие величины.

Содержание

Формулы площади трапеции
Площадь любых трапеций
Площадь равнобедренной трапеции
Определения трапеции
Элементы трапеции

Формулы площади трапеции

Площадь любых трапеций

Ⅰ. Площадь трапеции через основания и высоту:

\[ S = \frac{a+b}{2} \cdot h \]
a,b — основания трапеции;
h — высота трапеции;

Ⅱ. Площадь трапеции через высоту и среднюю линию:

\[ S = mh \]
m — средняя линия трапеции;
h — высота трапеции;

Ⅲ. Площадь трапеции через диагонали и угол между ними:

\[ S =\frac{1}{2}d_1d_2 \cdot \sin \alpha \]
\( d_1, d_2 \)- диагонали трапеции;
sin α — синус угла альфа в трапеции;

Ⅳ. 2}{2} \cdot \frac{\sin α \cdot \sin β}{\sin( α + β)} \]

a,b — основания трапеции;
α — угол при основании a в трапеции;
β — угол при основании b в трапеции;
sin α — синус угла альфа в трапеции;
sin β — синус угла бетта в трапеции;

Площадь равнобедренной трапеции

Ⅰ. Площадь трапеции через синус угла, среднюю линию и боковую сторону:

\[ S = ld \cdot \sin α \]

l — средняя линия равнобедренной трапеции;
d — боковая сторона равнобедренной трапеции;
α — угол альфа при боковой стороне d равнобедренной трапеции;
sin α — синус угла альфа в равнобедренной трапеции;

Ⅱ. Площадь трапеции через диагонали и синус угла:

\[ S = \frac{d^2}{2} \cdot \sin α \]

d — диагональ равнобедренной трапеции;
α — угол между двумя диагоналями в равнобедренной трапеции;
sin α — синус угла альфа в равнобедренной трапеции;

Ⅲ. Площадь трапеции через радиус вписанной окружности и основания:

\[ S = r( a+b) \]

r — радиус вписанной окружности равнобедренной трапеции;
a, b — основания равнобедренной трапеции;

Ⅳ. Площадь трапеции через основания:

\[ S = \sqrt{ab} \cdot {\frac{a+b}{2}} \]

a, b — основания равнобедренной трапеции;

Ⅴ. Площадь трапеции через основания и среднюю линию:

\[ S = l\sqrt{ab} \]

l — средняя линия равнобедренной трапеции;
a, b — основания равнобедренной трапеции;

Ⅵ. Площадь трапеции через синус угла и стороны:

\[ S = c \cdot \sin α \cdot (a-c \cdot \cos α) \]

a — нижнее основание равнобедренной трапеции;
с — боковая сторона равнобедренной трапеции;
sin α — синус угла альфа в равнобедренной трапеции;
cos α — косинус угла альфа в равнобедренной трапеции;

Ⅶ.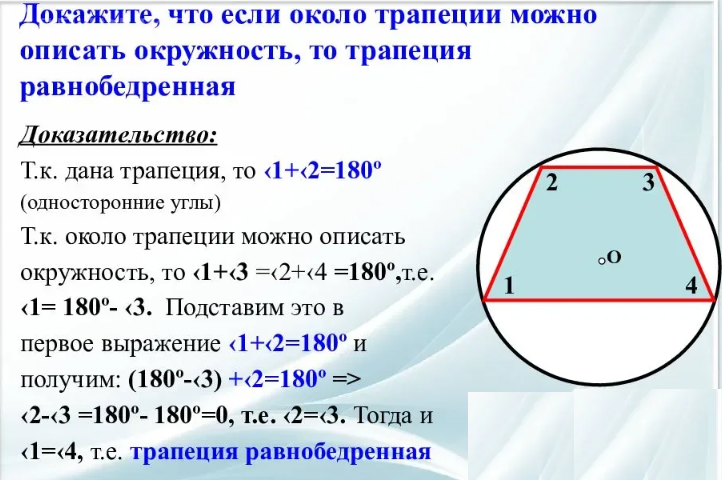 2}{\sin α} \]

r — радиус вписанной окружности равнобедренной трапеции;
sin α — синус угла альфа в равнобедренной трапеции;

Определения трапеции

Трапеция — это четырехугольник, у которого две
стороны параллельны а две другие нет.

Зная углы трапеции, можно определить, к какому виду
она относится. Всего различают три вида трапеций:

Обычная / стандартная трапеция: четыре угла и четыре стороны не равны.
Равнобедренная / равнобочная / равнобоковая трапеция:
два угла при основании равны, две боковые стороны равны.
Прямоугольная / прямая трапеция: один из углов прямой.

Площадь равнобедренной, прямоугольной трапеции,
можно найти через формулы площади обычной трапеции.

Формул, с помощью которых, можно найти площадь трапеции
через описанную окружность около трапеции, не существует.

Элементы трапеции

Любая трапеция является четырехугольником,
поэтому у трапеции 4 угла и 4 стороны.

Основание трапеции — это сторона, противолежащая
сторона которой параллельна.

Боковая сторона трапеции — это сторона, противолежащая
сторона которой не параллельна.

Средняя линия трапеции — это отрезок, соединяющий
середины боковых сторон трапеции.

Диагональ трапеции — это отрезок, соединяющий две
вершины, которые лежат в разных концах трапеции.

Высота трапеции — это отрезок, соединяющий меньшее основание с большим,
образуя при этом два угла по 90 градусов на большей стороне.

Основания у трапеции не могут быть никогда равны.
Боковые стороны могут быть равны только,
если трапеция — равнобедренная.

Площадь трапеции — это площадь геометрической фигуры,
у которой четыре стороны и четыре угла, причем только
две стороны параллельны а остальные нет.

Калькулятор площади трапеции

Создано Bogna Szyk

Отзыв Стивена Вудинга

Последнее обновление: 18 декабря 2022 г.

Содержание:
Что такое трапеция?
Как найти площадь трапеции?
Как найти периметр трапеции?
Использование калькулятора площади трапеции: пример
Часто задаваемые вопросы
Если у вас когда-либо возникали проблемы с запоминанием формул на уроках геометрии, эта область калькулятора трапеции обязательно вам поможет. Всего за несколько простых шагов вы сможете найти площадь трапеции и определить все остальные ее свойства, например длины сторон внутренних углов. Итак, если вас беспокоят такие вопросы, как «как найти периметр трапеции», не смотрите дальше — просто продолжайте читать, чтобы узнать!
Вы также можете воспользоваться нашим калькулятором длины окружности, чтобы более подробно проанализировать геометрию круга, или нашим калькулятором формулы окружности, чтобы узнать больше об уравнениях, лежащих в основе этой геометрии.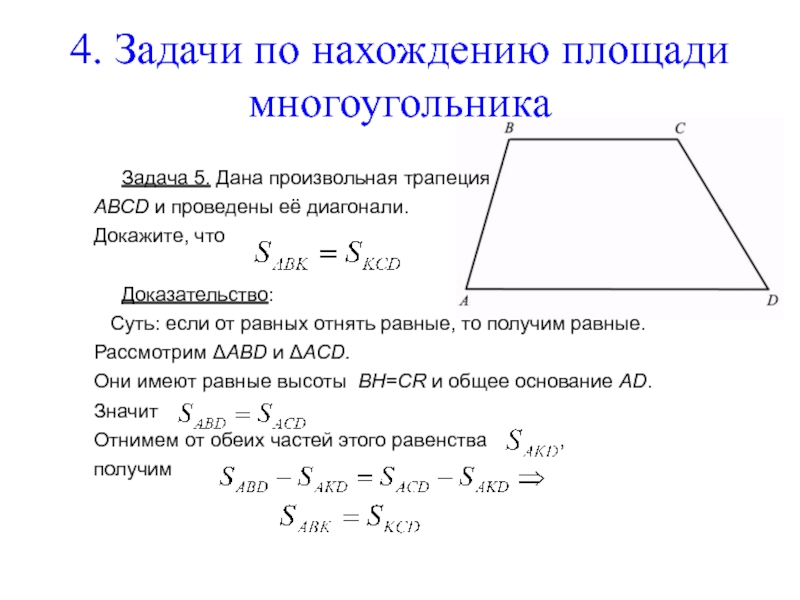
Что такое трапеция?
Трапеция – это четырехсторонняя геометрическая фигура, две стороны которой параллельны друг другу. Эти две стороны ( a и b на схеме) называются основаниями трапеции. Две другие стороны ( c и d ) называются ножками. h высота трапеции.
Сумма всех внутренних углов трапеции дает 360°. Кроме того, углы на одной стороне катета называются смежными и всегда дают в сумме 180°:
α + β = 180°
γ + δ = 180°
Как найти площадь трапеции?
Чтобы найти площадь трапеции (
A ), выполните следующие действия:
Найдите длину каждого основания ( a и b ).
Найдите высоту трапеции ( h ).
Подставьте эти значения в формулу площади трапеции: A = (a + b) × h / 2 .
Вы можете заметить, что для трапеции с a = b (и, следовательно, c = d = h) формула упрощается до A = a × h , что в точности соответствует формуле площади прямоугольника.
Как найти периметр трапеции?
Чтобы быстро найти периметр трапеции, выполните следующие действия:
Найдите длину всех сторон трапеции ( a , b , c и 9 0043 д ).
Сложите их вместе, чтобы получить периметр трапеции: P = a + b + c + d .
Вот оно! Это так просто.
В качестве альтернативы вы можете использовать калькулятор площади трапеции, который автоматически найдет для вас площадь и периметр трапеции.
Использование калькулятора площади трапеции: пример
Предположим, вы хотите вычислить площадь некоторой трапеции. Все данные приведены:
α = 30°
γ = 125°
В = 6 см
а = 4 см
Р = 25 см
Вычислите оставшиеся внутренние углы. Как α + β = 180° , β = 180° - 30° = 150° .
Аналогично, как γ + δ = 180° , δ = 180° - 125° = 55° .
Найдите длины катетов трапеции, используя формулу синуса угла:
sin 30° = c / h
sin 55° = д/ч
c = sin 30° × 6 = 12 см
d = sin 55° × 6 = 7,325 см
Вычтите значения a, c и d из периметра трапеции, чтобы найти длину второго основания:
b = P - a - c - d = 25 - 4 - 12 - 7,325 = 1,675 см
Наконец, применим формулу площади трапеции:
A = (a + b) × h / 2 = (4 + 1,675) × 6 / 2 = 17,026 см²
Не забудьте также взглянуть на шестигранный калькулятор!
Часто задаваемые вопросы
Чем трапеция отличается от других четырехугольников?
Трапеции отличаются от других четырехугольников тем, что они имеют ровно одну пару параллельных сторон .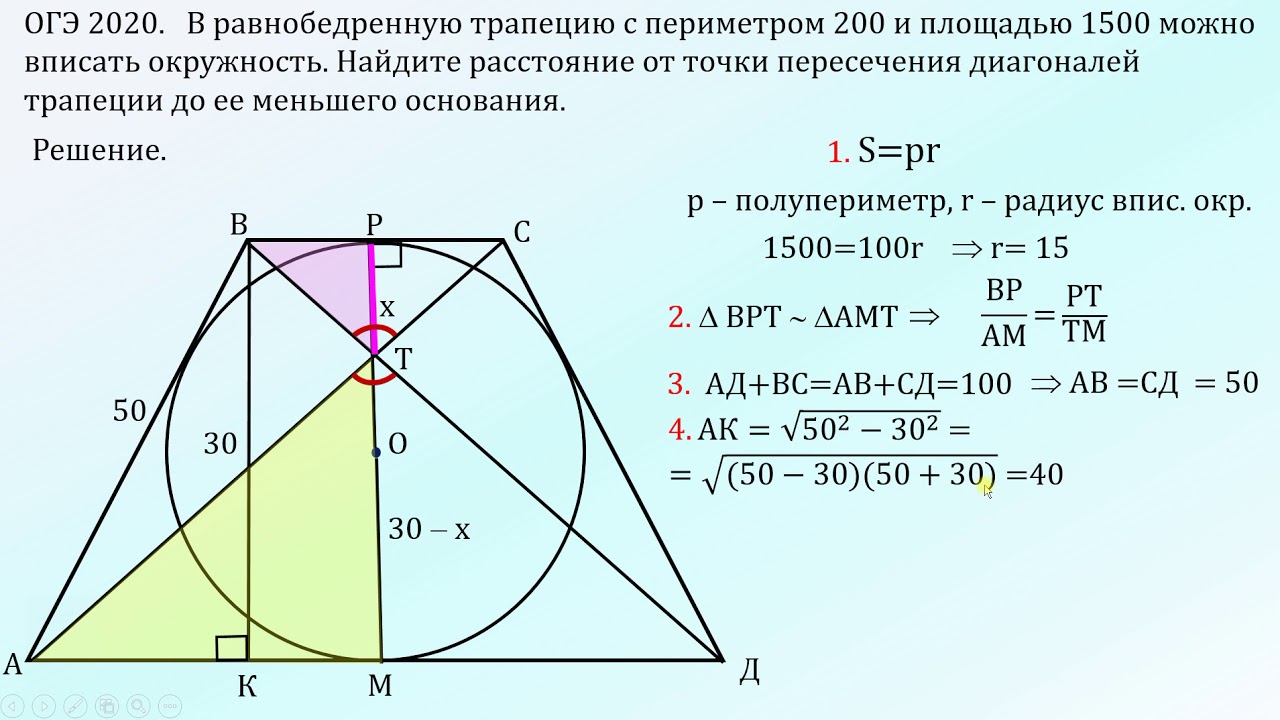 Они, по сути, четырехугольники, как прямоугольники и квадраты, но не параллелограммы.
Какова площадь трапеции с высотой 5 м и основаниями 8 м и 1 м?
Площадь этой трапеции равна 22,5 метра в квадрате . Для получения результата воспользуемся формулой площади трапеции: A = (a + b) × h / 2 и положим a = 8 м , b = 1 м , а h = 5 м внутри него.
Bogna Szyk
a (основание)
b (основание)
h (высота)
Периметр
Периметр
У углов
Проверьте 23 аналогичные 2D Геометрические калькуляторы 📏
Площадь с прямоугольником полумесяца… еще 20
Область трапеции — формула, примеры, решения
Студенты должны выполнять различные геометрические домашние работы. Однако больше всего трудностей возникает у учащихся средних классов, поскольку они изучали только математику и алгебру, и геометрию. Например, им нужно найти перпендикулярное расстояние, площадь поверхности или параллельные стороны трапеции.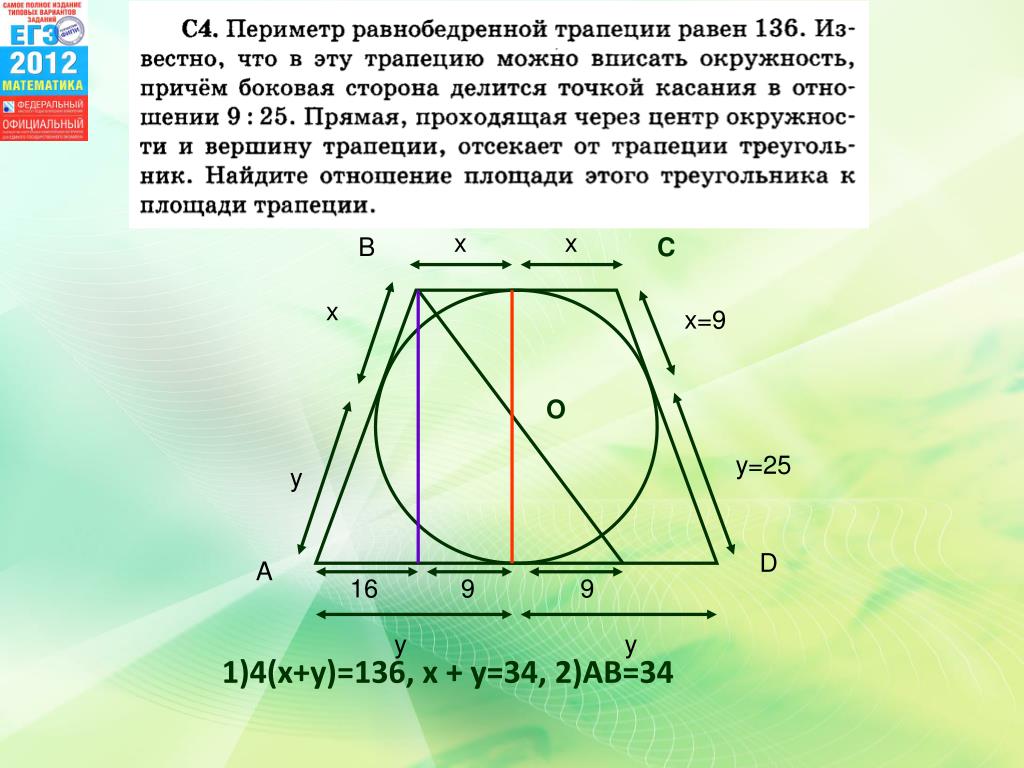 Сегодня мы поговорим именно о трапециях, нахождении площади и рассмотрении ее как одной из важнейших теорем.
Трапеция — что это за фигура?
Элементы трапеции
Теорема: площадь трапеции
Расчет площадей в прошлом
Расчет площадей в современном мире
Формула площади трапеции по основанию и высоте
Формула площади ловушки эзоид на Басе
Формула площади трапеции через
Формула площади трапеции через
Трапеция и созвездия
Трапеции в экспериментальной физике
Трапеция — что это за фигура?
Трапеция – это четырехугольник, имеющий две параллельные стороны и две непараллельные стороны. Параллельные стороны называются основаниями трапеции, а две другие — боковыми сторонами. Высота трапеции – это расстояние между прямыми, на которых лежат основания трапеции, любым общим перпендикуляром этих прямых. Средняя линия трапеции – это отрезок, соединяющий середины сторон.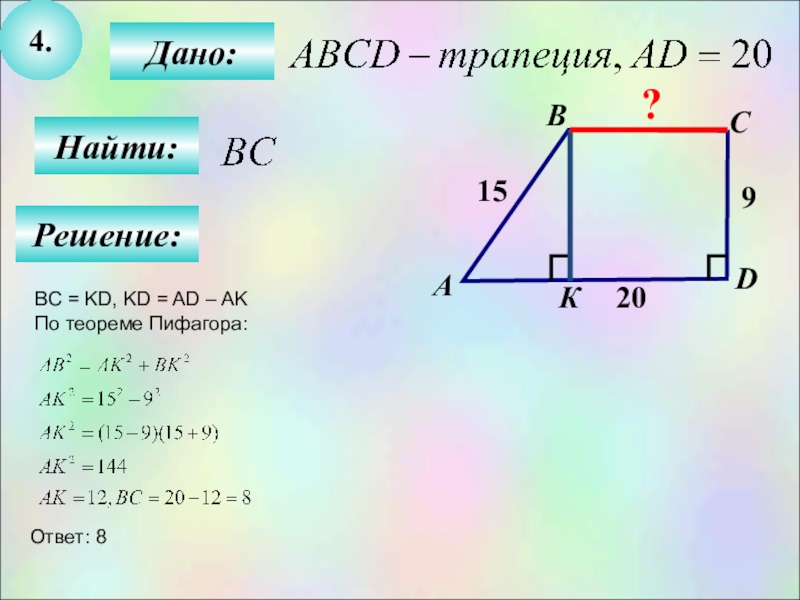
Черты трапеции
Если в трапецию вписана окружность, то сумма основ всегда совпадает с суммой сторон: a+b=c+d, а средняя линия всегда равна полусумме сторон:
Равнобедренной трапецией называется трапеция, стороны которой равны AB = CD. Тогда диагонали AC = BD и углы при основании равны:
Из всех трапеций только около равнобедренной трапеции можно описать окружность, если сумма противоположных прямых углов равна 180°. В равнобедренной трапеции расстояние от вершины одного основания до проекции противоположной вершины, которая непосредственно связана с основанием, всегда совпадает с осевой линией.
Прямоугольная трапеция — это разновидность трапеции, угол основания которой равен 90°.
Теорема: площадь трапеции
Чтобы вычислить площадь произвольного многоугольника, мы делаем следующее: делим многоугольник на треугольники и находим площадь треугольника. Сумма площадей этих треугольников равна площади многоугольника. С помощью этой методики выводим формулу расчета площади запасной части трапеции. Условимся называть высотой трапеции перпендикуляр, проведенный из любой точки одного из оснований на прямую, содержащую другое основание. На рисунке ниже мы указали, что отрезок линии BH является высотой трапеции ABCD:
Исходя из этого, получаем теорему: «Площадь трапеции равна произведению полусуммы ее оснований на высоту». Используя формулу площади, мы можем доказать эту теорему.
Дана трапеция: ABCD, AD, BC — длины оснований, BH — высота.
Докажите: площадь этой трапеции ABCD будет равна S = ½ (AD + BC) · BH.
Доказательство: проведите диагональ BD. Он делит трапецию на два треугольника ABD и BCD. Это означает, что периметр трапеции ABCD будет равен сумме площадей этих треугольников.
В треугольнике ABD: AD — основание, BH — высота. В треугольнике BCD: BC является основанием.
Нарисуем высоту DK. Площадь S треугольника ABD = 1/2 AD · BH; площадь S треугольника BCD = 1/2 BC · DK. Так как BH = DK, то площадь S треугольника BCD = 1/2 BC · BH. Таким образом, площадь S трапеции ABCD = 1/2 AD · BH + 1/2 BC · BH = 1/2 (AD + BC) · BH. Что требовалось доказать.
Вычисление площадей в прошлые времена
Еще 4-5 тысяч лет назад вавилоняне умели определять площадь трапеции в квадратных единицах. Древние египтяне 4000 лет назад использовали почти те же приемы, что и мы: сумму параллельных сторон делили пополам и умножали на высоту.
Определение площадей геометрических фигур — одна из древнейших практических задач. Люди не сразу нашли правильный подход к их решению. Один из самых простых и доступных способов вычисления площадей открыл Евклид. При расчете площадей он использовал простой прием, называемый методом разбиения.
Вычисление площадей в современном мире
Сегодня существует множество формул для вычисления длин сторон, вершин, параллельных оснований и площади трапеции. Мы рассмотрим самые основные из них. Приведенные ниже формулы просты в использовании, но если вам сложно их понять и вам нужна помощь с домашним заданием, вы всегда можете обратиться в нашу службу. Опытные авторы проконсультируют вас по всем заданиям, и вы значительно улучшите свою успеваемость.
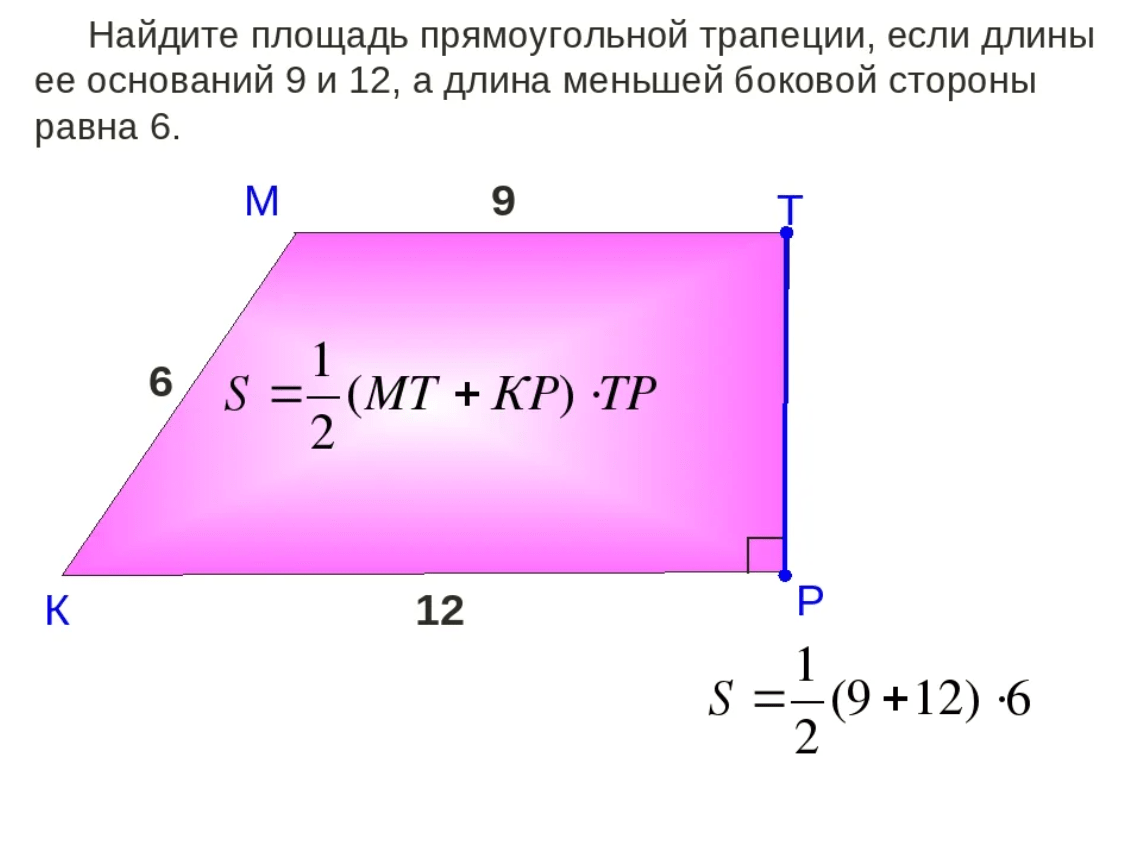
Формула площади трапеции по основанию и высоте
Дана произвольная трапеция. Для нахождения его площади используем следующую формулу:
В этой формуле:
а, b — основания трапеции;
hh — высота трапеции.
Представим, что нам нужно найти площадь трапеции, у которой известны основания, численно равные 10 см и 8 см. Также известный рост, 6 см в длину.
Решение:
а = 8;
б = 10;
ч = 6;
Сразу подставляем цифры в полученную формулу и вычисляем значение:
Ответ: 54 квадратных сантиметра.
Формула площади основания и центральной линии трапеции
Следует отметить, что средняя линия трапеции равна половине суммы ее оснований. Таким образом, нахождение площади через центральную линию есть не что иное, как метод, аналогичный первому. Насколько:
В этой формуле:
S = l ⋅ h;
l — средняя линия трапеции;
h – высота.
Предположим, нам нужно найти площадь трапеции, если известно, что средняя линия равна 5 см, а высота трапеции в два раза больше ее высоты.
Решение:
л = 5;
ч = 2 ⋅ л.
Найдите высоту трапеции:
h = 2 ⋅ 5 = 10
Площадь:
S = l ⋅ h = 5 ⋅ 10 = 50 см.кв.
Ответ: 50 квадратных сантиметров
Формула площади трапеции через радиус и угол вписанной окружности
Этот случай подходит только для равнобедренной трапеции:
В этой формуле:
р это радиус вписанной окружности;
α — угол между основанием и стороной.
Предположим, нам дан радиус вписанной окружности в трапецию, равный 4 см. Угол α равен 90 градусов. Нам нужно найти площадь трапеции.
Решение:
r = 4;
α = 90,
По формуле:
Ответ: 64 квадратных сантиметра.
Формула площади трапеции через диагонали и угол между ними
Существует простая формула для нахождения площади трапеции через диагонали и угол между ними:
В этой формуле:
d1, d2 — диагонали трапеций;
α — угол между диагоналями.
Пусть две диагонали трапеции равны 20 см и 7 см. При пересечении они образуют угол 30 градусов. Нам нужно найти площадь трапеции.
Решение:
d1 = 20;
д2 = 7;
α = 30°.
Площадь:
Ответ: 35 квадратных сантиметров.
Трапеция и созвездия
Трапеция встречается не только в домашних заданиях по математике. Эту цифру можно найти при изучении созвездий. Выдающимся астеризмом весеннего неба является трапеция Льва, которую можно наблюдать по вечерам с февраля по май. Эта фигура расположена в зодиакальном созвездии Льва, образуя тело животного, и по форме напоминает трапецию.
Четыре яркие звезды созвездия α, β, γ и δ расположены на вершинах трапеции – туловища льва. А голову льва образуют звезды, расположенные в виде серпа. Отсюда и название — трапеция Льва.
Трапеции в экспериментальной физике Посмотреть
Союз физики и математики предполагает непрерывное движение науки вперед. В физике ученые проводят опыты, суть которых становится полностью ясной только после математического анализа. Многие разделы математики обязаны своим возникновением и дальнейшим развитием новым физическим опытам. В качестве примера рассмотрим школьную лабораторную работу по физике.
Постановка вопроса: Рассмотрим фигуру — произвольную трапецию ABCD. Проведите две его диагонали AC и BD, которые делят трапецию на четыре треугольника — ABO, BCO, CDO и DAO. Треугольники ABO и CDO равны:
Формулировка цели опытной работы: с помощью взвешивания доказать, что массы треугольников, полученных диагоналями и сторонами трапеции, равны.
Ход лабораторной работы:
Учащимся необходимо взять: лист бумаги, линейку, карандаш, ластик, ножницы.
No related posts.