Период синуса: Тригонометрия, тригонометрические функции, синус, косинус, тангенс, котангенс

Период синуса, косинуса, тангенса и котангенса + область определений — вопрос №1858527 — Учеба и наука

Лучший ответ по мнению автора

26. 02.16 Лучший ответ по мнению автора

Михаил Александров Читать ответы

Андрей Андреевич Читать ответы

Eleonora Gabrielyan Читать ответы

Посмотреть всех экспертов из раздела Учеба и наука > Математика

Похожие вопросы

Данный пример использовался на экзамене upsc в декабре 2013 и лишь один человек смог решить его .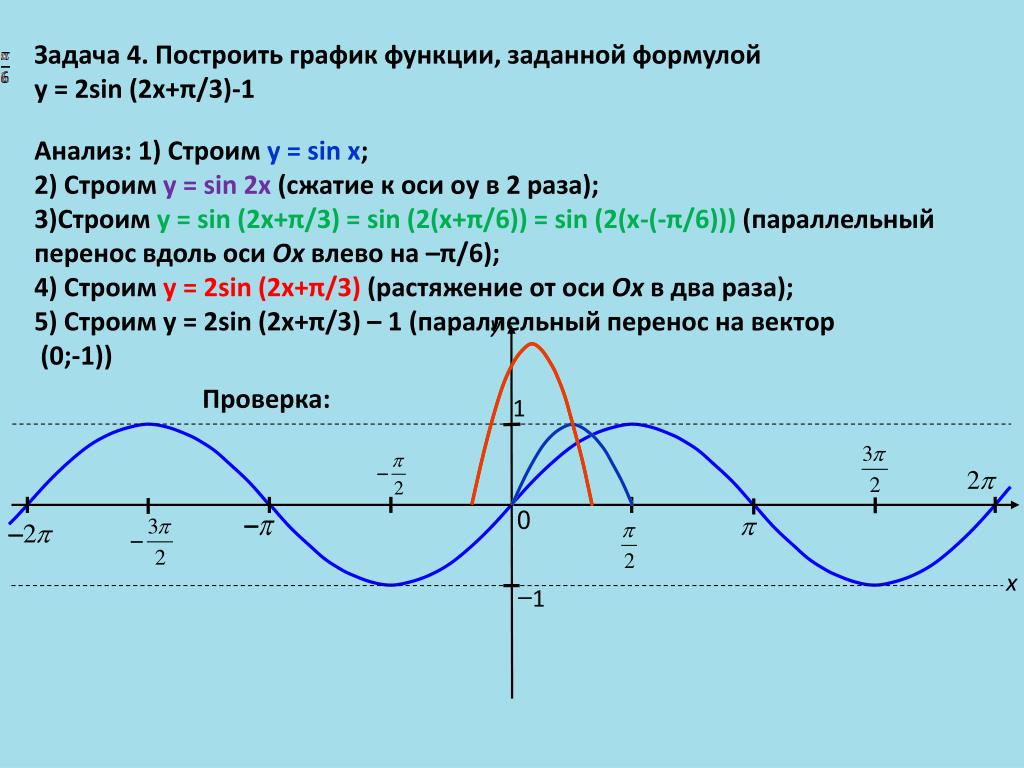 2 — 2x — 3. Найдите: а)наименьшее значение функции; б) значения x, при которых значение функции равно 5; в) значение…

шмель и оса полетели с…

Решено

Из пункта А в пункт В,расположенный ниже по течению реки,отправился плот. Одновременно с ним из пункта А вышел катер.Дойдя до В,катер сразу же…

Решено

два самолёта вылетели с аэродрома…

Пользуйтесь нашим приложением

Период функции y sin x. Синус (sin x) и косинус (cos x) – свойства, графики, формулы

Видеоурок «Периодичность функций у = sin х, у = cos х» раскрывает понятие периодичности функции, рассматривает описание примеров решения задач, в которых используется понятие периодичности функции. Данный видеоурок является наглядным пособием для объяснения темы ученикам. Также данное пособие может стать самостоятельной частью урока, освобождая учителя для проведения индивидуальной работы с учениками.

Наглядность в представлении данной темы очень важна. Чтобы представить поведение функции, построение графика, ее необходимо визуализировать. Произвести построения с помощью классной доски и мела не всегда удается так, чтобы они были понятны всем ученикам. В видеоуроке есть возможность при построении выделять части рисунка цветом, производить преобразования с помощью анимации. Таким образом, построения становятся более понятными большинству учеников. Также возможности видеоурока способствуют лучшему запоминанию материала.

Демонстрация начинается с представления темы урока, а также напоминания ученикам материала, изученного на прошлых уроках. В частности, подытоживается перечень свойств, которые были выявлены в функциях у = sin х, а также у = cos х. Среди свойств рассматриваемых функций отмечены область определения, область значений, четность (нечетность), другие особенности — ограниченность, монотонность, непрерывность, точки наименьшего (наибольшего) значения. Ученикам сообщается, что на данном уроке изучается еще одно свойство функции — периодичность.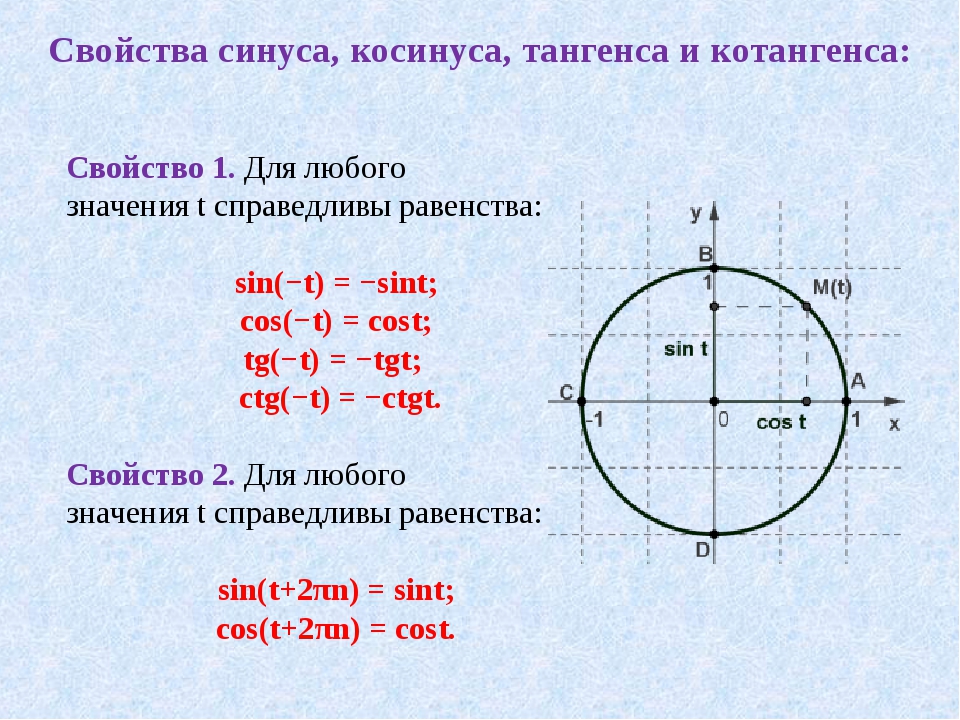

Представлено определение периодичной функции y=f(x), где xϵX, в которой выполняется условие f(x-Т)= f(x)= f(x+Т) для некоторого Т≠0. Иначе число Т называют периодом функции.

Для рассматриваемых функций синуса и косинуса выполнение условия проверяется, применяя формулы приведения. Очевидно, что вид тождества sin(x-2π)=sinx=sin(x+2π) соответствует виду выражения определяющего условие периодичности функции. Такое же равенство можно отметить для косинуса cos (x-2π)= cos x= cos (x+2π). Значит, данные тригонометрические функции являются периодическими.

Далее отмечается, как свойство периодичности помогает строить графики периодичных функций. Рассматривается функция у = sin х. На экране строится координатная плоскость, на которой отмечены абсциссы от -6π до 8π с шагом π. На плоскости строится часть графика синуса, представленный одной волной на отрезке . На рисунке демонстрируется, как график функции формируется на всей области определения сдвигом построенного фрагмента, и получая длинную синусоиду.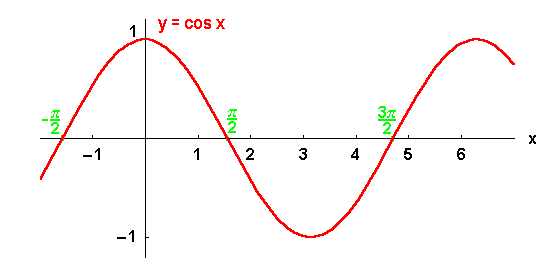

Строится график функции у = cos х, используя свойство ее периодичности. Для этого на рисунке строится координатная плоскость, на которой изображается фрагмент графика. Отмечается, что обычно такой фрагмент строится на отрезке [-π/2;3π/2]. Аналогично графику функции синуса, построение графика косинуса выполняется сдвигом фрагмента. В результате построения образуется длинная синусоида.

Построение графика периодичной функции имеет особенности, которые можно использовать. Поэтому они даются в обобщенном виде. Отмечается, что для построения графика такой функции сначала строят ветвь графика на некотором промежутке длиной Т. затем необходимо сдвинуть построенную ветвь вправо и влево на Т, 2Т, 3Т и т.д. при этом указывается еще на одну особенность периода — для любого целого k≠0 число kТ также является периодом функции. Однако Т называется основным периодом, так как он наименьших из всех. Для тригонометрических функций синуса и косинуса основным периодом является 2π. Однако также являются периодами 4π, 6π и т.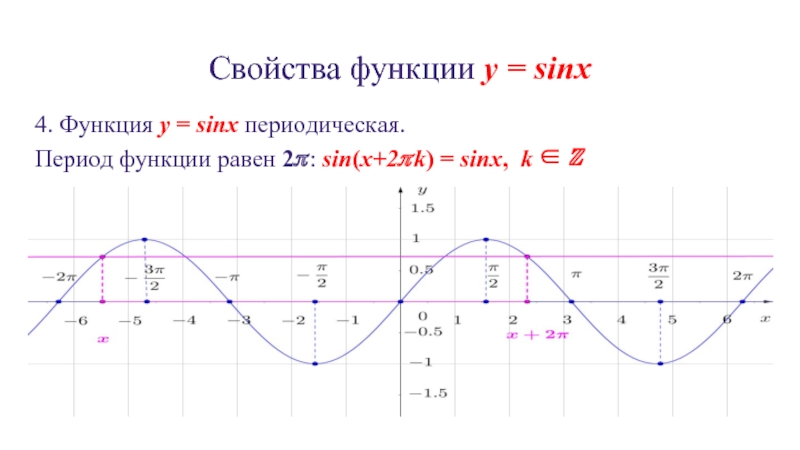

д.

Далее предлагается рассмотреть нахождение основного периода функции у = cos 5х. Решение начинается с предположением, что Т — период функции. Значит, необходимо выполнение условия f(x-Т)= f(x)= f(x+Т). В данном тождестве f(x)= cos 5х, а f(x+Т)=cos 5(x+Т)= cos (5x+5Т). При этом cos (5x+5Т)= cos 5х, следовательно 5Т=2πn. Теперь можно найти Т=2π/5. Задача решена.

Во второй задаче необходимо найти основной период функции y=sin(2x/7). Предполагается, что основной период функции Т. для данной функции f(x)= sin(2x/7), а через период f(x+Т)=sin(2x/7)(х+Т)= sin(2x/7+(2/7)Т). после приведения получаем (2/7)Т=2πn. Однако нам необходимо найти основной период, поэтому берем наименьшее значение (2/7)Т=2π, из которого находим Т=7π. Задача решена.

В конце демонстрации результаты примеров обобщаются, сформировав правило для определения основного периода функции. Отмечается, что для функций у=sinkxи y=coskx основными периодами являются 2π/k.

Видеоурок «Периодичность функций у = sin х, у = cos х» может применяться на традиционном уроке математики для повышения эффективности урока.

Также данный материал рекомендуется использовать учителю, осуществляющему дистанционное обучение для повышения наглядности объяснения. Видео может быть рекомендовано отстающему ученику для углубления понимания темы.

ТЕКСТОВАЯ РАСШИФРОВКА:

«Периодичность функций у = cos x, y =sin x».

Для построения графиков функций y =sin x и у = cos x были использованы свойства функций:

1 область определения,

2 область значения,

3 четность или нечетность,

4 монотонность,

5 ограниченность,

6 непрерывность,

7 наибольшее и наименьшее значение.

Сегодня мы изучим еще одно свойство: периодичность функции.

ОПРЕДЕЛЕНИЕ. Функцию у = f (x), где х ϵ Х(игрек равно эф от икс, где икс принадлежит множеству икс), называют периодической, если существует отличное от нуля число Т такое, что для любого х из множества Х выполняется двойное равенство: f (x — Т)= f (x) = f (x + Т)(эф от икс минус тэ равно эф от икс и равно эф от икс плюс тэ). Число Т, которое удовлетворяет такому двойному равенству, называют периодом функции

А так как синус и косинус определены на всей числовой прямой и для любого х выполняются равенства sin(x — 2π)= sin x= sin(x+ 2π) (синус от икс минус два пи равен синусу икс и равен синусу от икс плюс два пи) и

cos (x- 2π)= cos x = cos (x+ 2π) (косинус от икс минус два пи равен косинусу икс и равен косинусу от икс плюс два пи), то синус и косинус — это периодические функции с периодом 2π.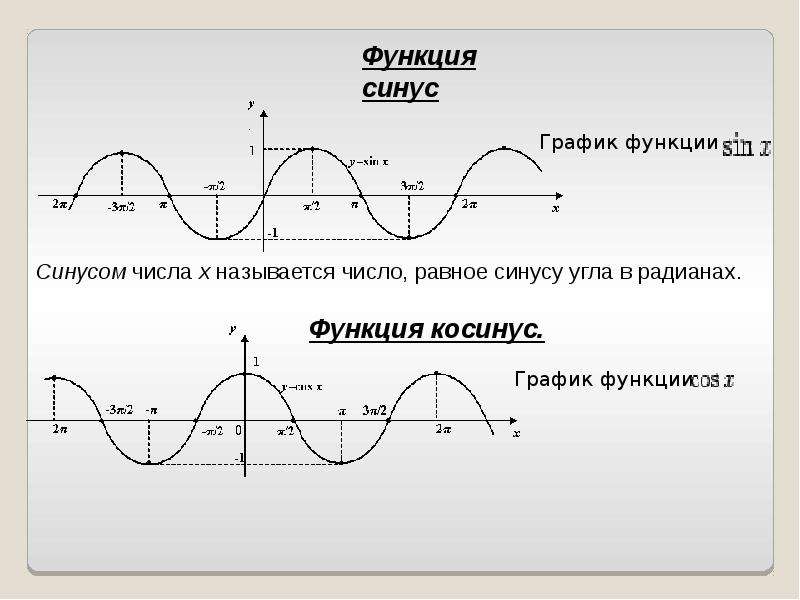

Периодичность позволяет быстро построить график функции. Ведь для того, что бы построить график функции y = sin x , достаточно построить одну волну (чаще всего на отрезке (от нуля до двух пи), а затем с помощью сдвига построенной части графика вдоль оси абсцисс вправо и влево на 2π, затем на 4π и так далее получить синусоиду.

(показать сдвиг вправо и влево на 2π, 4π)

Аналогично для графика функции

у = cos x, только строим одну волну чаще всего на отрезке [; ] (от минус пи на два до трех пи на два).

Обобщим выше сказанное и сделаем вывод: для построения графика периодической функции с периодом Т сначала нужно построить ветвь(или волну, или часть) графика на любом промежутке длины Т(чаще всего это промежуток с концами в точках 0 и Т или же — и (минус тэ на два и тэ на два), а затем сдвинуть эту ветвь вдоль оси х(икс) вправо и влево на Т, 2Т, 3Т и т. д.

Очевидно, что если функция периодическая с периодом Т, то при любом целом k0(ка не равном нулю) число вида kT(ка тэ) тоже период этой функции.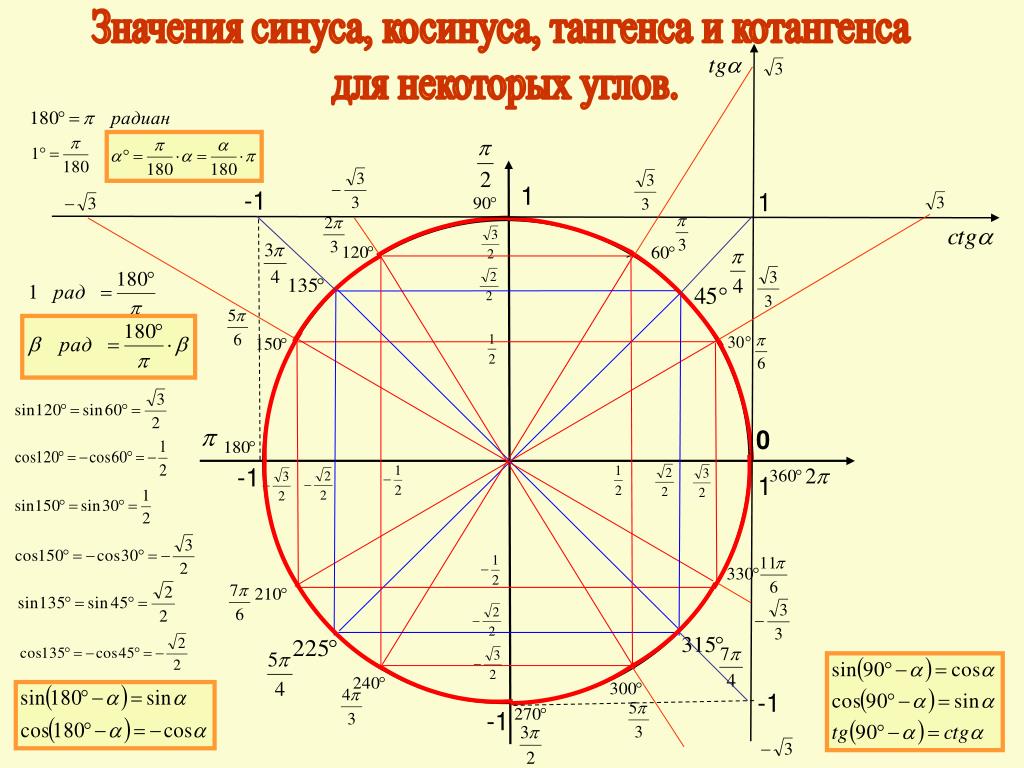 Обычно стараются выделить наименьший положительный период, который называют основным периодом.

В качестве периода функций у = cos x, y = sin x можно было бы взять — 4π, 4π,- 6π, 6π и т.д.(минус четыре пи, четыре пи, минус шесть пи, шесть пи и так далее). Но число 2π является основным периодом и той, и другой функции.

Рассмотрим примеры.

ПРИМЕР 1.Найти основной период функции у = сos5x (игрек равно косинус пяти икс).

Решение. Пусть Т — основной период функции у = сos5x. Положим

f (x) = сos5x, тогда f (x + Т)= сos5(x + Т)= сos (5x + 5Т) (эф от икс плюс тэ равно косинусу пяти, умноженного на сумму икса и тэ равно косинусу от суммы пяти икс и пяти тэ).

сos (5x + 5Т)= сos5x. Отсюда 5Т= 2πn (пять тэ равно два пи эн), но по условию нужно найти основной период, значит, 5Т= 2π. Получаем Т=

(период данной функции равен два пи, деленное на пять).

Ответ: Т=.

ПРИМЕР 2. Найти основной период функции у = sin (игрек равно синус частного двух икс на семь).

Решение. Пусть Т — основной период функции у = sin . Положим

f (x) = sin , тогда f (x + Т)= sin (x + Т) = sin (x + Т) (эф от икс плюс тэ равно синусу произведения двух седьмых и суммы икса и тэ равно синусу от суммы двух седьмых икс и двух седьмых тэ).

Чтобы число Т было периодом функции, должно выполнятся тождество

sin (x + Т) = sin . Отсюда Т= 2πn (две седьмые тэ равно два пи эн), но по условию нужно найти основной период, значит, Т= 2π. Получаем Т=7

(период данной функции равен семи пи).

Ответ: Т=7.

Обобщая результаты, полученные в примерах, можно сделать вывод: основной период функций y =sin kx или у = cos kx (игрек равно синус ка икс или игрек равно косинус ка икс) равен (два пи, деленное на ка).

С центром в точке A .
α — угол, выраженный в радианах.

Определение
Синус (sin α) — это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины противолежащего катета |BC| к длине гипотенузы |AC|.

Косинус (cos α) — это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины прилежащего катета |AB| к длине гипотенузы |AC|.

Принятые обозначения

;
;
.

;
;
.

График функции синус, y = sin x

График функции косинус, y = cos x

Свойства синуса и косинуса

Периодичность

Функции y = sin x и y = cos x периодичны с периодом 2 π .

Четность

Функция синус — нечетная. Функция косинус — четная.

Область определения и значений, экстремумы, возрастание, убывание

Функции синус и косинус непрерывны на своей области определения, то есть для всех x (см. доказательство непрерывности). Их основные свойства представлены в таблице (n — целое).

	y = sin x	y = cos x
Область определения и непрерывность	— ∞	— ∞
Область значений	-1 ≤ y ≤ 1	-1 ≤ y ≤ 1
Возрастание
Убывание
Максимумы, y = 1
Минимумы, y = -1
Нули, y = 0
Точки пересечения с осью ординат, x = 0	y = 0	y = 1

Основные формулы

Сумма квадратов синуса и косинуса

Формулы синуса и косинуса от суммы и разности

;
;

Формулы произведения синусов и косинусов

Формулы суммы и разности

Выражение синуса через косинус

;
;
;
.

Выражение косинуса через синус

;
;
;
.

Выражение через тангенс

; .

При , имеем:
; .

При :
; .

Таблица синусов и косинусов, тангенсов и котангенсов

В данной таблице представлены значения синусов и косинусов при некоторых значениях аргумента.

Выражения через комплексные переменные

;

Формула Эйлера

Выражения через гиперболические функции

;
;

Производные

; . Вывод формул > > >

Производные n-го порядка:
{ -∞

Секанс, косеканс

Обратные функции

Обратными функциями к синусу и косинусу являются арксинус и арккосинус , соответственно.

Арксинус, arcsin

Арккосинус, arccos

Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.

Инструкция

Чтобы найти период тригонометрической функции, возведенной в степень, оцените четность степени. 2х, то стандартный период 2П уменьшится в 2 раза, таким образом, период будет равен П. Обратите , функции tg, ctg в любой степени периодичны П.

Если вам дано уравнение, содержащее или частное двух тригонометрических функций, сначала найдите период для каждой из них отдельно. Затем найдите минимальное число, которое умещало бы в себе целое количество обоих . Например, дана функция у=tgx*cos5x. Для тангенса период П, для косинуса 5х – период 2П/5. Минимальное число, в которое можно уместить оба этих периода, это 2П, таким образом, искомый период – 2П.

Если вы затрудняетесь действовать предложенным образом или сомневаетесь в ответе, попытайтесь действовать по определению. Возьмите в качестве периода функции Т, он больше нуля. Подставьте в уравнение вместо х выражение (х+Т) и решите полученное равенство, как если бы Т было параметром или числом. В результате вы найдете значение тригонометрической функции и сможете подобрать минимальный период. Например, в результате упрощения у вас получилось тождество sin (Т/2)=0. Минимальное значение Т, при котором оно выполняется, 2П, это и будет задачи.

Источники:

• период sin

Периодической функцией называется функция, повторяющая свои значения через какой-то ненулевой период. Периодом функции называется число, при добавление которого к аргументу функции значение функции не меняется.

Вам понадобится

• Знания по элементарной математике и началам анализа.

Инструкция

Видео по теме

Обратите внимание

Все тригонометрические функции являются периодическими, а все полиномиальные со степенью больше 2 — апериодическими.

Полезный совет

Периодом функции, состоящей из двух периодический функций, является Наименьшее общее кратное периодов этих функций.

Тригонометрические уравнения — это уравнения, которые содержат в себе функции неизвестного аргумента (для примера: 5sinx-3cosx =7). Чтобы научиться решать их — нужно знать некоторые для этого методы.

Инструкция

Разложение уравнения на множители. Сначала переносим все члены влево и раскладываем на множители.

Важно помнить, что о четности и нечетности функции имеет прямую с областью определения функции. Если, например, четная либо нечетная функция не при х=5, то она не существует и при х=-5, чего нельзя сказать про функцию общего вида. При установлении четности и нечетности обращайте внимание на область определения функции.

Исследование функции на четность и нечетность коррелирует с нахождением множества значений функции. Для нахождения множества значений четной функции достаточно рассмотреть половину функции, правее либо левее нуля. Если при x>0 четная функция y(x) принимает от А до В, то те же значения она будет и при xДля нахождения множества значений, принимаемых нечетной функцией, тоже достаточно рассмотреть только одну функции. Если при x>0 нечетная функция y(x) принимает диапазон значений от А до В, то при x

«Тригонометрическими» когда-то стали называть функции, которые определяются зависимостью острых углов в прямоугольном треугольнике от длин его сторон. К таким функциям относят в первую очередь синус и косинус, во вторую — обратные этим функциям секанс и косеканс, производные от них тангенс и котангенс, а также обратные функции арксинус, арккосинус и др. Правильнее говорить не о «решении» таких функций, а об их «вычислении», то есть о нахождении численного значения.

Инструкция

Если аргумент тригонометрической неизвестен, то вычислить ее значение можно косвенным способом исходя из определений этих функций. Для этого требуется знать длины сторон треугольника, тригонометрическую для одного из углов которого требуется вычислить. Например, синус острого угла в прямоугольном треугольнике — это отношение длины противолежащего этому углу катета к длине гипотенузы. Из этого вытекает, что для угла достаточно знать длины этих двух сторон. Аналогичное гласит, что синусом острого угла является отношение длины прилежащего к этому углу катета к длине гипотенузы. Тангенс острого угла можно вычислить, разделив длину противолежащего ему катета на длину прилежащего, а требует деления длины прилежащего катета к длине противолежащего. Для вычисления секанса острого угла надо найти отношение длины гипотенузы к длине прилежащего к нужному углу катета, а косеканс определяется отношением длины гипотенузы к длине противолежащего катета.

Если же аргумент тригонометрической функции известен, то знать длины сторон треугольника не требуется — можно воспользоваться таблицами значений или калькуляторами тригонометрических функций. Такой есть среди стандартных программ операционной системы Windows. Для его запуска можно нажать сочетание клавиш Win + R, ввести команду calc и щелкнуть кнопку «OK». В интерфейсе программы следует раскрыть раздел «Вид» и пункт «Инженерный» или «Научный». После этого можно вводить аргумент тригонометрической функции. Для вычисления функций синус, косинус и достаточно после ввода значения щелкнуть по соответствующей кнопке интерфейса (sin, cos, tg), а для нахождения обратных им арксинуса, арккосинуса и следует предварительно поставить отметку в чекбоксе Inv.

Есть и альтернативные способы. Один из них — перейти на сайт поисковой системы Nigma или Google и ввести в качестве поискового запроса нужную функцию и ее аргумент (например, sin 0. 47). Эти поисковики имеют встроенные калькуляторы, поэтому после отправки такого запроса вы получите значение введенной вами тригонометрической функции.

Видео по теме

Тригонометрические функции вначале возникли как инструменты абстрактных математических вычислений зависимостей величин острых углов в прямоугольном треугольнике от длин его сторон. Сейчас они очень широко применяются как в научных, так и в технических областях человеческой деятельности. Для практических вычислений тригонометрических функций от заданных аргументов можно использовать разные инструменты — ниже описано несколько наиболее доступных из них.

Инструкция

Воспользуйтесь, например, устанавливаемой по умолчанию вместе с операционной системой программой-калькулятором. Она открывается выбором пункта «Калькулятор» в папке «Служебные» из подраздела «Стандартные», помещенного в раздел «Все программы». Этот раздел можно , открыв щелчком по кнопке «Пуск» главное меню операционной . Если вы используете версию Windows 7, то имеете возможность просто ввести «Калькулятор» в поле «Найти программы и файлы» главного меню, а затем щелкнуть по соответствующей ссылке в результатах поиска.

Введите угла, для которого надо рассчитать тригонометрическую функцию, а потом кликните по соответствующей этой кнопке — sin, cos или tan. Если вас интересуют обратные тригонометрические функции (арксинус, арккосинус или ), то сначала кликните кнопку с надписью Inv — она меняет присвоенные управляющим кнопкам функции на противоположные.

В более ранних версиях ОС (например, Windows XP) для доступа к тригонометрическим функциям надо раскрыть в меню калькулятора раздел «Вид» и выбрать строку «Инженерный». Кроме того, вместо кнопки Inv в интерфейсе старых версий программы присутствует чекбокс с же надписью.

Можно и без калькулятора, если у вас есть доступ в интернет. В сети много сервисов, которые предлагают по-разному организованные вычислители тригонометрических функций. Один их наиболее удобных встроен в поисковую систему Nigma. Перейдя на ее главную страницу, просто введите в поле поискового запроса интересующее вас значение — например, «арктангенс 30 ». После нажатия кнопки «Найти!» поисковик рассчитает и покажет результат вычисления — 0,482347907101025.

Видео по теме

Тригонометрия – раздел математики для изучения , выражающих различные зависимости сторон прямоугольного треугольника от величин острых углов при гипотенузе. Такие функции получили называние тригонометрических, а для упрощения работы с ними были выведены тригонометрические тождества .

Понятие тождества в означает равенство, которое выполняется при любых значениях аргументов входящих в него функций. Тригонометрические тождества – это равенства тригонометрических функций, доказанные и принятые для облегчения работы с тригонометрическими формулами.Тригонометрическая функция – это элементарная функция зависимости одного из катетов прямоугольного треугольника от величины острого угла при гипотенузе. Чаще всего используются шесть основных тригонометрических функций: sin (синус), cos (косинус), tg (тангенс), ctg (котангенс), sec (секанс) и cosec (косеканс). Эти функции называются прямыми, существуют также

Задание 1: Изучение синусоидальных кривых

Задание 1: Изучение синусоидальных кривых

Задание 1: Изучение синусоидальных кривых

Кристина Данбар, UGA

В этом задании мы будем исследуя график уравнения

с использованием разных значений a, b, и с.

 

 

В приведенном выше уравнении

• а это амплитуда синусоиды
• б есть период синусоиды
• с есть фаза сдвиг синусоиды

 

Что такое амплитуда синусоиды?

Амплитуда синусоиды равна ее высоте.

 

Что такое период синусоида?

Период синусоиды равен длине одного цикла кривой. Естественный период синуса кривая 2π. Итак, коэффициент b =1 эквивалентен периоду 2π. Чтобы получить период синусоиды для любого коэффициента b , просто разделите 2π на коэффициент b , чтобы получить новый период кривой.

Коэффициент b и период синусоиды имеют обратную зависимость, так как б получает меньше, длина одного цикла кривой становится больше.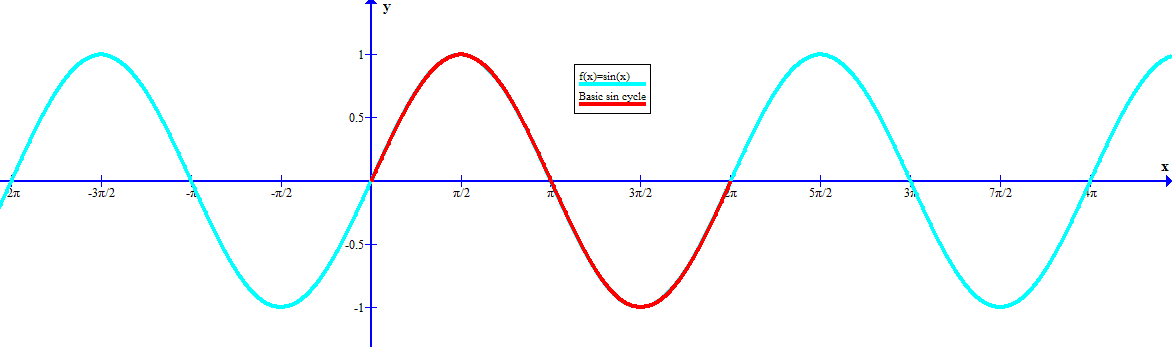 Точно так же, как вы увеличиваете b , период уменьшится.

 

Что такое фазовый сдвиг синусоида?

Фазовый сдвиг синусоидальной кривой, насколько кривая смещается от нуля. Если фазовый сдвиг равен нулю, кривая начинается в начале координат, но может двигаться влево или вправо в зависимости от фазового сдвига. Отрицательный фазовый сдвиг указывает движение вправо, а положительный фазовый сдвиг указывает на движение влево.

 

 

Давайте посмотрим на график y = sin x.

Глядя на график, помните, что числовое значение π составляет приблизительно 3,1416, поэтому 2π составляет приблизительно 6,2832.

 

На графике выше

• Амплитуда a равна 1. Это означает, что высота графика будет равна 1, а вершина первого «горб» 1.

• Период b имеет коэффициент 1, поэтому период равен (2π)/1 или просто 2π.

• Фазовый сдвиг c составляет ноль, поэтому кривая начинается в начале координат.

 

Вернуться на мою домашнюю страницу.

 

Давайте рассмотрим синусоиду с разными амплитуды.

Мы уже видели случай, когда амплитуда равна 1; это на графике выше. Как насчет других амплитуды?

 

у = 2 sin x

 

 

у = 5 sin x

 

у = -1 sin x

Чем отличается приведенный выше график? Это имеет коэффициент а = -1. Что это значит? Мы видим, что самая высокая точка кривой по-прежнему равна 1, но первый выступ равен -1 вместо 1. По сути, мы перевернули график.

 

Теперь давайте посмотрим на несколько различных синусоидальных графиков. вместе.

   

 

Вернуться на мою домашнюю страницу.

 

Давайте рассмотрим синусоиду с разными периоды.

Мы уже видели случай, когда коэффициент b равен 1; это на графике выше. Как насчет другие периоды?

Помните, б коэффициент и период кривой находятся в обратной зависимости.

 

у = грех (2x)

Коэффициент b на приведенном выше графике равен 2, поэтому период синусоиды изменился в 1/2 раза, в результате чего новый период π, или около 3,14.

 

 

у = sin (0,5x)

Для приведенного выше графика коэффициент b = 1/2, так что период синусоиды будет в два раза больше, чем обычно, или 4π.

 

 

у = грех (3x)

Обратите внимание, что новый период составляет 1/3 от исходного период, равный 2π/3, что составляет примерно 2.09.    

Теперь давайте рассмотрим несколько различных синусоидальных графики вместе, с разными периодами.

 

Вернуться на мою домашнюю страницу.

 

Рассмотрим синусоиду с фазой сдвиг.

Обычно синусоида не имеет фазы сдвига, поэтому переменная c равна 0. Это означает, что синусоида начинается с источник, как показано на первом графике в верхней части этой страницы.

Что делать, если с не равно нулю?

 

у = грех (х + п)  

На приведенном выше графике y = sin (x + π) , график был сдвинут на единицу π слева.

 

На самом деле положительный фазовый сдвиг c фактически указывает на сдвиг влево. давайте посмотрим на некоторые другие примеры:

 

 

у = грех (х + 1)

Синусоида сместилась на одну единицу в левый.

 

 

у = грех (х + π/2)

Кривая сместилась на π/2 единицы влево. Напомним, что π/2 примерно равно 1,57.

 

Что делать, если переменная c отрицательный?

у = грех (х — 1)

Кривая сместилась на 1 единицу вправо.

 

у = грех (х — №/2)

 

Давайте вместе посмотрим на несколько фазовых сдвигов:

 

 

Примечание:   Фазовый сдвиг π будет выглядеть точно так же, как фазовый сдвиг -π.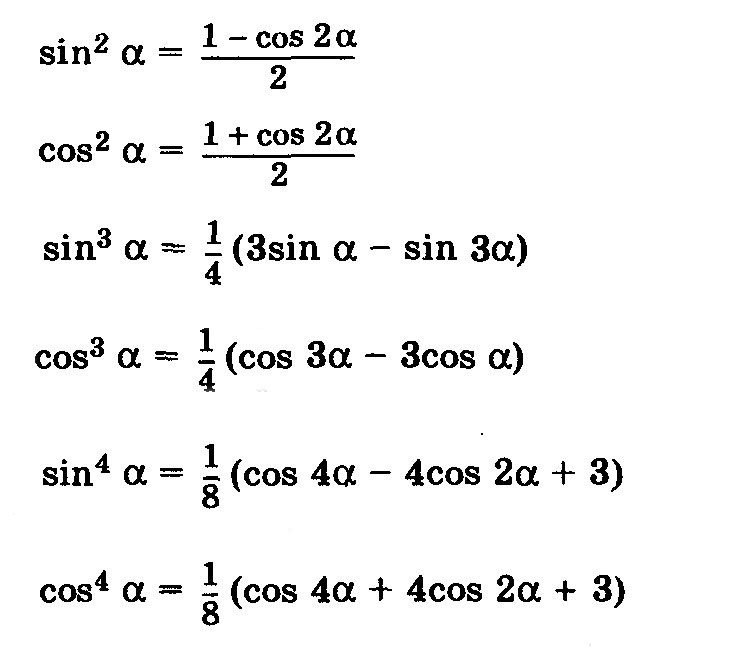

у = грех (х + π)

у = грех (х — π)

Вернуться на мою домашнюю страницу.

В приведенных выше упражнениях мы изучили, что происходит с синусоидой, когда мы варьируем коэффициенты a, b и c индивидуально. Что делать, если вы изменили более одного за раз?

у = 2 sin (2x)

а = 2    б=2 с=0

Амплитуда равна 2, а период равен 2π/2, или π. Фазового сдвига нет.

 

 

у = 2 sin (2x -1)

а = 2    б = 2 с = -1

Амплитуда равна 2, а период равен 2π/2, или π. Вся кривая сдвинута на одну единицу вправо.

 

 

у = 3 sin (2x + 2)

а = 3    б = 2 с = 2

Амплитуда равна 3, как и следовало ожидать. период графика равен 2π/2, или π. Мы ожидали, что фазовый сдвиг будет на две единицы влево, но мы видим, что Это не относится к делу. Почему? Поскольку фазовый сдвиг связан с Период. Период графика равен 1/2 его первоначального размера, а поэтому фазовый сдвиг также будет равен 1/2 коэффициента c или 1. Это показано на графике выше.

 

у = 0,5 sin (0,5x -3)

а = 0,5    б = 0,5 с = -3

Амплитуда 0,5, что мы ясно видим в график. Коэффициент b равен 0,5, поэтому период синусоиды вдвое больше. как обычно, или 4π (примерно 12,57). Так как период кривой в два раза больше, чем обычно фазовый сдвиг будет в два раза больше коэффициента с, или на 6 единиц к верно.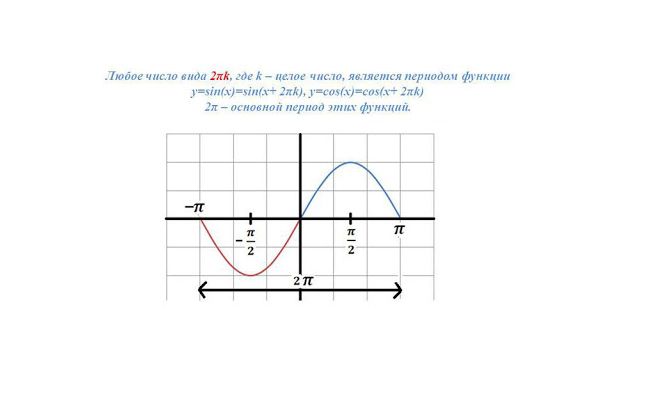

Вернуться на мою домашнюю страницу.

 

Хотите решить несколько практических задач? Кликните сюда.

 

Найти период функции синуса или косинуса

Все ресурсы для предварительного исчисления

12 диагностических тестов 380 практических тестов Вопрос дня Карточки Learn by Concept

Precalculus Помощь » Графики и обратные тригонометрические функции » График функций синуса и косинуса » Найдите период функции синуса или косинуса

Дано, каков период действия функции?

Возможные ответы:

Правильный ответ:

Объяснение:

Формула для периода функции синуса/косинуса .

В стандартной форме:

Так как , формула принимает вид .

Упрощенный, период .

Сообщить об ошибке

Каков период этого графика?

Возможные ответы:

Правильный ответ:

Объяснение:

Одна волна графика проходит точно от 0 до до повторения. Это означает, что период .

Сообщить об ошибке

Пожалуйста, выберите лучший ответ из следующих вариантов.

 

Найдите период следующей функции в радианах:

Возможные ответы:

Правильный ответ:

Объяснение:

Если вы посмотрите на график, то увидите, что период (длина одной волны) равен . Без графика вы можете разделить на частоту, которая в данном случае равна 1.

Сообщить об ошибке

Пожалуйста, выберите лучший ответ из следующих вариантов.

 

Найдите период следующей функции.

Возможные ответы:

Правильный ответ:

Объяснение:

Период определяется как длина одной волны функции. В этом случае одна полная волна составляет 180 градусов или радиан. Вы можете понять это, не глядя на график, разделив на частоту, которая в данном случае равна 2.

Сообщить об ошибке

Каков период этого синусоидального графика?

Возможные ответы:

Правильный ответ:

Объяснение:

На графике есть 3 волны между 0 и , что означает, что длина каждой из волн делится на 3, или .

Сообщить об ошибке

Напишите уравнение косинуса с минимумом в  и максимумом в .

Возможные ответы:

Правильный ответ:

Объяснение:

Уравнение для этого графика будет иметь вид, где A — амплитуда, f — частота, h — сдвиг по горизонтали, а k — сдвиг по вертикали.

Чтобы написать это уравнение, полезно начертить график:

Нарисовав максимум и минимум, мы можем видеть, что график находится в центре и имеет амплитуду 2.

Расстояние между максимумом а минимум составляет половину длины волны. Вот . Это означает, что полная длина волны равна , поэтому частота равна 1.

Минимум находится в середине графика, поэтому, чтобы выяснить, где он начинается, вычтите из координаты x минимума:

Уравнение этого графика:

.

Сообщить об ошибке

Задайте период и частоту для уравнения.

Возможные ответы:

Период: , Частота:

Период: , Частота:

Период: , Частота:

Период: , Частота:

Период: , Частота: 

Правильный ответ:

Период: , Частота:

Объяснение:

Наше уравнение имеет вид  

, где A – амплитуда, f – частота, h – сдвиг по горизонтали, а k – сдвиг по вертикали.

Мы можем посмотреть на уравнение и увидеть, что частота , равна .

Период , поэтому в данном случае .

Сообщить об ошибке

Каков период графика?

Возможные ответы:

Правильный ответ:

Объяснение:

Уравнение для этой функции имеет вид  

, где A – амплитуда, f – частота, h – сдвиг по горизонтали, а k – сдвиг по вертикали.

Глядя на уравнение, мы видим, что частота , равна .

Период , поэтому в данном случае .

Сообщить об ошибке

Какую функцию может выполнять следующий график?

Возможные ответы:

Правильный ответ:

Объяснение:

Какой может быть функция для следующего графика?

Для начала поймите, что мы имеем дело с периодической функцией, поэтому синус и косинус — лучший выбор.

Далее обратите внимание, что диапазон функции и что функция проходит через точку .

Из этой информации мы можем найти амплитуду:

Таким образом, наша функция должна иметь выход впереди.

Кроме того, из точки мы можем сделать вывод, что функция имеет вертикальный сдвиг положительной двойки.

Единственным оставшимся препятствием является то, является ли функция синусоидальной или косинусоидальной.