Период у синуса: Тригонометрия, тригонометрические функции, синус, косинус, тангенс, котангенс

alexxlab / / Разное

Mathway | Популярные задачи

1Найти точное значениеsin(30)
2Найти точное значениеsin(45)
3Найти точное значениеsin(30 град. )
4Найти точное значениеsin(60 град. )
5Найти точное значениеtan(30 град. )
6Найти точное значениеarcsin(-1)
7Найти точное значениеsin(pi/6)
8
Найти точное значение		cos(pi/4)
9Найти точное значениеsin(45 град. )
10Найти точное значениеsin(pi/3)
11Найти точное значениеarctan(-1)
12Найти точное значениеcos(45 град. )
13Найти точное значениеcos(30 град. )
14Найти точное значениеtan(60)
15
Найти точное значение		csc(45 град. )
16Найти точное значениеtan(60 град. )
17Найти точное значениеsec(30 град. )
18Найти точное значениеcos(60 град. )
19Найти точное значениеcos(150)
20Найти точное значениеsin(60)
21Найти точное значениеcos(pi/2)
22Найти точное значениеtan(45 град. )
23Найти точное значениеarctan(- квадратный корень из 3)
24Найти точное значениеcsc(60 град. )
25Найти точное значениеsec(45 град. )
26Найти точное значениеcsc(30 град. )
27Найти точное значениеsin(0)
28Найти точное значениеsin(120)
29Найти точное значениеcos(90)
30Преобразовать из радианов в градусыpi/3
31Найти точное значениеtan(30)
32Преобразовать из градусов в радианы45
33Найти точное значениеcos(45)
34Упроститьsin(theta)^2+cos(theta)^2
35Преобразовать из радианов в градусыpi/6
36Найти точное значениеcot(30 град. )
37Найти точное значениеarccos(-1)
38Найти точное значениеarctan(0)
39Найти точное значениеcot(60 град. )
40Преобразовать из градусов в радианы30
41Преобразовать из радианов в градусы(2pi)/3
42Найти точное значениеsin((5pi)/3)
43Найти точное значениеsin((3pi)/4)
44Найти точное значениеtan(pi/2)
45Найти точное значениеsin(300)
46Найти точное значениеcos(30)
47Найти точное значениеcos(60)
48Найти точное значениеcos(0)
49Найти точное значениеcos(135)
50Найти точное значениеcos((5pi)/3)
51Найти точное значениеcos(210)
52Найти точное значениеsec(60 град. )
53Найти точное значениеsin(300 град. )
54Преобразовать из градусов в радианы135
55Преобразовать из градусов в радианы150
56Преобразовать из радианов в градусы(5pi)/6
57Преобразовать из радианов в градусы(5pi)/3
58Преобразовать из градусов в радианы89 град.
59Преобразовать из градусов в радианы60
60Найти точное значениеsin(135 град. )
61Найти точное значениеsin(150)
62Найти точное значениеsin(240 град. )
63Найти точное значениеcot(45 град. )
64Преобразовать из радианов в градусы(5pi)/4
65Найти точное значениеsin(225)
66Найти точное значениеsin(240)
67Найти точное значениеcos(150 град. )
68Найти точное значениеtan(45)
69Вычислитьsin(30 град. )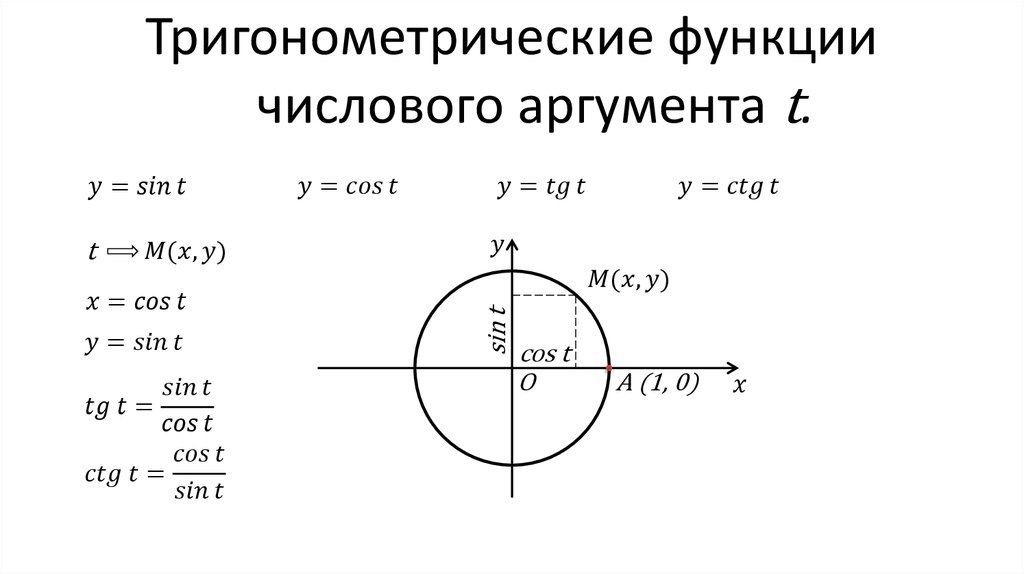
70Найти точное значениеsec(0)
71Найти точное значениеcos((5pi)/6)
72Найти точное значениеcsc(30)
73Найти точное значениеarcsin(( квадратный корень из 2)/2)
74Найти точное значениеtan((5pi)/3)
75Найти точное значениеtan(0)
76Вычислитьsin(60 град. )
77Найти точное значениеarctan(-( квадратный корень из 3)/3)
78Преобразовать из радианов в градусы(3pi)/4
79Найти точное значениеsin((7pi)/4)
80Найти точное значениеarcsin(-1/2)
81Найти точное значениеsin((4pi)/3)
82Найти точное значениеcsc(45)
83Упроститьarctan( квадратный корень из 3)
84Найти точное значениеsin(135)
85Найти точное значениеsin(105)
86Найти точное значениеsin(150 град. )
87Найти точное значение
sin((2pi)/3)
88Найти точное значениеtan((2pi)/3)
89Преобразовать из радианов в градусыpi/4
90Найти точное значениеsin(pi/2)
91Найти точное значениеsec(45)
92Найти точное значениеcos((5pi)/4)
93Найти точное значениеcos((7pi)/6)
94Найти точное значениеarcsin(0)
95Найти точное значениеsin(120 град. )
96Найти точное значениеtan((7pi)/6)
97Найти точное значениеcos(270)
98Найти точное значениеsin((7pi)/6)
99Найти точное значениеarcsin(-( квадратный корень из 2)/2)
100Преобразовать из градусов в радианы88 град.

Простейшие формулы

удовлетворяющих системе неравенств:

sin t > 0,

0 6 t 6 4π.

б) Рассмотрим множество чисел на числовой оси, удовлетворяющих системе неравенств:

sin x 6 0,

0 6 x 6 20π.

Найдите сумму длин отрезков, из которых состоит это множество.

В § 3 мы установили для острых углов α такую формулу:

 

 

 

sin2 α + cos2 α = 1.

 

 

 

 

 

 

 

Эта же формула

верна

и

в случае,

 

 

когда α — любое

число. В

самом де-

 

 

 

 

 

 

 

ле, пусть M — точка на тригонометри-

 

 

 

ческой окружности, соответствующая

 

 

числу α (рис. 7.1). Тогда

M имеет ко-

 

 

 

 

 

 

 

 

ординаты x = cos α, y

=

sin α. Од-

 

 

 

 

нако всякая точка (x; y), лежащая на

 

 

 

 

окружности единичного радиуса с цен-

 

 

 

 

тром в начале координат, удовлетво-

 

 

 

 

 

Рис. 7.1.

 

ряет уравнению x2 + y2

= 1, откуда

 

 

cos2 α + sin2 α = 1, что и требовалось.

Итак, формула cos2 α + sin2 α = 1 вытекает из уравнения окружности. Может показаться, что тем самым для острых углов мы дали новое доказательство этой формулы (по сравнению с указанным в § 3, где мы пользовались теоремой Пифагора). Отличие, однако, чисто внешнее: при выводе уравнения окружности x2 + y2 = 1 используется та же теорема Пифагора.

32

Для острых углов мы получали и другие формулы, напри-

мер cos α = 1/

1 + tg2 α. Для произвольных углов эта формула

в таком виде

верна быть не может: согласно общепринятому по-

 

p

√

ниманию символа , правая часть всегда неотрицательна, в то время как левая часть вполне может быть и отрицательной. Чтобы формула была верна при всех α, надо ее возвести в квадрат. Получится равенство: cos2 α = 1/(1 + tg2 α). Докажем, что эта формула верна при всех α:1

1/(1 + tg2

α) = 1

1 +

sin2 α

 

=

cos2 α

= cos2 α.

cos2 α

sin2 α + cos2 α

Задача 7.1. Выведите все формулы, приведенные ниже, из определений и формулы sin2 α + cos2 α = 1 (некоторые из них мы уже доказали):

sin2 α + cos2 α = 1;

tg2 α =

sin α

;

 

ctg α =

cos α

;

 

 

 

 

sin α

 

 

 

 

 

 

 

 

 

 

cos α

 

 

 

 

 

 

1

 

 

 

 

 

 

tg2 α

 

 

 

 

1

+ tg2

α =

 

 

;

sin2 α =

 

 

 

;

tg α · ctg α = 1;

cos2 α

1 + tg2 α

 

 

 

1

 

 

 

 

 

 

ctg2 α

 

 

 

 

1

+ ctg2

α =

 

 

;

cos2 α =

 

 

.

 

 

 

 

1 + ctg2 α

 

 

 

 

 

 

sin2

α

 

 

 

 

 

 

Эти формулы позволяют, зная значение одной из тригонометрических функций данного числа, почти найти все осталь-

ные. Пусть, например, мы знаем, что sin x = 1/2. Тогда cos2 x =

√ √

= 1−sin2 x = 3/4, так что cos x равен или 3/2, или − 3/2. Чтобы узнать, какому именно из этих двух чисел равен cos x, нужна дополнительная информация.

Задача 7.2. Покажите на примерах, что оба вышеуказанных случая возможны.

Задача 7.3. а) Пусть tg x = −1. Найдите sin x. Сколько ответов у этой задачи?

б) Пусть в дополнение к условиям пункта а) нам известно, что sin x < 0. Сколько теперь ответов у задачи?

1Для которых tg α определен, т. е. cos α 6= 0.

33

Задача 7.4. Пусть sin x = 3/5, x [π/2; 3π/2]. Найдите tg x.

Задача 7.5. Пусть tg x = 3, cos x > sin x. Найдите cos x, sin x.

Задача 7.6. Пусть tg x = 3/5. Найдите sin x + 2 cos x. cos x − 3 sin x

Задача 7.7. Докажите тождества:

а)

tg α + ctg β

=

tg α

;

б)

tg α sin α

=

 

tg α − sin α

;

ctg α + tg β

tg β

tg α + sin α

 

tg α sin α

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

1

 

 

в) sin α + cos α ctg α + sin α tg α + cos α =

 

+

 

.

 

sin α

cos α

 

Задача 7.8. Упростите выражения:

а) (sin α + cos α)2 + (sin α − cos α)2; б) (tg α + ctg α)2 + (tg α − ctg α)2;

в) sin α(2 + ctg α)(2 ctg α + 1) − 5 cos α.

Числам x, x+2π, x−2π соответствует одна и та же точка на тригонометрической окружности (если пройти по тригонометрической окружности лишний круг, то придешь туда, где был). Отсюда вытекают такие тождества, о которых уже шла речь в § 5:

sin(x + 2π) = sin(x − 2π) = sin x; cos(x + 2π) = cos(x − 2π) = cos x.

В связи с этими тождествами мы уже употребляли термин «период». Дадим теперь точные определения.

Определение. Число T 6= 0 называют периодом функции f, если для всех x верны равенства f(x − T ) = f(x + T ) = f(x) (подразумевается, что x + T и x − T входят в область определения функции, если в нее входит x). Функцию называют периодической, если она имеет период (хотя бы один).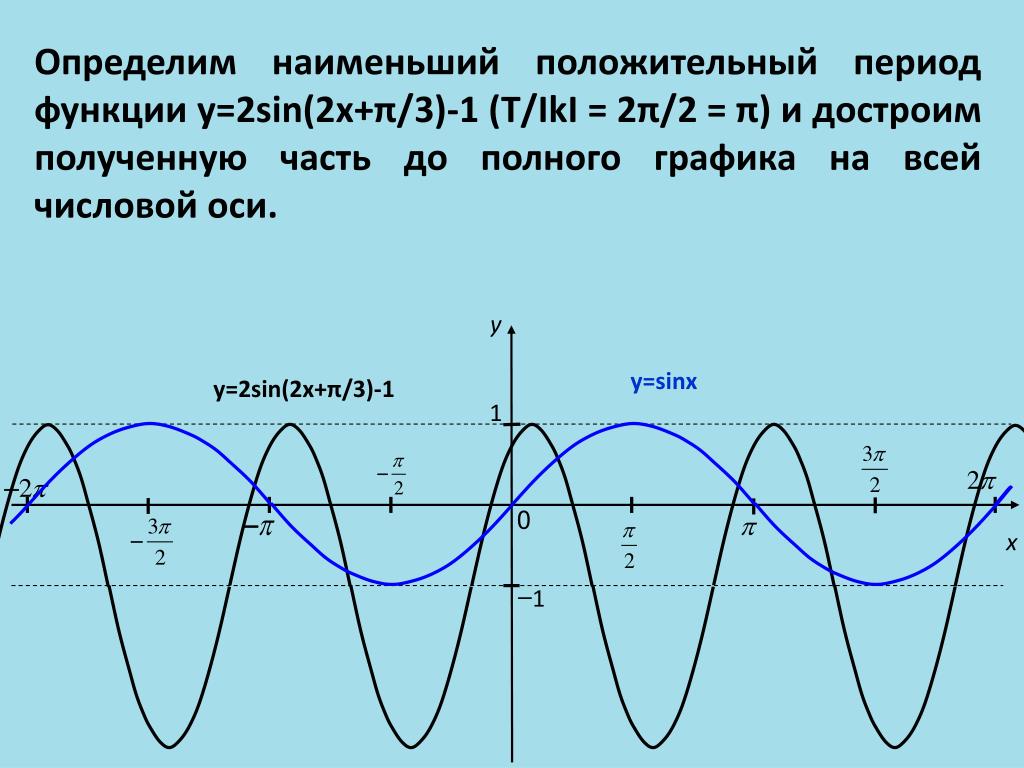

34

Периодические функции естественно возникают при описании колебательных процессов. Об одном из таких процессов речь уже шла в § 5. Вот еще примеры:

1)Пусть ϕ = ϕ(t) — угол отклонения качающегося маятника часов от вертикали в момент t. Тогда ϕ — периодическая функция от t.

2)Напряжение («разность потенциалов», как сказал бы физик) между двумя гнездами розетки в сети переменного тока, ес-

ли его рассматривать как функцию от времени, является периодической функцией1.

3)Пусть мы слышим музыкальный звук. Тогда давление воздуха в данной точке — периодическая функция от времени.

Если функция имеет период T , то периодами этой функции будут и числа −T , 2T , −2T . . . — одним словом, все числа nT , где n — целое число, не равное нулю. В самом деле, проверим, например, что f(x + 2T ) = f(x):

f(x + 2T ) = f((x + T ) + T ) = f(x + T ) = f(x).

Определение. Наименьшим положительным периодом функции f называется — в соответствии с буквальным смыслом слов — такое положительное число T , что T — период f и ни одно положительное число, меньшее T , периодом f уже не является.

Периодическая функция не обязана иметь наименьший положительный период (например, функция, являющаяся постоянной, имеет периодом вообще любое число и, стало быть, наименьшего положительного периода у нее нет). Можно привести примеры и непостоянных периодических функций, не имеющих наименьшего положительного периода. Тем не менее в большинстве интересных случаев наименьший положительный период у периодических функций существует.

1Когда говорят «напряжение в сети 220 вольт», имеют в виду его «среднеквадратичное значение», о котором мы будем говорить в § 21. Само же напряжение все время меняется.

35

Рис. 8.1. Период тангенса и котангенса.

В частности, наименьший положительный период как синуса, так и косинуса равен 2π. Докажем это, например, для функции y = sin x. Пусть вопреки тому, что мы утверждаем, у синуса есть такой период T , что 0 < T < 2π. При x = π/2 имеем sin x = = 1. Будем теперь увеличивать x. В точке x + T значение синуса должно быть также равно 1. Но в следующий раз синус будет равен 1 только при x = (π/2) + 2π. Поэтому период синуса быть меньше 2π не может. Доказательство для косинуса аналогично.

Наименьший положительный период функции, описывающей колебания (как в наших примерах 1–3), называется просто периодом этих колебаний.

Поскольку число 2π является периодом синуса и косинуса, оно будет также периодом тангенса и котангенса. Однако для этих функций 2π — не наименьший период: наименьшим положительным периодом тангенса и котангенса будет π. В самом деле, точки, соответствующие числам x и x + π на тригонометрической окружности, диаметрально противоположны: от точки x до точки x + 2π надо пройти расстояние π, в точности равное половине окружности. Теперь, если воспользоваться определением тангенса и котангенса с помощью осей тангенсов и котангенсов, равенства tg(x + π) = tg x и ctg(x + π) = ctg x станут очевидными (рис. 8.1). Легко проверить (мы предложим это сделать в задачах), что π — действительно наименьший положительный период тангенса и котангенса.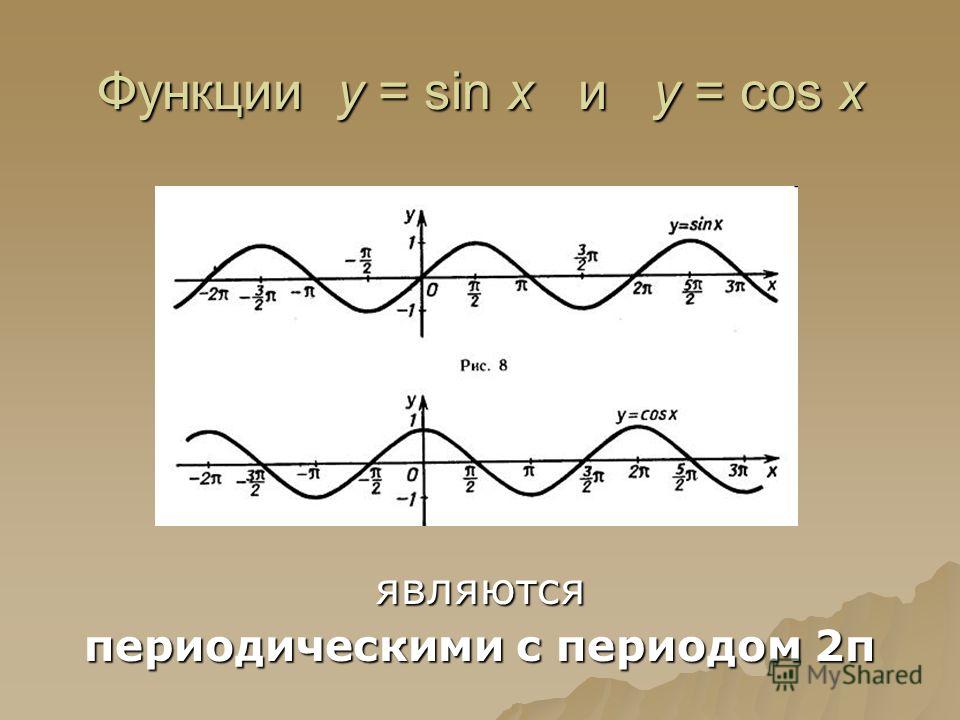

36

Одно замечание по поводу терминологии. Часто слова «период функции» употребляют в значении «наименьший положительный период». Так что если на экзамене у вас спросят: «Является ли 100π периодом функции синус?», не торопитесь с ответом, а уточните, имеется в виду наименьший положительный период или просто один из периодов.

Тригонометрические функции — типичный пример периодических функций: любую «не очень плохую» периодическую функцию можно в некотором смысле выразить через тригонометрические.

Задача 8.1. Найдите наименьшие положительные периоды функций:

а) y = sin 3x;

б) y = cos

x

;

в) y = cos πx;

2

г) y = cos x + cos(1,01x).

Задача 8.2. Зависимость напряжения в сети переменного тока от времени задается формулой U = U0 sin ωt (здесь t — время, U — напряжение, U0 и ω — постоянные величины). Частота переменного тока — 50 Герц (это означает, что напряжение совершает 50 колебаний в секунду).

а) Найдите ω, считая, что t измеряется в секундах;

б) Найдите (наименьший положительный) период U как функции от t.

Задача 8.3. а) Докажите, что наименьший положительный период косинуса равен 2π;

б) Докажите, что наименьший положительный период тангенса равен π.

Задача 8.4. Пусть наименьший положительный период функции f равен T . Докажите, что все остальные ее периоды имеют вид nT для некоторых целых чисел n.

Задача 8.5. Докажите, что следующие функции не являются периодическими:

37

Симптомы, причины, продолжительность и лечение. Синусы — это полые пространства в костях между глазами, за скулами и во лбу. Они производят слизь, которая увлажняет внутреннюю часть носа. Это, в свою очередь, помогает защитить от пыли, аллергенов и загрязняющих веществ.

Здоровые носовые пазухи заполнены воздухом. Но когда они блокируются и наполняются жидкостью, микробы могут расти и вызывать инфекцию.

Состояния, которые могут вызвать закупорку носовых пазух, включают:

  • Обычную простуду
  • Аллергический ринит, который представляет собой отек слизистой оболочки носа, вызванный аллергенами
  • Небольшие образования на слизистой оболочке носа, называемые носовыми полипами перегородка, представляющая собой сдвиг в полость носа

Типы

Вы можете услышать, как ваш врач использует следующие термины:

  • Острый синусит обычно начинается с симптомов простуды, таких как насморк, заложенность носа и боль в лице. Это может начаться внезапно и длиться от 2 до 4 недель.
  • Подострый синусит обычно длится от 4 до 12 недель.
  • Симптомы хронического синусита длятся 12 недель или дольше.
  • Рецидивирующий синусит бывает несколько раз в год.

Кто это получит?

Много людей. Около 35 миллионов американцев болеют синуситом не реже одного раза в год. Это более вероятно, если у вас есть:

  • Отек внутри носа, как при простуде
  • Блокировка дренажных протоков
  • Структурные различия, которые сужают эти протоки вызвать синусит включают:

    • Аллергии
    • Болезни от других детей в детском саду или школе
    • Пустышки
    • Питье из бутылочки лежа на спине
    • Дым в окружающей среде

    Основными причинами синусита у взрослых являются инфекции и курение.

    Acute Sinusitis Symptoms

    The main signs include:

    • Facial pain or pressure
    • «Stuffed-up» nose
    • Runny nose
    • Loss of smell
    • Cough or congestion

    You may also have:

    • Лихорадка
    • Неприятный запах изо рта
    • Усталость
    • Зубная боль

    Это может быть острый синусит, если у вас есть два или более симптомов или густые, зеленые или желтые выделения из носа.

    Симптомы хронического синусита

    Следующие симптомы могут наблюдаться в течение 12 недель и более:

    • Ощущение заложенности или распирания лица
    • Заложенность носа или заложенность носа
    • Гной в полости носа
      • Лихорадка Насморк или изменение цвета постназального отделяемого

    У вас также могут быть головные боли, неприятный запах изо рта и зубная боль. Вы можете чувствовать сильную усталость.

    Многие вещи могут вызывать подобные симптомы. Вам нужно обратиться к врачу, чтобы узнать, есть ли у вас синусит.

    Лечение

    Если у вас простая инфекция носовых пазух, врач может порекомендовать вам использовать противоотечное средство и солевой раствор для промывания носа. Однако вам не следует использовать безрецептурные противозастойные средства более 3 дней, потому что это может сделать вас более застойными.

    Вы можете попробовать другой безрецептурный вариант — биоэлектрическое устройство, излучающее волны микротоков. Устройство размещается на лице и излучает безболезненные вибрации, чтобы устранить заложенность носовых пазух.

    Если ваш врач пропишет вам антибиотики, вы, вероятно, будете принимать их в течение 10–14 дней. Симптомы обычно исчезают при лечении.

    Теплый влажный воздух может помочь при хроническом синусите. Вы можете использовать испаритель или вдыхать пар из кастрюли с теплой водой. Убедитесь, что вода не слишком горячая.

    Есть и другие способы помочь при хроническом синусите:

    • Теплые компрессы могут облегчить боль в носу и пазухах.
    • Пейте много жидкости, чтобы разжижать слизь.
    • Капли в нос с солевым раствором безопасны для домашнего использования.
    • Могут помочь безрецептурные противозастойные капли или спреи. Не принимайте их дольше, чем рекомендуется.

    В некоторых случаях врач может назначить стероиды вместе с антибиотиками.

    Другие варианты

    Вам также необходимо избегать любых триггеров, связанных с вашим синуситом.

    Если у вас аллергия , ваш врач может порекомендовать антигистаминный препарат.

    Если виноват грибок , вам выпишут рецепт на противогрибковый препарат.

    Если у вас есть определенные иммунодефициты, ваш врач может дать вам иммуноглобулин, который помогает бороться с вещами, на которые реагирует ваш организм.

    Можно ли предотвратить синусит?

    Надежного способа предотвратить синусит не существует. Но есть вещи, которые могут помочь.

    • Не курите и избегайте курения других людей.
    • Часто мойте руки, особенно в сезон простуды и гриппа, и старайтесь не касаться лица.
    • Держитесь подальше от вещей, на которые, как вы знаете, у вас аллергия. Поговорите со своим врачом, чтобы узнать, нужны ли вам лекарства, отпускаемые по рецепту, прививки от аллергии или другие формы иммунотерапии.

    Если ваши проблемы с носовыми пазухами продолжают возвращаться, спросите своего врача о плюсах и минусах операции по очистке и дренированию носовых пазух.

    Что произойдет, если синусит не лечить?

    Вы будете испытывать боль и дискомфорт, пока не начнете проходить. В редких случаях невылеченный синусит может привести к менингиту, абсцессу головного мозга или инфекции костей. Поговорите со своим врачом о своих опасениях.

    Далее Синусит (синусовая инфекция)

    Острый и хронический синусит

    Неаллергический синусит | Кедры-Синай

    ОБ ДИАГНОЗ ЛЕЧЕНИЕ

    Обзор

    Миллионы американцев, взрослых и детей, ежегодно страдают синуситом. Синусит может быть острым (длительностью от двух до трех месяцев) или хроническим (длительностью более трех месяцев), аллергическим или неаллергическим.

    Синусы представляют собой полые полости, заполненные воздухом, находящиеся в костях за щеками, лбом и глазами. Синусы вырабатывают слизь, которая очищает воздух, которым вы дышите, от бактерий и других частиц.

    Симптомы

    Симптомы неаллергического синусита, длящиеся от нескольких часов до нескольких дней, могут включать:

    • Сильный насморк или заложенность носа
    • Прозрачная или слегка окрашенная слизь
    • Постназальное затекание при упорном кашле
    • Лицевая боль, отек и давление
    • Измененное обоняние
    • Лихорадка

    В некоторых случаях при использовании безрецептурных препаратов облегчение не наступает или симптомы ухудшаются.

    Причины и факторы риска

    Люди, чувствительные к пыли, смогу, дыму, сильным запахам и химическим веществам, могут страдать неаллергическим синуситом. Изменения температуры, а также изменения влажности и стресса также могут быть триггерами.

    Другие причины могут включать:

    Инфекции — Вирусные инфекции, такие как простуда или грипп, могут вызывать неаллергический синусит. Хотя приступ может длиться короткое время, пациенты часто испытывают постоянное постназальное затекание, обесцвеченную слизь, давление на лицо и боль.

    Гормоны — Беременность, менструация, менопауза, гипотиреоз и использование оральных контрацептивов могут вызвать неаллергическую реакцию синусита.

    Диета — Алкогольные напитки и горячая, острая пища могут вызвать приступ неаллергического синусита.

    Лекарства — Противовоспалительные препараты, такие как аспирин и ибупрофен, бета-блокаторы, седативные средства, антидепрессанты, препараты для лечения эректильной дисфункции и, во многих случаях, чрезмерное использование противозастойных назальных спреев могут вызвать неаллергический синусит

    Диагностика

    Чтобы исключить аллергический синусит, врач обычно проводит анализы крови и/или кожи. Кожные тесты измеряют реакцию человека на определенный аллерген (например, пылевых клещей, пыльцу животных и т. д.). Анализы крови измеряют реакцию иммунной системы организма на распространенные аллергены.

    Другие диагностические тесты, помогающие оценить симптомы пациента, могут включать назальную эндоскопию, процедуру, при которой гибкая трубка вводится в носовые ходы, а оптоволоконный свет позволяет врачу увидеть даже малейшую аномалию

    Кроме того, компьютерная томография (КТ) пазух может помочь врачу оценить инфекции, травмы или другие отклонения.

    Лечение

    Если симптомы легкие, пациентам могут помочь безрецептурные средства, такие как:

    • Пероральные деконгестанты
    • Назальные спреи — солевые, антигистаминные, противоотечные назальные спреи
    • Ополаскиватели для носа для защиты носа от раздражающих веществ
    • Комнатные увлажнители воздуха
    • Увеличение потребления воды, сока или напитков без кофеина
    • Мягкое и регулярное сморкание
    • Избегание известных или предполагаемых триггеров

    В дополнение к некоторым методам лечения, описанным выше, хронический неаллергический синусит можно лечить с помощью:

    Баллонной синусопластики — Подобно баллонной ангиопластике, используемой для разрушения тромбов в артериях сердца, баллонная синусопластика использует маленькие баллоны для расширения отверстия синусов.

    No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *