Периодические функции, 10 класс — презентация онлайн
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
1. Периодические функции
Алгебра и начала анализа, 10 класс(профильный уровень)
А.Г.Мордкович, П.Е.Семёнов
Учитель Волкова С.Е.
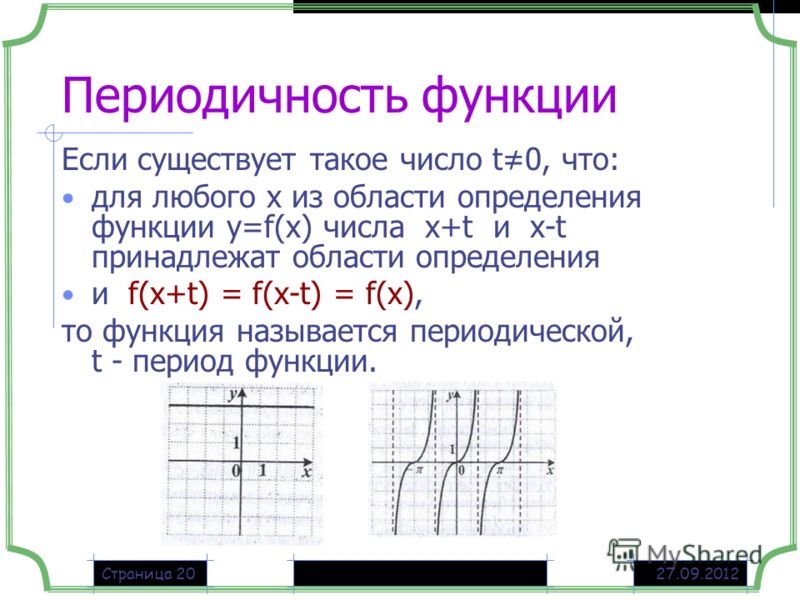
2. Определение 1
Говорят, что функцияy = f (x), x ∈ X имеет период Т, если для
любого х ∈ Х выполняется равенство
f (x – T) = f (x) = f (x + T).
Если функция с периодом Т определена в точке х,
то она определена и в точках
х + Т, х – Т.

Любая функция имеет период, равный нулю
при Т = 0 получим f(x – 0) = f(x) = f(x + 0).
3. Определение 2
Функцию, имеющую отличный от нуля периодТ, называют периодической.
Если функция y = f (x), x ∈ X имеет период Т, то
любое число, кратное Т (т.е. число вида кТ, к ∈ Z),
также является её периодом.
4. Доказательство
Пусть 2Т – период функции. Тогдаf(x) = f(x + T) = f((x + T) +T) = f(x +2T),
f(x) = f(x — T) = f((x — T) -T) = f(x — 2T).
Аналогично доказывается, что
f(x) = f(x + 3T) = f(x — 3T),
f(x) = f(x + 4T) = f(x — 4T) и т.д.
Итак, f(x — кТ) = f(x ) = f(x + кT)
5. Наименьший период среди положительных периодов периодической функции называется основным периодом данной функции.
6. Особенности графика периодической функции
Если Т – основной период функции y = f(x), тодостаточно:
— построить ветвь графика на одном из
промежутков длины Т
— выполнить параллельный перенос этой ветви вдоль
оси х на ±Т, ±2Т, ±3Т и т.
 д.
д.Обычно выбирают промежуток с концами в точках
Т
Т
( ;0)и ( ;0)
2
2
7. Свойства периодических функций
1.Если f(x) – периодическая функция с периодом Т,то функция g(x) = A f(kx + b), где к>0, также
является периодической с периодом Т1= Т/к.
2.Пусть функция f1(x) и f2(x) определены на всей
числовой оси и являются периодическими с
периодами Т1 > 0 и Т2 >0. Тогда при Т1/Т2 ∈Q
функция f(x) = f(x) +f2(x) – периодическая функция
с периодом Т, равным наименьшему общему
кратному чисел Т1 и Т2.
8. Примеры
1. Периодическая функция y = f(x) определена длявсех действительных чисел. Её период равен 3
и f(0) =4. Найти значение выражения 2f(3) – f(-3).
Решение .
Т = 3,
f(3) =f(0+3) = 4,
f(-3) = f(0–3) =4, f(0) = 4.
Подставив полученные значения в выражение
2f(3) – f(-3), получим 8 — 4 =4.
Ответ: 4.
9. Примеры
2. Периодическая функция y = f(x) определена длявсех действительных чисел.
 Её период равен 5,
Её период равен 5,а f(-1) = 1.Найти f(-12),если 2f(3) – 5f(9) = 9.
Решение
Т= 5
F(-1) = 1
f(9) = f(-1 +2T) = 1⇨ 5f(9) = 5
2f(3) = 9 + 5f(9) = 14 ⇨f(3)= 7
F(-12) = f(3 – 3T) = f(3) = 7
Ответ:7.
10. Используемая литература
А.Г.Мордкович, П.В.Семёнов. Алгебра и началаанализа (профильный уровень), 10 класс
А.Г.Мордкович, П.В.Семёнов. Алгебра и начала
анализа (профильный уровень), 10 класс.
Методическое пособие для учителя
English Русский Правила
этапы урока | Задания | Количество баллов | Самооценка | |
1 | Домашняя работа | 13 | ||
3 | 1 тип задач | 5 | ||
2 тип задач | 5 | |||
4 тип задач | 5 | |||
«5» — 27-28 баллов «4» — 22-26 баллов «3» — 17-21 балл | Итого: | 28 |
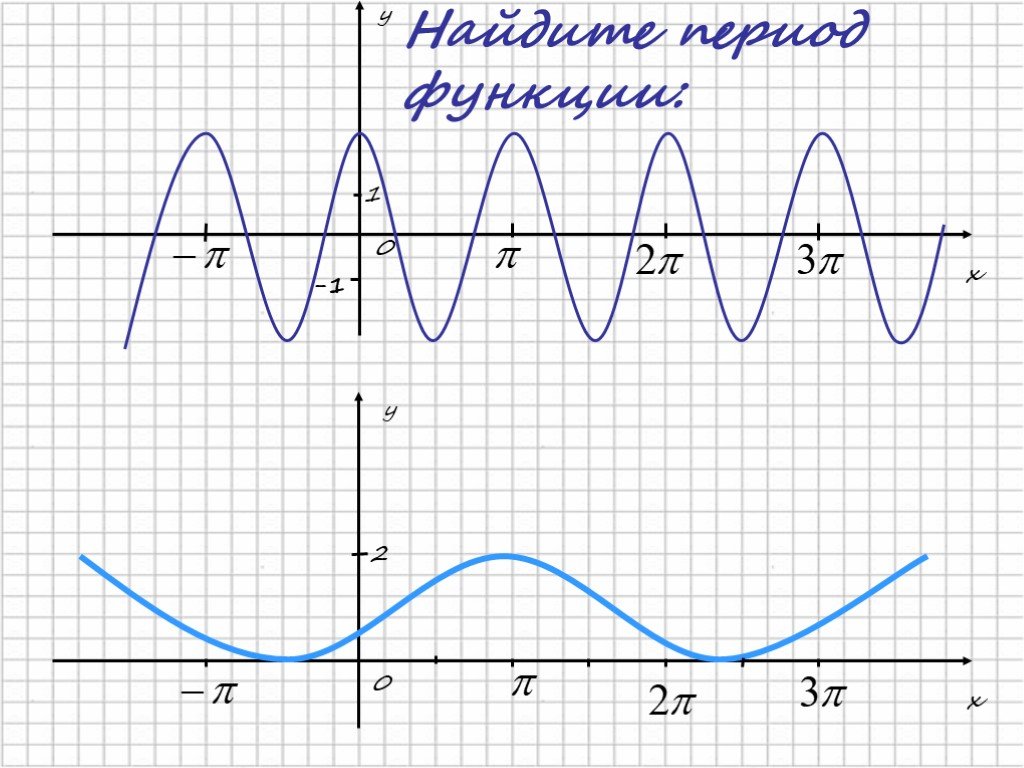
Периодические формулы с примерами — GeeksforGeeks
Период определяется как интервал времени между двумя моментами времени, а периодическая функция определяется как функция, которая повторяется через равные промежутки времени или периоды времени. Другими словами, периодическая функция — это функция, значения которой повторяются через определенный интервал времени. Периодическая функция представляется как f(x + p) = f(x), где «p» — период функции. Синусоидальная волна, треугольная волна, прямоугольная волна и пилообразная волна являются некоторыми примерами периодических функций. Ниже приведены графики некоторых периодических функций, и мы можем заметить, что график каждой периодической функции обладает трансляционной симметрией.
Другими словами, периодическая функция — это функция, значения которой повторяются через определенный интервал времени. Периодическая функция представляется как f(x + p) = f(x), где «p» — период функции. Синусоидальная волна, треугольная волна, прямоугольная волна и пилообразная волна являются некоторыми примерами периодических функций. Ниже приведены графики некоторых периодических функций, и мы можем заметить, что график каждой периодической функции обладает трансляционной симметрией.
Основной период функции
Область определения периодической функции охватывает все действительные числовые значения, а ее диапазон задан для фиксированного интервала. Периодическая функция — это функция, в которой существует положительное действительное число P такое, что f (x + p) = f (x), поскольку все x — действительные числа. Фундаментальный период функции — это наименьшее значение положительного действительного числа P или период, в течение которого функция повторяется.
f(x + P) = f(x)
, где
P — период функции, а f — периодическая функция.
Как определить период функции?
- Периодическая функция определяется как функция, которая повторяется через равные промежутки времени или периоды.
- Представляется как f(x + p) = f(x), где «p» — период функции, p ∈ R.
- Период означает интервал времени между двумя появлениями волны.
Периоды тригонометрических функций
Тригонометрические функции являются периодическими функциями, а периоды тригонометрических функций следующие:
- Период Sin x и Cos x равен 2π .
т. е. sin(x + 2π) = sin x и cos(x + 2π) = cos x
- Период Tan x и Cot x равен π.
т. е. tan(x + π) = tan x и cot(x + π) = cot x
- Период Sec x и Cosec x равен 2π.
т. е. sec(x + 2π) = sec x и cosec(x + 2π) = cosec x
Период функции называется расстоянием между повторениями любой функции. Период тригонометрической функции — это длина одного полного цикла. Амплитуда определяется как максимальное смещение частицы в волне от равновесия. Проще говоря, это расстояние между самой высокой или самой низкой точкой и средней точкой на графике функции. В тригонометрии есть три фундаментальные функции, а именно sin, cos и tan, периоды которых составляют 2π, 2π и π периодов соответственно. За точку отсчета графика любой тригонометрической функции принимается x = 0,9.0003
Период тригонометрической функции — это длина одного полного цикла. Амплитуда определяется как максимальное смещение частицы в волне от равновесия. Проще говоря, это расстояние между самой высокой или самой низкой точкой и средней точкой на графике функции. В тригонометрии есть три фундаментальные функции, а именно sin, cos и tan, периоды которых составляют 2π, 2π и π периодов соответственно. За точку отсчета графика любой тригонометрической функции принимается x = 0,9.0003
Например, если мы посмотрим на приведенный ниже график косинуса, мы увидим, что расстояние между двумя вхождениями равно 2π, т. е. период функции косинуса равен 2π. Его амплитуда равна 1.
График косинуса
Периодические формулы
- Если «p» — период периодической функции f (x), то 1/f (x) также является периодической функцией и будет иметь тот же фундаментальный период p, что и f (x).
Если f (x + p) = f (x),
F (x) = 1/f (x) , тогда F (x + p) = F (x).

- Если «p» — период периодической функции f(x), то f (ax + b), a>0 — тоже периодическая функция с периодом p/|a|.
- Период Sin (ax + b) и Cos (ax + b) равен 2π/|a|.
- Период Tan (ax + b) и Cot (ax + b) равен π/|a|.
- Период Sec (ax + b) и Cosec (ax + b) равен 2π/|a|.
- Если «p» — период периодической функции f(x), то af(x) + b, a>0 — также периодическая функция с периодом p.
- Период [a Sin x + b] и [a Cos x + b] равен 2π.
- Период [a Tan x + b] и [a Cot x + b] равен π.
- Период [a Sec x + b] и [a Cosec x + b] равен 2π.
Практические задачи на основе периодической функции
Задача 1. Определить период периодической функции cos(5x + 4).
Решение:
Заданная функция: cos (5x + 4)
Коэффициент при x = a = 5,
Мы знаем, что
Период cos x равен 2π.
Итак, период cos(5x + 4) равен 2π/ |a| = 2π/5.
Следовательно, период cos(5x + 4) равен 2π/5.
Задача 2: Найдите период f(x) = cot 4x + sin 3x/2.
Решение:
Дана периодическая функция: f(x) = cot 4x + sin 3x/2
Мы знаем, что
Период cot x равен π, а период sin x равен 2π.
Итак, период раскладушки 4x равен π/4.
Итак, период sin 3x/2 равен 2π/(3/2) = 4π/3.
Теперь расчет периода функции f(x) = cot 4x + sin 3x/2 is,
Период f(x) = (НОК π и 4π)/(HCF 3 и 4) = 4π/1 = 4π.
Следовательно, период cot 4x + sin 3x/2 равен 4π.
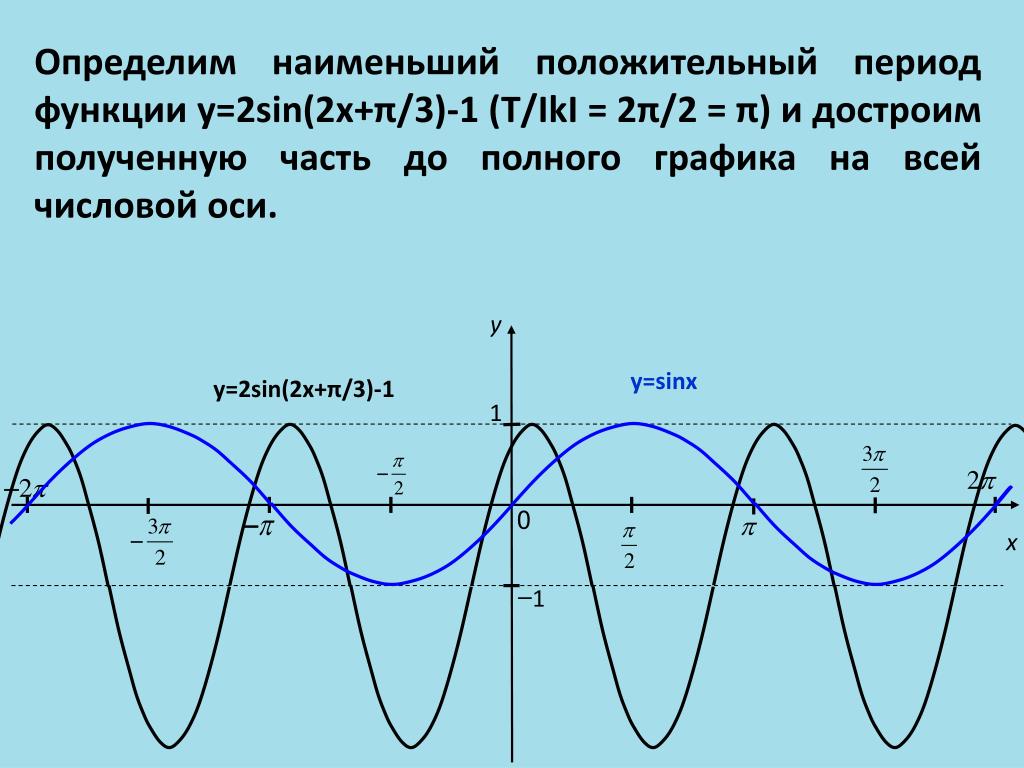
Задача 3. Нарисуйте график y = 3 sin 3x+ 5.
Решение:
Учитывая, что y = 3 sin 3x + 5
Данная волна = а грех бх + с
На приведенном выше графике мы можем написать следующее:
- Период = 2π/|b| = 2π/3
- Ось: y = 0 [ось X]
- Амплитуда: 3
- Максимальное значение = (3 × 1) + 5 = 8
- Минимальное значение = (3 × -1) + 5 = 2
- Домен: { x : x ∈ R }
- Диапазон = [ 8, 2]
Задача 4.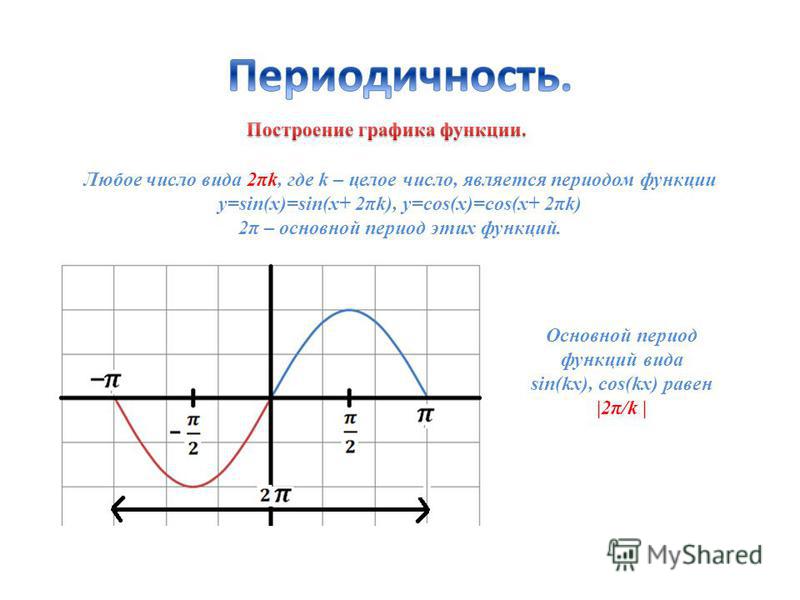 Определить период заданной периодической функции 5 sin(2x + 3).
Определить период заданной периодической функции 5 sin(2x + 3).
Решение:
Заданная функция: 5 sin(2x + 3)
Коэффициент при x = a = 2.
Мы знаем, что
Период cos x равен 2π.
Итак, период 5 sin(2x + 3) равен 2π/ |a| = 2π/2 = π.
Следовательно, период 5 sin(2x + 3) равен π.
Задача 5: Найдите период f (x) = tan 3x + cos 5x.
Решение:
Дана периодическая функция: f(x) =tan 3x + cos 6x.
Мы знаем, что
Период tan x равен π, а период cos x равен 2π.
Итак, период тангенса 3x равен π/3.
Итак, период cos 6x равен 2π/5.
Теперь расчет периода функции f(x) = tan 3x + cos 6x равен
Период f(x) = (НОК π и 2π)/(HCF 3 и 5) = 2π /1 = 2π.
Следовательно, период f (x) = tan 3x + cos 5x равен 2π.
Периодическая функция — определение, формула, свойства, график, примеры
Периодическая функция — это функция, которая повторяется через равные промежутки времени.
Давайте узнаем больше о периодической функции, свойствах периодических функций и примерах периодических функций.
| 1. | Что такое периодическая функция? |
| 2. | Периоды некоторых важных периодических функций |
| 3. | Свойства периодических функций |
| 4. | Некоторые важные функции периода |
| 4. | Примеры периодической функции |
| 5. | Практические вопросы |
| 6. | Часто задаваемые вопросы о периодической функции |
Что такое периодическая функция?
Функция y = f(x) называется периодической, если существует положительное действительное число P такое, что f(x + P) = f(x), для всех x принадлежит действительным числам. Наименьшее значение положительного действительного числа P называется фундаментальным периодом функции. Этот основной период функции также называют периодом функции, на котором функция повторяется.
Наименьшее значение положительного действительного числа P называется фундаментальным периодом функции. Этот основной период функции также называют периодом функции, на котором функция повторяется.
f(x + P) = f(x)
Функция синуса является периодической функцией с периодом 2π. Sin(2π + x) = Sinx.
Ниже приведены графики некоторых периодических функций. График каждой из перечисленных ниже периодических функций имеет трансляционную симметрию.
Периоды некоторых важных периодических функций
Период функции помогает нам узнать интервал, после которого диапазон периодической функции повторяется. Область определения периодической функции f(x) включает действительные числовые значения x, диапазон периодической функции представляет собой ограниченный набор значений в пределах интервала. Длина этого повторяющегося интервала или интервал, после которого диапазон функции повторяется, называется периодом периодической функции.
Период некоторых важных периодических функций следующий.
- Период Sinx и Cosx равен 2π.
- Период Tanx и Cotx равен π.
- Период Secx и Cosecx равен 2π.
Свойства периодических функций
Следующие свойства полезны для более глубокого понимания концепции периодической функции.
- График периодической функции симметричен и повторяется вдоль горизонтальной оси.
- Область определения периодической функции включает все значения действительных чисел, а диапазон периодической функции определяется для фиксированного интервала.
- Период периодической функции, относительно которого период повторяется, равен константе во всем диапазоне функции.
- Если f(x) — периодическая функция с периодом P, то 1/f(x) также будет периодической функцией с тем же фундаментальным периодом P.
- Если f(x) периодическая функция с периодом P, то f(ax + b) также периодическая функция с периодом P/|a|.
- Если f(x) — периодическая функция с периодом P, то af(x) + b — также периодическая функция с периодом P.

Некоторые важные периодические функции
Ниже приведены некоторые расширенные периодические функции, которые можно изучить подробнее.
Формула Эйлера: Формула комплексного числа e ix = Coskx + iSinkx состоит из функций косинуса и синуса, которые являются периодическими функциями. Здесь эти две функции являются периодическими, а формула Эйлера представляет периодическую функцию и имеет период 2π/k.
Ряд Фурье: Ряд Фурье представляет собой суперпозицию различных периодических рядов волновой функции, образующую сложную периодическую функцию. Обычно он состоит из функций синуса и косинуса, и суммирование этих волновых функций осуществляется путем присвоения этим рядам соответствующих весовых составляющих. Ряд Фурье имеет приложения для представления тепловых волн, анализа вибрации, квантовой механики, электротехники, обработки сигналов, обработки изображений.
Обычно он состоит из функций синуса и косинуса, и суммирование этих волновых функций осуществляется путем присвоения этим рядам соответствующих весовых составляющих. Ряд Фурье имеет приложения для представления тепловых волн, анализа вибрации, квантовой механики, электротехники, обработки сигналов, обработки изображений.
Связанные темы
Следующие темы помогают лучше понять периодические функции.
- Отношения и функции
- Типы функций
- Тригонометрические функции
- Логарифмические функции
- Сигнум-функция
- Ряд Фурье Формула
Часто задаваемые вопросы о периодической функции
Что такое периодическая функция в математике?
Функция y=f(x) называется -периодической функцией , если существует положительное действительное число P такое, что f(x + P) = f(x), для всех x принадлежит действительным числам. Наименьшее значение положительного действительного числа P называется фундаментальным периодом функции. Этот основной период функции также называют периодом функции, на котором функция повторяется. f(x + P) = f(x)
Этот основной период функции также называют периодом функции, на котором функция повторяется. f(x + P) = f(x)
Как узнать, является ли функция периодической функцией?
Функция может быть идентифицирована как периодическая функция, если диапазон функции повторяется через равные промежутки времени, и функция имеет вид f(X + P) = F(X).
Что такое формула периодической функции?
Формула периодической функции: f(X + P) = F(x). Здесь функция повторяется для разных доменов.
Каковы примеры периодической функции?
Примерами периодических функций являются тригонометрические функции, обратные тригонометрические функции, гиперболические функции и все функции, которые представляют периодические или круговые движения в физике.
Что такое период в периодической функции?
Период периодической функции — это интервал, после которого диапазон функции повторяется. Периодическая функция f(x + p) = f(x) имеет такое же значение диапазона для более высоких значений домена.


 )
)
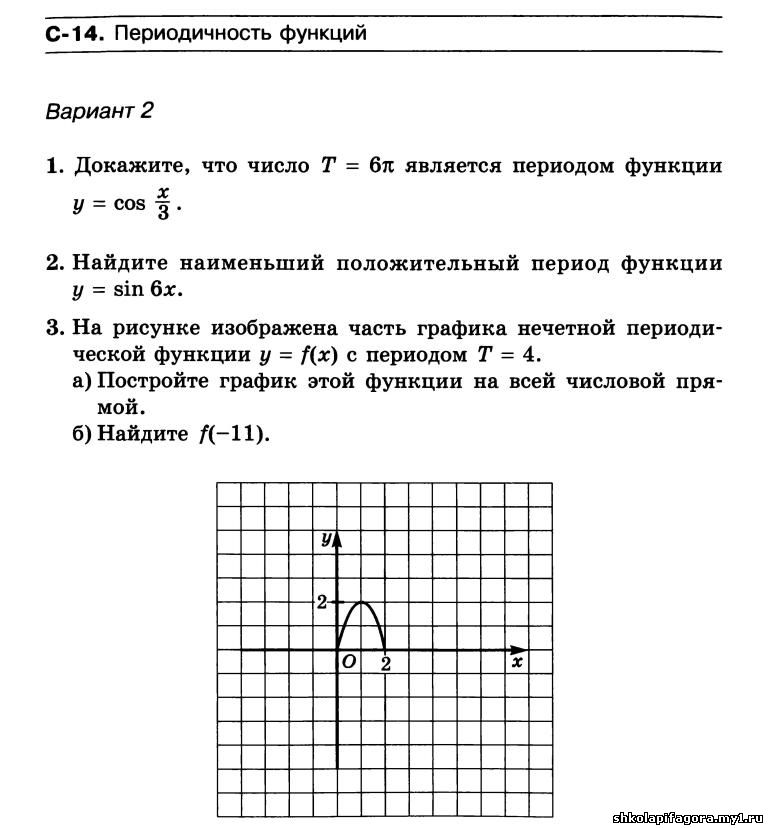
 На промежутке [ 0;2 ) эта функция совпадает с функцией у= х2 – 2. Сколько раз пересекаются графики функций у= f(х) и у = 1 на отрезке [ 1;7]?
На промежутке [ 0;2 ) эта функция совпадает с функцией у= х2 – 2. Сколько раз пересекаются графики функций у= f(х) и у = 1 на отрезке [ 1;7]? Объясните свой выбор.( Задачи 3, 5)
Объясните свой выбор.( Задачи 3, 5)

 Функция g(х) на промежутке [0;4) задается
Функция g(х) на промежутке [0;4) задается
 Найдите значение функции f(24).
Найдите значение функции f(24).