Периодичность функции как проверить: Периодические функции — урок. Алгебра, 10 класс.

Простая физика — EASY-PHYSIC

В этой статье обсуждаем периодичность функций: как определить, периодична ли  функция, и каков ее период.

Функция периодична, если  некоторый набор ее значений повторяется раз за разом, и точки с одинаковыми значениями функции расположены на числовой оси с равными промежутками. Это расстояние и будем называть периодом. Периодичная функция может иметь и несколько периодов, самый маленький положительный из них будем называть основным.

Тогда, если мы знаем период, мы можем, зная все значения функции на протяжении данного периода, достроить функцию, либо узнать ее значения в любой точке числовой оси – то есть при любом аргументе.

Периодичная функция

 

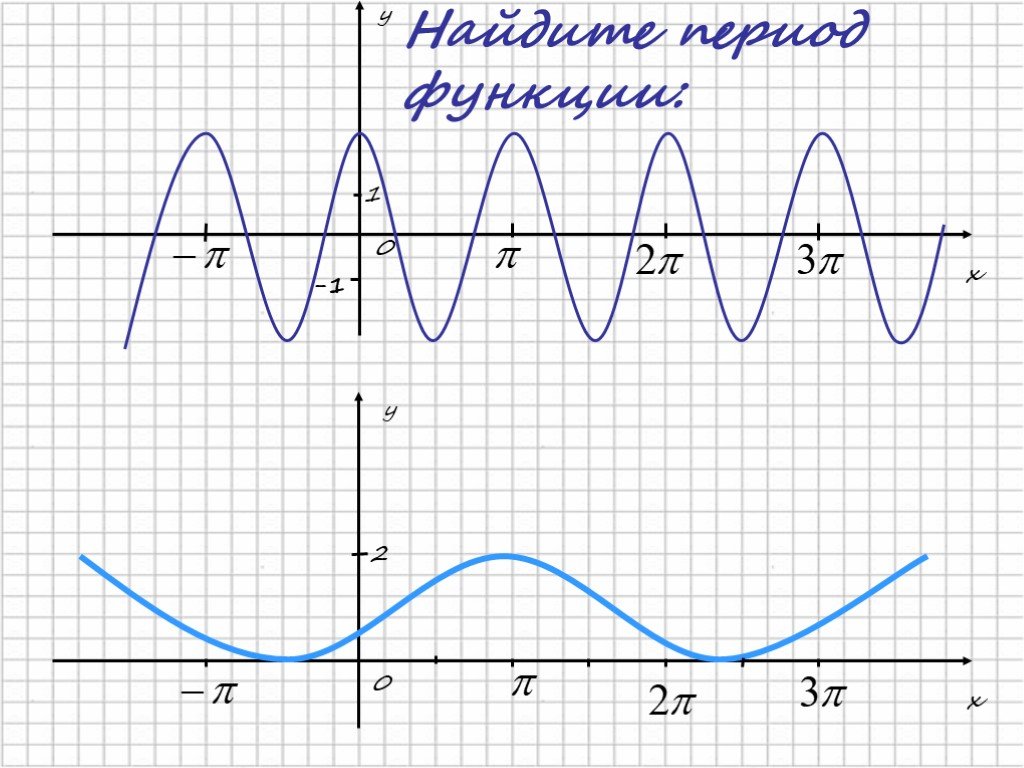
Пример 1: функция имеет период, равный 2: и при . Найдите значение выражения .

Раз наша функция принимает форму части параболы на отрезке [-2; 0] при периоде, равном 2, значит, такую же форму она будет иметь и на следующем отрезке – [0;2], и на отрезке [2;4]. Изобразим ее:

Определение значения периодичной функции

Видно, что функция принимает одинаковые значения в точках, отстоящих друг от друга на 2, 4, 6  единиц и т.д., тогда . Найдем эти значения функции. В точке (-1) функция принимает значение , в точке (3,5) функция принимает значение .

Теперь найдем значение искомого выражения: .

Строго говоря, функция периодична, если есть такое число Т, что .

Попробуем научиться определять, периодична ли функция или нет. Для этого рассмотрим несколько примеров.

Пример 2. Проверим, периодична ли функция .

Установим, выполняется ли условие: , то есть ? Очевидно, что данное условие не выполняется. Значит, функция непериодична.

Пример 3. Проверим, периодична ли функция .

Функцию для удобства представим в виде: .

Установим, выполняется ли условие: , то есть ? Очевидно, что данное условие не выполняется: . Значит, функция непериодична.

Пример 4. Проверим, периодична ли функция . Если функция периодична, то будет выполняться условие: , то есть . Поскольку нам все равно, в какой точке числовой оси мы проведем свое исследование, то очень удобно начать с точки . Тогда  , или . Это означает, что либо  , либо ,  то есть либо ,  либо ,  а так как главным считается наименьший  положительный период, то .

Определение периода функции

В данном примере делать проверку необязательно, но проверка бывает очень полезна в более сложных задачах, поэтому сделаем ее здесь для тренировки: .

 

Пример 5. Определить периодичность функции .

Если Т – период, то .

В это равенство подставим какие-нибудь «удобные» точки, например, . Получим:

Далее есть два пути отыскания периода, первый – решение этого уравнения, второй – составление еще одного уравнения такого же вида. Если функция имеет период Т, то верно и следующее: . Подставим  «удобную» точку :

Пользуясь четностью косинуса  и нечетностью синуса можем записать:

Имеем систему:

Уравнения сложим, и получим

, откуда

, при получим  – ведь нам нужен наименьший период.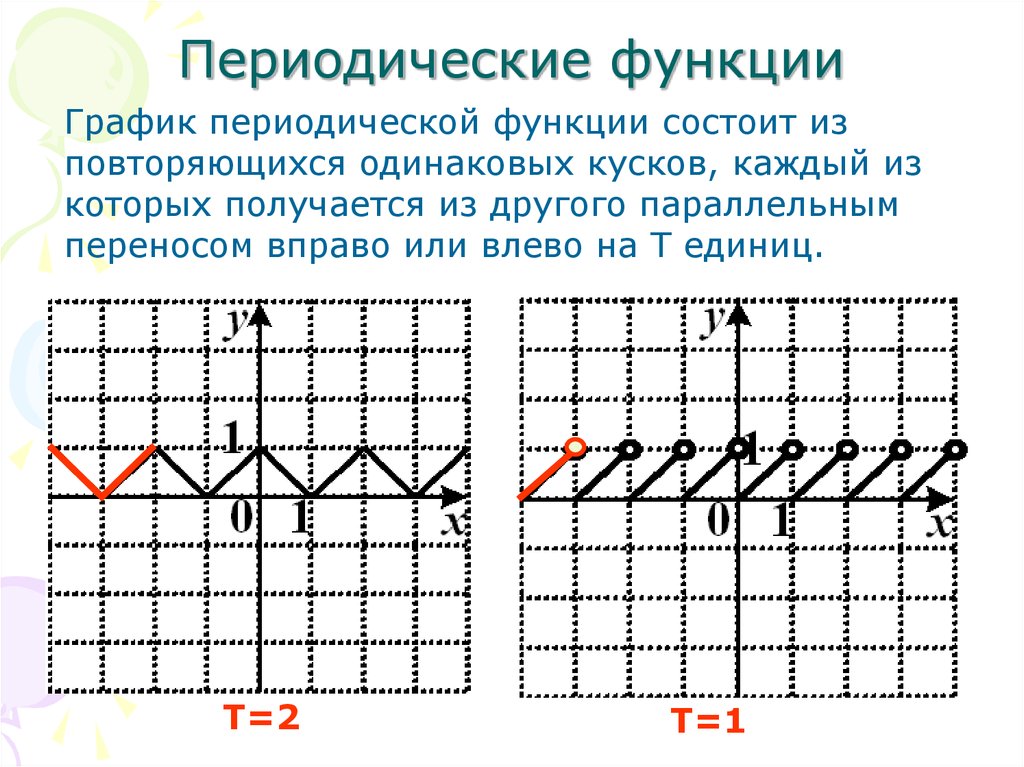

Теперь испробуем второй путь, решим это уравнение: . Из основного тригонометрического тождества:

Оставим в левой части только корень:

Возведем в квадрат:

Тогда либо , либо и .

Это уравнение имеет два решения, одно из которых (второе) – посторонний корень, появившийся при возведении в квадрат. Проверка подстановкой его в исходное уравнение позволит нам выявить его и отбросить. Таким образом, получаем:

и наименьшим будет период при , то есть .

Здесь также необходимо сделать проверку. Подставим полученный период в условие  :

, то есть

период данной функции — .

Определение периода функции

Пример 6. Определить периодичность функции и найти ее основной период.

Если Т – период, то

Подставим , имеем

,

Или , , наименьший период при , .

Проверим:

Определение периода функции

Пример 7. Определим период функции .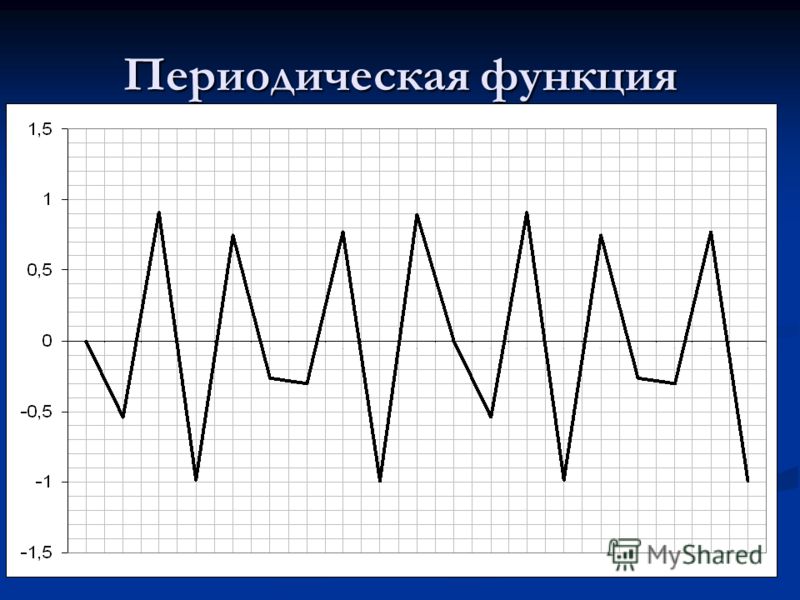

Запишем условие периодичности:

, если , то

, откуда  , . При , , при , . Проверкой можно показать, что периодом не является. Тогда . Действительно:

Определение периода функции

Пример 8. Доказать, что периодом функции является .

Тогда:

Пример 9. Доказать, что периодом функции является .

Тогда:

Если , то

, а  так как и —  одна и та же точка на единичной окружности, то равенство выполняется.

Удачи вам в учебе и надеюсь, эта статья вам помогла.

Периодическая функция | Алгебра

Периодическая функция — это функция, значения которой не изменяются при добавлении к значениям её аргумента некоторого числа T (отличного от нуля).

Определение

Функция y=f(x) называется периодической, если существует такое число T≠0, что для любого x из области определения этой функции выполняются равенства:

f(x-T)= f(x)=f(x+T).

Число T называют периодом функции y=f(x).

Из определения следует, что значения x-T и x+T также входят в область определения функции y=f(x).

Свойства периодических функций

1. Если число T является периодом функции y=f(x), то и число  -T также является периодом этой функции.
2. Если числа T₁ и T₂ являются периодами функции y=f(x) и T ₁+T₂≠0, то и число T₁+T₂ также является периодом функции y=f(x).
3. Если число T является периодом функции y=f(x), то и любое число вида nT, где n∈Ζ и n≠0 также является периодом этой функции.
4. Если число T является периодом функции y=f(x), то число T/k является периодом функции y=f(kx+b) (где k≠0).
5. Если число T является периодом функции y=f(x) и функции y=g(x), то сумма, разность, произведение и частное этих функций являются периодическими функциями с тем же периодом T.

Доказательство:

1) По определению периодической функции для любого x из области определения y=f(x) если T — период функции, то f(x-T)= f(x)=f(x+T).

Вместо каждого T подставим в это равенство -T:

f(x-(-T))= f(x)=f(x+(-T)), откуда

f(x+T)=f(x)=f(x-T), то есть -T также является периодом функции y=f(x).

2) Для любого x из области определения y=f(x) если T₁ — период функции, то

f(x-T₁)= f(x)=f(x+T₁).

Так как T₂ также является периодом функции y=f(x), то для аргумента x-T₁

f((x-T₁)-T₂)=f(x-T₁),

f(x-(T₁+T₂))=f(x-T₁)=f(x).

Для аргумента x+T₁

f(x+T₁)=f((x+T₁)+T₂),

f(x)=f(x+T₁)=f(x+(T₁+T₂)).

Таким образом, f(x-(T₁+T₂))=f(x)=f(x+(T₁+T₂)).

Следовательно, число T₁+T₂ является периодом функции y=f(x).

3) Это свойство непосредственно вытекает из свойства 2, если T взять в качестве слагаемого n раз.

4) Если T — период функции f(x), то для аргумента kx+b

f((kx+b)-T)=f(kx+b)=f((kx+b)+T),

f((kx-T)+b))=f(kx+b)=f((kx+T)+b),

   

   

Значит число T/k — период функции f(kx+b).

5) Эти свойства следуют непосредственно из определения.

Например, для суммы f(x) и g(x):

f(x-T)+g(x-T)=f(x)+g(x)=f(x+T)+g(x+T).

 

Из свойства 3 следует, что каждая периодическая функция имеет бесконечно много периодов.

Если среди всех периодов функции y=f(x) существует наименьший положительный период, то его называют главным (или основным) периодом функции.

 

Примеры периодических функций

1) Поскольку для любого x выполняются равенства

sin (x-2π)=sin x = sin (x-2π),

cos (x-2π)=cos x = cos (x-2π),

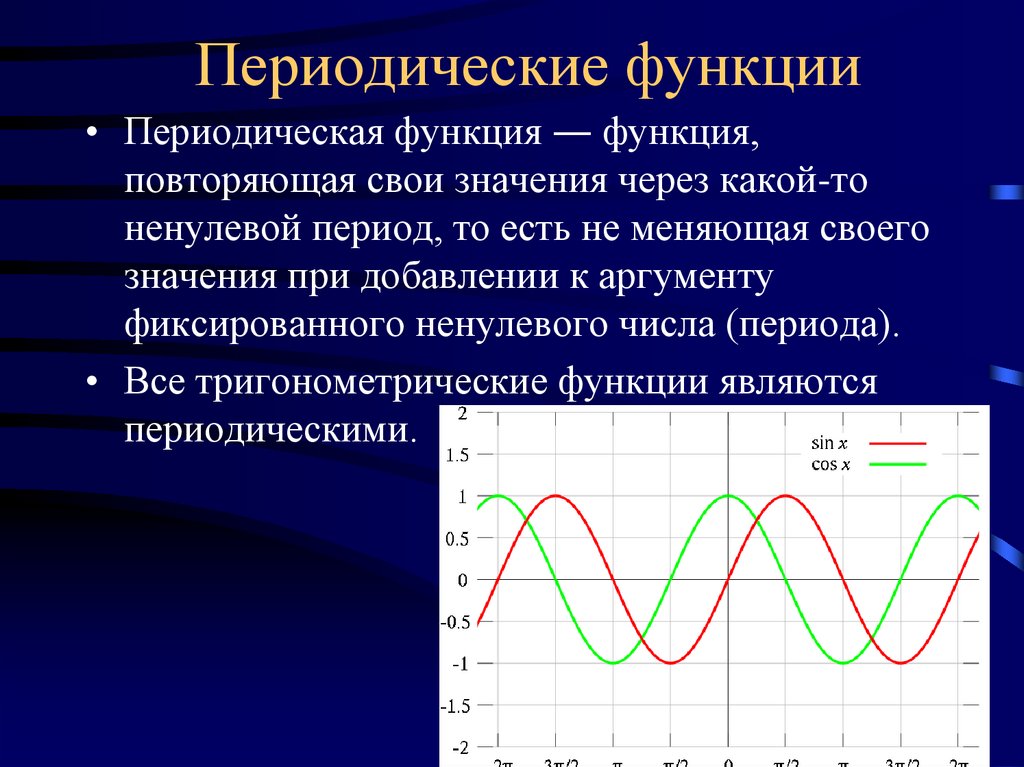
то функции y=sin x и y=cos x являются периодическими с периодом T=2π.

2) Так как для любого x из области определения функции y=tg x выполняется равенство

tg (x-π)=tg x =tg (x-π), то y=tg x — периодическая функция с периодом T=π.

Аналогично, y=ctg x — периодическая функция с периодом T=π.

3) Так как для любого действительного числа x и любого рационального числа k выполняется равенство D(x+k)=D(x), то функция Дирихле D(x) — периодическая с периодом T=k, где k∈Q, k≠0.

Поскольку k — любое рациональное число, невозможно его указать наименьшее положительное значение. Следовательно, функция Дирихле не имеет главного периода.

4) Рассмотрим частный случай линейной функции y=b, b — действительное число (b∈R). Эта функция определена на множестве действительных чисел и при любых значениях аргумента принимает единственное значение y=b, то есть для любого действительного числа m (m∈R), y(x)=y(x+m)=b.

Значит y=b — периодическая функция с периодом T=m, где m∈R, m≠0.

Так как m — любое действительное число, оно не имеет наименьшего положительного значения. Поэтому функция y=b не имеет главного периода.

5) Так как для любого действительного x и любого целого k выполняется равенство {x+k}={x}, то функция дробной части числа y={x} — периодическая с периодом T=k, где k∈Ζ, k≠0.

Наименьшим положительным целым числом является единица. Следовательно, T=1 — главный период функции y={x}.

 

Утверждения

Главный период функций y=sin x и y=cos x T=2π.

Главный период функций y=tg x и y=ctg x T=π.

Доказательство:

Если T — период функции y=sin x, то sin (x-2π)=sin x = sin (x-2π) для любого x.

В частности, при x= -T/2:

   

и, поскольку

   

получаем

   

Отсюда

   

   

   

Так как

   

   

   

То есть любой период функции y=sin x имеет вид 2πn, n∈Z.

Наименьшее положительное значение это выражение принимает при n=1 и оно равно T=2π.

Таким образом, 2π — главный период функции y=sin x.

Аналогично доказываются утверждения о главном периоде функций y=cos x, y=tg x и y=ctg x.

 

Из 4-го свойства периодических функций непосредственно следует, что для функций y=sin (kx+b) и y=cos (kx+b) (k≠0) наименьший положительный период

   

а для функций y=tg (kx+b) и y=ctg (kx+b) (k≠0) наименьший положительный период

   

 

График периодической функции повторяется через промежутки длиной T (на оси Ox).

Поэтому периодичность функции используют для построения графика: достаточно построить часть графика на любом промежутке, длина которого равна величине наименьшего положительного периода T (например, на отрезке [0;T]), а затем выполнить параллельный перенос построенной части вдоль оси Ox на ±T, ±2T, ±3T, … .

Пример.

 

Дана часть графика

периодической функции

с периодом T на

промежутке длиной T.

 

 

Чтобы построить график функции, выполняем параллельный перенос этой части графика вдоль оси Ox на ±T, ±2T,… :

Рубрика: Функции | Комментарии         Исчисление

— Доказательство периодичности функции!

спросил 8 лет, 6 месяцев назад

Изменено 8 лет, 6 месяцев назад

Просмотрено 6к раз

$\begingroup$

У меня проблемы с освоением периодической функции.

Позвольте мне сказать вам, что я уже провел семестр анализа Фурье, но просмотр первой главы запутал меня в тривиальном уравнении. Функция периодична, если она удовлетворяет условию: $x(t) = x(t+T_0)$, где наименьший $T_0$ — это основной период.

Возьмем, например, $\sin(x)$. Я интуитивно вижу, что период равен $2\pi$, НО $\sin(0)=\sin(\pi)$. Под этим я подразумеваю, что значение $\sin(x)$ одинаково при $x=0$ и $x=pi$, тогда $T_0$ не должно быть $\pi$, потому что $T_0$ является фундаментальным для наименьшее значение $T_0$, которое я только что показал, равно $1$, а НЕ $2$.

пожалуйста, помогите мне в этом тривиальном вопросе.

• исчисление

$\endgroup$

2

$\begingroup$

Для периодичности с периодом $p$ требуется $\sin(x+p) = \sin x$ для всех $x$ (а не только для отдельных значений $x$).

Разверните: $\sin(x+p) = \sin x \cos p + \cos x \sin p$.

Приравнять коэффициенты: $\cos p = 1$ и $\sin p = 0$.

Единственные значения $p$, удовлетворяющие обоим условиям, имеют вид $p = 2k\pi, k \in \mathbb{Z}$. Фундаментальный период наступает при $k=1$, т.е. $2\pi$.

(Если взять, например, $p = \pi$, то получится $\cos \pi = -1$, что является нарушением требуемых условий).

$\endgroup$

1

$\begingroup$

Я думаю, что вас смущает тот факт, что период является наименьшим числом T, так что для всех x мы имеем $$ f(x+T)=f(x)$$. Для примерно x (например, в вашем примере sinx $sin(0)=sin(\pi)$, может быть так, что существует некоторый $T’ < T$, так что$ f(x+T ')=f(x)$, но у вас должен быть $T$, работающий за

все х.

$\endgroup$

$\begingroup$

Вам следует внимательно посмотреть, что именно означают ваши определения. Функция $f$ периодична на множестве $D$ с периодом $T$ тогда и только тогда, когда $f(x+T) = f(x)$ для любого $x \in D$ . Если вы выберете некоторый $T$, и есть только один $x$, который не удовлетворяет этому уравнению, то выбранный вами $T$ не будет даже периодом, не говоря уже о фундаментальном периоде. Фундаментальный период впоследствии определяется как минимальный положительный период, если он существует. Обратите внимание, что постоянная функция имеет произвольно малые периоды и, следовательно, не имеет фундаментального периода.

$\endgroup$

4

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

Предварительное исчисление алгебры. Как определить, является ли следующая функция периодической?

Задавать вопрос

спросил 8 лет, 1 месяц назад

Изменено 6 лет, 10 месяцев назад

Просмотрено 35 тысяч раз

$\begingroup$

В моем учебнике задан вопрос о том, является ли функция $f(x)=\cos(3x)+\sin(x)$ периодической. Я не верю, что это так, поскольку аргументы синуса и косинуса различны, и поэтому их нельзя записать в виде синусоиды. Как я могу определить, является ли функция периодической или нет?

Вот моя попытка ответить на мой собственный вопрос, пожалуйста, покритикуйте, где это возможно.

Функция периодическая, если $f(x+p)=f(x) \следовательно \cos(3(x+p)) + \sin(x+p) = \cos(3x) + \sin(x )$

Пусть $x = 0$:

$\cos(0)+\sin(0)=\cos(3p)+\sin(p)$

$1=\cos(3p)+\sin(p )$

Куда мне идти дальше? Я знаю, что это будет иметь место, когда: синус равен 0, а косинус равен 1 ИЛИ когда косинус равен 0, а синус равен 1. Однако как мне установить, для какого значения P это происходит?

• алгебра-предварительное исчисление
• функции
• тригонометрия
• периодические функции

$\endgroup$

3

$\begingroup$

Подумайте об этой проблеме интуитивно. Рассмотрим дрэг-рейсер, у которого радиус задних колес в 3 раза больше радиуса меньших передних колес. Если мы пометим колеса (с одной стороны автомобиля) желтым мелом в том месте, где они первоначально касаются земли, как часто желтый мел на обоих колесах будет касаться земли одновременно?

$\endgroup$

8

$\begingroup$

Подсказка: функция $f$ периодична с периодом $T$, если $f(x) = f(x + T)$. $T$ не должен быть равен нулю.

Можете ли вы найти общий период для обоих слагаемых?

Попробуйте построить график функции, чтобы понять, что происходит.

$\endgroup$

2

$\begingroup$

Подсказка: $$ \начать{выравнивать} \cos(3(x+2\pi))+\sin(x+2\pi) &=\cos(3x+6\pi)+\sin(x+2\pi)\\ ]\конец{выравнивание} $$ Теперь применим тот факт, что $\sin(x+2\pi)=\sin(x)$ и $\cos(x+2\pi)=\cos(x)$.

Обратите внимание, что последнее тождество говорит, что $\cos(x+6\pi)=\cos(x+4\pi)=\cos(x+2\pi)=\cos(x)$.

$\endgroup$

$\begingroup$

Чтобы проверить, повторяется ли функция во времени, т. е. через фиксированный интервал времени.

Итак, нам просто нужно интерпретировать, когда функция будет повторяться.