Первообразная 2: Mathway | Популярные задачи

2

Математический анализ — 2 — тест 35

Математический анализ — 2 — тест 35

Решение тестов Intuit

игра брюс 2048

Главная / Математика / Математический анализ — 2 / Тест 35

Упражнение 1:

---

Номер 1

Функция  называется первообразной функции  на интервале , если функция  дифференцируема

Ответ:

&nbsp(1) &nbsp

&nbsp(2) &nbsp

&nbsp(3) для некоторых &nbsp

&nbsp(4) для некоторых &nbsp

---

Номер 2

Функция  называется первообразной функции  на интервале , если функция  дифференцируема

Ответ:

&nbsp(1) &nbsp

&nbsp(2) &nbsp

&nbsp(3) в некоторых &nbsp

&nbsp(4) в некоторых &nbsp

---

Номер 3

Если функция  является первообразной функции  на интервале , то на этом интервале

Ответ:

&nbsp(1) &nbsp

&nbsp(2) &nbsp

&nbsp(3) &nbsp

&nbsp(4) &nbsp

&nbsp(5) &nbsp

&nbsp(6) &nbsp

---

Упражнение 2:

---

Номер 1

Отметьте промежутки, на которых функция  является первообразной для функции :

Ответ:

&nbsp(1) &nbsp

&nbsp(2) &nbsp

&nbsp(3) &nbsp

---

Номер 2

Отметьте промежутки, на которых функция  является первообразной для функции  :

Ответ:

&nbsp(1) &nbsp

&nbsp(2) &nbsp

&nbsp(3) &nbsp

&nbsp(4) все варианты неверны&nbsp

---

Номер 3

Отметьте промежутки, на которых функция  является первообразной для функции :

Ответ:

&nbsp(1) &nbsp

&nbsp(2) &nbsp

&nbsp(3) &nbsp

---

Упражнение 3:

---

Номер 1

Отметьте верные утверждения:

Ответ:

&nbsp(1) если — первообразная для некоторой функции на промежутке , то — непрерывная функция на этом промежутке&nbsp

&nbsp(2) любая функция , определенная на промежутке , имеет первообразную на этом промежутке&nbsp

&nbsp(3) если — первообразные для некоторой функции на промежутке , то их разность равна некоторой постоянной&nbsp

---

Номер 2

 Отметьте верные утверждения:

Ответ:

&nbsp(1) если — первообразная для некоторой функции на промежутке , то — дифференцируемая функция на этом промежутке&nbsp

&nbsp(2) если функция на промежутке имеет первообразную, то она имеет на бесконечное множество первообразных&nbsp

&nbsp(3) если функция имеет первообразную на промежутке , то и каждая из функция также имеет первообразную на этом промежутке&nbsp

---

Номер 3

Отметьте верные утверждения:

Ответ:

&nbsp(1) если — первообразная для некоторой функции на промежутке , то функция — также первообразная для на этом промежутке&nbsp

&nbsp(2) если каждая из функций имеет первообразную на промежутке , то и функция также имеет первообразную на этом промежутке&nbsp

&nbsp(3) любая функция , непрерывная на промежутке , имеет первообразную на этом промежутке&nbsp

---

Упражнение 4:

---

Номер 1

Найдите первообразную для функции , которая в точке  принимает значение, равное 5

Ответ:

&nbsp(1) &nbsp

&nbsp(2) &nbsp

&nbsp(3) &nbsp

&nbsp(4) &nbsp

---

Номер 2

Найдите первообразную для функции , которая в точке  принимает значение, равное 5

Ответ:

&nbsp(1) &nbsp

&nbsp(2) &nbsp

&nbsp(3) &nbsp

&nbsp(4) &nbsp

---

Номер 3

Найдите первообразную для функции , которая в точке  принимает значение, равное 8

Ответ:

&nbsp(1) &nbsp

&nbsp(2) &nbsp

&nbsp(3) &nbsp

&nbsp(4) &nbsp

---

Упражнение 5:

---

Номер 1

Пусть  - неопределенный интеграл от функции  на интервале .  Тогда он

Ответ:

&nbsp(1) является совокупностью некоторых первообразных для функции &nbsp

&nbsp(2) является совокупностью всех первообразных для функции &nbsp

&nbsp(3) равен , где — первообразная для — произвольная константа&nbsp

&nbsp(4) равен где — первообразная для — некоторая константа&nbsp

---

Номер 2

Отметьте верные утверждения:

Ответ:

&nbsp(1) функция , определенная на промежутке , имеет неопределенный интеграл на этом промежутке&nbsp

&nbsp(2) функция , непрерывная на промежутке , имеет неопределенный интеграл на этом промежутке&nbsp

&nbsp(3) функция , имеющая первообразную на промежутке , имеет неопределенный интеграл на этом промежутке&nbsp

---

Номер 3

Неопределенный интеграл от функции  на интервале  существует, если функция 

Ответ:

&nbsp(1) определена на интервале &nbsp

&nbsp(2) непрерывна на интервале &nbsp

&nbsp(3) непрерывна в некоторой точке интервала &nbsp

---

Упражнение 6:

---

Номер 1

Отметьте верное равенство:

Ответ:

&nbsp(1) &nbsp

&nbsp(2) &nbsp

&nbsp(3) &nbsp

---

Номер 2

Отметьте верные равенства:

Ответ:

&nbsp(1) &nbsp

&nbsp(2) &nbsp

&nbsp(3) &nbsp

---

Номер 3

Отметьте верные равенства:

Ответ:

&nbsp(1) &nbsp

&nbsp(2) &nbsp

&nbsp(3) &nbsp

---

Упражнение 7:

---

Номер 1

Отметьте верные равенства:

Ответ:

&nbsp(1) &nbsp

&nbsp(2) &nbsp

&nbsp(3) &nbsp

&nbsp(4) &nbsp

---

Номер 2

Отметьте верные равенства:

Ответ:

&nbsp(1) &nbsp

&nbsp(2) &nbsp

&nbsp(3) &nbsp

&nbsp(4) &nbsp

---

Номер 3

Отметьте верные равенства:

Ответ:

&nbsp(1) &nbsp

&nbsp(2) &nbsp

&nbsp(3) &nbsp

&nbsp(4) &nbsp

---

Главная / Математика / Математический анализ — 2 / Тест 35

Первообразная — Вычисление | Как найти первообразную?

Первообразная функции также известна как интеграл. При дифференцировании первообразной функции получается исходная функция. Интеграция — это процесс, противоположный дифференциации, отсюда и название «анти» производные.

Первообразные обычно известны как неопределенные интегралы. Однако с помощью основной теоремы исчисления первообразные также можно связать с определенными интегралами. В этой статье мы узнаем об первообразных, их формулах, правилах и различных приложениях.

1.	Что такое первообразная?
2.	Антипроизводные формулы
3.	Вычисление первообразной
4.	Антидеривативы Правило
5.	Первообразная триггерных функций
6.	Первообразная экспоненциальной функции
7.	Свойства первообразных производных
8.	Часто задаваемые вопросы по антидеривативам

Что такое первообразная?

Первопроизводная , F, функции f может быть определена как функция, которую можно дифференцировать для получения исходной функции f.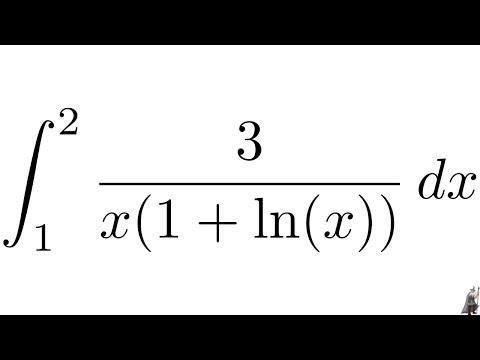 т. е. первообразная математически определяется следующим образом: ∫ f(x) dx = F(x) + C, где

• производная от F(x) равна f(x). т. е. F'(x) = f(x) и
• C — постоянная интегрирования

У данной функции может быть много первообразных, поэтому они не уникальны. Производные функции x могут быть такими: x ² /2 + 2, x ² /2 — 32, x ² /2 + 19,2 и т. д. (попытайтесь продифференцировать каждое из них и найти результат для быть х). Таким образом, можно сказать, что первообразные функции будут отличаться на константу. Антипроизводные можно разделить на два типа:

• неопределенные производные
• определенные производные

Неопределенная первообразная

Когда определяется общая первообразная функции, она называется неопределенной первообразной (или) неопределенным интегралом. Такая первообразная не имеет никаких пределов/границ. Интегрирование, которое является обратным процессом дифференцирования, используется для вычисления неопределенной первообразной функции. Предположим, что есть функция f(x) и ее первообразная, если F(x). Написано так:

∫ f(x) dx = F(x) + C

где C — действительное число и постоянная интегрирования. ‘∫’ — знак интеграла.

Определенная первообразная

Если первообразная функции вычисляется между двумя конечными точками, то она известна как определенная первообразная (или) определенный интеграл. Определенный интеграл функции используется для вычисления площади под кривой. Такая первообразная будет иметь определенное значение. Предположим, что первообразная функции f(x) должна быть вычислена между двумя точками (или пределами) a и b, тогда она записывается следующим образом:0003

∫ _a ^b f(x) = [F(x)] _a ^b = F(b) — F(a)

Это следует из основной теоремы исчисления.

Антипроизводные формулы

Существует несколько различных формул первообразных, которые помогают найти первообразную заданной функции с помощью процесса интегрирования. Это помогает увеличить скорость и точность выполнения вычислений. Некоторые первообразные формулы приведены ниже:

• ∫ x ⁿ dx = x ^{n + 1} /(n + 1) + C
• ∫ е ^х dx = е ^х + С
• ∫ 1/x dx = log |x| + С

Вычисление первообразной

Процесс вычисления первообразной зависит от сложности функции. Шаги для вычисления первообразных различных типов функций перечислены ниже:

• Проверьте тип интеграла. Простые интегралы можно решить, используя правила прямого интегрирования.
• Некоторые интегралы можно решить методом подстановки.
• Рациональные алгебраические функции могут быть решены с помощью интегрирования методом частных дробей.
• Функции, выраженные в виде произведения, могут быть решены путем интегрирования по частям.
• Для определенного интеграла сначала вычислите первообразную, используя один из приведенных выше примеров, а затем примените пределы, используя формулу ∫ _a ^b f(x)dx = F(b) — F(a), чтобы получить окончательный результат отвечать.

Антидеривативные правила

Существуют некоторые важные правила, которые необходимо соблюдать при интегрировании функции для получения ее первообразных. Эти правила перечислены ниже:

• Правило суммы: Первообразная суммы равна сумме первообразных. Если f(x) и g(x) две функции, то ∫ [f(x) + g(x)]dx = ∫ f(x)dx + ∫ g(x)dx
• Правило разности: Это правило утверждает, что первообразная разности равна разнице первообразных. Это можно выразить как ∫ [f(x) — g(x)]dx = ∫ f(x)dx — ∫ g(x)dx
• Правило констант: Скаляр можно вынести из интеграла по правилу констант. Если k скаляр или константа, то ∫ k f(x)dx = k∫ f(x)dx

Наиболее важным правилом является правило мощности, которое будет изучено в следующем разделе.

Правило степени первообразной

Правило степени первообразной также является общей формулой, используемой для решения простых интегралов. Он показывает, как интегрировать функцию вида x ⁿ , где n ≠ -1. Это правило также можно использовать для объединения выражений с радикалами в них. Степенное правило для первообразных дается следующим образом:

∫ x ⁿ dx = x ^{n + 1} /(n + 1) + C, где C — постоянная интегрирования.

Предположим, есть функция x ³ . Тогда, поскольку мощность функции равна 3, что не равно -1, для ее интегрирования можно использовать правило мощности. ∫ x ³ dx = x ^{3 + 1} /(3 + 1) = x ⁴ / 4 + C — первая производная x ³ .

Первообразная триггерных функций

Существует шесть основных тригонометрических функций. Это синус (sin), косинус (cos), тангенс (tan), косеканс (cosec), секанс (sec) и котангенс (cot). cosec, sec и cot являются обратными функциями sin, cos и tan соответственно. Ниже приведены первообразные тригонометрических функций:

• Первообразная sin x равна, ∫ sin x dx = -cos x + C
• Первообразная cos x равна ∫ cos x dx = sin x + C
• Первообразная tan x равна ∫ tan x dx = -ln |cos x| + С = пер |сек х| + С
• Первообразная кроватки x равна ∫ кроватки x dx = ln |sin x| + C = -ln |cosec x| + С
• Первообразная sec x равна ∫ sec x dx = ln |sec x + tan x| + С
• Первообразная cosec x равна ∫ cosec x dx = — ln |cosec x + cot x| + С
• ∫ cos (ax + b)x dx = (1/a) sin (ax + b) + C
• ∫ sin (ax + b)x dx = -(1/a) cos (ax + b) + C

Существуют определенные функции, которые дают обратные тригонометрические функции как первообразные при интегрировании. Они задаются следующим образом:

• ∫1/√(1 — x ² ).dx = sin ^-1 x + C
• ∫ 1/(1 — x ² ).dx = -cos ^-1 x + C
• ∫1/(1 + x ² ).dx = тангенс ^-1 х + С
• ∫ 1/(1 + x ² ).dx = -cot ^-1 x + C
• ∫ 1/x√(x ² — 1).dx = сек ^-1 x + C
• ∫ 1/x√(x ² — 1).dx = -cosec ^-1 x + C

Кроме того, у нас есть формулы приведения, которые говорят о первообразных sin ⁿ x, cos ⁿ x и tan ⁿ x.

Первообразная экспоненциальной функции

Экспоненциальные функции широко используются для моделирования таких ситуаций, как финансовый рост, рост населения и т. д. Это связано с тем, что e обычно ассоциируется с ускорением или нарастанием роста. Экспоненциальная функция e ^x является собственной первообразной и производной. Правило степени нельзя использовать для интегрирования экспоненциальной функции. Первообразная экспоненциальной функции задается следующим образом:

• Первообразная e ^x равна, ∫ e ^x дх = е ^х + С
• ∫ e ​​ ^cx dx = (1/c) e ^cx + C

Предположим, что постоянное число возведено в степень x, тогда первообразная такой функции будет следующей: + C

Еще одна важная формула, подпадающая под категорию экспоненциальных функций, — это первообразная логарифмической функции. Логарифмическую функцию можно проинтегрировать по следующим формулам:

• Первообразная log x равна ∫ log x dx = xlog x — x + C
• Первообразная ln x равна ∫ ln x dx = x ln x — x + C.

Свойства первообразных производных

Свойства первообразных помогают упростить сложное выражение, чтобы упростить вычисления. Вот некоторые важные свойства первообразных:

• ∫ f(x) dx = ∫ g(x) dx, если ∫ [f(x) — g(x)]dx = 0. Это следствие правила разности .
• ∫ [k ₁ f ₁ (x) + k ₂ f ₂ (x) + …+k _n f _n (x)]dx = k 909101 2 f ₁ (x)dx + k ₂ ∫ f ₂ (x)dx + … + k _n ∫ f _n (x)dx. Это свойство является следствием правила сумм и правила констант.

☛ Статьи по теме:

• Формулы интегрирования
• Дифференциальные уравнения
• Тригонометрия

Важные замечания по первообразным:

• При применении обратного процесса дифференцирования, т. е. интегрирования, к функции полученный таким образом результат известен как первообразная.
• Добавить константу C после нахождения любой первообразной.
• У заданной функции может быть несколько первообразных, отличающихся константой.
• Правило степени — это наиболее важное правило первообразной, заданное ∫ x ⁿ dx = x ^{n + 1} /(n + 1) + C
• Первообразная — это неопределенный интеграл. Когда ограничения применяются к первообразным, используя Фундаментальную теорему исчисления, они становятся определенными интегралами.

Часто задаваемые вопросы по антидеривативам

Что такое антидеривативы?

Первообразные — это функции, которые получаются после интегрирования данной функции. Первообразные являются частью интегрального исчисления. Если дифференцируется первообразная, получается исходная функция.

Каково назначение первообразных производных?

Процесс, обращающий результат дифференциации, известен как первообразная. Функцию можно интегрировать, чтобы получить первообразную и константу интегрирования.

Как найти первообразные производные?

Чтобы найти первообразные, проинтегрируйте заданную функцию по формулам, методом подстановки, интегрированием по частям или интегрированием по неполным дробям. Конечный результат будет иметь константу интегрирования, если в исходной функции не указаны пределы.

Являются ли первообразные такими же, как интегралы?

Первообразные аналогичны неопределенным интегралам. Однако если в данной функции заданы некоторые пределы, то первообразная работает как определенный интеграл.

Какие существуют методы расчета первообразных производных?

Некоторые первообразные можно вычислить, просто применяя правила первообразных. Но для вычисления некоторых первообразных нам потребуются такие методы, как метод подстановки, интегрирование по частям, интегрирование по неполным дробям и т. д. Чтобы подробно изучить эти методы, нажмите здесь.

Что такое степенное правило для первообразных производных?

Степенное правило для первообразных применяется к функциям вида x ⁿ , где n не равно -1. Оно задается как ∫ x ⁿ dx = x ^{n + 1} /(n + 1) + C.

Что такое первообразная 1 / x?

Первообразная 1 / x равна ln|x| + C. Это потому, что производная от ln x равна 1/x.

Каковы применения первообразных производных?

Первообразные широко используются для объяснения связи между скоростью, положением и скоростью. Например, интегрирование ускорения приводит к скорости движущегося объекта вместе с константой.

Антипроизводные.html

Определение первообразной

Мы говорим, что является производной от на интервале I, если для всех х в I.

Пример: Функции и оба являются первообразными .

Когда мы изучали теорему о среднем значении, мы разработали теорему, которая показывает, что любые две первообразные функции (на интервале) должны отличаться на константу. Следовательно, если является первообразной для , то для любой постоянной , также является первообразной для .

Пример: Каждый участник семейства функций (куда постоянна) является первообразной .

Определение неопределенного интеграла

если и только если является первообразной для .

Мы говорим, что общая первообразная является .

Процесс антидифференцирования (то есть процесс нахождения первообразной функции) по существу является обратным процессу дифференцирования. Каждому разработанному нами правилу дифференциации соответствует правило антидифференцирования.

Рассмотрим правило степени дифференцирования. У нас есть это для всех действительных чисел . Соответствующее утверждение о неопределенном интеграле дает нам правило степени для интегралов.

Степенное правило для интегралов

, для всех не равно -1.

Пример: .

Предположим, что мы расширяем последний пример, рассматривая неопределенный интеграл от степени общей функции . Обратите внимание, что по правилу Powerchain для дифференцирования

.

Соответствующее утверждение о неопределенном интеграле — это обобщенная степень интегралов.